Effect of Process Conditions and Colloidal Properties of Cellulose Nanocrystals Suspensions on the Production of Hydrogel Beads
Abstract
:1. Introduction
2. Results
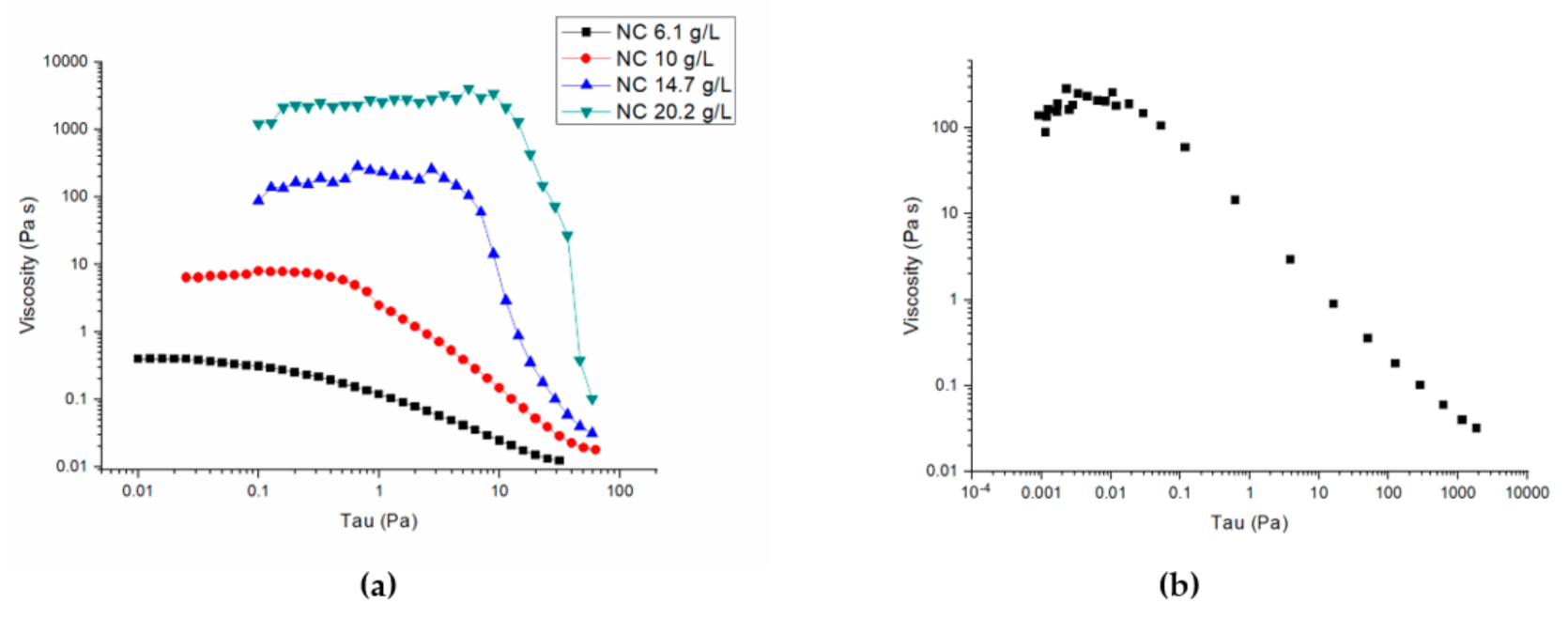
2.1. Physical–Chemical Peroperties of CNC Solutions
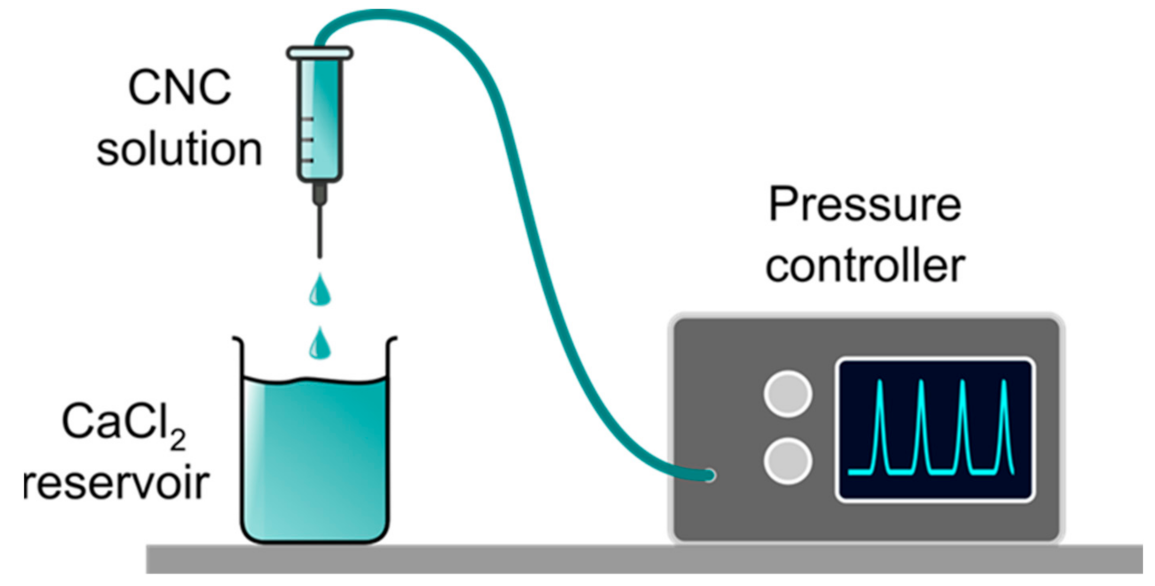
2.2. Production of Hydrogel Beads by Pump-Driven External Gelation
2.3. Determination of the Ohnesorge Number
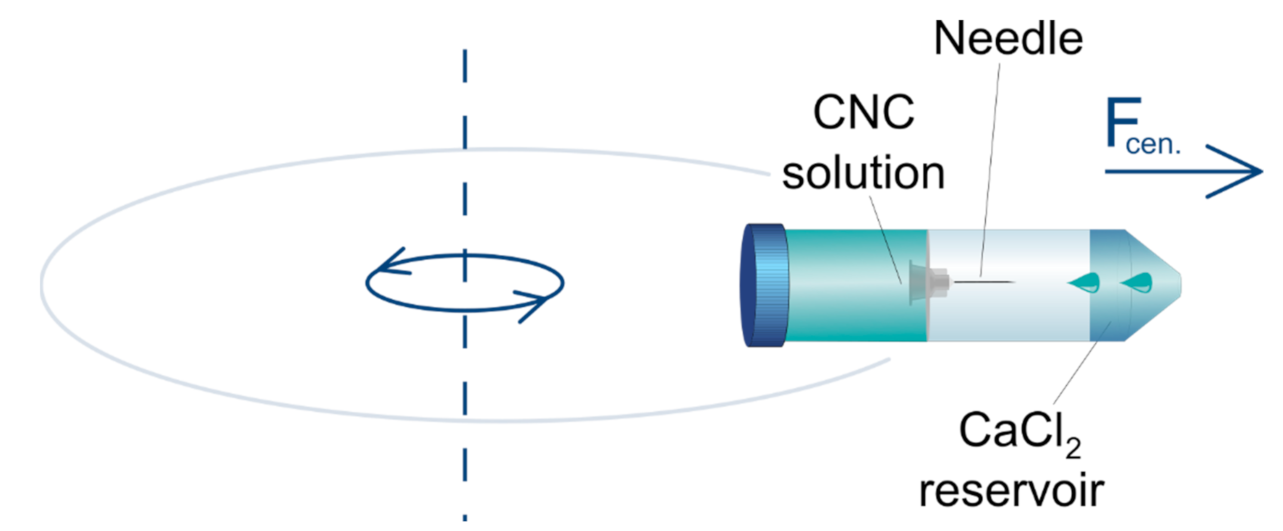
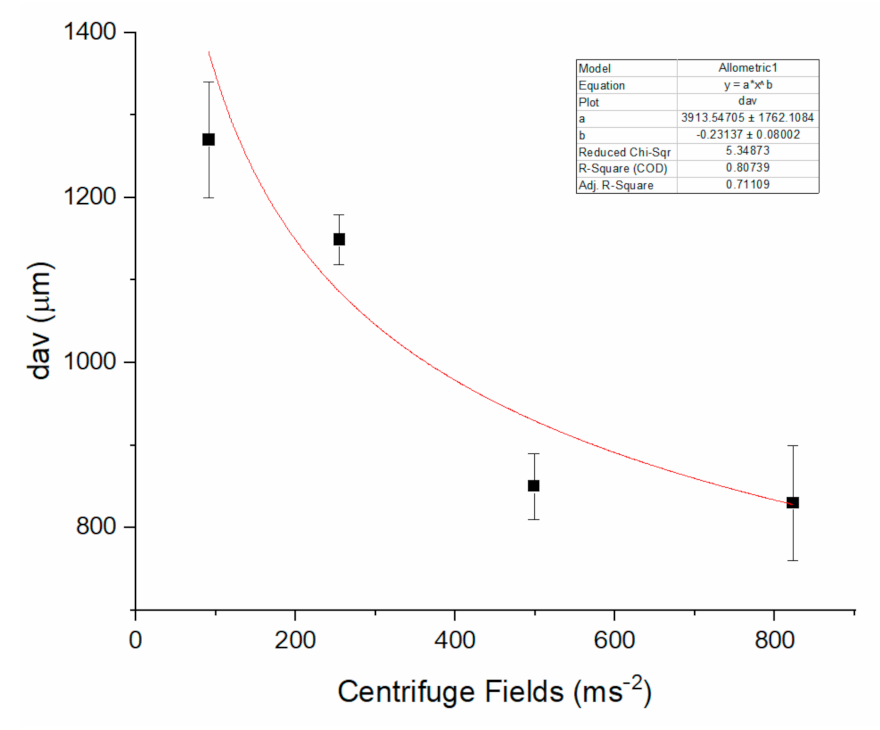
2.4. Production of Beads by a Centrifugal-Force-Driven Micronozzle System External Gelation
3. Materials and Methods
3.1. Materials
3.2. Measurement of the Density of CNC Solutions
3.3. Extrusion Dripping Experiments
3.4. Centrifugally Driven Pulse-Free Flow Experiments
3.5. Bead Analysis
3.6. Shrinkage Factor (SF) Determination
3.7. Lost Factor Determination
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Zhao, Q.; Cui, H.; Wang, Y.; Du, X. Microfluidic Platforms toward Rational Material Fabrication for Biomedical Applications. Small 2020, 16, 1903798. [Google Scholar] [CrossRef]
- Negro, A.; Cherbuin, T.; Lutolf, M.P. 3D Inkjet Printing of Complex, Cell-Laden Hydrogel Structures. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Ghasemiyeh, P.; Mohammadi-Samani, S. Hydrogels as Drug Delivery Systems; Pros and Cons. Trends Pharm. Sci. 2019, 5, 7–24. [Google Scholar]
- Castiaux, A.D.; Spence, D.M.; Martin, R.S. Review of 3D cell culture with analysis in microfluidic systems. Anal. Methods 2019, 11, 4220–4232. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Marchant, R.E. Design properties of hydrogel tissue-engineering scaffolds. Expert Rev. Med Devices 2011, 8, 607–626. [Google Scholar] [CrossRef] [PubMed]
- Jung, I.Y.; Kim, J.S.; Choi, B.R.; Lee, K.; Lee, H. Hydrogel Based Biosensors for In Vitro Diagnostics of Biochemicals, Proteins, and Genes. Adv. Heal. Mater. 2017, 6, 1601475. [Google Scholar] [CrossRef]
- Yin, Y.; Xia, Y. Self-Assembly of Monodispersed Spherical Colloids into Complex Aggregates with Well-Defined Sizes, Shapes, and Structures. Adv. Mater. 2001, 13, 267–271. [Google Scholar] [CrossRef]
- Chan, E.-S.; Lee, B.-B.; Ravindra, P.; Poncelet, D. Prediction models for shape and size of ca-alginate macrobeads produced through extrusion–dripping method. J. Colloid Interface Sci. 2009, 338, 63–72. [Google Scholar] [CrossRef]
- Lee, B.B.; Ravindra, P.; Chan, E.S. Size and Shape of Calcium Alginate Beads Produced by Extrusion Dripping. Chem. Eng. Technol. 2013, 36, 1627–1642. [Google Scholar] [CrossRef]
- Lin, N.; Huang, J.; Dufresne, A. Preparation, properties and applications of polysaccharide nanocrystals in advanced functional nanomaterials: A review. Nanoscale 2012, 4, 3274–3294. [Google Scholar] [CrossRef]
- Maestri, C.A.; Motta, A.; Moschini, L.; Bernkop-Schnürch, A.; Baus, R.A.; Lecca, P.; Scarpa, M. Composite nanocellulose-based hydrogels with spatially oriented degrada-tion and retarded release of macromolecules. J. Biomed. Mater. Res. Part A 2020, 108, 1509–1519. [Google Scholar] [CrossRef]
- Maestri, C.A.; Bettotti, P.; Scarpa, M. Fabrication of complex-shaped hydrogels by diffusion controlled gelation of nanocellulose crystallites. J. Mater. Chem. B 2017, 5, 8096–8104. [Google Scholar] [CrossRef]
- Xu, Y.; Atrens, A.; Stokes, J.R. A review of nanocrystalline cellulose suspensions: Rheology, liquid crystal ordering and colloidal phase behaviour. Adv. Colloid Interface Sci. 2020, 275, 102076. [Google Scholar] [CrossRef]
- Pääkkö, M.; Ankerfors, M.; Kosonen, H.; Nykänen, A.; Ahola, S.; Österberg, M.; Ruokolainen, J.; Laine, J.; Larsson, P.T.; Ikkala, O.; et al. Enzymatic hydrolysis combined with mechanical shearing and high-pressure homogenization for nanoscale cellulose fibrils and strong gels. Biomacromolecules 2007, 8, 1934–1941. [Google Scholar] [CrossRef] [PubMed]
- Poncelet, D.; Babak, V.; Neufeld, R.; Goosen, M.; Burgarski, B. Theory of electrostatic dispersion of polymer solutions in the production of microgel beads containing biocatalyst. Adv. Colloid Interface Sci. 1999, 79, 213–228. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Ballinger, S.; Pelton, R.; Cranston, E.D. Surfactant-enhanced cellulose nanocrystal Pickering emulsions. J. Colloid Interface Sci. 2015, 439, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Hoorfar, M.; Kurz, M.A.; Policova, Z.; Hair, M.L.; Neumann, A.W. Do polysaccharides such as dextran and their monomers really increase the surface tension of water? Langmuir 2006, 22, 52–56. [Google Scholar] [CrossRef]
- Lapasin, R.; Pricl, S.; Lapasin, R. Rheology of Industrial Polysaccharides: Theory and Applications; Springer: Boston, MA, USA, 1995; pp. 162–249. ISBN 978-1-4613-5915-9. [Google Scholar]
- Steffe, J.F.; Daubert, C.R. Bioprocessing Pipelines: Rheology and Analysis; Freeman Press: East Lansing, MI, USA, 2006; p. 8. [Google Scholar]
- Eral, H.B.; Safai, E.R.; Keshavarz, B.; Kim, J.J.; Lee, J.; Doyle, P.S.; Lee, J. Governing Principles of Alginate Microparticle Synthesis with Centrifugal Forces. Langmuir 2016, 32, 7198–7209. [Google Scholar] [CrossRef]
- Middleman, S.; Gavis, J. Expansion and Contraction of Capillary Jets of Newtonian Liquids. Phys. Fluids 1961, 4, 355–359. [Google Scholar] [CrossRef]
- Middleman, S.; Gavis, J. Expansion and Contraction of Capillary Jets of Viscoelastic Liquids. Phys. Fluids 1961, 4, 963. [Google Scholar] [CrossRef]
- Saito, T.; Isogai, A. TEMPO-Mediated Oxidation of Native Cellulose. The Effect of Oxidation Conditions on Chemical and Crystal Structures of the Water-Insoluble Fractions. Biomacromolecules 2004, 5, 1983–1989. [Google Scholar] [CrossRef] [PubMed]
- Bettotti, P.; Maestri, C.A.; Guider, R.; Mancini, I.; Nativ-Roth, E.; Golan, Y.; Scarpa, M. Dynamics of Hydration of Nanocellulose Films. Adv. Mater. Interface. 2016, 3, 1500415. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
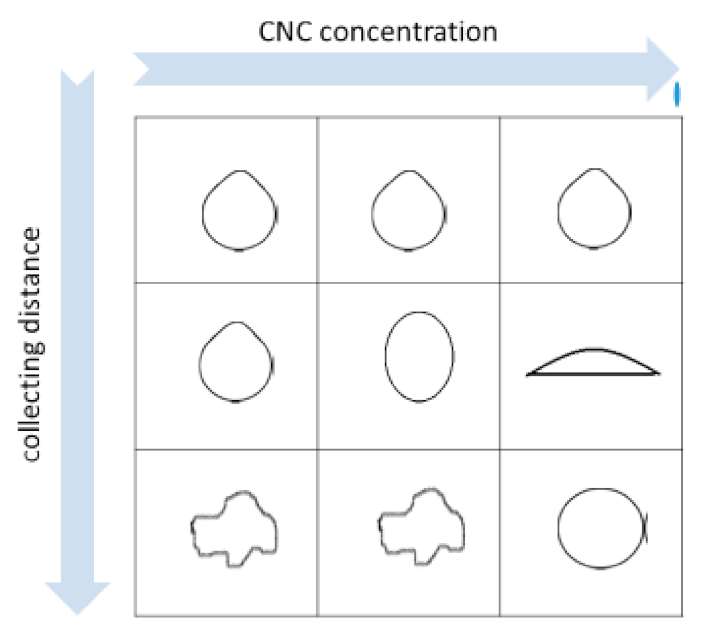
| Collecting Distance (cm) | dmax (µm) | dmin (µm) | SF | AR |
|---|---|---|---|---|
| 1 | 3000 ± 100 | 2600 ± 100 | 0.07 ± 0.04 | 1.15 ± 0.08 |
| 2 | 3100 ± 200 | 2600 ± 100 | 0.09 ± 0.06 | 1.2 ± 0.1 |
| 3 | 3200 ± 200 | 2600 ± 200 | 0.10 ± 0.06 | 1.2 ± 0.2 |
| 5 | 3600 ± 100 | 2300 ± 200 | 0.22 ± 0.08 | 1.5 ± 0.2 |
| 20 | 3200 ± 200 | 2600 ± 200 | 0.10 ± 0.08 | 1.2 ± 0.2 |
| 30 | 3800 ± 200 | 2600 ± 200 | 0.20 ± 0.08 | 1.5 ± 0.3 |
| Collecting Distance (mm) | dmax (µm) | dmin (µm) | SF | AR |
|---|---|---|---|---|
| 2 | 1270 ± 60 | 1180 ± 70 | 0.037 | 1.08 |
| 5 | 1710 ± 70 | 1520 ± 80 | 0.059 | 1.125 |
| 10 | 1930 ± 90 | 1570 ± 60 | 0.103 | 1.23 |
| 15 | 2000 ± 100 | 1710 ± 50 | 0.078 | 1.17 |
| RCF xg | dmax (µm) | dmin (µm) | SF | AR |
|---|---|---|---|---|
| 9.3 ± 0.1 | 1270 ± 60 | 1180 ± 70 | 0.037 | 1.08 |
| 26.0 ± 0.1 | 1149 ± 40 | 1050 ± 20 | 0.045 | 1.09 |
| 50.9 ± 0.1 | 850 ± 30 | 760 ± 50 | 0.056 | 1.12 |
| 84.0 ± 0.2 | 830 ± 70 | 700 ± 70 | 0.085 | 1.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari, N.; Maestri, C.A.; Bettotti, P.; Grassi, M.; Abrami, M.; Scarpa, M. Effect of Process Conditions and Colloidal Properties of Cellulose Nanocrystals Suspensions on the Production of Hydrogel Beads. Molecules 2021, 26, 2552. https://doi.org/10.3390/molecules26092552
Ferrari N, Maestri CA, Bettotti P, Grassi M, Abrami M, Scarpa M. Effect of Process Conditions and Colloidal Properties of Cellulose Nanocrystals Suspensions on the Production of Hydrogel Beads. Molecules. 2021; 26(9):2552. https://doi.org/10.3390/molecules26092552
Chicago/Turabian StyleFerrari, Nicola, Cecilia Ada Maestri, Paolo Bettotti, Mario Grassi, Michela Abrami, and Marina Scarpa. 2021. "Effect of Process Conditions and Colloidal Properties of Cellulose Nanocrystals Suspensions on the Production of Hydrogel Beads" Molecules 26, no. 9: 2552. https://doi.org/10.3390/molecules26092552






