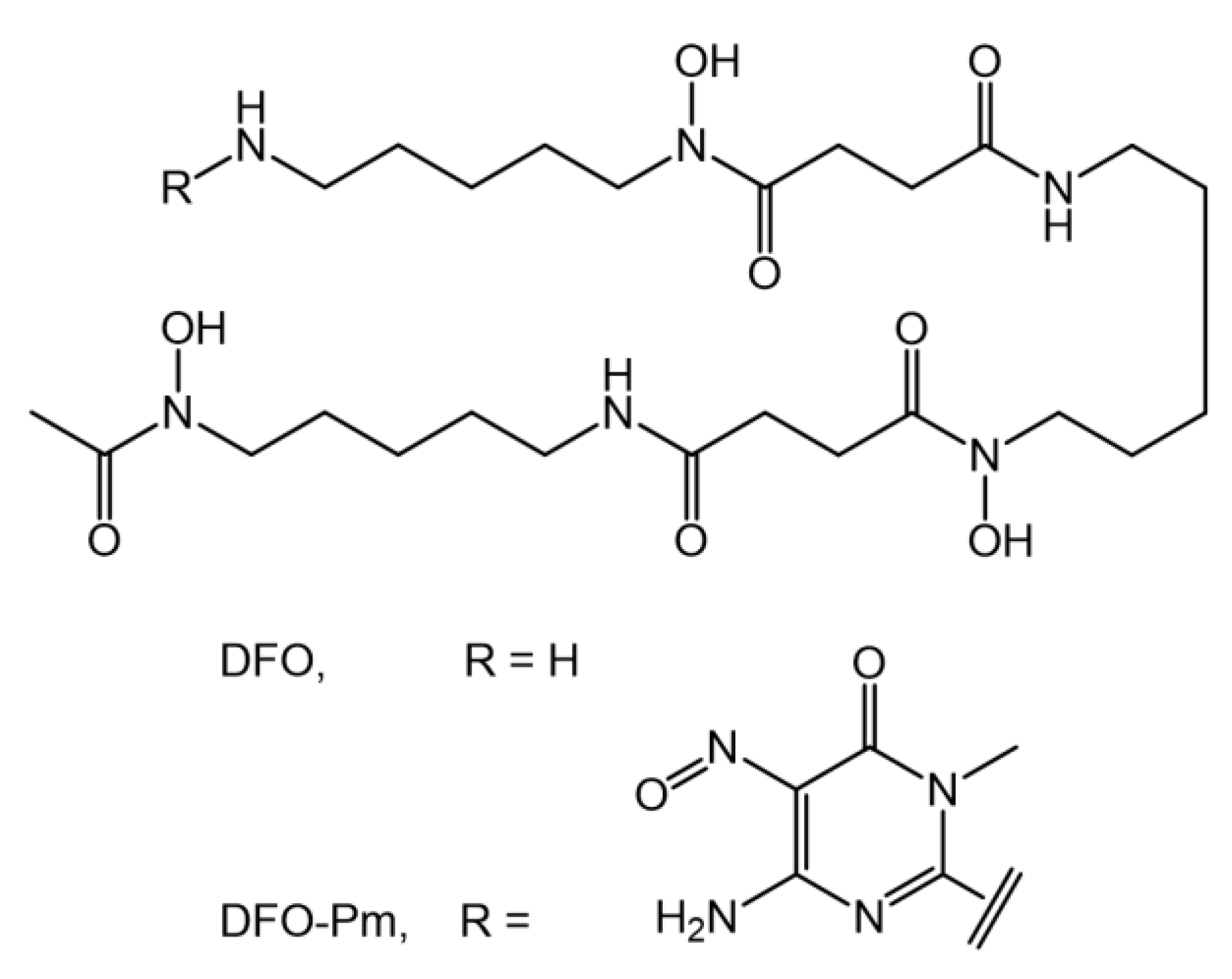
Metal Coordination Properties of a Chromophoric Desferrioxamine (DFO) Derivative: Insight on the Coordination Stoichiometry and Thermodynamic Stability of Zr4+ Complexes
Abstract
:1. Introduction
2. Results and Discussion
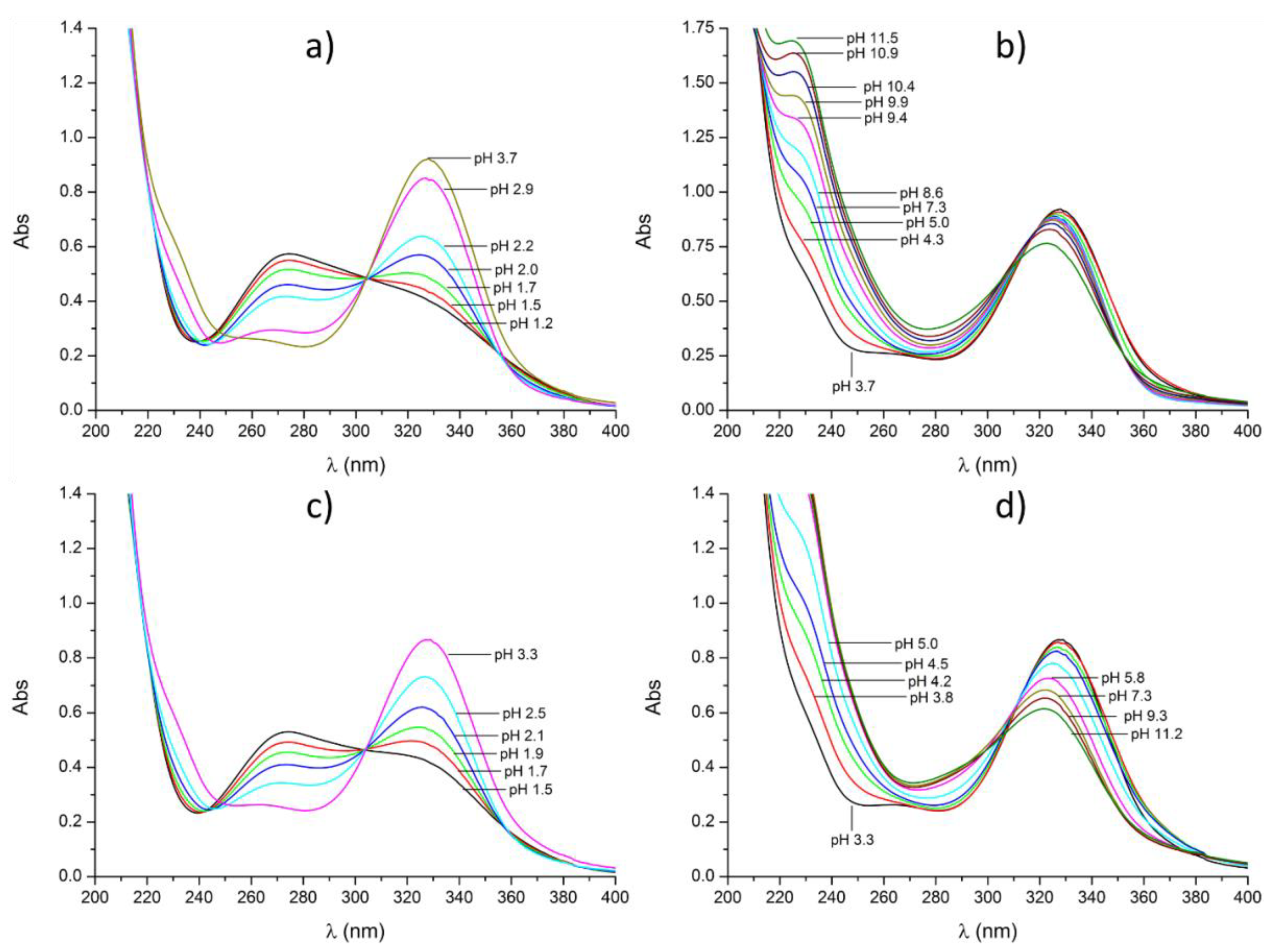
2.1. Protonation/Deprotonation Equilibria of DFO–Pm
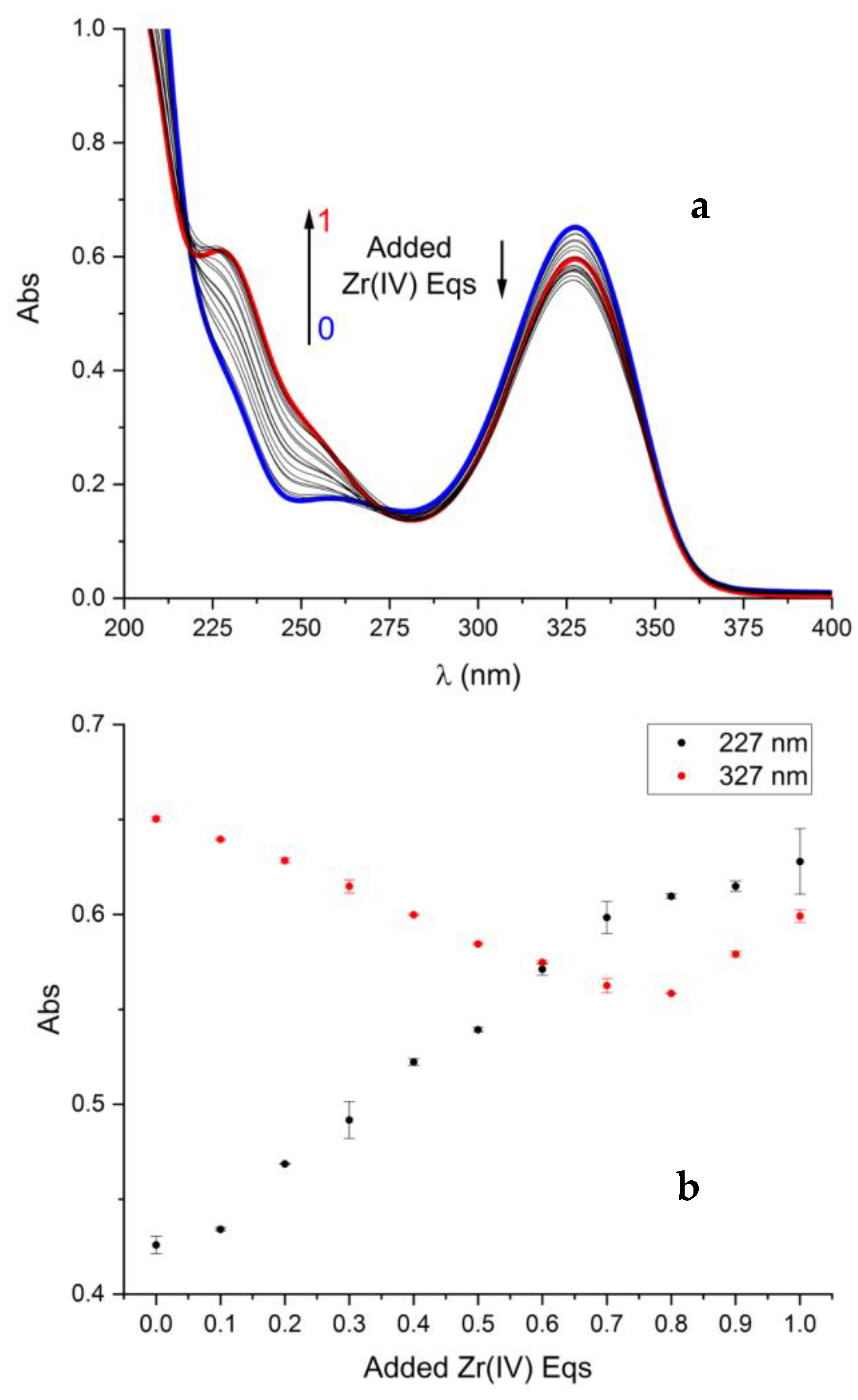
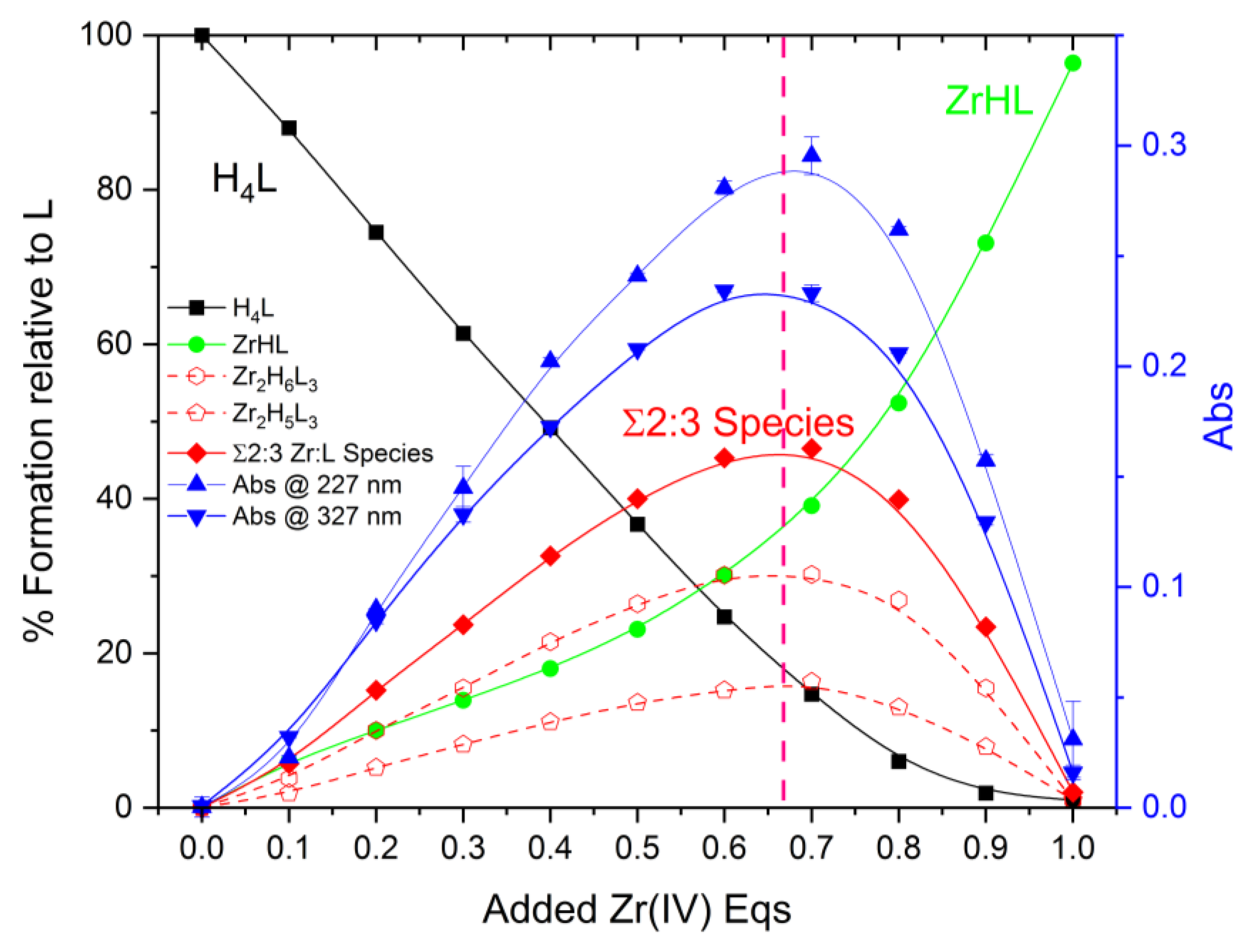
2.2. Formation of Metal Complexes
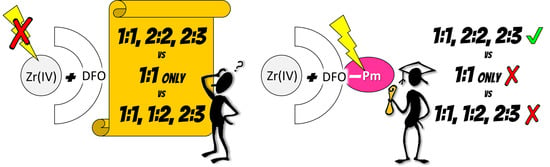
2.3. On the Stoichiometry of Zr4+ Complexes
2.4. An Attempt to Arrive at an Unified Model for the Zr4+/DFO System
2.4.1. Model by Imura et al.
2.4.2. Model by Toporivska et al.
2.4.3. Model by Savastano et al.
2.4.4. A Unified Model for Zr(IV):DFO System?
3. Materials and Methods
3.1. Materials
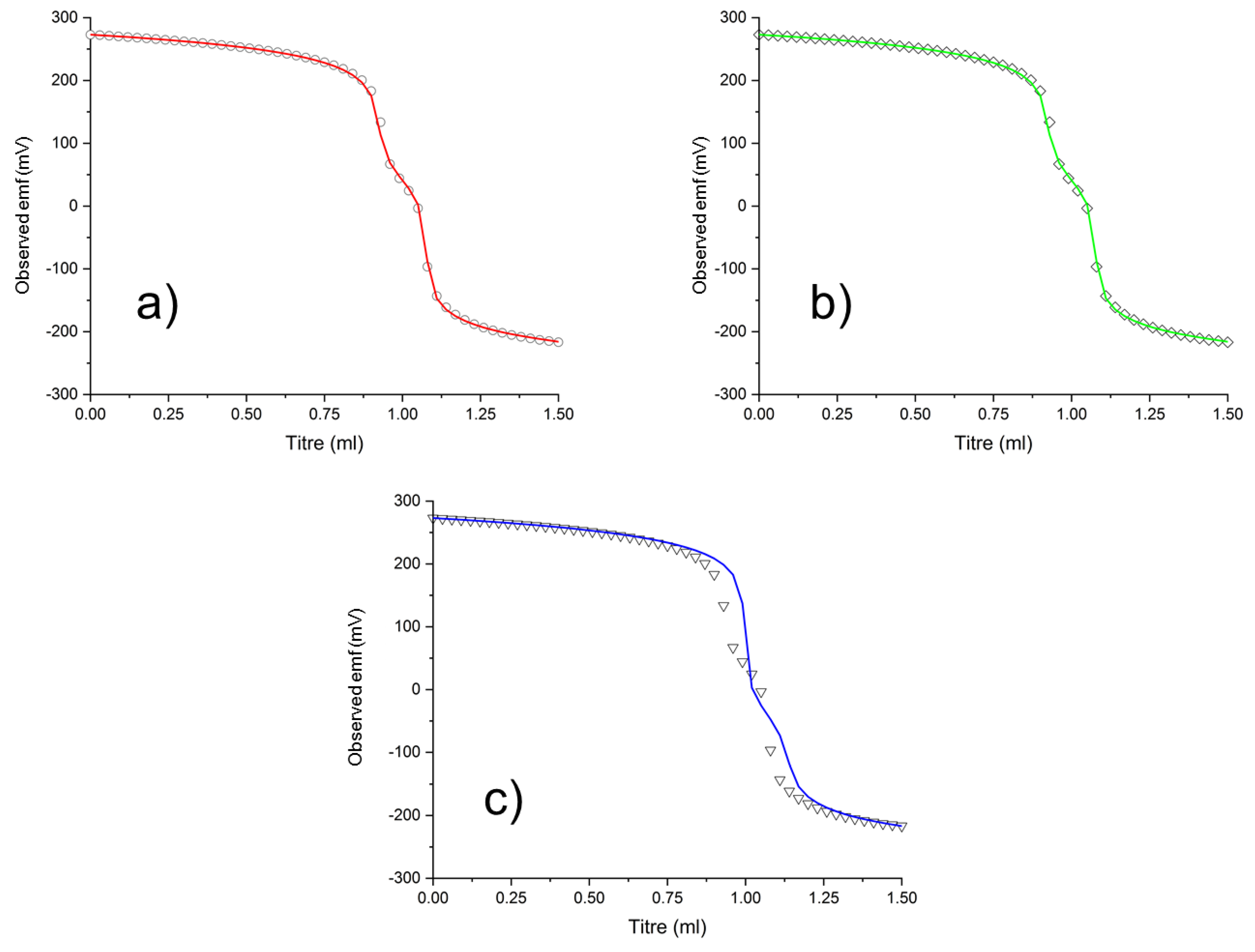
3.2. Potentiometric Measurements
3.3. Spectrophotometric Measurements
3.4. Mass Spectrometry
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Dilworth, J.R.; Pascu, S.I. The chemistry of PET imaging with zirconium-89. Chem. Soc. Rev. 2018, 47, 2554–2571. [Google Scholar] [CrossRef]
- Price, E.W.; Orvig, C. Matching chelators to radiometals for radiopharmaceuticals. Chem. Soc. Rev. 2014, 43, 260–290. [Google Scholar] [CrossRef]
- Deri, M.A.; Zeglis, B.M.; Francesconi, L.C.; Lewis, J.S. PET imaging with 89Zr: From radiochemistry to the clinic. Nucl. Med. Biol. 2013, 40, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Jauw, Y.W.; Menke-vander Houven van Oordt, C.W.; Hoekstra, O.S.; Hendrikse, N.H.; Vugts, D.J.; Zijlstra, J.M.; Huisman, M.C.; van Dongen, G.A. Immuno-Positron Emission Tomography with Zirconium-89-Labeled Monoclonal Antibodies in Oncology: What Can We Learn from Initial Clinical Trials? Front. Pharmacol. 2016, 7, 131. [Google Scholar] [CrossRef]
- Abou, D.S.; Ku, T.; Smith-Jones, P.M. In vivo biodistribution and accumulation of 89Zr in mice. Nucl. Med. Biol. 2011, 38, 675–681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dhunganga, S.; White, P.S.; Crumbliss, A.L. Crystal structure of ferrioxamine B: A comparative analysis and implications for molecular recognition. J. Biol. Inorg. Chem. 2001, 6, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.P.; Divilov, V.; Bander, N.H.; Smith-Jones, P.M.; Larson, S.M.; Lewis, J.S. 89Zr-DFO-J591 for ImmunoPET of Prostate-Specific Membrane Antigen Expression In Vivo. J. Nucl. Med. 2010, 51, 1293–1300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savastano, M.; Bazzicalupi, C.; Ferraro, G.; Fratini, E.; Gratteri, P.; Bianchi, A. Tales of the Unexpected: The Case of Zirconium(IV) Complexes with Desferrioxamine. Molecules 2019, 24, 2098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holland, J.P. Predicting the Thermodynamic Stability of Zirconium Radiotracers. Inorg. Chem. 2020, 59, 2070–2082. [Google Scholar] [CrossRef]
- Guerard, F.; Lee, Y.-S.; Tripier, R.; Szajek, L.P.; Deschamps, J.R.; Brechbiel, M.W. Investigation of Zr(IV) and 89Zr(IV) complexation with hydroxamates: Progress towards designing a better chelator than desferrioxamine B for immuno-PET imaging. Chem. Commun. 2013, 49, 1002–1004. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, A.; Savastano, M. Comment on “Investigation of Zr(iv) and 89Zr(iv) complexation with hydroxamates: Progress towards designing a better chelator than desferrioxamine B for immuno-PET imaging” by F. Guérard, Y.-S. Lee, R. Tripier, L.P. Szajek, J.R. Deschamps and M. W. Brechbiel, Chem. Commun., 2013, 49, 1002. Chem. Commun 2020, 56, 12664–12666. [Google Scholar]
- Meijes, W.E.; Herscheid, J.D.M.; Haisma, H.J.; Pinedo, H.M. Evaluation of desferal as a bifunctional chelating agent for labeling antibodies with Zr-89. Appl. Rodiat. Isot. 1992, 43, 1443–1447. [Google Scholar] [CrossRef]
- Toporivska, Y.; Gumienna-Kontecka, E. The solution thermodynamic stability of desferrioxamine B (DFO) with Zr(IV). J. Inorg. Biochem. 2019, 198, 110753. [Google Scholar] [CrossRef] [PubMed]
- Farkas, E.; Csóka, H.; Micera, G.; Dessi, A. Copper(II), nickel(II), zinc(II), and molybdenum(VI) complexes of desferrioxamine B in aqueous solution. J. Inorg. Biochem. 1997, 65, 281–286. [Google Scholar] [CrossRef]
- Hernlem, B.J.; Vane, L.M.; Sayles, G.D. Stability constants for complexes of the siderophore desferrioxamine B with selected heavy metal cations. Inorg. Chim. Acta 1996, 244, 179–184. [Google Scholar] [CrossRef]
- Crumbliss, A.L. Aqueous Solution Equilibrium and Kinetic Studies of iron Siderophore and Model Siderophore Complexes. In Handbook of Microbial Iron Chelates; CRC Press: Boca Raton, FL, USA, 1991; pp. 177–233. [Google Scholar]
- Imura, R.; Ida, H.; Sasaki, I.; Ishioka, N.S.; Watanabe, S. Re-Evaluations of Zr-DFO Complex Coordination Chemistry for the Estimation of Radiochemical Yields and Chelator-to-Antibody Ratios of 89Zr Immune-PET Tracers. Molecules 2021, 26, 4977. [Google Scholar] [CrossRef]
- Godino-Salido, M.L.; Santiago-Medina, A.; López-Garzón, R.; Gutiérrez-Valero, M.D.; Arranz-Mascarós, P.; López de la Torre, M.D.; Domingo-García, M.; López-Garzón, F.J. Preparation and characterization of trihydroxamic acid functionalized carbon materials for the removal of Cu(II) ions from aqueous solution. Appl. Surf. Sci. 2016, 387, 128–138. [Google Scholar] [CrossRef]
- Gutiérrez-Valero, M.D.; Godino-Salido, M.L.; Arranz-Mascarós, P.; López-Garzón, R.; Cuesta, R.; García-Martín, J. Adsorption of designed pyrimidine derivative ligands on an activated carbon for the removal of Cu(II) ions from aqueous solution. Langmuir 2007, 23, 5995–6003. [Google Scholar] [CrossRef] [PubMed]
- Godino-Salido, M.L.; Santiago-Medina, A.; Arranz-Mascarós, P.; López-Garzón, R.; Gutiérrez-Valero, M.D.; Melguizo, M.; López-Garzón, F.J. Novel active carbon/crown ether derivative hybrid material for the selective removal of Cu(II) ions: The crucial role of the surface chemical functions. Chem. Eng. Sci. 2014, 114, 94–104. [Google Scholar] [CrossRef]
- Savastano, M.; Arranz-Mascarós, P.; Bazzicalupi, C.; Clares, M.P.; Godino-Salido, M.L.; Gutiérrez-Valero, M.D.; Inclán, M.; Bianchi, A.; García-España, E.; López-Garzón, R. Construction of green nanostructured heterogeneous catalysts via non-covalent surface decoration of multi-walled carbon nanotubes with Pd(II) complexes of azamacrocycles. J. Catal. 2017, 353, 239–249. [Google Scholar] [CrossRef]
- Savastano, M.; Arranz-Mascarós, P.; Clares, M.P.; Cuesta, R.; Godino-Salido, M.L.; Guijarro, L.; Gutiérrez-Valero, M.D.; Inclán, M.; Bianchi, A.; García-España, E.; et al. A New Heterogeneous Catalyst Obtained via Supramolecular Decoration of Graphene with a Pd2+ Azamacrocyclic Complex. Molecules 2019, 24, 2714. [Google Scholar] [CrossRef] [Green Version]
- Savastano, M.; Passaponti, M.; Giurlani, W.; Lari, L.; Bianchi, A.; Innocenti, M. Multi-Walled Carbon Nanotubes Supported Pd(II) Complexes: A Supramolecular Approach towards Single-Ion Oxygen Reduction Reaction Catalysts. Energies 2020, 13, 5539. [Google Scholar] [CrossRef]
- Savastano, M.; Zoppi, C.; Bianchi, A.; Bazzicalupi, C. Synthesis and coordination properties of a new ligand designed for surface functionalization of carbon substrates. Inorg. Chim. Acta 2020, 511, 119793. [Google Scholar] [CrossRef]
- Savastano, M.; Passaponti, M.; Giurlani, W.; Lari, L.; Calisi, N.; Delgado-Pinar, E.; Serrano, E.S.; Garcia-España, E.; Innocenti, M.; Lazarov, V.K.; et al. Linear, tripodal, macrocyclic: Ligand geometry and ORR activity of supported Pd(II) complexes. Inorg. Chim. Acta 2021, 518, 120250. [Google Scholar] [CrossRef]
- Bellotti, D.; Remelli, M. Deferoxamine B: A Natural, Excellent and Versatile Metal Chelator. Molecules 2021, 26, 3255. [Google Scholar] [CrossRef]
- Gans, P.; Sabatini, A.; Vacca, A. Investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs. Talanta 1996, 43, 1739–1753. [Google Scholar]
- Savastano, M.; Arranz-Mascarós, P.; Bazzicalupi, C.; Clares, M.P.; Godino-Salido, M.L.; Guijarro, L.; Gutiérrez-Valero, M.D.; Bianchi, A.; García-España, E.; López-Garzón, R. Polyfunctional Tetraaza-Macrocyclic Ligands: Zn(II), Cu(II) Binding and Formation of Hybrid Materials with Multiwalled Carbon Nanotubes. ACS Omega 2017, 2, 3868–3877. [Google Scholar] [CrossRef]
- Alderighi, L.; Gans, P.; Ienco, A.; Peters, D.; Sabatini, A.; Vacca, A. Hyperquad simulation and speciation (HySS): A utility program for the investigation of equilibria involving soluble and partially soluble species. Coord. Chem. Rev. 1999, 184, 311–318. [Google Scholar] [CrossRef]
- Feiner, I.V.J.; Brandt, M.; Cowell, J.; Demuth, T.; Vugts, D.; Gasser, G.; Mindt, T.L. The Race for Hydroxamate-Based Zirconium-89 Chelators. Cancers 2021, 13, 4466. [Google Scholar] [CrossRef]
- Sasaki, T.; Kobayashi, T.; Takagi, I.; Moriyama, H. Hydrolysis Constant and Coordination Geometry of Zirconium(IV). J. Nucl. Sci. Technol. 2008, 45, 735–739. [Google Scholar] [CrossRef]
- Schneider, H.-J.; Yatsimirsky, A. Priciples and Methods in Supramolecular Chemistry; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Ekberg, C.; Kallvenius, G.; Albinsson, Y.; Brown, P.L. Studies on the Hydrolytic Behavior of Zirconium(IV). J. Solut. Chem. 2004, 33, 47–79. [Google Scholar] [CrossRef]
- Perera, W.N.; Hefter, G. Mononuclear Cyano- and Hydroxo-Complexes of Iron(III). Inorg. Chem. 2003, 42, 5917–5923. [Google Scholar] [CrossRef] [PubMed]
- Rai, D.; Kitamura, A.; Altmaier, M.; Rosso, K.M.; Sasaki, T.; Kobayashi, T. A Thermodynamic Model for ZrO2(am) Solubility at 25 °C in the Ca2+–Na+–H+–Cl−–OH−–H2O System: A Critical Review. J. Solut. Chem. 2018, 47, 855–891. [Google Scholar] [CrossRef]
- Brown, P.; Curti, E.; Grambow, B.; Ekberg, C. Chemical Thermodynamics of Zirconium. In Chemical Thermodynamics; Mompean, F.J., Perrone, J., Illemassène, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 8. [Google Scholar]
- Bazzicalupi, C.; Bianchi, A.; Biver, T.; Giorgi, C.; Santarelli, S.; Savastano, M. Formation of Double-Strand Dimetallic Helicates with a Terpyridine-Based Macrocycle. Inorg. Chem. 2014, 53, 12215–12224. [Google Scholar] [CrossRef]
- Fontanelli, M.; Micheloni, M. Proceedings of the I Spanish-Italian Congress on Thermodynamics of Metal Complexes; Diputación de Castellón: Castellón, Spain, 1990; pp. 41–43. [Google Scholar]
- Savastano, M.; Fiaschi, M.; Ferraro, G.; Gratteri, P.; Mariani, P.; Bianchi, A.; Bazzicalupi, C. Sensing Zn2+ in Aqueous Solution with a Fluorescent Scorpiand Macrocyclic Ligand Decorated with an Anthracene Bearing Tail. Molecules 2020, 25, 1355. [Google Scholar] [CrossRef] [Green Version]
- Gran, G. Determination of the equivalence point in potentiometric titrations. Part II. Analyst 1952, 77, 661–671. [Google Scholar]
- Kraus, K.A.; Johnson, J.S. Hydrolytic polymerization of Zr(IV). J. Am. Chem. Soc. 1953, 75, 5769. [Google Scholar] [CrossRef]
- Johnson, J.S.; Kraus, K.A. Hydrolytic Behavior of Metal Ions. VI. Ultracentrifugation of Zirconium(IV) and Hafnium(IV); Effect of Acidity on the Degree of Polymerization. J. Am. Chem. Soc. 1956, 78, 3937–3943. [Google Scholar]
- Connick, R.E.; McVey, W.H. The Aqueous Chemistry of Zirconium. J. Am. Chem. Soc. 1949, 71, 3182–3191. [Google Scholar] [CrossRef] [Green Version]
- Connick, R.E.; Reas, W.H. The Hydrolysis and Polymerization of Zirconium in Perchloric Acid Solution. J. Am. Chem. Soc. 1951, 73, 1171–1176. [Google Scholar] [CrossRef]
- Connick, R.E.; Zielen, A.J. The Hydrolytic Polymerization of Zirconium in Perchloric Acid Solutions. J. Am. Chem. Soc. 1956, 78, 5785–5792. [Google Scholar]
- Baes, C.F.; Mesmer, R.E. The Hydrolysis of Cations; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Thoenen, T.; Hummel, W.; Berner, U.; Curti, E. The PSI/Nagra Chemical Thermodynamic Database 12/07, Nuclear Energy and Safety Research Department Laboratory for Waste Management (LES); Paul Scherrer Institute: Villigen, Switzerland, 2014. [Google Scholar]

| Equilibria | logK | Equilibria | logK |
|---|---|---|---|
| L4− + H+ = HL3− | 10.70(2) | H3L− + Zn2+ = [ZnH3L]+ | 5.4(1) |
| HL3−+ H+ = H2L2− | 9.53(3) | H4L + Zn2+ = [ZnH4L]2+ | 3.43(3) |
| H2L2− + H+ = H3L− | 9.07(3) | ||
| H3L− + H+ = H4L | 8.40(3) | L4− + Cu2+ = [CuL]2− | 15.44(8) |
| H4L + H+ = H5L+ | 2.67(3) | HL3− + Cu2+ = [CuHL]− | 14.29(9) |
| H2L2− + Cu2+ = [CuH2L] | 13.49(7) | ||
| L4− + Na+ = [NaL]3− | 2.35(5) | H3L− + Cu2+ = [CuH3L]+ | 8.89(3) |
| HL3− + Na+ = [NaHL]2− | 1.6(1) | ||
| L4− + Zr4+ = [ZrL] | 37.40(5) | ||
| L4− + K+ = [KL]3− | 2.11(7) | HL3− + Zr4+ = [ZrHL]+ | 35.97(8) |
| L4− + Zr4+ + 2H+ = [ZrH2L]2+ | 51.51(8) | ||
| L4− + Mg2+ = [MgL]2− | 4.42(3) | 2L4− + 2Zr4+ + H+ = [Zr2HL2]+ | 88.63(5) |
| HL3− + Mg2+ = [MgHL]− | 4.30(3) | 2L4− + 2Zr4+ + 3H+ = [Zr2H3L2]3+ | 102.3(1) |
| H2L2− + Mg2+ = [MgH2L] | 3.16(8) | 3L4− + 2Zr4+ + 4H+ = [Zr2H4L3] | 125.12(6) |
| 3L4− + 2Zr4+ + 5H+ = [Zr2H5L3]+ | 134.0(2) | ||
| L4− + Ca2+ =[CaL]2− | 3.82(6) | 3L4−+2Zr4++6H+=[Zr2H6L3]2+ | 142.4(2) |
| HL3− + Ca2+=[CaHL]− | 3.35(7) | ||
| DFO3− + Na+ = [NaDFO]2− | 1.70(9) | ||
| L4− + Zn2+ = [ZnL]2− | 10.88(5) | ||
| HL3− + Zn2+ = [ZnHL]− | 10.54(4) | DFO3− + K+ = [KDFO]2− | 1.57(7) |
| H2L2− + Zn2+ = [ZnH2L] | 8.62(3) |
| Stoichio-Metry | Species a | Formula | Experim. | Calculated | Error (ppm) |
|---|---|---|---|---|---|
| 2:3 | H4L3Zr2Na+ | C90H148O30N30NaZr2 | 2331.88818 | 2331.89639 | −3.52 |
| 2:3 | H4L3Zr2Na+ −169 | C85H141O28N25NaZr2 | 2162.93740 | 2162.83642 | 0.45 |
| 1:2 | H4L2ZrNa+ | C60H100O20N20NaZr | 1533.63483 | 1533.63620 | 1.45 |
| 1:2 | H4L2ZrNa+ −169 | C55H93O18N15NaZr | 1364.57874 | 1364.57623 | 1.84 |
| 1:1 | HLZr+ | C30H49O10N10Zr | 799.26849 | 799.26747 | 1.28 |
| 1:1 | LZrNa+ | C30H48O10N10ZrNa | 821.25037 | 821.24941 | 1.17 |
| H4LNa+ | C30H52N10O10Na | 735.37598 | 735.37677 | 0.790 |
| Zr,H,DFO Species | 1 logβ Ref [8] | 2 logβ Ref [13] | 3 Alternative logβ, Set 1 | 4 Alternative logβ, Set 2 | 5 logK a Column 1 | 6 logK a Column 3 |
|---|---|---|---|---|---|---|
| 101 | 36.02(9) | 40.04(3) | 40.95(9) | 41.29(6) | ||
| 111 | b | 46.4(1) | 49.01(7) | |||
| 121 | 49.06(6) | 53.87(6) | 51.8(1) | 13.04 c | 12.92 c | |
| 1-11 | 26.15(4) | 29.15(9) | 30.96(4) | 30.6(1) | −9.87 c | −9.99 c |
| 212 | 86.3(1) | 95.9(1) | 14.3 c | 14.0 c | ||
| 222 | 92.9(2) | 102.55(2) | 20.9 c | 20.6 c | ||
| 232 | 99.1(1) | 108.7(1) | 27.1 c | 26.8 c | ||
| 253 | 134.1(1) | 143.7(1) | 62.1 c | 61.8 c | ||
| 263 | 138.0(1) | 147.6(1) | 66.0 c | 65.7 c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savastano, M.; Boscaro, F.; Bianchi, A. Metal Coordination Properties of a Chromophoric Desferrioxamine (DFO) Derivative: Insight on the Coordination Stoichiometry and Thermodynamic Stability of Zr4+ Complexes. Molecules 2022, 27, 184. https://doi.org/10.3390/molecules27010184
Savastano M, Boscaro F, Bianchi A. Metal Coordination Properties of a Chromophoric Desferrioxamine (DFO) Derivative: Insight on the Coordination Stoichiometry and Thermodynamic Stability of Zr4+ Complexes. Molecules. 2022; 27(1):184. https://doi.org/10.3390/molecules27010184
Chicago/Turabian StyleSavastano, Matteo, Francesca Boscaro, and Antonio Bianchi. 2022. "Metal Coordination Properties of a Chromophoric Desferrioxamine (DFO) Derivative: Insight on the Coordination Stoichiometry and Thermodynamic Stability of Zr4+ Complexes" Molecules 27, no. 1: 184. https://doi.org/10.3390/molecules27010184