Spectroscopic Characterization of 3-Aminoisoxazole, a Prebiotic Precursor of Ribonucleotides
Abstract
:1. Introduction
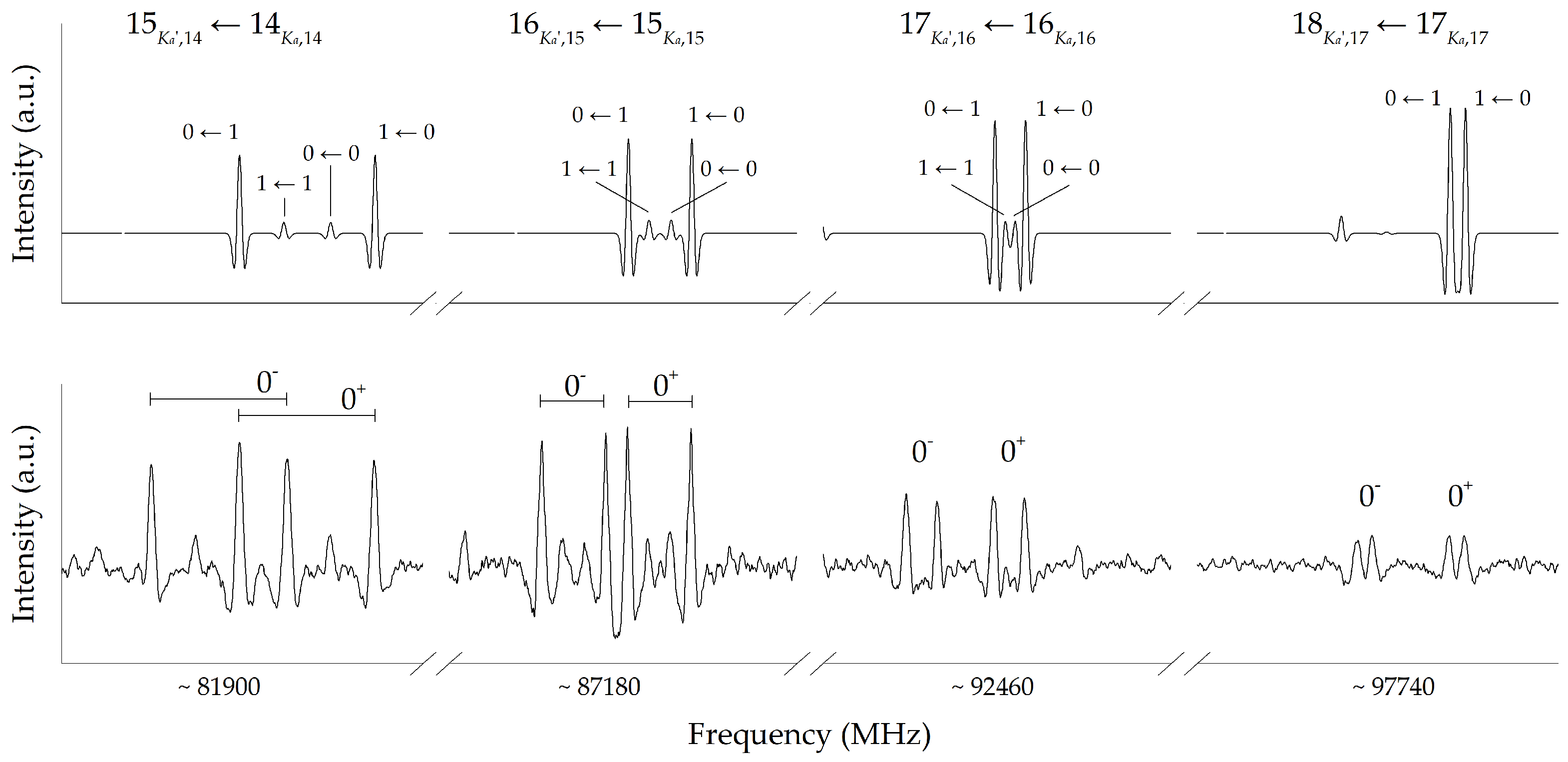
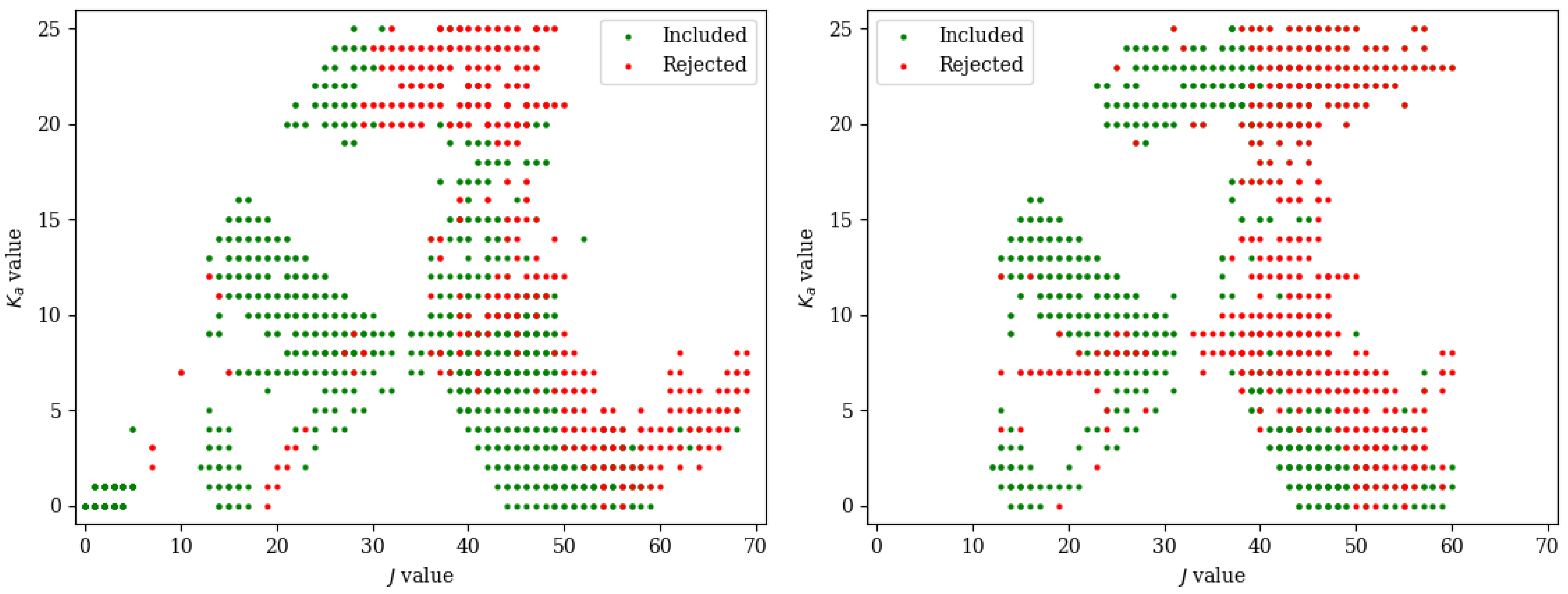
2. Results and Discussion
3. Materials and Methods
3.1. Computational Details
3.2. Experimental Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilbert, W. Origin of life: The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Fuller, W.D.; Sanchez, R.A.; Orgel, L.E. Studies in prebiotic synthesis: VI. Synthesis of purine nucleosides. J. Mol. Biol. 1972, 67, 25–33. [Google Scholar] [CrossRef]
- Leslie, E.O. Prebiotic chemistry and the origin of the RNA world. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 99–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powner, M.W.; Gerland, B.; Sutherland, J.D. Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions. Nature 2009, 459, 239–242. [Google Scholar] [CrossRef]
- Becker, S.; Thoma, I.; Deutsch, A.; Gehrke, T.; Mayer, P.; Zipse, H.; Carell, T. A high-yielding, strictly regioselective prebiotic purine nucleoside formation pathway. Science 2016, 352, 833–836. [Google Scholar] [CrossRef]
- Becker, S.; Schneider, C.; Okamura, H.; Crisp, A.; Amatov, T.; Dejmek, M.; Carell, T. Wet-dry cycles enable the parallel origin of canonical and non-canonical nucleosides by continuous synthesis. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Becker, S.; Feldmann, J.; Wiedemann, S.; Okamura, H.; Schneider, C.; Iwan, K.; Crisp, A.; Rossa, M.; Amatov, T.; Carell, T. Unified prebiotically plausible synthesis of pyrimidine and purine RNA ribonucleotides. Science 2019, 366, 76–82. [Google Scholar] [CrossRef] [Green Version]
- Chyba, C.; Sagan, C. Endogenous Production, Exogenous Delivery and Impact-Shock Synthesis of Organic Molecules: An Inventory for the Origins of Life. Nature 1992, 355, 125. [Google Scholar] [CrossRef]
- Pierazzo, E.; Chyba, C. Amino acid survival in large cometary impacts. Meteorit. Planet. Sci. 1999, 34, 909–918. [Google Scholar] [CrossRef]
- Bertrand, M.; Van Der Gaast, S.; Vilas, F.; Hörz, F.; Haynes, G.; Chabin, A.; Brack, A.; Westall, F. The fate of amino acids during simulated meteoritic impact. Astrobiology 2009, 9, 943–951. [Google Scholar] [CrossRef]
- McCaffrey, V.; Zellner, N.; Waun, C.; Bennett, E.; Earl, E. Reactivity and survivability of glycolaldehyde in simulated meteorite impact experiments. Orig. Life Evol. Biosph. 2014, 44, 29–42. [Google Scholar] [CrossRef] [PubMed]
- Rivilla, V.; Drozdovskaya, M.N.; Altwegg, K.; Caselli, P.; Beltrán, M.; Fontani, F.; Van Der Tak, F.; Cesaroni, R.; Vasyunin, A.; Rubin, M.; et al. ALMA and ROSINA detections of phosphorus-bearing molecules: The interstellar thread between star-forming regions and comets. Mon. Not. R. Astron. Soc. 2020, 492, 1180–1198. [Google Scholar] [CrossRef]
- Todd, Z.R.; Öberg, K.I. Cometary delivery of hydrogen cyanide to the early Earth. Astrobiology 2020, 20, 1109–1120. [Google Scholar] [CrossRef]
- Zellner, N.E.; McCaffrey, V.P.; Butler, J.H. Cometary Glycolaldehyde as a Source of pre-RNA Molecules. Astrobiology 2020, 20, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Kimmich, N.; Belisle, W.; Sarinana, J.; Brabham, K.; Garrel, L. Carbonaceous meteorites as a source of sugar-related organic compounds for the early Earth. Nature 2001, 414, 879–883. [Google Scholar] [CrossRef] [PubMed]
- Herbst, E.; Van Dishoeck, E.F. Complex organic interstellar molecules. Ann. Rev. Astron. Astrophys. 2009, 47, 427–480. [Google Scholar] [CrossRef]
- Turner, B. Detection of interstellar cyanoacetylene. Astrophys. J. 1971, 163, L35. [Google Scholar] [CrossRef]
- Turner, B.; Liszt, H.; Kaifu, N.; Kisliakov, A. Microwave detection of interstellar cyanamide. Astrophys. J. 1975, 201, L149–L152. [Google Scholar] [CrossRef]
- Rivilla, V.M.; Martín-Pintado, J.; Jiménez-Serra, I.; Martín, S.; Rodríguez-Almeida, L.F.; Requena-Torres, M.A.; Rico-Villas, F.; Zeng, S.; Briones, C. Prebiotic precursors of the primordial RNA world in space: Detection of NH2OH. Astrophys. J. Lett. 2020, 899, L28. [Google Scholar] [CrossRef]
- Hollis, J.M.; Lovas, F.J.; Jewell, P.R. Interstellar glycolaldehyde: The first sugar. Astrophys. J. 2000, 540, L107. [Google Scholar] [CrossRef]
- Rivilla, V.M.; Colzi, L.; Jiménez-Serra, I.; Martín-Pintado, J.; Megías, A.; Melosso, M.; Bizzocchi, L.; López-Gallifa, A.; Martínez-Henares, A.; Massalkhi, S. Precursors of the RNA-world in space: Detection of (Z)-1,2-ethenediol in the interstellar medium, a key intermediate in sugar formation. Astrophys. J. Lett. 2022, 929, L11. [Google Scholar] [CrossRef]
- Belloche, A.; Garrod, R.; Müller, H.; Menten, K.; Medvedev, I.; Thomas, J.; Kisiel, Z. Re-exploring Molecular Complexity with ALMA (ReMoCA): Interstellar detection of urea. Astron. Astrophys. 2019, 628, A10. [Google Scholar] [CrossRef] [Green Version]
- McGuire, B.A.; Burkhardt, A.M.; Kalenskii, S.; Shingledecker, C.N.; Remijan, A.J.; Herbst, E.; McCarthy, M.C. Detection of the aromatic molecule benzonitrile (c-C6H5CN) in the interstellar medium. Science 2018, 359, 202–205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGuire, B.A.; Loomis, R.A.; Burkhardt, A.M.; Lee, K.L.K.; Shingledecker, C.N.; Charnley, S.B.; Cooke, I.R.; Cordiner, M.A.; Herbst, E.; Kalenskii, S.; et al. Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering. Science 2021, 371, 1265–1269. [Google Scholar] [CrossRef]
- Burkhardt, A.M.; Lee, K.L.K.; Changala, P.B.; Shingledecker, C.N.; Cooke, I.R.; Loomis, R.A.; Wei, H.; Charnley, S.B.; Herbst, E.; McCarthy, M.C.; et al. Discovery of the pure polycyclic aromatic hydrocarbon indene (c-C9H8) with GOTHAM observations of TMC-1. Astrophys. J. Lett. 2021, 913, L18. [Google Scholar] [CrossRef]
- Cernicharo, J.; Agúndez, M.; Kaiser, R.; Cabezas, C.; Tercero, B.; Marcelino, N.; Pardo, J.; de Vicente, P. Discovery of two isomers of ethynyl cyclopentadiene in TMC-1: Abundances of CCH and CN derivatives of hydrocarbon cycles. Astron. Astrophys. 2021, 655, L1. [Google Scholar] [CrossRef]
- McNaughton, D.; Jahn, M.K.; Travers, M.J.; Wachsmuth, D.; Godfrey, P.D.; Grabow, J.U. Laboratory rotational spectroscopy of cyano substituted polycyclic aromatic hydrocarbons. Mon. Not. R. Astron. Soc. 2018, 476, 5268–5273. [Google Scholar] [CrossRef]
- McCarthy, M.C.; McGuire, B.A. Aromatics and cyclic molecules in molecular clouds: A new dimension of interstellar organic chemistry. J. Phys. Chem. A 2021, 125, 3231–3243. [Google Scholar] [CrossRef]
- Kruse, F.M.; Teichert, J.S.; Trapp, O. Prebiotic Nucleoside Synthesis: The Selectivity of Simplicity. Chem. Eur. J. 2020, 26, 14776–14790. [Google Scholar] [CrossRef]
- Crisp, A. Non-Canonical Nucleosides and Proto-Urea-RNA at the Chemical Origins of Life. Ph.D. Thesis, LMU, Munich, Germany, 2021. [Google Scholar]
- Tran, Q.P.; Adam, Z.R.; Fahrenbach, A.C. Prebiotic reaction networks in water. Life 2020, 10, 352. [Google Scholar] [CrossRef]
- Møllendal, H.; Konovalov, A. Microwave spectrum of 2-aminooxazole, a compound of potential prebiotic and astrochemical interest. J. Phys. Chem. A 2010, 114, 2151–2156. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Serra, I.; Martín-Pintado, J.; Rivilla, V.M.; Rodríguez-Almeida, L.; Alonso Alonso, E.R.; Zeng, S.; Cocinero, E.J.; Martín, S.; Requena-Torres, M.; Martín-Domenech, R.; et al. Toward the RNA-world in the interstellar medium. Detection of urea and search of 2-amino-oxazole and simple sugars. Astrobiology 2020, 20, 1048–1066. [Google Scholar] [CrossRef] [PubMed]
- Kydd, R.; Mills, I. Microwave spectrum of 2-aminopyridine. J. Mol. Spectrosc. 1972, 42, 320–326. [Google Scholar] [CrossRef]
- Ye, E.; Bettens, R.P. Millimeter wave measurement and assignment of the rotational spectrum of 2-aminopyridine. J. Mol. Spectrosc. 2004, 223, 73–79. [Google Scholar] [CrossRef]
- Christen, D.; Norbury, D.; Lister, D.G.; Palmieri, P. Microwave spectra and structure of the amine group in 3-aminopyridine and 4-aminopyridine. Ab initio molecular orbital calculations of the structure of the amine group in the aminopyridines. J. Chem. Soc. Faraday Trans. II 1975, 71, 438–446. [Google Scholar] [CrossRef]
- Lister, D.G.; Tyler, J.K. Non-planarity of the aniline molecule. Chem. Commun. 1966, 6, 152–153. [Google Scholar] [CrossRef]
- Hatta, A.; Suzuki, M.; Kozima, K. Nuclear quadrupole effects in the microwave spectrum and dipole moment of aniline. Bull. Chem. Soc. Jpn. 1973, 46, 2321–2323. [Google Scholar] [CrossRef]
- Lister, D.; Tyler, J.; Høg, J.; Larsen, N.W. The microwave spectrum, structure and dipole moment of aniline. J. Mol. Struct. 1974, 23, 253–264. [Google Scholar] [CrossRef]
- Roussy, G.; Nonat, A. Determination of the equilibrium molecular structure of inverting molecules by microwave spectroscopy: Application to aniline. J. Mol. Spectrosc. 1986, 118, 180–188. [Google Scholar] [CrossRef]
- Kleibömer, B.; Sutter, D. The vibrational state dependence of the 14N quadrupole coupling tensor in aniline. A microwave Fourier-transform study combined with semirigid bender calculations. Z. Naturforsch. A 1988, 43, 561–571. [Google Scholar] [CrossRef]
- Lupi, J.; Puzzarini, C.; Cavallotti, C.; Barone, V. State-of-the-Art Quantum Chemistry Meets Variable Reaction Coordinate Transition State Theory to Solve the Puzzling Case of the H2S + Cl System. J. Chem. Theory Comput. 2020, 16, 5090–5104. [Google Scholar] [CrossRef] [PubMed]
- Lupi, J.; Alessandrini, S.; Puzzarini, C.; Barone, V. junChS and junChS-F12 Models: Parameter-free efficient yet accurate composite schemes for energies and structures of noncovalent complexes. J. Chem. Theory Comput. 2021, 17, 6974–6992. [Google Scholar] [CrossRef] [PubMed]
- Ceselin, G.; Barone, V.; Tasinato, N. Accurate biomolecular structures by the nano-LEGO approach: Pick the bricks and build your geometry. J. Chem. Theory Comput. 2021, 17, 7290–7311. [Google Scholar] [CrossRef] [PubMed]
- Western, C.M. PGOPHER: A program for simulating rotational, vibrational and electronic spectra. J. Quant. Spectrosc. Ra. 2017, 186, 221–242. [Google Scholar] [CrossRef] [Green Version]
- Pickett, H.M. The fitting and prediction of vibration-rotation spectra with spin interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
- Watson, J.K.G. Aspects of quartic and sextic centrifugal effects on rotational energy levels. In Vibrational Spectra and Structure; Durig, J.R., Ed.; Elsevier: New York, NY, USA, 1977; pp. 1–89. [Google Scholar]
- Brown, R.; Godfrey, P.; Kleibomer, B.; Pierlot, A.; McNaughton, D. Submillimeter-wave spectrum, far-infrared spectrum, and inversion potential of vinylamine. J. Mol. Spectrosc. 1990, 142, 195–204. [Google Scholar] [CrossRef]
- Puzzarini, C.; Stanton, J.F.; Gauss, J. Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. Int. Rev. Phys. Chem. 2010, 29, 273–367. [Google Scholar] [CrossRef]
- Puzzarini, C.; Bloino, J.; Tasinato, N.; Barone, V. Accuracy and interpretability: The devil and the holy grail. New routes across old boundaries in computational spectroscopy. Chem. Rev. 2019, 119, 8131–8191. [Google Scholar] [CrossRef]
- Barone, V.; Ceselin, G.; Fusè, M.; Tasinato, N. Accuracy meets interpretability for computational spectroscopy by means of hybrid and double-hybrid functionals. Front. Chem. 2020, 8, 859. [Google Scholar] [CrossRef]
- Barone, V.; Alessandrini, S.; Biczysko, M.; Cheeseman, J.R.; Clary, D.C.; McCoy, A.B.; DiRisio, R.J.; Neese, F.; Melosso, M.; Puzzarini, C. Computational molecular spectroscopy. Nat. Rev. Methods Prim. 2021, 1, 1–27. [Google Scholar] [CrossRef]
- Melli, A.; Barone, V.; Puzzarini, C. Unveiling bifunctional hydrogen bonding with the help of quantum Chemistry: The imidazole-water adduct as test case. J. Phys. Chem. A 2021, 125, 2989–2998. [Google Scholar] [CrossRef] [PubMed]
- Santra, G.; Sylvetsky, N.; Martin, J.M. Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 2019, 123, 5129–5143. [Google Scholar] [CrossRef] [PubMed]
- Papajak, E.; Truhlar, D.G. Convergent partially augmented basis sets for post-Hartree-Fock calculations of molecular properties and reaction barrier heights. J. Chem. Theory Comput. 2011, 7, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Dunning Jr, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Alessandrini, S.; Barone, V.; Puzzarini, C. Extension of the “cheap” composite approach to noncovalent interactions: The jun-ChS scheme. J. Chem. Theory Comput. 2019, 16, 988–1006. [Google Scholar] [CrossRef]
- Puzzarini, C.; Barone, V. Extending the molecular size in accurate quantum-chemical calculations: The equilibrium structure and spectroscopic properties of uracil. Phys. Chem. Chem. Phys. 2011, 13, 7189–7197. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618. [Google Scholar] [CrossRef] [Green Version]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Mills, I.M. Vibration-Rotation Structure in Asymmetric- and Symmetric-Top Molecules. In Molecular Spectroscopy: Modern Research; Rao, K.N., Matthews, C.W., Eds.; Academic Press: Cambridge, MA, USA, 1972; Volume 1, pp. 115–140. [Google Scholar]
- Grabow, J.U.; Stahl, W.; Dreizler, H. A multioctave coaxially oriented beam-resonator arrangement Fourier-transform microwave spectrometer. Rev. Sci. Instrum. 1996, 67, 4072–4084. [Google Scholar] [CrossRef]
- Melosso, M.; Conversazioni, B.; Degli Esposti, C.; Dore, L.; Cané, E.; Tamassia, F.; Bizzocchi, L. The Pure Rotational Spectrum of 15ND2 Observed by Millimetre and Submillimetre-Wave Spectroscopy. J. Quant. Spectrosc. Rad. 2019, 222, 186–189. [Google Scholar] [CrossRef]
- Melosso, M.; Bizzocchi, L.; Tamassia, F.; Degli Esposti, C.; Canè, E.; Dore, L. The rotational spectrum of 15ND. Isotopic-independent Dunham-type analysis of the imidogen radical. Phys. Chem. Chem. Phys. 2019, 21, 3564–3573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
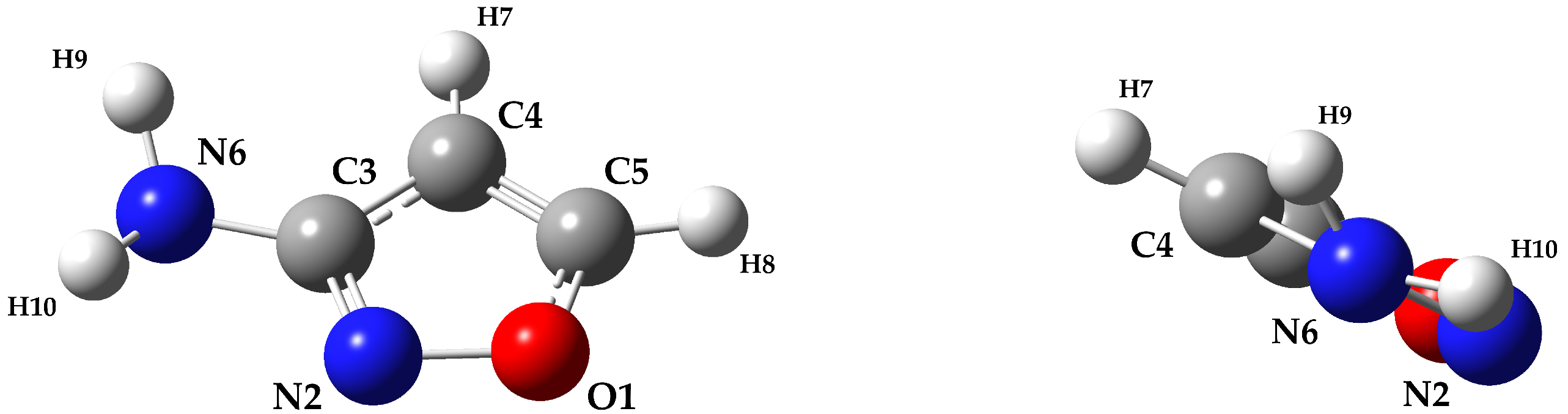

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| N2-O1 | 1.3993 | C3-N2-O1 | 105.43 |
| C3-N2 | 1.3098 | C4-C3-N2 | 111.98 |
| C4-C3 | 1.4256 | C5-O1-N2 | 108.55 |
| C5-O1 | 1.3359 | N6-C3-N2 | 121.03 |
| N6-C3 | 1.3822 | H7-C4-C3 | 128.57 |
| H7-C4 | 1.0738 | H8-C5-O1 | 115.95 |
| H8-C5 | 1.0755 | H9-N6-C3 | 113.83 |
| H9-N6 | 1.0048 | H10-N6-C3 | 112.74 |
| H10-N6 | 1.0067 | H9-N6-C3-N2 | 143.82 |
| H10-N6-C3-N2 | 14.90 |
| Atom | Parameter | Unit 1 | Experimental 2 | Theoretical 3 | |
|---|---|---|---|---|---|
| A | MHz | 9356.38319(10) | 9353.34396(32) | 9365.17 | |
| B | 3669.785470(65) | 3667.50297(15) | 3673.88 | ||
| C | 2642.302812(47) | 2642.25405(11) | 2645.93 | ||
| kHz | 0.233858(13) | 0.228365(35) | 0.22 | ||
| 1.60119(21) | 1.55578(35) | 1.49 | |||
| 1.53764(25) | 1.57235(33) | 1.53 | |||
| −0.0770640(78) | −0.076715(14) | −0.072 | |||
| −0.0217051(39) | −0.0240627(65) | −0.022 | |||
| N2 | MHz | 8.6397(17) | – | 8.97 | |
| −0.74480(68) | – | −0.79 | |||
| N6 | 3.8032(25) | – | 3.64 | ||
| 1.39391(64) | – | 1.46 | |||
| D | (y) | (y) | 1.19 | ||
| (y) | (y) | 3.08 | |||
| (n) | (n) | 1.09 | |||
| ad. | 623 | 529 | |||
| 0, 68 | 0, 60 | ||||
| 0, 25 | 0, 24 | ||||
| 01.47 | 01.50 | ||||
| kHz | 40.40 | 44.80 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melli, A.; Melosso, M.; Lengsfeld, K.G.; Bizzocchi, L.; Rivilla, V.M.; Dore, L.; Barone, V.; Grabow, J.-U.; Puzzarini, C. Spectroscopic Characterization of 3-Aminoisoxazole, a Prebiotic Precursor of Ribonucleotides. Molecules 2022, 27, 3278. https://doi.org/10.3390/molecules27103278
Melli A, Melosso M, Lengsfeld KG, Bizzocchi L, Rivilla VM, Dore L, Barone V, Grabow J-U, Puzzarini C. Spectroscopic Characterization of 3-Aminoisoxazole, a Prebiotic Precursor of Ribonucleotides. Molecules. 2022; 27(10):3278. https://doi.org/10.3390/molecules27103278
Chicago/Turabian StyleMelli, Alessio, Mattia Melosso, Kevin G. Lengsfeld, Luca Bizzocchi, Víctor M. Rivilla, Luca Dore, Vincenzo Barone, Jens-Uwe Grabow, and Cristina Puzzarini. 2022. "Spectroscopic Characterization of 3-Aminoisoxazole, a Prebiotic Precursor of Ribonucleotides" Molecules 27, no. 10: 3278. https://doi.org/10.3390/molecules27103278
APA StyleMelli, A., Melosso, M., Lengsfeld, K. G., Bizzocchi, L., Rivilla, V. M., Dore, L., Barone, V., Grabow, J.-U., & Puzzarini, C. (2022). Spectroscopic Characterization of 3-Aminoisoxazole, a Prebiotic Precursor of Ribonucleotides. Molecules, 27(10), 3278. https://doi.org/10.3390/molecules27103278







