Millimeter-Wave Spectroscopy of Methylfuran Isomers: Local vs. Global Treatments of the Internal Rotation
Abstract
:1. Introduction
2. Results
2.1. Global Fit of the Vibrational Ground State and First Torsional State of 2-MF
2.2. Global Fit of the Vibrational Ground State and First Torsional State of 3-MF
3. Discussion
3.1. “Local” versus “Global” Approach
3.2. Influence of the Isomerism on the Internal Rotation of the Methyl Group, Comparison with Other Heterocyclic Compounds
4. Materials and Methods
4.1. Theoretical Methods
4.1.1. Quantum Chemistry Calculations
4.1.2. Internal Rotation Hamiltonian
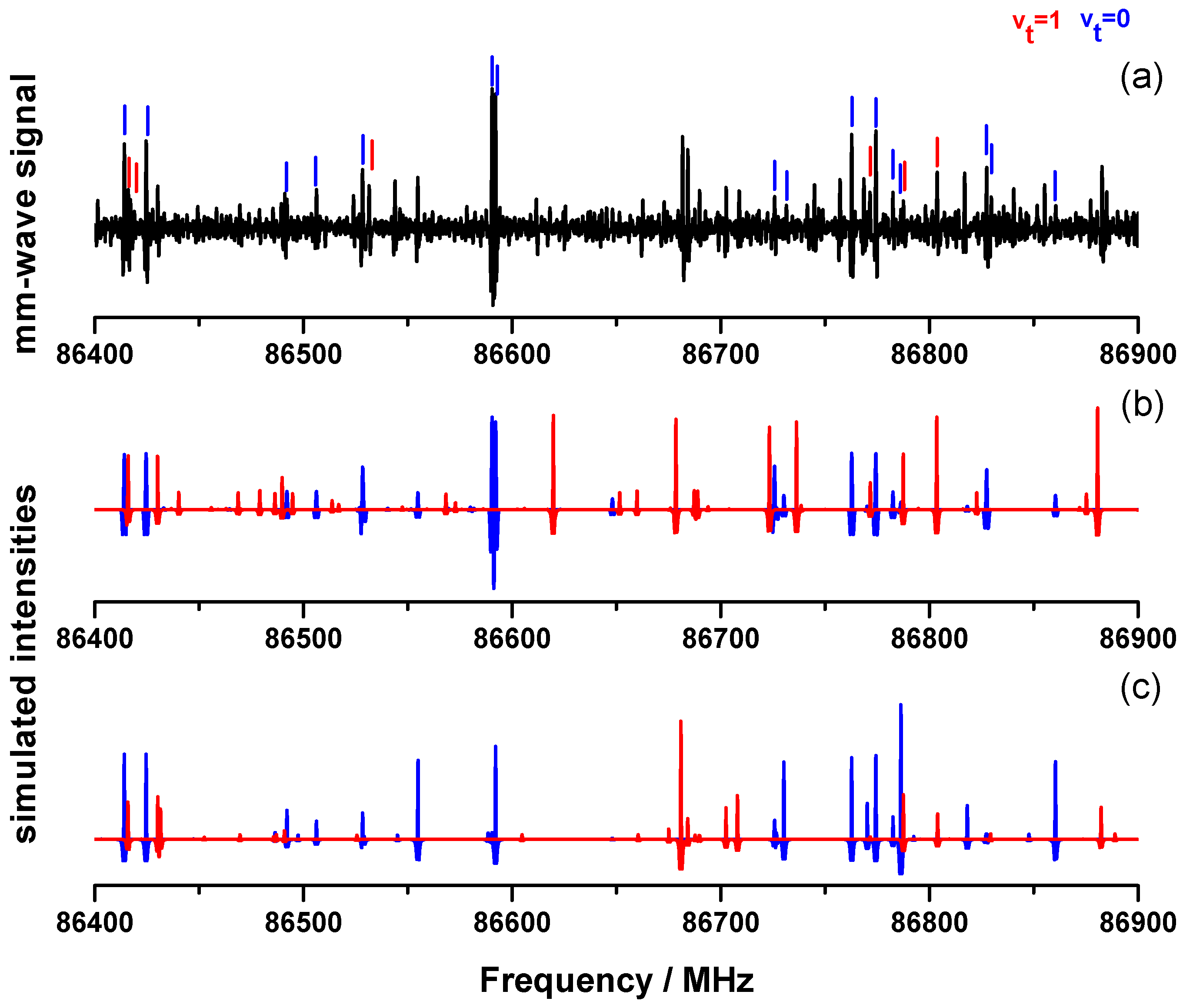
4.2. Room Temperature Millimeter-Wave Spectroscopy
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
The Following Abbreviations Are Used in This Manuscript
| B3LYP | Becke, 3-parameter, Lee-Yang-Parr |
| CAM | Combined Axis Method |
| DFT | Density Functional Theory |
| ERHAM | Effective Rotational-torsional HAMiltonian |
| FFT | Fast Fourier Transform |
| GC-MS | Gas Chromatography—Mass Spectrometry |
| GS | Ground State |
| IR | InfraRed |
| MF | Methyl Furan |
| MP | Methyl Pyrrole |
| MT | Methyl Tiophene |
| MP2 | Møller-Plesset perturbation theory at 2nd order |
| PAM | Principal Axis Method |
| PAS | Principal Axis System |
| RAM | Rho Axis Method |
| RAS | Rho Axis System |
| RMS | Root Mean Square |
| WRMS | Weighted Root Mean Square |
| RAS | Rho Axis System |
| SOA | Secondary Organic Aerosol |
| VOC | Volatile Organic Compound |
| XIAM | eXtended Internal Axis Method |
| ZBD | Zero Bias Detector |
References
- Jiang, X.; Tsona, N.T.; Jia, L.; Liu, S.; Zhang, H.; Xu, Y.; Du, L. Secondary organic aerosol formation from photooxidation of furan: Effects of NOx and humidity. Atmos. Chem. Phys. 2019, 19, 13591–13609. [Google Scholar] [CrossRef] [Green Version]
- Tapia, A.; Villanueva, F.; Salgado, M.S.; Cabañas, B.; Martínez, E.; Martín, P. Atmospheric degradation of 3-methylfuran: Kinetic and products study. Atmos. Chem. Phys. 2011, 11, 3227–3241. [Google Scholar] [CrossRef] [Green Version]
- Newland, M.J.; Ren, Y.; McGillen, M.R.; Michelat, L.; Daële, V.; Mellouki, A. NO3 chemistry of wildfire emissions: A kinetic study of the gas-phase reactions of furans with the NO3 radical. Atmos. Chem. Phys. 2022, 22, 1761–1772. [Google Scholar] [CrossRef]
- Gilman, J.B.; Lerner, B.M.; Kuster, W.C.; Goldan, P.D.; Warneke, C.; Veres, P.R.; Roberts, J.M.; de Gouw, J.A.; Burling, I.R.; Yokelson, R.J. Biomass burning emissions and potential air quality impacts of volatile organic compounds and other trace gases from fuels common in the US. Atmos. Chem. Phys. 2015, 15, 13915–13938. [Google Scholar] [CrossRef] [Green Version]
- Elwardany, A.; Es-sebbar, E.; Khaled, F.; Farooq, A. A chemical kinetic study of the reaction of hydroxyl with furans. Fuel 2016, 166, 245–252. [Google Scholar] [CrossRef] [Green Version]
- Intergovernmental panel on climate change Clouds and aerosols. In Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 571–658. [CrossRef]
- Yokelson, R.J.; Burling, I.R.; Gilman, J.B.; Warneke, C.; Stockwell, C.E.; de Gouw, J.; Akagi, S.K.; Urbanski, S.P.; Veres, P.; Roberts, J.M.; et al. Coupling field and laboratory measurements to estimate the emission factors of identified and unidentified trace gases for prescribed fires. Atmos. Chem. Phys. 2013, 13, 89–116. [Google Scholar] [CrossRef] [Green Version]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Wlodarczak, G.; Martinache, L.; Demaison, J.; Van Eijck, B.P. The millimeter-wave spectra of furan, pyrrole, and pyridine: Experimental and theoretical determination of the quartic centrifugal distortion constants. J. Mol. Spectrosc. 1988, 127, 200–208. [Google Scholar] [CrossRef]
- Motiyenko, R.A.; Alekseev, E.A.; Dyubko, S.F.; Lovas, F.J. Microwave spectrum and structure of furfural. J. Mol. Spectrosc. 2006, 240, 93–101. [Google Scholar] [CrossRef]
- Ogata, T.; Kozima, K. Microwave spectrum, barrier height to internal rotation of methyl group, and dipole moment of 3-methylfuran. Bull. Chem. Soc. Jpn. 1971, 44, 2344–2346. [Google Scholar] [CrossRef] [Green Version]
- Finneran, I.A.; Shipman, S.T.; Widicus Weaver, S.L. Rotational spectroscopy of 2-methylfuran from 8.7 to 960 GHz. J. Mol. Spectrosc. 2012, 280, 27–33. [Google Scholar] [CrossRef]
- Tokaryk, D.; Culligan, S.; Billinghurst, B.; van Wijngaarden, J. Synchrotron-based far-infrared spectroscopy of furan: Rotational analysis of the ν14, ν11, ν18 and ν19 vibrational levels. J. Mol. Spectrosc. 2011, 270, 56–60. [Google Scholar] [CrossRef]
- Jabri, A.; Fontanari, D.; Roucou, A.; Bray, C.; Hindle, F.; Dhont, G.; Mouret, G.; Bocquet, R.; Cuisset, A. Conformational landscape and inertial defect of methoxyphenol isomers studied by mm-wave spectroscopy and quantum chemistry calculations. J. Chem. Phys. 2019, 150, 104303. [Google Scholar] [CrossRef] [PubMed]
- Bruckhuisen, J.; Dhont, G.; Roucou, A.; Jabri, A.; Bayoudh, H.; Tran, T.T.; Goubet, M.; Martin-Drumel, M.A.; Cuisset, A. Intramolecular H-bond dynamics of catechol investigated by THz high-resolution spectroscopy of its low-frequency modes. Molecules 2021, 26, 3645. [Google Scholar] [CrossRef]
- Cuisset, A.; Hindle, F.; Mouret, G.; Bocquet, R.; Bruckhuisen, J.; Decker, J.; Pienkina, A.; Bray, C.; Fertein, E.; Boudon, V. Terahertz rotational spectroscopy of greenhouse gases using long interaction path-lengths. Appl. Sci. 2021, 11, 1229. [Google Scholar] [CrossRef]
- Decker, J.; Fertein, E.; Bruckhuisen, J.; Houzel, N.; Kulinski, P.; Fang, B.; Zhao, W.; Hindle, F.; Dhont, G.; Bocquet, R.; et al. MULTICHARME: A modified Chernin-type multi-pass cell designed for IR and THz long-path absorption measurements in the CHARME atmospheric simulation chamber. Atmos. Meas. Tech. 2022, 15, 1201–1215. [Google Scholar] [CrossRef]
- Andresen, U.; Dreizler, H. Dipolmoment des 2-Methylfurans. Z. Naturforsch. A 1970, 25, 570. [Google Scholar] [CrossRef]
- Drouin, B.J.; Maiwald, F.W.; Pearson, J.C. Application of cascaded frequency multiplication to molecular spectroscopy. Rev. Sci. Instrum. 2005, 76, 093113. [Google Scholar] [CrossRef] [Green Version]
- Mouret, G.; Guinet, M.; Cuisset, A.; Croize, L.; Eliet, S.; Bocquet, R.; Hindle, F. Versatile sub-THz spectrometer for trace gas analysis. IEEE Sens. J. 2013, 13, 133–138. [Google Scholar] [CrossRef]
- Hartwig, H.; Dreizler, H. The microwave spectrum of trans-2,3-dimethyloxirane in torsional excited states. Z. Naturforsch. A 1996, 51, 923–932. [Google Scholar] [CrossRef]
- Groner, P. Effective rotational Hamiltonian for molecules with two periodic large-amplitude motions. J. Chem. Phys. 1997, 107, 4483–4498. [Google Scholar] [CrossRef]
- Hougen, J.T.; Kleiner, I.; Godefroid, M. Selection rules and intensity calculations for a Cs asymmetric top molecule containing a methyl group internal rotor. J. Mol. Spectrosc. 1994, 163, 559–586. [Google Scholar] [CrossRef]
- Williams, T.; Kelley, C. Gnuplot 5.4: An Interactive Plotting Program. 2020. Available online: http://www.gnuplot.info (accessed on 1 April 2022).
- Kleiner, I. Asymmetric-top molecules containing one methyl-like internal rotor: Methods and codes for fitting and predicting spectra. J. Mol. Spectrosc. 2010, 260, 1–18. [Google Scholar] [CrossRef]
- Nguyen, T.; Stahl, W.; Nguyen, H.V.L.; Kleiner, I. Local vs global approaches to treat two equivalent methyl internal rotations and 14N nuclear quadrupole coupling of 2,5-dimethylpyrrole. J. Chem. Phys. 2021, 154, 204304. [Google Scholar] [CrossRef] [PubMed]
- Groner, P. Large-amplitude motion tunneling parameters in effective rotational Hamiltonians from rotation-internal rotation theory. J. Mol. Spectrosc. 1992, 156, 164–189. [Google Scholar] [CrossRef]
- Roucou, A.; Goubet, M.; Kleiner, I.; Bteich, S.; Cuisset, A. Large amplitude torsions in nitrotoluene isomers studied by rotational spectroscopy and quantum chemistry calculations. ChemPhysChem 2020, 21, 1–17. [Google Scholar] [CrossRef]
- Tudorie, M.; Kleiner, I.; Hougen, J.; Melandri, S.; Sutikdja, L.; Stahl, W. A fitting program for molecules with two inequivalent methyl tops and a plane of symmetry at equilibrium: Application to new microwave and millimeter-wave measurements of methyl acetate. J. Mol. Spectrosc. 2011, 269, 211–225. [Google Scholar] [CrossRef]
- Ilyushin, V.; Alekseev, E.A.; Dorovskaya, O.; Kalambet, M.; Margulès, L.; Motiyenko, R.A.; Goubet, M.; Pirali, O.; Bauerecker, S.; Maul, C.; et al. Isolated Small-Amplitude Fundamental Embedded in a Pure Torsional Bath: FIR and MW Spectra of the ν10 Vibrational Mode and Hot Torsional Bands of Acetaldehyde. In Proceedings of the 74th International Symposium on Molecular Spectroscopy, Champaign-Urbana, IL, USA, 17–21 June 2019; Available online: https://hal.archives-ouvertes.fr/hal-02397248 (accessed on 1 April 2022).
- Mjöberg, P.J.; Ralowski, W.M.; Ljunggren, S.O. Microwave spectrum and barrier to internal rotation of 5-methylisoxazole. Z. Naturforsch. A 1975, 30, 1279–1281. [Google Scholar] [CrossRef]
- Nguyen, T.; Dindic, C.; Stahl, W.; Nguyen, H.V.L.; Kleiner, I. 14N nuclear quadrupole coupling and methyl internal rotation in the microwave spectrum of 2-methylpyrrole. Mol. Phys. 2020, 118, 1668572. [Google Scholar] [CrossRef]
- Ogata, T.; Kozima, K. Microwave spectrum, barrier height to internal rotation of methyl group of 3-methylthiophene, and dipole moments of 3-methylthiophene and thiophene. J. Mol. Spectrosc. 1972, 42, 38–46. [Google Scholar] [CrossRef]
- Nguyen, T.; Stahl, W.; Nguyen, H.V.L.; Kleiner, I. 14N nuclear quadrupole coupling and methyl internal rotation in 3-methylpyrrole investigated by microwave spectroscopy. J. Mol. Spectrosc. 2020, 372, 111351. [Google Scholar] [CrossRef]
- Kleiner, I.; Godefroid, M.; Herman, M.; McKellar, A. The fundamental torsion band in acetaldehyde. J. Mol. Spectrosc. 1990, 142, 238–253. [Google Scholar] [CrossRef]
- Bermúdez, C.; Tercero, B.; Motiyenko, R.A.; Margulès, L.; Cernicharo, J.; Ellinger, Y.; Guillemin, J.-C. The millimeter-wave spectrum of methyl ketene and the astronomical search for it. A&A 2018, 619, A92. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C.; Merke, I.; Stahl, W. Microwave and theoretical investigation of the internal rotation in m-cresol. J. Chem. Phys. 2006, 124, 204305. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many–electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Kisiel, Z. PROSPE: Programs for ROtational SPEctroscopy. 1999. Available online: http://www.ifpan.edu.pl/~kisiel/prospe.htm (accessed on 1 April 2022).
- Kleiner, I.; Hougen, J.T. Rho-axis-method Hamiltonian for molecules having one methyl rotor and C1 point-group symmetry at equilibrium. J. Chem. Phys. 2003, 119, 5505–5509. [Google Scholar] [CrossRef]
- Ilyushin, V.V.; Kisiel, Z.; Pszczókowski, L.; Mäder, H.; Hougen, J.T. A new torsion–rotation fitting program for molecules with a sixfold barrier: Application to the microwave spectrum of toluene. J. Mol. Spectrosc. 2010, 259, 26–38. [Google Scholar] [CrossRef]
- Kirtman, B. Interactions between ordinary vibrations and hindered internal rotation. I. Rotational energies. J. Chem. Phys. 1962, 37, 2516–2539. [Google Scholar] [CrossRef]
- Lees, R.M.; Baker, J.G. Torsion–vibration–rotation interactions in methanol. I. Millimeter wave spectrum. J. Chem. Phys. 1968, 48, 5299–5318. [Google Scholar] [CrossRef]
- Herbst, E.; Messer, J.; De Lucia, F.C.; Helminger, P. A new analysis and additional measurements of the millimeter and submillimeter spectrum of methanol. J. Mol. Spectrosc. 1984, 108, 42–57. [Google Scholar] [CrossRef]
- Lin, C.C.; Swalen, J.D. Internal rotation and microwave spectroscopy. Rev. Mod. Phys. 1959, 31, 841–892. [Google Scholar] [CrossRef]
- Roucou, A.; Fontanari, D.; Dhont, G.; Jabri, A.; Bray, C.; Mouret, G.; Bocquet, R.; Cuisset, A. Large amplitude torsions in full conformational landscape of 3-methoxyphenol revealed by room temperature mm-wave rotational spectroscopy supported by quantum chemistry calculations. ChemPhysChem 2018, 19, 1–8. [Google Scholar] [CrossRef] [PubMed]
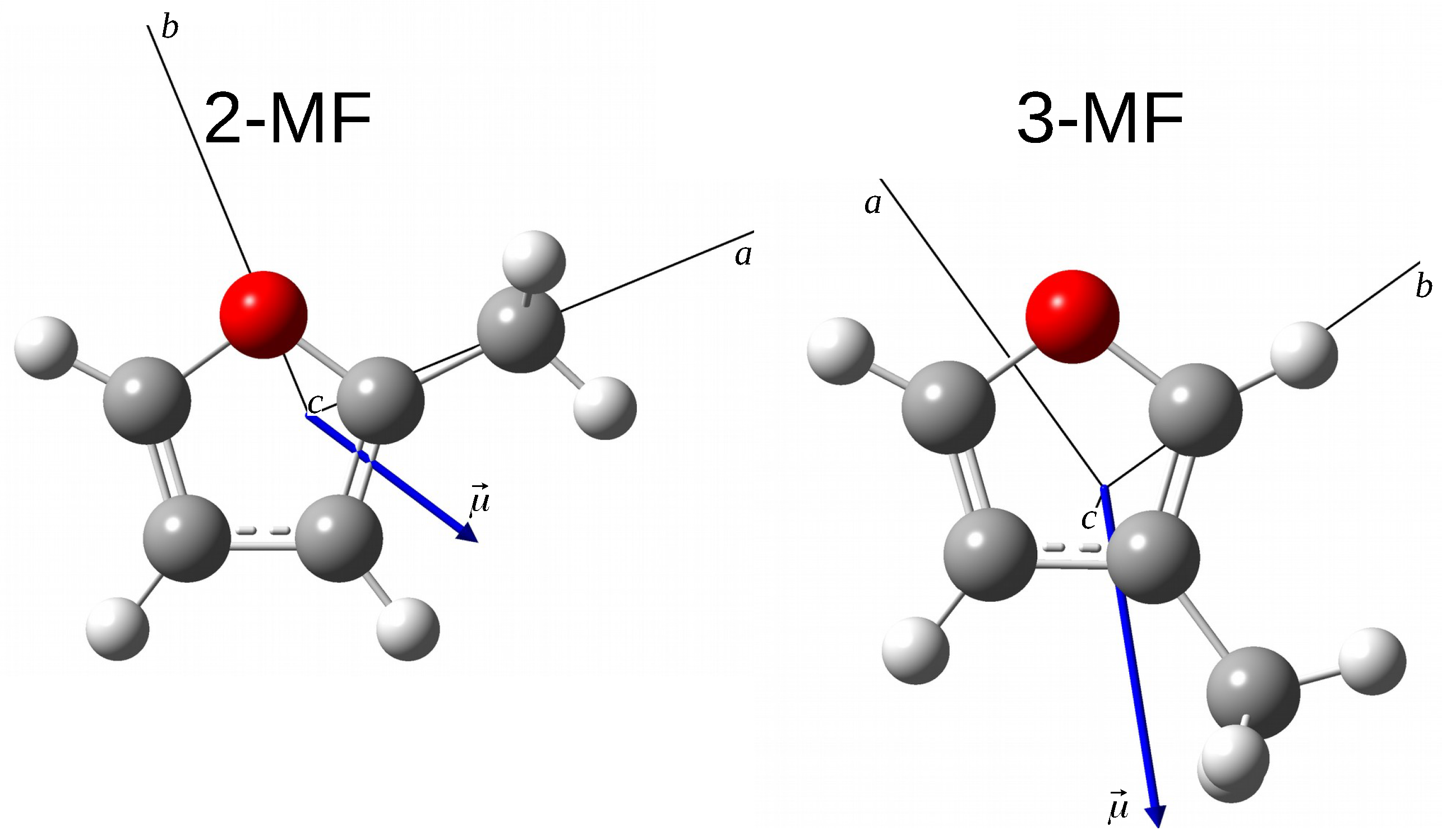


| Unit | B3LYP | XIAM v | ERHAM v | ERHAM v | BELGI-C v | |
|---|---|---|---|---|---|---|
| Present Work | Ref. [12] | Ref. [12] | Ref. [12] | Present Work | ||
| A | MHz | 8871.678 | 8792.22489 (33) | 8791.54486 (12) | 8790.0922 (18) | 8792.209 (28) |
| B | MHz | 3548.740 | 3542.64071 (20) | 3543.321804 (46) | 3540.94203 (22) | 3544.381 (32) |
| C | MHz | 2575.200 | 2565.560151 (38) | 2565.603243 (36) | 2564.946450 (65) | 2565.8202 (91) |
| kHz | 0.26076 | 1.539273 (68) | 0.2645388 (58) | 0.268855 (50) | ||
| kHz | 1.3921 | −2.41323 (31) | 1.408544 (66) | 1.8300 (31) | ||
| kHz | 0.991 | 0.99269 (31) | 1.000997 (83) | −1.947 (21) | ||
| kHz | 0.071346 | 0.564919 (32) | 0.0724207 (24) | 0.074930 (24) | ||
| kHz | 0.7186 | −0.46139 (17) | 0.687123 (86) | 0.6824 (14) | ||
| mHz | −0.669 (45) | −0.6653 (83) | −2.852 (63) | |||
| mHz | 0.568 (50) | [0.0] | [0.0] | |||
| mHz | [0.0] | 1.882 (20) | −7.01 (64) | |||
| mHz | −0.502 (29) | [0.0] | [0.0] | |||
| unitless | 0.0549 | 0.0549511 (44) | 0.0550406 (14) | 0.0554463 (90) | 0.0551544 (10) | |
| F | GHz | 170.257 | 169.30759 | 169.0829 | ||
| 376.12(22 e) | 412.873 (74) | 420.3157 (35) | ||||
| −1.49(22 e) | −9.010 (11) | |||||
| MHz | −119.459 (11) | 3781.55 (72) | ||||
| degree | 4.48 | 3.30 (13) | 4.6345 (53) | |||
| degree | 85.52 | 86.70 (13) | 85.3655 (83) | |||
| degree | 90.00 | 90.009 (18) | 90.00 | |||
| degree | 1.908 (13) | 2.1785 (31) | 1.871 | |||
| unitless | 29.435 | 32.492 | 33.1218 | |||
| 95 | 120 | 117 | 70 | |||
| 53 | 54 | 15 | 53 | |||
| (A; E) | 8006 (2495; 5511) | 11793 | 14152 (7766; 6386) | |||
| (A; E) | 2580 | 3742 (1836; 1906) | ||||
| WRMS | unitless | 1.754 | 0.718 | 0.753 | 1.0733; 1.1431 | |
| RMS | kHz | 263 | 108 | 113 | 107; 114 |
| Unit | B3LYP | Ref. [11] | XIAM v = 0 | XIAM v = 1 | BELGI-C v | |
|---|---|---|---|---|---|---|
| A | MHz | 8956.659 | 8890.83 (15) | 8890.9101 (10) | 8891.799 (11) | 8890.483 (14) |
| B | MHz | 3379.791 | 3366.91 (5) | 3367.05272 (32) | 3364.7173 (25) | 3368.235 (13) |
| C | MHz | 2491.517 | 2479.32 (5) | 2479.20065 (31) | 2478.2235 (23) | 2479.69788 (28) |
| kHz | 0.24058 | 0.24309 (12) | 0.24004 (90) | |||
| kHz | 1.5663 | 1.59104 (88) | 1.6429 (25) | |||
| kHz | 0.97 | 1.4636 (30) | 1.717 (56) | |||
| kHz | 0.06369 | 0.064188 (34) | 0.06267 (30) | |||
| kHz | 0.7979 | 0.7466 (26) | 0.4967 (45) | |||
| mHz | −18.1 (13) | −18.1 | ||||
| mHz | −12.1 (12) | −12.1 | ||||
| unitless | 0.0554 | 0.055676201 | 0.055620821 | 0.05564643 (33) | ||
| F | GHz | 171.195 | 167.8 | 169.1046 e | 169.2800 e | 159.541(78) |
| degree | 179.43 | 179.9438 | 179.9425 | 179.9425 | 179.495 (39) | |
| degree | 89.43 | 89.9438 | 89.9425 | 89.9425 | 89.483 (38) | |
| degree | 90.00 | 89.999866 | 90.0000 | 90.0000 | 90.000 | |
| 348.92 (50 ) | 381 (1) | 382.032 (44) | 385.4706 (44) | 357.77(22) | ||
| −10.81(50 ) | −2.481 (13) | |||||
| s | unitless | 27.156 | 30.22 (8) | 30.101 | 30.3406 | 29.879 (17) |
| 50 | 50 | 50 | ||||
| 31 | 31 | 31 | ||||
| N(v=0) (A; E) | 36 (20; 16) | 2463 (1296; 1167) | 2463 (1296; 1167) | |||
| N(v=1) (A; E) | 0 | 2016 (1003; 1013) | 2017 (1003;1014) | |||
| WRMS (v = 0; v = 1) | unitless | 1.3 | 10.0 | 1.21; 1.16 | ||
| RMS (v = 0; v = 1) | kHz | 200.6 | 1500 | 181; 174 |
| Molecule | /cm | /cm | 100 |
|---|---|---|---|
| 2-MF | 376.12 (22) [420.3157 (35)] | −1.49 (22) [−9.010 (11)] | −0.40 [−2.143] |
| 2-MT | 198.08 (33) [194.1] | 1.71 (33) | 0.86 |
| 2-MP | 263.62 (67) [279.7183 (26)] | 1.96 (67) | 0.74 |
| 3-MF | 348.92 (50) [357.77 (22)] | −10.81 (50) [−2.481 (13)] | −3.10 [−0.693] |
| 3-MT | 254.47 (20) [259] | −8.27 (20) | −3.25 |
| 3-MP | 223.55 (34) [245.14101 (89)] e | −7.71 (34) | −3.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruckhuisen, J.; Chawananon, S.; Kleiner, I.; Roucou, A.; Dhont, G.; Bracquart, C.; Asselin, P.; Cuisset, A. Millimeter-Wave Spectroscopy of Methylfuran Isomers: Local vs. Global Treatments of the Internal Rotation. Molecules 2022, 27, 3591. https://doi.org/10.3390/molecules27113591
Bruckhuisen J, Chawananon S, Kleiner I, Roucou A, Dhont G, Bracquart C, Asselin P, Cuisset A. Millimeter-Wave Spectroscopy of Methylfuran Isomers: Local vs. Global Treatments of the Internal Rotation. Molecules. 2022; 27(11):3591. https://doi.org/10.3390/molecules27113591
Chicago/Turabian StyleBruckhuisen, Jonas, Sathapana Chawananon, Isabelle Kleiner, Anthony Roucou, Guillaume Dhont, Colwyn Bracquart, Pierre Asselin, and Arnaud Cuisset. 2022. "Millimeter-Wave Spectroscopy of Methylfuran Isomers: Local vs. Global Treatments of the Internal Rotation" Molecules 27, no. 11: 3591. https://doi.org/10.3390/molecules27113591
APA StyleBruckhuisen, J., Chawananon, S., Kleiner, I., Roucou, A., Dhont, G., Bracquart, C., Asselin, P., & Cuisset, A. (2022). Millimeter-Wave Spectroscopy of Methylfuran Isomers: Local vs. Global Treatments of the Internal Rotation. Molecules, 27(11), 3591. https://doi.org/10.3390/molecules27113591








