The Relevance of Experimental Charge Density Analysis in Unraveling Noncovalent Interactions in Molecular Crystals
Abstract
:1. Introduction
2. Understanding Noncovalent Interactions in Terms of Descriptors from X-ray Charge Density Analysis
2.1. Halogen Bonds
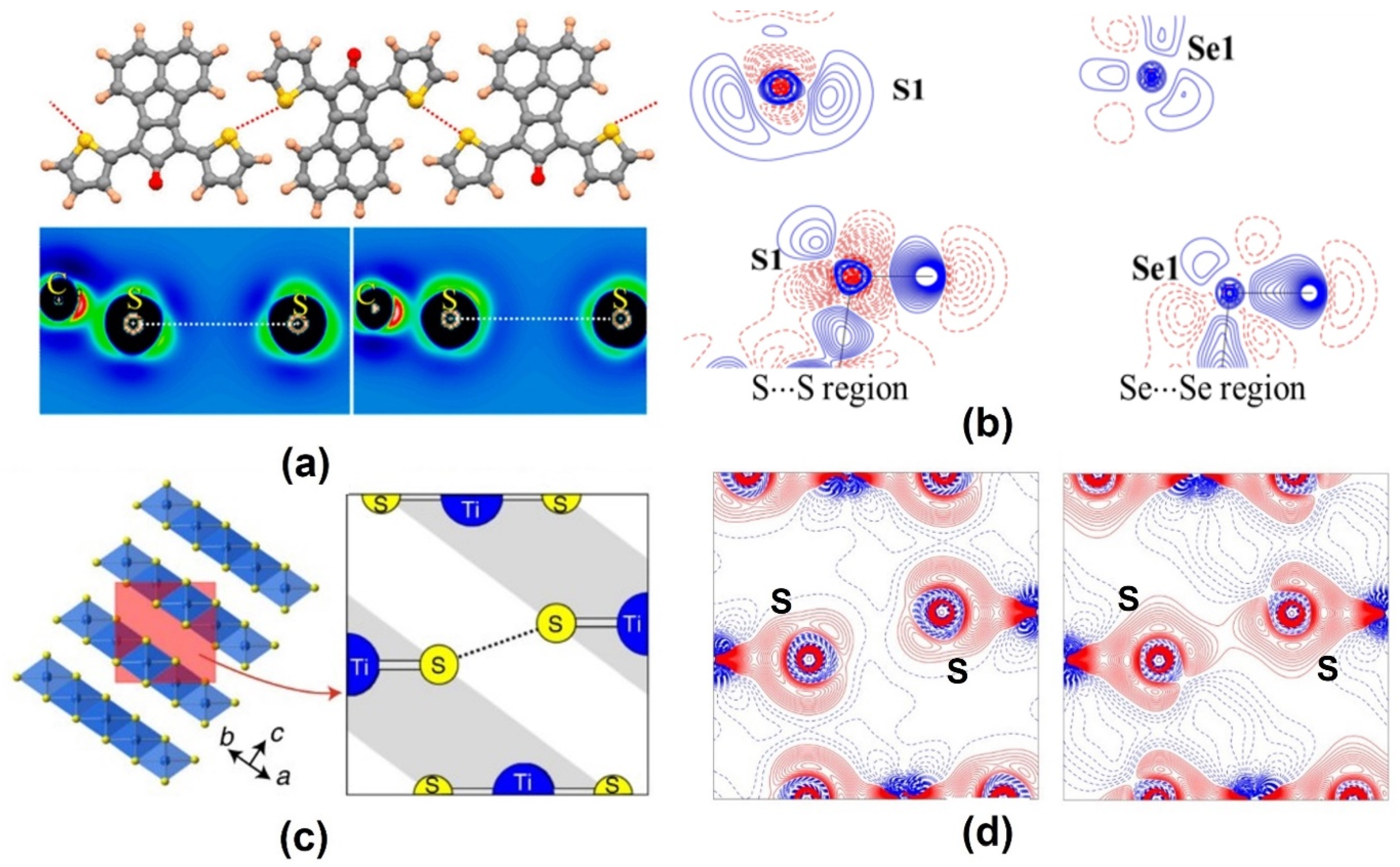
2.2. Chalcogen Bonds
| Interaction | Rij (Å) | ρ (e Å−3) | ∇2ρ (e Å−5) | V | |V|/G | Comment |
|---|---|---|---|---|---|---|
| Se∙∙∙O | 2.5331 | 0.251 | 2.452 | −84.7 | 1.12 | Thomas, Row et al. [48] |
| Se-C | 1.8842 | 1.03 | 0.50 | −661.0 | 1.96 | Thomas, Row et al. [48] |
| Se-N | 1.8987 | 0.94 | 3.20 | −592.7 | 1.74 | Thomas, Row et al. [48] |
| Se∙∙∙O | 3.355 | 0.049 | 0.62 | −9.7 | 0.73 | Espinosa et al. [51] |
| Se∙∙∙H | 2.974 | 0.05 | 0.51 | −8.9 | 0.78 | Espinosa et al. [51] |
| Se∙∙∙Se | 3.822 | 0.051 | 0.37 | −7.7 | 0.87 | Espinosa et al. [51] |
| S∙∙∙S | 3.227 | 0.092 | 0.76 | −18.6 | 0.95 | Owczarzak et al. [58] |
| S∙∙∙S | 3.365 | 0.083 | 0.34 | −13.0 | 1.17 | Owczarzak et al. [58] |
| S∙∙∙S | 3.459 | 0.072 | 0.65 | −13.7 | 0.87 | Owczarzak et al. [58] |
| S∙∙∙S | 3.443 | 0.086 | 0.691 | −16.7 | 0.94 | Iversen et al. [57] |
| S∙∙∙S | 3.6291 | 0.071 | 0.547 | −12.6 | 0.92 | Bai, Row et al. [55] |
| S∙∙∙S | 3.7927 | 0.042 | 0.376 | −6.6 | 0.78 | Bai, Row et al. [55] |
| S∙∙∙S | 3.5837 | 0.07 | 0.6 | −12.9 | 0.88 | Thomas, Row et al. [56] |
| Se∙∙∙Se | 3.7562 | 0.05 | 0.5 | −8.8 | 0.78 | Thomas, Row et al. [56] |
| S-H∙∙∙S | 3.1078 | 0.02 | 0.4 | −4.6 | 0.59 | Thomas, Row et al. [56] |
| Se-H∙∙∙Se | 3.0882 | 0.03 | 0.5 | −6.3 | 0.64 | Thomas, Row et al. [56] |
2.3. Carbon Bonding, Pnicogen Bonding, and Hydrophobic Interactions
2.4. π-Holes Interactions
3. Applications of Charge Density Analysis in Crystal Engineering and Pharmaceutical Sciences
3.1. Charge Density Studies of Pharmaceutical Compounds (APIs)
3.1.1. Insights on Polymorphism and Relative Stability of Polymorphs
3.1.2. Predicting Chemical Reactivity/Mechanism of Action of APIs
3.1.3. Applications in Formulation Development
3.1.4. Investigations on Exotic Non-Covalent Interactions in APIs
3.1.5. Salt vs. Cocrystal Nature
3.2. Charge Density Studies to Understand Protein-Ligand Interactions
4. Summary and Outlook
Funding
Conflicts of Interest
Abbreviations
| ADP | Anisotropic displacement parameter |
| AIM | Atoms in molecules |
| API | Active pharmaceutical ingredient |
| BCP | Bond critical point |
| CC | Charge concentration |
| CD | Charge depletion |
| CD | Charge density |
| CDMM | Charge density multipole modeling |
| CSD | Cambridge structural database |
| ED | Electron density |
| EDD | Electron density distribution |
| ELMO | Extremely localized molecular orbitals |
| ESP | Electrostatic potential |
| FTIR | Fourier transform infrared |
| HI | Hydrophobic interaction |
| HAR | Hirshfeld Atom Refinement |
| IUCr | International Union of Crystallography |
| IUPAC | International union of pure and applied chemistry |
| LUMO | Lowest unoccupied molecular orbital |
| MESP | Molecular electrostatic potential |
| NCI | Non-covalent interactions |
| NOESY | Nuclear overhauser effect spectroscopy |
| PDB | Protein data bank |
| QTAIM | Quantum theory of atoms in molecules |
| RCP | Ring critical points |
| VSCC | Valence shell charge concentration |
| XB | Halogen bond |
| XWR | X-ray wavefunction refinement |
References
- Coppens, P.; Sabine, T.M.; Delaplane, G.; Ibers, J.A. An experimental determination of the asphericity of the atomic charge distribution in oxalic acid dihydrate. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 2451–2458. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Electron Population Analysis of Accurate Diffraction Data.6. Testing Aspherical Atom Refinements on Small-Molecule Data Sets. Acta Crystallogr. Sect. A 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Stewart, R. Electron population analysis with rigid pseudoatoms. Acta Crystallogr. Sect. A 1976, 32, 565–574. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Can X-Ray Data Distinguish Bonding Effects from Vibrational Smearing. Acta Crystallogr. Sect. A 1976, 32, 239–244. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge-Densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Koritsanszky, T.S.; Coppens, P. Chemical Applications of X-ray Charge-Density Analysis. Chem. Rev. 2001, 101, 1583–1627. [Google Scholar] [CrossRef]
- Spackman, M.A. Molecular electric moments from x-ray diffraction data. Chem. Rev. 1992, 92, 1769–1797. [Google Scholar] [CrossRef]
- Van der Waals, J.D. Over de Continuited van den Gas-en Vloeistoftoestand. Ph.D. Thesis, University of Leiden, Leiden, The Netherlands, 1873. [Google Scholar]
- Desiraju, G.R. Crystal Engineering: From Molecule to Crystal. J. Am. Chem. Soc. 2013, 135, 9952–9967. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules—A Quantum Theory; Oxford University Press: Oxford, UK, 1990; Volume 22, p. 438. [Google Scholar]
- Koritsanszky, T.; Macchi, P.; Gatti, C.; Farrugia, L.; Mallinson, P.; Volkov, A.; Richter, T. XD2016-a Computer Program Package for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental and Theoretical Structure Factors. 2016. Available online: https://www.chem.gla.ac.uk/~louis/xd-home/avail.html (accessed on 12 April 2022).
- Guillot, B.; Viry, L.; Guillot, R.; Lecomte, C.; Jelsch, C. Refinement of proteins at subatomic resolution with MOPRO. J. Appl.Crystallogr. 2001, 34, 214–223. [Google Scholar] [CrossRef]
- Meindl, K.; Henn, J. Foundations of residual-density analysis. Acta Crystallogr. Sect. A 2008, 64, 404–418. [Google Scholar] [CrossRef]
- Henn, J.; Meindl, K. Statistical tests against systematic errors in data sets based on the equality of residual means and variances from control samples: Theory and applications. Acta Crystallogr. Sect. A 2015, 71, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Nyburg, S.C. ‘Polar flattening’: Non-spherical effective shapes of atoms in crystals. Acta Crystallogr. Sect. A 1979, 35, 641–645. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other sigma-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Hassel, O.; Hvoslef, J. The Structure of Bromine 1,4-Dioxanate. Acta Chem. Scand. 1954, 8, 873. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R.; Murray-Rust, P. Angular preferences of intermolecular forces around halogen centers: Preferred directions of approach of electrophiles and nucleophiles around carbon-halogen bond. J. Am. Chem. Soc. 1986, 108, 4308. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Parthasarathy, R. The nature of halogen.cntdot..cntdot..cntdot.halogen interactions: Are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms? J. Am. Chem. Soc. 1989, 111, 8725. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Row, T.N.G. Nature of Cl...Cl Intermolecular Interactions via Experimental and Theoretical Charge Density Analysis: Correlation of Polar Flattening Effects with Geometry. J. Phys. Chem. A 2010, 114, 13434–13441. [Google Scholar] [CrossRef]
- Stevens, E.D. Experimental electron density distribution of molecular chlorine. Mol. Phys. 1979, 37, 27–45. [Google Scholar] [CrossRef]
- Tsirelson, V.G.; Zou, P.F.; Tang, T.H.; Bader, R.F.W. Topological Definition of Crystal-Structure - Determination of the Bonded Interactions in Solid Molecular Chlorine. Acta Crystallogr. Sect. A 1995, 51, 143–153. [Google Scholar] [CrossRef]
- Bui, T.T.T.; Dahaoui, S.; Lecomte, C.; Desiraju, G.R.; Espinosa, E. The Nature of Halogen...Halogen Interactions: A Model Derived from Experimental Charge-Density Analysis. Angew. Chem. Int. Ed. 2009, 48, 3838–3841. [Google Scholar] [CrossRef]
- Chopra, D.; Row, T.N.G. Role of Organic Fluorine in Crystal Engineering. Crystengcomm 2011, 13, 2175–2186. [Google Scholar] [CrossRef]
- Pavan, M.S.; Prasad, K.D.; Row, T.N.G. Halogen Bonding in Fluorine: Experimental Charge Density Study on Intermolecular F...F and F...S Donor-Acceptor Contacts. Chem. Commun. 2013, 49, 7558–7560. [Google Scholar] [CrossRef] [PubMed]
- Hathwar, V.R.; Chopra, D.; Panini, P.; Row, T.N.G. Revealing the Polarizability of Organic Fluorine in the Trifluoromethyl Group: Implications in Supramolecular Chemistry. Cryst. Growth Des. 2014, 14, 5366–5369. [Google Scholar] [CrossRef]
- Dey, D.; Bhandary, S.; Sirohiwal, A.; Hathwar, V.R.; Chopra, D. “Conformational Lock” via Unusual Intramolecular C-F...O=C and C-H...Cl-C Parallel Dipoles Observed in In Situ Cryocrystallized Liquids. Chem. Commun. 2016, 52, 7225–7228. [Google Scholar] [CrossRef]
- Dikundwar, A.G.; Row, T.N.G. Evidence for the “Amphoteric” Nature of Fluorine in Halogen Bonds: An Instance of Cl···F Contact. Cryst. Growth Des. 2012, 12, 1713–1716. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Row, T.N.G. Charge Density Analysis of Heterohalogen (Cl...F) and Homohalogen (F...F) Intermolecular Interactions. Cryst. Growth Des. 2011, 11, 1338–1346. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Gonnade, R.G.; Munshi, P.; Bhadbhade, M.M.; Row, T.N.G. Halogen Bonding in 2,5-Dichloro-1,4-benzoquinone: Insights from Experimental and Theoretical Charge Density Analysis. Cryst. Growth Des. 2011, 11, 1855–1862. [Google Scholar] [CrossRef]
- Pavan, M.S.; Jana, A.K.; Natarajan, S.; Guru Row, T.N. Halogen Bonding and Chalcogen Bonding in 4,7-Dibromo-5,6-dinitro-2,1,3-benzothiadiazole. J. Phys. Chem. B 2015, 119, 11382–11390. [Google Scholar] [CrossRef] [PubMed]
- Pavan, M.S.; Guru Row, T.N. Analysis of an unusual hetero-halogen bonded trimer using charge density analysis: A case of concerted type I Br⋯Br and type II Br⋯Cl interactions. J. Chem. Sci. 2016, 128, 1579–1587. [Google Scholar] [CrossRef]
- Sarkar, S.; Row, T.N.G. A heuristic approach to evaluate peri interactions versus intermolecular interactions in an overcrowded naphthalene. IUCrJ 2017, 4, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, T.; Pavan, M.S.; Guru Row, T.N. Do halogen bonds dictate the packing preferences in solid solutions? Faraday Discuss. 2017, 203, 201–212. [Google Scholar] [CrossRef]
- Chopra, D.; Cameron, T.S.; Ferrara, J.D.; Row, T.N.G. Pointers Toward the Occurrence of C-F...F-C Interaction: Experimental Charge Density Analysis of 1-(4-Fluorophenyl)-3,6,6-Trimethyl-2-phenyl-1,5,6,7-Tetrahydro-4H-indol-4-one and 1-(4-Fluorophenyl)-6-Methoxy-2-phenyl-1,2,3,4-Tetrahydroisoquinoline. J. Phys. Chem A 2006, 110, 10465–10477. [Google Scholar] [CrossRef]
- Eraković, M.; Cinčić, D.; Molčanov, K.; Stilinović, V. A Crystallographic Charge Density Study of the Partial Covalent Nature of Strong N⋅⋅⋅Br Halogen Bonds. Angew. Chem. Int. Ed. 2019, 58, 15702–15706. [Google Scholar] [CrossRef]
- Wang, R.; Hartnick, D.; Englert, U. Short is strong: Experimental electron density in a very short N···I halogen bond. Z. Kristallogr. Cryst. Mater. 2018, 233, 733–744. [Google Scholar] [CrossRef]
- Wang, R.; Dols, T.S.; Lehmann, C.W.; Englert, U. The halogen bond made visible: Experimental charge density of a very short intermolecular Cl⋯Cl donor–acceptor contact. Chem. Commun. 2012, 48, 6830–6832. [Google Scholar] [CrossRef]
- Bianchi, R.; Forni, A.; Pilati, T. The experimental electron density distribution in the complex of (E)-1,2-bis(4-pyridyl) ethylene with 1,4-diiodotetrafluorobenzene at 90 K. Chem. Eur. J. 2003, 9, 1631–1638. [Google Scholar] [CrossRef]
- Bianchi, R.; Forni, A.; Pilati, T. Experimental electron density study of the supramolecular aggregation between 4,4 ′-dipyridyl-N,N ′-dioxide and 1,4-diiodotetrafluorobenzene at 90 K. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 2004, 60, 559–568. [Google Scholar] [CrossRef]
- Wang, R.; Kalf, I.; Englert, U. Insight into trifluoromethylation – experimental electron density for Togni reagent I. RSC Adv. 2018, 8, 34287–34290. [Google Scholar] [CrossRef] [PubMed]
- Nelyubina, Y.V.; Antipin, M.Y.; Dunin, D.S.; Kotov, V.Y.; Lyssenko, K.A. Unexpected "amphoteric" character of the halogen bond: The charge density study of the co-crystal of N-methylpyrazine iodide with I-2. Chem. Commun. 2010, 46, 5325–5327. [Google Scholar] [CrossRef] [PubMed]
- Shukla, R.; Claiser, N.; Souhassou, M.; Lecomte, C.; Balkrishna, S.J.; Kumar, S.; Chopra, D. Exploring the simultaneous [σ]-hole/[π]-hole bonding characteristics of a Br...[π] interaction in an ebselen derivative via experimental and theoretical electron-density analysis. IUCrJ 2018, 5, 647–653. [Google Scholar] [CrossRef] [PubMed]
- Aubert, E.; Espinosa, E.; Nicolas, I.; Jeannin, O.; Fourmigué, M. Toward a reverse hierarchy of halogen bonding between bromine and iodine. Faraday Discuss. 2017, 203, 389–406. [Google Scholar] [CrossRef]
- Thomas, S.P.; Satheeshkumar, K.; Mugesh, G.; Row, T.N.G. Unusually Short Chalcogen Bonds Involving Organoselenium: Insights into the Se-N Bond Cleavage Mechanism of the Antioxidant Ebselen and Analogues. Chem. Eur. J. 2015, 21, 6793–6800. [Google Scholar] [CrossRef]
- Otte, F.; Kleinheider, J.; Hiller, W.; Wang, R.; Englert, U.; Strohmann, C. Weak yet Decisive: Molecular Halogen Bond and Competing Weak Interactions of Iodobenzene and Quinuclidine. J. Am. Chem. Soc. 2021, 143, 4133–4137. [Google Scholar] [CrossRef]
- Thomas, S.P.; Kumar, V.; Alhameedi, K.; Guru Row, T.N. Non-Classical Synthons: Supramolecular Recognition by S⋅⋅⋅O Chalcogen Bonding in Molecular Complexes of Riluzole. Chem. Eur. J. 2019, 25, 3591–3597. [Google Scholar] [CrossRef]
- Brezgunova, M.E.; Lieffrig, J.; Aubert, E.; Dahaoui, S.; Fertey, P.; Lebegue, S.; Angyan, J.G.; Fourmigue, M.; Espinosa, E. Chalcogen Bonding: Experimental and Theoretical Determinations from Electron Density Analysis. Geometrical Preferences Driven by Electrophilic-Nucleophilic Interactions. Cryst. Growth Des. 2013, 13, 3283–3289. [Google Scholar] [CrossRef]
- Domagała, M.; Lutyńska, A.; Palusiak, M. Extremely Strong Halogen Bond. The Case of a Double-Charge-Assisted Halogen Bridge. J. Phys. Chem. A 2018, 122, 5484–5492. [Google Scholar] [CrossRef]
- Kuznetsov, M.L. Strength of the [Z–I···Hal]− and [Z–Hal···I]− Halogen Bonds: Electron Density Properties and Halogen Bond Length as Estimators of Interaction Energy. Molecules 2021, 26, 2083. [Google Scholar] [CrossRef]
- Thomas, S.P.; Guru Row, T.N. Observation of a conserved ’selenium bond synthon’ involving Se...O interaction. Acta Crystallogr. Sect. A 2011, 67, C448. [Google Scholar] [CrossRef]
- Bai, M.; Thomas, S.P.; Kottokkaran, R.; Nayak, S.K.; Ramamurthy, P.C.; Guru Row, T.N. A Donor–Acceptor–Donor Structured Organic Conductor with S···S Chalcogen Bonding. Cryst. Growth Des. 2014, 14, 459–466. [Google Scholar] [CrossRef]
- Thomas, S.P.; Sathishkumar, R.; Guru Row, T.N. Organic alloys of room temperature liquids thiophenol and selenophenol. Chem. Commun. 2015, 51, 14255–14258. [Google Scholar] [CrossRef] [PubMed]
- Kasai, H.; Tolborg, K.; Sist, M.; Zhang, J.; Hathwar, V.R.; Filsø, M.Ø.; Cenedese, S.; Sugimoto, K.; Overgaard, J.; Nishibori, E.; et al. X-ray electron density investigation of chemical bonding in van der Waals materials. Nat. Mater. 2018, 17, 249–252. [Google Scholar] [CrossRef]
- Owczarzak, A.; Dutkiewicz, Z.; Kurczab, R.; Pietruś, W.; Kubicki, M.; Grześkiewicz, A.M. Role of Staple Molecules in the Formation of S···S Contact in Thioamides: Experimental Charge Density and Theoretical Studies. Cryst. Growth Des. 2019, 19, 7324–7335. [Google Scholar] [CrossRef]
- Thomas, S.P.; Jayatilaka, D.; Row, T.N.G. S...O Chalcogen Bonding in Sulfa Drugs: Insights from Multipole Charge Density and X-ray Wavefunction of acetazolamide. Phys. Chem. Chem. Phys. 2015, 17, 25411–25420. [Google Scholar] [CrossRef]
- Thomas, S.P.; Veccham, S.P.K.P.; Farrugia, L.J.; Row, T.N.G. "Conformational Simulation" of Sulfamethizole by Molecular Complexation and Insights from Charge Density Analysis: Role of Intramolecular S...O Chalcogen Bonding. Cryst. Growth Des. 2015, 15, 2110–2118. [Google Scholar] [CrossRef]
- Sovago, I.; Gutmann, M.J.; Hill, J.G.; Senn, H.M.; Thomas, L.H.; Wilson, C.C.; Farrugia, L.J. Experimental Electron Density and Neutron Diffraction Studies on the Polymorphs of Sulfathiazole. Cryst. Growth Des. 2014, 14, 1227–1239. [Google Scholar] [CrossRef]
- Menon, P.K.; Krishnaraj, K.U.; Anabha, E.R.; Devaky, K.S.; Thomas, S.P. Synthesis, crystal structure and electron density analysis of a sulfanyl 2-pyridone analogue: Tautomeric preference and conformation locking by S···O chalcogen bonding. J. Mol. Struct. 2020, 1222, 128798. [Google Scholar] [CrossRef]
- Sarkar, S.; Pavan, M.S.; Cherukuvada, S.; Guru Row, T.N. Acetazolamide polymorphism: A case of hybridization induced polymorphism? Chem. Commun. 2016, 52, 5820–5823. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. The X-C...Y (X = O/F, Y = O/S/F/Cl/Br/N/P) ’carbon bond’ and hydrophobic interactions. Phys. Chem. Chem. Phys. 2013, 15, 14377–14383. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Pavan, M.S.; Row, T.G. Experimental evidence for ‘carbon bonding’in the solid state from charge density analysis. Chem. Commun. 2014, 50, 49–51. [Google Scholar] [CrossRef] [PubMed]
- Heywood, V.L.; Alford, T.P.J.; Roeleveld, J.J.; Lekanne Deprez, S.J.; Verhoofstad, A.; van der Vlugt, J.I.; Domingos, S.R.; Schnell, M.; Davis, A.P.; Mooibroek, T.J. Observations of tetrel bonding between sp3-carbon and THF. Chem. Sci. 2020, 11, 5289–5293. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A. Tetrel Bonding Interactions Involving Carbon at Work: Recent Advances in Crystal Engineering and Catalysis. C 2020, 6, 60. [Google Scholar] [CrossRef]
- Mundlapati, V.R.; Sahoo, D.K.; Bhaumik, S.; Jena, S.; Chandrakar, A.; Biswal, H.S. Noncovalent Carbon-Bonding Interactions in Proteins. Angew. Chem. Int. Ed. 2018, 57, 16496–16500. [Google Scholar] [CrossRef]
- Sarkar, S.; Pavan, M.S.; Guru Row, T.N. Experimental validation of ’pnicogen bonding’ in nitrogen by charge density analysis. Phys. Chem. Chem. Phys. 2015, 17, 2330–2334. [Google Scholar] [CrossRef]
- Bauer, S.; Tschirschwitz, S.; Lönnecke, P.; Frank, R.; Kirchner, B.; Clarke, M.L.; Hey-Hawkins, E. Enantiomerically Pure Bis(phosphanyl)carbaborane(12) Compounds. Eur. J. Inorg. Chem. 2009, 2009, 2776–2788. [Google Scholar] [CrossRef]
- Zahn, S.; Frank, R.; Hey-Hawkins, E.; Kirchner, B. Pnicogen bonds: A new molecular linker? Chem. Eur. J. 2011, 17, 6034–6038. [Google Scholar] [CrossRef]
- Scheiner, S. The pnicogen bond: Its relation to hydrogen, halogen, and other noncovalent bonds. Acc. Chem. Res. 2012, 46, 280–288. [Google Scholar] [CrossRef]
- Li, Q.; Zhuo, H.; Yang, X.; Cheng, J.; Li, W.; Loffredo, R.E. Cooperative and Diminutive Effects of Pnicogen Bonds and Cation–π Interactions. ChemPhysChem 2014, 15, 500–506. [Google Scholar] [CrossRef]
- Li, Q.-Z.; Li, R.; Liu, X.-F.; Li, W.-Z.; Cheng, J.-B. Pnicogen–Hydride Interaction between FH2X (X = P and As) and HM (M = ZnH, BeH, MgH, Li, and Na). J. Phys. Chem. A 2012, 116, 2547–2553. [Google Scholar] [CrossRef] [PubMed]
- Moaven, S.; Andrews, M.C.; Polaske, T.J.; Karl, B.M.; Unruh, D.K.; Bosch, E.; Bowling, N.P.; Cozzolino, A.F. Triple-Pnictogen Bonding as a Tool for Supramolecular Assembly. Inorg. Chem. 2019, 58, 16227–16235. [Google Scholar] [CrossRef] [PubMed]
- Moaven, S.; Watson, B.T.; Polaske, T.J.; Karl, B.M.; Unruh, D.K.; Bowling, N.P.; Cozzolino, A.F. Self-Assembly of Complementary Components Using a Tripodal Bismuth Compound: Pnictogen Bonding or Coordination Chemistry? Inorg. Chem. 2021, 60, 11242–11250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wei, J.; Ding, W.-Y.; Li, S.; Xiang, S.-H.; Tan, B. Asymmetric Pnictogen-Bonding Catalysis: Transfer Hydrogenation by a Chiral Antimony(V) Cation/Anion Pair. J. Am. Chem. Soc. 2021, 143, 6382–6387. [Google Scholar] [CrossRef]
- Sarkar, S.; Thomas, S.P.; Potnuru, L.R.; Edwards, A.J.; Grosjean, A.; Ramanathan, K.V.; Guru Row, T.N. Experimental Insights into the Electronic Nature, Spectral Features, and Role of Entropy in Short CH3···CH3 Hydrophobic Interactions. J. Phys. Chem. Lett. 2019, 10, 7224–7229. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Korlyukov, A.A.; Lyssenko, K.A. Experimental Charge Density Evidence for Pnicogen Bonding in a Crystal of Ammonium Chloride. ChemPhysChem 2015, 16, 676–681. [Google Scholar] [CrossRef]
- Sjoberg, P.; Politzer, P. Use of the electrostatic potential at the molecular surface to interpret and predict nucleophilic processes. J. Phys. Chem. 1990, 94, 3959–3961. [Google Scholar] [CrossRef]
- Meyer, E.E.; Rosenberg, K.J.; Israelachvili, J. Recent progress in understanding hydrophobic interactions. Proc. Natl. Acad. Sci. USA 2006, 103, 15739–15746. [Google Scholar] [CrossRef]
- Davis, A.M.; Teague, S.J. Hydrogen Bonding, Hydrophobic Interactions, and Failure of the Rigid Receptor Hypothesis. Angew. Chem. Int. Ed. 1999, 38, 736–749. [Google Scholar] [CrossRef]
- Maibaum, L.; Dinner, A.R.; Chandler, D. Micelle Formation and the Hydrophobic Effect. J. Phys. Chem. B 2004, 108, 6778–6781. [Google Scholar] [CrossRef]
- Fang, N.; Chan, V.; Mao, H.-Q.; Leong, K.W. Interactions of Phospholipid Bilayer with Chitosan: Effect of Molecular Weight and pH. Biomacromolecules 2001, 2, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Shi, M.W.; Koutsantonis, G.A.; Jayatilaka, D.; Edwards, A.J.; Spackman, M.A. The Elusive Structural Origin of Plastic Bending in Dimethyl Sulfone Crystals with Quasi-isotropic Crystal Packing. Angew. Chem. Int. Ed. 2017, 56, 8468–8472. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, W.; Jin, W.J. σ-Hole Bond vs π-Hole Bond: A Comparison Based on Halogen Bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef] [PubMed]
- Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Zeitschrift für Physik 1921, 5, 17–26. [Google Scholar] [CrossRef]
- Hibbs, D.E.; Austin-Woods, C.J.; Platts, J.A.; Overgaard, J.; Turner, P. Experimental and theoretical charge density study of the neurotransmitter taurine. Chem. Eur. J. 2003, 9, 1075–1084. [Google Scholar] [CrossRef] [PubMed]
- Pal, R.; Nagendra, G.; Samarasimhareddy, M.; Sureshbabu, V.V.; Guru Row, T.N. Observation of a reversible isomorphous phase transition and an interplay of “σ-holes” and “π-holes” in Fmoc-Leu-ψ[CH2-NCS]. Chem. Commun. 2015, 51, 933–936. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Thakur, T.S.; Dubey, R.; Pavan, M.S.; Row, T.N.G.; Desiraju, G.R. Extending the Supramolecular Synthon Based Fragment Approach (SBFA) for Transferability of Multipole Charge Density Parameters to Monofluorobenzoic Acids and their Cocrystals with Isonicotinamide: Importance of C-H...O, C-H...F, and F...F Intermolecular Regions. J. Phys. Chem. A 2011, 115, 12852–12863. [Google Scholar] [CrossRef]
- Munshi, P.; Row, T.N.G. Exploring the Lower Limit in Hydrogen Bonds: Analysis of Weak C-H...O and C-H...π Interactions in Substituted Coumarins from Charge Density Analysis. J. Phys. Chem A 2005, 109, 659–672. [Google Scholar] [CrossRef]
- Thomas, S.P.; Pavan, M.S.; Guru Row, T.N. Charge Density Analysis of Ferulic Acid: Robustness of a Trifurcated C–H···O Hydrogen Bond. Cryst. Growth Des. 2012, 12, 6083–6091. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Glukhov, I.V.; Antipin, M.Y.; Lyssenko, K.A. "Higher density does not mean higher stability" mystery of paracetamol finally unraveled. Chem. Commun. 2010, 46, 3469–3471. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Spackman, M.A. How Reliable Are Intermolecular Interaction Energies Estimated from Topological Analysis of Experimental Electron Densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
- Krawczuk, A.; Macchi, P. Charge Density Analysis for Crystal Engineering. Chem. Cent. J. 2014, 8, 68. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, B.; Matta, C.F. Contributions of Charge-Density Research to Medicinal Chemistry. IUCrJ 2014, 1, 457–469. [Google Scholar] [CrossRef] [PubMed]
- Soave, R.; Barzaghi, M.; Destro, R. Progress in the Evaluation of Intermolecular Interaction Energies from X-ray Diffraction Data. Available online: https://www.academia.edu/17563845/PROGRESS_IN_THE_EVALUATION_OF_INTERMOLECULAR_INTERACTION_ENERGIES_FROM_X_RAY_DIFFRACTION_DATA2008 (accessed on 12 April 2022).
- Soave, R.; Barzaghi, M.; Destro, R. Progress in the Understanding of Drug–Receptor Interactions, Part 2: Experimental and Theoretical Electrostatic Moments and Interaction Energies of an Angiotensin II Receptor Antagonist (C30H30N6O3S). Chem. Eur. J. 2007, 13, 6942–6956. [Google Scholar] [CrossRef]
- Rajalakshmi, G.; Hathwar, V.R.; Kumaradhas, P. Topological Analysis of Electron Density and the Electrostatic Properties of Isoniazid: An Experimental and Theoretical Study. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 2014, 70, 331–341. [Google Scholar] [CrossRef]
- Wagner, A.; Flaig, R.; Dittrich, B.; Schmidt, H.; Koritsánszky, T.; Luger, P. Charge density and experimental electrostatic potentials of two penicillin derivatives. Chem. Eur. J. 2004, 10, 2977–2982. [Google Scholar] [CrossRef]
- Zhurova, E.A.; Zhurov, V.V.; Chopra, D.; Stash, A.I.; Pinkerton, A.A. 17α-estradiol· 1/2 H2O: Super-structural ordering, electronic properties, chemical bonding, and biological activity in comparison with other estrogens. J. Am. Chem. Soc. 2009, 131, 17260–17269. [Google Scholar] [CrossRef]
- Grabowsky, S.; Pfeuffer, T.; Morgenroth, W.; Paulmann, C.; Schirmeister, T.; Luger, P. A comparative study on the experimentally derived electron densities of three protease inhibitor model compounds. Org. Biomol. Chem. 2008, 6, 2295–2307. [Google Scholar] [CrossRef]
- Kirby, I.L.; Brightwell, M.; Pitak, M.B.; Wilson, C.; Coles, S.J.; Gale, P.A. Systematic experimental charge density analysis of anion receptor complexes. Phys. Chem. Chem. Phys. 2014, 16, 10943–10958. [Google Scholar] [CrossRef] [PubMed]
- Overgaard, J.; Hibbs, D.E. The experimental electron density in polymorphs A and B of the anti-ulcer drug famotidine. Acta Crystallogr. Sect. A 2004, 60, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Ghermani, N.E.; Spasojević-de Biré, A.; Bouhmaida, N.; Ouharzoune, S.; Bouligand, J.; Layre, A.; Gref, R.; Couvreur, P. Molecular reactivity of busulfan through its experimental electrostatic properties in the solid state. Pharm. Res. 2004, 21, 598–607. [Google Scholar] [CrossRef] [PubMed]
- Zhurova, E.A.; Matta, C.F.; Wu, N.; Zhurov, V.V.; Pinkerton, A.A. Experimental and theoretical electron density study of estrone. J. Am. Chem. Soc. 2006, 128, 8849–8861. [Google Scholar] [CrossRef] [PubMed]
- Yearley, E.J.; Zhurova, E.A.; Zhurov, V.V.; Pinkerton, A.A. Binding of genistein to the estrogen receptor based on an experimental electron density study. J. Am. Chem. Soc. 2007, 129, 15013–15021. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Pal, R.; Row, T.N.G. Charge Density Analysis of Crystals of Nicotinamide with Salicylic Acid and Oxalic Acid: An Insight into the Salt to Cocrystal Continuum. Cryst. Growth Des. 2010, 10, 3306–3310. [Google Scholar] [CrossRef]
- Domagała, S.; Fournier, B.; Liebschner, D.; Guillot, B.; Jelsch, C. An improved experimental databank of transferable multipolar atom models–ELMAM2. Construction details and applications. Acta Crystallogr. Sect. A 2012, 68, 337–351. [Google Scholar] [CrossRef]
- Jarzembska, K.N.; Dominiak, P.M. New version of the theoretical databank of transferable aspherical pseudoatoms, UBDB2011–towards nucleic acid modelling. Acta Crystallogr. Sect. A 2012, 68, 139–147. [Google Scholar] [CrossRef]
- Dittrich, B.; Hübschle, C.B.; Pröpper, K.; Dietrich, F.; Stolper, T.; Holstein, J. The generalized invariom database (GID). Acta Crystallogr. Sect. B Struct. Sci. Crystal Eng. Mater. 2013, 69, 91–104. [Google Scholar] [CrossRef]
- Dominiak, P.; Espinosa, E.; Angyán, J.G. Modern Charge-Density Analysis; Gatti, C., Macchi, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Guillot, B.; Jelsch, C.; Podjarny, A.; Lecomte, C. Charge-density analysis of a protein structure at subatomic resolution: The human aldose reductase case. Acta Crystallogr. Sect. D Biol. Crystallogr. 2008, 64, 567–588. [Google Scholar] [CrossRef]
- Lichtenthaler, F.W. 100 years “Schlüssel-Schloss-Prinzip”: What made Emil Fischer use this analogy? Angew. Chem. Int. Ed. 1995, 33, 2364–2374. [Google Scholar] [CrossRef]
- Muzet, N.; Guillot, B.; Jelsch, C.; Howard, E.; Lecomte, C. Electrostatic complementarity in an aldose reductase complex from ultra-high-resolution crystallography and first-principles calculations. Proc. Natl. Acad. Sci. USA 2003, 100, 8742–8747. [Google Scholar] [CrossRef] [PubMed]
- Dominiak, P.M.; Volkov, A.; Dominiak, A.P.; Jarzembska, K.N.; Coppens, P. Combining crystallographic information and an aspherical-atom data bank in the evaluation of the electrostatic interaction energy in an enzyme–substrate complex: Influenza neuraminidase inhibition. Acta Crystallogr. Sect. D Biol. Crystallogr. 2009, 65, 485–499. [Google Scholar] [CrossRef] [PubMed]
- Malińska, M.; Jarzembska, K.N.; Goral, A.M.; Kutner, A.; Woźniak, K.; Dominiak, P.M. Sunitinib: From charge-density studies to interaction with proteins. Acta Crystallogr. Sect. D Biol. Crystallogr. 2014, 70, 1257–1270. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, B.; Bond, C.S.; Kalinowski, R.; Spackman, M.A.; Jayatilaka, D. Revised electrostatics from invariom refinement of the 18-residue peptaibol antibiotic trichotoxin A50E. Crystengcomm 2010, 12, 2419–2423. [Google Scholar] [CrossRef]
- Pröpper, K.; Holstein, J.J.; Hübschle, C.B.; Bond, C.S.; Dittrich, B. Invariom refinement of a new monoclinic solvate of thiostrepton at 0.64 Å resolution. Acta Crystallogr. Sect. D Biol. Crystallogr. 2013, 69, 1530–1539. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.; Lamzin, V.S. Veni, vidi, vici—atomic resolution unravelling the mysteries of protein function. Curr. Opin. Struct. Biol. 2002, 12, 698–703. [Google Scholar] [CrossRef]
- Vrielink, A.; Sampson, N. Sub-Ångstrom resolution enzyme X-ray structures: Is seeing believing? Curr. Opin. Struct. Biol. 2003, 13, 709–715. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
- Scheiner, S. Understanding noncovalent bonds and their controlling forces. J. Chem. Phys. 2020, 153, 140901. [Google Scholar] [CrossRef]


















| Interaction Geometry | Rij (Å) | θ1/θ2 (°) | ρBCP eÅ−3 | ∇2ρBCP eÅ−5 | ε | G(rBCP) (kJ mol−1 bohr−3) | V(rBCP) (kJ mol−1 bohr−3) | H(rBCP) (kJ mol−1 bohr−3) | |
|---|---|---|---|---|---|---|---|---|---|
| Cl1∙∙∙Cl1 (cis) | 3.3172(1) | 158.7/158.7 | 0.05 0.06 | 0.66 0.72 | 0.02 0.03 | 13.5 15.4 | −9.2 −11.2 | 4.3 4.2 | 0.68 0.73 |
| Cl1∙∙∙Cl1 (trans) | 3.5747(2) | 150.6/150.6 | 0.03 0.04 | 0.41 0.44 | 0.11 0.11 | 7.8 9.1 | −4.9 −6.1 | 2.9 3.0 | 0.62 0.67 |
| Cl1∙∙∙Cl1 (L) | 3.4668(2) | 168.3/103.6 | 0.03 0.05 | 0.47 0.57 | 0.03 0.07 | 9.0 11.8 | −5.6 −7.9 | 3.4 3.9 | 0.63 0.68 |
| Interaction | Rij (Å) | ρ (e Å−3) | ∇2ρ (e Å−5) | V | |V|/G | Comment |
|---|---|---|---|---|---|---|
| Cl∙∙∙Cl | 3.3172(1) | 0.05 | 0.66 | −10.2 | 0.73 | Hathwar et al. [23] |
| Cl∙∙∙Cl | 3.5747(2) | 0.03 | 0.41 | −5.5 | 0.66 | Hathwar et al. [23] |
| Cl∙∙∙Cl | 3.4668(2) | 0.03 | 0.47 | −6.1 | 0.64 | Hathwar et al. [23] |
| Cl∙∙∙Cl | 3.4343 | 0.06 | 0.6 | −11.2 | 0.81 | Bui et al. [26] |
| Cl∙∙∙Cl | 3.4618 | 0.05 | 0.6 | −9.7 | 0.74 | Bui et al. [26] |
| Cl∙∙∙Cl | 3.6129 | 0.04 | 0.5 | −7.5 | 0.71 | Bui et al. [26] |
| Cl∙∙∙F | 3.0207(2) | 0.05 | 0.84 | −11.9 | 0.68 | Hathwar et al. [32] |
| F∙∙∙F | 2.8187(1) | 0.04 | 0.82 | −10.4 | 0.63 | Hathwar et al. [32] |
| Cl∙∙∙O | 3.0562(3) | 0.05 | 0.80 | −11.5 | 0.69 | Hathwar et al. [33] |
| Br∙∙∙O | 2.922 | 0.11 | 1.33 | −27.9 | 0.87 | Pavan et al. [34] |
| Br∙∙∙Br | 3.6673 | 0.06 | 0.54 | −10.6 | 0.84 | Pavan et al. [35] |
| Br∙∙∙Cl | 3.7327 | 0.04 | 0.40 | −6.6 | 0.75 | Pavan et al. [35] |
| Br∙∙∙Cl | 3.6133 | 0.05 | 0.51 | −8.9 | 0.78 | Pavan et al. [35] |
| Cl∙∙∙Cl | 2.9941 | 0.12 | 1.51 | −32.0 | 0.87 | Sarkar et al. [36] |
| Br∙∙∙Br | 3.6673 | 0.05 | 0.46 | −8.4 | 0.80 | Pramanik et al. [37] |
| Br∙∙∙Cl | 3.7327 | 0.04 | 0.43 | −6.8 | 0.74 | Pramanik et al. [37] |
| Br∙∙∙Cl | 3.313 | 0.08 | 0.82 | −16.7 | 0.86 | Pramanik et al. [37] |
| Br∙∙∙Br | 3.2324 | 0.06 | 0.67 | −11.8 | 0.79 | Pavan et al. [34] |
| Br∙∙∙Br | 3.7098 | 0.04 | 0.51 | −7.6 | 0.70 | Pavan et al. [34] |
| F∙∙∙F | 2.6627 | 0.06 | 1.3 | −17.6 | 0.66 | Pavan et al. [34] |
| F∙∙∙F | 2.824 | 0.04 | 0.9 | −11.1 | 0.62 | Pavan et al. [34] |
| F∙∙∙F | 2.8091 | 0.05 | 1.03 | −13.6 | 0.65 | Chopra et al. [38] |
| F∙∙∙F | 2.569 | 0.07 | 0.93 | −15.9 | 0.77 | Chopra et al. [38] |
| Br∙∙∙O | 2.7575 | 0.135 | 1.87 | −39.2 | 0.87 | Erakovic et al. [39] |
| Br∙∙∙N | 2.3194(4) | 0.379 | 3.63 | −157.0 | 1.23 | Erakovic et al. [39] |
| N∙∙∙I | 2.6625 | 0.36 | 1.95 | −131.6 | 1.42 | Wang et al. [40] |
| Cl∙∙∙Cl | 3.1912(6) | 0.11 | 1.102 | −25.8 | 0.92 | Wang et al. [41] |
| I∙∙∙N | 2.7804 | 0.24 | 1.96 | −75.7 | 1.17 | Bianchi et al. [42] |
| I∙∙∙O | 2.7523 | 0.20 | 2.04 | −61.3 | 1.05 | Bianchi et al. [43] |
| I∙∙∙O | 2.9824 | 0.10 | 1.307 | −25.3 | 0.83 | Wang et al. [44] |
| I∙∙∙I | 2.789 | 0.40 | 2.02 | −154.0 | 1.47 | Nelyubina et al. [45] |
| Molecule | Rij for S∙∙∙O(Å) | ρ(eÅ−3) | ∇2ρ (eÅ−5) | |V|/G | 2G/|V| | G/ρ | Method |
|---|---|---|---|---|---|---|---|
| Sulfamethizole-sulfate [60] | 2.816 | 0.13 | 1.50 | 0.92 | 2.18 | 0.74 | MM |
| 2.753 | 0.15 | 1.60 | 0.97 | 2.06 | 0.72 | ||
| Acetazolamide (form I) [59] | 2.752 | 0.14 | 0.42 | 1.41 | 1.42 | 0.36 | XWR |
| Acetazolamide (form II) [63] | 2.608 | 0.16 | 2.19 | 0.91 | 2.21 | 0.88 | MM |
| Sulfathiazole Polymorphs [61] Ia, | 2.9913 | 0.10 | 1.11 | 0.88 | 2.28 | 0.69 | MM |
| Ib | 2.9694 | 0.09 | 1.09 | 0.83 | 2.40 | 0.73 | MM |
| II | 2.9583 | 0.10 | 0.96 | 0.92 | 2.18 | 0.62 | MM |
| IIIa | 2.9382 | 0.10 | 1.11 | 0.88 | 2.28 | 0.69 | MM |
| IIIb | 2.8834 | 0.11 | 1.23 | 0.89 | 2.24 | 0.71 | MM |
| IV | 2.9006 | 0.11 | 1.16 | 0.91 | 2.20 | 0.68 | MM |
| Molecules | Rij (Å) | ρ (eÅ−3) | ∇2ρ (eÅ−5) | ε | G a | |V|/G |
|---|---|---|---|---|---|---|
| Caff-3HNA | 3.0453 | 0.047(4) | 0.451(1) | 1.02 | 10.1 | 0.81 |
| Caff-PZCA | 3.0893 | 0.037(4) | 0.409(2) | 2.68 | 8.7 | 0.75 |
| Theo-25DFBZA | 3.3037 | 0.009(4) | 0.434(1) | 1.51 | 8.0 | 0.53 |
| TMP-OA | 3.2694 | 0.037(3) | 0.598(1) | 0.64 | 12.1 | 0.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomas, S.P.; Dikundwar, A.G.; Sarkar, S.; Pavan, M.S.; Pal, R.; Hathwar, V.R.; Row, T.N.G. The Relevance of Experimental Charge Density Analysis in Unraveling Noncovalent Interactions in Molecular Crystals. Molecules 2022, 27, 3690. https://doi.org/10.3390/molecules27123690
Thomas SP, Dikundwar AG, Sarkar S, Pavan MS, Pal R, Hathwar VR, Row TNG. The Relevance of Experimental Charge Density Analysis in Unraveling Noncovalent Interactions in Molecular Crystals. Molecules. 2022; 27(12):3690. https://doi.org/10.3390/molecules27123690
Chicago/Turabian StyleThomas, Sajesh P., Amol G. Dikundwar, Sounak Sarkar, Mysore S. Pavan, Rumpa Pal, Venkatesha R. Hathwar, and Tayur N. Guru Row. 2022. "The Relevance of Experimental Charge Density Analysis in Unraveling Noncovalent Interactions in Molecular Crystals" Molecules 27, no. 12: 3690. https://doi.org/10.3390/molecules27123690
APA StyleThomas, S. P., Dikundwar, A. G., Sarkar, S., Pavan, M. S., Pal, R., Hathwar, V. R., & Row, T. N. G. (2022). The Relevance of Experimental Charge Density Analysis in Unraveling Noncovalent Interactions in Molecular Crystals. Molecules, 27(12), 3690. https://doi.org/10.3390/molecules27123690