Molybdenum Disulphide Precipitation in Jet Reactors: Introduction of Kinetics Model for Computational Fluid Dynamics Calculations
Abstract
1. Introduction
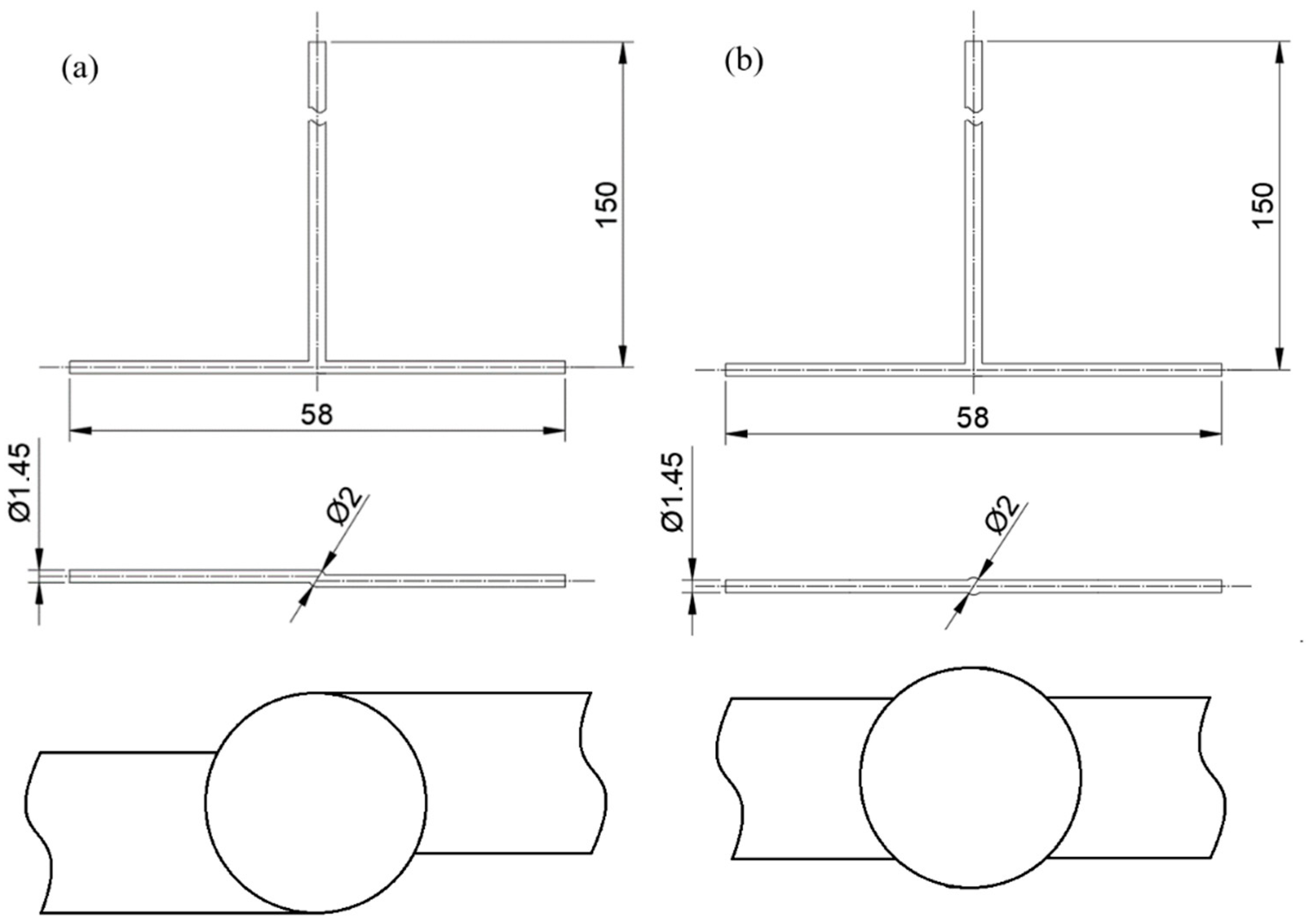
2. Materials and Methods
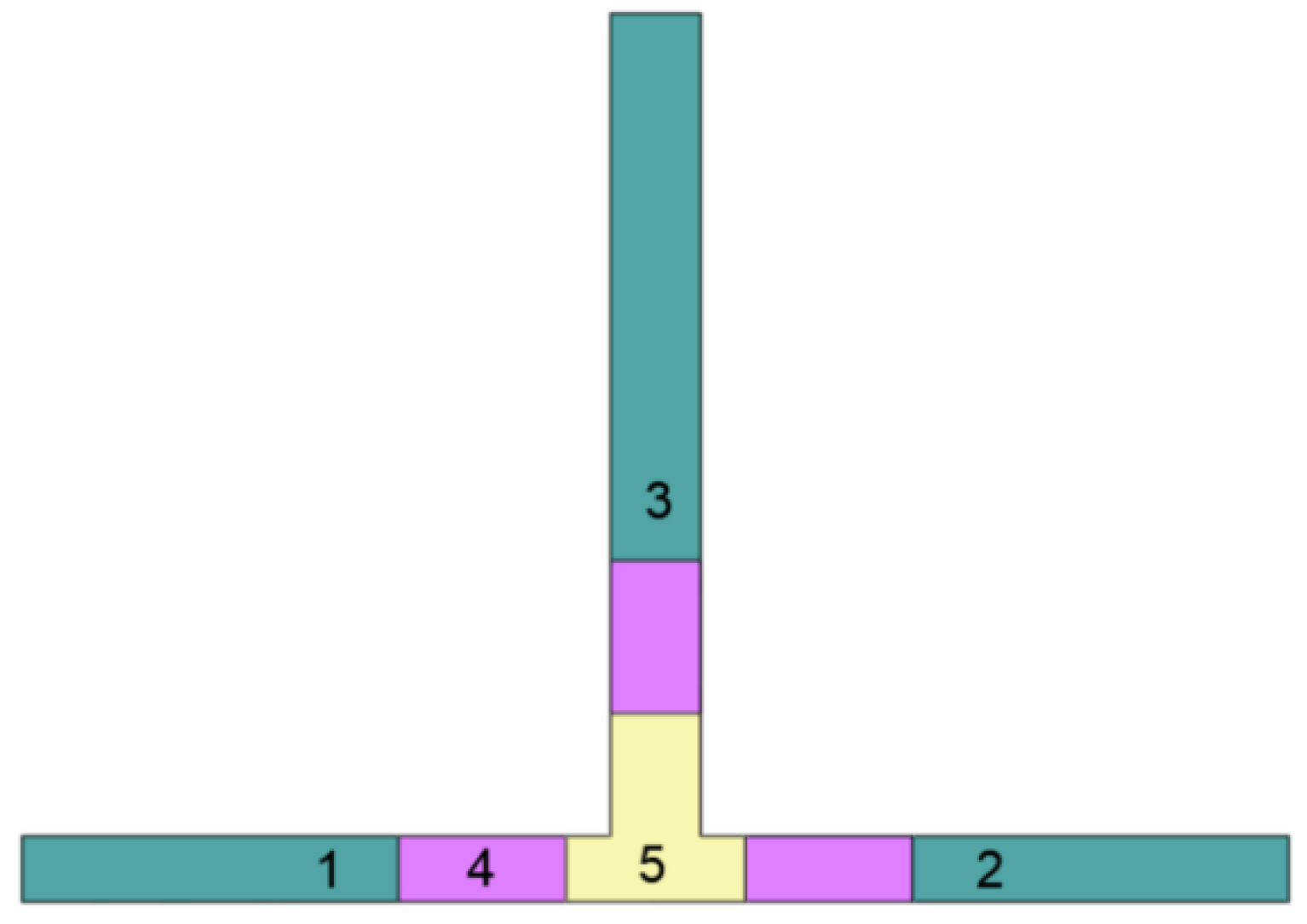
3. CFD Modeling
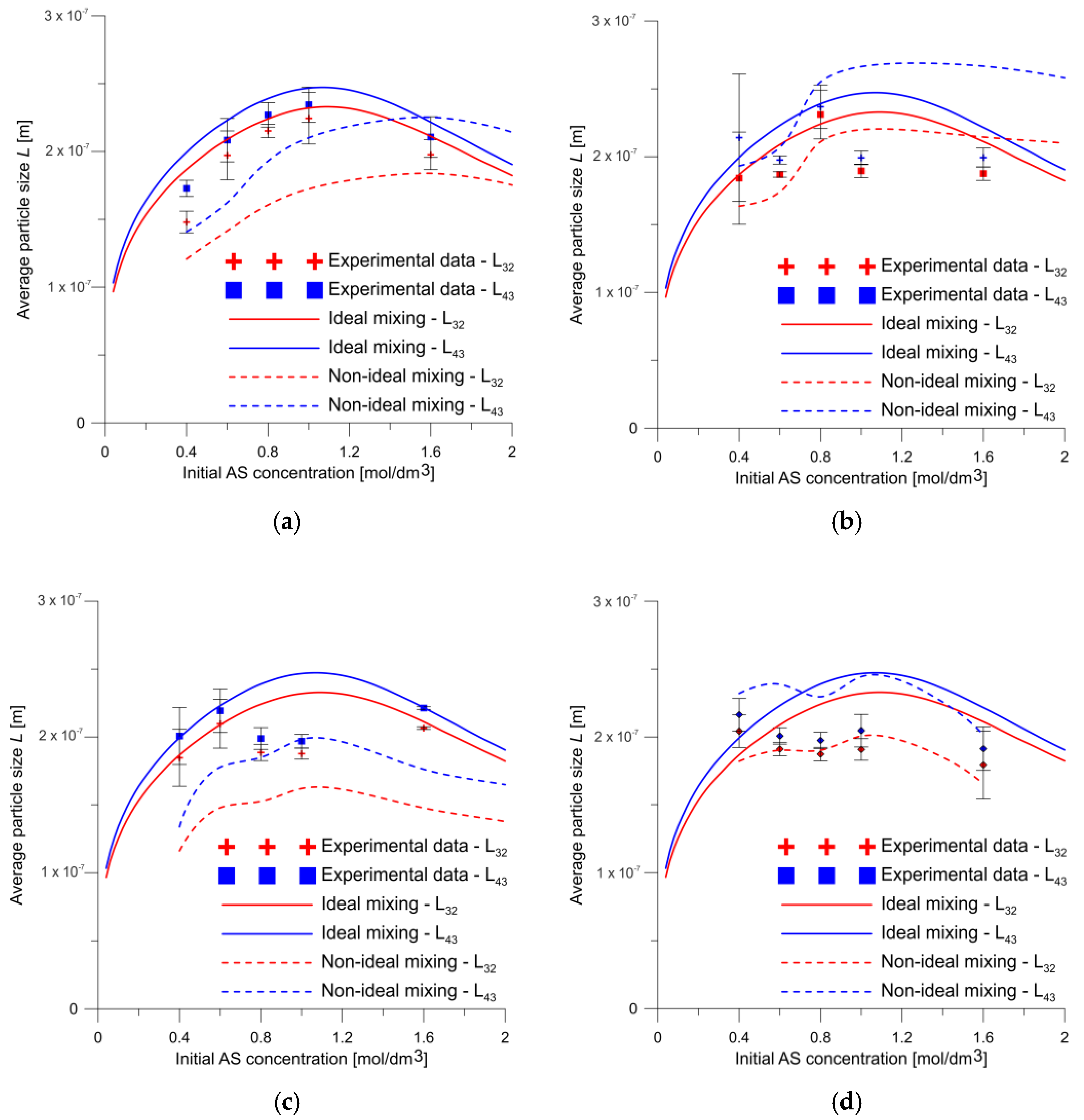
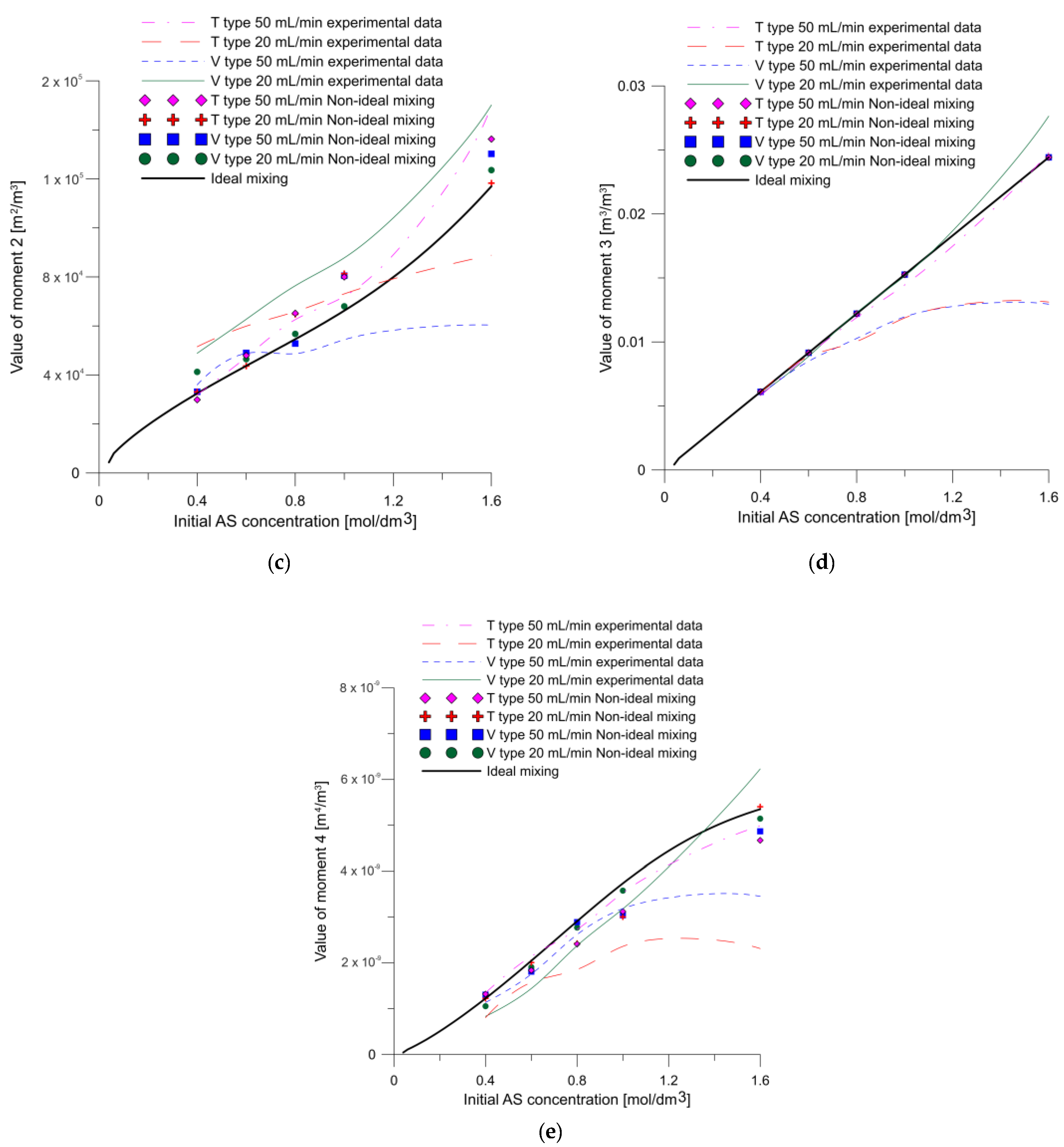
4. Results and Discussion
5. Conclusions
- The model enables kinetic constants to be determined for other complex chemical reactions, even with limited knowledge of the reaction mechanism, and can be applied with CFD to various reaction processes;
- The effect of the mixing conditions on the chemical reaction was determined using the SST k–ω model combined with the developed kinetic model to calculate results close to the experimental ones. In addition, the modelling and experimental results deviated more markedly at higher concentrations and lower flow rates, which may be because the reactant mixing was worse and, consequently, deviated even further from the ideal mixing conditions. Under these conditions the viscosity is higher due to the higher concentration of citric acid, what strongly affects the flow parameters, and thus the mixing-limited reaction;
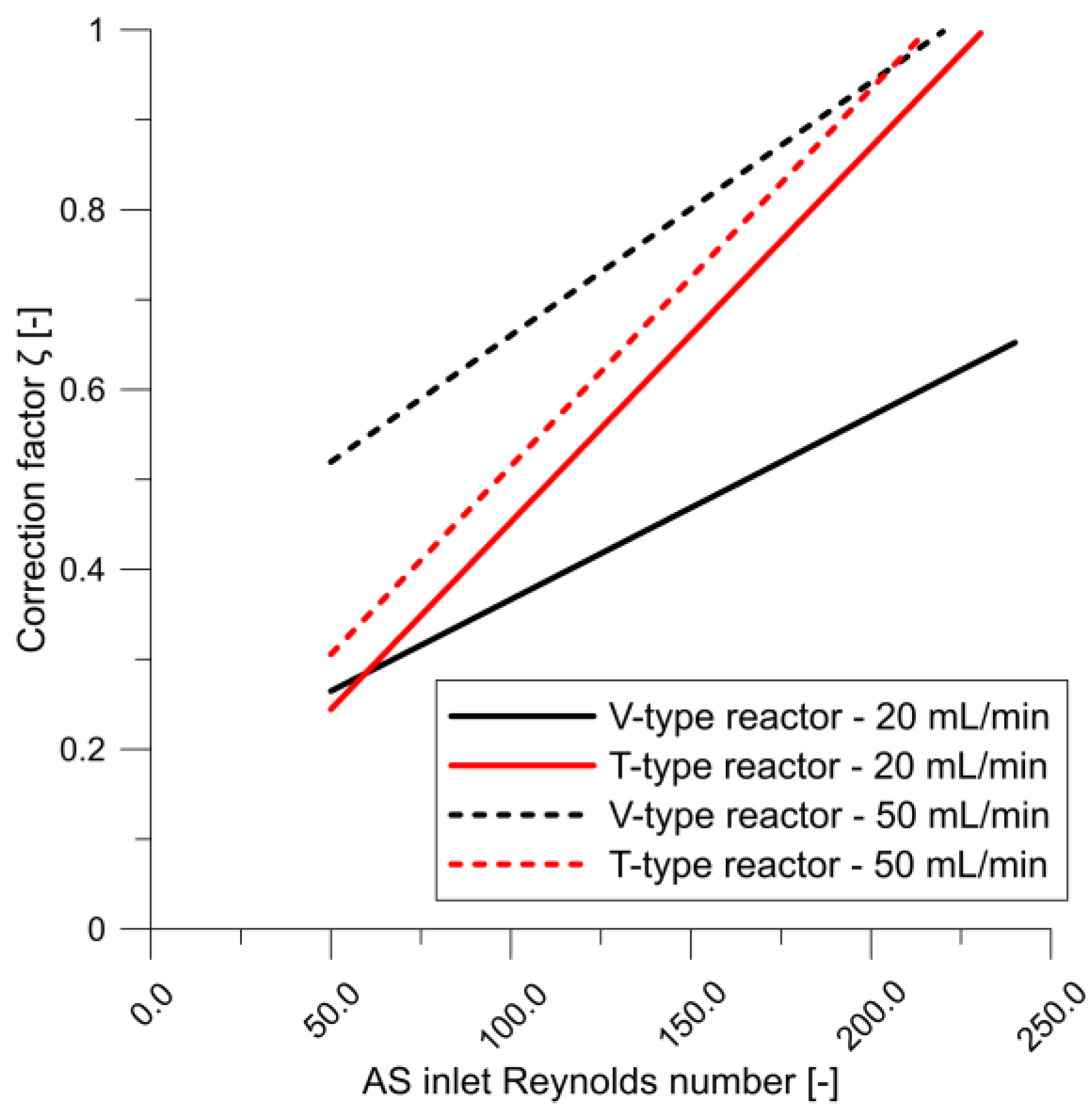
- The concentration and velocity contour plots indicate that the V-type reactor exhibited superior fluid mixing than the T-type one at the same flow rate. However, although this is associated with a more marked pressure drop, the particles were better mixed and nucleated over a much larger area. Fluid mixing is also affected by reagent concentration because fluid viscosity increases with increasing reagent concentration, which affects the Reynolds number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Nomenclature
| share function constant | ||
| heterogenous nucleation rate constant for sulfur particles | ||
| heterogenous nucleation rate constant for MoS2 particles | ||
| homogenous nucleation rate constant for sulfur particles | ||
| homogenous nucleation rate constant for MoS2 particles | ||
| heterogenous nucleation rate constant for sulfur particles | ||
| heterogenous nucleation rate constant for MoS2 particles | ||
| homogenous nucleation rate constant for sulfur particles | ||
| homogenous nucleation rate constant for MoS2 particles | ||
| birth rate | ||
| ammonium sulphide concentration | ||
| ammonium heptamolybdate concentration | ||
| death rate | ||
| auxiliary function in equation for turbulent viscosity in SST k–ω model | ||
| auxiliary function in equation for turbulent viscosity in SST k–ω model | ||
| total particle growth rate | ||
| particle growth rate for MoS2 particles | ||
| particle growth rate for sulfur particles | ||
| turbulence kinetic energy | ||
| surface shape factor | ||
| linear growth rate constant for sulfur particles | ||
| linear growth rate constant for MoS2 particles | ||
| solubility index | ||
| m | particle size | |
| m | characteristic dimension | |
| m | characteristic dimension | |
| m | characteristic dimension | |
| m | characteristic dimension | |
| molar mass | ||
| m0 | moment 0 | |
| m1 | moment 1 | |
| m2 | moment 2 | |
| m3 | moment 3 | |
| m4 | moment 4 | |
| moment index | ||
| substrate consumption rate | ||
| total nucleation rate | ||
| nucleation rate for MoS2 particles | ||
| nucleation rate for sulfur particles | ||
| S | supersaturation | |
| t | s | time |
| particle velocity component | ||
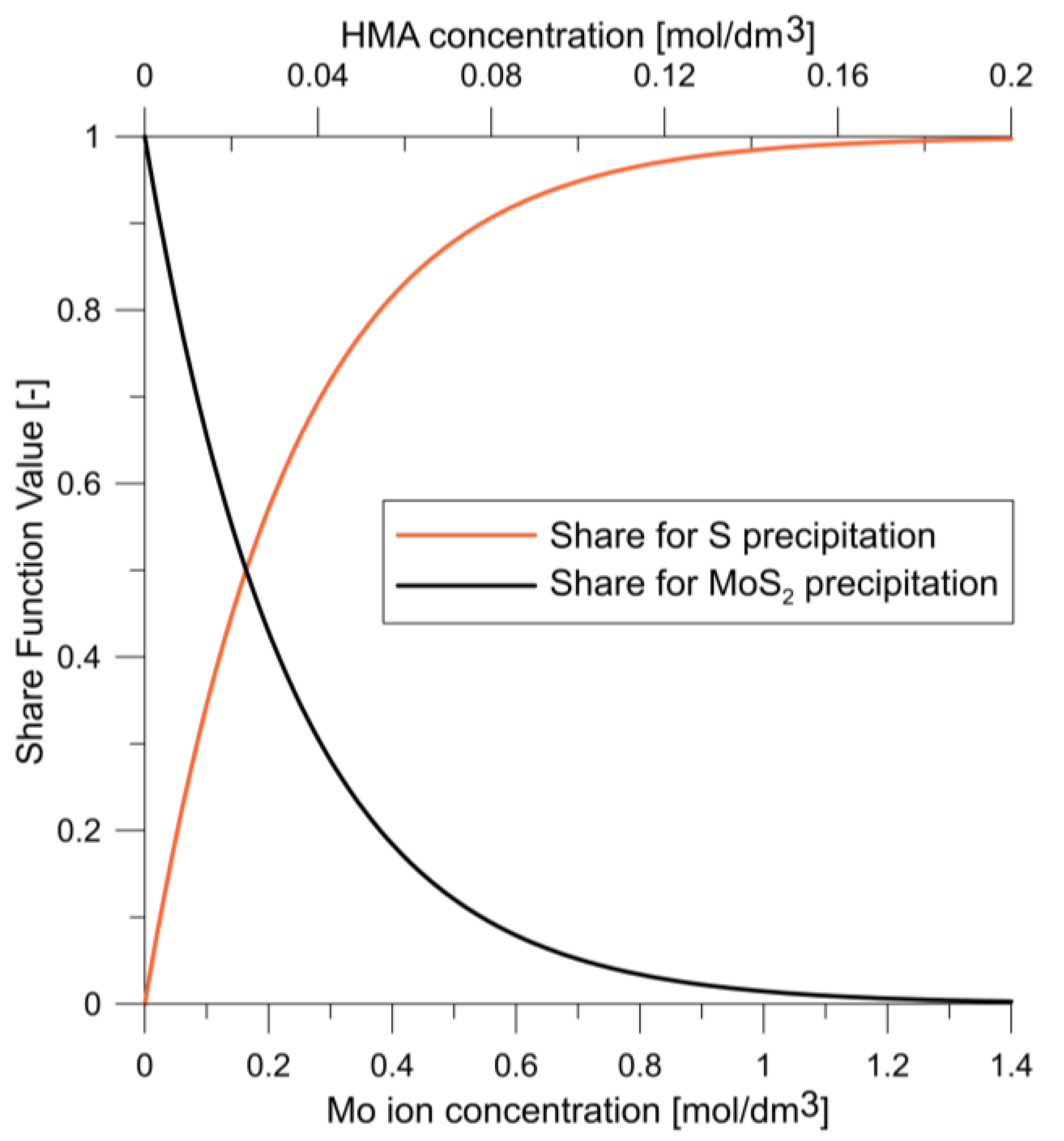
| MoS2 precipitation share function | ||
| S precipitation share function | ||
| volume | ||
| m | Cartesian coordinates | |
| Greek symbols | ||
| density | ||
| share function | ||
References
- Baldyga, J.; Bourne, J.R. Turbulent Mixing and Chemical Reactions, 1st ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fox, R.O. Computational Models for Turbulent Reacting Flows; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Wojtas, K.; Makowski, Ł.; Orciuch, W. Barium sulfate precipitation in jet reactors: Large eddy simulations, kinetics study and design considerations. Chem. Eng. Res. Des. 2020, 158, 64–76. [Google Scholar] [CrossRef]
- Wojtas, K.; Orciuch, W.; Makowski, Ł. Large eddy simulations of reactive mixing in jet reactors of varied geometry and size. Processes 2020, 8, 1101. [Google Scholar] [CrossRef]
- Battistini, A.; Cammi, A.; Lorenzi, S.; Colombo, M.; Fairweather, M. Development of a CFD—LES model for the dynamic analysis of the DYNASTY natural circulation loop. Chem. Eng. Sci. 2021, 237, 116520. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, C.; Mao, Z.S. CFD-PBE simulation of premixed continuous precipitation incorporating nucleation, growth and aggregation in a stirred tank with multi-class method. Chem. Eng. Sci. 2012, 68, 469–480. [Google Scholar] [CrossRef]
- Metzger, L.; Kind, M. The influence of mixing on fast precipitation processes—A coupled 3D CFD-PBE approach using the direct quadrature method of moments (DQMOM). Chem. Eng. Sci. 2017, 169, 284–298. [Google Scholar] [CrossRef]
- Sultan, M.A.; Fonte, C.P.; Dias, M.M.; Lopes, J.C.B.; Santos, R.J. Experimental study of flow regime and mixing in T-jets mixers. Chem. Eng. Sci. 2012, 73, 388–399. [Google Scholar] [CrossRef]
- Johnson, N.K.; Richardson, L.F. Weather Prediction by Numerical Process. Math. Gaz. 1922, 11, 125–127. [Google Scholar] [CrossRef][Green Version]
- Anderson, J. Computational Fluid Dynamics: The Basics with Applications; McGrawhill Inc.: New York, NY, USA, 1995; pp. 1–547. [Google Scholar]
- Patankar, S.V. Numerical heat transfer and fluid flow. Nucl. Sci. Eng. 1981, 78, 196–197. [Google Scholar] [CrossRef]
- Wojtas, K.; Orciuch, W.; Makowski, Ł. Comparison of large eddy simulations and k-ε Modelling of fluid velocity and tracer concentration in impinging jet mixers. Chem. Process Eng. 2015, 36, 251–262. [Google Scholar] [CrossRef]
- Wojtas, K.; Orciuch, W.; Wysocki, Ł.; Makowski, Ł. Modeling and experimental validation of subgrid scale scalar variance at high Schmidt numbers. Chem. Eng. Res. Des. 2017, 123, 141–151. [Google Scholar] [CrossRef]
- Makowski, Ł.; Bałdyga, J. Large Eddy Simulation of mixing effects on the course of parallel chemical reactions and comparison with k-ε modeling. Chem. Eng. Process. Process Intensif. 2011, 50, 1035–1040. [Google Scholar] [CrossRef]
- Vicum, L.; Ottiger, S.; Mazzotti, M.; Makowski, Ł.; Bałdyga, J. Multi-scale modeling of a reactive mixing process in a semibatch stirred tank. Chem. Eng. Sci. 2004, 59, 1767–1781. [Google Scholar] [CrossRef]
- Hai-Dou, W.; Bin-Shi, X.; Jia-Jun, L.; Da-Ming, Z. Characterization and anti-friction on the solid lubrication MoS2 film prepared by chemical reaction technique. Sci. Technol. Adv. Mater. 2005, 6, 535–539. [Google Scholar] [CrossRef][Green Version]
- He, B.; Chen, L.; Jing, M.; Zhou, M.; Hou, Z.; Chen, X. 3D MoS2-rGO@Mo nanohybrids for enhanced hydrogen evolution: The importance of the synergy on the Volmer reaction. Electrochim. Acta 2018, 283, 357–365. [Google Scholar] [CrossRef]
- Voiry, D.; Salehi, M.; Silva, R.; Fujita, T.; Chen, M.; Asefa, T.; Shenoy, V.B.; Eda, G.; Chhowalla, M. Conducting MoS2 Nanosheets as Catalysts for Hydrogen Evolution Reaction. Nano Lett. 2013, 13, 6222–6227. [Google Scholar] [CrossRef]
- Si, K.; Ma, J.; Guo, Y.; Zhou, Y.; Lu, C.; Xu, X.; Xu, X. Improving photoelectric performance of MoS2 photoelectrodes by annealing. Ceram. Int. 2018, 44, 21153–21158. [Google Scholar] [CrossRef]
- Merki, D.; Fierro, S.; Vrubel, H.; Hu, X. Amorphous molybdenum sulfide films as catalysts for electrochemical hydrogen production in water. Chem. Sci. 2011, 2, 1262–1267. [Google Scholar] [CrossRef]
- Bojarska, Z.; Kopytowski, J.; Mazurkiewicz-Pawlicka, M.; Bazarnik, P.; Gierlotka, S.; Rożeń, A.; Makowski, Ł. Molybdenum disulfide-based hybrid materials as new types of oil additives with enhanced tribological and rheological properties. Tribol. Int. 2021, 160, 106999. [Google Scholar] [CrossRef]
- Deorsola, F.A.; Russo, N.; Blengini, G.A.; Fino, D. Synthesis, characterization and environmental assessment of nanosized MoS2 particles for lubricants applications. Chem. Eng. J. 2012, 195–196, 1–6. [Google Scholar] [CrossRef]
- Santillo, G.; Deorsola, F.A.; Bensaid, S.; Russo, N.; Fino, D. MoS2 nanoparticle precipitation in turbulent micromixers. Chem. Eng. J. 2012, 207–208, 322–328. [Google Scholar] [CrossRef]
- Wojtalik, M.; Orciuch, W.; Makowski, Ł. Nucleation and growth kinetics of MoS2 nanoparticles obtained by chemical wet synthesis in a jet reactor. Chem. Eng. Sci. 2020, 225, 55–65. [Google Scholar] [CrossRef]
- Wojtalik, M.; Bojarska, Z.; Makowski, Ł. Experimental studies on the chemical wet synthesis for obtaining high-quality MoS2 nanoparticles using impinging jet reactor. J. Solid State Chem. 2020, 285, 121254. [Google Scholar] [CrossRef]
- Wojtalik, M.; Przybyt, P.; Zubańska, K.; Żuchowska, M.; Bojarska, Z.; Arasimowicz-Andres, M.; Rożeń, A.; Makowski, Ł. Production of synthetic particles of MoS2 using wet chemical synthesis. Przem. Chem. 2019, 98, 1817–1821. [Google Scholar] [CrossRef]
- Al-Tarazi, M.; Heesink, A.B.M.; Versteeg, G.F. New method for the determination of precipitation kinetics using a laminar jet reactor. Chem. Eng. Sci. 2005, 60, 805–814. [Google Scholar] [CrossRef]
- Al-Tarazi, M.; Heesink, A.B.M.; Versteeg, G.F. Precipitation of metal sulphides using gaseous hydrogen sulphide: Mathematical modelling. Chem. Eng. Sci. 2004, 59, 567–579. [Google Scholar] [CrossRef]
- Bardina, J.E.; Huang, P.G.; Coakley, T.J. Turbulence Modeling Validation, Testing, and Development; Nasa Technical Memorandum; NASA: Washington, DC, USA, 1997.
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Simion, A.I.; Grigoraş, C.G.; Gavrilă, L.G. Modelling of the thermophysical properties of citric acid aqueous solutions. Density and viscosity. Ann. Food Sci. Technol. 2014, 1, 193–202. [Google Scholar]


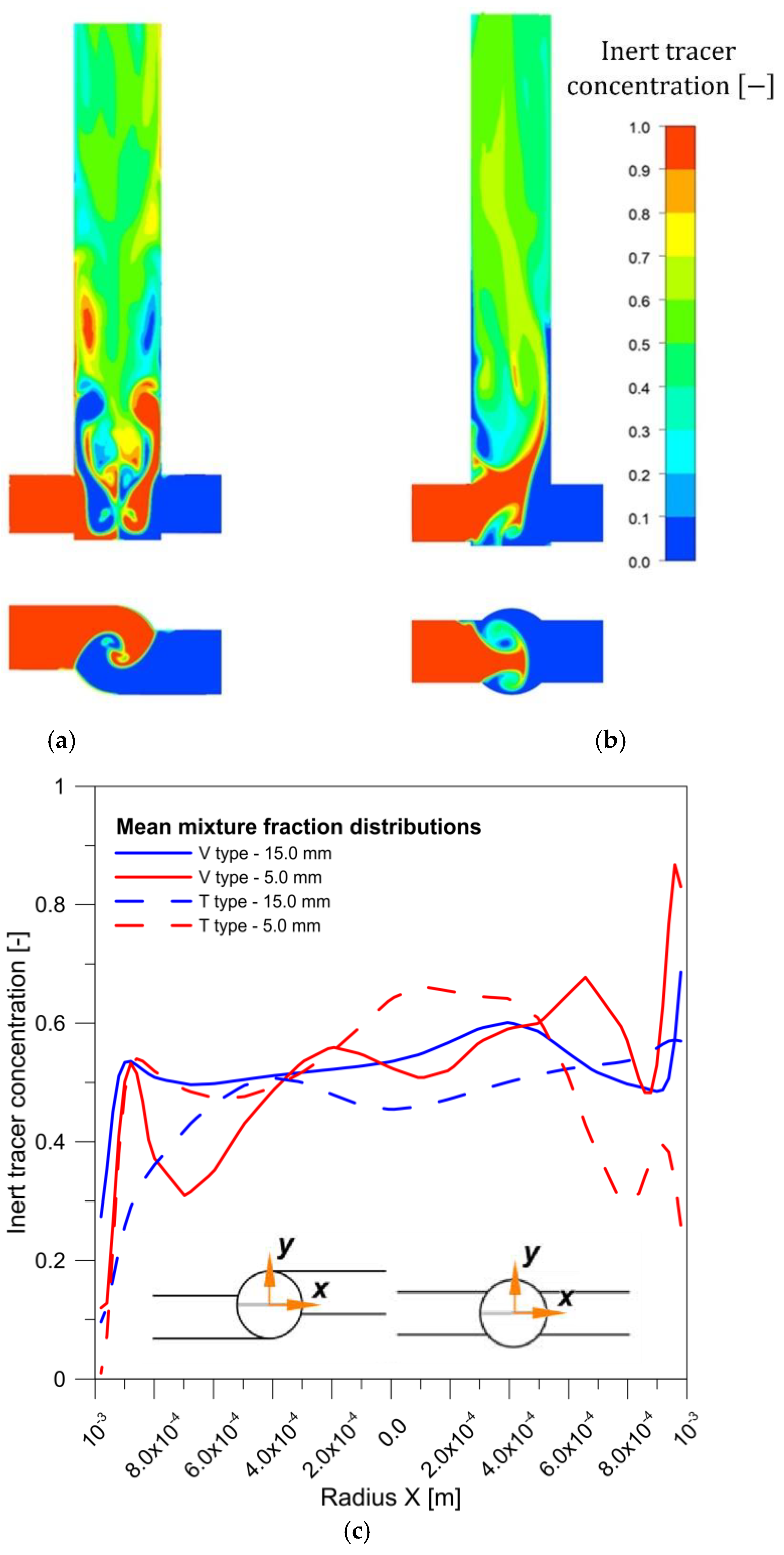
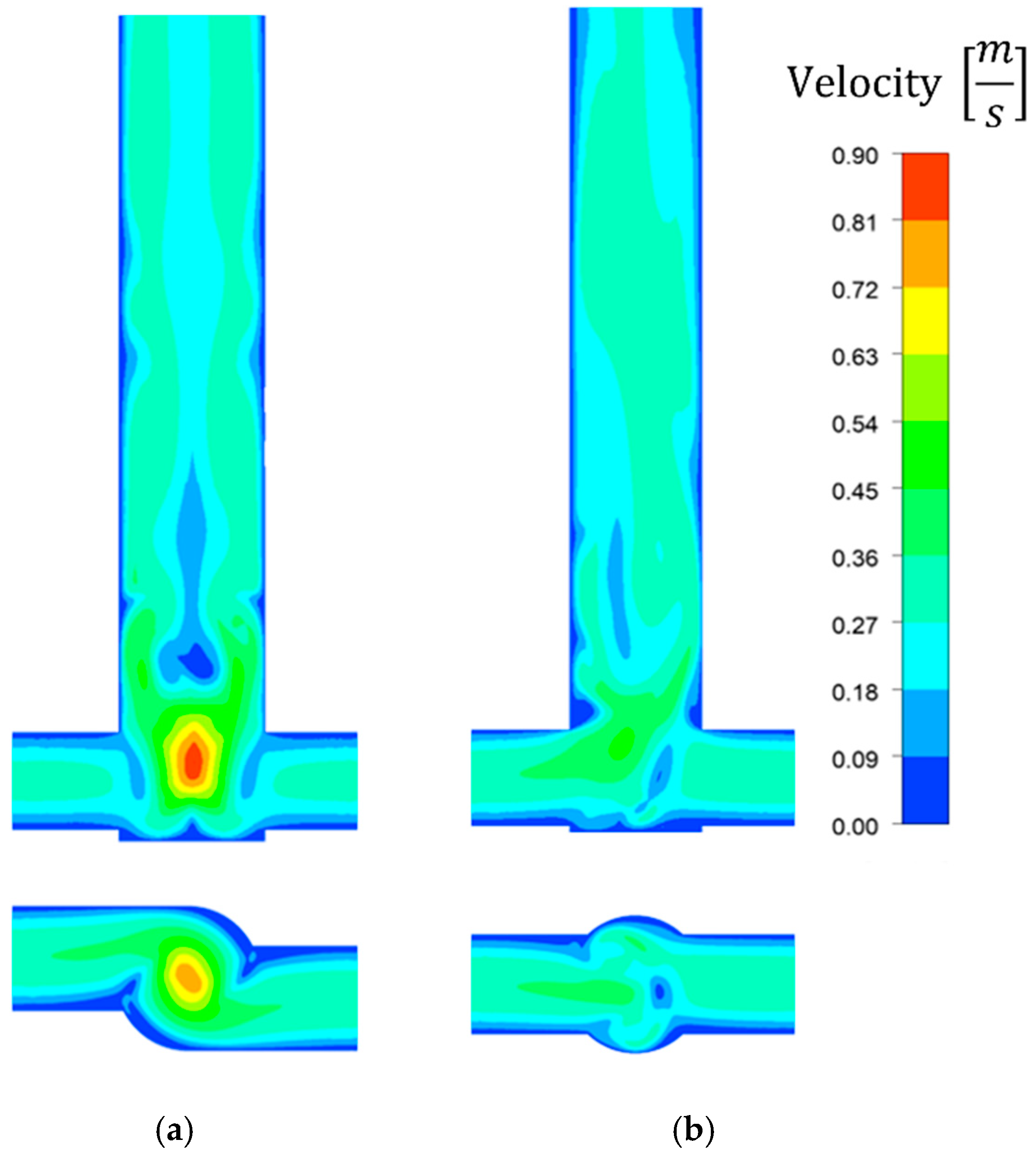
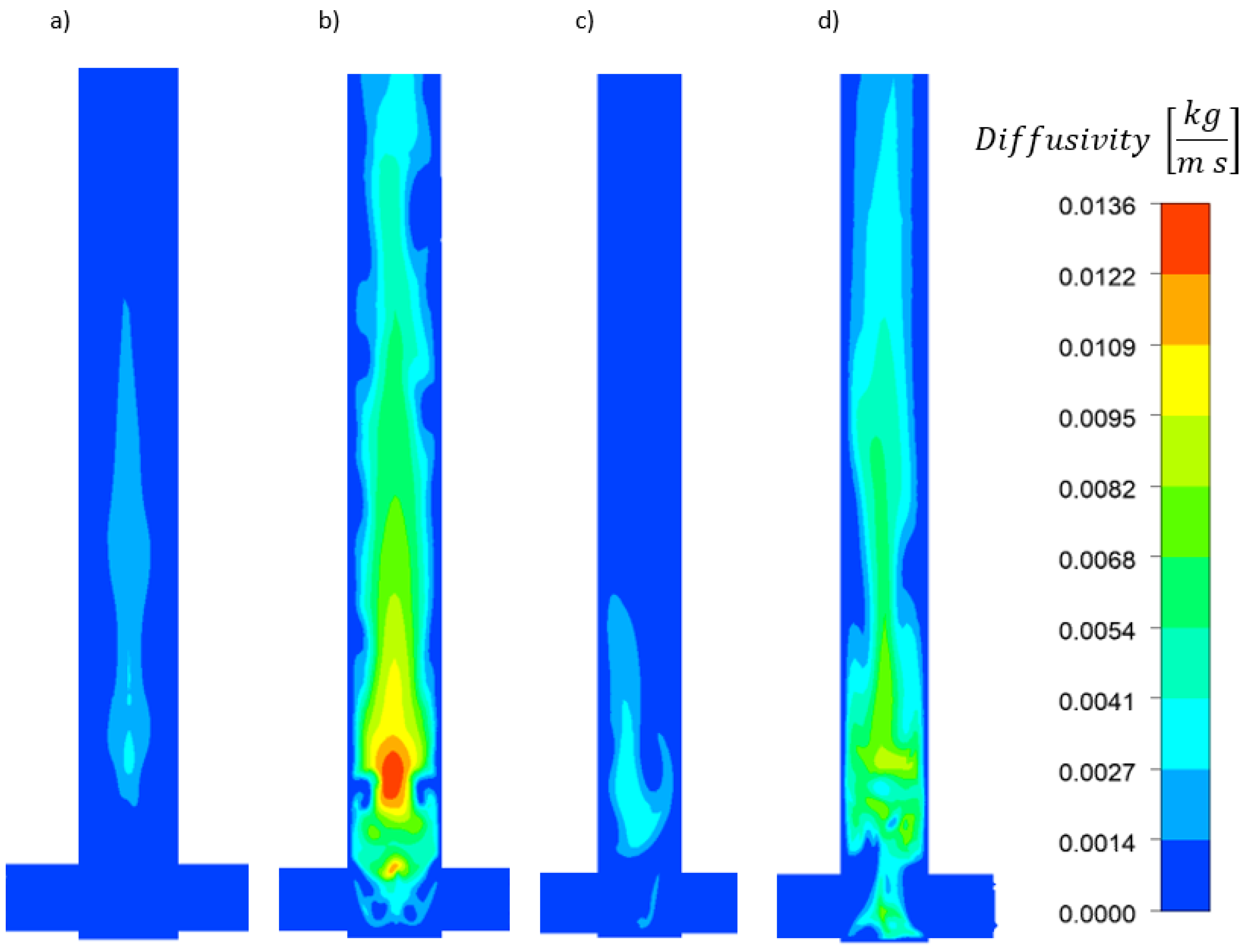

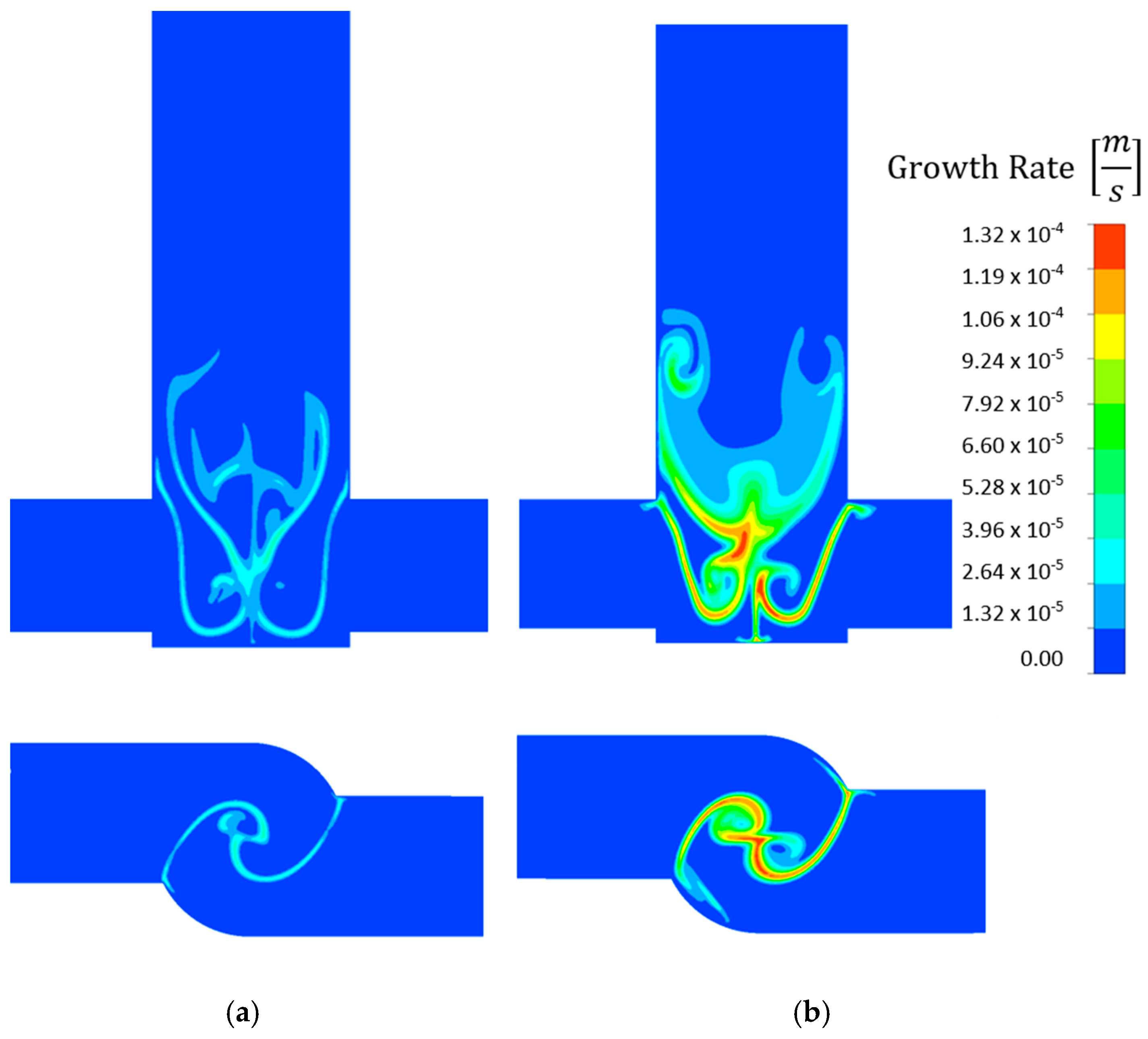



| Supersaturation = product of sulphide ion equilibrium constants) | (1) | |
| Rate of formation from MoS2 precipitation | (2) | |
| Rate of formation from S precipitation | (3) | |
| Linear growth rate coefficient from MoS2 precipitation | (4) | |
| Linear growth rate coefficient from S precipitation | (5) | |
| MoS2 precipitation kinetics share function in model | (6) | |
| S precipitation kinetics share function in model | (7) | |
| Total formation rate | (8) | |
| Total linear growth rate coefficient | (9) | |
| Substrate consumption rate | (10) | |
| HMA balance | (11) | |
| AS balance | (12) | |
| Zero-moment balance | (13) | |
| Higher-moment balance (for n = 1, 2, 3, or 4) | (14) | |
| Volumetric change (zero for pipe reactor) | (15) |
| Constant | Value | Unit |
|---|---|---|
| 5.25 × 1022 | ||
| 3.97 × 1023 | ||
| 1.89 | ||
| 6.58 | ||
| 3.05 × 1015 | ||
| 1.31 × 1016 | ||
| 24.04 | ||
| 1.04 × 10−11 | ||
| 0.3533 | ||
| 0.0102 | ||
| 3.21 × 10−9 | ||
| 0.034 |
| CA Mass Concentration [−] | CA Dynamic Viscosity [Pa s] | CA Density [kg/m3] |
|---|---|---|
| 0.0000 | 8.94 × 10−4 | 997.0 |
| 0.0643 | 1.05 × 10−3 | 1022.5 |
| 0.0994 | 1.12 × 10−3 | 1035.3 |
| 0.1699 | 1.28 × 10−3 | 1059.4 |
| 0.1982 | 1.37 × 10−3 | 1068.5 |
| 0.2518 | 1.53 × 10−3 | 1085.0 |
| 0.3000 | 1.69 × 10−3 | 1099.0 |
| 0.3400 | 1.84 × 10−3 | 1110.1 |
| 0.3994 | 2.12 × 10−3 | 1125.7 |
| Parameter | V-Type Reactor | T-Type Reactor |
|---|---|---|
| Number of cells | 2,030,910 | 2,018,986 |
| Minimum Orthogonal Quality | 0.354 | 0.351 |
| Maximum Aspect Ratio | 34.13 | 33.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wojtalik, M.; Wojtas, K.; Gołębiowska, W.; Jarząbek, M.; Orciuch, W.; Makowski, Ł. Molybdenum Disulphide Precipitation in Jet Reactors: Introduction of Kinetics Model for Computational Fluid Dynamics Calculations. Molecules 2022, 27, 3943. https://doi.org/10.3390/molecules27123943
Wojtalik M, Wojtas K, Gołębiowska W, Jarząbek M, Orciuch W, Makowski Ł. Molybdenum Disulphide Precipitation in Jet Reactors: Introduction of Kinetics Model for Computational Fluid Dynamics Calculations. Molecules. 2022; 27(12):3943. https://doi.org/10.3390/molecules27123943
Chicago/Turabian StyleWojtalik, Michał, Krzysztof Wojtas, Weronika Gołębiowska, Maria Jarząbek, Wojciech Orciuch, and Łukasz Makowski. 2022. "Molybdenum Disulphide Precipitation in Jet Reactors: Introduction of Kinetics Model for Computational Fluid Dynamics Calculations" Molecules 27, no. 12: 3943. https://doi.org/10.3390/molecules27123943
APA StyleWojtalik, M., Wojtas, K., Gołębiowska, W., Jarząbek, M., Orciuch, W., & Makowski, Ł. (2022). Molybdenum Disulphide Precipitation in Jet Reactors: Introduction of Kinetics Model for Computational Fluid Dynamics Calculations. Molecules, 27(12), 3943. https://doi.org/10.3390/molecules27123943






