Does Hamiltonian Replica Exchange via Lambda-Hopping Enhance the Sampling in Alchemical Free Energy Calculations?
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
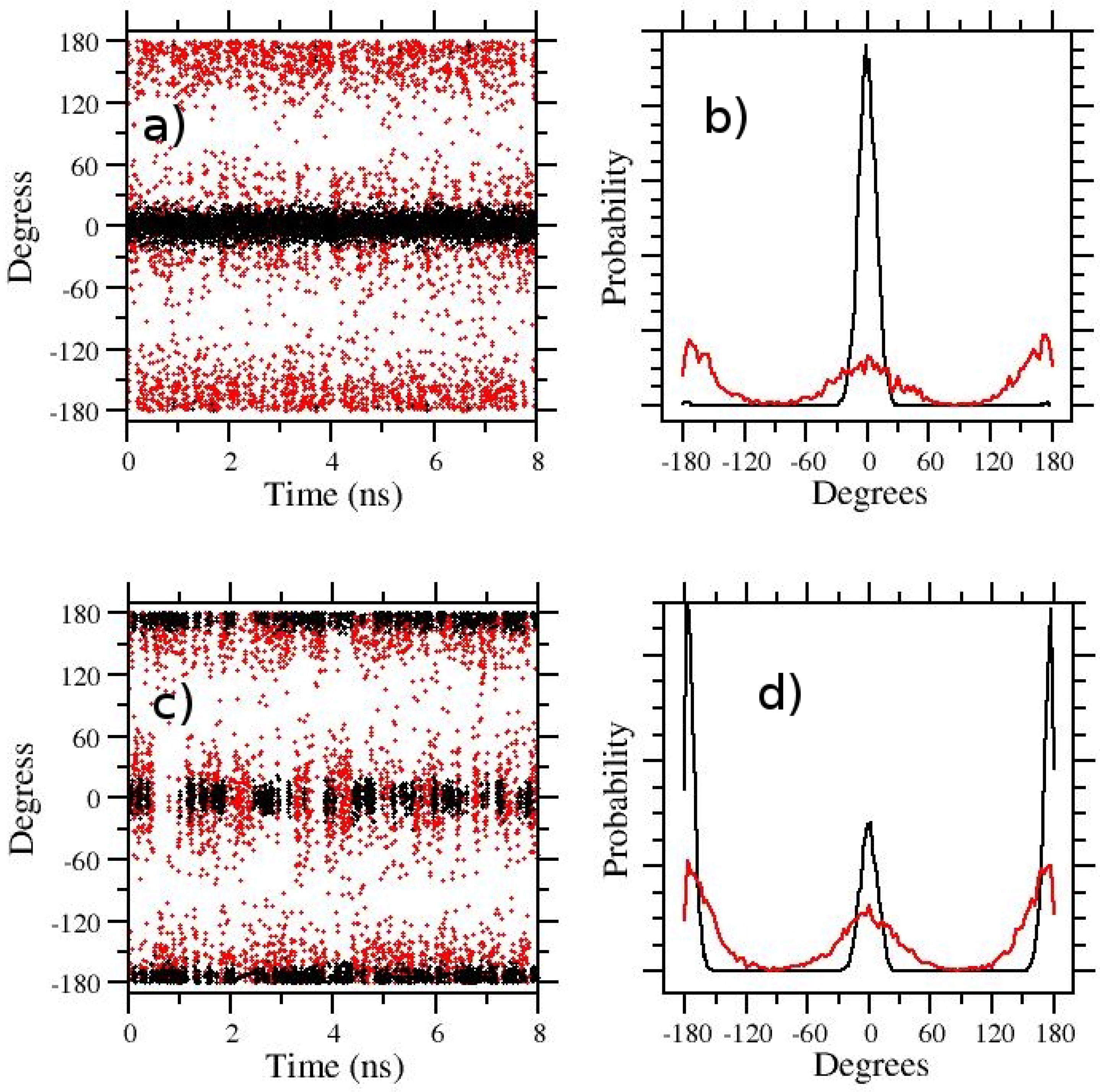
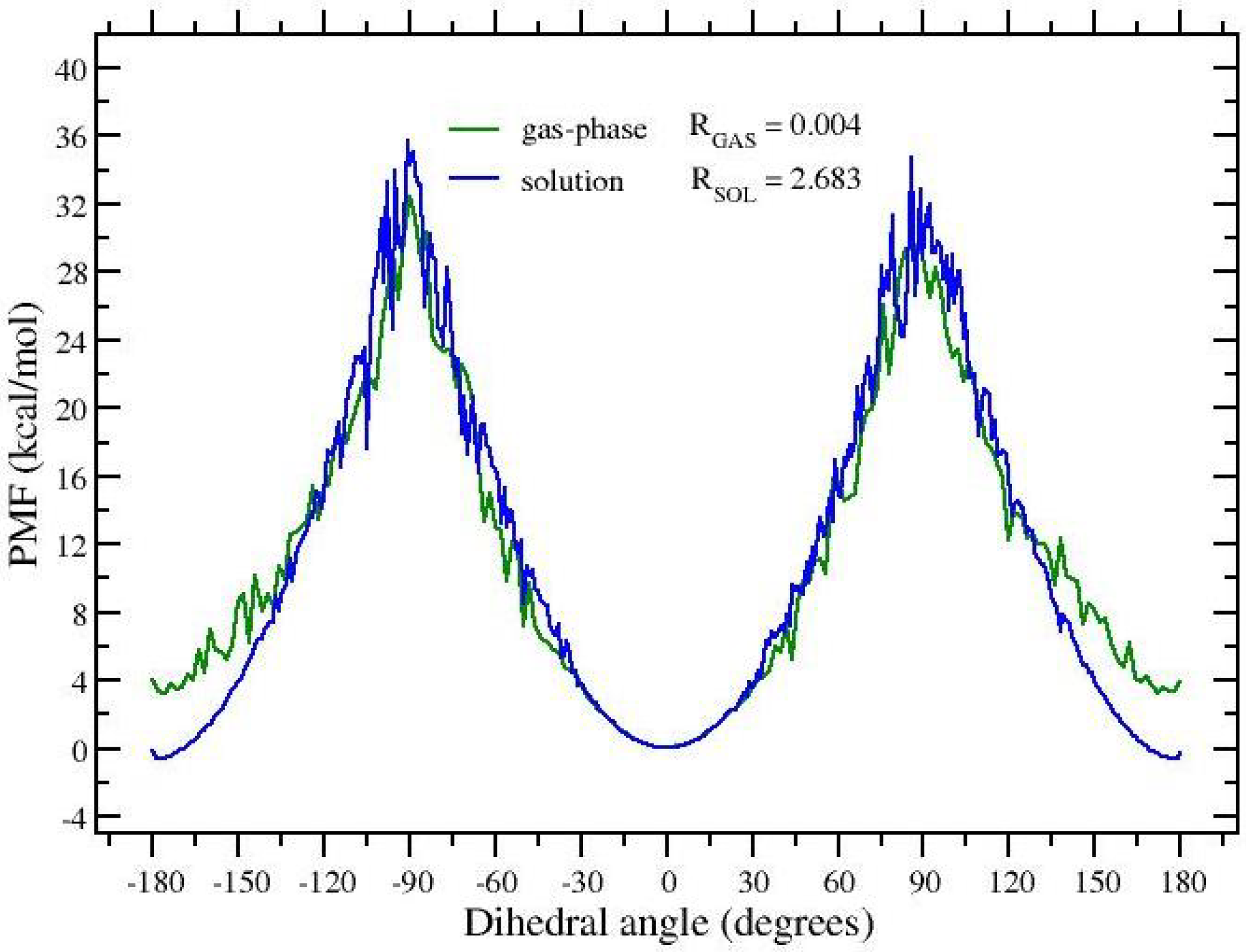
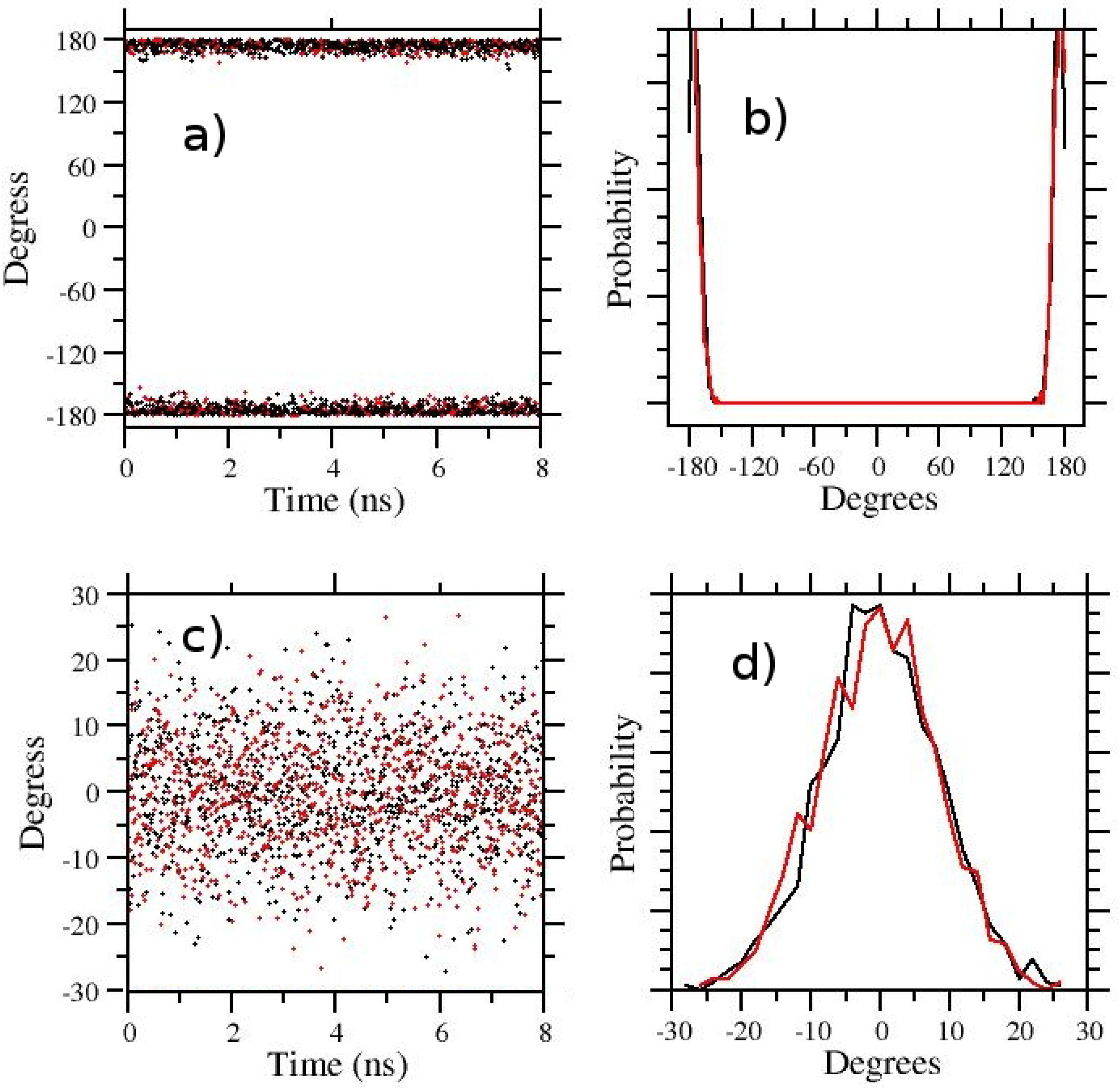
3.1. t-REM and ST-HREM of APA in the Gas-Phase and in Solution
3.2. -Hopping and FEP Results
3.3. Hydration Free Energy of APA with -Hopping
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BFE | Binding free energy |
| MD | Molecular dynamics |
| FEP | Free energy perturbation |
| HREM | Hamiltonian Replica Exchange Method |
| t-REM | Temperature Replica Exchange Method |
| APA | 5-Aminopent-3-enoic acid |
| RTT | round-trip time |
| ER | Exchange ratio |
| MBAR | Multiple Bennett acceptance ratio |
| ST | Solute tempering |
References
- In-Silico Drug Discovery Market. 2022. Available online: https://www.psmarketresearch.com/market-analysis/in-silico-drug-discovery-market (accessed on 12 June 2022).
- Jorgensen, W.L.; Buckner, J.K.; Boudon, S.; TiradoRives, J. Efficient computation of absolute free energies of binding by computer simulations. Application to the methane dimer in water. J. Chem Phys. 1988, 89, 3742–3746. [Google Scholar] [CrossRef]
- Pohorille, A.; Jarzynski, C.; Chipot, C. Good Practices in Free-Energy Calculations. J. Phys. Chem. B 2010, 114, 10235–10253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Coveney, P.V.; Wan, S. On the calculation of equilibrium thermodynamic properties from molecular dynamics. Phys. Chem. Chem. Phys. 2016, 18, 30236–30240. [Google Scholar] [CrossRef] [Green Version]
- Bhati, A.P.; Wan, S.; Hu, Y.; Sherborne, B.; Coveney, P.V. Uncertainty Quantification in Alchemical Free Energy Methods. J. Chem. Theory Comput. 2018, 14, 2867–2880. [Google Scholar] [CrossRef]
- Gapsys, V.; Perez-Benito, L.; Aldeghi, M.; Seeliger, D.; van Vlijmen, H.; Tresadern, G.; de Groot, B.L. Large scale relative protein ligand binding affinities using non-equilibrium alchemy. Chem. Sci. 2020, 11, 1140–1152. [Google Scholar] [CrossRef] [Green Version]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Woods, C.J.; Essex, J.W.; King, M.A. Enhanced Configurational Sampling in Binding Free-Energy Calculations. J. Phys. Chem. B 2003, 107, 13711–13718. [Google Scholar] [CrossRef]
- Bitetti-Putzer, R.; Yang, W.; Karplus, M. Generalized ensembles serve to improve the convergence of free energy simulations. Chem. Phys. Lett. 2003, 377, 633–641. [Google Scholar] [CrossRef]
- Hritz, J.; Oostenbrink, C. Hamiltonian replica exchange molecular dynamics using soft-core interactions. J. Chem. Phys. 2008, 128, 144121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Berne, B.J.; Friesner, R.A. On achieving high accuracy and reliability in the calculation of relative protein-ligand binding affinities. Proc. Natl. Acad. Sci. USA 2012, 109, 1937–1942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M.K.; Greenwood, J.; et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015, 137, 2695–2703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, W.; Roux, B. Free Energy Perturbation Hamiltonian Replica-Exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory Comput. 2010, 6, 2559–2565. [Google Scholar] [CrossRef] [Green Version]
- Baumann, H.M.; Gapsys, V.; de Groot, B.L.; Mobley, D.L. Challenges Encountered Applying Equilibrium and Nonequilibrium Binding Free Energy Calculations. J. Phys. Chem. 2021, 125, 4241–4261. [Google Scholar] [CrossRef]
- Gonzalez, D.; Macaya, L.; Vöhringer-Martinez, E. Molecular Environment-Specific Atomic Charges Improve Binding Affinity Predictions of SAMPL5 Host–Guest Systems. J. Chem. Inf. Model. 2021, 61, 4462–4474. [Google Scholar] [CrossRef]
- Bannan, C.C.; Burley, K.H.; Chiu, M.; Shirts, M.R.; Gilson, M.K.; Mobley, D.L. Blind prediction of cyclohexane-water distribution coefficients from the SAMPL5 challenge. J. Comput.-Aided Mol. Des. 2016, 30, 927–944. [Google Scholar] [CrossRef] [Green Version]
- Markthaler, D.; Fleck, M.; Stankiewicz, B.; Hansen, N. Exploring the Effect of Enhanced Sampling on Protein Stability Prediction. J. Chem. Theory Comput. 2022, 18, 2569–2583. [Google Scholar] [CrossRef]
- Gapsys, V.; Yildirim, A.; Aldeghi, M.; Khalak, Y.; van der Spoel, D.; de Groot, B.L. Accurate absolute free energies for ligand-protein binding based on non-equilibrium approaches. Comm. Chem. 2021, 4, 61. [Google Scholar] [CrossRef]
- Wan, S.; Tresadern, G.; Perez-Benito, L.; van Vlijmen, H.; Coveney, P.V. Accuracy and Precision of Alchemical Relative Free Energy Predictions with and without Replica-Exchange. Adv. Theory Simul. 2020, 3, 1900195. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marsili, S.; Signorini, G.F.; Chelli, R.; Marchi, M.; Procacci, P. ORAC: A Molecular Dynamics Simulation Program to Explore Free Energy Surfaces in Biomolecular Systems at the Atomistic Level. J. Comput. Chem. 2010, 31, 1106–1116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chemicalize Was Used for Prediction of the pKa’s in APA, Developed by ChemAxon. 2021. Available online: https://chemicalize.com/ (accessed on 1 March 2022).
- Sun, D. Recent Advances in Macrocyclic Drugs and Microwave-Assisted and/or Solid-Supported Synthesis of Macrocycles. Molecules 2022, 27, 1012. [Google Scholar] [CrossRef] [PubMed]
- Baillargeon, P.; Bernard, S.; Gauthier, D.; Skouta, R.; Dory, Y. Efficient Synthesis and Astonishing Supramolecular Architectures of Several Symmetric Macrolactams. Chem. Eur. J. 2007, 13, 9223–9235. [Google Scholar] [CrossRef]
- Saltiel, J.; Sun, Y.-P. Cis-trans Isomerization of C=C Double Bonds; Elsevier: Amsterdam, The Netherlands, 2003; Chapter Photochromism; pp. 64–164. [Google Scholar]
- Dugave, C.; Demange, L. Cis-Trans Isomerization of Organic Molecules and Biomolecules: Implications and Applications. Chem. Rev. 2003, 103, 2475–2532. [Google Scholar] [CrossRef]
- Procacci, P. PrimaDORAC: A Free Web Interface for the Assignment of Partial Charges, Chemical Topology, and Bonded Parameters in Organic or Drug Molecules. J. Chem. Inf. Model. 2017, 57, 1240–1245. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.; Caldwell, J.; Kollman, P.; Case, D. Development and testing of a general AMBER force field. J. Comp. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- GAFF and GAFF2 Are Public Domain Force Fields and Are Part of the AmberTools Distribution. According to the AMBER Development Team, the Improved Version of GAFF, GAFF2, Is an Ongoing Poject Aimed at “Reproducing Both the High Quality Interaction Energies and Key Liquid Properties such as Density, Heat of Vaporization and Hydration Free Energy”. GAFF2 is Expected “to Be an Even More Successful General Purpose Force Field and that GAFF2-Based Scoring Functions will Significantly Improve the Successful Rate of Virtual Screenings”. Available online: https://amber.org (accessed on 22 January 2022).
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Izadi, S.; Onufriev, A.V. Accuracy limit of rigid 3-point water models. J. Chem. Phys. 2016, 145, 074501. [Google Scholar] [CrossRef] [Green Version]
- Marchi, M.; Procacci, P. Coordinates scaling and multiple time step algorithms for simulation of solvated proteins in the NPT ensemble. J. Chem. Phys. 1998, 109, 5194–5202. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Procacci, P. Hybrid MPI/OpenMP Implementation of the ORAC Molecular Dynamics Program for Generalized Ensemble and Fast Switching Alchemical Simulations. J. Chem. Inf. Model. 2016, 56, 1117–1121. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Friesner, R.A.; Berne, B.J. Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2). J. Phys. Chem. 2011, 115, 9431–9438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iannone, F.; Ambrosino, F.; Bracco, G.; De Rosa, M.; Funel, A.; Guarnieri, G.; Migliori, S.; Palombi, F.; Ponti, G.; Santomauro, G.; et al. Cresco Enea HPC clusters: A working example of a multifabric GPFS Spectrum Scale layout. In Proceedings of the 2019 International Conference on High Performance Computing Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; pp. 1051–1052. [Google Scholar]
- Wang, L.; Deng, Y.; Knight, J.L.; Wu, Y.; Kim, B.; Sherman, W.; Shelley, J.C.; Lin, T.; Abel, R. Modeling Local Structural Rearrangements Using FEP/REST: Application to Relative Binding Affinity Predictions of CDK2 Inhibitors. J. Chem. Theory Comput. 2013, 9, 1282–1293. [Google Scholar] [CrossRef]
- The Advantages of Free Energy Perturbation Calculations. Available online: http://xxx.lanl.gov/abs/www.schrodinger.com/products/fep (accessed on 11 February 2022).
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comp. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [Green Version]
- Procacci, P. Multiple Bennett acceptance ratio made easy for replica exchange simulations. J. Chem. Phys. 2013, 139, 124105. [Google Scholar] [CrossRef]


| Gas-Phase | ||||||
| Rep. | S | Time/ns | Exch. | RTT/ps | ||
| t-REM | 8 | 0.1 | 8.0 | 42–58% | 103 ± 12 | −3.0 ± 0.5 |
| t-REM | 8 | 0.05 | 8.0 | 15–44% | 134 ± 14 | −2.8 ± 0.6 |
| t-REM | 4 | 0.05 | 8.0 | 8–44% | 80 ± 3 | −3.3 ± 0.8 |
| Solution | ||||||
| Rep. | S | Time/ns | Exch. | RTT/ps | ||
| ST-HREM | 8 | 0.1 | 8.0 | 58–81% | 6.9 ± 0.7 | −0.17 ± 0.07 |
| ST-HREM | 8 | 0.05 | 8.0 | 44–79% | 7.1 ± 0.6 | 0.63 ± 0.1 |
| ST-HREM | 8 | 0.05 | 16.0 | 44–79% | 7.1 ± 0.6 | 0.53 ± 0.06 |
| ST-HREM | 4 | 0.05 | 16.0 | 15–44% | 6.3 ± 0.4 | 0.59 ± 0.06 |
| ST-HREM | 4 | 0.05 | 32.0 | 15–44% | 6.3 ± 0.3 | 0.51 ± 0.05 |
| Solution (FEP/FEP with -hopping) | ||||||
| Rep. | S | Time/ns | Exch. | RTT/ps | ||
| -hop | 16 | 1.0 | 12.0 | 75–87% | 11 ± 1 | n/a |
| -hop | 16 | 0.25 | 12.0 | 75–87% | 15 ± 1 | n/a |
| -hop | 16 | 0.1 | 12.0 | 47–84% | 15 ± 2 | 0.81 ± 0.22 |
| -hop | 16 | 0.05 | 8.0 | 33–78% | 24 ± 2 | 0.70 ± 0.11 |
| -hop | 16 | 0.05 | 16.0 | 33–78% | 24 ± 2 | 0.68 ± 0.09 |
| -hop | 16 | 0.05 | 32.0 | 33–78% | 24 ± 2 | 0.75 ± 0.07 |
| Time/ns | (Equation (3)) | (FEP) | ||
|---|---|---|---|---|
| 8 | −18.61 | −15.97 | −18.44(−18.43) | −18.29 |
| 16 | −18.57 | −15.91 | −18.41(−18.36) | −18.25 |
| 32 | −18.58 | −15.92 | −18.41(−18.35) | −18.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Procacci, P. Does Hamiltonian Replica Exchange via Lambda-Hopping Enhance the Sampling in Alchemical Free Energy Calculations? Molecules 2022, 27, 4426. https://doi.org/10.3390/molecules27144426
Procacci P. Does Hamiltonian Replica Exchange via Lambda-Hopping Enhance the Sampling in Alchemical Free Energy Calculations? Molecules. 2022; 27(14):4426. https://doi.org/10.3390/molecules27144426
Chicago/Turabian StyleProcacci, Piero. 2022. "Does Hamiltonian Replica Exchange via Lambda-Hopping Enhance the Sampling in Alchemical Free Energy Calculations?" Molecules 27, no. 14: 4426. https://doi.org/10.3390/molecules27144426
APA StyleProcacci, P. (2022). Does Hamiltonian Replica Exchange via Lambda-Hopping Enhance the Sampling in Alchemical Free Energy Calculations? Molecules, 27(14), 4426. https://doi.org/10.3390/molecules27144426






