1. Introduction
Water is the basis of life on our planet, ensuring the existence of humanity. Various natural and anthropogenic factors can lead to the contamination of water resources with toxic pollutants, among which heavy metal compounds are the most hazardous and carcinogenic [
1,
2,
3,
4,
5]. The growing technological impact of modern industrial enterprises and factories on the quality and purity of water contributes to the active growth of research on the effective removal of these contaminants from aqueous media using adsorption methods [
6]. In recent decades, nano materials are gaining importance in many fields [
7,
8,
9]. In particular, carbon nanotubes (CNTs), due to their highly developed surface, low mass density, effective porosity and ease of modification, are widely used to remove various heavy metals [
8]. At the same time, an increase in the accessibility of the CNT surface is facilitated by their dispersed stability through oxidation. For example, commercial single-walled and multi-walled carbon nanotubes (CNTs) were used to purify water from zinc ions Zn
2+ [
9]. To impart hydrophilicity, the CNTs were heat-treated at 350 °C for 30 min, cleaned with 70% sodium hypochlorite solution and subjected to ultrasonic cleaning for 20 min in a water bath (at 85 °C). The adsorption capacity for Zn (II) was 43.66 mg/g.
Carbon nanotubes oxidized with H
2O
2, KMnO
4 and HNO
3 were used to adsorb Cd (II) ions [
10]. Due to the functional groups introduced by oxidation, the adsorption capacity of Cd (II) reached 2.6, 5.1 and 11.0 mg g
−1 for CNTs oxidized with H
2O
2, HNO
3 and KMnO
4, respectively, at an equilibrium concentration of Cd (II) of 4 mg L
−1. The specific surface area and specific pore volume of CNTs increased after the oxidation of H
2O
2, HNO
3 and KMnO
4. Also, dispersions of oxidized multi-walled CNTs (o-CNTs) were used to remove heavy metals from acidic solutions [
11]. Oxidized multiwalled CNTs (in 65% nitric acid) were dispersed in deionized water using ultrasound in the presence of various surfactants. Numerous studies have noted that surface modification of CNTs leads to an increase in the adsorption capacity of negatively charged surfaces of modified CNTs [
12]. An even higher sorption capacity was demonstrated by a 2D carbon material. Melezhik et al. [
13] coated graphene oxide (GO) with various oxygen-containing groups and reported a high surface area. Zhao et al. [
14] described 106.3 and 68.2 mg/g sorption capacity of Cd (II) and Co (II) on graphene oxide at pH 6.0 ± 0.1 and T = 303 K. Wang et al. [
15] used ethylenediamine as a reducing agent and the obtained GO showed an adsorption capacity of 413.22, 162.33, 55.34 and 42.46 mg/g for Pb (II), Cd (II), Cu (II) and Mn (II), respectively. GO reduced by thiourea dioxide was studied for the adsorption of Th (IV) from aqueous solutions by Pan et al. [
16]. The maximum theoretical adsorption capacity of Th (IV) was 0.21 mmol at 298.15 K. It was also shown that the adsorption of Th (IV) on r-GO was described by pseudo-second-order and Langmuir isotherm models. In addition, thermodynamic parameters were determined (Δ
H0 = 4.32 kJ/mol, Δ
S0 = 69.47 J/mol K and Δ
G0 = −16.39 kJ/mol at 298.15 K), which showed that the adsorption process was spontaneous and endothermic in nature.
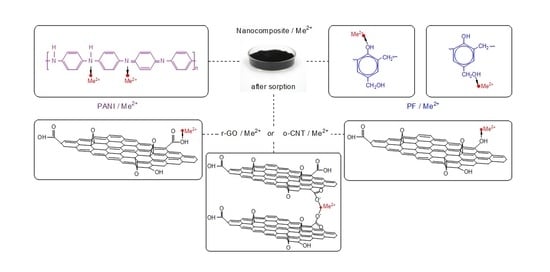
An important advantage of r-GO is the possibility of chemical modification of its surface without damage to the bulk and structural properties of the material, which made it possible to noticeably increase the adsorption capacity. As a result, r-GO is a more promising 2D material than the original GO due to the possibility of compacting and forming various commercial adsorbents for use in aqueous media. Polyaniline (PANI) is a very promising modifying agent, which contains alternating iminoquinoid and phenylenediamine groups. This is capable of adsorbing cationic and anionic contaminants through various electrostatic interactions [
17,
18]. The combination of PANI with carbon nanomaterials made it possible to adsorb heavy metal ions. For example, GO obtained by polymerization at temperatures below −20 °C with PANI nanodots showed a high Cr (VI) adsorption capacity of 1149.4 mg g
−1 in combination with the reduction to Cr (III). Another three-dimensional PANI/GO composite showed 80.7 mg g
−1 at pH 5 adsorption capacity for Hg (II). In general, it was observed that PANI/GO composites absorb heavy metals efficiently, but most publications focus on the most common Zn (II), Cd (II), Pb (II) and Cu (II) ions. Hajjaoui et al. [
19] reported good removal capacities of heavy metal ions by modifying multilayer CNTs with polyaniline. However, the use of PANI is limited by its extremely low solubility in water and most known solvents, as well as poor mechanical properties—the polymer powder does not adhere to other materials. One of the ways to eliminate this disadvantage is to obtain composite systems that combine the effective functional properties of PANI and the dispersion stability of the carrier adsorbent [
20]. There is a method for obtaining an aqueous colloidal solution of PANI, which can be used, in particular, to obtain composite graphene materials [
21]. To obtain a colloidal solution, the polyaniline base is sonicated in an aqueous solution of a resole-type phenol-formaldehyde resin. It is reasonable to assume that even more effective adsorbents can be nanocomposites in which a mixture of carbon nanomaterials is modified with polyaniline. The possibility of forming such a composite (GNS/CNT/PANI) is mentioned by Rahman et al. [
22]. Polyaniline (PANI) is a famous conductive polymer, and it has received tremendous consideration from researchers in the field of nanotechnology for the improvement of material properties including sorbents. PANI is doped easily because of its easy synthesis and remarkable environmental stability. PANI is one of the most effective organic polymeric materials used to remove various cationic and anionic pollutants from aqueous media, due to the significant content of phenylenediamine and quinonediamine functional groups. Due to its high nitrogen functionality, this polymer is often used in the extraction of heavy metal ions from aqueous media [
23]. Keeping all these facts into consideration, this article implements the synthesis of a hybrid nanostructured adsorbent based on r-GO modified with PANI. In this method, o-CNTs played a role of a structure-forming agent and as an additional component that improved the efficiency of zinc and lead metal ions removal. The developed functional nanomaterial is a multicomponent cryogel obtained using the lyophilization method.
2. Materials and Methods
2.1. Materials
To prepare a nanocomposite (cryogel r-GO/o-CNTs/PANI), the substances and materials used were oxidized CNTs (o-CNTs) obtained by oxidation of Taunit-M CNTs (NanoTechCenter LLC, Tambov, Russia). Besides this, a solution of sodium hypochlorite in the form of an aqueous paste with a mass content of 11.48% dry matter; r-GO (NanoTechCenter LLC, Tambov, Russia; prepared by reduction of graphene oxide with ascorbic acid); acetic acid (1.5 M CH3COOH) (Nevinnomyssky AZOT JSC, Nevinnomyssk, Russia); resole water-soluble PF Fenotam-GR-326 (Krata PJSC, Tambov, Russia; with a dry matter content of 50%; aniline hydrochloric acid; ammonium persulfate; aqueous ammonia containing 25% ammonia and hydrochloric acid (JSC REACHIM LLC, Moscow, Russia) were used. To determine the adsorption capacity of the cryogel for heavy metals, model solutions of nitrates were used, that is, zinc nitrate Zn(NO3)2·6H2O and lead (II) nitrate Pb(NO3)2 (Scientific and Production Kama Chemical Company LLC, Perm, Russia).
2.2. Preparation Methods
2.2.1. Polyaniline Preparation Method
PANI was produced under laboratory conditions by the standard method, including the oxidative polymerization of aniline in an acidic medium [
24]. In 0.115 M HCl 97.2 g (0.75 mol) of aniline hydrochloride was added and stirred until complete dissolution. Separately, an aqueous solution was prepared of 213.93 g (0.9375 mol) of ammonium persulfate in 375 mL water, which was then added to the hydrochloric acid solution of aniline hydrochloride with continuous stirring in an argon atmosphere, after which the stirring process was continued for another 2 h. Then the mixture was kept for 11 h to complete the polymerization process. Then the reaction mixture was transferred to a filter and washed first with a 0.1 M hydrochloric acid solution until a colorless filtrate was obtained following washing with distilled water until pH ≈ 6. Further, for deprotonation, the product was washed on the filter with a 1 M ammonia solution and then with distilled water until the filtrate had a neutral pH. Excess moisture was filtered out using a vacuum pump, and the finished product was packed in a sealed container. To determine the mass content of dry matter in the resulting paste, a portion of the sample was dried in an oven at 110 °C to constant weight. The mass content of dry matter was 11%. The final material was used in the form of an aqueous paste since complete drying leads to a strong and irreversible agglomeration of the particles.
2.2.2. Nanocomposite Preparation Method
Synthesis of the base hydrogel was carried out at room temperature without preliminary preparation of materials. Aqueous pastes of the initial components (r-GO/o-CNTs/PANI/FFS) were taken in an amount corresponding to 1 g of dry matter, mixed in a ratio of 1:1:1:1 in distilled water, bringing the total weight to 100 g. Then, the mixture was subjected to ultrasonication for an hour (frequency 22 ± 0.4 kHz) to destroy particle aggregates and uniformly distribute the mixture components. Then, 25 mL of 9% acetic acid was added to the resulting colloid to coagulate the solution. The mixture was kept for 1 h to complete coagulation and then filtered on a polypropylene microfilter and washed with distilled water to remove reaction side-products. Excess moisture was removed with a vacuum filter for 10 min. To prepare a dry r-GO/o-CNTs/PANI nanocomposite, the solvent was removed from the hydrogel pores by freeze-drying at a temperature of −40…−50 °C and a pressure of about 5–8 Pa using a Scientz-10n unit (Science, Ningbo, China).
2.3. Characterization Methods
Micrographs of the materials were obtained using a scanning electron microscope (SEM) MERLIN (Carl Zeiss, Jena, Germany) and a transmission electron microscope (TEM) JEM-2010 instrument (JEOL, Tokyo, Japan). The structural characteristics of the initial components and the nanocomposite were analyzed by X-ray phase analysis using a Thermo Scientific ARL Equinox 1000 X-ray diffractometer (TechTrend Science Co., Ltd., Taoyuan, Taiwan). The diffraction patterns were taken at a wavelength of λ = 0.1540562 nm (copper anode). Data registration was carried out in the range of 2θ angles from 10° to 110°. Using the diffraction patterns, the structure of crystalline substances and phase composition were studied. The sizes of crystallites (regions of coherent scattering) were determined by the Debye–Scherrer formula (1) [
25]
where
D is crystallite size, nm;
n is the coefficient depending on the particle shape and close to 1; λ is the wavelength of X-ray radiation, nm; β is the half-width of the peak in the diffraction pattern, rad; θ is peak maximum angle, deg.
To study the dependence of the change in mass with temperature, a combined thermal analysis was carried out involving the simultaneous use of thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) using a NETZSCH STA 449 F3 Jupiter instrument. The study was carried out in air at a heating rate of 10 K/min. The specific surface area and pore space parameters were measured by nitrogen adsorption at 77 K using an Autosorb iQ automatic analyzer (Quantachrome Instruments). The multipoint Brunauer–Emmett–Teller (BET) method was used to determine the specific surface area, and a mathematical model based on the density functional theory (DFT) was used to determine the volume and pore size. The degassing procedure was carried out at 200 °C and a pressure of 1.3 × 10−3 Pa for 8–10 h. For calculating the specific surface area, P/P0 values up to 0.3 were used. Samples were analyzed using a DXR Raman Microscope with an excitation laser wavelength of λ = 633 nm and a range of 100–3500 cm–1. To obtain the FT-IR spectra of the initial components and the nanocomposite, a Jasco FT/IR 6700 IR Fourier spectrometer was used. FTIR measurements were performed using KBr pellets. Number of scans—16. Resolution—4 cm−1. Samples were prepared for analysis. The aqueous pastes and suspensions were dried in an oven at 50 °C to constant weight and pressed into tablets with potassium bromide.
2.4. Adsorption Study
The equilibrium concentration of heavy metal ions in selected aliquots of aqueous solutions (deionized water) was measured using energy dispersive X-ray fluorescence spectrometry (ARLQuant ThermoScientific spectrometer, ThermoScientific, Waltham, MA, USA).
Static sorption capacity of sorbents
, mg g
−1 was calculated by the formula:
where
C0 and
Ce are initial and final concentrations of substances in solution, mg L
−1;
V is the solution volume, L;
m is the weight of sorbent sample, g.
2.4.1. pH Effect
The study of the effect of the solution pH on the sorption capacity of the r-GO/o-CNTs/PANI nanocomposite was carried out using an H1 2210 pH Meter. A buffer system with a given pH value was gotten by adding the required acids (hydrochloric, acetic and amino acetic) and alkali (NaOH) to deionized water in given proportions. The experiments were carried out at room temperature. Stock solutions were obtained using zinc nitrate [Zn(NO3)2·6H2O] and lead (II) nitrate [Pb(NO3)2] of analytical grade by dissolving weighed portions in 1 L of deionized water, which were then diluted to the required concentrations. The sorbent weighing 0.005 g was placed in conical tubes with a capacity of 50 mL and poured into 30 mL of a model solution of heavy metals with C0 = 100 mg L−1. The tubes were shaken for an hour on a rotator, then the solution was filtered to distinguish the solid phase. All experimental situations for the process were stable for each sample.
2.4.2. Dosage Effect
For precise valuation of the sorption activity of the material, it is essential to use the weight of the adsorbent sample at which the sorption ability for each extractable component is maximum under the designated experimental situations of the process. To regulate the effect of the weight of the adsorbent on its sorption capacity, samples were used, which are acetic acetate buffer systems with a volume of 30 mL, containing solutions of Zn(NO3)2·6H2O and Pb(NO3)2 with C0 = 150 mg L−1. For experimental studies, the sorbent weights used were 0.001, 0.005, 0.01, 0.02, 0.03 and 0.05 g. The tubes were stunned for 30 min on a rotator, then the solution was cleaned to separate the solid phase, and the equilibrium concentration of ions in the solution was measured.
2.4.3. Kinetic Study
To determine the optimal sorption time of Pb (II) and Zn (II) ions on the synthesized nanocomposite, kinetic experiments were carried out in a limited volume (batch kinetics experiments). The sorbent weighing 0.005 g was placed in 30 mL of heavy metal solution with C0 = 100 mg L−1. Given the significant sorption activity in the initial period of the process, it is necessary to determine a larger number of samples in the preliminary period of time. The experiments were carried out at 5, 10, 15, 30, 45 and 60 min time intervals. Then the solution was filtered to discrete the solid phase, and the equilibrium amount of ions in the solution was decided.
2.4.4. Isotherm Study
The study of the state of adsorption equilibrium was carried out using samples of model solutions of metal ions with varying concentrations at a sorbent dose of 0.005 g. A solution of the required concentration was made by sequential dilution of acetic acetate buffer solutions with an amount of 300 mg L−1 (solutions with C0 = 20, 50, 100, 200 and 300 mg L−1 were obtained). The tubes were shaken in a rotator for 30 min and filtered to discrete the solid phase. Then the equilibrium amount of ions in the solution was measured.
2.4.5. Thermodynamic Study
To confirm the correctness of the expectations around the nature of the studied sorption procedures on the made nanocomposite, it is required to examine the effect of temperature on the efficacy of ion removal from aqueous solutions. For this, 30 mL solutions of various concentrations C0 = 20, 50, 100, 200, 300, 400 mg L−1 were used. Sorbent in the amount of 0.005 g was added to the solution and then shaken for 30 min. In this case, the isotherms were obtained at different temperatures: 25, 35 and 45 °C. The solution was filtered to remove the solid, and the equilibrium amount of ions in the solution was measured.
2.4.6. Desorption Study
To study the effect of desorption, 30 mL of a solution with a given concentration and 0.005 g of a sorbent were taken. The initial solution was prepared by successive dilution of acetic-acetate buffer solutions of lead and zinc ions with C0 = 400 mg L−1 (solutions were obtained C0 = 20, 50, 100, 200, 300, 400 mg L−1). The tubes were shaken on a rotator for 30 min, and the filtrate was taken to measure the equilibrium concentration. Then, after separating the solid phase, it was dried at a temperature of 55 °C for ~15 min to remove surface moisture. After that, the dried nanocomposite was poured with a 30 mL buffer solution with pH = 6 and shaken for an hour on a programmable rotator. The suspension was then filtered and the equilibrium concentration was measured after the desorption stage.
2.5. Process Modeling
2.5.1. Adsorption Kinetics
To describe kinetics, models are traditionally used that simulate the processes of mass transfer using formal equations of chemical kinetics. This is due to the complexity of the quantitative description of diffusion processes using simple models. This approach most often involves the use of pseudo-first- and pseudo-second-order models [
26,
27].
The pseudo-first-order equation of the Lagergren model has the following form.
where
is adsorption at equilibrium, mg g
−1;
is adsorption at time t, mg g
−1;
is pseudo-first-order adsorption rate constant, min
−1.
After integration and application of boundary conditions (from
to
and
to and
) the equation takes the following form.
It should be noted that the equation of the pseudo-first-order kinetics model coincides mathematically with the equation characteristic of diffusion processes. However, the value of the sorption rate constant was used here as a fixed parameter of the model. In the case of diffusion, the rate of the process depends on the size of the sorbent particles and the film thickness. If the limiting stage is chemical kinetics, then the sorption rate does not depend on the above factors but depends only on the concentration and temperature. Thus, when the sorption process kinetics is described by a pseudo-first-order kinetics model, the sorption of a substance is preceded by its diffusion.
The classical form of the equation of the pseudo-second-order kinetics model [
28,
29] has the following form.
where
is pseudo-second-order adsorption rate constant (g mg
−1 min
−1).
After integration and application of boundary conditions (from
to
and
to and
) the equation takes the following form.
The linearized form of the equation that is most commonly reported in the literature has the following form.
The applicability of this model indicated the occurrence of a chemical reaction that limits the sorption kinetics. Azizian [
30] and Liu and Shen [
31] showed that Langmuir kinetics could be reduced to either pseudo-first-order velocity equations or second-order velocity equations. However, there are works in which the pseudo-second-order model is considered a rather flexible mathematical formula capable of modeling the sorption kinetics of internal mass transfer (diffusion) for systems with flat and spherical particles [
32].
The Elovich model is mainly used to describe chemical adsorption on highly heterogeneous adsorbents, but it does not suggest any specific mechanism for the adsorbate–adsorbent interaction [
33].
The equation of the Elovich model has the form:
where
α is the preliminary adsorption rate constant (min
−1 mg g
−1);
β is the surface coverage and activation energy of chemisorption (g mg
−1).
Weber and Morris described the intraparticle [
34] uptake of the adsorption process to be proportional to the half-power of time:
where
kid is the internal diffusion coefficient (mg g
−1min
−0.5);
C is the boundary layer thickness (mg g
−1).
2.5.2. Adsorption Isotherms
The Langmuir equation deals with monolayer adsorption [
35]. Adsorption occurs on a homogeneous surface covered with adsorption sites. The free centers of the sorbent and the adsorbate form an interaction in an ideal solution.
The linear form of the Langmuir isotherm has the following form:
where
is maximum sorption capacity, mg g
−1;
is adsorbent–adsorbate affinity distribution (adsorption energy), L mg
−1.
The Freundlich isotherm is one of the earliest empirical equations used to describe non-ideal sorption equilibrium data and describes polymolecular adsorption. According to Freundlich’s theory, the absorption process is most often initial surface adsorption followed by condensation resulting from strong interactions [
35].
The linear form of the Freundlich isotherm is given below.
where
and
are Freundlich constants,
giving an indication of how favorable the adsorption process and
(mg g
−1 L mg
−1) is the adsorption capacity of the adsorbent.
The Temkin isotherm contains a parameter that takes into account interactions between adsorption sites and the adsorbate. The model assumes that the heat of adsorption of all molecules in the layer decreases linearly as the layer is filled. This process proceeds to a greater extent according to a linear law than according to a logarithmic one [
36].
The linear form of the Temkin isotherm is given below.
where
is equilibrium binding constant corresponding to the maximum binding energy (L.mg
−1)
is the Temkin isotherm constant.
is an absolute temperature (K).
is a universal gas constant (8.314 J (mol K)
−1).
is a constant related to the heat of sorption (J.moL
−1).
2.5.3. Adsorption Thermodynamics
To determine the spontaneity of the adsorption process and describe the absorption mechanism, enthalpy change (ΔH°), entropy change (ΔS°) and free energy change (ΔG°) are measured [
37].
The Gibbs equation is used to study the effect of temperature on equilibrium adsorption. The equation can be represented as follows:
is a thermodynamic equilibrium constant (L mol
−1), which can be found through the following equation:
where
is the equilibrium concentration of the adsorbate adsorbed on the sorbent (mg L
−1) and
is an equilibrium concentration of adsorbate in solution (mg L
−1).
The value of the enthalpy of the sorption process is found by graphical interpolation of experimental data using the Van’t Hoff isotherm equation.
2.5.4. Desorption
To calculate the desorption, we used the following equation.
where
are equilibrium concentrations in solution during desorption, initial concentration of the solution and equilibrium concentration in solution during adsorption, respectively [
38].
4. Conclusions
The article proposed a new nanocomposite material based on reduced graphene oxide and oxidized CNTs modified with polyaniline. To stabilize the composite in an aqueous medium, the phenol-formaldehyde resin was added as a component. Physical-chemical, textural, structural and morphological properties were studied using SEM and TEM, Raman and IR-Fourier spectroscopy, XRD and TG/DSC. To preserve the structure and volume of the porous space at the final stage of preparation, the nanocomposite was dried using lyophilic treatment. In this study, the sorption properties of nanocomposite were studied for the elimination of lead and zinc metal ions from water. The adsorption kinetics of metal ions removal was pseudo-second-order, Elovich and intraparticle diffusion models. When describing the equilibrium state of adsorption, the Langmuir and Temkin models were fitted well. The removal capacities were 346 and 581 mg/g at pH 6.5, 0.005 g/30 mL dose and 15 min contact time. These conditions made this method highly applicable, nature-friendly and fast. Therefore, the reported method may be used successfully for the removal of lead and zinc from water.