Temperature Dependence of the Electrical Properties of Na2Ti3O7/Na2Ti6O13/POMA Composites
Abstract
:1. Introduction
2. Results and Discussion
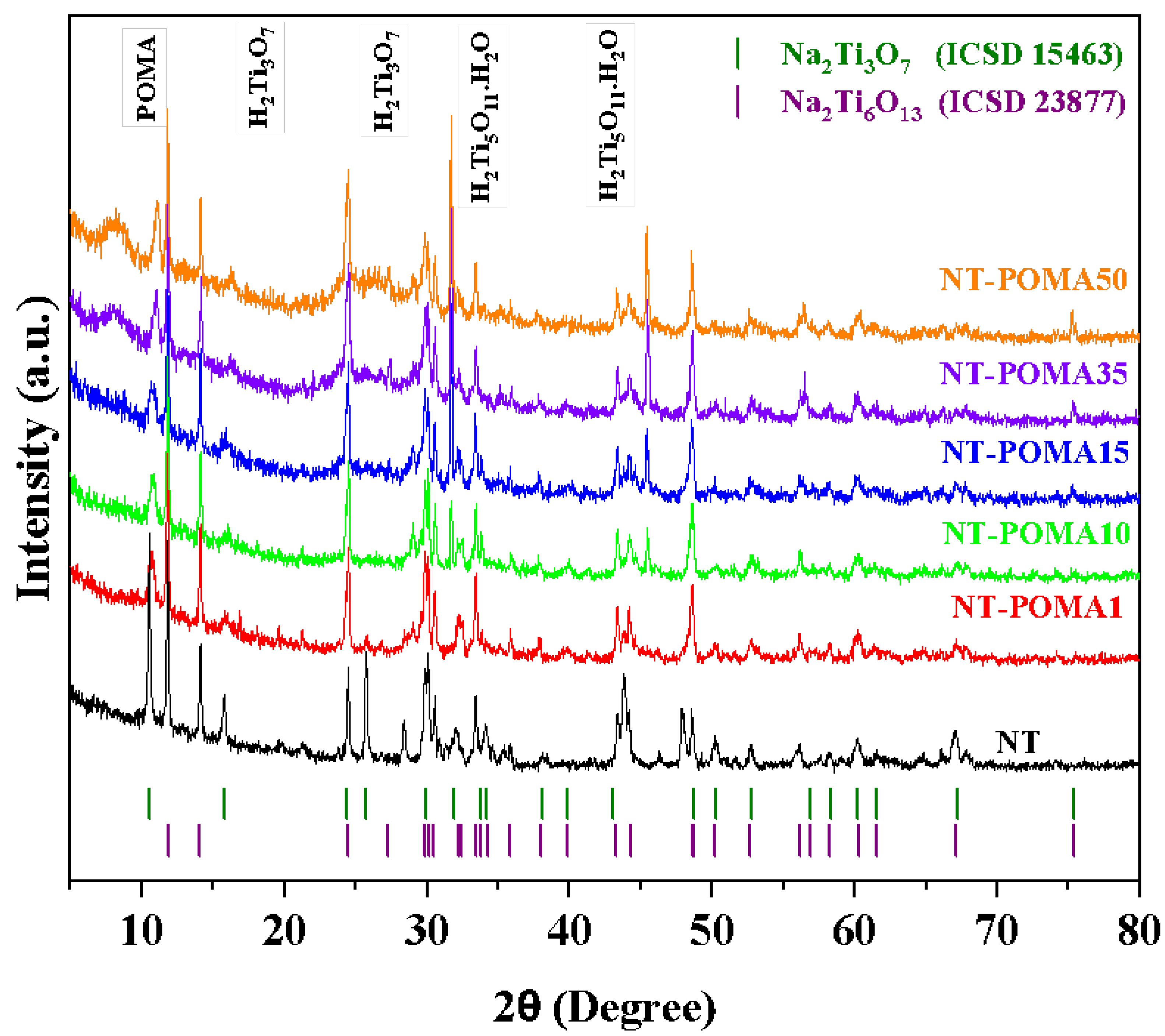
2.1. X-ray Diffraction (XRD) Analysis
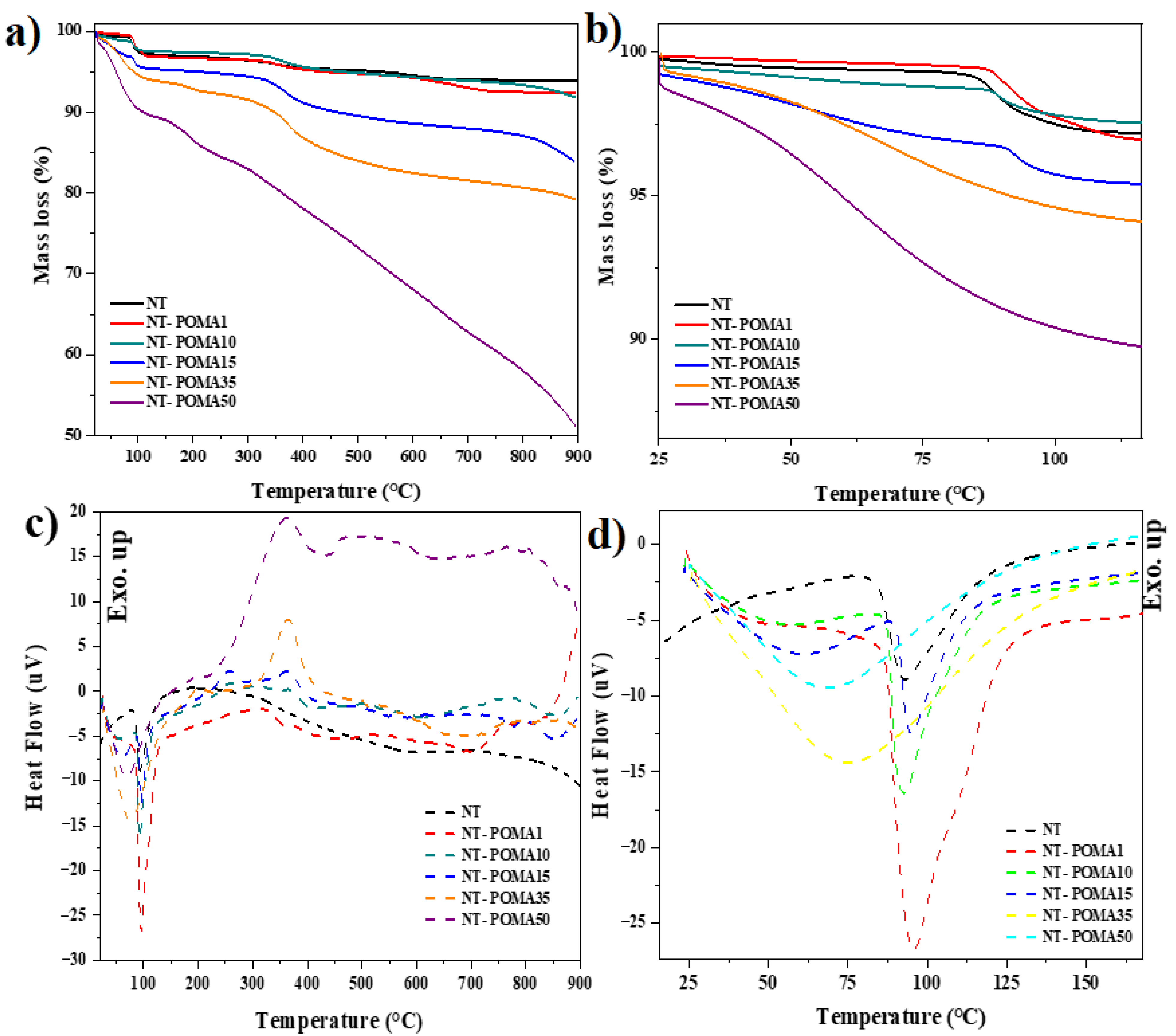
2.2. Thermogravimetric (TGA) and Differential Thermal Analysis (DTA)
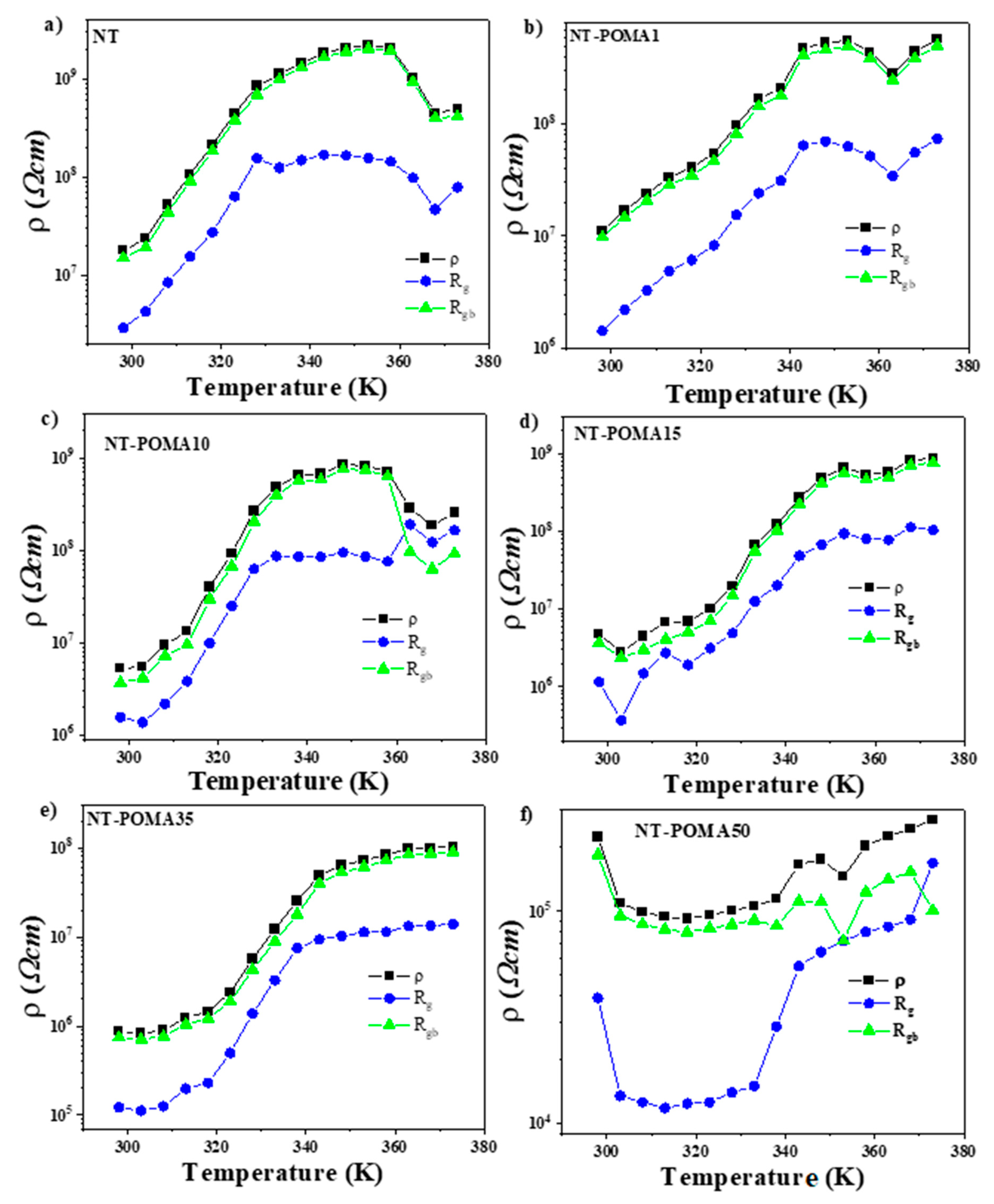
2.3. Electrical Behavior
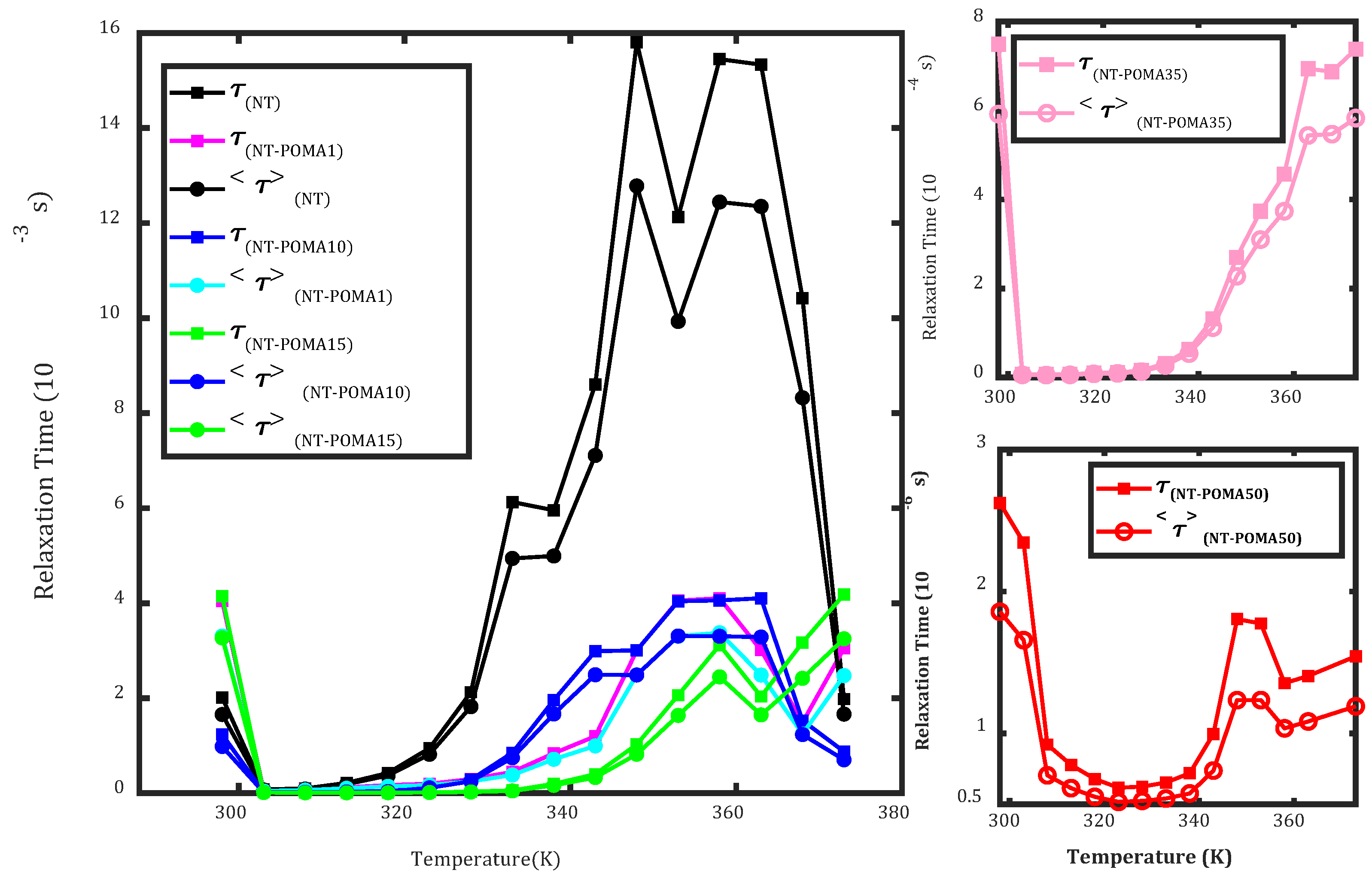
Electrical Properties in the Time and Frequency Domains
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, S.; Li, B.; Wang, J. Hydrothermal Growth of PX-PbTiO3 Nanowires with K2Ti6O13 as Precursors. J. Cryst. Growth 2020, 546, 125792. [Google Scholar] [CrossRef]
- Goyal, R.K.; Rokade, K.A.; Kapadia, A.S.; Selukar, B.S.; Garnaik, B. PEEK/SiO2 Composites with High Thermal Stability for Electronic Applications. Electron. Mater. Lett. 2013, 9, 95–100. [Google Scholar] [CrossRef]
- Folorunso, O.; Hamam, Y.; Sadiku, R.; Ray, S.S.; Adekoya, G.J. Synthesis Methods of Borophene, Graphene-Loaded Polypyrrole Nanocomposites and Their Benefits for Energy Storage Applications: A Brief Overview. FlatChem. 2021, 26, 100211. [Google Scholar] [CrossRef]
- Capiglia, C.; Mustarelli, P.; Quartarone, E.; Tomasi, C.; Magistris, A. Effects of Nanoscale SiO2 on the Thermal and Transport Properties of Solvent-Free, Poly(Ethylene Oxide) (PEO)-Based Polymer Electrolytes. Solid State Ionics 1999, 118, 73–79. [Google Scholar] [CrossRef]
- Chung, S.H.; Wang, Y.; Persi, L.; Croce, F.; Greenbaum, S.G.; Scrosati, B.; Plichta, E. Enhancement of Ion Transport in Polymer Electrolytes by Addition of Nanoscale Inorganic Oxides. J. Power Sources 2001, 97–98, 644–648. [Google Scholar] [CrossRef]
- Weston, J.E.; Steele, B.C.H. Effects of Preparation Method on Properties of Lithium Salt-Poly(Ethylene Oxide) Polymer Electrolytes. Solid State Ionics 1982, 7, 81–88. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, C.; Peng, G.; Chen, X.; Yao, X.; Bai, Y.; Wu, F.; Chen, S.; Xu, X. A New Solid Polymer Electrolyte Incorporating Li10GeP2S12 into a Polyethylene Oxide Matrix for All-Solid-State Lithium Batteries. J. Power Sources 2016, 301, 47–53. [Google Scholar] [CrossRef]
- Chen, F.; Yang, D.; Zha, W.; Zhu, B.; Zhang, Y.; Li, J.; Gu, Y.; Shen, Q.; Zhang, L.; Sadoway, D.R. Solid Polymer Electrolytes Incorporating Cubic Li7La3Zr2O12 for All-Solid-State Lithium Rechargeable Batteries. Electrochim. Acta 2017, 258, 1106–1114. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Y.; Liu, X.; Zhong, H.; Xu, H.; Xu, Z.; Shao, H.; Ding, F. Suppression of Lithium Dendrite Formation by Using LAGP-PEO (LiTFSI) Composite Solid Electrolyte and Lithium Metal Anode Modified by PEO (LiTFSI) in All-Solid-State Lithium Batteries. ACS Appl. Mater. Interfaces 2017, 9, 13694–13702. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.; Li, S.P.; Fan, L.Z.; Nan, C.W.; Goodenough, J.B. PEO/Garnet Composite Electrolytes for Solid-State Lithium Batteries: From “Ceramic-in-Polymer” to “Polymer-in-Ceramic”. Nano Energy 2018, 46, 176–184. [Google Scholar] [CrossRef]
- Deivanayaki, S.; Ponnuswamy, V.; Ashokan, S.; Jayamurugan, P.; Mariappan, R. Synthesis and Characterization of TiO2-Doped Polyaniline Nanocomposites by Chemical Oxidation Method. Mater. Sci. Semicond. Process. 2013, 16, 554–559. [Google Scholar] [CrossRef]
- Lai, C.; Li, G.R.; Dou, Y.Y.; Gao, X.P. Mesoporous Polyaniline or Polypyrrole/Anatase TiO2 Nanocomposite as Anode Materials for Lithium-Ion Batteries. Electrochim. Acta 2010, 55, 4567–4572. [Google Scholar] [CrossRef]
- Folorunso, O.; Onibonoje, M.O.; Hamam, Y.; Sadiku, R.; Ray, S.S. Fabrication and Model Characterization of the Electrical Conductivity of PVA/PPy/RGO Nanocomposite. Molecules 2022, 27, 3696. [Google Scholar] [CrossRef] [PubMed]
- de Souza Pinto, S.; Machado, J.P.B.; Gomes, N.A.S.; Rezende, M.C. Electromagnetic, Morphological and Structural Characterization of Microwave Absorbers Based on POMA/Magnetic Filament Composites. J. Magn. Magn. Mater. 2018, 449, 406–414. [Google Scholar] [CrossRef]
- Raposo, M.; Oliveira, O.N. Adsorption of Poly(o-Methoxyaniline) in Layer-by-Layer Films. Langmuir 2002, 18, 6866–6874. [Google Scholar] [CrossRef]
- Diniz, M.O.; Coelho, R.S.; Bianchi, R.F.; Guerra, E.M. Electrical Impedance of V2O5/POMA Hybrid Film Deposited by Casting for Application in Ammonia Gas Sensor. J. Electron. Mater. 2021, 50, 450–455. [Google Scholar] [CrossRef]
- Gao, R.; Zhu, H.; Gao, S.; Liu, L.; Xu, Y.; Zhang, X.; Cheng, X.; Huo, L. Synthesis of ZnO@poly-o-Methoxyaniline Nanosheet Composite for Enhanced NH3-Sensing Performance at Room Temperature. Microchim. Acta 2020, 187, 510. [Google Scholar] [CrossRef]
- Mohammadi, A.; Peighambardoust, S.J.; Entezami, A.A.; Arsalani, N. High Performance of Covalently Grafted Poly(o-Methoxyaniline) Nanocomposite in the Presence of Amine-Functionalized Graphene Oxide Sheets (POMA/f-GO) for Supercapacitor Applications. J. Mater. Sci. Mater. Electron. 2017, 28, 5776–5787. [Google Scholar] [CrossRef]
- Tsai, C.H.; Huang, W.C.; Hsu, Y.C.; Shih, C.J.; Teng, I.J.; Yu, Y.H. Poly(o-Methoxyaniline) Doped with an Organic Acid as Cost-Efficient Counter Electrodes for Dye-Sensitized Solar Cells. Electrochim. Acta 2016, 213, 791–801. [Google Scholar] [CrossRef]
- Sangamithirai, D.; Munusamy, S.; Narayanan, V.; Stephen, A. Fabrication of Neurotransmitter Dopamine Electrochemical Sensor Based on Poly(o-Anisidine)/CNTs Nanocomposite. Surf. Interfaces 2016, 4, 27–34. [Google Scholar] [CrossRef]
- Dawn, A.; Nandi, A.K. Slow Doping Rate in DNA-Poly(o-Methoxyaniline) Hybrid: Uncoiling of Poly(o-Methoxyaniline) Chain on DNA Template. Macromolecules 2005, 38, 10067–10073. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lin, J.C.; Wu, S.H. One-Step Growth of Na2Ti3O7 Nanorods for Enhanced Photocatalytic Activities and Recyclability. J. Alloys Compd. 2018, 749, 955–960. [Google Scholar] [CrossRef]
- Ramýìrez-Salgado, J.; Fabry, P. Feasibility of Potentiometric Oxygen Gas Sensor Based on Perovskite and Sodium Titanate Measuring Electrode. Sens. Actuators B Chem. 2002, 82, 34–39. [Google Scholar] [CrossRef]
- Gao, L.; Chen, S.; Zhang, L.; Yang, X. High Performance Sodium Ion Hybrid Supercapacitors Based on Na2Ti3O7 Nanosheet Arrays. J. Alloys Compd. 2018, 766, 284–290. [Google Scholar] [CrossRef]
- Dong, S.; Shen, L.; Li, H.; Pang, G.; Dou, H.; Zhang, X. Flexible Sodium-Ion Pseudocapacitors Based on 3D Na2Ti3O7 Nanosheet Arrays/Carbon Textiles Anodes. Adv. Funct. Mater. 2016, 26, 3703–3710. [Google Scholar] [CrossRef]
- Cao, Y.; Ye, Q.; Wang, F.; Fan, X.; Hu, L.; Wang, F.; Zhai, T.; Li, H. A New Triclinic Phase Na2Ti3O7 Anode for Sodium-Ion Battery. Adv. Funct. Mater. 2020, 30, 2003733. [Google Scholar] [CrossRef]
- Dynarowska, M.; Kotwiñski, J.; Leszczynska, M.; Marzantowicz, M.; Krok, F. Ionic Conductivity and Structural Properties of Na2Ti3O7 Anode Material. Solid State Ionics 2017, 301, 35–42. [Google Scholar] [CrossRef]
- Hwang, J.; Setiadi Cahyadi, H.; Chang, W.; Kim, J. Uniform and Ultrathin Carbon-Layer Coated Layered Na2Ti3O7 and Tunnel Na2Ti6O13 Hybrid with Enhanced Electrochemical Performance for Anodes in Sodium Ion Batteries. J. Supercrit. Fluids 2019, 148, 116–129. [Google Scholar] [CrossRef]
- Leyet, Y.; Guerrero, F.; Anglada-Rivera, J.; de Souza, R.F.B.; Brito, W.R.; Aguilera, L.; Pocrifka, L.A.; Peña-Garcia, R.; Padrón-Hernández, E.; de la Cruz Pérez, J. Synthesis of Na2Ti3O7 Nanoparticles by Sonochemical Method for Solid State Electrolyte Applications. J. Solid State Electrochem. 2018, 22, 1315–1319. [Google Scholar] [CrossRef]
- da Silva, J.P.; Biondo, M.M.; Nobre, F.X.; Anglada-Rivera, J.; Almeida, A.; Agostinho-Moreira, J.; Sanches, E.A.; da S. Paula, M.M.; Aguilera, L.; Leyet, Y. Structure and Electrical Properties of the Composite Na2Ti3O7/ Na2Ti6O13/POMA: A Study of the Effect of Adding POMA. J. Alloys Compd. 2021, 867, 159025. [Google Scholar] [CrossRef]
- Basilio, L.A.L.; Silva, J.H.L.; Xavier, F.; Aguilera, L.; Guerrero, F.; Antonelli, E.; Anglada-Rivera, J.; Garcia, J.E.; Silva, R.S.; Leyet, Y. Toward a New PTCR Material Based on the Na2Ti6O13/Na2Ti3O7 System. Mater. Res. Bull. 2021, 140, 111311. [Google Scholar] [CrossRef]
- Badran, H.A.; Hussain, H.F.; Ajeel, K.I. Nonlinear Characterization of Conducting Polymer and Electrical Study for Application as Solar Cells and Its Antibacterial Activity. Opt. Int. J. Light Electron Opt. 2016, 127, 5301–5309. [Google Scholar] [CrossRef]
- Michalik, A.; Tzavalas, S.; Singh, B.; Le, H.D. Semiconductive Polymeric Coatings for Outdoor Polymeric Insulation. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1402–1408. [Google Scholar] [CrossRef]
- Huybrechts, B.; Ishizaki, K.; Takata, M. The Positive Temperature Coefficient of Resistivity in Barium Titanate. J. Mater. Sci. 1995, 30, 2463–2474. [Google Scholar] [CrossRef]
- Biondo, M.M.; de Oliveira, L.M.; Lima, S.X.; de Souza, A.C.; Rocha, A.L.F.; da Silva, J.P.; Ruiz, Y.L.; Giacon, V.M.; Campelo, P.H.; Sanches, E.A. Chemically Synthesized Poly(o-Methoxyaniline): Influence of Counterions on the Structural and Electrical Properties. J. Mol. Struct. 2020, 1205, 127588. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. Magnetic Structure Determination from Powder Diffraction Using the Program FullProf. In Applied Crystallography; World Scientific Publishing: Singapore, 2001; pp. 30–36. [Google Scholar] [CrossRef]
- Andersson, S.; Wadsley, A.D. The Crystal Structure of Na2Ti3O7. Acta Crystallogr. 1961, 14, 1245–1249. [Google Scholar] [CrossRef]
- Andersson, S.; Wadsley, A.D. The Structures of Na2Ti6O13 and Rb2Ti6O13 and the Alkali Metal Titanates. Acta Crystallogr. 1962, 15, 194–201. [Google Scholar] [CrossRef]
- Supothina, S.; Rattanakam, R.; Tawkaew, S. Hydrothermal Synthesis and Photocatalytic Activity of Anatase TiO2 Nanofiber. J. Nanosci. Nanotechnol. 2012, 12, 4998–5003. [Google Scholar] [CrossRef]
- Cho, S.H.; Adhikari, R.; Kim, S.H.; Kim, T.H.; Lee, S.W. Microwave Assisted Hydrothermal Synthesis and Structural Characterization of TiO2 Nanotubes. J. Nanosci. Nanotechnol. 2015, 15, 7391–7394. [Google Scholar] [CrossRef]
- Torres-Martínez, L.M.; Juárez-Ramírez, I.; Del Ángel-Sánchez, K.; Garza-Tovar, L.; Cruz-López, A.; Del Ángel, G. Rietveld Refinement of Sol-Gel Na2Ti6O13 and Its Photocatalytic Performance on the Degradation of Methylene Blue. J. Sol-Gel Sci. Technol. 2008, 47, 158–164. [Google Scholar] [CrossRef]
- Xu, Y.; Bauer, D.; Lübke, M.; Ashton, T.E.; Zong, Y.; Darr, J.A. High-Power Sodium Titanate Anodes; a Comparison of Lithium vs. Sodium-Ion Batteries. J. Power Sources 2018, 408, 28–37. [Google Scholar] [CrossRef]
- Sauvet, A.L.; Baliteau, S.; Lopez, C.; Fabry, P. Synthesis and Characterization of Sodium Titanates Na 2Ti 3O 7 and Na 2Ti 6O 13. J. Solid State Chem. 2004, 177, 4508–4515. [Google Scholar] [CrossRef]
- Baliteau, S.; Sauvet, A.L.; Lopez, C.; Fabry, P. Controlled Synthesis and Characterization of Sodium Titanate Composites Na2Ti3O7/Na2Ti6O13. Solid State Ionics 2007, 178, 1517–1522. [Google Scholar] [CrossRef]
- Fagundes, N.G.; Nobre, F.X.; Basilio, L.A.L.; Melo, A.D.; Bandeira, B.; Sales, J.C.C.; Andrade, J.C.S.; Anglada-Rivera, J.; Aguilera, L.; Pérez de la Cruz, J.; et al. Novel and Simple Way to Synthesize Na2Ti6O13 Nanoparticles by Sonochemical Method. Solid State Sci. 2019, 88, 63–66. [Google Scholar] [CrossRef]
- Alves, W.F.; Venancio, E.C.; Leite, F.L.; Kanda, D.H.F.; Malmonge, L.F.; Malmonge, J.A.; Mattoso, L.H.C. Thermo-Analyses of Polyaniline and Its Derivatives. Thermochim. Acta 2010, 502, 43–46. [Google Scholar] [CrossRef]
- Gomes, C.E.; Oliveira, A.S.M. Chemical Polymerization of Aniline in Hydrochloric Acid (HCl) and Formic Acid (HCOOH) Media. Differences Between the Two Synthesized Polyanilines. Am. J. Polym. Sci. 2012, 2, 5–13. [Google Scholar] [CrossRef]
- Sreedhar, B.; Sairam, M.; Chattopadhyay, D.K.; Mitra, P.P.; Mohan Rao, D.V. Thermal and XPS Studies on Polyaniline Salts Prepared by Inverted Emulsion Polymerization. J. Appl. Polym. Sci. 2006, 101, 499–508. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy Theory, Experiment and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; Volume 125, ISBN 0-471-64749-7. [Google Scholar]
- Léon, C.; Rivera, A.; Várez, A.; Sanz, J.; Santamaria, J.; Ngai, K.L. Origin of Constant Loss in Ionic Conductors. Phys. Rev. Lett. 2001, 86, 1279–1282. [Google Scholar] [CrossRef]
- Feldman, Y.; Puzenko, A.; Ryabov, Y. Non-Debye Dielectric Relaxation in Complex Materials. Chem. Phys. 2002, 284, 139–168. [Google Scholar] [CrossRef]
- León, C.; Lucía, M.; Santamaría, J.; Sánchez-Quesada, F. Universal Scaling of the Conductivity Relaxation in Crystalline Ionic Conductors. Phys. Rev. B Condens. Matter Mater. Phys. 1998, 57, 41–44. [Google Scholar] [CrossRef]
- Teo, L.P. Impedance Spectroscopy Analysis of Li2SnO3. Ionics 2017, 23, 309–317. [Google Scholar] [CrossRef]
- Dzwonkowski, P.; Eddrief, M.; Julien, C.; Balkanski, M. Electrical AC Conductivity of B2O3xLi2O Glass Thin Films and Analysis Using the Electric Modulus Formalism. Mater. Sci. Eng. B 1991, 8, 193–200. [Google Scholar] [CrossRef]
- Rivera-Calzada, A.; Kaminski, K.; Leon, C.; Paluch, M. Ion Dynamics under Pressure in an Ionic Liquid. J. Phys. Chem. B 2008, 112, 3110–3114. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dos Santos Costa, S.; Pereira da Silva, J.; Moraes Biondo, M.; Sanches, E.A.; Da Silva Paula, M.M.; Xavier Nobre, F.; Anglada Rivera, J.; Alexis Zulueta, Y.; Torikachvili, M.S.; Vieira Sampaio, D.; et al. Temperature Dependence of the Electrical Properties of Na2Ti3O7/Na2Ti6O13/POMA Composites. Molecules 2022, 27, 5756. https://doi.org/10.3390/molecules27185756
Dos Santos Costa S, Pereira da Silva J, Moraes Biondo M, Sanches EA, Da Silva Paula MM, Xavier Nobre F, Anglada Rivera J, Alexis Zulueta Y, Torikachvili MS, Vieira Sampaio D, et al. Temperature Dependence of the Electrical Properties of Na2Ti3O7/Na2Ti6O13/POMA Composites. Molecules. 2022; 27(18):5756. https://doi.org/10.3390/molecules27185756
Chicago/Turabian StyleDos Santos Costa, Salomão, Juliana Pereira da Silva, Matheus Moraes Biondo, Edgar Aparecido Sanches, Marcos Marques Da Silva Paula, Francisco Xavier Nobre, José Anglada Rivera, Yohandys Alexis Zulueta, Milton S. Torikachvili, David Vieira Sampaio, and et al. 2022. "Temperature Dependence of the Electrical Properties of Na2Ti3O7/Na2Ti6O13/POMA Composites" Molecules 27, no. 18: 5756. https://doi.org/10.3390/molecules27185756
APA StyleDos Santos Costa, S., Pereira da Silva, J., Moraes Biondo, M., Sanches, E. A., Da Silva Paula, M. M., Xavier Nobre, F., Anglada Rivera, J., Alexis Zulueta, Y., Torikachvili, M. S., Vieira Sampaio, D., Vinicius Dias Vermelho, M., Ţălu, Ş., Aguilera Dominguez, L., & Leyet, Y. (2022). Temperature Dependence of the Electrical Properties of Na2Ti3O7/Na2Ti6O13/POMA Composites. Molecules, 27(18), 5756. https://doi.org/10.3390/molecules27185756






