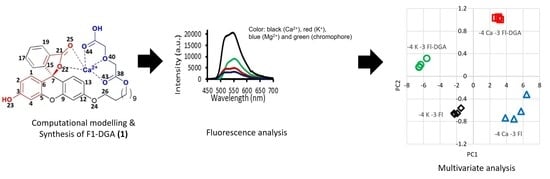
Rational Design of a Fluorescent Chromophore as a Calcium Receptor via DFT and Multivariate Approaches
Abstract
:1. Introduction
2. Results and Discussion
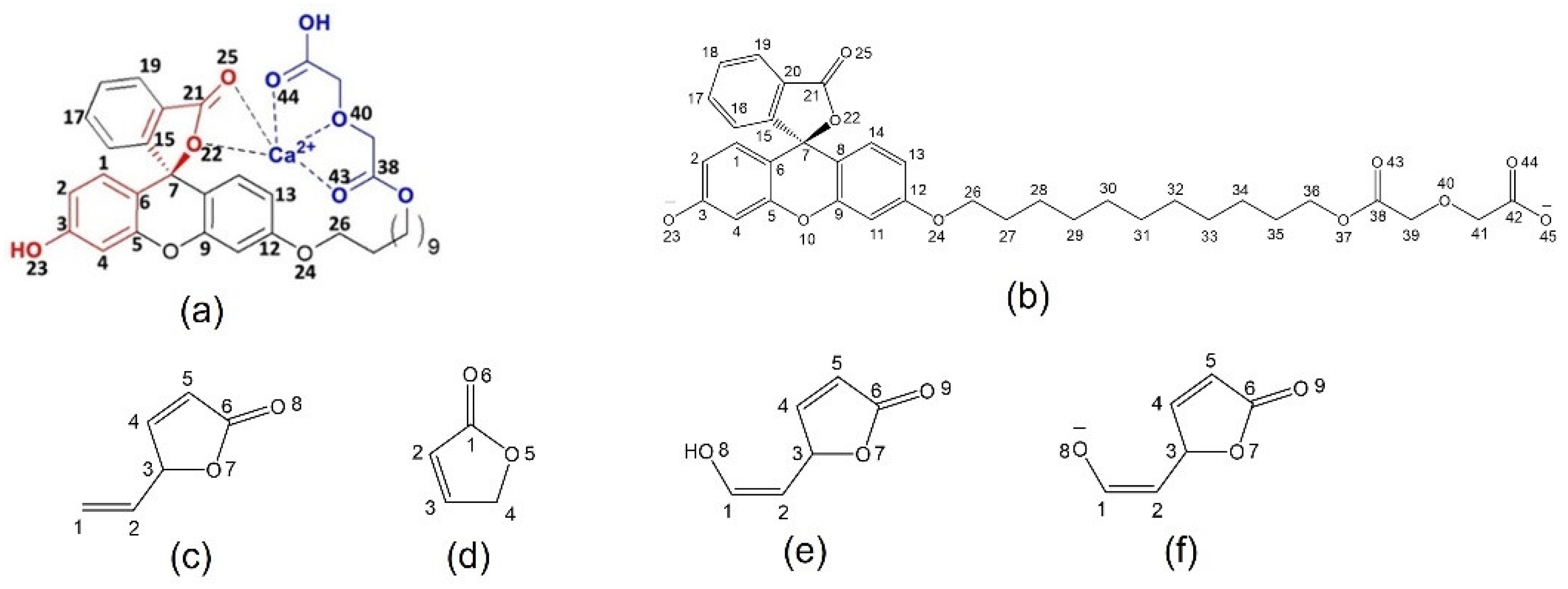
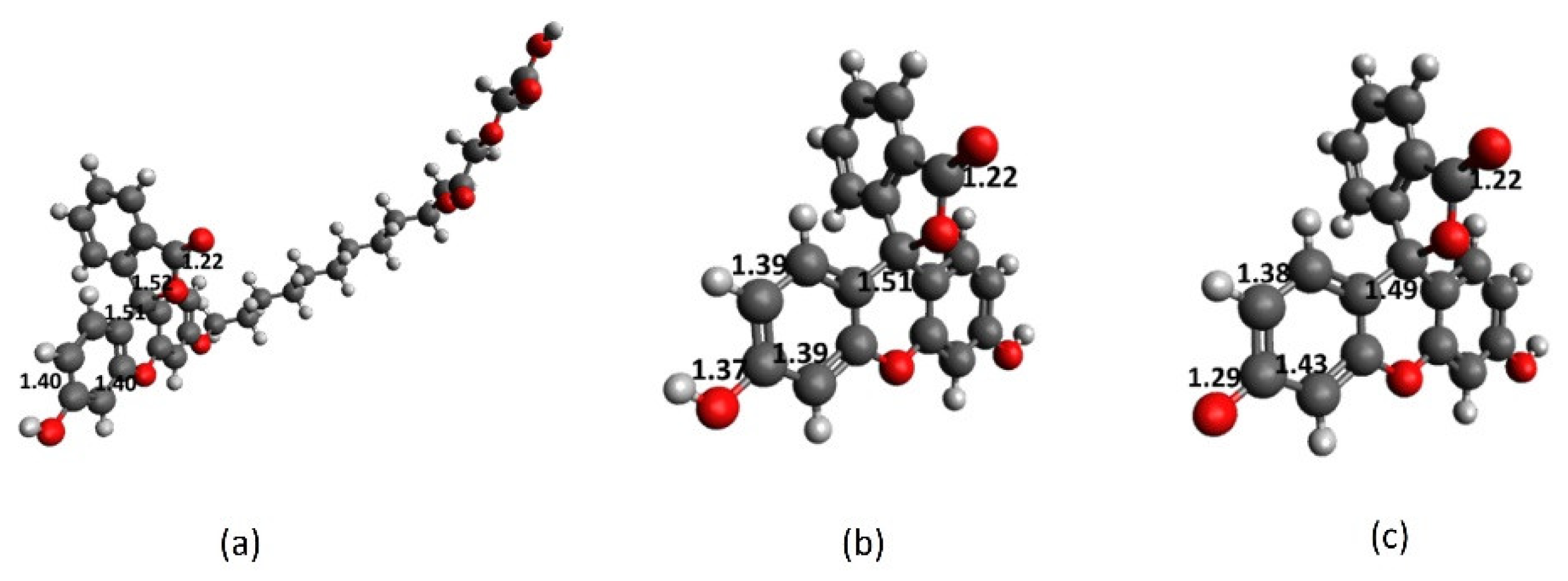
2.1. Full-Structure Computations
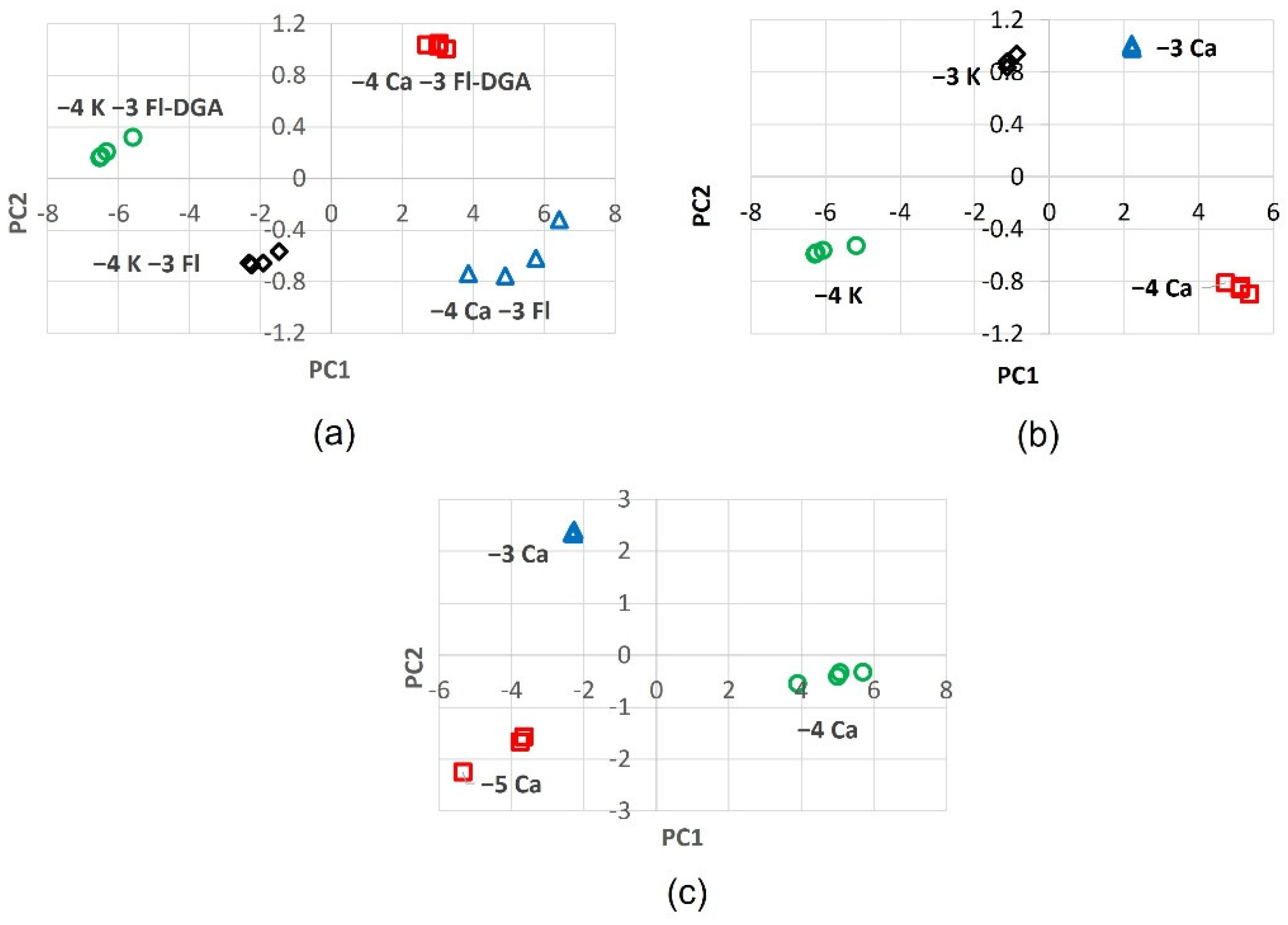
2.2. Chromophore Models and Computational PCA
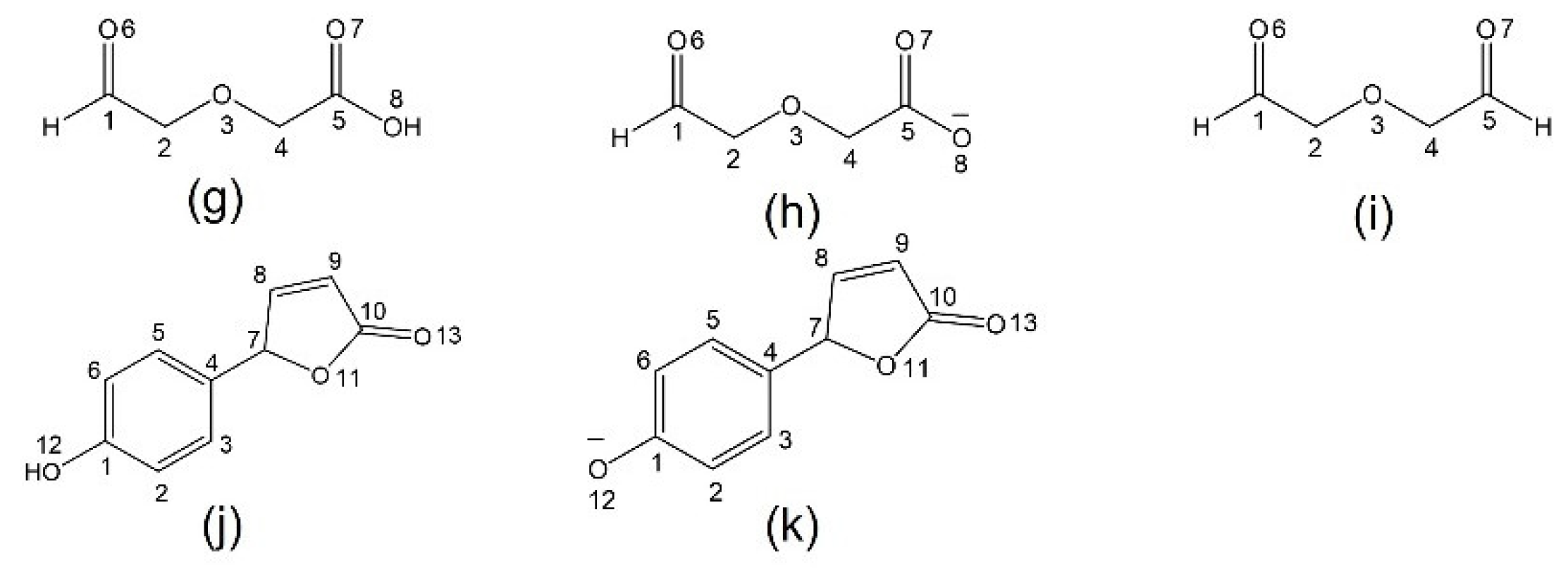
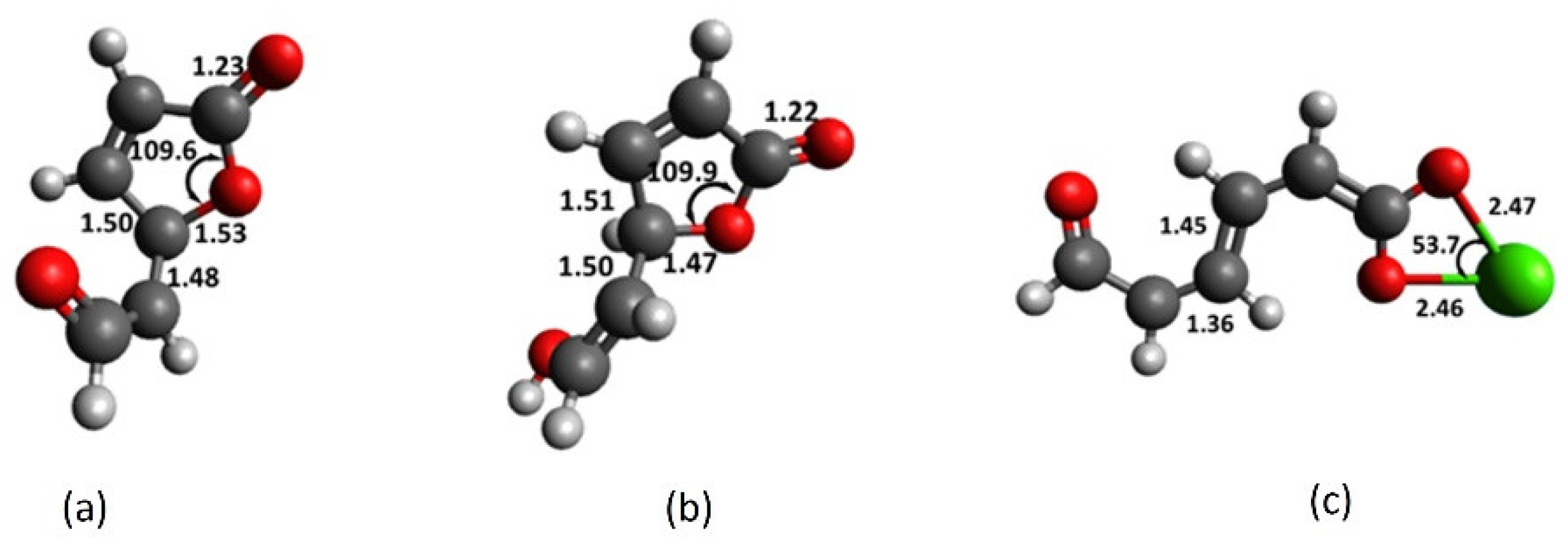
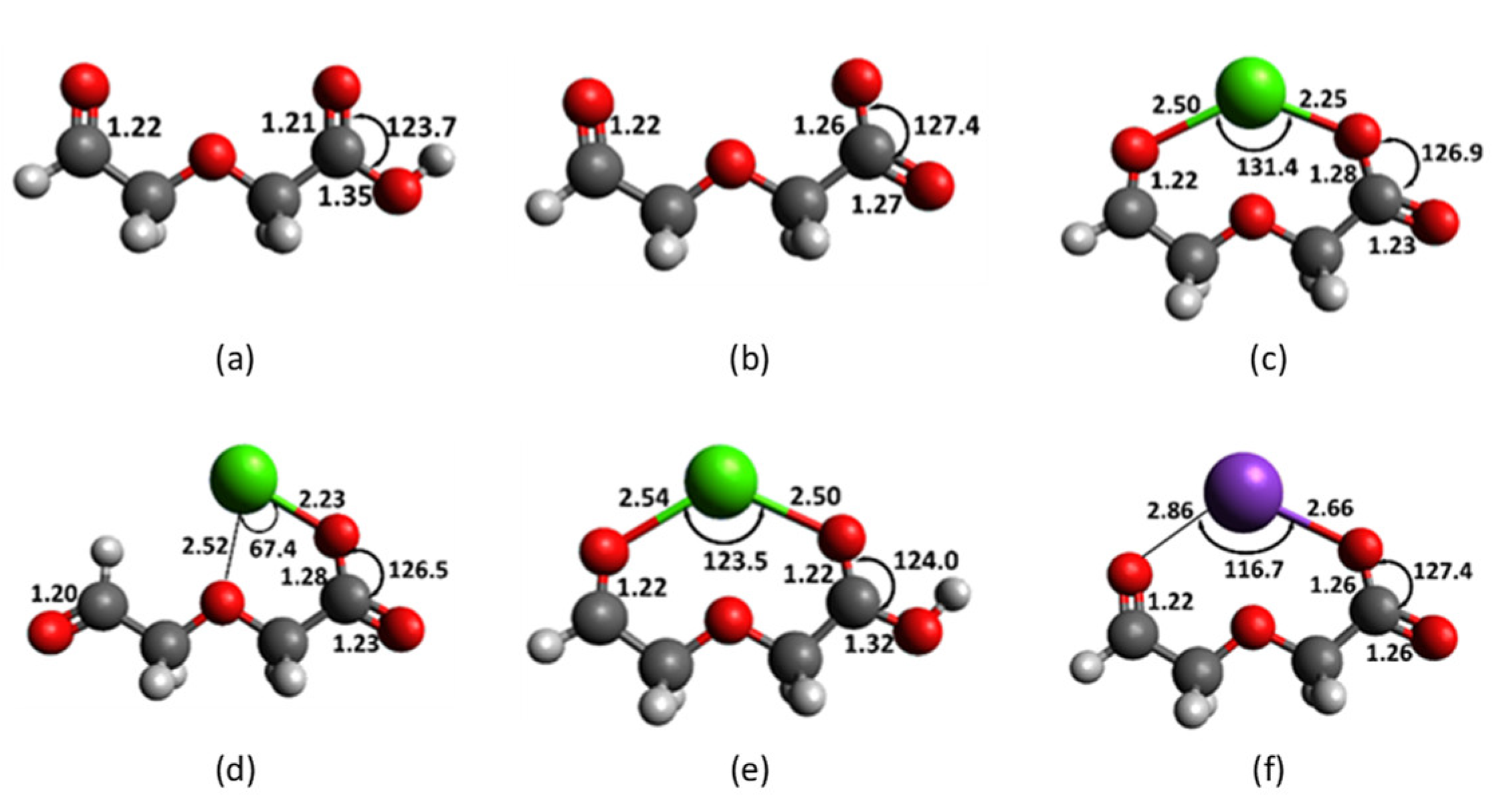
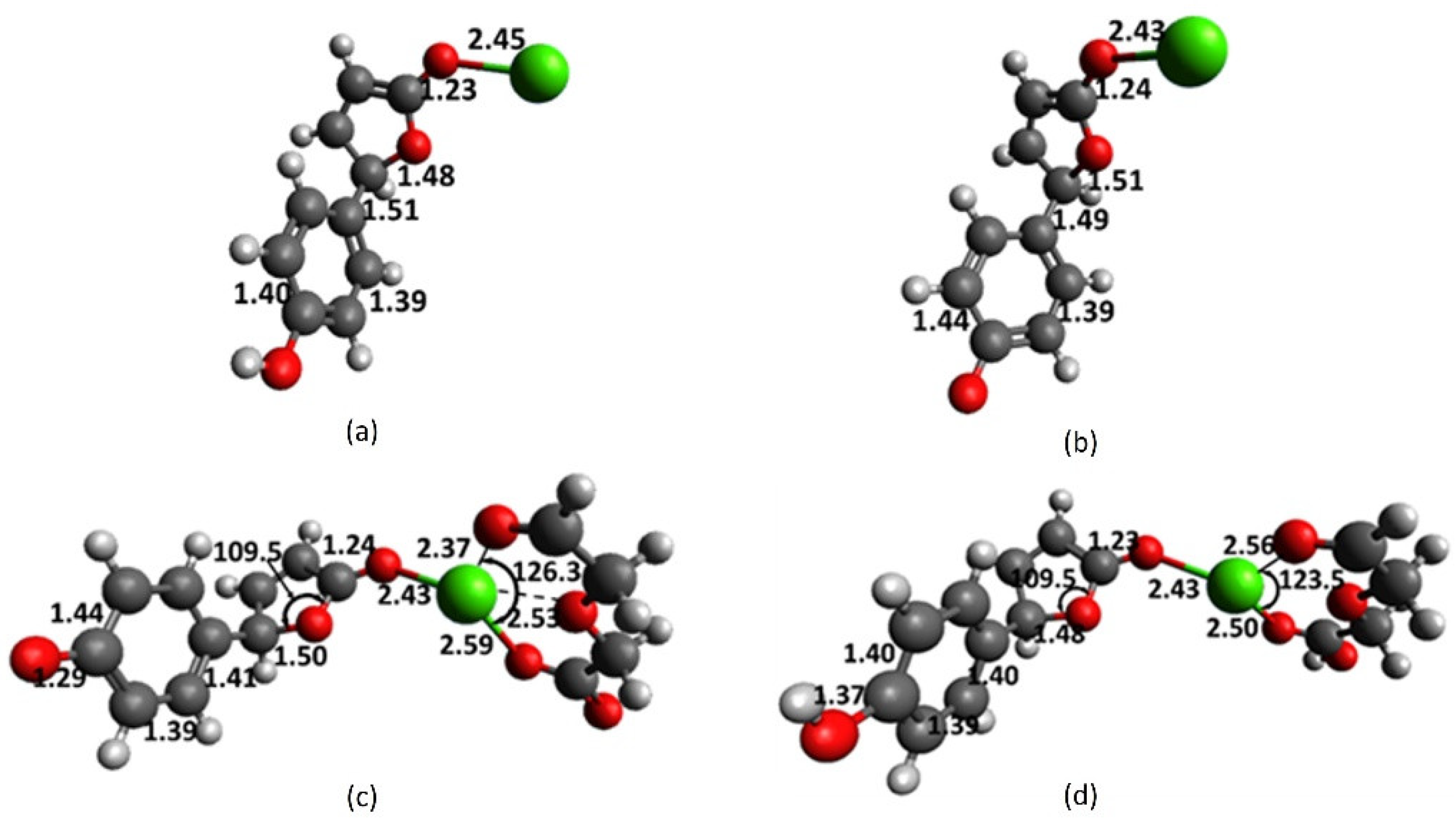
2.3. Diglycolic Ca2+ Receptor Models
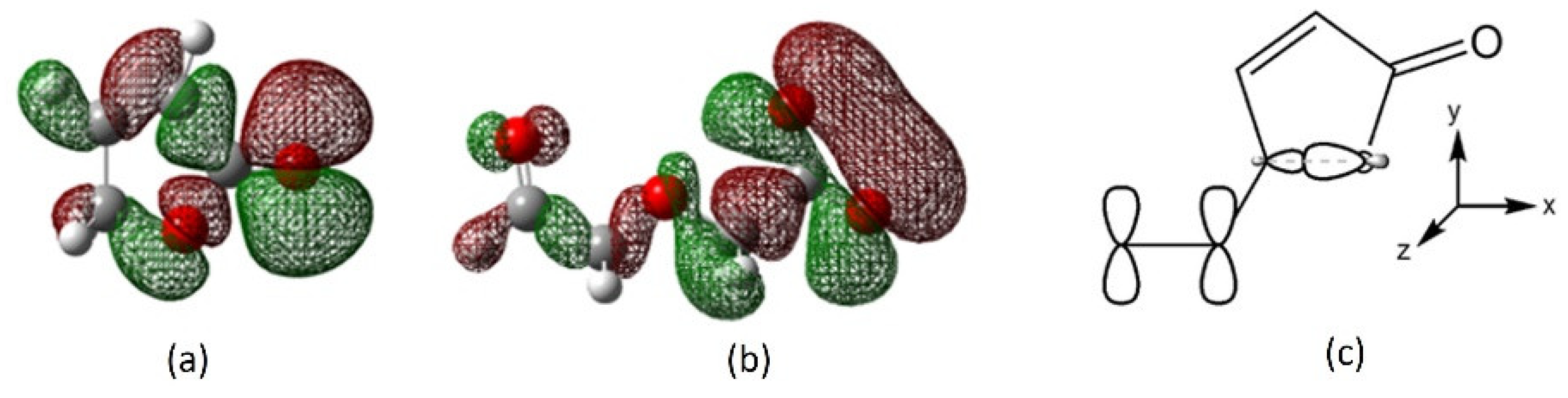
2.4. Interaction of Receptor and Chromophore Fragments with Cation
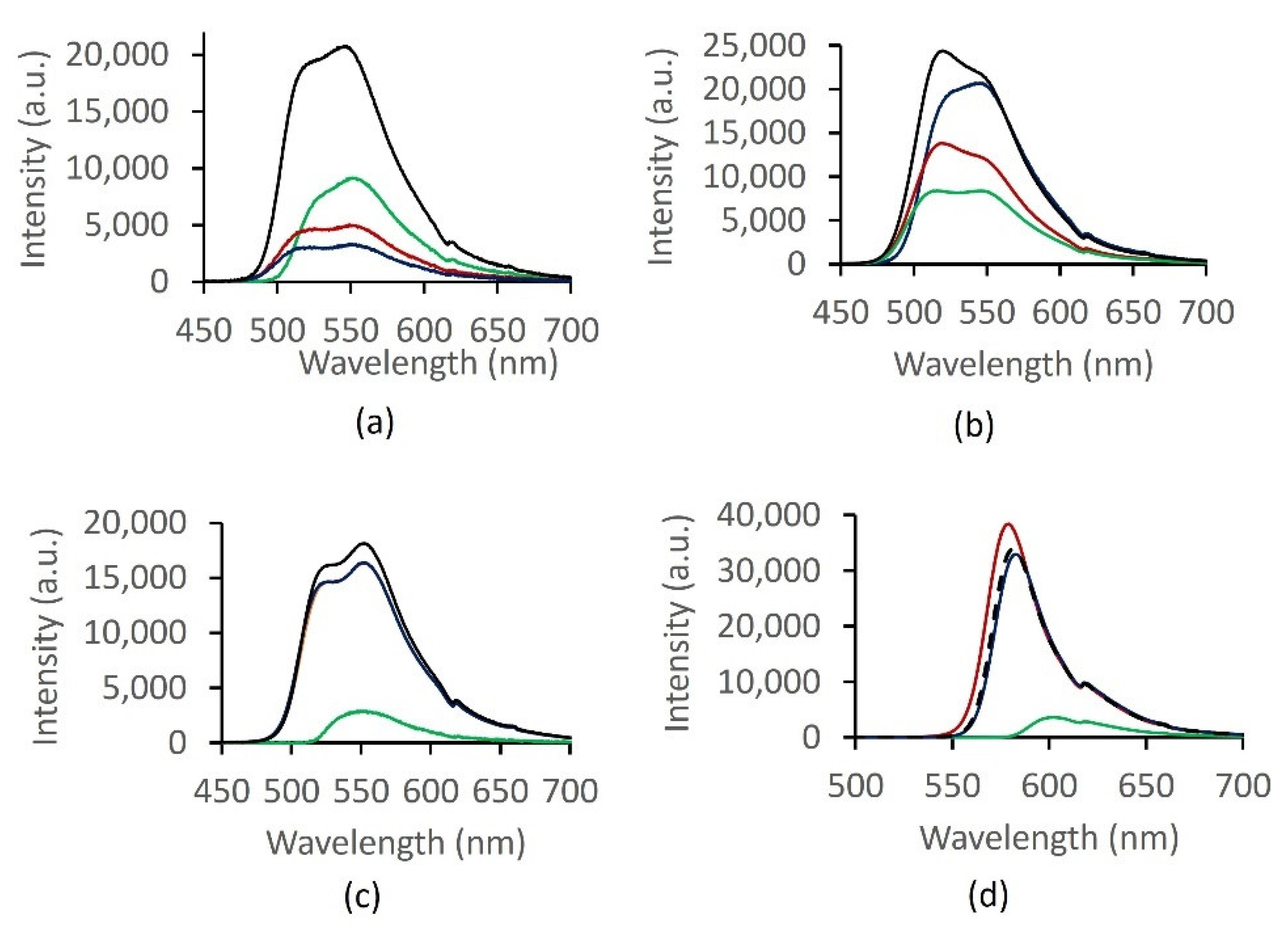
2.5. Optical Response Characterization
2.6. PCA of Optical Responses
2.7. Mechanistic Insights and Rationale for Calcium Selectivity
3. Conclusions
4. Experimental Section
4.1. Materials and Methods
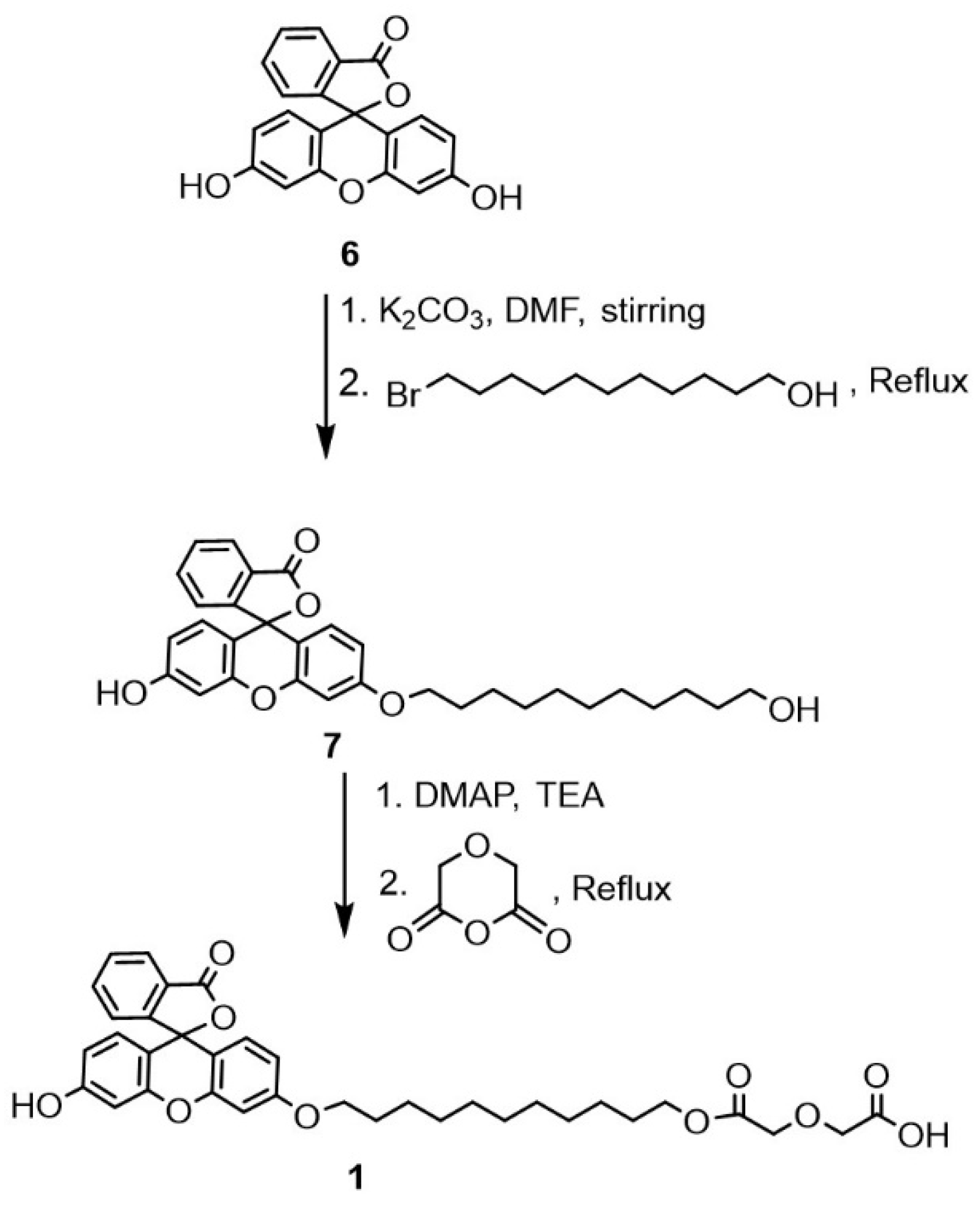
4.2. Synthesis
4.3. Computational Details
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robertson, T.; Bunel, F.; Roberts, M.S. Fluorescein Derivatives in Intravital Fluorescence Imaging. Cells 2013, 2, 591–606. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Zhong, C.; Liu, M.; Yuan, Y.; Zhu, H.; Gao, Y. Rational design and bioimaging application of water-soluble Fe3+ fluorescent probes. N. J. Chem. 2021, 45, 5184–5194. [Google Scholar] [CrossRef]
- Zhong, C.; Qiu, J.; Liu, M.; Yuan, Y.; Zhu, H.; Gao, Y. Rational design and bioimaging application of cholesterol conjugated fluorescence probe for Cu2+ detection. J. Photochem. Photobiol. A Chem. 2021, 414, 113267. [Google Scholar] [CrossRef]
- Wu, X.; Gong, X.; Dong, W.; Ma, J.; Chao, J.; Li, C.; Wang, L.; Dong, C. A novel fluorescein-based colorimetric probe for Cu2+ detection. RSC Adv. 2016, 6, 59677–59683. [Google Scholar] [CrossRef]
- Wysocki, L.M.; Grimm, J.B.; Tkachuk, A.; Brown, T.; Betzig, E.; Lavis, L.D. Facile and General Synthesis of Photoactivatable Xanthene Dyes. Angew. Chem. Int. Ed. 2011, 50, 11206–11209. [Google Scholar] [CrossRef]
- Cook, M.P.; Ando, S.; Koide, K. One-step synthesis of a fluorescein derivative and mechanistic studies. Tetrahedron Lett. 2012, 53, 5284–5286. [Google Scholar] [CrossRef]
- Batistela, V.R.; Cedran, J.D.C.; de Oliveira, H.P.M.; Scarminio, I.S.; Ueno, L.T.; Machado, A.E.D.H.; Hioka, N. Protolytic fluorescein species evaluated using chemometry and DFT studies. Dye. Pigment. 2010, 86, 15–24. [Google Scholar] [CrossRef]
- Carter, K.P.; Young, A.M.; Palmer, A.E. Fluorescent Sensors for Measuring Metal Ions in Living Systems. Chem. Rev. 2014, 114, 4564–4601. [Google Scholar] [CrossRef]
- Xu, W.; Park, J.Y.; Kattel, K.; Ahmad, W.; Alam Bony, B.; Heo, W.C.; Jin, S.; Park, J.W.; Chang, Y.; Kim, T.J.; et al. Fluorescein-polyethyleneimine coated gadolinium oxide nanoparticles as T1 magnetic resonance imaging (MRI)–cell labeling (CL) dual agents. RSC Adv. 2012, 2, 10907–10915. [Google Scholar] [CrossRef]
- Peterlik, M.; Kállay, E.; Cross, H.S. Calcium Nutrition and Extracellular Calcium Sensing: Relevance for the Pathogenesis of Osteoporosis, Cancer and Cardiovascular Diseases. Nutrients 2013, 5, 302–327. [Google Scholar] [CrossRef]
- Tripathi, D.K.; Singh, V.P.; Chauhan, D.K.; Prasad, S.M.; Dubey, N.K. Role of macronutrients in plant growth and acclimation: Recent advances and future prospective. In Improvement of Crops in the Era of Climatic Changes; Ahmad, P., Wani, M.R., Azooz, M.M., Phan Tran, L.S., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Maathuis, F.J.M. Physiological functions of mineral macronutrients. Curr. Opin. Plant Biol. 2009, 12, 250–258. [Google Scholar] [CrossRef]
- de Bang, T.C.; Husted, S.; Laursen, K.H.; Persson, D.P.; Schjoerring, J.K. The molecular–physiological functions of mineral macronutrients and their consequences for deficiency symptoms in plants. New Phytol. 2020, 229, 2446–2469. [Google Scholar] [CrossRef]
- Osório, C.R.W.D.S.; Teixeira, G.C.M.; Barreto, R.F.; Campos, C.N.S.; Leal, A.J.F.; Teodoro, P.E.; Prado, R.D.M. Macronutrient deficiency in snap bean considering physiological, nutritional, and growth aspects. PLoS ONE 2020, 15, e0234512. [Google Scholar] [CrossRef]
- Bedlechowicz, I.; Maj-Żurawska, M.; Sokalski, T.; Hulanicki, A. Effect of a plasticizer on the detection limit of calcium-selective electrodes. J. Electroanal. Chem. 2002, 537, 111–118. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, P.; Liang, R.; Qin, W. Improving the Biocompatibility of Polymeric Membrane Potentiometric Ion Sensors by Using a Mussel-Inspired Polydopamine Coating. Anal. Chem. 2019, 91, 6424–6429. [Google Scholar] [CrossRef]
- Souza, S.S.; Cruz, A.G.; Walter, E.H.; Faria, J.A.; Celeghini, R.M.; Ferreira, M.M.; Granato, D.; Sant’Ana, A.D.S. Monitoring the authenticity of Brazilian UHT milk: A chemometric approach. Food Chem. 2011, 124, 692–695. [Google Scholar] [CrossRef]
- Feron, V.; Groten, J. Toxicological evaluation of chemical mixtures. Food Chem. Toxicol. 2002, 40, 825–839. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1992; Volume 4. [Google Scholar]
- Rosli, A.N.; Abu Bakar, M.A.; Manan, N.S.A.; Woi, P.M.; Lee, V.S.; Zain, S.; Ahmad, M.R.; Alias, Y. G3 Assisted Rational Design of Chemical Sensor Array Using Carbonitrile Neutral Receptors. Sensors 2013, 13, 13835–13860. [Google Scholar] [CrossRef]
- Woi, P.M.; Bakar, M.A.A.; Rosli, A.N.; Lee, V.S.; Ahmad, M.R.; Zain, S.; Alias, Y. Does cation break the cyano bond? A critical evaluation of nitrile-cation interaction. J. Mol. Model. 2014, 20, 2219. [Google Scholar] [CrossRef]
- Rosli, A.N.; Abu Bakar, M.A.; Lee, V.S.; Zain, S.; Ahmad, M.R.; Manan, N.S.A.; Alias, Y.; Woi, P.M. Rational design of carbonitrile-carboxaldehyde cation receptor models: Probing the nature of the heteroatom–metal interaction. J. Mol. Model. 2014, 20, 2428. [Google Scholar] [CrossRef]
- He, H.; Jenkins, K.; Lin, C. A fluorescent chemosensor for calcium with excellent storage stability in water. Anal. Chim. Acta 2008, 611, 197–204. [Google Scholar] [CrossRef]
- Fink, D.W.; Koehler, W.R. pH Effects on fluorescence of umbelliferone. Anal. Chem. 1970, 42, 990–993. [Google Scholar] [CrossRef]
- Haupts, U.; Maiti, S.; Schwille, P.; Webb, W.W. Dynamics of fluorescence fluctuations in green fluorescent protein observed by fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA 1998, 95, 13573–13578. [Google Scholar] [CrossRef]
- Pratt, L.M.; Nguỹên, N.V.; Ramachandran, B. Computational Strategies for Evaluating Barrier Heights for Gas-Phase Reactions of Lithium Enolates. J. Org. Chem. 2005, 70, 4279–4283. [Google Scholar] [CrossRef]
- Ahmad, M.R.; Dahlke, G.D.; Kass, S.R. The Thio-Wittig Rearrangement of Deprotonated Allyl Methyl Sulfide. A Gas-Phase Unimolecular Isomerization Probed with a Variable Temperature Flowing Afterglow-Triple Quadrupole Device. J. Am. Chem. Soc. 1996, 118, 1398–1407. [Google Scholar] [CrossRef]
- Evans, D.A.; Golob, A.M. [3,3]Sigmatropic rearrangements of 1,5-diene alkoxides. Powerful accelerating effects of the alkoxide substituent. J. Am. Chem. Soc. 1975, 97, 4765–4766. [Google Scholar] [CrossRef]
- Greeves, N.; Lee, W.-M. Synthetic Applications (I) of the Tandem [2,3]-Wittig-Anionic Oxy-Cope Rearrangement: Stereoselective Disubstituted Tetrahydropyran Synthesis by Electrophile Initiated Cyclisation. Tetrahedron Lett. 1997, 38, 6449–6452. [Google Scholar] [CrossRef]
- Glassey, W.V.; Hoffmann, R. A comparative study of Hamilton and overlap population methods for the analysis of chemical bonding. J. Chem. Phys. 2000, 113, 1698–1704. [Google Scholar] [CrossRef]
- Le Roy, J.J.; Jeletic, M.; Gorelsky, S.I.; Korobkov, I.; Ungur, L.; Chibotaru, L.F.; Murugesu, M. An Organometallic Building Block Approach To Produce a Multidecker 4f Single-Molecule Magnet. J. Am. Chem. Soc. 2013, 135, 3502–3510. [Google Scholar] [CrossRef]
- Wiberg, K.B. Basis set effects on calculated geometries: 6-311++G** vs. aug-cc-pVDZ. J. Comput. Chem. 2004, 25, 1342–1346. [Google Scholar] [CrossRef]
- Fleming, I. Frontier Orbitals and Organic Chemical Reactions; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor—Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gorelsky, S. AOMix-Software Package for Electronic Structure Analysis, Revision 6.87 d; Ottawa, ON, Canada, 2013.
- Schreckenbach, G.; Ziegler, T. Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory. J. Phys. Chem. 1995, 99, 606–611. [Google Scholar] [CrossRef]
- Zhu, M.; Ghodsi, A. Automatic dimensionality selection from the scree plot via the use of profile likelihood. Comput. Stat. Data Anal. 2006, 51, 918–930. [Google Scholar] [CrossRef]
- Brereton, R.G. Chemometrics: Data Analysis for the Laboratory and Chemical Plant; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976, A32, 751–766. [Google Scholar] [CrossRef]
- Tirado, M.; Polfer, N.C. Defying Entropy: Forming Large Head-to-Tail Macrocycles in the Gas Phase. Angew. Chem. 2012, 124, 6542–6544. [Google Scholar] [CrossRef]
- Barrow, D.A.; Lentz, B.R. Quinine as a fluorescence lifetime standard: Conditions for effectively homogeneous decay. Chem. Phys. Lett. 1984, 104, 163–167. [Google Scholar] [CrossRef]
- Grynkiewicz, G.; Poenie, M.; Tsien, R.Y. A new generation of Ca2+ indicators with greatly improved fluorescence properties. J. Biol. Chem. 1985, 260, 3440–3450. [Google Scholar] [CrossRef]
- Ahmad, S.; Reynolds, D. Monitoring of water quality using fluorescence technique: Prospect of on-line process control. Water Res. 1999, 33, 2069–2074. [Google Scholar] [CrossRef]
- Ayala, P.Y.; Schlegel, H.B. A combined method for determining reaction paths, minima, and transition state geometries. J. Chem. Phys. 1997, 107, 375–384. [Google Scholar] [CrossRef]
- Liu, C.; Hermann, T. Characterization of ionomycin as a calcium ionophore. J. Biol. Chem. 1978, 253, 5892–5894. [Google Scholar] [CrossRef]
- Ertekin, K. Fiber optic sodium and potassium sensing by using a newly synthesized squaraine dye in PVC matrix. Talanta 2002, 58, 719–727. [Google Scholar] [CrossRef]
- Zhang, W.; Jenny, L.; Spichiger, U.E. A Comparison of Neutral Mg2+-Selective Ionophores in Solvent Polymeric Membranes: Complex Stoichiometry and Lipophilicity. Anal. Sci. 2000, 16, 11–18. [Google Scholar] [CrossRef]
- Ninham, A.B.W.; Yaminsky, V. Ion Binding and Ion Specificity: The Hofmeister Effect and Onsager and Lifshitz Theories. Langmuir 1997, 13, 2097–2108. [Google Scholar] [CrossRef]
- Zhang, D.; Cochrane, J.R.; Martinez, A.; Gao, G. Recent advances in H2PO4− fluorescent sensors. RSC Adv. 2014, 4, 29735–29749. [Google Scholar] [CrossRef]
- Rai, A.; Bhaskar, S.; Battampara, P.; Reddy, N.; Ramamurthy, S.S. Integrated Photo-Plasmonic Coupling of Bioinspired Sharp-Edged Silver Nano-particles with Nano-films in Extended Cavity Functional Interface for Cellphone-aided Femtomolar Sensing. Mater. Lett. 2022, 316, 132025. [Google Scholar] [CrossRef]
- Rai, A.; Bhaskar, S.; Mohan, G.K.; Ramamurthy, S.S. Biocompatible Gellucire® Inspired Bimetallic Nanohybrids for Augmented Fluorescence Emission Based on Graphene Oxide Interfacial Plasmonic Architectures. ECS Trans. 2022, 107, 4527–4535. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09 rev. D 01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Kim, K.; Jordan, K.D. Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer. J. Phys. Chem. 1994, 98, 10089–10094. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Mayer, I. Bond order and valence indices: A personal account. J. Comput. Chem. 2006, 28, 204–221. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
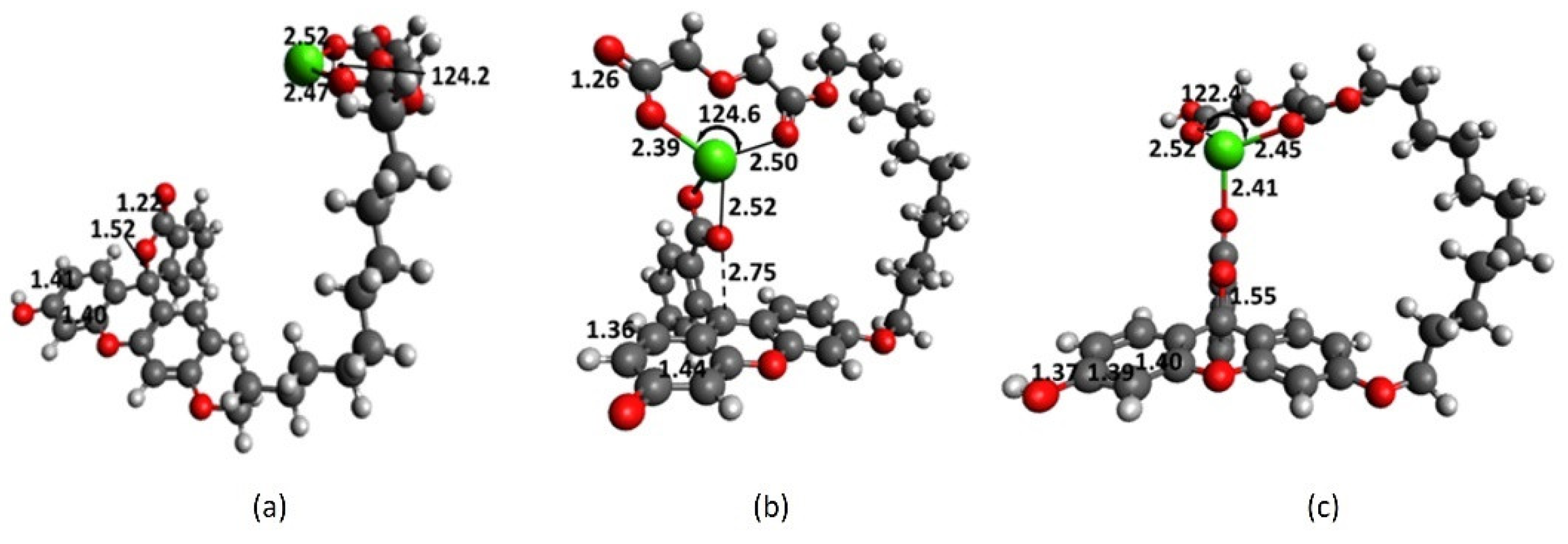


| Parameter | a 1-Ca2+ | b 1a-Ca2+ |
|---|---|---|
| Ca Valence | 0.43 | 0.41 |
| Ca Charge | 1.89 | 1.79 |
| C6 p-Character | 68.6 | 64.0 |
| Ca-O25 TOP | 0.092 | 0.090 |
| C7-O22 BD | 1.55 | 2.75 |
| C7 Valence | 4.90 | 3.56 |
| O22 Valence | 1.95 | 1.70 |
| Dissociation Reaction | BDE (kcal mol−1) |
|---|---|
| a2a-Mg2+ → 2a + Mg2+ | 18.2 |
| a2a-Ca2+ → 2a + Ca2+ | 9.1 |
| a2a-Na+ → 2a + Na+ | 4.3 |
| a2a-K+ → 2a + K+ | 3.5 |
| b4-Mg2+ → 4 + Mg2+ | 29.5 |
| b4-Ca2+ → 4 + Ca2+ | 11.8 |
| b4-K+ → 4 + K+ | 7.2 |
| b4a-Mg2+ → 4a + Mg2+ | 53.7 |
| b4a-Ca2+ → 4a + Ca2+ | 27.2 |
| b4a-K+ → 4a + K+ | 12.6 |
| b2-Ca2+ → 2 + Ca2+ | 6.5 |
| b4b-Ca2+ → 4b + Ca2+ | 11.6 |
| b2–4b-Ca2+ → 2 + 4b-Ca2+ | 5.6 |
| c3a-Ca2+ → 3a + Ca2+ | 22.1 |
| Parameter | a 5-4-Ca2+ | b 5a-4a-Ca2+ |
|---|---|---|
| Ca Valence | 0.42 | 0.47 |
| Ca Charge | 1.88 | 1.86 |
| C4 p-Character | 69.5 | 69.1 |
| C7-O11 TOP | 0.412 | 0.028 |
| C7-O11 Bond Order | 1.34 | 1.25 |
| C7 Valence | 3.07 | 3.32 |
| O11 Valence | 1.85 | 1.81 |
| C4 NMR | 129.9 | 110.1 |
| C7 NMR | 96.5 | 100.8 |
| [Fl-DGA] (mM) | 3.2 | 1.0 | 0.3 | 0.1 |
| λmax(nm) | 544 | 544 | 544 | 544 |
| Im/I0 | 1.0 | 5.2 | 2.1 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narimani, L.; Lee, V.S.; Alias, Y.; Manan, N.S.; Woi, P.M. Rational Design of a Fluorescent Chromophore as a Calcium Receptor via DFT and Multivariate Approaches. Molecules 2022, 27, 6248. https://doi.org/10.3390/molecules27196248
Narimani L, Lee VS, Alias Y, Manan NS, Woi PM. Rational Design of a Fluorescent Chromophore as a Calcium Receptor via DFT and Multivariate Approaches. Molecules. 2022; 27(19):6248. https://doi.org/10.3390/molecules27196248
Chicago/Turabian StyleNarimani, Leila, Vannajan Sanghiran Lee, Yatimah Alias, Ninie Suhana Manan, and Pei Meng Woi. 2022. "Rational Design of a Fluorescent Chromophore as a Calcium Receptor via DFT and Multivariate Approaches" Molecules 27, no. 19: 6248. https://doi.org/10.3390/molecules27196248
APA StyleNarimani, L., Lee, V. S., Alias, Y., Manan, N. S., & Woi, P. M. (2022). Rational Design of a Fluorescent Chromophore as a Calcium Receptor via DFT and Multivariate Approaches. Molecules, 27(19), 6248. https://doi.org/10.3390/molecules27196248