Thermodynamic and Computational (DFT) Study of Non-Covalent Interaction Mechanisms of Charge Transfer Complex of Linagliptin with 2,3-Dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) and Chloranilic acid (CHA)
Abstract
:1. Introduction
2. Results and Discussion
2.1. Optimization of the Reaction Conditions
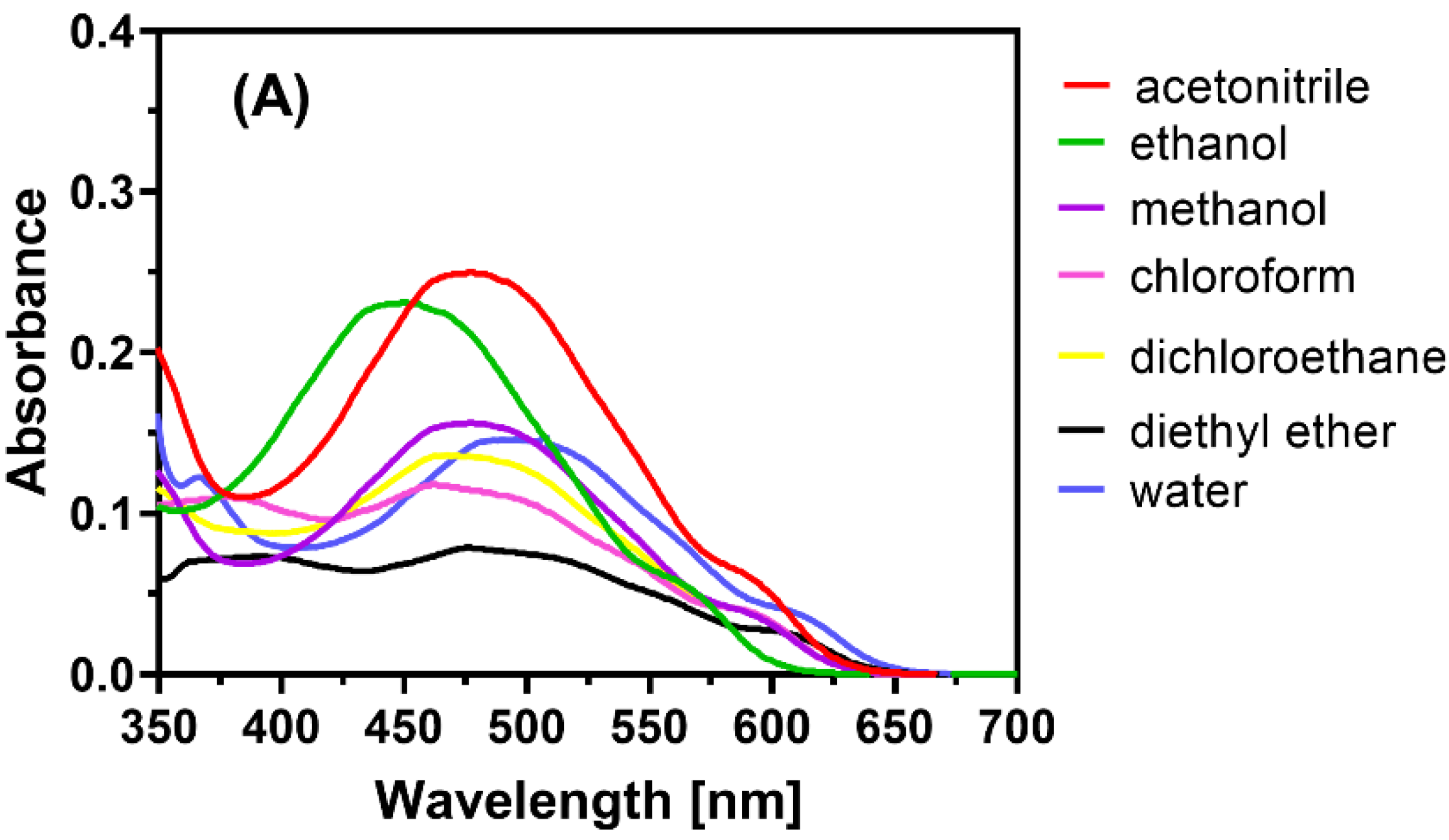
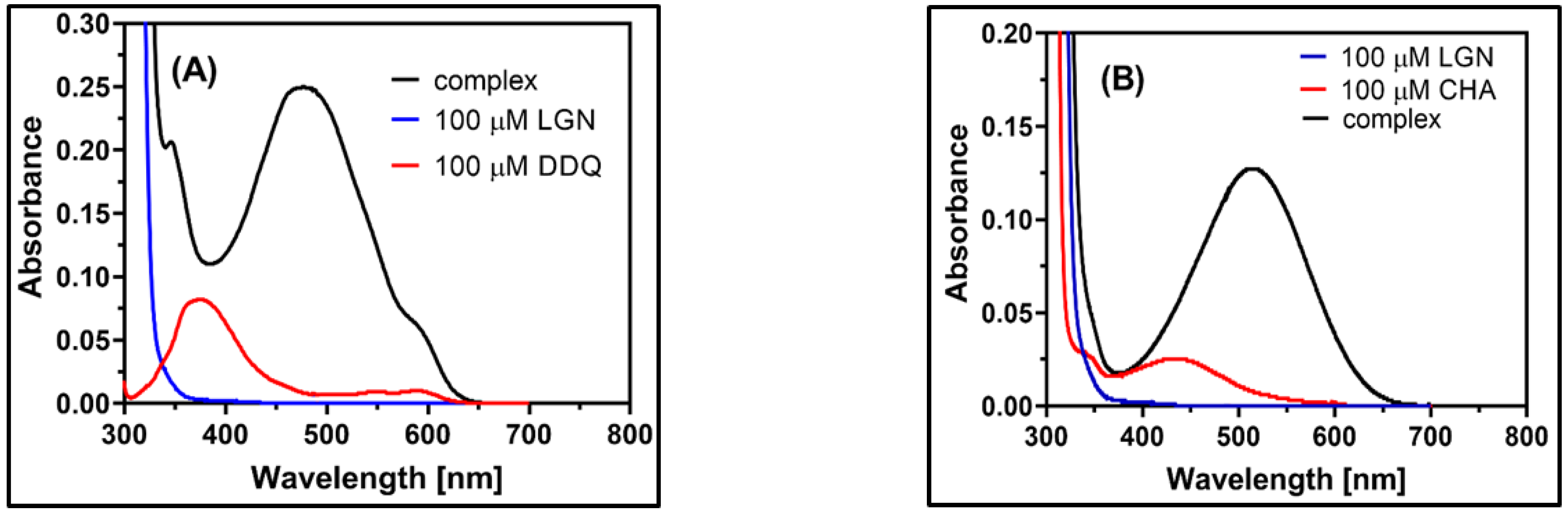
2.2. Observation of CT Electronic Spectra
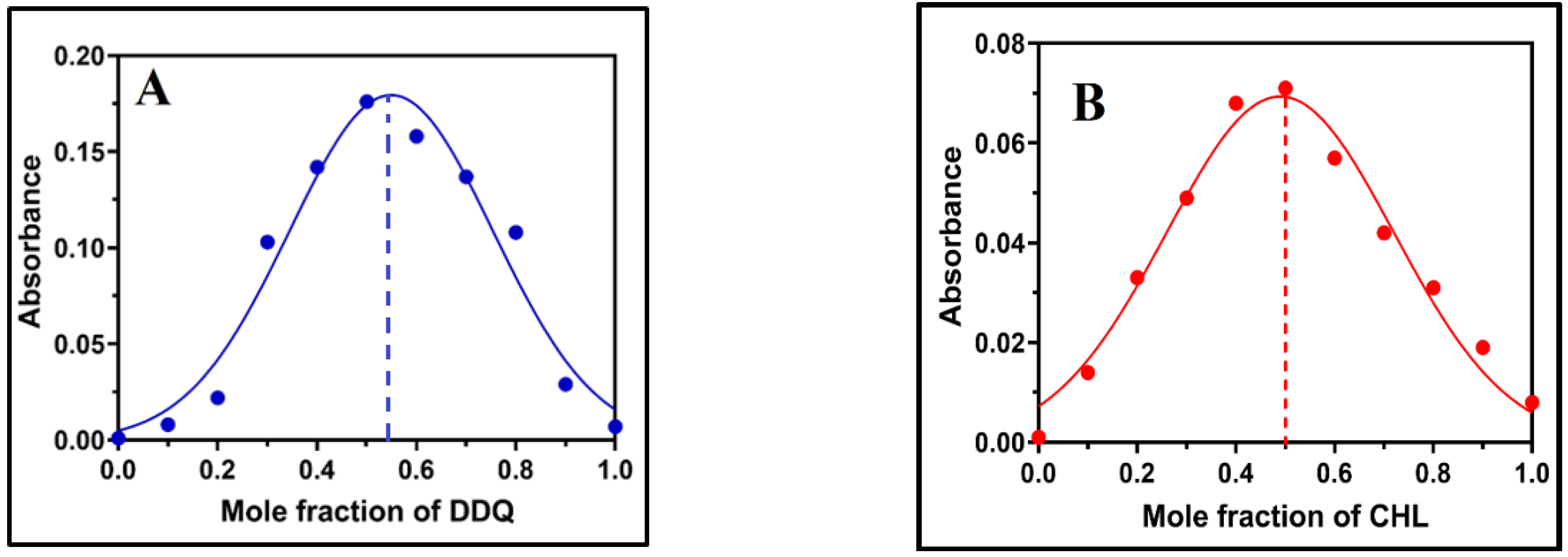
2.3. Physical Composition of the CT Complex
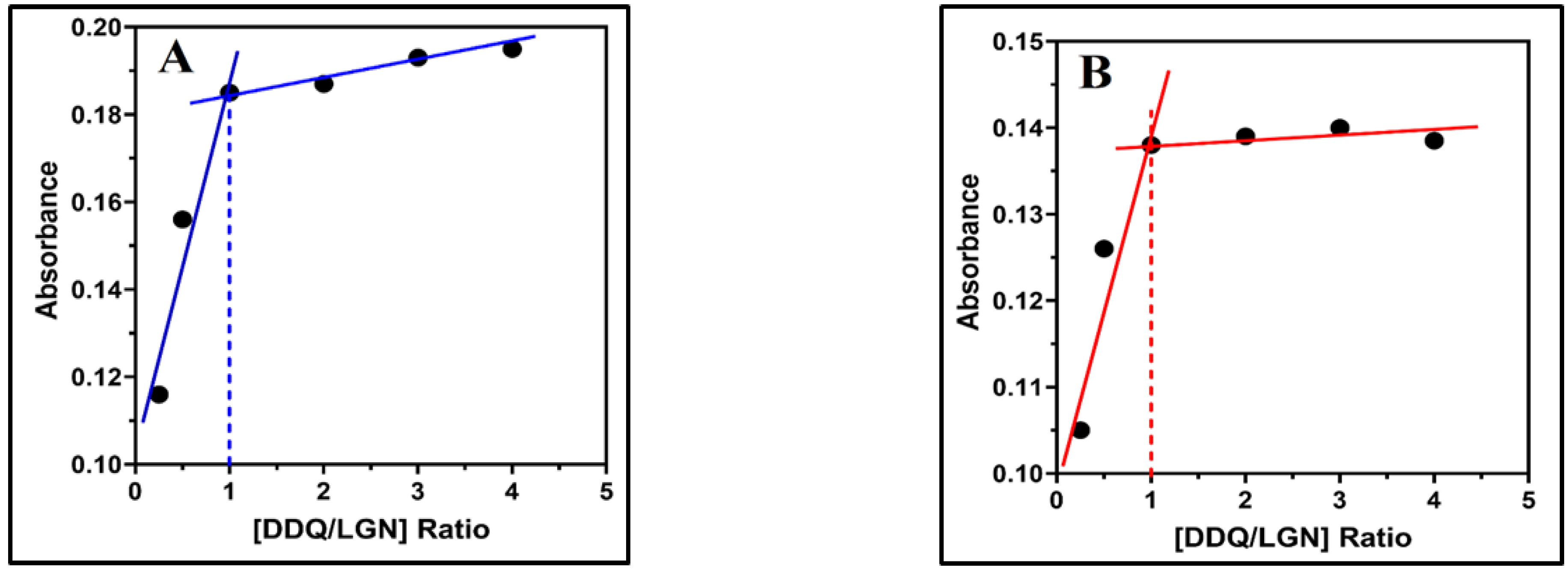
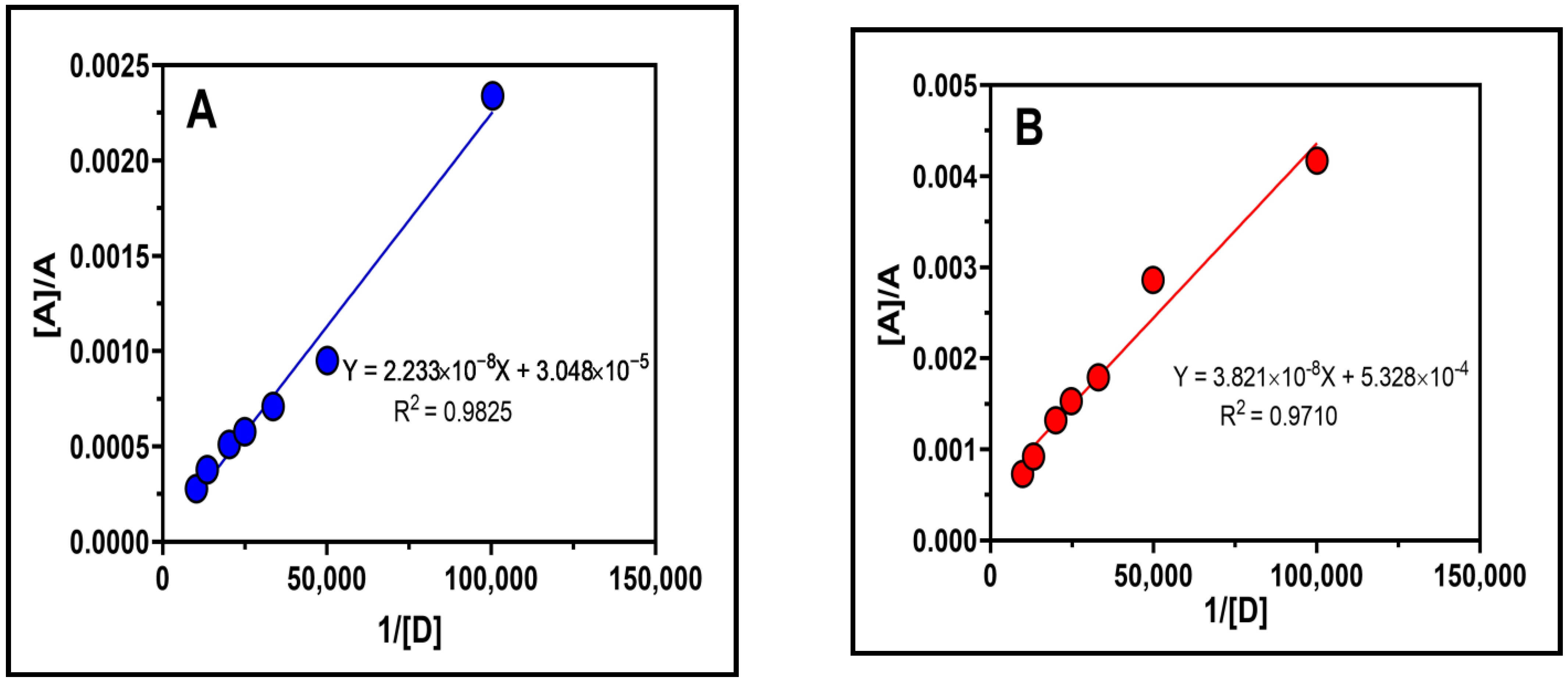
2.4. Association Constant, Free Energy Change and Ionization Potential
2.5. Computational Analysis
2.5.1. Interaction Energies (IE)
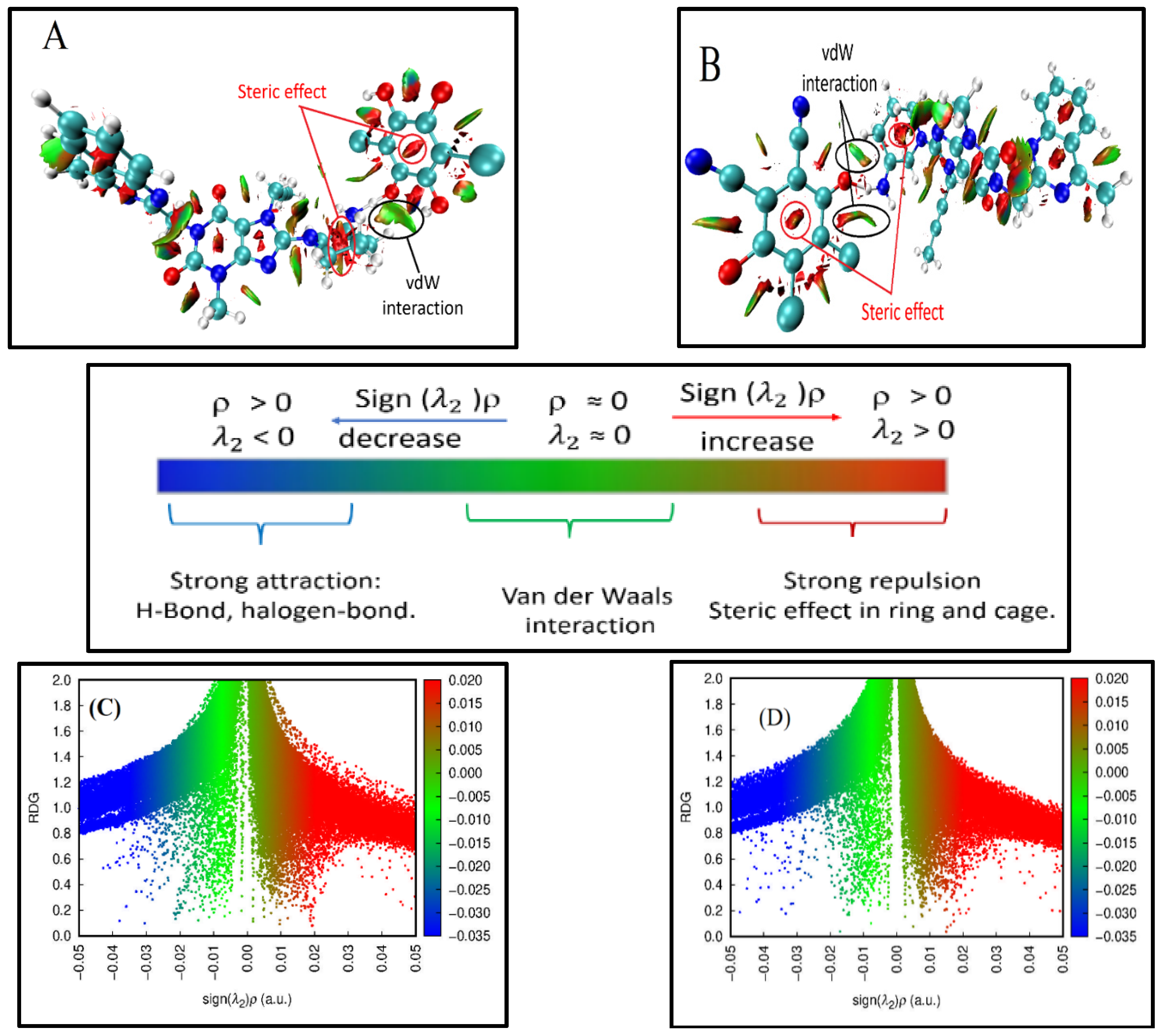
2.5.2. Non-Covalent Interaction (NCI) Index
2.5.3. Reduced Density Gradient (RDG)
2.5.4. Quantum Theory of Atoms in Molecules (QTAIM)
- (1)
- Weak bonds are specified by ∇2ρ(r) > 0 and H(r) >0
- (2)
- Moderate bonds are specified by ∇2ρ(r) > 0 and H(r) < 0
- (3)
- Strong bonds are specified by ∇2ρ(r) < 0 and H(r) < 0
2.5.5. Molecular Electrostatic Potential (MESP) Analysis
2.5.6. UV–Visible Analysis
2.6. Validation of Spectrophotometric Determination
2.6.1. Linear Range and Sensitivity
2.6.2. Precision and Accuracy
3. Materials and Methods
3.1. Reference Samples and Reagents
3.2. Apparatus
3.3. LGN Standard Preparation
3.4. The Molar Ratio and the Association Constant
3.5. Computational
3.5.1. Calculations of Electronic Structure
3.5.2. Interaction Energies (IE)
3.5.3. Non-Covalent Interaction (NCI) Index
3.5.4. Quantum Theory of Atoms in Molecules (QTAIM)
3.5.5. Molecular Electrostatic Potential (MESP)
3.5.6. Ultraviolet–Visible Spectra (UV–Vis)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fuchs, H.; Runge, F.; Held, H.-D. Excretion of the dipeptidyl peptidase-4 inhibitor linagliptin in rats is primarily by biliary excretion and P-gp-mediated efflux. Eur. J. Pharm. Sci. 2012, 45, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Mulliken, R.S. Molecular compounds and their spectra. II. J. Am. Chem. Soc. 1952, 74, 811–824. [Google Scholar] [CrossRef]
- Mulliken, R.S. Molecular compounds and their spectra. III. The interaction of electron donors and acceptors. J. Phys. Chem. 1952, 56, 801–822. [Google Scholar] [CrossRef]
- Foster, R. Organic Charge-Transfer Complexes; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Mostafa, G.A.; Bakheit, A.; AlMasoud, N.; AlRabiah, H. Charge Transfer Complexes of Ketotifen with 2, 3-Dichloro-5, 6-dicyano-p-benzoquinone and 7, 7, 8, 8-Tetracyanoquodimethane: Spectroscopic Characterization Studies. Molecules 2021, 26, 2039. [Google Scholar] [CrossRef]
- Basha, M.T.; Alghanmi, R.M.; Soliman, S.M.; Alharby, W.J. Synthesis, spectroscopic, thermal, structural characterization and DFT/TD-DFT computational studies for charge transfer complexes of 2, 4-diamino pyrimidine with some benzoquinone acceptors. J. Mol. Liq. 2020, 309, 113210. [Google Scholar] [CrossRef]
- Abbu, V.; Nampally, V.; Baindla, N.; Tigulla, P. Stoichiometric, thermodynamic and computational DFT analysis of charge transfer complex of 1-benzoylpiperazine with 2, 3-dichloro-5, 6-dicyano-1, 4-benzoquinone. J. Solut. Chem. 2019, 48, 61–81. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Meyer, E.A.; Castellano, R.K.; Diederich, F. Interactions with aromatic rings in chemical and biological recognition. Angew. Chem. Int. Ed. 2003, 42, 1210–1250. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond: In Structural Chemistry and Biology; International Union of Crystal, Oxford University Press: New York, NY, USA, 2001; Volume 9. [Google Scholar]
- Steiner, T. The hydrogen bond in the solid state. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Legon, A.C. The halogen bond: An interim perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef]
- Scholfield, M.R.; Zanden CM, V.; Carter, M.; Ho, S. Halogen bonding (X-bonding): A biological perspective. Protein Sci. 2013, 22, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Erdelyi, M. Halogen bonding in solution. Chem. Soc. Rev. 2012, 41, 3547–3557. [Google Scholar] [CrossRef] [PubMed]
- Parisini, E.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen bonding in halocarbon–protein complexes: A structural survey. Chem. Soc. Rev. 2011, 40, 2267–2278. [Google Scholar] [CrossRef] [PubMed]
- Gumus, I.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Hirshfeld surface analyses and crystal structures of supramolecular self-assembly thiourea derivatives directed by non-covalent interactions. J. Mol. Struct. 2018, 1157, 78–88. [Google Scholar] [CrossRef]
- Patel, K.D.; Patel, U.H. Quantitative analysis of weak interactions by Lattice energy calculation, Hirshfeld surface and DFT studies of sulfamonomethoxine. J. Mol. Struct. 2017, 1128, 127–134. [Google Scholar] [CrossRef]
- Venkatesan, P.; Cerón, M.; Thamotharan, S.; Robles, F.; Percino, M.J. Quantitative analysis of weak non-covalent interactions in (Z)-3-(4-halophenyl)-2-(pyridin-2/3/4-yl) acrylonitriles. CrystEngComm 2018, 20, 2681–2697. [Google Scholar] [CrossRef]
- Sangeetha, R.; Subashri, T. Analysis of linagliptin in tablet dosage form by UV spectroscopy method, its derivatives and difference spectra. Eur. J. Pharm. Med. Res. 2016, 3, 536–540. [Google Scholar]
- Sri, K.V.; Anusha, A.; Sudhakar, M. UV-Spectrophotometry Method for the Estimation of Linagliptin in Bulk and Pharmaceutical Formulations. Asian J. Res. Chem. 2016, 9, 47. [Google Scholar] [CrossRef]
- Banik, S.; Karmakar, P.; Miah, M.A.H. Development and validation of a UV-spectrophotometric method for determination of vildagliptin and linagliptin in bulk and pharmaceutical dosage forms. Bangladesh Pharm. J. 2015, 18, 163–168. [Google Scholar] [CrossRef]
- Lilian, S. Development of economic UV spectrophotometric method for determination of linagliptin in its ternary mixture with empagliflozin and metformin: Comparison to economic pharmaceutical analysis in literature. Der Pharm. Lett. 2016, 8, 267–269. [Google Scholar]
- El-Bagary, R.I.; Elkady, E.F.; Ayoub, B.M. Spectrophotometric methods for the determination of linagliptin in binary mixture with metformin hydrochloride and simultaneous determination of linagliptin and metformin hydrochloride using high performance liquid chromatography. Int. J. Biomed. Sci. IJBS 2013, 9, 41. [Google Scholar] [PubMed]
- Aher, S.; Saudagar, S. Spectrophotometric and chromatographic estimation of linagliptin in bulk and tablet dosage form. Int. J. ChemTech Res. 2017, 10, 736–744. [Google Scholar]
- Banik, S.; Kaisar, M.; Hossain, M. Development and validation of a simple and rapid uv spectrophotometer method for assay of linagliptin in bulk and marketed dosage form. Indian. J. Nov. Drug. Deliv. 2013, 5, 221–224. [Google Scholar]
- Abdalla, O.M.; Abdel-Megied, A.M.; Saad, A.S.; Soliman, S.S. Simultaneous spectrophotometric determination of compounds having relatively disparate absorbance and concentration ranges; application to antidiabetic formulation of linagliptin and metformin. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 203, 112–117. [Google Scholar] [CrossRef]
- Derakhshan, M.S.; Sohrabi, M.R.; Davallo, M. Developed rapid spectrophotometric method for simultaneous quantitative determination of metformin and linagliptin mixture as antidiabetic drugs by artificial intelligence methodology in biological fluid and pharmaceutical sample. Optik 2021, 241, 166922. [Google Scholar] [CrossRef]
- Gurrala, S.; Anumolu, P.D.; Menkana, S.; Gandla, N.; Toddi, K. Spectrophotometric estimation of linagliptin using ion-pair complexation and oxidative coupling reactions–A green approach. Thai J. Pharm. Sci. (TJPS) 2020, 44, 245–250. [Google Scholar]
- Mathew, C.; Varma, S. Green Analytical Methods based on Chemometrics and UV spectroscopy for the simultaneous estimation of Empagliflozin and Linagliptin. Asian J. Pharm. Anal. 2022, 12, 1–11. [Google Scholar] [CrossRef]
- Tejashree, R.K.; Dashetwar, A.R.; Kardile, D.P.; Jadhav, A.P.; Bhagat, V.C.; Shete, R.V. Q-absorbance ratio spectrophotometric method for the simultaneous estimation of metformin hydrochloride and voglibose in tablet dosage form. Res. J. Pharm. Technol. 2021, 14, 3179–3183. [Google Scholar] [CrossRef]
- Moradi, M.; Sohrabi, M.R.; Mortazavinik, S. Simultaneous ultra-trace quantitative colorimetric determination of antidiabetic drugs based on gold nanoparticles aggregation using multivariate calibration and neural network methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 234, 118254. [Google Scholar] [CrossRef]
- Anumolu, P.D.; SNS RANI; Galennagari, R.; Achanta, R.; Gurrala, S. Quantification of Linagliptin by Chemical Derivatization with Appliance of Chromogenic Reagents. Sci. Inf. Database 2017, 11, 39–50. [Google Scholar]
- Omar, M.A.; Ahmed, H.M.; Batakoushy, H.A.; Hamid, M.A.A. New spectrofluorimetric analysis of empagliflozin in its tablets and human plasma using two level full factorial design. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 235, 118307. [Google Scholar] [CrossRef] [PubMed]
- Aref, H.A.; Hammad, S.F.; Elgawish, M.S.; Darwish, K.M. Novel spectrofluorimetric quantification of linagliptin in biological fluids exploiting its interaction with 4-chloro-7-nitrobenzofurazan. Luminescence 2020, 35, 626–635. [Google Scholar] [CrossRef] [PubMed]
- Elmasry, M.S.; Hasan, M.A.; Hassan, W.S.; Merey, H.A.; Nour, I.M. Flourimetric study on antidiabetic combined drugs; empagliflozin and linagliptin in their pharmaceutical formulation and human plasma. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 248, 119258. [Google Scholar] [CrossRef] [PubMed]
- Donepudi, S.; Achanta, S. Validated HPLC-UV method for simultaneous estimation of linagliptin and empagliflozin in human plasma. Int. J. Appl. Pharm. 2018, 10, 56–61. [Google Scholar]
- Rajbangshi, J.C.; Alam, M.M.; Hossain, M.S.; Islam, M.S.; Rouf, A.S.S. Development and validation of a RP-HPLC method for quantitative analysis of Linagliptin in bulk and dosage forms. Dhaka Univ. J. Pharm. Sci. 2018, 17, 175–182. [Google Scholar] [CrossRef]
- Sivagami, B.; Purushotham, A.; Sikdar, P.; Chandrasekar, R.; Babu, M.N. A validated method for the simultaneous estimation of Linagliptin and metformin in tablet dosage forms by RP-HPLC. Res. J. Pharm. Technol. 2020, 13, 1266–1270. [Google Scholar] [CrossRef]
- Moussa, B.A.; Mahrouse, M.A.; Fawzy, M.G. Application of experimental design in HPLC method optimization and robustness for the simultaneous determination of canagliflozin, empagliflozin, linagliptin, and metformin in tablet. Biomed. Chromatogr. 2021, 35, e5155. [Google Scholar] [CrossRef]
- Airinei, A.; Homocianu, M.; Dorohoi, D.O. Changes induced by solvent polarity in electronic absorption spectra of some azo disperse dyes. J. Mol. Liq. 2010, 157, 13–17. [Google Scholar] [CrossRef]
- Harvey, A.E.; Manning, D.L. Spectrophotometric methods of establishing empirical formulas of colored complexes in solution. J. Am. Chem. Soc. 1950, 72, 4488–4493. [Google Scholar] [CrossRef]
- Kuntz, I., Jr.; Gasparro, F.P.; Johnston, M.D., Jr.; Taylor, R.P. Molecular interactions and the Benesi-Hildebrand equation. J. Am. Chem. Soc. 1968, 90, 4778–4781. [Google Scholar] [CrossRef]
- Pandeeswaran, M.; Elango, K. Solvent effect on the charge transfer complex of oxatomide with 2, 3-dichloro-5, 6-dicyanobenzoquinone. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2006, 65, 1148–1153. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory Oxford University; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Popelier, P.L.A.; Bader, R.F.W. The existence of an intramolecular C─H─O hydrogen bond in creatine and carbamoyl sarcosine. Chem. Phys. Lett. 1992, 189, 542–548. [Google Scholar] [CrossRef]
- Sokolova, I.; Orlovskaya, L.; Zhigalova, E. Application of the molecular electrostatic potential (MESP) method to the study of the reactivity of aliphatic carbonyl compounds. J. Struct. Chem. 1980, 21, 46–51. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Mulholland, M.; Hibbert, D.B. Linearity and the limitations of least squares calibration. J. Chromatogr. A 1997, 762, 73–82. [Google Scholar] [CrossRef]
- Guideline, I. Q2 (R1): Validation of Analytical Procedure: Text and Methodology; ICH: London, UK, 2005. [Google Scholar]
- Ghabbour, H.A.; Bakheit, A.H.; Ezzeldin, E.; Mostafa, G.A. Synthesis Characterization and X-ray Structure of 2-(2,6-Dichlorophenylamino)-2-imidazoline Tetraphenylborate: Computational Study. Appl. Sci. 2022, 12, 3568. [Google Scholar] [CrossRef]
- Abuelizz, H.A.; Taie, H.A.; Bakheit, A.H.; Marzouk, M.; Abdellatif, M.M.; Al-Salahi, R. Biological Evaluation of 4-(1H-triazol-1-yl) benzoic Acid Hybrids as Antioxidant Agents: In Vitro Screening and DFT Study. Appl. Sci. 2021, 11, 11642. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting noncovalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem 2012, 33, 580–592. [Google Scholar]
- Bader, R.F. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Bader, R.F. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Abuelizz, H.A.; Taie, H.A.; Bakheit, A.H.; Mostafa, G.A.; Marzouk, M.; Rashid, H.; Al-Salahi, R. Investigation of 4-Hydrazinobenzoic Acid Derivatives for Their Antioxidant Activity: In Vitro Screening and DFT Study. ACS Omega 2021, 6, 31993–32004. [Google Scholar] [CrossRef]
- Murray, J.S.; Paulsen, K.; Politze, P. Molecular surface electrostatic potentials in the analysis of non-hydrogen-bonding noncovalent interactions. In Proceedings of the Indian Academy of Sciences-Chemical Sciences; Springer: Berlin/Heidelberg, Germany, 1994; Volume 106, pp. 267–275. [Google Scholar]
- Sjoberg, P.; Politzer, P. Use of the electrostatic potential at the molecular surface to interpret and predict nucleophilic processes. J. Phys. Chem. 1990, 94, 3959–3961. [Google Scholar] [CrossRef]
- Politzer, P.; Laurence, P.R.; Jayasuriya, K. Molecular electrostatic potentials: An effective tool for the elucidation of biochemical phenomena. Environ. Health Perspect. 1985, 61, 191–202. [Google Scholar] [CrossRef]
- Sen, K.; Politzer. Characteristic features of the electrostatic potentials of singly negative monoatomic ions. J. Chem. Phys. 1989, 90, 4370–4372. [Google Scholar] [CrossRef]
- Murray, J.S.; Sen, K. Molecular Electrostatic Potentials: Concepts and Applications; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Tomasi, J.; Bonaccorsi, R.; Cammi, R. Theoretical Models of Chemical Bonding (Ed: R. Maksic) Springer, Berlin, 1990, 230; b) RK Pathak, SR Gadre. J. Chem. Phys. 1990, 93, 1770. [Google Scholar]
- Politzer, P.; Murray, J.S. The fundamental nature and role of the electrostatic potential in atoms and molecules. Theor. Chem. Acc. 2002, 108, 134–142. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Peralta-Inga, Z. Molecular surface electrostatic potentials in relation to noncovalent interactions in biological systems. Int. J. Quantum Chem. 2001, 85, 676–684. [Google Scholar] [CrossRef]
- Kazachenko, A.S.; Akman, F.; Sagaama, A.; Issaoui, N.; Malyar, Y.N.; Vasilieva, N.Y.; Borovkova, V.S. Theoretical and experimental study of guar gum sulfation. J. Mol. Modeling 2021, 27, 5. [Google Scholar] [CrossRef] [PubMed]
- ChemAxon. MarvinSketch. Budapest, Hungary: ChemAxon. (Internal Build ID: 21.19.0-13698). Available online: https://chemaxon.com/ (accessed on 7 December 2021).
- Burke, K.; Werschnik, J.; Gross, E.K. Time-dependent density functional theory: Past, present, and future. J. Chem. Phys. 2005, 123, 1904586. [Google Scholar] [CrossRef]
- Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys. 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
- Boyle, N.; Tenderholt, A.; Langner, K.M. Gausssum 3.0. J. Comput. Chem. 2008, 29, 839–845. [Google Scholar]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]





| Complexes | (∆E) Raw kcal/mol | ∆EBSSE | (∆E) Corrected kcal/mol |
|---|---|---|---|
| LGN-DDQ | –75.32 | 0.00338 | –73.20 |
| LGN-CHA | –77.30 | 0.00638 | –73.30 |
| Complex | BCP | Bond and Bond Distance (Å) | ρ(r) (a.u.) | K(r) (a.u.) | V(r) (a.u.) | H(r) (a.u.) | ∇2ρ(r) (a.u.) | |V(r)|/G(r) (a.u.) |
|---|---|---|---|---|---|---|---|---|
| LGN–CHA | 121 | O(71)⋯H(45)-C(10) 2.78298 | 5.15 × 10−3 | −6.84 × 10−4 | −3.16 × 10−3 | 6.84 × 10−4 | 1.81 × 10−2 | 0.823 |
| 149 | O(71)⋯H(49)-N(12) 1.76989 | 3.87 × 10−2 | 1.34 × 10−4 | −36.6 × 10−3 | −1.34 × 10−4 | 14.5 × 10−2 | 1.003 | |
| LGN–DDQ | 126 | N(12)-H(49)⋯O(74) 1.67704 | 4.70 × 10−2 | 2.60 × 10−3 | −4.73 × 10−2 | −2.60 × 10−3 | 2.13 × 10−2 | 1.057 |
| 150 | C(13)-H(50)⋯O(74) 2.46133 | 9.95 × 10−3 | −1.14 × 10−3 | −6.27 × 10−3 | 1.14 × 10−3 | 3.42 × 10−2 | 0.847 | |
| 163 | C(13)-H(50)⋯Cl(72) 2.97070 | 5.43 × 10−3 | −1.04 × 10−3 | −2.49 × 10−3 | 1.04 × 10−3 | 1.83 × 10−2 | 0.705 |
| Complex | Experimental | Theoretical (TD–DFT Calculation) | ||||
|---|---|---|---|---|---|---|
| (λmax) nm | Band Gap (eV) | Excited State | Band Gap (eV) | Oscillator Strength (f) | * Transition State (Coefficient) | |
| LGN⋯DDQ | 546.28 | 2.27 | 0.0245 | HOMO → LUMO (99%) | ||
| 487.5 | 2.54 | 424.48 | 2.92 | 0.0448 | HOMO → LUMO + 1 (100%) | |
| 346.0 | 3.58 | 371.66 | 3.34 | 0.0000 | HOMO − 1 → LUMO (99%) | |
| LGN⋯CHA. | 514.0 | 2.41 | 510.58 | 2.43 | 0.0039 | HOMO → LUMO (100%) |
| 487.5 | 2.54 | 420.17 | 2.95 | 0.0000 | HOMO − 1 → LUMO (99%) | |
| 379.0 | 3.27 | 371.73 | 3.34 | 0.0012 | HOMO → LUMP + 1 (100%) | |
| Parameter | LGN-DDQ | LGN-CHA |
|---|---|---|
| Linear range (µM) | 2.5–100 | 5–100 |
| Intercept | 0.04729 | 0.01416 |
| Standard deviation of intercept | 0.0009602 | 0.0005387 |
| Slope | 0.002922 | 0.001234 |
| Standard deviation of slope | 1.980 × 10–5 | 1.048 × 10–5 |
| Correlation coefficient | 0.9997 | 0.9996 |
| LOD (µM) | 1.0844 | 1.4406 |
| LOQ (µM) | 3.2861 | 4.3655 |
| Taken Concentration (µM) | Precision: Relative Standard Deviation (%) | Accuracy: Recovery (% ± SD) | |
|---|---|---|---|
| Intra–Assay | Inter–Assay | ||
| LGN–DDQ complex | |||
| 10 | 1.039 | 0.383 | 101.12 ± 0.41 |
| 30 | 0.733 | 0.839 | 98.91 ± 0.62 |
| 50 | 0.374 | 1.017 | 98.80 ± 0.90 |
| 100 | 1.235 | 1.177 | 99.57 ± 1.25 |
| LGN–CHA complex | |||
| 10 | 0.411 | 0.681 | 99.34 ± 0.29 |
| 30 | 1.355 | 1.107 | 98.72 ± 0.86 |
| 50 | 1.013 | 0.852 | 102.73 ± 1.72 |
| 100 | 0.710 | 0.751 | 100.756 ± 1.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakheit, A.H.; Al-Salahi, R.; Al-Majed, A.A. Thermodynamic and Computational (DFT) Study of Non-Covalent Interaction Mechanisms of Charge Transfer Complex of Linagliptin with 2,3-Dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) and Chloranilic acid (CHA). Molecules 2022, 27, 6320. https://doi.org/10.3390/molecules27196320
Bakheit AH, Al-Salahi R, Al-Majed AA. Thermodynamic and Computational (DFT) Study of Non-Covalent Interaction Mechanisms of Charge Transfer Complex of Linagliptin with 2,3-Dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) and Chloranilic acid (CHA). Molecules. 2022; 27(19):6320. https://doi.org/10.3390/molecules27196320
Chicago/Turabian StyleBakheit, Ahmed H., Rashad Al-Salahi, and Abdulrahman A. Al-Majed. 2022. "Thermodynamic and Computational (DFT) Study of Non-Covalent Interaction Mechanisms of Charge Transfer Complex of Linagliptin with 2,3-Dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) and Chloranilic acid (CHA)" Molecules 27, no. 19: 6320. https://doi.org/10.3390/molecules27196320
APA StyleBakheit, A. H., Al-Salahi, R., & Al-Majed, A. A. (2022). Thermodynamic and Computational (DFT) Study of Non-Covalent Interaction Mechanisms of Charge Transfer Complex of Linagliptin with 2,3-Dichloro-5,6-dicyano-1,4-benzoquinone (DDQ) and Chloranilic acid (CHA). Molecules, 27(19), 6320. https://doi.org/10.3390/molecules27196320









