Electronic Structure-, Phonon Spectrum-, and Effective Mass- Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
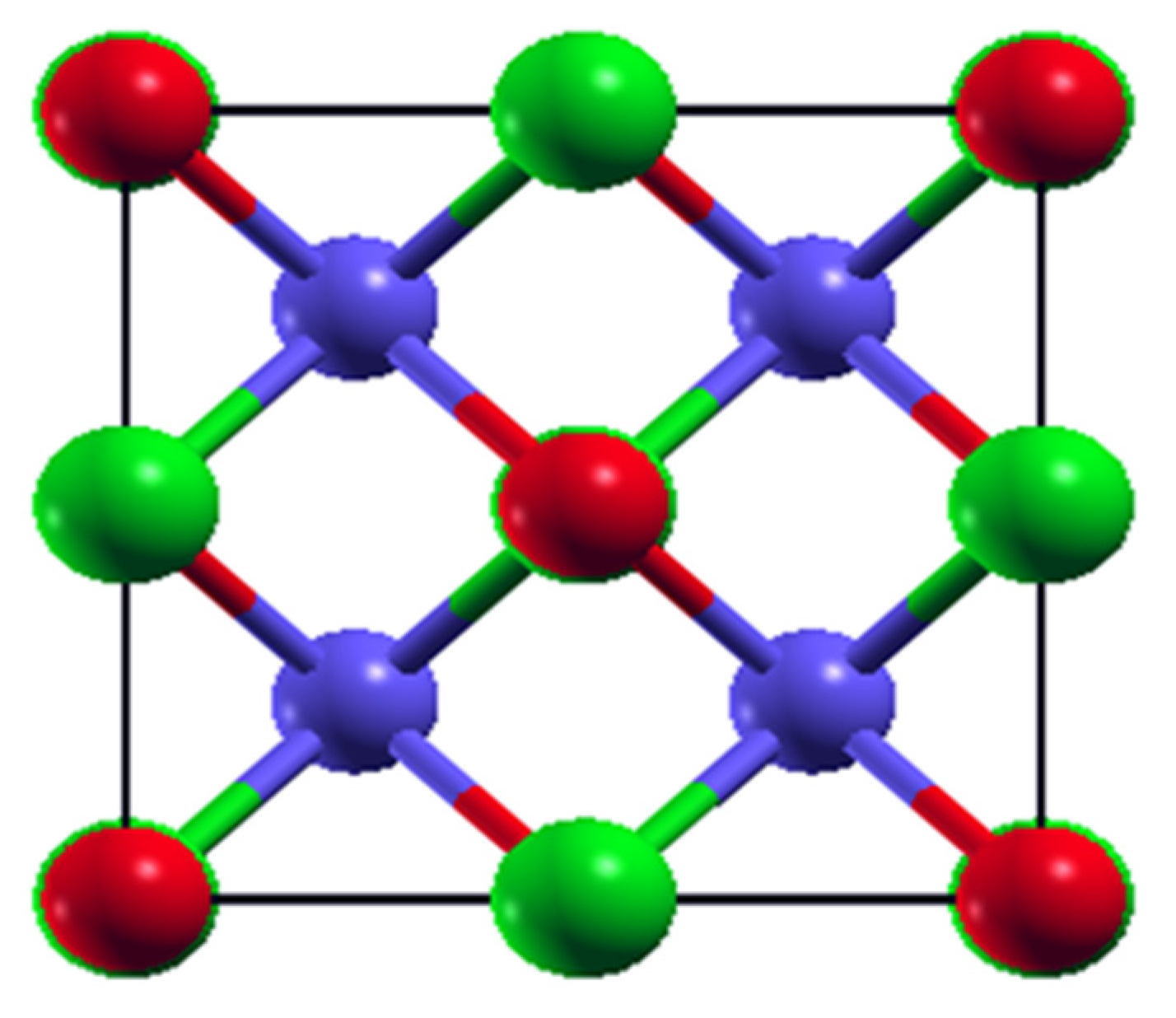
3.1. Structure and Stability
| Parameter | Lattice Constant (Ǻ) | Band Gap (eV) |
|---|---|---|
| PdZrSn | 6.41 (this work) | 0.91 (this work) |
| 6.32 [48] | 0.49 [48] | |
| 6.321 [49] | 0.43 [49] | |
| 6.392 [50] | ||
| PdHfSn | 6.38 (this work) | 0.82 (this work) |
| 6.354 [32] | 0.40 [32] | |
| 6.30 [48] | 0.38 [48] |
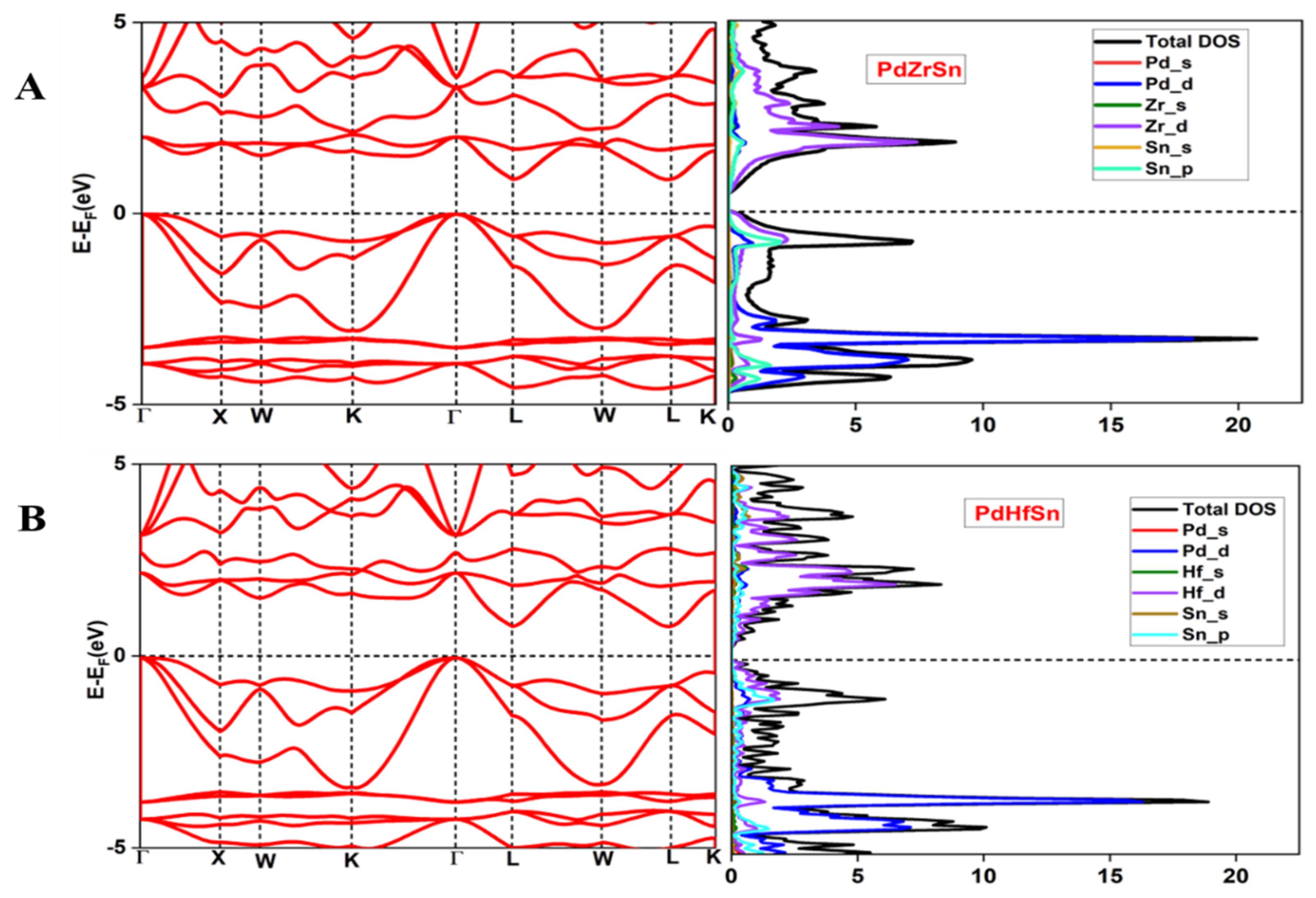
3.2. Electronic Structure
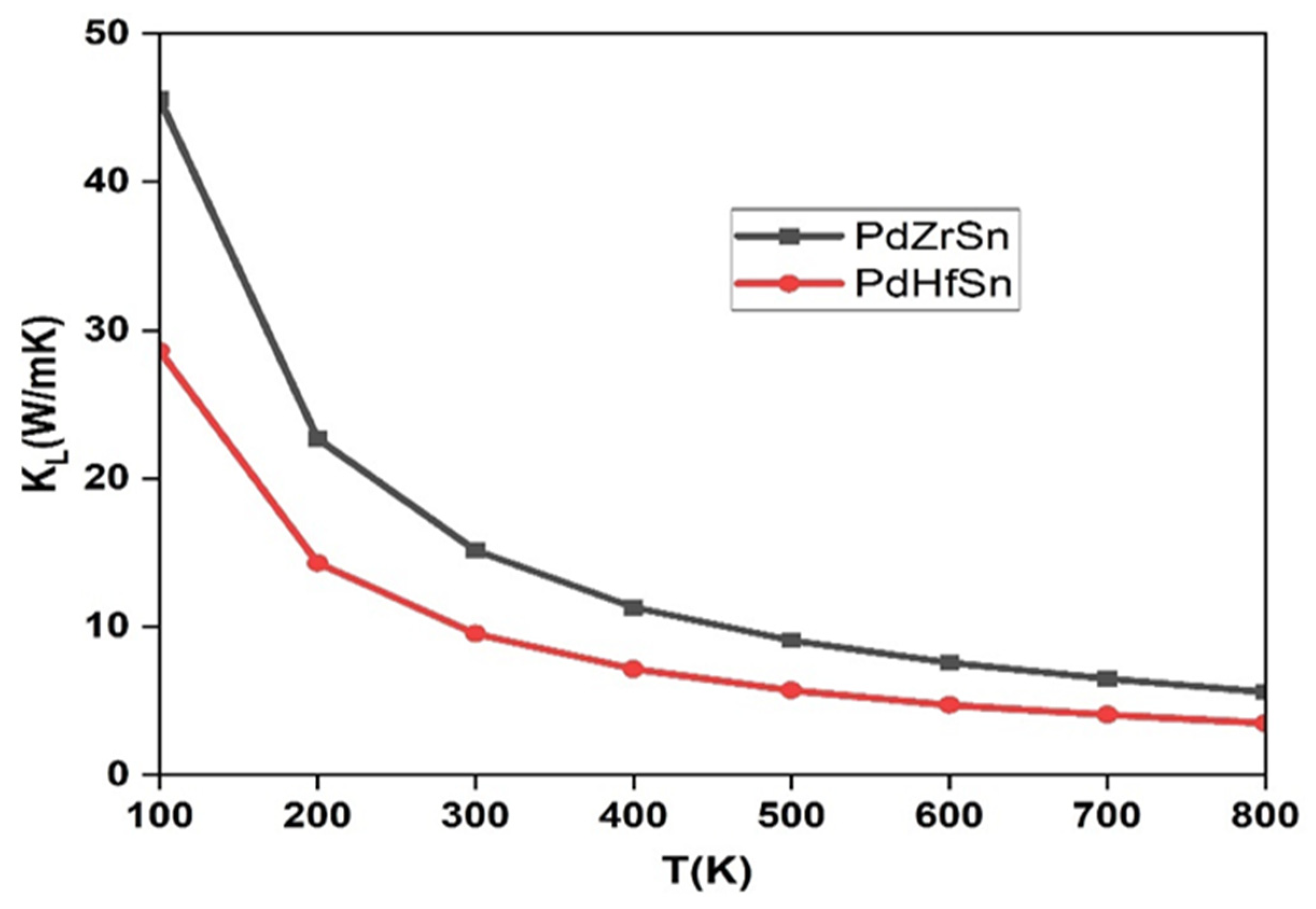
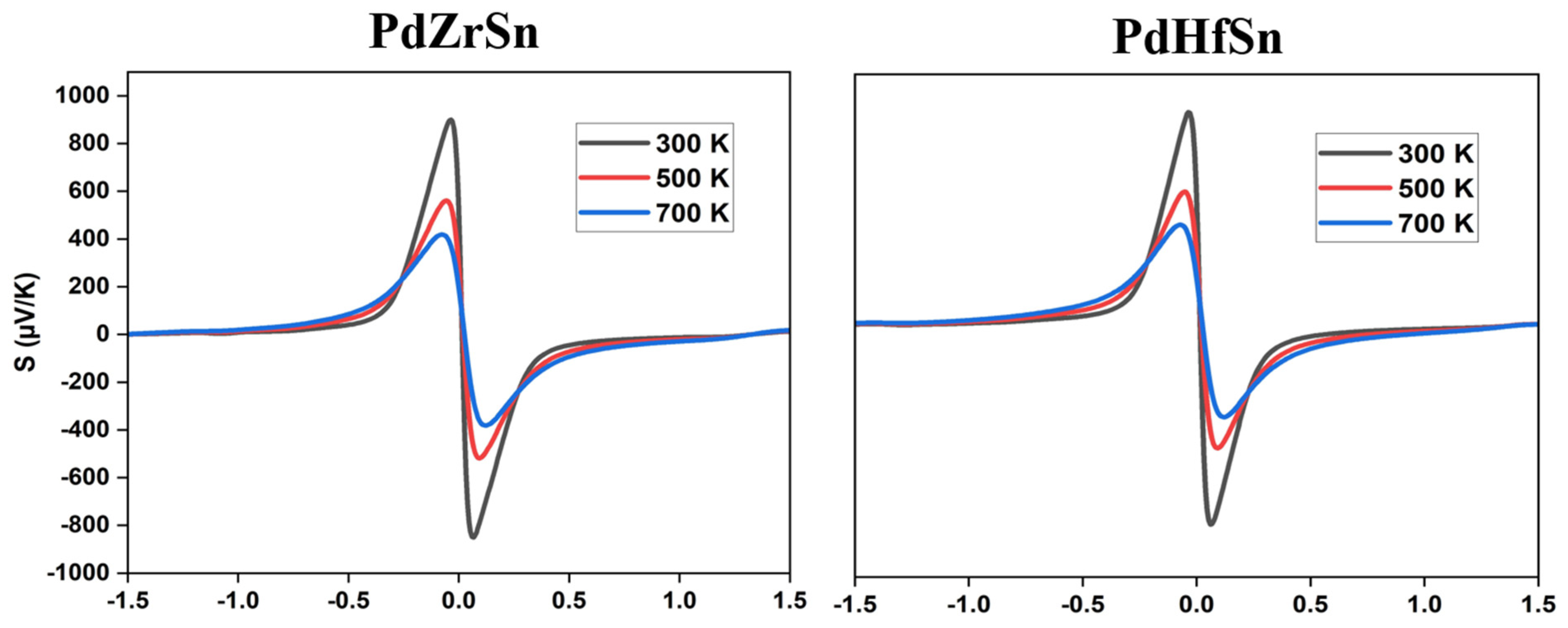
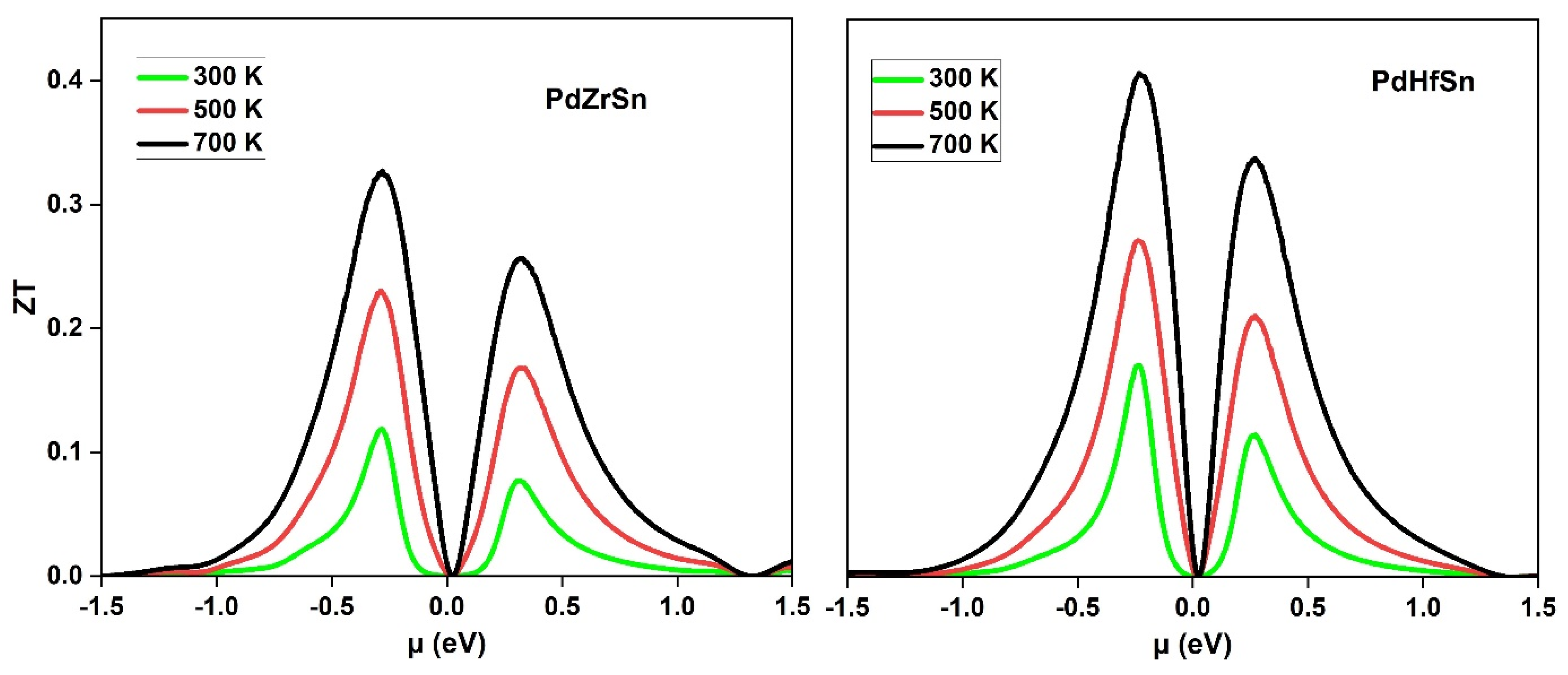
3.3. Thermoelectric Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DiSalvo, F.J. Thermoelectric Cooling and Power Generation. Science 1999, 285, 703–706. [Google Scholar] [CrossRef] [PubMed]
- Zeeshan, M.; Singh, H.K.; Van Den Brink, J.; Kandpal, H.C. Ab Initio Design of New Cobalt-Based Half-Heusler Materials for Thermoelectric Applications. Phys. Rev. Mater. 2017, 1, 075407–075415. [Google Scholar] [CrossRef]
- Zhang, Q.; Liao, B.; Lan, Y.; Lukas, K.; Liu, W.; Esfarjani, K.; Opeil, C.; Broido, D.; Chen, G.; Ren, Z. High Thermoelectric Performance by Resonant Dopant Indium in Nanostructured SnTe. Proc. Natl. Acad. Sci. USA 2013, 110, 13261–13266. [Google Scholar] [CrossRef]
- Jia, B.; Huang, Y.; Wang, Y.; Zhou, Y.; Zhao, X.; Ning, S.; Xu, X.; Lin, P.; Chen, Z.; Jiang, B.; et al. Realizing High Thermoelectric Performance in Non-Nanostructured n-Type PbTe. Energy Environ. Sci. 2022, 15, 1920–1929. [Google Scholar] [CrossRef]
- Sakane, S.; Ishibe, T.; Mizuta, K.; Fujita, T.; Kiyofuji, Y.; Ohe, J.I.; Kobayashi, E.; Nakamura, Y. Anomalous Enhancement of Thermoelectric Power Factor by Thermal Management with Resonant Level Effect. J. Mater. Chem. A 2021, 9, 4851–4857. [Google Scholar] [CrossRef]
- Lue, C.S.; Kuo, Y.K. Thermoelectric Properties of the Semimetallic Heusler Compounds (Formula Presented) (Formula Presented) Ga. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 66, 085121–085125. [Google Scholar] [CrossRef]
- El Krimi, Y.; Masrour, R.; Jabar, A.; Labidi, S.; Bououdina, M.; Ellouze, M. Structural, Electronic, Magnetic and Thermoelectric Properties of Full-Heusler Fe2MnSi: Ab Initio Calculations. Results Phys. 2020, 18, 103252. [Google Scholar] [CrossRef]
- Hu, Y.; Jin, Y.; Zhang, G.; Yan, Y. Electronic Structure and Thermoelectric Properties of Full Heusler Compounds Ca2YZ (Y = Au, Hg; Z = As, Sb, Bi, Sn and Pb). RSC Adv. 2020, 10, 28501–28508. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, R. Giant Thermoelectric Performance of Novel TaIrSn Half Heusler Compound. Phys. Lett. A 2017, 381, 3760–3765. [Google Scholar] [CrossRef]
- Rahman, J.U.; Nam, W.H.; Van Du, N.; Rahman, G.; Rahman, A.U.; Shin, W.H.; Seo, W.S.; Kim, M.H.; Lee, S. Oxygen Vacancy Revived Phonon-Glass Electron-Crystal in SrTiO3. J. Eur. Ceram. Soc. 2019, 39, 358–365. [Google Scholar] [CrossRef]
- Zhu, T.; Swaminathan-Gopalan, K.; Stephani, K.; Ertekin, E. Thermoelectric Phonon-Glass Electron-Crystal via Ion Beam Patterning of Silicon. Phys. Rev. B 2018, 97, 174201–174220. [Google Scholar] [CrossRef]
- Ramiere, A.; Li, F.; Chen, Y.; Fu, Y. Thermoelectric Properties and Low Thermal Conductivity of Nanocomposite ZrTe5 under Magnetic Field. J. Alloys Compd. 2020, 840, 155651. [Google Scholar] [CrossRef]
- Shen, J.; Xie, T.; Zhang, L.; Wang, P.; Fang, Z. Si2Ge: A New VII-Type Clathrate with Ultralow Thermal Conductivity and High Thermoelectric Property. Sci. Rep. 2020, 10, 3068. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Sturm, C.; Kleinke, H. Chalcogenides as Thermoelectric Materials. J. Solid State Chem. 2019, 270, 273–279. [Google Scholar] [CrossRef]
- Rogl, G.; Rogl, P. Skutterudites, a Most Promising Group of Thermoelectric Materials. Curr. Opin. Green Sustain. Chem. 2017, 4, 50–57. [Google Scholar] [CrossRef]
- Ohtaki, M. Recent Aspects of Oxide Thermoelectric Materials for Power Generation from Mid-to-High Temperature Heat Source. J. Ceram. Soc. Japan 2011, 119, 770–775. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Xing, C.; Xing, C.; Zhang, T.; Li, M.; Pacios, M.; Yu, X.; Arbiol, J.; Arbiol, J.; et al. Tin Selenide Molecular Precursor for the Solution Processing of Thermoelectric Materials and Devices. ACS Appl. Mater. Interfaces 2020, 12, 27104–27111. [Google Scholar] [CrossRef]
- Ma, J.; Hegde, V.I.; Munira, K.; Xie, Y.; Keshavarz, S.; Mildebrath, D.T.; Wolverton, C.; Ghosh, A.W.; Butler, W.H. Computational Investigation of Half-Heusler Compounds for Spintronics Applications. Phys. Rev. B 2017, 95, 024411–024435. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti Substitution on the Thermoelectric Properties of (Zr, Hf)NiSn Half-Heusler Compounds. Appl. Phys. Lett. 2005, 86, 082105–082107. [Google Scholar] [CrossRef]
- Yan, X.; Liu, W.; Chen, S.; Wang, H.; Zhang, Q.; Chen, G.; Ren, Z. Thermoelectric Property Study of Nanostructured P-Type Half-Heuslers (Hf, Zr, Ti)CoSb0.8 Sn0.2. Adv. Energy Mater. 2013, 3, 1195–1200. [Google Scholar] [CrossRef]
- Rausch, E.; Balke, B.; Ouardi, S.; Felser, C. Enhanced Thermoelectric Performance in the P-Type Half-Heusler (Ti/Zr/Hf)CoSb0.8Sn0.2 System via Phase Separation. Phys. Chem. Chem. Phys. 2014, 16, 25258–25262. [Google Scholar] [CrossRef] [PubMed]
- Jia, K.; Yang, C.L.; Wang, M.S.; Ma, X.G.; Yi, Y.G. First-Principles Investigation on the Thermoelectric Performance of Half-Heusler Compound CuLiX(X = Se, Te). J. Phys. Condens. Matter 2020, 33, 095501. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Bai, S.; Liu, Y.; Tang, Y.; Chen, L.; Zhao, X.; Zhu, T. Realizing High Figure of Merit in Heavy-Band p-Type Half-Heusler Thermoelectric Materials. Nat. Commun. 2015, 6, 8144–8150. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Fu, C.; Liu, Y.; Zhao, X.; Zhu, T. Enhancing Thermoelectric Performance of FeNbSb Half-Heusler Compound by Hf-Ti Dual-Doping. Energy Storage Mater. 2018, 10, 69–74. [Google Scholar] [CrossRef]
- Bamgbose, M.K. First-Principles Study of Electronic Structure and Thermoelectric Properties of p-Type XIrSb(X = Ti, Zr and Hf) Half-Heusler Compounds. Mater. Sci. Semicond. Process. 2021, 129, 105792. [Google Scholar] [CrossRef]
- Fang, T.; Zheng, S.; Zhou, T.; Yan, L.; Zhang, P. Computational Prediction of High Thermoelectric Performance in P-Type Half-Heusler Compounds with Low Band Effective Mass. Phys. Chem. Chem. Phys. 2017, 19, 4411–4417. [Google Scholar] [CrossRef]
- Meghoufel, Z.F.; Cherifi, F.; Boukra, A. Ab-Initio Investigation on the Electronic and Thermoelectric Properties of New Half-Heusler Compounds KBi X ( X = Ba and Sr ). J. Phys. Condens. Matter 2021, 33, 395701. [Google Scholar] [CrossRef]
- Ahmed, R.; Masuri, N.S.; Ul Haq, B.; Shaari, A.; AlFaifi, S.; Butt, F.K.; Muhamad, M.N.; Ahmed, M.; Tahir, S.A. Investigations of Electronic and Thermoelectric Properties of Half-Heusler Alloys XMgN (X = Li, Na, K) by First-Principles Calculations. Mater. Des. 2017, 136, 196–203. [Google Scholar] [CrossRef]
- Kangsabanik, J.; Enamullah; Alam, A. Bismuth Based Half-Heusler Alloys with Giant Thermoelectric Figures of Merit. J. Mater. Chem. A 2017, 5, 6131–6139. [Google Scholar] [CrossRef]
- Zeeshan, M.; Nautiyal, T.; Van Den Brink, J.; Kandpal, H.C. FeTaSb and FeMnTiSb as Promising Thermoelectric Materials: An Ab Initio Approach. Phys. Rev. Mater. 2018, 2, 065407–065416. [Google Scholar] [CrossRef]
- Vora-ud, A.; Jiang, Q.; Wan, R.; Zhang, Z.; Lei, Y. High Thermoelectric Performance of Half-Heusler Zr X Pb ( X = Ni, Pd, and Pt ). J. Phys. Condens. Matter Pap. 2021, 33, 465501–465510. [Google Scholar]
- Nagura, J.; Ashani, T.M.; Adebambo, P.O.; Ayedun, F.; Adebayo, G.A. Thermoelectric and Mechanical Properties of XHfSn (X = Ni, Pd and Pt) Semiconducting Half-Heusler Alloys: A First-Principles Study. Comput. Condens. Matter 2021, 26, e00539. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502–3955019. [Google Scholar] [CrossRef] [PubMed]
- TroullierMartinsPhysRevB.43.1993.Pdf. PhysRevB. 1991, 43, 1993–2006.
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Wu, M.; Hinokuma, S.; Ohto, T.; Wakisaka, M.; Fujita, J.; Ito, Y. Boosting Electrochemical Water Splitting via Ternary NiMoCo Hybrid Nanowire Arrays. J. Mater. Chem. A 2019, 7, 2156–2164. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Scheidemantel, J.; Ambrosch-Draxl, C.; Thonhauser, T.; Badding, V.; Sofo, O. Transport Coefficients from First-Principles Calculations. Phys. Rev. B—Condens. Matter Mater. Phys. 2003, B 68, 25210–25215. [Google Scholar] [CrossRef]
- Jodin, L.; Tobola, J.; Pecheur, P.; Scherrer, H.; Kaprzyk, S. Effect of Substitutions and Defects in Half-Heusler FeVSb Studied by Electron Transport Measurements and KKR-CPA Electronic Structure Calculations. Phys. Rev. B—Condens. Matter Mater. Phys. 2004, B 70, 184207. [Google Scholar] [CrossRef]
- Nielsen, M.D.; Ozolins, V.; Heremans, J.P. Lone Pair Electrons Minimize Lattice Thermal Conductivity. Energy Environ. Sci. 2013, 6, 570–578. [Google Scholar] [CrossRef]
- Morelli, D.T.; Slack, G.A. High Lattice Thermal Conductivity Solids. In High Thermal Conductivity Materials; Springer: New York, NY, USA, 2006; pp. 37–68. [Google Scholar] [CrossRef]
- Skoug, E.J.; Cain, J.D.; Morelli, D.T. Structural Effects on the Lattice Thermal Conductivity of Ternary Antimony- and Bismuth-Containing Chalcogenide Semiconductors. Appl. Phys. Lett. 2010, 96, 181905–181908. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Xue, Q.Y.; Liu, H.J.; Fan, D.D.; Cheng, L.; Zhao, B.Y.; Shi, J. LaPtSb: A Half-Heusler Compound with High Thermoelectric Performance. Phys. Chem. Chem. Phys. 2016, 18, 17912–17916. [Google Scholar] [CrossRef] [PubMed]
- Murnaghan, F.D. The Volume Changes of Five Gases under High Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed]
- Kaur, K.; Kumar, R. On the Possibility of Thermoelectricity in Half Heusler XRuSb (X = V, Nb, Ta) Materials: A First Principles Prospective. J. Phys. Chem. Solids 2017, 110, 108–115. [Google Scholar] [CrossRef]
- Ahmad Khandy, S.; Kaur, K.; Dhiman, S.; Singh, J.; Kumar, V. Exploring Thermoelectric Properties and Stability of Half-Heusler PtXSn (X = Zr, Hf) Semiconductors: A First Principle Investigation. Comput. Mater. Sci. 2021, 188, 110232. [Google Scholar] [CrossRef]
- Roy, A.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Half-Heusler Semiconductors as Piezoelectrics. Phys. Rev. Lett. 2012, 109, 037602–037606. [Google Scholar] [CrossRef]
- Xing, G.; Sun, J.; Li, Y.; Fan, X.; Zheng, W.; Singh, D.J. Electronic Fitness Function for Screening Semiconductors as Thermoelectric Materials. Phys. Rev. Mater. 2017, 1, 065405–065416. [Google Scholar] [CrossRef]
- Schlipf, M.; Gygi, F. Optimization Algorithm for the Generation of ONCV Pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef]
- Born, M.; Fürth, R. The Stability of Crystal Lattices. III: An Attempt to Calculate the Tensile Strength of a Cubic Lattice by Purely Static Considerations. Math. Proc. Camb. Philos. Soc. 1940, 36, 454–465. [Google Scholar] [CrossRef]
- Hill, R. Related Content The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Sisodia, P.; Verma, M.P. Shear moduli of polycrystalline cubic elements. J. Phys.Chem. Solids 1989, 50, 223–224. [Google Scholar]
- SOGA, N.; ANDERSON, O.L. Simplified Method for Calculating Elastic Moduli of Ceramic Powder from Compressibility and Debye Temperature Data. J. Am. Ceram. Soc. 1966, 49, 318–322. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Hossain, M.A.; Rahman, M.T.; Khatun, M.; Haque, E. Structural, Elastic, Electronic, Magnetic and Thermoelectric Properties of New Quaternary Heusler Compounds CoZrMnX (X = Al, Ga, Ge, In). Comput. Condens. Matter 2018, 15, 31–41. [Google Scholar] [CrossRef]
- Khandy, S.A.; Chai, J.D. Thermoelectric Properties, Phonon, and Mechanical Stability of New Half-Metallic Quaternary Heusler Alloys: FeRhCrZ (Z = Si and Ge). J. Appl. Phys. 2020, 127, 165102–165104. [Google Scholar] [CrossRef]
- Singh, J.; Kaur, K.; Khandy, S.A.; Dhiman, S.; Goyal, M.; Verma, S.S. Structural, Electronic, Mechanical, and Thermoelectric Properties of LiTiCoX (X = Si, Ge) Compounds. Int. J. Energy Res. 2021, 45, 16891–16900. [Google Scholar] [CrossRef]
- Shastri, S.S.; Pandey, S.K. Two Functionals Approach in DFT for the Prediction of Thermoelectric Properties of Fe2ScX (X = P, As, Sb) Full-Heusler Compounds. J. Phys. Condens. Matter 2019, 31, 435701–435712. [Google Scholar] [CrossRef]
- Paquin, F.; Rivnay, J.; Salleo, A.; Stingelin, N.; Silva, C. Multi-Phase Semicrystalline Microstructures Drive Exciton Dissociation in Neat Plastic Semiconductors. J. Mater. Chem. C 2015, 3, 10715–10722. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, R.; Rai, D.P. A Promising Thermoelectric Response of HfRhSb Half Heusler Compound at High Temperature: A First Principle Study. J. Alloys Compd. 2018, 763, 1018–1023. [Google Scholar] [CrossRef]
- Qiu, P.; Yang, J.; Huang, X.; Chen, X.; Chen, L. Effect of Antisite Defects on Band Structure and Thermoelectric Performance of ZrNiSn Half-Heusler Alloys. Appl. Phys. Lett. 2010, 96, 152105–152108. [Google Scholar] [CrossRef]
- Kimura, Y.; Zama, A. Thermoelectric Properties of P-Type Half-Heusler Compound HfPtSn and Improvement for High-Performance by Ir and Co Additions. Appl. Phys. Lett. 2006, 89, 172110–172113. [Google Scholar] [CrossRef]



| Compound | Electrons | Holes | ||||||
|---|---|---|---|---|---|---|---|---|
| Ed (eV) | Cii (GPa) | τ (fs) | Ed (eV) | Cii (GPa) | τ (fs) | |||
| PdZrSn | 0.13 | 37.88 | 166.7 | 0.690 | 1.28 | 35.33 | 166.7 | 0.026 |
| PdHfSn | 0.128 | 38.21 | 163 | 0.698 | 1.12 | 35.74 | 163 | 0.030 |
| Property | PdZrSn (This Work) | PdHfSn (This Work) | (PdHfSn) Others 26 |
|---|---|---|---|
| C11 (GPa) | 178.8 | 175.1 | 179.5 |
| C12 (GPa) | 96.6 | 90.4 | 88.6 |
| C44 (GPa) | 76.7 | 79.0 | 69.6 |
| ρ (gcm−3) | 7.96 | 10.29 | - |
| (ms−1) | 5055.9 | 4417.7 | - |
| (ms−1) | 2738.0 | 2445.7 | - |
| B (GPa) | 124.0 | 118.6 | 117.0 |
| G (GPa) | 59.7 | 61.7 | 59.5 |
| (K) | 322.5 | 288.6 | - |
| Pugh’s ratio (B/G) | 2.07 | 1.92 | - |
| Compound | S (µV/K) | (S/m) | (W/mK) | ZT Value |
|---|---|---|---|---|
| PdZrSn (our work) | 900 | 13.96 × 106 | 15.16 | 0.32 |
| PdHfSn (our work) | 763 | 17.46 × 106 | 9.53 | 0.40 |
| PtZrSn [47] | 1533 | 4.00 × 105 | 16.96 | 0.24 |
| PtHfSn [47] | 1649 | 6.42 × 105 | 10.04 | 0.57 |
| HfRhSb [61] | 252 | 1.5 × 105 | 17.35 | 0.42 |
| ZrNiSn [62] | 275 | 4 × 105 | 7.00 | 0.64 |
| ZrIrBi | 255.9 | 26.5× 104 | 2.00 | 0.42 |
| ZrRhBi | 319.8 | 8.7× 104 | - | 0.43 |
| HfPtSn [63] | 196 | 5.2 | 14.90 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rani, B.; Wani, A.F.; Sharopov, U.B.; Patra, L.; Singh, J.; Ali, A.M.; Abd El-Rehim, A.F.; Khandy, S.A.; Dhiman, S.; Kaur, K. Electronic Structure-, Phonon Spectrum-, and Effective Mass- Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers. Molecules 2022, 27, 6567. https://doi.org/10.3390/molecules27196567
Rani B, Wani AF, Sharopov UB, Patra L, Singh J, Ali AM, Abd El-Rehim AF, Khandy SA, Dhiman S, Kaur K. Electronic Structure-, Phonon Spectrum-, and Effective Mass- Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers. Molecules. 2022; 27(19):6567. https://doi.org/10.3390/molecules27196567
Chicago/Turabian StyleRani, Bindu, Aadil Fayaz Wani, Utkir Bahodirovich Sharopov, Lokanath Patra, Jaspal Singh, Atif Mossad Ali, A. F. Abd El-Rehim, Shakeel Ahmad Khandy, Shobhna Dhiman, and Kulwinder Kaur. 2022. "Electronic Structure-, Phonon Spectrum-, and Effective Mass- Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers" Molecules 27, no. 19: 6567. https://doi.org/10.3390/molecules27196567
APA StyleRani, B., Wani, A. F., Sharopov, U. B., Patra, L., Singh, J., Ali, A. M., Abd El-Rehim, A. F., Khandy, S. A., Dhiman, S., & Kaur, K. (2022). Electronic Structure-, Phonon Spectrum-, and Effective Mass- Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers. Molecules, 27(19), 6567. https://doi.org/10.3390/molecules27196567








