Graphene Nanoplatelets’ Effect on the Crystallization, Glass Transition, and Nanomechanical Behavior of Poly(ethylene 2,5-furandicarboxylate) Nanocomposites
Abstract
1. Introduction
2. Results
2.1. SEM Observations of the PEF and PEF/GNPs Nanocomposites
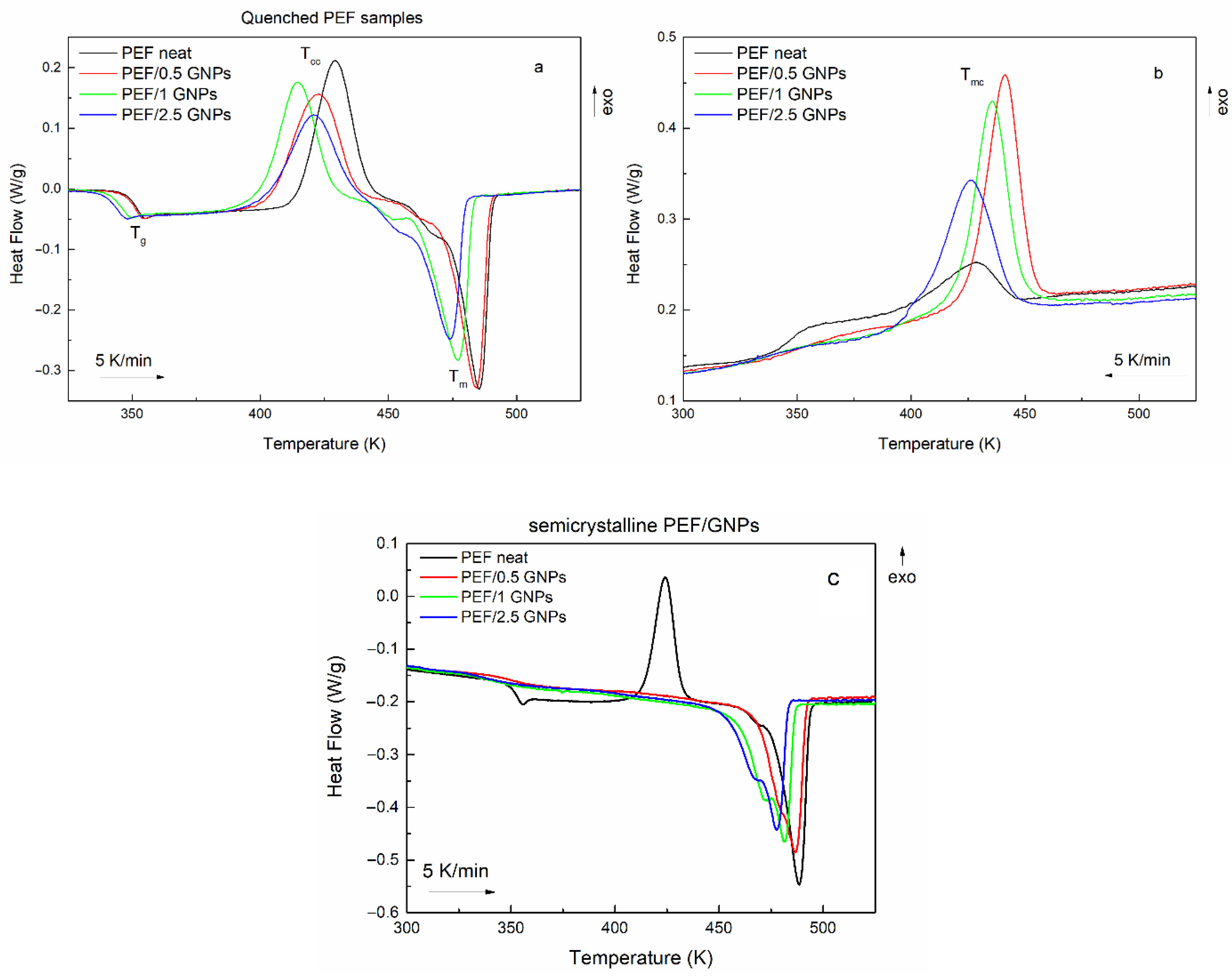
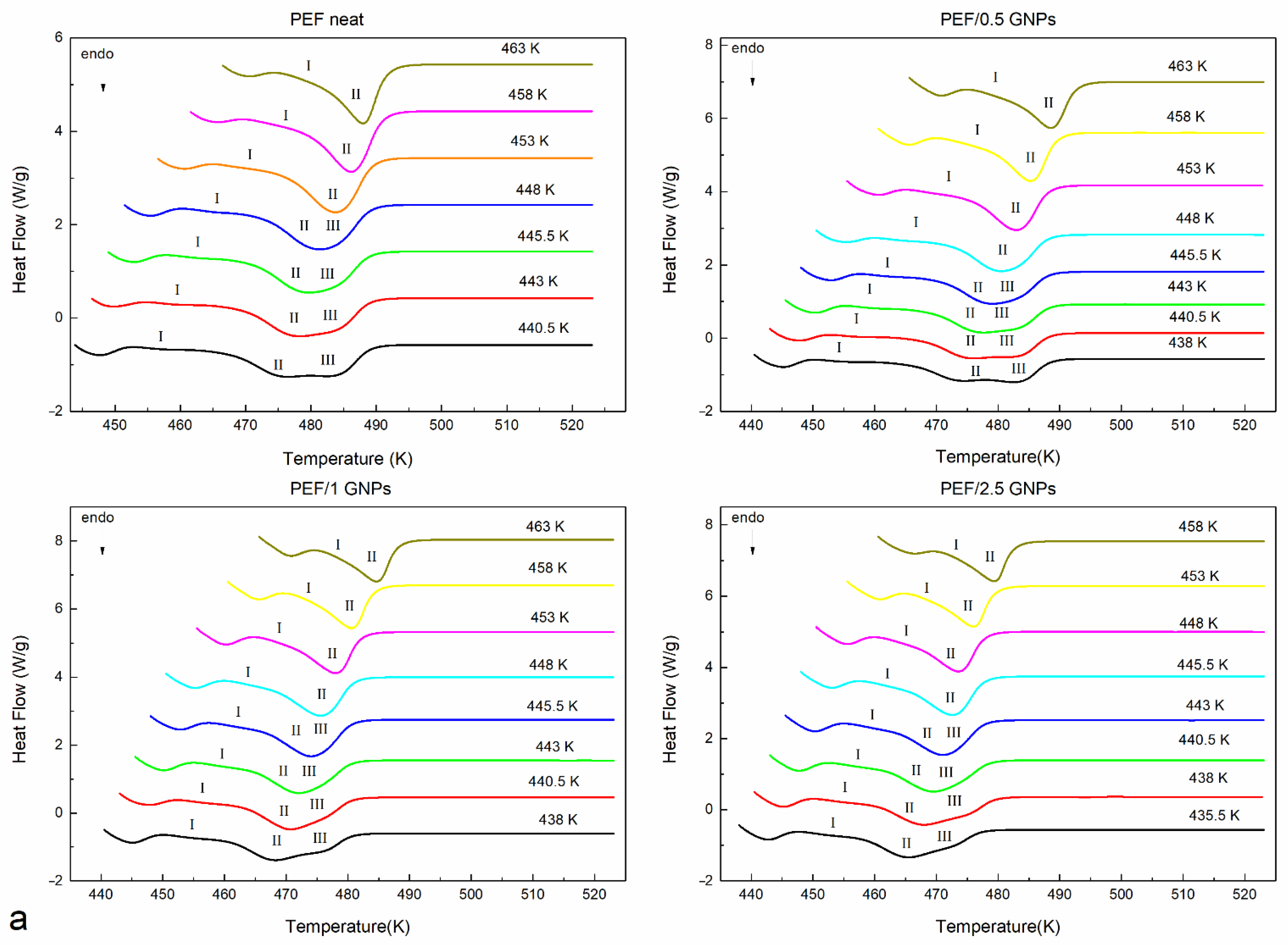
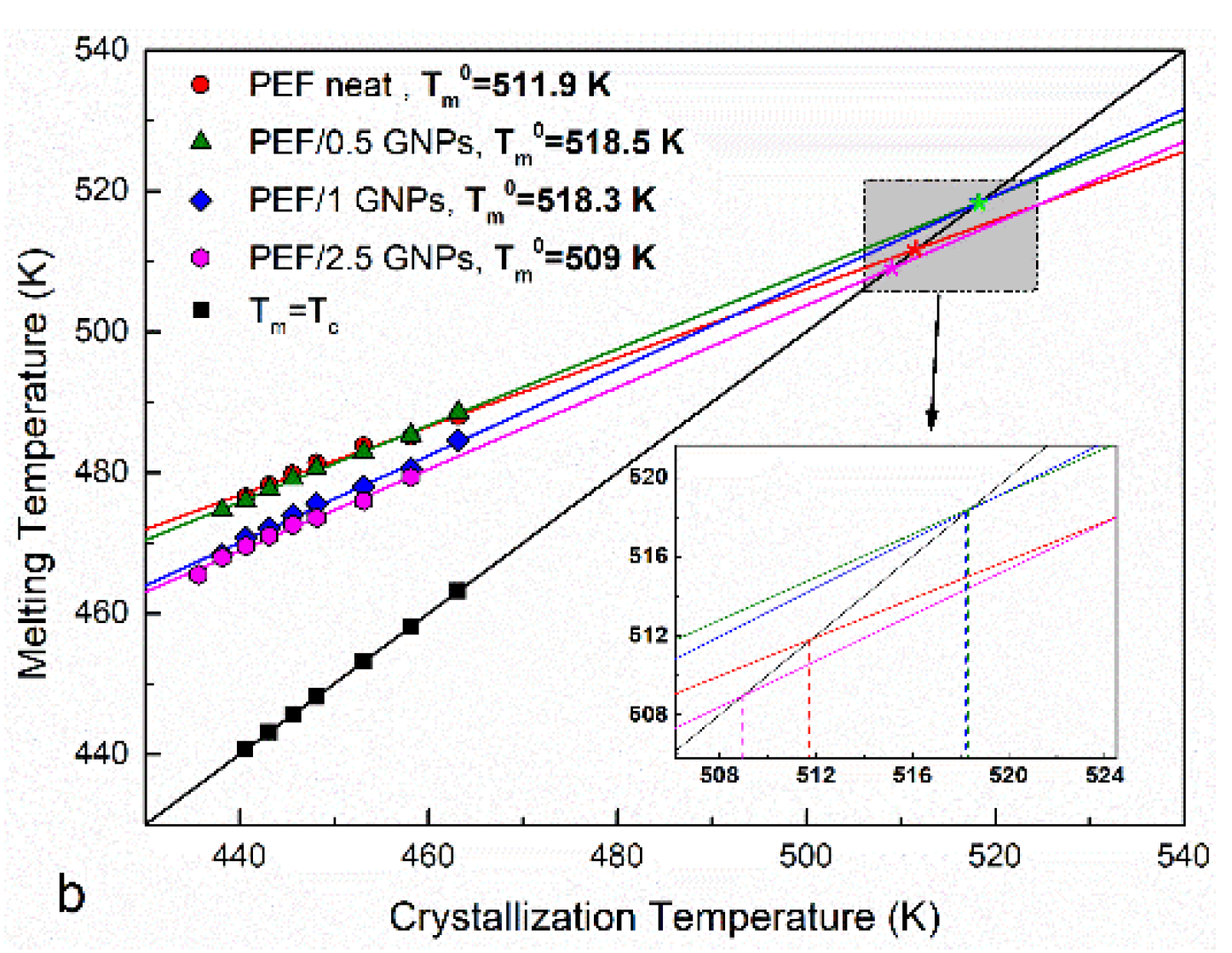
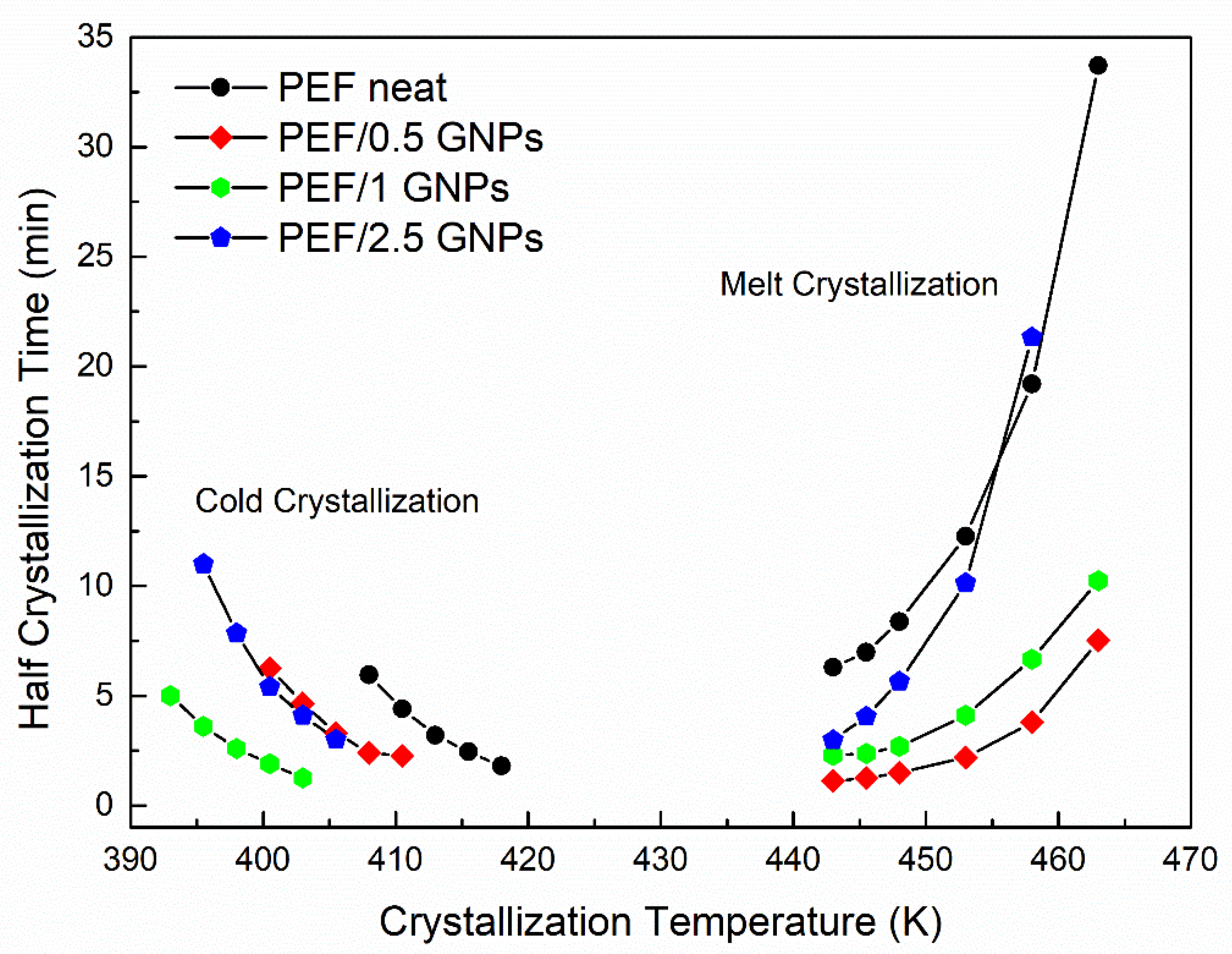
2.2. Crystallization of the Neat PEF and PEF/GNP Nanocomposites
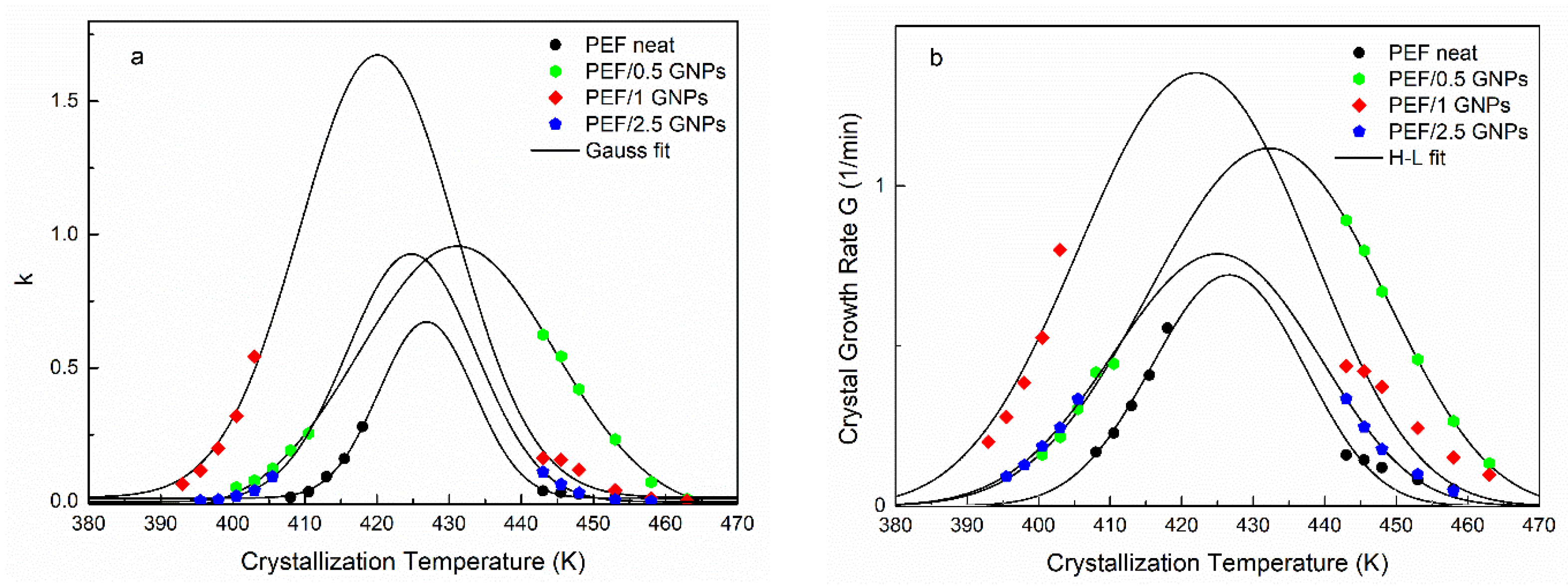
2.2.1. Isothermal Crystallization Kinetics of the Neat PEF and PEF/GNP Nanocomposites
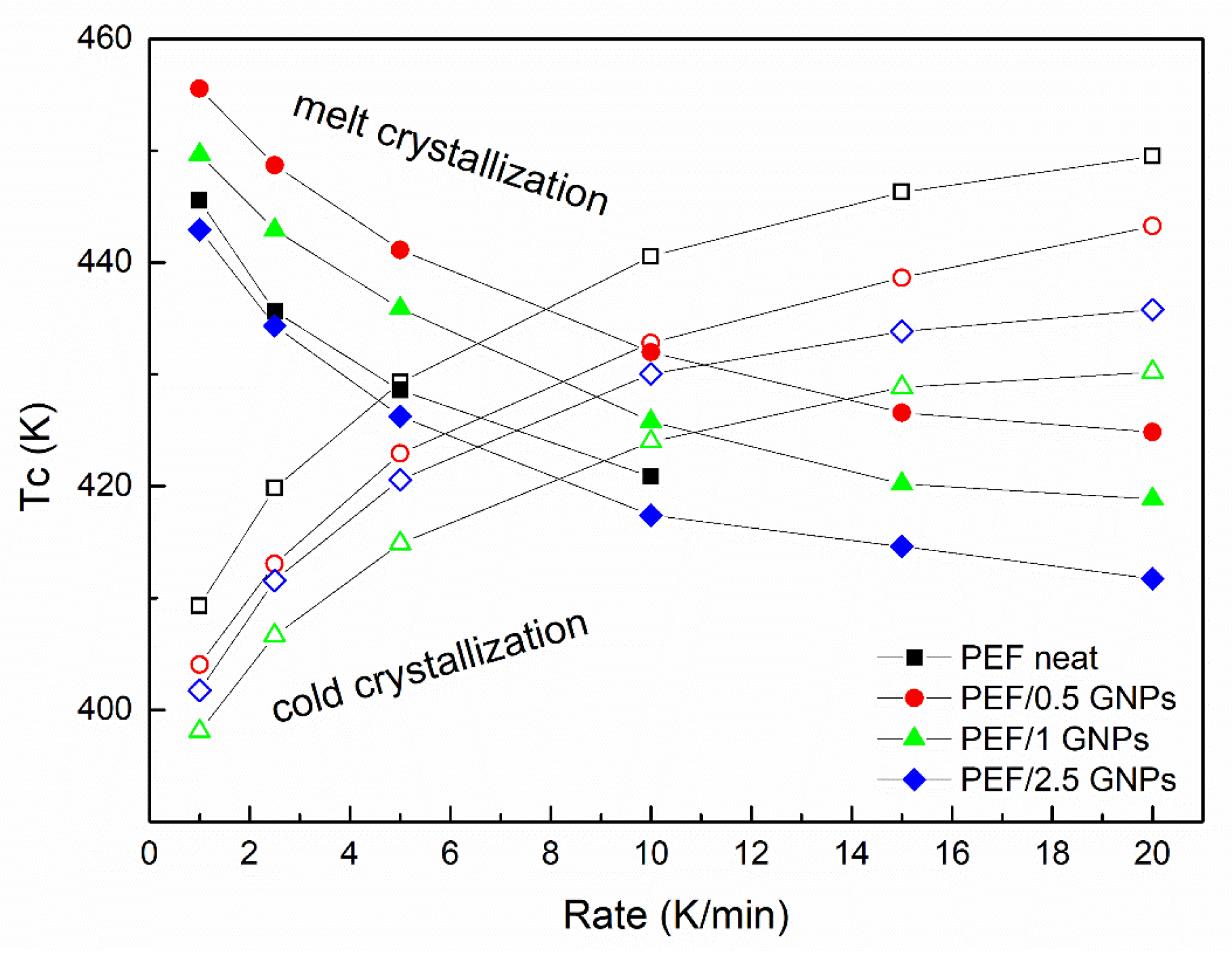
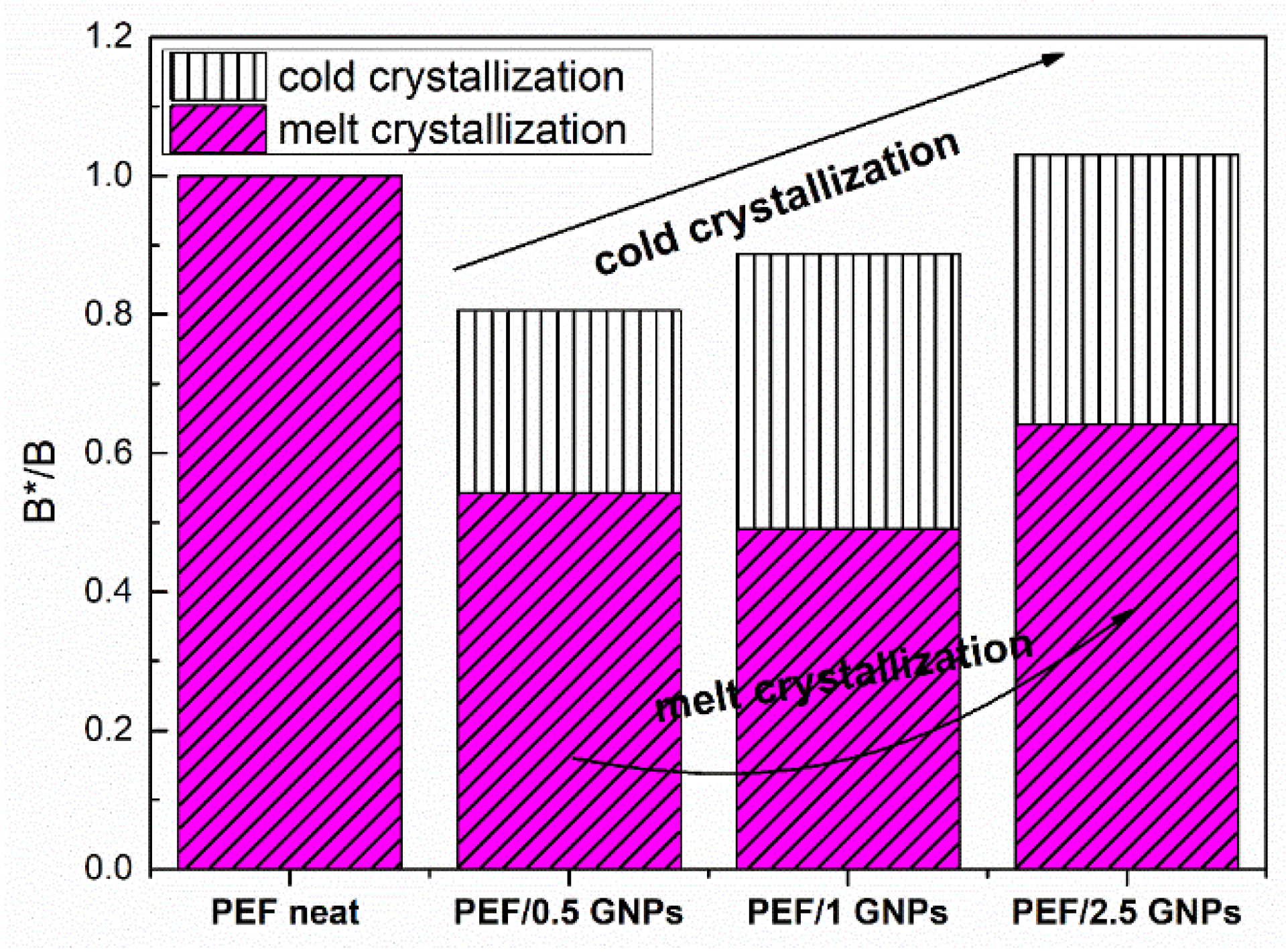
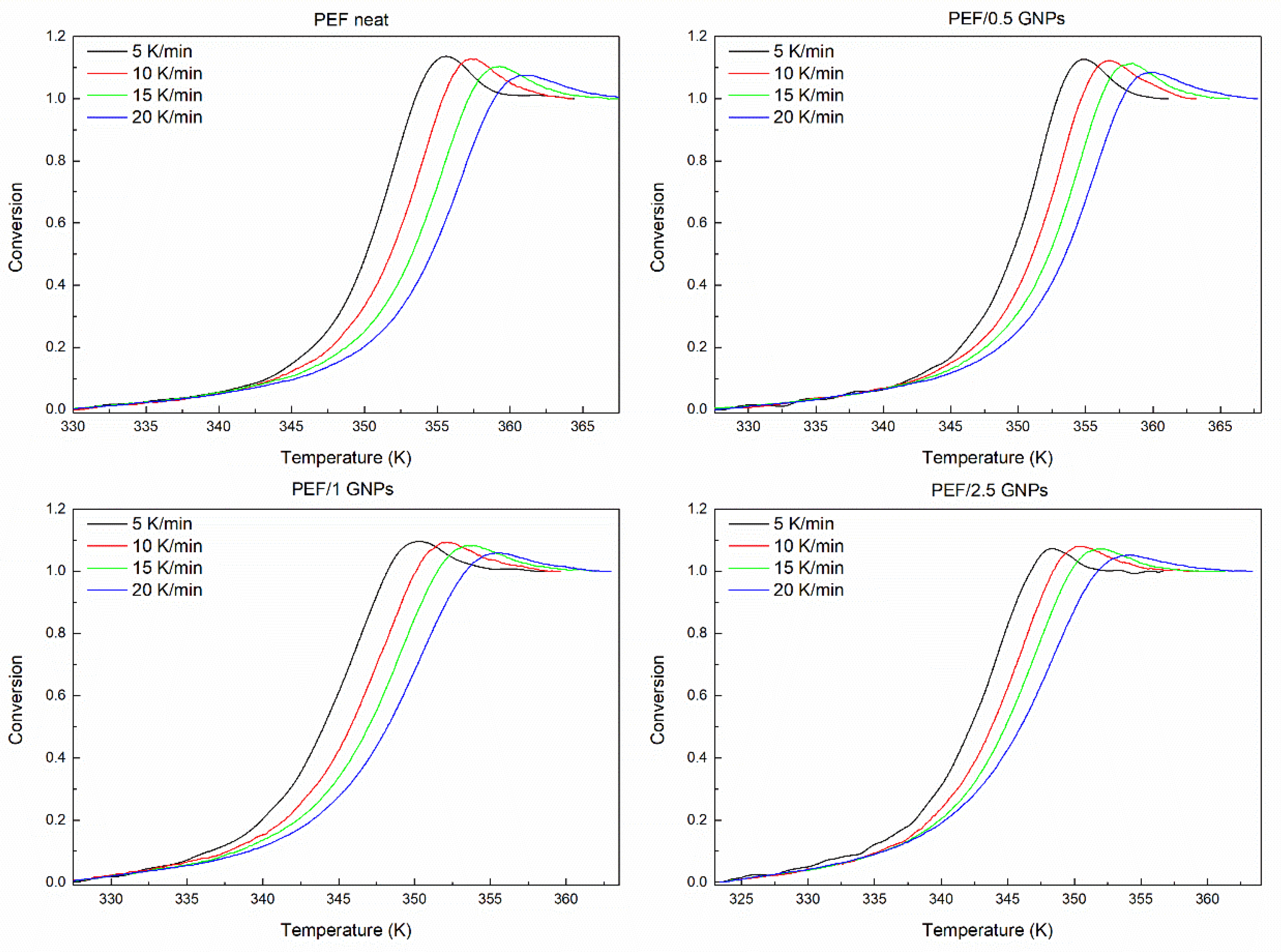
2.2.2. Non-isothermal Crystallization of the Neat PEF and PEF/GNP Nanocomposites
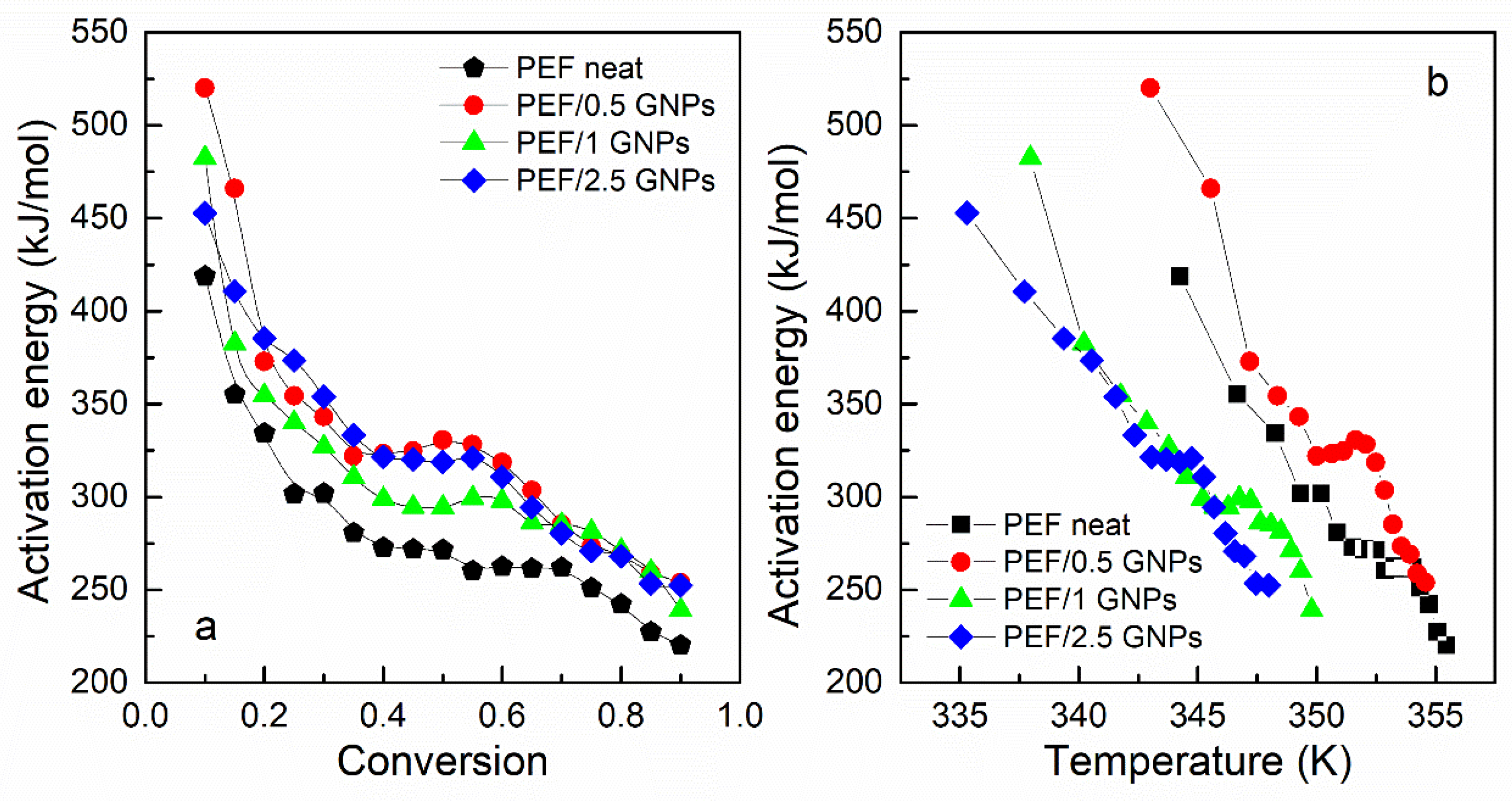
2.2.3. Glass Transition Kinetics of the Amorphous Neat PEF and PEF/GNP Nanocomposites
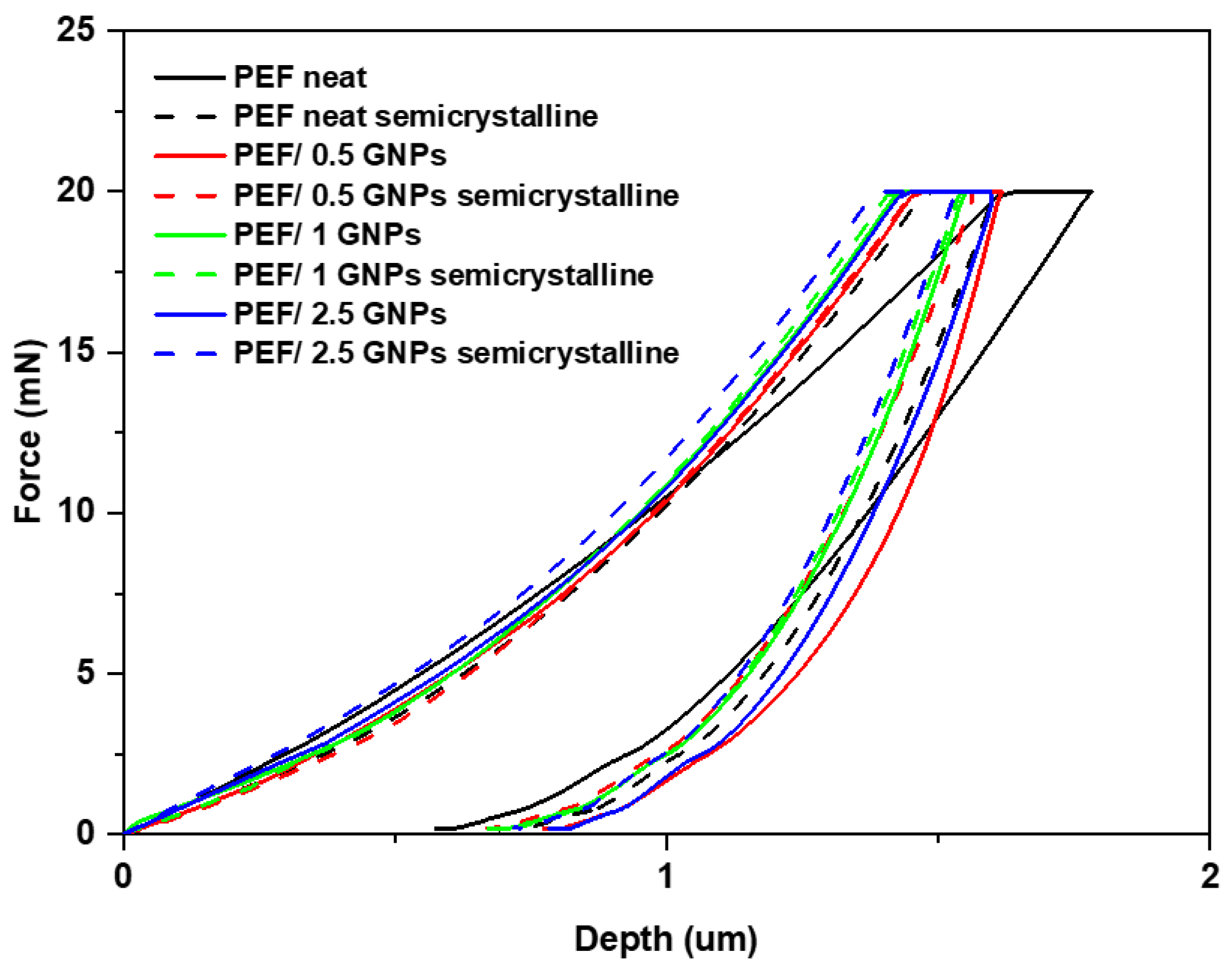
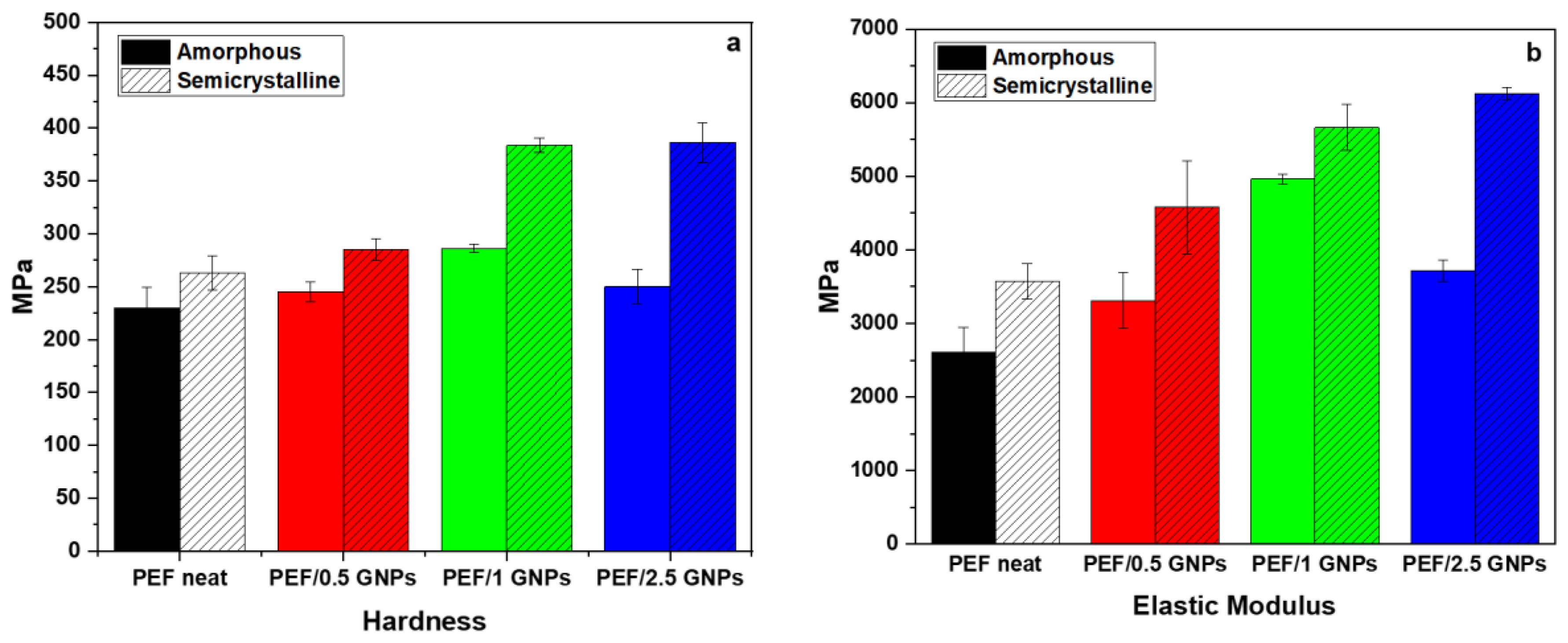
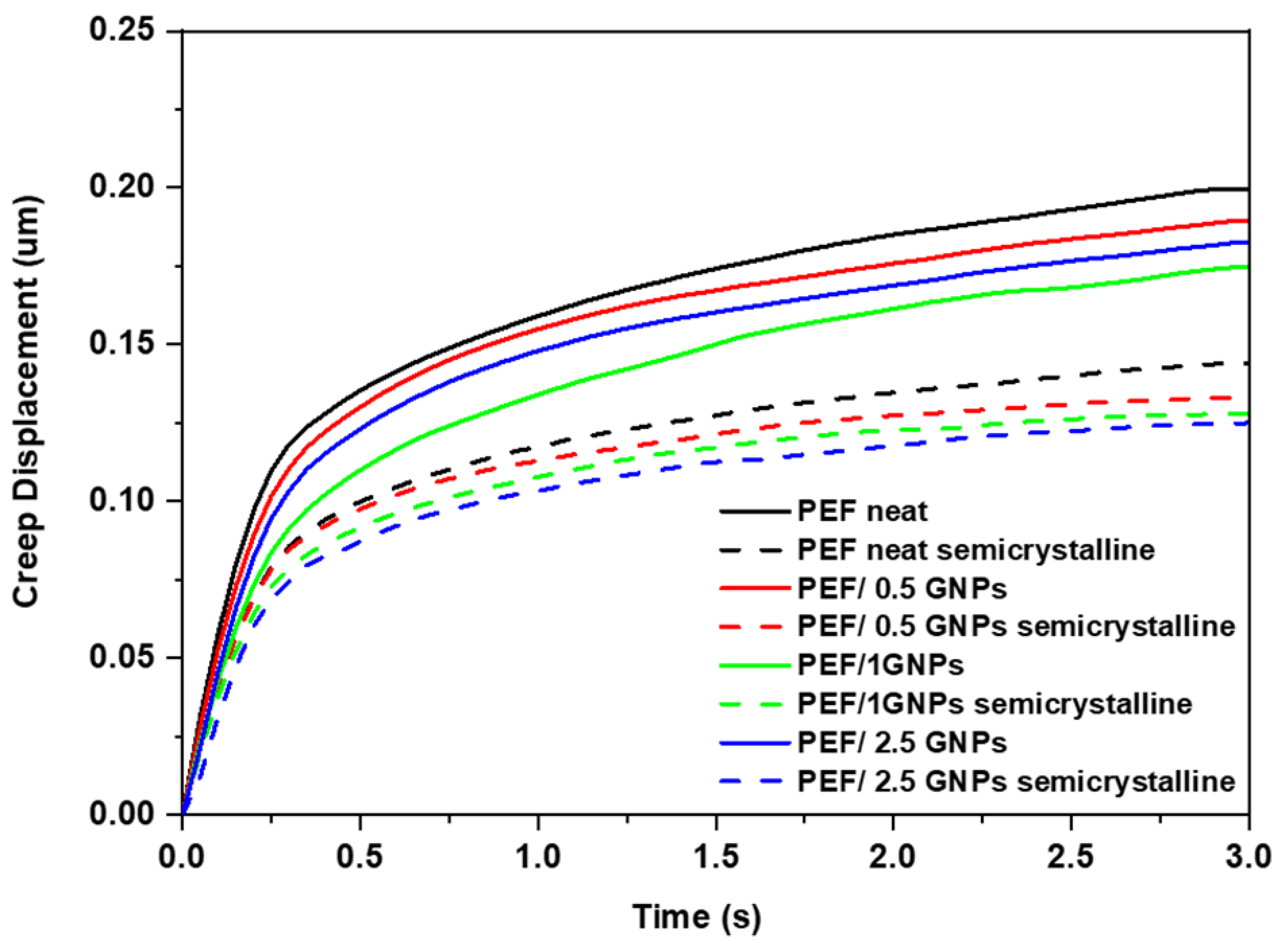
2.3. Nanoindentation Tests of the Neat PEF and PEF/GNP Nanocomposites
3. Materials and Methods
3.1. Materials
3.2. Synthesis of Poly(ethylene 2,5-furandicarboxylate)/Carbon Nanotube Nanocomposites (PEF/GNPs)
3.3. Characterization Techniques
Scanning Electron Microscopy (SEM)
3.4. Differential Scanning Calorimetry (DSC)
3.5. Nanoindentation Tests
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muhammad Shamsuddin, I. Bioplastics as Better Alternative to Petroplastics and Their Role in National Sustainability: A Review. Adv. Biosci. Bioeng. 2017, 5, 63. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Tsetsou, I.; Ioannidis, R.O.; Nikolaidis, G.N.; Exarhopoulos, S.; Kasmi, N.; Bikiaris, D.N.; Achilias, D.S.; Papageorgiou, G.Z. A new era in engineering plastics: Compatibility and perspectives of sustainable alipharomatic poly(ethylene terephthalate)/poly(ethylene 2,5-furandicarboxylate) blends. Polymers 2021, 13, 70. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, G.Z.; Papageorgiou, D.G.; Terzopoulou, Z.; Bikiaris, D.N. Production of bio-based 2,5-furan dicarboxylate polyesters: Recent progress and critical aspects in their synthesis and thermal properties. Eur. Polym. J. 2016, 83, 202–229. [Google Scholar] [CrossRef]
- Xanthopoulou, E.; Terzopoulou, Z.; Zamboulis, A.; Papadopoulos, L.; Tsongas, K.; Tzetzis, D.; Papageorgiou, G.Z.; Bikiaris, D.N. Poly(propylene vanillate): A Sustainable Lignin-Based Semicrystalline Engineering Polyester. ACS Sustain. Chem. Eng. 2021, 9, 1383–1397. [Google Scholar] [CrossRef]
- Fei, X.; Fei, X.; Fei, X.; Wang, J.; Wang, J.; Zhu, J.; Zhu, J.; Wang, X.; Liu, X.; Liu, X. Biobased Poly(ethylene 2,5-furancoate): No Longer an Alternative, but an Irreplaceable Polyester in the Polymer Industry. ACS Sustain. Chem. Eng. 2020, 8, 8471–8485. [Google Scholar] [CrossRef]
- Li, F.; Li, X.L.; Li, C.; Shi, J.; Fu, Y. Aerobic oxidative esterification of 5-hydroxymethylfurfural to dimethyl furan-2,5-dicarboxylate by using homogeneous and heterogeneous PdCoBi/C catalysts under atmospheric oxygen. Green Chem. 2018, 20, 3050–3058. [Google Scholar] [CrossRef]
- Loos, K.; Zhang, R.; Pereira, I.; Agostinho, B.; Hu, H.; Maniar, D.; Sbirrazzuoli, N.; Silvestre, A.J.D.; Guigo, N.; Sousa, A.F. A Perspective on PEF Synthesis, Properties, and End-Life. Front. Chem. 2020, 8, 585. [Google Scholar] [CrossRef]
- Tsanaktsis, V.; Vouvoudi, E.; Papageorgiou, G.Z.; Papageorgiou, D.G.; Chrissafis, K.; Bikiaris, D.N. Thermal degradation kinetics and decomposition mechanism of polyesters based on 2,5-furandicarboxylic acid and low molecular weight aliphatic diols. J. Anal. Appl. Pyrolysis 2015, 112, 369–378. [Google Scholar] [CrossRef]
- Papadopoulos, L.; Terzopoulou, Z.; Vlachopoulos, A.; Klonos, P.A.; Kyritsis, A.; Tzetzis, D.; Papageorgiou, G.Z.; Bikiaris, D. Synthesis and characterization of novel polymer/clay nanocomposites based on poly (butylene 2,5-furan dicarboxylate). Appl. Clay Sci. 2020, 190, 105588. [Google Scholar] [CrossRef]
- Jiang, M.; Liu, Q.; Zhang, Q.; Ye, C.; Zhou, G. A series of furan-aromatic polyesters synthesized via direct esterification method based on renewable resources. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 1026–1036. [Google Scholar] [CrossRef]
- Codou, A.; Guigo, N.; Van Berkel, J.; De Jong, E.; Sbirrazzuoli, N. Non-isothermal Crystallization Kinetics of Biobased Poly(ethylene 2,5-furandicarboxylate) Synthesized via the Direct Esterification Process. Macromol. Chem. Phys. 2014, 215, 2065–2074. [Google Scholar] [CrossRef]
- Van Berkel, J.G.; Guigo, N.; Kolstad, J.J.; Sipos, L.; Wang, B.; Dam, M.A.; Sbirrazzuoli, N. Isothermal crystallization kinetics of poly (ethylene 2,5-furandicarboxylate). Macromol. Mater. Eng. 2015, 300, 466–474. [Google Scholar] [CrossRef]
- Eirasa, D.; Pessan, L.A. Mechanical properties of polypropylene/calcium carbonate nanocomposites. Mater. Res. 2009, 12, 517–522. [Google Scholar] [CrossRef]
- Bartczak, Z.; Vozniak, A. Deformation instabilities and lamellae fragmentation during deformation of cross-linked polyethylene. Polymers 2019, 11, 1954. [Google Scholar] [CrossRef] [PubMed]
- Araujo, C.F.; Nolasco, M.M.; Ribeiro-Claro, P.J.A.; Rudić, S.; Silvestre, A.J.D.; Vaz, P.D.; Sousa, A.F. Inside PEF: Chain Conformation and Dynamics in Crystalline and Amorphous Domains. Macromolecules 2018, 51, 3515–3526. [Google Scholar] [CrossRef]
- Maini, L.; Gigli, M.; Gazzano, M.; Lotti, N.; Bikiaris, D.; Papageorgiou, G. Structural Investigation of Poly(ethylene furanoate) Polymorphs. Polymers 2018, 10, 296. [Google Scholar] [CrossRef] [PubMed]
- Vassiliou, A.A.; Papageorgiou, G.Z.; Achilias, D.S.; Bikiaris, D.N. Non-isothermal crystallisation kinetics of in situ prepared poly(ε-caprolactone)/ surface-treated SiO2 nanocomposites. Macromol. Chem. Phys. 2007, 208, 364–376. [Google Scholar] [CrossRef]
- Klonos, P.A.; Papadopoulos, L.; Tzetzis, D.; Kyritsis, A.; Papageorgiou, G.Z.; Bikiaris, D.N. Thermal, nanoindentation and dielectric study of nanocomposites based on poly(propylene furanoate) and various inclusions. Mater. Today Commun. 2019, 20, 100585. [Google Scholar] [CrossRef]
- Penghabluran, K.; Poli, K.; Asid, L.; Kenaf, S. Non-Isothermal Crystallization Kinetics of Poly (Lactic Acid)/Kenaf Fiber Composites. Sains Malays. 2020, 49, 2169–2185. [Google Scholar]
- Alshammari, B.A.; Al-Mubaddel, F.S.; Karim, M.R.; Hossain, M.; Al-Mutairi, A.S.; Wilkinson, A.N. Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling. Polymers 2019, 11, 1411. [Google Scholar] [CrossRef] [PubMed]
- Lotti, N.; Munari, A.; Gigli, M.; Gazzano, M.; Tsanaktsis, V.; Bikiaris, D.N.; Papageorgiou, G.Z. Thermal and structural response of in situ prepared biobased poly(ethylene 2,5-furan dicarboxylate) nanocomposites. Polymer 2016, 103, 288–298. [Google Scholar] [CrossRef]
- Achilias, D.S.; Chondroyiannis, A.; Nerantzaki, M.; Adam, K.-V.; Terzopoulou, Z.; Papageorgiou, G.Z.; Bikiaris, D.N. Solid State Polymerization of Poly(Ethylene Furanoate) and Its Nanocomposites with SiO2 and TiO2. Macromol. Mater. Eng. 2017, 302, 1700012. [Google Scholar] [CrossRef]
- Martino, L.; Niknam, V.; Guigo, N.; Gabriël van Berkel, J.; Sbirrazzuoli, N. Morphology and thermal properties of novel clay-based poly(ethylene 2,5-furandicarboxylate) (PEF) nanocomposites. RSC Adv. 2016, 6, 59800–59807. [Google Scholar] [CrossRef]
- Kourtidou, D.; Klonos, P.A.; Papadopoulos, L.; Kyritsis, A.; Bikiaris, D.N.; Chrissafis, K. Molecular mobility and crystallization of renewable poly(ethylene furanoate) in situ filled with carbon nanotubes and graphene nanoparticles. Soft Matter 2021, 17, 5815–5828. [Google Scholar] [CrossRef]
- Dimitra, K.; Konstantinos, C. Nonisothermal Crystallization Kinetics: Studying the Validity of Different Johnson–Mehl–Avrami–Erofeev–Kolmogorov (JMAEK) Based Equations. Thermochim. Acta 2021, 704, 179030. [Google Scholar] [CrossRef]
- Xie, H.; Meng, H.; Wu, L.; Li, B.G.; Dubois, P. In-situ synthesis, thermal and mechanical properties of biobased poly(ethylene 2,5-furandicarboxylate)/montmorillonite (PEF/MMT) nanocomposites. Eur. Polym. J. 2019, 121, 109266. [Google Scholar] [CrossRef]
- Codou, A.; Guigo, N.; Van Berkel, J.G.; De Jong, E.; Sbirrazzuoli, N. Preparation and characterization of poly(ethylene 2,5-furandicarboxylate/nanocrystalline cellulose composites via solvent casting. J. Polym. Eng. 2017, 37, 869–878. [Google Scholar] [CrossRef]
- Long, L.; Ye, B.; Wei, J.; Wu, B.; Li, Y.; Wang, Z. Structure and enhanced mechanical properties of biobased poly(ethylene 2,5-furandicarboxylate) by incorporating with low loadings of talc platelets. Polymer 2021, 237, 124351. [Google Scholar] [CrossRef]
- Jia, S.; Yu, D.; Zhu, Y.; Wang, Z.; Chen, L.; Fu, L. Morphology, Crystallization and Thermal Behaviors of PLA-Based Composites: Wonderful Effects of Hybrid GO/PEG via Dynamic Impregnating. Polymers 2017, 9, 528. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, G.Z.; Tsanaktsis, V.; Bikiaris, D.N. Synthesis of poly(ethylene furandicarboxylate) polyester using monomers derived from renewable resources: Thermal behavior comparison with PET and PEN. Phys. Chem. Chem. Phys. 2014, 16, 7946–7958. [Google Scholar] [CrossRef]
- Stoclet, G.; Gobius Du Sart, G.; Yeniad, B.; De Vos, S.; Lefebvre, J.M. Isothermal crystallization and structural characterization of poly(ethylene-2,5-furanoate). Polymer 2015, 72, 165–176. [Google Scholar] [CrossRef]
- Gabriël van Berkel, J. On the Physical Properties of Poly(ethylene 2,5-furandicarboxylate). Ph.D. Thesis, Université Côte d’Azur, Aix-en-Provence, France, 2018. [Google Scholar]
- Hoffman, J.D.; Weeks, J.J. Melting process and the equilibrium melting temperature of polychlorotrifluoroethylene. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1962, 66A, 13. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.X.; Gu, K.; Soman, A.; Gu, T.; Arnold, C.B.; Register, R.A.; Loo, Y.L.; Priestley, R.D. Epitaxially crystallized polyethylene exhibiting near-equilibrium melting temperatures*. Polym. Eng. Sci. 2022, 62, 841–847. [Google Scholar] [CrossRef]
- Drzewicz, A.; Juszyńska-Gałązka, E.; Jasiurkowska-Delaporte, M.; Kula, P. Insight into cold- and melt crystallization phenomena of a smectogenic liquid crystal. CrystEngComm 2022, 24, 3074–3087. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Bikiaris, D.N.; Achilias, D.S. Effect of molecular weight on the cold-crystallization of biodegradable poly(ethylene succinate). Thermochim. Acta 2007, 457, 41–54. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I: General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Non-Isothermal Crystallization of Polymer Melts. J. Therm. Anal. Calorim. 2003, 72, 681–686. [Google Scholar] [CrossRef]
- Lauritzen, J.I.; Hoffman, J.D. Extension of theory of growth of chain-folded polymer crystals to large undercoolings. J. Appl. Phys. 1973, 44, 4340–4352. [Google Scholar] [CrossRef]
- Chan, T.W.; Isayev, A.I. Quiescent polymer crystallization: Modelling and measurements. Polym. Eng. Sci. 1994, 34, 461–471. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Frolen, L.J.; Ross, G.S.; Lauritzen, J.I. On the growth rate of spherulites and axialites from the melt in polyethylene fractions: Regime I and regime II crystallization. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1975, 79A, 671. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Davis, G.T.; Lauritzen, J.I. The Rate of Crystallization of Linear Polymers with Chain Folding. In Treatise on Solid State Chemistry; Springer: Boston, MA, USA, 1976; pp. 497–614. [Google Scholar]
- Seo, J.; Zhang, X.; Schaake, R.P.; Rhoades, A.M.; Colby, R.H. Dual Nakamura model for primary and secondary crystallization applied to nonisothermal crystallization of poly(ether ether ketone). Polym. Eng. Sci. 2021, 61, 2416–2426. [Google Scholar] [CrossRef]
- Van Berkel, J.G.; Guigo, N.; Visser, H.A.; Sbirrazzuoli, N. Chain Structure and Molecular Weight Dependent Mechanics of Poly(ethylene 2,5-furandicarboxylate) Compared to Poly(ethylene terephthalate). Macromolecules 2018, 51, 8539–8549. [Google Scholar] [CrossRef]
- Dobreva, A.; Gutzow, I. Activity of substrates in the catalyzed nucleation of glass-forming melts. I. Theory. J. Non. Cryst. Solids 1993, 162, 1–12. [Google Scholar] [CrossRef]
- Dobreva, A.; Gutzow, I. Activity of substrates in the catalyzed nucleation of glass-forming melts. II. Experimental evidence. J. Non. Cryst. Solids 1993, 162, 13–25. [Google Scholar] [CrossRef]
- Tarani, E.; Črešnar, K.P.; Zemljič, L.; Chrissafis, K.; Papageorgiou, G.; Lambropoulou, D.; Zamboulis, A.; Bikiaris, D.N.; Terzopoulou, Z. Cold Crystallization Kinetics and Thermal Degradation of PLA Composites with Metal Oxide Nanofillers. Appl. Sci. 2021, 11, 3004. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the IntegralIsoconversional Method to Accountfor Variation in the Activation Energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Hodge, I.M. Enthalpy relaxation and recovery in amorphous materials. J. Non. Cryst. Solids 1994, 169, 211–266. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N.; Dranca, I. Variation in activation energy of the glass transition for polymers of different dynamic fragility. Macromol. Chem. Phys. 2006, 207, 1126–1130. [Google Scholar] [CrossRef]
- Codou, A.; Moncel, M.; Van Berkel, J.G.; Guigo, N.; Sbirrazzuoli, N. Glass transition dynamics and cooperativity length of poly(ethylene 2,5-furandicarboxylate) compared to poly(ethylene terephthalate). Phys. Chem. Chem. Phys. 2016, 18, 16647–16658. [Google Scholar] [CrossRef] [PubMed]
- Saharudin, M.S.; Shyha, I.; Inam, F. Viscoelastic and Mechanical Properties of Multi-layered- Graphene Polyester Composites. In Proceedings of the 2nd International Conference on Advances in Mechanical Engineering, Istanbul, Turkey, 20–22 October 2016; pp. 10–13. [Google Scholar]
- Okoro, A.M.; Lephuthing, S.S.; Rasiwela, L.; Olubambi, P.A. Nondestructive measurement of the mechanical properties of graphene nanoplatelets reinforced nickel aluminium bronze composites. Heliyon 2021, 7, e07978. [Google Scholar] [CrossRef] [PubMed]
- Djukic, S.; Bocahut, A.; Bikard, J.; Long, D.R. Mechanical properties of amorphous and semi-crystalline semi-aromatic polyamides. Heliyon 2020, 6, e03857. [Google Scholar] [CrossRef]
- Balani, K.; Verma, V.; Agarwal, A.; Narayan, R. Physical, Thermal, and Mechanical Properties of Polymers. Biosurfaces 2015, 329–344. [Google Scholar] [CrossRef]
- Gu, X.W.; Ye, X.; Koshy, D.M.; Vachhani, S.; Hosemann, P.; Alivisatos, A.P. Tolerance to structural disorder and tunable mechanical behavior in self-assembled superlattices of polymer-grafted nanocrystals. Proc. Natl. Acad. Sci. USA 2017, 114, 2836–2841. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Tzetzis, D.; Tsongas, K.; Mansour, G. Determination of the mechanical properties of epoxy silica nanocomposites through FEA-supported evaluation of ball indentation test results. Mater. Res. 2017, 20, 1571–1578. [Google Scholar] [CrossRef]
- Tsongas, K.; Tzetzis, D.; Karantzalis, A.; Banias, G.; Exarchos, D.; Ahmadkhaniha, D.; Zanella, C.; Matikas, T.; Bochtis, D. Microstructural, surface topology and nanomechanical characterization of electrodeposited Ni-P/SiC nanocomposite coatings. Appl. Sci. 2019, 9, 2901. [Google Scholar] [CrossRef]
- Mansour, G.; Tzetzis, D. Nanomechanical Characterization of Hybrid Multiwall Carbon Nanotube and Fumed Silica Epoxy Nanocomposites. Polym. Plast. Technol. Eng. 2013, 52, 1054–1062. [Google Scholar] [CrossRef]
- Tzetzis, D.; Mansour, G.; Tsiafis, I.; Pavlidou, E. Nanoindentation measurements of fumed silica epoxy reinforced nanocomposites. J. Reinf. Plast. Compos. 2013, 32, 163–173. [Google Scholar] [CrossRef]
- Mansour, G.; Tzetzis, D.; Bouzakis, K.D. A nanomechanical approach on the measurement of the elastic properties of epoxy reinforced carbon nanotube nanocomposites. Tribol. Ind. 2013, 35, 190–199. [Google Scholar]
- Grigora, M.; Terzopoulou, Z.; Tsongas, K.; Bikiaris, D.N.; Tzetzis, D. Physicochemical Characterization and Finite Element Analysis-Assisted Mechanical Behavior of Polylactic Acid-Montmorillonite 3D Printed Nanocomposites. Nanomaterials 2022, 12, 2641. [Google Scholar] [CrossRef] [PubMed]

| Heating of Quenched Samples | Melt Crystallization | |||||||
|---|---|---|---|---|---|---|---|---|
| Sample | Tcc (K) | Tg (K) | ΔHcc (J/gr) | Tm (K) | ΔHm (J/gr) | Tmc (K) | ΔHmc (J/gr) | Xc % |
| neat PEF | 429 | 352 | 44.4 | 486 | 47.8 | 429 | 16.4 | 13 |
| PEF/0.5 GNPs | 423 | 351 | 45.6 | 484 | 50.9 | 441 | 50.2 | 36.1 |
| PEF/1 GNPs | 415 | 346 | 45.1 | 477 | 47.7 | 436 | 51.9 | 36.4 |
| PEF/2.5 GNPs | 421 | 344 | 39.7 | 474 | 42 | 426 | 45.6 | 35.2 |
| Sample | Kg (K2) × 105 | U* (kJ/mol) | Tmax (K) | R2 |
|---|---|---|---|---|
| neat PEF | 7.4 | 16.9 | 428 | 0.962 |
| PEF/0.5 GNPs | 3.6 | 8.5 | 432 | 0.995 |
| PEF/1 GNPs | 4.8 | 8.2 | 422 | 0.908 |
| PEF/2.5 GNPs | 5 | 12.7 | 425 | 0.965 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourtidou, D.; Grigora, M.-E.; Tzetzis, D.; Bikiaris, D.N.; Chrissafis, K. Graphene Nanoplatelets’ Effect on the Crystallization, Glass Transition, and Nanomechanical Behavior of Poly(ethylene 2,5-furandicarboxylate) Nanocomposites. Molecules 2022, 27, 6653. https://doi.org/10.3390/molecules27196653
Kourtidou D, Grigora M-E, Tzetzis D, Bikiaris DN, Chrissafis K. Graphene Nanoplatelets’ Effect on the Crystallization, Glass Transition, and Nanomechanical Behavior of Poly(ethylene 2,5-furandicarboxylate) Nanocomposites. Molecules. 2022; 27(19):6653. https://doi.org/10.3390/molecules27196653
Chicago/Turabian StyleKourtidou, Dimitra, Maria-Eirini Grigora, Dimitrios Tzetzis, Dimitrios N. Bikiaris, and Konstantinos Chrissafis. 2022. "Graphene Nanoplatelets’ Effect on the Crystallization, Glass Transition, and Nanomechanical Behavior of Poly(ethylene 2,5-furandicarboxylate) Nanocomposites" Molecules 27, no. 19: 6653. https://doi.org/10.3390/molecules27196653
APA StyleKourtidou, D., Grigora, M.-E., Tzetzis, D., Bikiaris, D. N., & Chrissafis, K. (2022). Graphene Nanoplatelets’ Effect on the Crystallization, Glass Transition, and Nanomechanical Behavior of Poly(ethylene 2,5-furandicarboxylate) Nanocomposites. Molecules, 27(19), 6653. https://doi.org/10.3390/molecules27196653









