Parameter Optimization of Support Vector Machine to Improve the Predictive Performance for Determination of Aflatoxin B1 in Peanuts by Olfactory Visualization Technique
Abstract
:1. Introduction
2. Results
2.1. Division of the Sample Set
2.2. Response Results of Colorimetric Sensor Array
2.3. Feature Optimization Results Based on GA-BPNN
3. Discussion
4. Materials and Methods
4.1. Moldy Peanut Sample Preparation
4.2. Determination of the Aflatoxin B1
4.3. Colorimetric Sensor Array Preparation
4.4. Sensor Data Collection and Preprocessing
4.5. Data Analyses Methods
4.5.1. Back Propagation Neural Network
4.5.2. Genetic Algorithm
4.5.3. Support Vector Regression
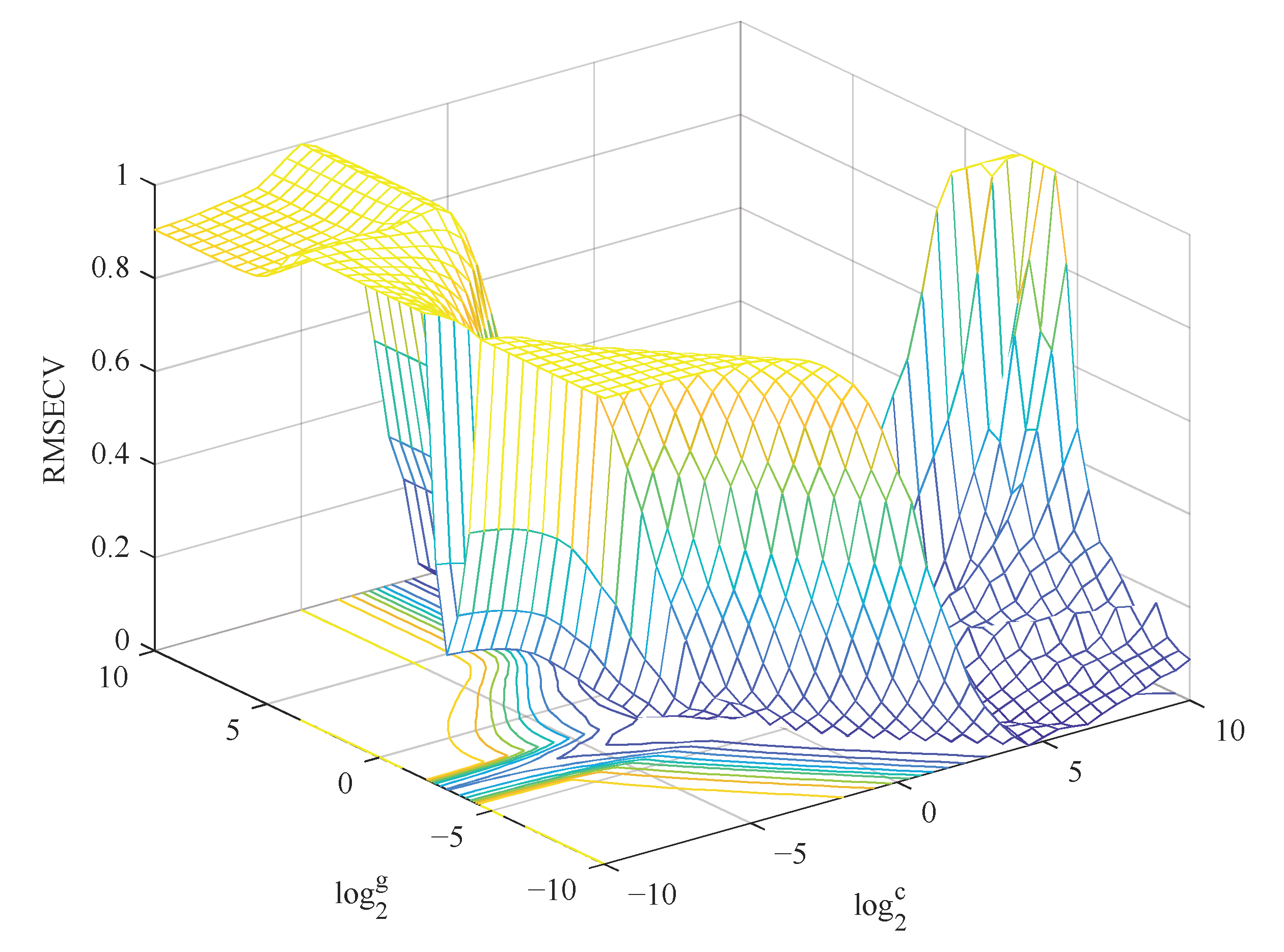
4.5.4. Parameter Optimization Algorithm
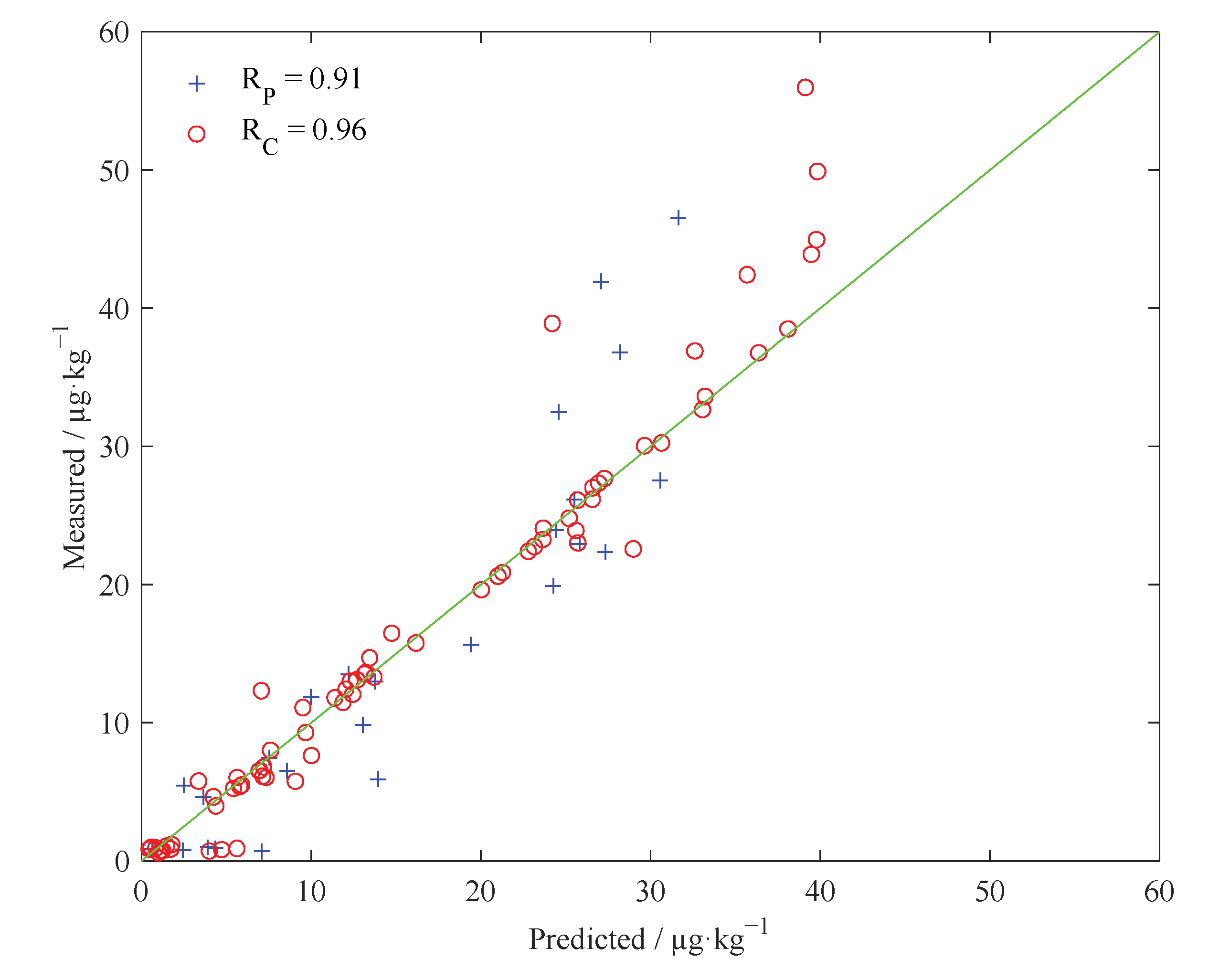
4.5.5. Model Evaluation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Schmitt, C.; Bastek, T.; Stelzer, A.; Schneider, T.; Fischer, M.; Hackl, T. Detection of peanut adulteration in food samples by nuclear magnetic resonance spectroscopy. J. Agric. Food Chem. 2020, 68, 14364–14373. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.W.; Liu, H.Z.; Wang, Q.; van Ruth, S. Evaluation of portable and benchtop NIR for classification of high oleic acid peanuts and fatty acid quantitation. Lwt Food Sci. Technol. 2020, 128, 109398. [Google Scholar] [CrossRef]
- Salve, A.R.; LeBlanc, J.G.; Arya, S.S. Effect of processing on polyphenol profile, aflatoxin concentration and allergenicity of peanuts. J. Food Sci. Technol. Mysore 2021, 58, 2714–2724. [Google Scholar] [CrossRef] [PubMed]
- Bonku, R.; Yu, J.M. Health aspects of peanuts as an outcome of its chemical composition. Food Sci. Hum. Wellness 2020, 9, 21–30. [Google Scholar] [CrossRef]
- Pinto Vieira, I.G.; Oliveira Freire, F.D.C.; Alves Andrade, J.; Pereira Mendes, F.N.; Nascimento Monteiro, M.D.C. Determination of aflatoxins in cashew kernels by thin layer chromatography. Rev. Cienc. Agron. 2007, 38, 430–435. [Google Scholar]
- Larionova, D.A.; Goryacheva, I.Y.; Van Peteghem, C.; De Saeger, S. Thin-layer chromatography of aflatoxins and zearalenones with beta-cyclodextrins as mobile phase additives. World Mycotoxin J. 2011, 4, 113–117. [Google Scholar] [CrossRef]
- Braicu, C.; Puia, C.; Bodoki, E.; Socaciu, C. Screening and quantification of aflatoxins and ochratoxin a in different cereals cultivated in romania using thin-layer chromatography-densitometry. J. Food Qual. 2008, 31, 108–120. [Google Scholar] [CrossRef]
- Hidalgo-Ruiz, J.L.; Romero-Gonzalez, R.; Martinez Vidal, J.L.; Garrido Frenich, A. A rapid method for the determination of mycotoxins in edible vegetable oils by ultra-high performance liquid chromatography-tandem mass spectrometry. Food Chem. 2019, 288, 22–28. [Google Scholar] [CrossRef]
- Hidalgo-Ruiz, J.L.; Romero-Gonzalez, R.; Martinez Vidal, J.L.; Garrido Frenich, A. Determination of mycotoxins in nuts by ultra high-performance liquid chromatography-tandem mass spectrometry: Looking for a representative matrix. J. Food Compos. Anal. 2019, 82, 103228. [Google Scholar] [CrossRef]
- Asadi, M. Separation and quantification of aflatoxins in grains using modified dispersive liquid-liquid microextraction combined with high-performance liquid chromatography. J. Food Meas. Charact. 2020, 14, 925–930. [Google Scholar] [CrossRef]
- Wu, Y.X.; Yu, J.Z.; Li, F.; Li, J.L.; Shen, Z.Q. A calibration curve implanted enzyme-linked immunosorbent assay for simultaneously quantitative determination of multiplex mycotoxins in cereal samples, soybean and peanut. Toxins 2020, 12, 718. [Google Scholar] [CrossRef] [PubMed]
- Leszczynska, J.; Kucharska, U.; Zegota, H. Aflatoxins in nuts assayed by immunological methods. Eur. Food Res. Technol. 2000, 210, 213–215. [Google Scholar] [CrossRef]
- Dou, W.T.; Wang, X.; Liu, T.T.; Zhao, S.W.; Liu, J.J.; Yan, Y.; Li, J.; Zhang, C.Y.; Sedgwick, A.C.; Tian, H.; et al. A homogeneous high-throughput array for the detection and discrimination of influenza A viruses. Chem 2022, 8, 1750–1761. [Google Scholar] [CrossRef]
- Dou, W.-T.; Han, H.-H.; Sedgwick, A.C.; Zhu, G.-B.; Zang, Y.; Yang, X.-R.; Yoon, J.; James, T.D.; Li, J.; He, X.-P. Fluorescent probes for the detection of disease-associated biomarkers. Sci. Bull. 2022, 67, 853–878. [Google Scholar] [CrossRef]
- Li, Z.; Askim, J.R.; Suslick, K.S. The optoelectronic nose: Colorimetric and fluorometric sensor arrays. Chem. Rev. 2019, 119, 231–292. [Google Scholar] [CrossRef]
- Rakow, N.A.; Suslick, K.S. A colorimetric sensor array for odour visualization. Nature 2000, 406, 710–713. [Google Scholar] [CrossRef]
- Huang, X.-W.; Zou, X.-B.; Shi, J.-Y.; Li, Z.-H.; Zhao, J.-W. Colorimetric sensor arrays based on chemo-responsive dyes for food odor visualization. Trends Food Sci. Technol. 2018, 81, 90–107. [Google Scholar]
- Liu, T.; Jiang, H.; Chen, Q. Qualitative identification of rice actual storage period using olfactory visualization technique combined with chemometrics analysis. Microchem. J. 2020, 159, 105339. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, T.; He, P.; Ding, Y.; Chen, Q. Rapid measurement of fatty acid content during flour storage using a color-sensitive gas sensor array: Comparing the effects of swarm intelligence optimization algorithms on sensor features. Food Chem. 2021, 338, 127828. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, T.; He, P.; Chen, Q. Quantitative analysis of fatty acid value during rice storage based on olfactory visualization sensor technology. Sens. Actuator B-Chem. 2020, 309, 127816. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, W.; Chen, Q. Determination of tea polyphenols in green tea by homemade color sensitive sensor combined with multivariate analysis. Food Chem. 2020, 319, 126584. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Xu, W.; Chen, Q. Evaluating aroma quality of black tea by an olfactory visualization system: Selection of feature sensor using particle swarm optimization. Food Res. Int. 2019, 126, 108605. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Sun, C.; Ouyang, Q.; Wang, Y.; Liu, A.; Li, H.; Zhao, J. Classification of different varieties of Oolong tea using novel artificial sensing tools and data fusion. LWT-Food Sci. Technol. 2015, 60, 781–787. [Google Scholar] [CrossRef]
- Li, L.; Xie, S.; Zhu, F.; Ning, J.; Chen, Q.; Zhang, Z. Colorimetric sensor array-based artificial olfactory system for sensing Chinese green tea’s quality: A method of fabrication. Int. J. Food Prop. 2017, 20, 1762–1773. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, B.; Hu, W.; Liu, Y.; Dong, C.; Chen, Q. Monitoring black tea fermentation using a colorimetric sensor array-based artificial olfaction system. J. Food Process Preserv. 2018, 42, e16648. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Chen, Q. High-precision recognition of wheat mildew degree based on colorimetric sensor technique combined with multivariate analysis. Microchem. J. 2021, 168, 106468. [Google Scholar] [CrossRef]
- Gobbi, E.; Falasconi, M.; Torelli, E.; Sberveglieri, G. Electronic nose predicts high and low fumonisin contamination in maize cultures. Food Res. Int. 2011, 44, 992–999. [Google Scholar] [CrossRef]
- Paolesse, R.; Alimelli, A.; Martinelli, E.; Di Natale, C.; D’Amico, A.; D’Egidio, M.G.; Aureli, G.; Ricelli, A.; Fanelli, C. Detection of fungal contamination of cereal grain samples by an electronic nose. Sens. Actuator B-Chem. 2006, 119, 425–430. [Google Scholar] [CrossRef]
- Leggieri, M.C.; Mazzoni, M.; Fodil, S.; Moschini, M.; Bertuzzi, T.; Prandini, A.; Battilani, P. An electronic nose supported by an artificial neural network for the rapid detection of aflatoxin B-1 and fumonisins in maize. Food Control. 2021, 123, 107722. [Google Scholar] [CrossRef]
- Paul, C.; Vishwakarma, G.K. Back propagation neural networks and multiple regressions in the case of heteroskedasticity. Commun. Stat. Simul. Comput. 2017, 46, 6772–6789. [Google Scholar] [CrossRef]
- Niazi, A.; Leardi, R. Genetic algorithms in chemometrics. J. Chemom. 2012, 26, 345–351. [Google Scholar] [CrossRef]
- Gammermann, A. Support vector machine learning algorithm and transduction. Comput. Stat. 2000, 15, 31–39. [Google Scholar] [CrossRef]
- Yao, L.; Fang, Z.; Xiao, Y.; Hou, J.; Fu, Z. An intelligent fault diagnosis method for lithium battery systems based on grid search support vector machine. Energy 2021, 214, 118866. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Wang, F. A learning sparrow search algorithm. Comput. Intell. Neurosci. 2021, 2021. [Google Scholar] [CrossRef]
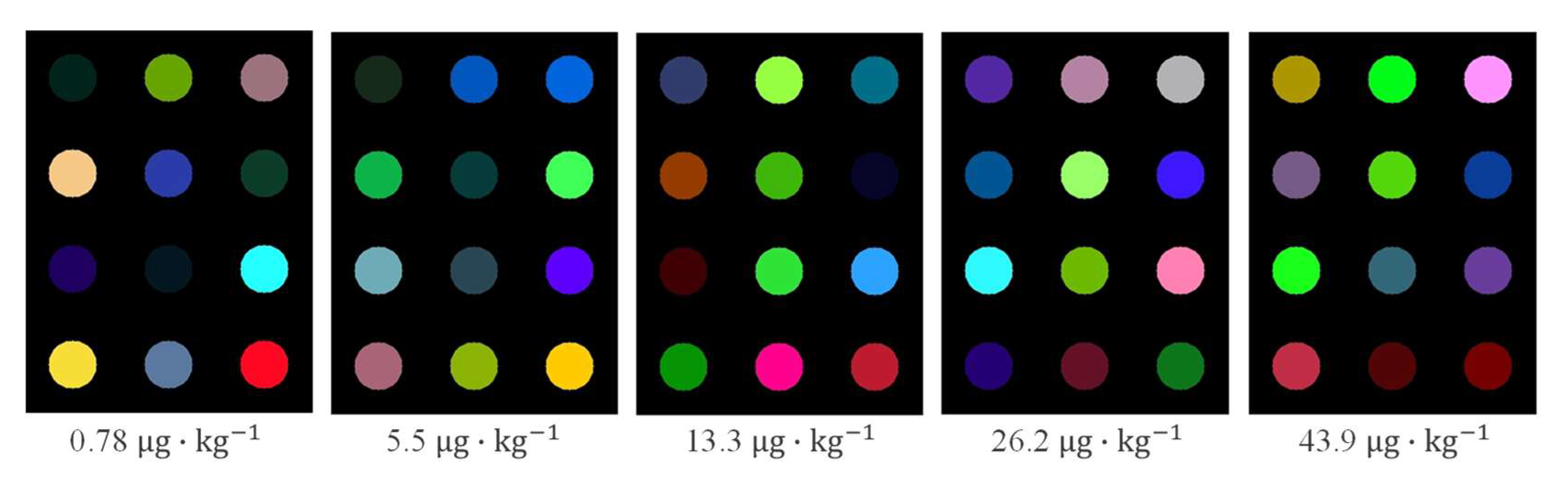


| Subsets | Sample Number | Units | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Calibration set | 75 | 0.60 | 56.0 | 16.2 | 13.8 | |
| Prediction set | 25 | 0.71 | 46.5 | 15.9 | 13.6 |
| Model | Mode | Number of Variables | Parameter Combination | Calibration Set | Validation Set | |||
|---|---|---|---|---|---|---|---|---|
| RC | RMSEC | RP | RMSEP | RPD | ||||
| GS-SVR | Case 1 | 13 | C = 0.50 g = 0.18 | 0.91 | 5.7 | 0.89 | 6.1 | 2.2 |
| Case 2 | 7 | C = 1.1 g = 0.50 | 0.94 | 4.5 | 0.90 | 5.8 | 2.3 | |
| Case 3 | 3 | C = 5.7 g = 0.35 | 0.81 | 8.0 | 0.81 | 8.0 | 1.7 | |
| SSA-SVR | Case 1 | 13 | C = 17.9 g = 1.5 | 0.94 | 4.7 | 0.91 | 5.8 | 2.3 |
| Case 2 | 7 | C = 50.3 g = 1.56 | 0.96 | 3.4 | 0.91 | 5.7 | 2.4 | |
| Case 3 | 3 | C = 85.8 g = 11.6 | 0.86 | 7.1 | 0.75 | 9.2 | 1.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Deng, J.; Jiang, H. Parameter Optimization of Support Vector Machine to Improve the Predictive Performance for Determination of Aflatoxin B1 in Peanuts by Olfactory Visualization Technique. Molecules 2022, 27, 6730. https://doi.org/10.3390/molecules27196730
Zhu C, Deng J, Jiang H. Parameter Optimization of Support Vector Machine to Improve the Predictive Performance for Determination of Aflatoxin B1 in Peanuts by Olfactory Visualization Technique. Molecules. 2022; 27(19):6730. https://doi.org/10.3390/molecules27196730
Chicago/Turabian StyleZhu, Chengyun, Jihong Deng, and Hui Jiang. 2022. "Parameter Optimization of Support Vector Machine to Improve the Predictive Performance for Determination of Aflatoxin B1 in Peanuts by Olfactory Visualization Technique" Molecules 27, no. 19: 6730. https://doi.org/10.3390/molecules27196730
APA StyleZhu, C., Deng, J., & Jiang, H. (2022). Parameter Optimization of Support Vector Machine to Improve the Predictive Performance for Determination of Aflatoxin B1 in Peanuts by Olfactory Visualization Technique. Molecules, 27(19), 6730. https://doi.org/10.3390/molecules27196730






