The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]arene Derivatives
Abstract
:1. Introduction
2. Results and Discussion
2.1. Complexation of Alkali Metal Cations with L in Methanol
2.2. Complexation of Alkali Metal Cations with L in Acetonitrile
2.3. Complexation of Alkali Metal Cations with L in N,N-Dimethylformamide
2.4. Complexation of Alkali Metal Cations with Compound l in Methanol and N,N-Dimethylformamide
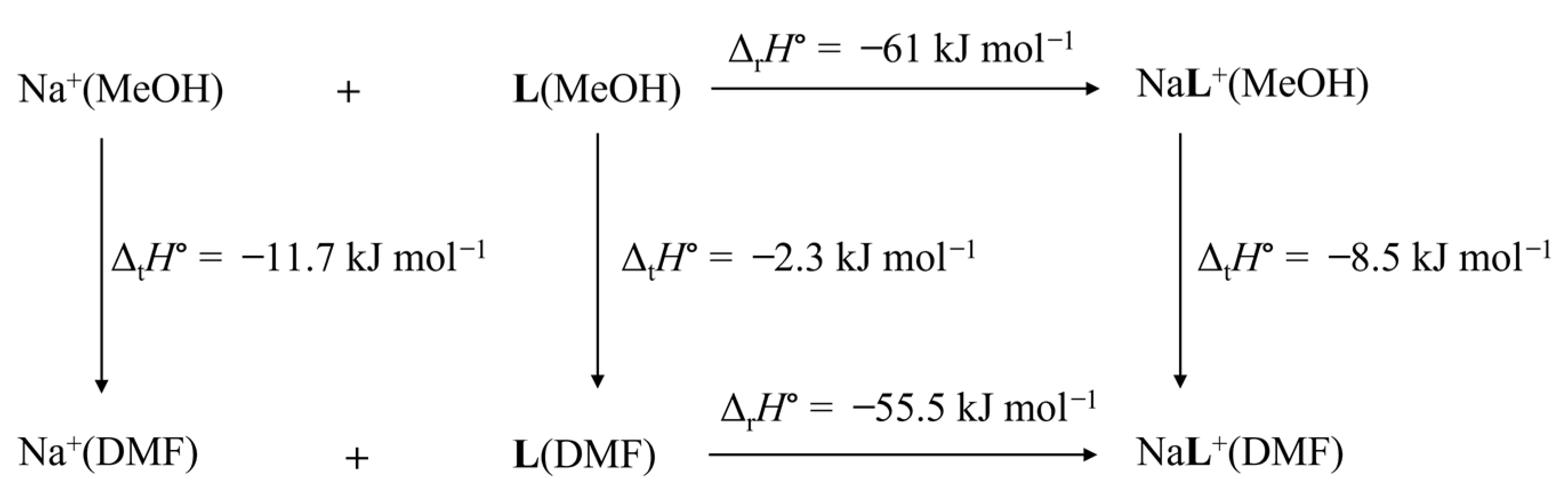
2.5. The Solvation of Receptors in Studied Solvents
2.6. The Solvent Effect on the Alkali Metal Complexation and Comparison of L and l Binding Affinities
2.7. Molecular Dynamics Simulations
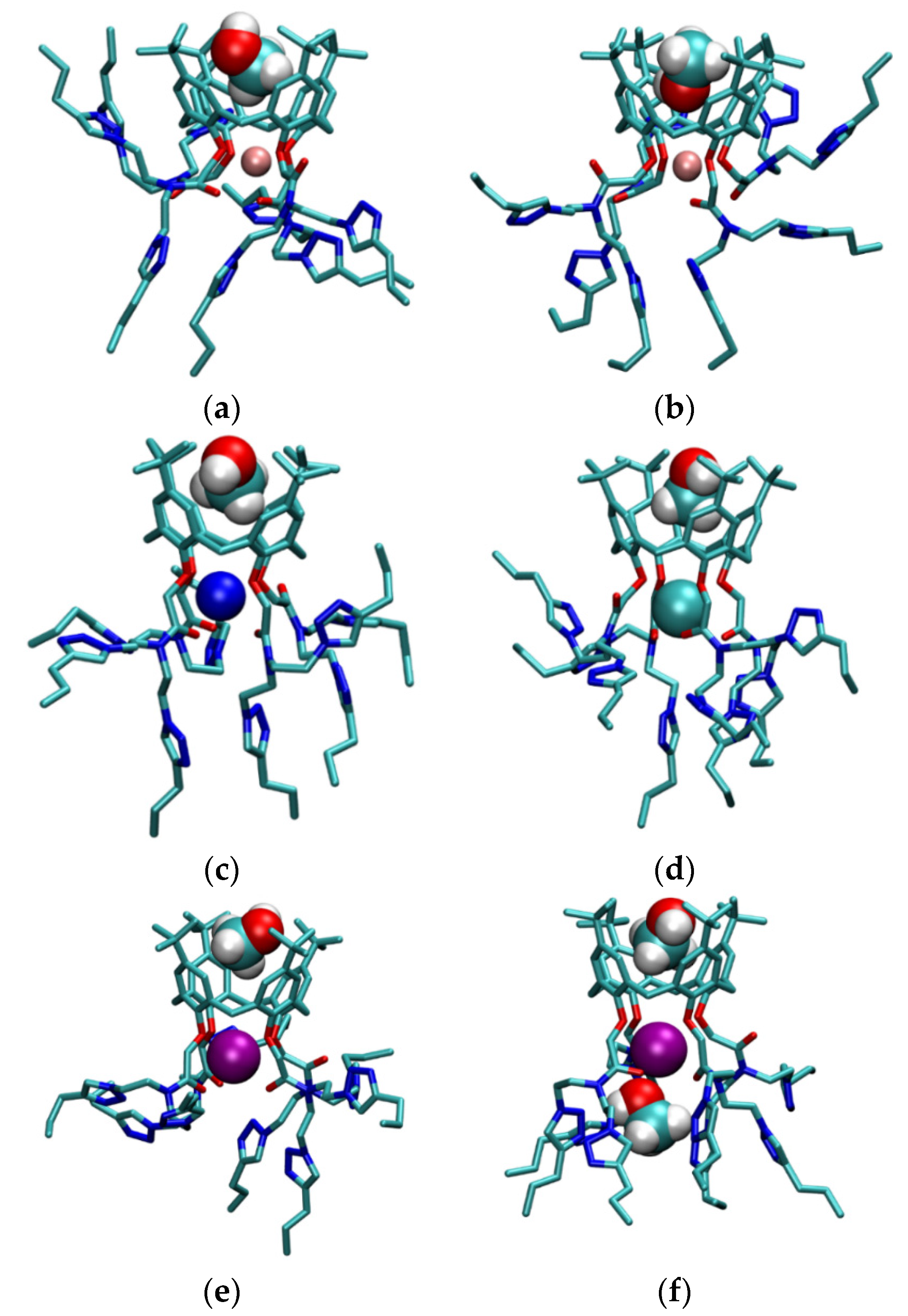
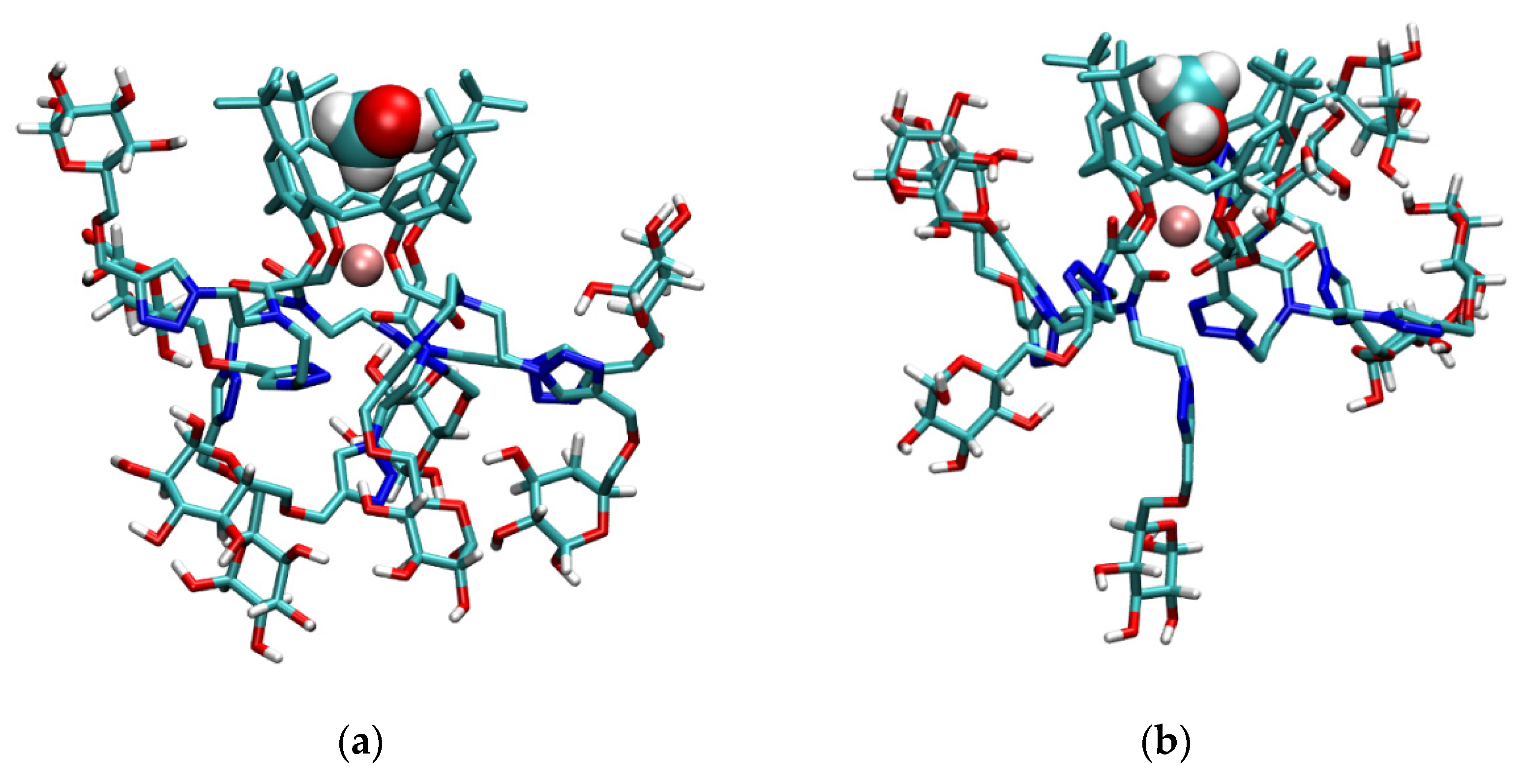
2.7.1. MD Investigations of Receptors
2.7.2. MD Investigations of Alkali Metal Cation Complexes with L
2.7.3. MD Investigations of Alkali Metal Cation Complexes with l
3. Materials and Methods
3.1. Materials for Synthesis and Physicochemical Investigations
3.2. Synthesis of Compound L
3.3. Methods
3.3.1. Microcalorimetry
3.3.2. NMR Investigations
3.3.3. Spectrophotometry
3.3.4. Solubility Measurements
3.3.5. Dissolution Enthalpies
3.3.6. Molecular Dynamics Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Asfari, Z.; Böhmer, V.; Harrowfield, J.; Vicens, J. Calixarenes 2001, 2001st ed.; Asfari, Z., Böhmer, V., Harrofield, J., Vicens, J., Eds.; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Danil de Namor, A.F.; Cabaleiro, M.C.; Vuano, B.M.; Salomona, M.; Pieroni, O.I.; Pacheco Tanaka, D.A.; Ng, C.Y.; Llosa Tanco, M.A.; Rodríguez, N.M.; Cárdenas García, J.D.; et al. Thermodynamic and electrochemical aspects of the interactions of functionalised calix(4)arenes and metal cations in “Allosteric Media”. Pure Appl. Chem. 1994, 66, 435–440. [Google Scholar] [CrossRef] [Green Version]
- Danil De Namor, A.F.; Cleverley, R.M.; Zapata-Ormachea, M.L. Thermodynamics of calixarene chemistry. Chem. Rev. 1998, 98, 2495–2525. [Google Scholar] [CrossRef] [PubMed]
- Creaven, B.S.; Donlon, D.F.; McGinley, J. Coordination chemistry of calix[4]arene derivatives with lower rim functionalisation and their applications. Coord. Chem. Rev. 2009, 253, 893–962. [Google Scholar] [CrossRef]
- Sliwa, W.; Girek, T. Calixarene complexes with metal ions. J. Incl. Phenom. Macrocycl. Chem. 2010, 66, 15–41. [Google Scholar] [CrossRef]
- Schühle, D.T.; Peters, J.A.; Schatz, J. Metal binding calixarenes with potential biomimetic and biomedical applications. Coord. Chem. Rev. 2011, 255, 2727–2745. [Google Scholar] [CrossRef]
- Danil de Namor, A.F.; Kowalska, D.; Castellano, E.E.; Piro, O.E.; Sueros Velarde, F.J.; Salas, J.V. Lower rim calix(4)arene ketone derivatives and their interaction with alkali metal cations. structural and thermodynamic (solution and complexation) characterisation of the tetraphenyl ketone derivative and its sodium complex. Phys. Chem. Chem. Phys. 2001, 3, 4010–4021. [Google Scholar] [CrossRef]
- Sansone, F.; Chierici, E.; Casnati, A.; Ungaro, R. Thiourea-Linked upper rim calix[4]arene neoglycoconjugates: Synthesis, conformations and binding properties. Org. Biomol. Chem. 2003, 1, 1802–1809. [Google Scholar] [CrossRef] [PubMed]
- Arena, G.; Contino, A.; Longo, E.; Spoto, G.; Arduini, A.; Pochini, A.; Secchi, A.; Massera, C.; Ugozzoli, F. An integrated approach to the study of the recognition of guests containing CH3 and CH2 acidic groups by differently rigidified cone p-tert-butylcalix[4]arene derivatives. New J. Chem. 2004, 28, 56–61. [Google Scholar] [CrossRef]
- Horvat, G.; Stilinović, V.; Hrenar, T.; Kaitner, B.; Frkanec, L.; Tomišić, V. An integrated approach (thermodynamic, structural, and computational) to the study of complexation of alkali-metal cations by a lower-rim calix[4]arene amide derivative in acetonitrile. Inorg. Chem. 2012, 51, 6264–6278. [Google Scholar] [CrossRef]
- Horvat, G.; Stilinović, V.; Kaitner, B.; Frkanec, L.; Tomišić, V. The effect of specific solvent-solute interactions on complexation of alkali-metal cations by a lower-rim calix[4]arene amide derivative. Inorg. Chem. 2013, 52, 12702–12712. [Google Scholar] [CrossRef] [PubMed]
- Tranfić Bakić, M.; Jadreško, D.; Hrenar, T.; Horvat, G.; Požar, J.; Galić, N.; Sokol, V.; Tomaš, R.; Alihodžić, S.; Žinić, M.; et al. Fluorescent phenanthridine-based calix[4]arene derivatives: Synthesis and thermodynamic and computational studies of their complexation with alkali-metal cations received. RSC Adv. 2015, 5, 23900–23914. [Google Scholar] [CrossRef] [Green Version]
- Bregović, N.; Cindro, N.; Frkanec, L.; Tomišić, V. Complexation of fluoride anion and its ion pairs with alkali metal cations by tetra-substituted lower rim calix[4]arene tryptophan derivative. Supramol. Chem. 2016, 28, 608–615. [Google Scholar] [CrossRef]
- Horvat, G.; Frkanec, L.; Cindro, N.; Tomišić, V. A comprehensive study of the complexation of alkali metal cations by lower rim calix[4]arene amide derivatives. Phys. Chem. Chem. Phys. 2017, 19, 24316–24329. [Google Scholar] [CrossRef]
- Požar, J.; Nikšić-Franjić, I.; Cvetnić, M.; Leko, K.; Cindro, N.; Pičuljan, K.; Borilović, I.; Frkanec, L.; Tomišić, V. Solvation effect on complexation of alkali metal cations by a calix[4]arene ketone derivative. J. Phys. Chem. B. 2017, 121, 8539–8550. [Google Scholar] [CrossRef]
- Cindro, N.; Požar, J.; Barišić, D.; Bregović, N.; Pičuljan, K.; Tomaš, R.; Frkanec, L.; Tomišić, V. Neutral glycoconjugated amide-based calix[4]arenes: Complexation of alkali metal cations in water. Org. Biomol. Chem. 2018, 16, 904–912. [Google Scholar] [CrossRef]
- Dantz, D.A.; Buschmann, H.-J.; Schollmeyer, E. Effects of the benzosubstitution of cryptands for the complex formation between protons, alkali and alkaline earth cations in water. Polyhedron 1998, 17, 1891–1895. [Google Scholar] [CrossRef]
- Takeda, Y.; Mochizuki, Y.; Tanaka, M.; Kudo, Y.; Katsuta, S.; Ouchi, M. Conductance study of 1:1 19-crown-6 complexes with various mono-and bivalent metal ions in water. J. Inclusion Phenom. Macrocyclic Chem. 1999, 33, 217–231. [Google Scholar] [CrossRef]
- Guo, D.S.; Wang, K.; Liu, Y. Selective binding behaviors of p-sulfonatocalixarenes in aqueous solution. J. Incl. Phenom. Macrocycl. Chem. 2008, 62, 1–21. [Google Scholar] [CrossRef]
- Francisco, V.; Piñeiro, A.; Nau, W.M.; García-Río, L. The “true” affinities of metal cations to p-sulfonatocalix[4] arene: A thermodynamic study at neutral PH reveals a pitfall due to salt effects in microcalorimetry. Chem.Eur. J. 2013, 19, 17809–17820. [Google Scholar] [CrossRef]
- Atwood, J.L.; Barbour, L.J.; Hardie, M.J.; Raston, C.L. Metal sulfonatocalix[4,5]arene complexes: Bi-layers, capsules, spheres, tubular arrays and beyond. Coord. Chem. Rev. 2001, 222, 3–32. [Google Scholar] [CrossRef]
- Sansone, F.; Casnati, A. Multivalent glycocalixarenes for recognition of biological macromolecules: Glycocalyx mimics capable of multitasking. Chem. Soc. Rev. 2013, 42, 4623–4639. [Google Scholar] [CrossRef]
- Tiwari, V.K.; Mishra, B.B.; Mishra, K.B.; Mishra, N.; Singh, A.S.; Chen, X. Cu-catalyzed click reaction in carbohydrate chemistry. Chem. Rev. 2016, 116, 3086–3240. [Google Scholar] [CrossRef]
- Ryu, E.H.; Zhao, Y. Efficient synthesis of water-soluble calixarenes using click chemistry. Org. Lett. 2005, 7, 1035–1037. [Google Scholar] [CrossRef] [Green Version]
- Bew, S.P.; Brimage, R.A.; L’Hermite, N.; Sharma, S.V. Upper rim appended hybrid calixarenes via click chemistry. Org. Lett. 2007, 9, 3713–3716. [Google Scholar] [CrossRef]
- Song, M.; Sun, Z.; Han, C.; Tian, D.; Li, H.; Kim, J.S. Calixarene-based chemosensors by means of click chemistry. Chem. Asian J. 2014, 9, 2344–2357. [Google Scholar] [CrossRef]
- Agrahari, A.K.; Bose, P.; Jaiswal, M.K.; Rajkhowa, S.; Singh, A.S.; Hotha, S.; Mishra, N.; Tiwari, V.K. Cu(I)-catalyzed click chemistry in glycoscience and their diverse applications. Chem. Rev. 2021, 121, 7638–7956. [Google Scholar] [CrossRef]
- Molenveld, P.; Engbersen, J.F.J.; Reinhoudt, D.N. Dinuclear Bisimidazolyl-Cu(II) calix[4]arenes as metalloenzyme models. synthesis and bifunctional catalysis in phosphate diester transesterification. J. Org. Chem. 1999, 64, 6337–6341. [Google Scholar] [CrossRef]
- Cao, Y.D.; Zheng, Q.Y.; Chen, C.F.; Hu, H.M.; Huang, Z.T. Synthesis of a novel three-coordinate copper(i) complex: A structural mimic of the reduced form of type 1 site in copper protein. Inorg. Chim. Acta 2004, 357, 316–320. [Google Scholar] [CrossRef]
- Zhou, J.; Rao, L.; Yu, G.; Cook, T.R.; Chen, X.; Huang, F. Supramolecular cancer nanotheranostics. Chem. Soc. Rev. 2021, 50, 2839–2891. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, Q.; Li, E.; Liu, J.; Zhou, J.; Huang, F. Vapochromic behaviors of a solid-state supramolecular polymer based on exo-wall complexation of perethylated pillar[5]arene with 1,2,4,5-tetracyanobenzene. Angew. Chem. Int. Ed. Engl. 2021, 60, 8115–8120. [Google Scholar] [CrossRef] [PubMed]
- Marcus, Y. Ion Properties; Taylor & Francis: New York, NY, USA, 1997. [Google Scholar]
- Leko, K.; Bregović, N.; Cvetnić, M.; Cindro, N.; Bakić, M.T.; Požar, J.; Tomišić, V. Complexation of alkali metal cations by a tertiary amide calix[4]arene derivative in strongly cation solvating solvents. Croat. Chem. Acta 2017, 90, 307–314. [Google Scholar] [CrossRef]
- Gutmann, V. Solvent effects on the reactivities of organometallic compounds. Coord. Chem. Rev. 1976, 18, 225–255. [Google Scholar] [CrossRef]
- Požar, J.; Preočanin, T.; Frkanec, L.; Tomišić, V. Thermodynamics of complexation of alkali metal cations by a lower-rim calix[4]arene amino acid derivative. J. Sol. Chem. 2010, 39, 835–848. [Google Scholar] [CrossRef]
- Danil De Namor, A.F.; Hill, T. Free energies of transfer of 1:1 electrolytes from water to nitro benzene partition of ions in the water + nitrobenzene system. J. Chem. Soc., Faraday Trans. 1 1983, 79, 2113–2122. [Google Scholar]
- Katayama, M.; Shinoda, M.; Ozutsumi, K.; Funahashi, S.; Inada, Y. Reevaluation of donor number using titration calorimetry. Anal. Sci. 2012, 28, 103–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cataldo, F. A revision of the gutmann donor numbers of a series of phosphoramides including TEPA. Eur. Chem. Bull. 2015, 4, 92–97. [Google Scholar] [CrossRef]
- de Araujo, A.S.; Piro, O.E.; Castellano, E.E.; de Namor, A.F.D. Combined cristallographic and solution molecular dynamics study of allosteric effects in ester and ketone p-tert-butylcalix[4]arene derivatives and their complexes with acetonitrile, cd(ii), and pb(ii). J. Phys. Chem. A 2008, 112, 11885–11894. [Google Scholar] [CrossRef] [PubMed]
- Gans, P.; Sabatini, A.; Vacca, A. investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs. Talanta 1996, 43, 1739–1753. [Google Scholar] [CrossRef]
- Frassineti, C.; Ghelli, S.; Gans, P.; Sabatini, A.; Moruzzi, M.S.; Vacca, A. Nuclear magnetic resonance as a tool for determining protonation constants of natural polyprotic bases in solution 1. Anal. Biochem. 1995, 231, 374–382. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; van der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Model. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Szilárd, P.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling exascale software challenges in molecular dynamics simulations with GROMACS. In Lecture Notes in Computer Science; Markidis, S., Laure, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 8759, pp. 3–27. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [Green Version]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanommeslaeghe, K.; MacKerell, A.D. Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D. Automation of the CHARMM general force field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M.L. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Goga, N.; Rzepiela, A.J.; de Vries, A.H.; Marrink, S.J.; Berendsen, H.J.C. Efficient algorithms for langevin and DPD dynamics. J. Chem. Theory Comput. 2012, 8, 3637–3649. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Arnaud-Neu, F.; Schwing-Weill, M.-J.; Ziat, K.; Cremin, S.; Harris, S.J.; McKervey, M.A. Selective alkali and alkaline earth cation complexation by calixarene amides. New J. Chem. 1991, 15, 33–37. [Google Scholar]
- Arnaud-Neu, F.; Barrett, G.; Fanni, S.; Marrs, D.; McGregor, W.; McKervey, M.A.; Schwing-Weill, M.J.; Vetrogon, V.; Wechsler, S. Extraction and solution thermodynamics of complexation of alkali and alkaline-earth cations by calix[4]arene amides. J. Chem. Soc. Perkin Trans. 1995, 2, 453–461. [Google Scholar] [CrossRef]
- Danil De Namor, A.F.; Matsufuji-Yasuda, T.T.; Zegarra-Fernandez, K.; Webb, O.A.; el Gamouz, A. An enchiridion of supramolecular thermodynamics: Calix[n]arene (N = 4,5,6) tertiary amide derivatives and their ionic recognition. Croat. Chem. Acta 2013, 86, 1–19. [Google Scholar] [CrossRef]











| Solvent | Cation | ||||
|---|---|---|---|---|---|
| MeOH | Li+ | 2.83 ± 0.01 | −16.13 ± 0.05 | −17.3 ± 0.2 | −4 ± 1 |
| Na+ | 7.37 ± 0.02 | −42.1 ± 0.1 | −61.0 ± 0.3 | −63.4 ± 0.1 | |
| K+ | 4.49 ± 0.01 | −25.63 ± 0.07 | −45.0 ± 0.2 | −65.2 ± 0.7 | |
| Rb+ | 1.97 ± 0.02 | −11.3 ± 0.1 | −47 ± 2 | −122 ± 7 | |
| MeCN | Li+ | 10.27 ± 0.02 | −58.6 ± 0.1 | −49.2 ± 0.1 | 32 ± 2 |
| Na+ | 11.51 ± 0.01 | −65.71 ± 0.07 | −75.0 ± 0.9 | −31 ± 2 | |
| K+ | 7.30 ± 0.01 | −41.69 ± 0.04 | −57.0 ± 0.5 | −51 ± 2 | |
| Rb+ | 4.73 ± 0.01 | −27.01 ± 0.06 | −46.0 ± 0.4 | −64 ± 1 | |
| Cs+ | 2.375 ± 0.002 2.49 ± 0.01 a | −13.56 ± 0.01 −13.04 ± 0.04 a | −32.2 ± 0.9 | −62 ± 3 | |
| DMF | Li+ | 1.89 ± 0.01 | −10.81 ± 0.08 | −30.3 ± 0.5 | −65 ± 2 |
| Na+ | 5.19 ± 0.01 | −29.65 ± 0.01 | −55.5 ± 0.1 | −86.5 ± 0.3 | |
| K+ | 1.97 ± 0.01 | −11.25 ± 0.03 | −26.5 ± 0.2 | −51.2 ± 0.7 |
| Solvent | Cation | ||||
|---|---|---|---|---|---|
| MeOH | Li+ | 3.12 ± 0.04 | −17.8 ± 0.2 | −19 ± 2 | −3 ± 6 |
| Na+ | 7.24 ± 0.04 a | −41.3 ± 0.2 a | −59.1 ± 0.5 a | −59.7 ± 0.9 a | |
| K+ | 4.57 ± 0.01 | −26.07 ± 0.04 | −45.3 ± 0.4 | −64 ± 1 | |
| Rb+ | 2.28 ± 0.01 | −13.0 ± 0.1 | −39 ± 5 | −89 ± 16 | |
| DMF | Li+ | 2.15 ± 0.01 | −12.27 ± 0.07 | −24.6 ± 0.7 | −41 ± 2 |
| Na+ | 5.40 ± 0.01 | −30.80 ± 0.06 | −54.57 ± 0.05 | −79.7 ± 0.4 | |
| K+ | 2.29 ± 0.01 | −13.06 ± 0.08 | −19.3 ± 0.5 | −21 ± 2 |
| Compound(s) | Solvent (S) | s/mol·dm−3 | ||
|---|---|---|---|---|
| L | MeOH | > 0.1 | 22.0 | − |
| DMF | > 0.1 | 19.7 | −2.3 | |
| MeCN | 4.13 × 10−3 | 29.8 | 7.8 | |
| l | MeOH | 3.69 × 10−3 | −23.7 | − |
| DMF | > 0.1 | −107 | −83.3 | |
| MeCN | <1 × 10−5 | − a | ||
| Glc | MeOH | > 0.1 | 17.2 | − |
| DMF | 9.3 | −7.9 | ||
| MeCN | − a | |||
| L + 8 Glc | MeOH | 159.6 | – | |
| DMF | 94.1 | −65.5 | ||
| MeCN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Požar, J.; Cvetnić, M.; Usenik, A.; Cindro, N.; Horvat, G.; Leko, K.; Modrušan, M.; Tomišić, V. The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]arene Derivatives. Molecules 2022, 27, 470. https://doi.org/10.3390/molecules27020470
Požar J, Cvetnić M, Usenik A, Cindro N, Horvat G, Leko K, Modrušan M, Tomišić V. The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]arene Derivatives. Molecules. 2022; 27(2):470. https://doi.org/10.3390/molecules27020470
Chicago/Turabian StylePožar, Josip, Marija Cvetnić, Andrea Usenik, Nikola Cindro, Gordan Horvat, Katarina Leko, Matija Modrušan, and Vladislav Tomišić. 2022. "The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]arene Derivatives" Molecules 27, no. 2: 470. https://doi.org/10.3390/molecules27020470
APA StylePožar, J., Cvetnić, M., Usenik, A., Cindro, N., Horvat, G., Leko, K., Modrušan, M., & Tomišić, V. (2022). The Role of Triazole and Glucose Moieties in Alkali Metal Cation Complexation by Lower-Rim Tertiary-Amide Calix[4]arene Derivatives. Molecules, 27(2), 470. https://doi.org/10.3390/molecules27020470










