Scheme 1.
Chemical structures of azoles and azines commonly employed in high-energy heterocyclic compounds.
Scheme 1.
Chemical structures of azoles and azines commonly employed in high-energy heterocyclic compounds.
Scheme 2.
Chemical structures of the studied triazolo[4,3-b][1,2,4,5]tetrazine derivatives.
Scheme 2.
Chemical structures of the studied triazolo[4,3-b][1,2,4,5]tetrazine derivatives.
Figure 1.
P-V diagrams of reaction products from the state of compressed cold plasma to normal temperature: (a,b) TTDA; (c,d) TTGA; (e,f) DNTT.
Figure 1.
P-V diagrams of reaction products from the state of compressed cold plasma to normal temperature: (a,b) TTDA; (c,d) TTGA; (e,f) DNTT.
Figure 2.
Appearance of synthesized samples and micromorphology of particles: (a,d,g) TTDA; (b,e,h) TTGA; (c,f,i) DNTT.
Figure 2.
Appearance of synthesized samples and micromorphology of particles: (a,d,g) TTDA; (b,e,h) TTGA; (c,f,i) DNTT.
Figure 3.
Thermograms of a TTDA sample with a separate stage of gas-phase decomposition (a) (heating rates of 4 and 10 min−1) and solid-phase decomposition with gas-phase assistance (b) (heating rates of 30 and 100 min−1).
Figure 3.
Thermograms of a TTDA sample with a separate stage of gas-phase decomposition (a) (heating rates of 4 and 10 min−1) and solid-phase decomposition with gas-phase assistance (b) (heating rates of 30 and 100 min−1).
Figure 4.
Thermograms of a TTGA sample with a separate stage of gas-phase decomposition (a) (heating rates of 2.5 and 4 min−1) and solid-phase decomposition with gas-phase assistance (b) (heating rates of 6, 10 and 30 min−1).
Figure 4.
Thermograms of a TTGA sample with a separate stage of gas-phase decomposition (a) (heating rates of 2.5 and 4 min−1) and solid-phase decomposition with gas-phase assistance (b) (heating rates of 6, 10 and 30 min−1).
Figure 5.
Thermograms of a DNTT sample with a separate stage of gas-phase decomposition (a) (heating rate 1 and 2.5 min−1) and solid-phase decomposition with gas-phase assisted (b) (heating rates 4 and 10 min−1).
Figure 5.
Thermograms of a DNTT sample with a separate stage of gas-phase decomposition (a) (heating rate 1 and 2.5 min−1) and solid-phase decomposition with gas-phase assisted (b) (heating rates 4 and 10 min−1).
Figure 6.
Differential decomposition curves of samples TTDA (a); TTGA (b) and DNTT (c,d).
Figure 6.
Differential decomposition curves of samples TTDA (a); TTGA (b) and DNTT (c,d).
Figure 7.
Integral decomposition curves of samples TTDA (a,b); TTGA (c); DNTT (d).
Figure 7.
Integral decomposition curves of samples TTDA (a,b); TTGA (c); DNTT (d).
Figure 8.
Mass spectra of gaseous products of TTDA reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 8.
Mass spectra of gaseous products of TTDA reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 9.
Mass spectra of gaseous products of TTGA reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 9.
Mass spectra of gaseous products of TTGA reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 10.
Mass spectra of gaseous products of DNTT reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 10.
Mass spectra of gaseous products of DNTT reactions at the peak of decomposition at heating rates from 1.5 to 2000 s−1.
Figure 11.
X-ray diffraction data of a powdered sample of the α-phase of carbon nitride.
Figure 11.
X-ray diffraction data of a powdered sample of the α-phase of carbon nitride.
Figure 12.
Crystallographic model of the structure of g-C3N4.
Figure 12.
Crystallographic model of the structure of g-C3N4.
Figure 13.
Points of change in the mechanism of chemical reactions in the studied compounds for: TTDA (a,b); TTGA (c) and DNTT (d). DTA-I-parameters of the process of intensive decomposition (maximum exothermic effect) carried out by the method of differential thermal analysis; DTG-I-parameters of the intensive decomposition process (maximum exothermic effect) carried out by thermogravimetric analysis; DTA-II-parameters of the slow decomposition process (previous exothermic effect) carried out by differential thermal analysis; DTG-II-parameters of the slow decomposition process (previous exothermic effect) carried out by thermogravimetric analysis.
Figure 13.
Points of change in the mechanism of chemical reactions in the studied compounds for: TTDA (a,b); TTGA (c) and DNTT (d). DTA-I-parameters of the process of intensive decomposition (maximum exothermic effect) carried out by the method of differential thermal analysis; DTG-I-parameters of the intensive decomposition process (maximum exothermic effect) carried out by thermogravimetric analysis; DTA-II-parameters of the slow decomposition process (previous exothermic effect) carried out by differential thermal analysis; DTG-II-parameters of the slow decomposition process (previous exothermic effect) carried out by thermogravimetric analysis.
Figure 14.
Changes in the induction energy of intensive decomposition processes depending on the catalytic contribution (taking into account gas-phase decomposition and in the absence of gas-phase decomposition) for: TTDA (a); TTGA (b) and DNTT (c,d).
Figure 14.
Changes in the induction energy of intensive decomposition processes depending on the catalytic contribution (taking into account gas-phase decomposition and in the absence of gas-phase decomposition) for: TTDA (a); TTGA (b) and DNTT (c,d).
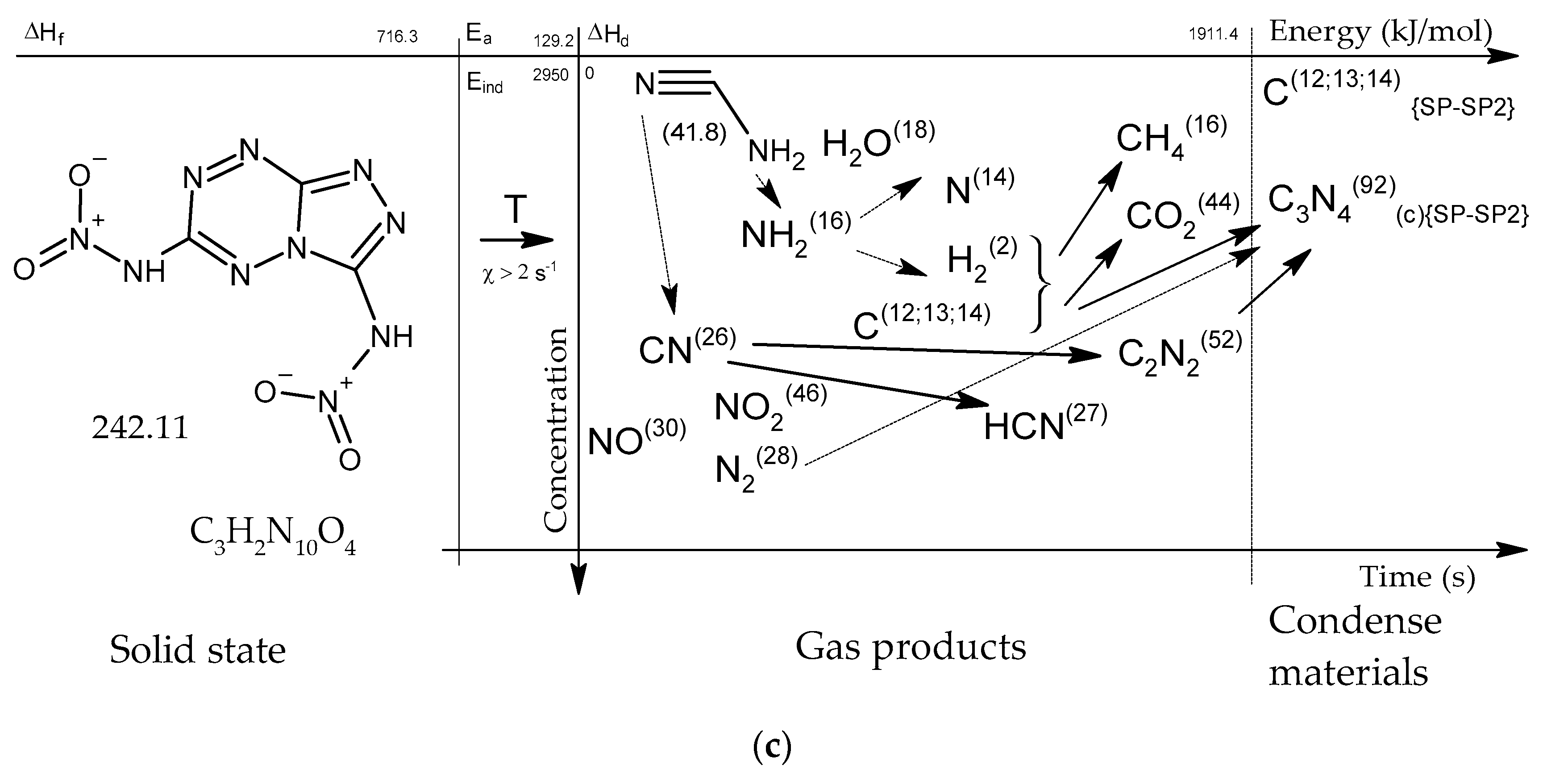
Figure 15.
Concentration-energy diagrams of thermal decomposition reactions of [1,2,4]triazolo[4,3-b][1,2,4,5]tetrazine derivatives: TTDA (a), TTGA (b), DNTT (c) at heating rates of more than 100 min−1.
Figure 15.
Concentration-energy diagrams of thermal decomposition reactions of [1,2,4]triazolo[4,3-b][1,2,4,5]tetrazine derivatives: TTDA (a), TTGA (b), DNTT (c) at heating rates of more than 100 min−1.
Scheme 3.
The synthesis of triazolo[4,3-b][1,2,4,5]tetrazine derivatives.
Scheme 3.
The synthesis of triazolo[4,3-b][1,2,4,5]tetrazine derivatives.
Table 1.
The known characteristics of the studied high-energy compounds.
Table 1.
The known characteristics of the studied high-energy compounds.
| Sample | Tdec [°C] | ρmc [g/cc] | ΔfH(S) [kJ/mol] | D [m s−1] | P [GPa] | IS [J] | FS [N] |
|---|
| TTDA | | 1.61 | 593.12 | 7190 [30] | 21.43 | | |
| DNTT | 138 | 1.91 | 740.9 | 9301 [2,3,13,14] | 38.3 | 3 | >5 |
Table 2.
Calculated characteristics of high-energy compounds.
Table 2.
Calculated characteristics of high-energy compounds.
| Sample | Gross
Formula | MW
[Dalton] | ρmc
[g/cc] | OB
[%] | ΔfHSE [kJ/mol] | V [m3/kg] | Z | D
[m s−1] |
|---|
| TTDA | C3H4N8 | 152.121 | 1.592 | −84.21 | 565.1 | 0.814 | 0.1579 | 7040 |
| TTGA | C3H5N9 | 167.13 | 1.586 | −81.44 | 558.5 | 0.852 | 0.1258 | 6960 |
| DNTT | C3H2N10O4 | 242.112 | 1.914 | −19.83 | 716.3 | 0.767 | 0.074 | 9290 |
Table 3.
Crystal structure of energetic compounds.
Table 3.
Crystal structure of energetic compounds.
| Sample | c [%] | Ds [Å] | Symmetry Group | Unit Cell Parameter |
|---|
| a [Å] | b [Å] | c [Å] | α [°] | β [°] | γ [°] | Z | ρ [g/cc] | V [Å3] |
|---|
| TTDA | 99 | 276 | P21 21 21 | 10.653 | 8.988 | 6.437 | 90 | 90 | 90 | 4 | 1.640 | 616.37 |
| TTGA | 97 | 293 | P2/m | 13.620 | 7.97 | 13.230 | 90 | 97.93 | 90 | 8 | 1.561 | 1422.4 |
| DNTT | 83 | 316 | P-1 | 14.669 | 11.775 | 9.412 | 104.89 | 73.94 | 96.56 | 8 | 1.896 | 1508.17 |
Table 4.
Decomposition points of samples according to DTA data.
Table 4.
Decomposition points of samples according to DTA data.
| Sample | β [°C/min] | Exothermic Effect-I | Exothermic Effect-II | ΣdQ
[kJ/mol] |
|---|
| Tsd [°C] | Tmax [°C] | Te [°C] | Tsd [°C] | Tmax [°C] | Te [°C] |
|---|
| TTDA | 4 | 332.4 | 339.3 | - | 349.7 | 357.2 | 355.9 | 150.43 |
| 10 | 332.6 (325.9) | 344.1 | - | 351.7 | 359.8 | 360.3 | 226.99 |
| 20 | | 324.2 | 345.5 | 346.7 | 363.8 | 378.1 | 255.97 |
| 30 | | | | 346 (324.8) | 361.7 | 369.8 | 319.71 |
| 100 | | | | 356.6 (343.8) | 375.3 | 417.8 | 407.97 |
| TTGA | 2.5 | 161.2 | 167.7 | 179.07 | 182.8 | 194.2 | 194.6 | 274.26 |
| 4 | 165.1 | 172.3 | 179.8 | 183.4 | 197.7 | 197.7 | 316.80 |
| 6 | | | | | 182.1 | 183.8 | 324.45 |
| 10 | 170.3 | 180.9 | - | 179.1 | 184.3 | 194.8 | 335.77 |
| 30 | 186.1 | 189.8 | - | 188.7 | 194.4 | 234.7 | 370.32 |
| DNTT | 1 | 96.4 | 106.9 | 116.5 | 118.1 | 124.7 | 133.8 | 354.96 |
| 2.5 | 101.2 | 115.3 | 120.4 | 121.5 | 127.6 | 140.2 | 413.27 |
| 4 | 110.5 | 115.7 | 116.5 | - | 117.6 | 120.5 | 516.34 |
| 10 | 112.7 | 116.1 | 116.8 | - | 119.4 | 122.6 | 1567.86 |
Table 5.
Decomposition points of samples according to gravimetry data II exothermic effect.
Table 5.
Decomposition points of samples according to gravimetry data II exothermic effect.
| Sample | β
[°C/min] | TG | DTGA |
|---|
| T0s[°C] | Tsid [°C] | Z1(T) [%] | Tsd [°C] | Tsid [°C] | Te [°C] |
|---|
| TTDA | 4 | 110 | 317 | 42.5 | | 350.5 | 358.1 |
| 10 | 175 | 332 | 47.8 | 240.3 | 352.6 | 368.7 |
| 20 | 180 | 342 | 45.4 | 299.6 (348.8) | 352.6 | 365.5 |
| 30 | 180 | 346 | 50.6 | 283.4 | 347.5 | 367.5 |
| 100 | 194 | 357 | 44.5 | 300.1 | 357.5 | 381.2 |
| TTGA | 2.5 | 165.5 | 191.1 | 14.7 | | | |
| 4 | 168.6 | 195.1 | 14.4 | | | |
| 6 | 176.8 | 178.3 | 12.6 | 178.6 | 179.1 | 181.3 |
| 10 | 178.4 | 179.8 | 14.7 | 179.8 | 180.6 | 183.9 |
| 30 | 183.3 | 188.9 | 14.1 | 188.8 | 189.7 | 193.4 |
| DNTT | 1 | 102.9 | | 37 | 99.3 | 109.2 | 113.4 |
| 2.5 | 109.8 | | 41 | 104.8 | 117.6 | 119.7 |
| 4 | 112.5 | 115.7 | - | 118.3 | 115.6 | 117.7 |
| 10 | 113.5 | 116.2 | - | 115.9 | 116.2 | 118.3 |
Table 6.
Experimentally determined characteristics of the studied substances.
Table 6.
Experimentally determined characteristics of the studied substances.
| Sample | Tsid [°C] | Tsd [°C] | Qp, J/g | Z0 | Z1(T) | Z2(T) |
|---|
| TTDA | 351 | 335 | 1231 | 0.762–0.997 | 0.47(366) | 0.45(400) |
| TTGA | 180 | 176 | 1961 | 0.988–0.998 | 0.142(187) | 0.113(250) |
| DNTT | 115 | 110 | 5786 | 0.989–1.00 | 0.08(118)
(thermal explosion) | - |
Table 7.
Crystal structure of the obtained α-phase of carbon nitride.
Table 7.
Crystal structure of the obtained α-phase of carbon nitride.
| Sample | c [%] | Ds [Å] | Symmetry Group | Cell Parameters |
|---|
| a [Å] | b [Å] | c [Å] | α [°] | β [°] | γ [°] | Z | ρ [g/cc] | V [Å3] |
|---|
| TTDA | 99 | 96 | P-6 | 6.694 | 6.694 | 6.649 | 90 | 90 | 120 | 2 | 2.652 | 249.45 |
| TTGA | 97 | 93 | P1 | 6.723 | 6.723 | 6.948 | 90 | 90 | 120 | 2 | 2.550 | 253.37 |
Table 8.
Kinetic parameters of the limiting stage of thermal decomposition in the solid phase obtained by the Kissenger method.
Table 8.
Kinetic parameters of the limiting stage of thermal decomposition in the solid phase obtained by the Kissenger method.
| Sample | Stage | Kinetic Parameters According to the Data |
|---|
| DTA/DSC | DTGA |
|---|
| E [kJ·mol−1] | A [s−1] | R2 | E [kJ·mol−1] | A [s−1] | R2 |
|---|
| TTDA | I (cat) | 784.0 | 1.63 × 1060 | 0.96 | 1939.6 | 1.4 × 10158 | 0.81 |
| II | 292.2 | 4.91 × 1019 | 1.0 | 381.3 | 7.51 × 1027 | 1.0 |
| III (ing) | 169.4 | 2.70 × 10−20 | 0.83 | | | |
| TTGA | I | 237.7 | 2.11 × 1021 | 1.0 | 216.5 | 1.04 × 1019 | 1.0 |
| II | 212.2 | 3.09 × 1019 | 0.98 | 238.0 | 5.04 × 1022 | 0.96 |
| III | 57.4 | 8.28 | 1.0 | | | |
| DNTT | I | | | | 129.0 | 7.56 × 1011 | 1.0 |
| II | 2170 | 7.6 × 10287 | 0.966 | 1914 | 2.4 × 10253 | 1.0 |
Table 9.
Kinetic parameters of TTDA at heating rates less than 20 min−1.
Table 9.
Kinetic parameters of TTDA at heating rates less than 20 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.1 | 404.5 | 3.4 × 1017 | 409.3 | 6.0 × 1031 | 414.2 | 9.7 × 1033 |
| 0.2 | 319.8 | 4.0 × 1013 | 321.3 | 6.7 × 1022 | 326.4 | 2.2 × 1025 |
| 0.3 | 346.4 | 2.9 × 1014 | 348.6 | 5.3 × 1024 | 353.8 | 2.7 × 1027 |
| 0.4 | 673.2 | 1.0 × 1027 | 687.2 | 1.8 × 1053 | 692.4 | 1.2 × 1056 |
| 0.5 | 1254.7 | 1.1 × 1049 | 1289.7 | 4.5 × 10103 | 1294.9 | 3.8 × 10106 |
| 0.6 | 1689.3 | 2.9 × 1065 | 1740.0 | 2.0 × 10141 | 1745.2 | 2.0 × 10144 |
| 0.7 | 1315.9 | 1.9 × 1051 | 1353.1 | 5.8 × 10108 | 1358.3 | 7.0 × 10111 |
| 0.8 | 956.5 | 3.6 × 1037 | 980.7 | 2.2 × 1077 | 985.9 | 3.0 × 1080 |
| 0.9 | 579.8 | 1.2 × 1023 | 590.3 | 2.1 × 1044 | 595.5 | 3.2 × 1047 |
| Mean | 837.8 | | 857.8 | | 863.0 | |
Table 10.
Kinetic parameters of TTDA at heating speeds of more than 20 min−1.
Table 10.
Kinetic parameters of TTDA at heating speeds of more than 20 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.1 | 368.6 | 6.4 × 1015 | 371.8 | 6.4 × 1027 | 376.9 | 1.1 × 1030 |
| 0.2 | 365.0 | 2.4 × 1015 | 367.9 | 6.7 × 1026 | 373.1 | 2.3 × 1029 |
| 0.3 | 370.8 | 3.7 × 1015 | 373.8 | 1.7 × 1027 | 379.0 | 8.9 × 1029 |
| 0.4 | 354.0 | 8.0 × 1014 | 356.4 | 5.5 × 1025 | 361.6 | 3.8 × 1028 |
| 0.5 | 333.2 | 1.2 × 1014 | 334.8 | 7.4 × 1023 | 340.0 | 6.4 × 1026 |
| 0.6 | 322.9 | 4.6 × 1013 | 324.1 | 8.4 × 1022 | 329.3 | 8.7 × 1025 |
| 0.7 | 330.4 | 8.3 × 1013 | 331.9 | 3.1 × 1023 | 337.2 | 3.8 × 1026 |
| 0.8 | 473.1 | 2.0 × 1019 | 479.7 | 4.7 × 1035 | 485.0 | 6.5 × 1038 |
| 0.9 | 442.6 | 1.0 × 1018 | 448.0 | 5.5 × 1032 | 453.3 | 8.7 × 1035 |
| Mean | 373.4 | | 376.5 | | 381.7 | |
Table 11.
Kinetic parameters of TTGA at heating rates less than 6 min−1.
Table 11.
Kinetic parameters of TTGA at heating rates less than 6 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.1 | 211.1 | 3.0 × 1011 | 210.9 | 2.4 × 1018 | 214.8 | 3.1 × 1020 |
| 0.2 | 215.0 | 4.7 × 1011 | 215.0 | 6.8 × 1018 | 218.9 | 1.8 × 1021 |
| 0.3 | 215.0 | 4.7 × 1011 | 215.0 | 6.9 × 1018 | 218.9 | 2.7 × 1021 |
| 0.4 | 216.7 | 5.8 × 1011 | 216.8 | 1.1 × 1019 | 220.7 | 5.7 × 1021 |
| 0.5 | 215.6 | 5.1 × 1011 | 215.7 | 8.1 × 1018 | 219.5 | 5.2 × 1021 |
| 0.6 | 214.6 | 4.5 × 1011 | 214.6 | 6.0 × 1018 | 218.4 | 4.7 × 1021 |
| 0.7 | 215.2 | 4.8 × 1011 | 215.2 | 7.1 × 1018 | 219.1 | 6.4 × 1021 |
| 0.8 | 212.6 | 3.5 × 1011 | 212.5 | 3.4 × 1018 | 216.4 | 3.5 × 1021 |
| 0.9 | 219.0 | 7.4 × 1011 | 219.2 | 1.9 × 1019 | 223.1 | 2.2 × 1022 |
| Mean | 215.0 | | 215.0 | | 218.9 | |
Table 12.
Kinetic parameters of TTGA at heating rates of more than 6 min−1.
Table 12.
Kinetic parameters of TTGA at heating rates of more than 6 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.1 | 235.1 | 1.8 × 1013 | 235.9 | 2.8 × 1022 | 239.8 | 3.5 × 1024 |
| 0.2 | 234.2 | 1.6 × 1013 | 235.0 | 2.1 × 1022 | 238.8 | 5.4 × 1024 |
| 0.3 | 232.6 | 1.3 × 1013 | 233.4 | 1.4 × 1022 | 237.2 | 5.3 × 1024 |
| 0.4 | 232.6 | 1.3 × 1013 | 233.4 | 1.4 × 1022 | 237.2 | 7.0 × 1024 |
| 0.5 | 231.6 | 1.2 × 1013 | 232.4 | 1.0 × 1022 | 236.2 | 6.5 × 1024 |
| 0.6 | 230.7 | 1.0 × 1013 | 231.4 | 7.9 × 1021 | 235.2 | 6.0 × 1024 |
| 0.7 | 230.6 | 1.0 × 1013 | 231.3 | 7.5 × 1021 | 235.1 | 6.7 × 1024 |
| 0.8 | 233.3 | 1.4 × 1013 | 234.1 | 1.6 × 1022 | 238.0 | 1.6 × 1025 |
| 0.9 | 232.8 | 1.3 × 1013 | 233.6 | 1.3 × 1022 | 237.4 | 1.4 × 1025 |
| Mean | 232.6 | | 233.4 | | 237.2 | |
Table 13.
Kinetic parameters of DNTT at heating rates less than 3 min−1.
Table 13.
Kinetic parameters of DNTT at heating rates less than 3 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.005 | 43.4 | 4.3 × 103 | 38.9 | 2.6 × 101 | 41.9 | 1.3 × 102 |
| 0.01 | 74.4 | 6.2 × 105 | 71.0 | 1.2 × 106 | 74.0 | 1.2 × 107 |
| 0.015 | 98.8 | 2.5 × 107 | 96.2 | 4.3 × 109 | 99.3 | 6.7 × 1010 |
| 0.02 | 111.9 | 1.8 × 108 | 109.8 | 3.2 × 1011 | 112.9 | 6.6 × 1012 |
| 0.025 | 116.7 | 3.4 × 108 | 114.7 | 1.3 × 1012 | 117.8 | 3.5 × 1013 |
| 0.03 | 123.0 | 8.4 × 108 | 121.1 | 9.9 × 1012 | 124.3 | 3.1 × 1014 |
| 0.035 | 126.3 | 1.3 × 109 | 124.6 | 2.7 × 1013 | 127.7 | 1.0 × 1015 |
| 0.04 | 129.8 | 2.2 × 109 | 128.2 | 8.1 × 1013 | 131.3 | 3.4 × 1015 |
| 0.045 | 132.4 | 3.1 × 109 | 130.9 | 1.8 × 1014 | 134.0 | 8.6 × 1015 |
| 0.1 | 159.9 | 2.4 × 1010 | 159.3 | 1.5 × 1016 | 162.5 | 1.6 × 1018 |
| 0.2 | 220.8 | 1.0 × 1014 | 222.3 | 2.2 × 1024 | 225.5 | 4.7 × 1026 |
| 0.3 | 282.4 | 3.8 × 1017 | 286.0 | 2.6 × 1032 | 289.3 | 8.6 × 1034 |
| 0.4 | 318.8 | 4.1 × 1019 | 323.7 | 1.1 × 1037 | 327.0 | 4.7 × 1039 |
| 0.5 | 355.0 | 3.5 × 1021 | 361.1 | 2.6 × 1041 | 364.5 | 1.4 × 1044 |
| 0.6 | 339.3 | 1.7 × 1020 | 344.7 | 2.5 × 1038 | 348.2 | 1.7 × 1041 |
| 0.7 | 294.5 | 2.3 × 1017 | 298.1 | 6.9 × 1031 | 301.6 | 5.5 × 1034 |
| 0.8 | 301.5 | 3.7 × 1017 | 305.3 | 1.9 × 1032 | 308.9 | 1.8 × 1035 |
| 0.9 | 472.3 | 6.3 × 1026 | 482.2 | 1.9 × 1053 | 485.8 | 2.1 × 1056 |
Table 14.
Kinetic parameters of DNTT at heating rates of more than 3 min−1.
Table 14.
Kinetic parameters of DNTT at heating rates of more than 3 min−1.
| Conversion | FWO | KAS | Friedman |
|---|
| E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] | E [kJ·mol−1] | A [s−1] |
|---|
| 0.005 | 210.7 | 6.3 × 1014 | 212.0 | 1.7 × 1026 | 215.1 | 8.7 × 1026 |
| 0.01 | 196.7 | 5.7 × 1013 | 197.4 | 7.1 × 1023 | 200.6 | 7.5 × 1024 |
| 0.015 | 205.0 | 1.6 × 1014 | 206.0 | 7.2 × 1024 | 209.2 | 1.2 × 1026 |
| 0.02 | 297.4 | 9.0 × 1019 | 301.7 | 7.6 × 1037 | 305.0 | 1.6 × 1039 |
| 0.025 | 450.0 | 2.2 × 1029 | 459.8 | 1.9 × 1059 | 463.1 | 5.1 × 1060 |
| 0.03 | 749.9 | 4.8 × 1047 | 770.5 | 1.6 × 10101 | 773.8 | 5.2 × 10102 |
| 0.035 | 1566.2 | 2.1 × 1097 | 1616.4 | 1.2 × 10215 | 1619.6 | 4.4 × 10216 |
| 0.04 | 2853.7 | 2.2 × 10175 | 2950.4 | 1.92 × 10394 | 2953.7 | 2.86 × 10396 |
| 0.045 | 2853.7 | 2.2 × 10175 | 2950.4 | 1.92 × 10394 | 2953.7 | 2.86 × 10396 |
| 0.1…0.9 | 2782.7 | 1.1 × 10171 | 2876.9 | 1.92 × 10384 | 2880.1 | 7.77 × 10386 |
Table 15.
Thermodynamic properties of the decomposition process in DTA cell.
Table 15.
Thermodynamic properties of the decomposition process in DTA cell.
| Sample | TSADT | Tm | ΔG* | ΔH* | ΔS* |
|---|
| [°C] | [°C] | [kJ·mol−1] | [kJ·mol−1] | [J·mol−1·K−1] |
|---|
| TTDA | 349.5 | 358.2 | 183.3 | 376.1 | 308.3 |
| TTGA | 190.3 | 198.0 | 135.9 | 234.1 | 211.8 |
| DNTT | 113.4 | 114.1 | 121.4 | 1911.4 | 4629.4 |