Abstract
Totally ignoring that the five enthalpies of reaction—bond dissociation enthalpy (BDE), adiabatic ionization potential (IP), proton dissociation enthalpy (PDE), proton affinity (PA), and electron transfer enthalpy (ETE)—characterizing the three free radical scavenging mechanisms—direct hydrogen atom transfer (HAT), sequential electron transfer proton transfer (SET-PT), and stepwise proton loss electron transfer (SPLET)—are not independent of each other, a recent publication on the antioxidant activity of dietary vitamins compared various vitamins and “found” different quantities, which should be strictly equal by virtue of energy conservation. Aiming to clarify this point, as well as to avoid such mistakes in future studies and to unravel errors in the previous literature, in the present paper we formulate two theorems that any sound results on antioxidation should obey. The first theorem states that the sums of the enthalpies characterizing the individual steps of SET-PT and SPLET are equal: IP+PDE = PA+ETE (=H2). This is a mathematical identity emerging from the fact that both the reactants and the final products of SET-PT and SPLET are chemically identical. The second theorem, which is also a mathematical identity, states that H2 − BDE = IP > 0, where IP is the ionization potential of the H-atom in the medium (e.g., gas or solvent) considered. Due to their general character, these theorems may/should serve as necessary sanity tests for any results on antioxidant activity, whatever the method employed in their derivation. From a more general perspective, they should represent a serious word of caution regarding attempts to assign the preferred free radical scavenging pathway based merely on thermochemical descriptors.
Keywords:
radical scavenging activity; antioxidant mechanisms; HAT; SPLET; SET-PT; BDE; IP; PDE; PA; ETE; thermochemistry; quantum chemistry 1. Introduction
Oxidative stress is an extremely dangerous phenomenon caused by the rapid production of free radicals (R) in the human body [1,2,3,4,5]. Owing to their unpaired electron, free radicals can seriously damage a variety of biomolecules related to a plethora of pathological processes, including, but not limited to, cardiovascular and neurodegenerative diseases [6,7,8,9,10,11,12,13,14,15,16,17]. Antioxidants (AXH) are molecules that can scavenge free radicals by H-atom donation (AXH + R → AX + RH), and can neutralize free radicals through single-step (direct H-atom transfer, HAT) or two-step mechanisms. The latter can proceed either via stepwise electron transfer–proton transfer (SET-PT) or via sequential proton loss–electron transfer (SPLET). A certain environment (solvent polarity) may selectively favor one over the other aforementioned pathways. By and large, there is a consensus that free radical scavenging by bio-relevant antioxidants (e.g., dietary vitamins and drugs against lipoprotein oxidation) proceeds as a single-step process (HAT) in non-polar solvents and as a two-step process in polar solvents. The most “popular” disputes (for vitamin E, see, e.g., [18,19,20]) on the antioxidant activity are on whether SET-PT or SPLET prevails in polar media. The most frequent challenge related to this dilemma is that differentiating between SET-PT and SPLET is a difficult issue that cannot be merely couched in terms of the antioxidant’s thermodynamical descriptors.
An adequate analysis of the preferred radical scavenging mechanism should not only consider the properties of the antioxidant but also the properties of the radical [19,21,22]. The conclusions of such an analysis can be surprising, as in the case of atorvastatin-based species [22].
In this vein, it was the recent claim made in [23] (even in the abstract) that HAT, rather than SET-PT or SPLET, is the preferred pathway along which dietary vitamins scavenge free radicals in aqueous solution—without any specific consideration of the free radicals to be neutralized—that attracted our attention. As elaborated below, this is only one of the severe flaws that plague [23]. An even more important source of errors in the reported results is the fact that [23] completely overlooked and failed to adequately account for the fact that even the thermodynamical descriptors characterizing the free radical scavenging activity of a given antioxidant are not molecular properties independent of each other. This is exactly what is stated by the two theorems presented below.
To avoid creating the impression that the present work is a “declaration of war” to the free radical/antioxidant community, we will deliberately restrict ourselves to naming a few previous works [23,24,25] and show how the two theorems, used as sanity checks, can easily unravel inadequate results of quantum chemical calculations. The fact that we are going to refer below to the works [23,24,25] (out of many others) should by no means be understood as an “attack” on these studies. It should become clear from the analysis that follows that these theorems are of great significance in diverse areas of chemistry.
2. Computational Details
The quantum chemical calculations carried out in conjunction with the specific molecule (vitamin B3) considered in this study used the GAUSSIAN 16 suite of programs [26], similar to those in our recent study on atorvastatin [22]. In order to make this paper self-contained, they will be briefly described again.
Geometry optimizations without constraints, frequency calculations (checking that all vibrational frequencies were real), and electronic energy calculations were carried out at the DFT level of theory using the hybrid B3LYP exchange correlation functional [27,28,29,30] and 6-311G(d,p) and 6-311++G(d,p) basis sets [31,32]. The solvent (water) was treated within the polarized continuum model (PCM) [33] using the integral equation formalism (IEF) [34]. Similar to other cases studied recently [35,36,37], spin contamination did not appear to be an issue for the unrestricted spin (UB3LYP) approaches, as witnessed by the values of the total spin values before and after the annihilation of the first spin contaminant presented in the following. For reasons explained below, we also performed restricted open-shell (ROB3LYP) calculations, which are more computationally demanding for larger molecules. The small differences between the unrestricted and restricted open-shell methods revealed that dynamic electron correlations brought about by spin polarization effects are weak; still, it should be made clear that claims (often formulated in the literature on antioxidation) of chemical accuracy (∼1 kcal/mol) are totally unrealistic. Achieving chemical accuracy for bond dissociation enthalpies and proton affinity (BDE and PA, quantities entering the discussion that follows) is often illusory, even for extremely computationally demanding state-of-the-art compound model chemistries (CBS-QB3, CBS-APNO, G4, W1BD) and smaller molecular sizes [38].
All enthalpies listed below refer to the temperature K.
3. Results and Discussion
3.1. Enthalpies of Reaction Characterizing the Antioxidant Activity
As noted in the Introduction, an antioxidant can transfer an H-atom to a free radical in one- or two-step processes. Again, to make the paper self-contained, let us be reminded that the three antioxidative mechanisms (HAT, SET-PT, and SPLET) and the corresponding reaction enthalpies (BDE, IP and PDE, and PA and ETE, respectively) can be expressed as follows:
Direct hydrogen atom transfer (HAT) [39,40,41]
Stepwise electron transfer–proton transfer (SET-PT) [42,43]
Sequential proton loss–electron transfer (SPLET) [44,45]
In specific cases of interest for antioxidation, X stands for an O, N, or S atom. The above definitions should make clear that all aforementioned reaction enthalpies (in particular, IP) are adiabatic rather than vertical properties [46,47]; they should be evaluated at the global electronic energy minima of the various reaction products/reactants.
3.2. Theorems on Antioxidation
The first theorem stated below expresses the chemical fact that both the reactants and the final products of the two two-step antioxidative mechanisms are identical.
Theorem 1.
Whatever the antioxidant and the environment, the combined enthalpies pertaining to the two-step SET-PT and SPLET mechanisms are equal:
Proof of Theorem 1.
The theorem straightforwardly follows by adding, term by term, the left- and right-hand sides of Equations (2a), (2b), (3a) and (3b)
As is visible, the right-hand sides of Equations (5a) and (5b) are identical. □
Corollary 1.
The second theorem establishes a relationship between the enthalpies of reactions characterizing the single-step and two-step antioxidative mechanisms.
Theorem 2.
The combined enthalpy of reaction pertaining to the two-step (SET-PT and SPLET) mechanisms exceeds the enthalpy of the direct H-atom transfer reaction. Whatever the antioxidant, the difference is equal to the ionization enthalpy of the H-atom in the corresponding environment:
Proof of Theorem 2.
The theorem straightforwardly follows by subtracting, term by term, the left- and right-hand sides of Equations (2) (or Equation (3)) and (1), and observing that the difference thus obtained represents the ionization enthalpy of the hydrogen atom:
□
Corollary 2.
Being equal to the ionization enthalpy of the H-atom (cf. Equation (8)), the difference between the enthalpies of the total two- and single-step pathways merely depends on the medium; it is the same for all antioxidant species
Remark 1.
Remark on Theorems 1 and 2. We referred above to enthalpies of reaction because these are usually examined in studies on antioxidants, but Gibbs free enthalpies satisfy the same equations.
3.3. Implications of Theorem 1
The results presented in the literature on antioxidants violating Theorem 1 (and hence being incorrect) fall into two categories.
Studies reporting values different from belong to the first category. Because the main aim of this work is to draw attention to the necessary sanity tests rather than amply documenting incorrect results on antioxidative activity reported in the literature in the past, we will only give here a single but notorious example, to which, unpleasantly, we return to repeatedly below.
We named [23], which is a notorious case because, unfortunately, all values presented for the dietary vitamins investigated (A, B1, B3, B6, and C) fail to obey Theorem 1. This is obvious by inspecting the last column of Table 1, where the pertaining results are collected. It is pure nonsense to settle between SET-PT and SPLET by “comparing” (as in [23]) the combined enthalpies of the pertaining reactions and . Provided that they are correctly estimated, they should be strictly equal to each other, whatever the computational method utilized.

Table 1.
The enthalpies of reaction (in kJ/mol) for dietary vitamins in aqueous solution taken from Table 1 of [23] violate Theorem 1; the values in the fourth column should be zero (cf. Equation (4)) but they are not. They also violate Theorem 2; all values of the fifth column should be equal to the H-atom ionization enthalpy in water (sixth column) but they are closer to that in the gas phase (seventh column). All quantities shown here are averages of the values computed using the Minnesota functionals M052x and M062x.
The second category comprises studies adjudicating between SET-PT and SPLET based on the reaction enthalpy of the first step. For example, SPLET is claimed to be the thermodynamically preferred pathway because . This is incorrect because it contradicts Corollary 1. If this was the case, thermodynamically speaking, the second, rate-determining step (electron transfer, ETE) would act as bottleneck of SPLET (, cf. Equation (6b)).
Equation (6) makes it clear that in all cases, it is the specific free radical and/or the reaction kinetics that settles whether SET-PL or SPLET prevails. Merely considering antioxidant’s enthalpies of reaction can never discriminate between these two pathways.
3.4. Implications of Theorem 2
There are at least two practical issues related to Theorem 2.
First, the theorem shows that it is incorrect to assign HAT as the preferred antioxidant pathway based on the fact that is smaller than (or ). Theorem 2 states that correctly estimated enthalpies should always satisfy this inequality. This refutes the claim made in [23] on this basis, that HAT is the thermodynamically preferred pathway for dietary vitamins to scavenge free radicals in aqueous solution.
Above, we said “correctly estimated” because, unfortunately, this is not always the case in the literature; for example, in [25], where enormous values of kcal/mol, much larger than all the other reaction enthalpies, were obtained (see [22,48]). At odds with Equation (7), the largest value of reported in the mentioned study are smaller than BDE; none exceeds ∼150 kcal/mol (cf. Table 2 of [25]).
Second, Theorem 2 emphasizes the particularly important role of the ionization enthalpy of the H-atom . For this reason, in Table 2 we present extensive data for the enthalpy of the H-atom. We used these data in Table 3 and Table 4 for computing in gas and solvents using popular functionals (B3LYP, PBE0, M052x, and M062x) and frequently employed Pople basis sets.

Table 2.
Enthalpies of the H-atom at K obtained by adding the thermal correction of 0.002361 hartree (common for all compound model chemistries from GAUSSIAN 16) to the electronic energies, computed as indicated below. As visible here, notwithstanding the different number of basis functions, the results using the basis sets 6-311+G(d,p) and 6-311G(d,p), and 6-31+G(d,p) and 6-31G(d,p) are identical. Likewise, including more polarization functions, G(d,p) → G(2d,2p) or 6-311++(3df,3pd), has no impact on the values presented here.

Table 3.
Ionization enthalpies (IP) of the H-atom in common environments. As already noted in the caption of Table 2, the results using the basis sets 6-311+G(d,p) and 6-311G(d,p), and 6-31+G(d,p) and 6-31G(d,p) are identical. Likewise, including more polarization functions, G(d,p) → G(2d,2p) or 6-311++(3df,3pd), has no impact on the values presented here.

Table 4.
Ionization enthalpies (IP) of the H-atom in common solvents. As already noted in the caption of Table 2, the results using the basis sets 6-311+G(d,p) and 6-311G(d,p), and 6-31+G(d,p) and 6-31G(d,p) are identical. Likewise, including more polarization functions, G(d,p) → G(2d,2p) or 6-311++(3df,3pd), has no impact on the values presented here.
Regarding the values of , a twofold word of caution is in order.
First, estimating as the Kohn–Sham HOMO energy with reversed sign (Koopmans’ theorem) lamentably fails in a twofold sense; see Table 5 and Table 6. Because Kohn–Sham “orbitals” are mathematical objects rather than true molecular orbitals [47,49], these estimates are inadequate. The differences between the B3LYP- and PBE0-based Koopmans’ values and the -DFT-based values [50,51,52] are unacceptable even in the gas phase: ∼4–5 eV for B3LYP and PBE0 (cf. Table 5) and ∼3.5 eV for M062x and M052x (cf. Table 6). These differences grow to enormous values in polar solvents (∼12 eV, cf. Table 5 and Table 6). This dramatic deterioration of the description based on Koopmans’ theorem is fully in line with findings reported in previous studies on molecules in solvents [46,53].

Table 5.
Ionization enthalpies (IP) of the H-atom in common environments (poorly) approximated as Kohn–Sham HOMO energy with reversed sign (Koopmans’ theorem). As already noted in the caption of Table 2, the results using the basis sets 6-311+G(d,p) and 6-311G(d,p), and 6-31+G(d,p) and 6-31G(d,p) are identical. Likewise, including more polarization functions, G(d,p) → G(2d,2p) or 6-311++(3df,3pd), has no impact on the values presented here.

Table 6.
Ionization enthalpies (IP) of the H-atom in common environments (poorly) approximated as Kohn–Sham HOMO energy with reversed sign (Koopmans’ theorem). Results using Minnesota functionals M062x and M052x and basis sets 6-31+G(d,p).
Second, differences in the values of antioxidant thermodynamic descriptors in solvents as large as ∼0.5 eV (12 kcal/mol, 50 kJ/mol) reported in various publications do not necessarily reflect real physical and chemical differences. They can simply stem from the utilization of different values of the electron and/or hydrogen atom enthalpy of solvation circulated in the literature (e.g., kJ/mol [54] versus kJ/mol [55] for a proton in water).
According to Theorem 2, the difference between and BDE should be equal to the ionization enthalpy of the H-atom in the medium (solvent) in question. It should be, but unfortunately, data in the literature exist for which this condition is not fulfilled.
In the upper part of Table 7, we reproduce enthalpies reported at the B3LYP/6-31+G(d,p)(/IEFPCM) level of theory for the natural food colorant peonidin in gas and aqueous phases [24].

Table 7.
The enthalpies of reaction (in kcal/mol) of peonidin according to [24].
It might be questionable whether the difference between the values = 392.87 kcal/mol and kcal/mol represents an obscure numerical artifact or a violation of Theorem 1. In fact, this should not be the case, given the fact that Theorem 1 is a mathematical identity that must be satisfied at any approximate level of theory provided that all antioxidant descriptors were correctly computed using the same method.
Anyway, letting alone this aspect, the values estimated for kcal/mol and kcal/mol differ too much from IP kcal/mol; they obviously do not satisfy Theorem 2.
Pleasantly, no objection can be raised against the enthalpies estimated in [24] for peonidin in the gas phase. They satisfy both Theorems 1 and 2.
Let us next refer again to notorious case of [23]. Relevant results are depicted in Table 1. The inspection of the fifth column of Table 1 reveals values that drastically differ from the ionization enthalpy of the H-atom in water (cf. Table 4). Furthermore, those values also significantly depend on the molecular species, which should not be the case if they were correct.
As a specific illustration of the latter aspect noted above, let us examine the results computed for atorvastatin (ATV) and its ortho- and para-hydroxy metabolites (o-ATV, p-ATV) in methanol at the B3LYP/6-31+G(d,p) level of theory [22]. As visible in Table 8 and Figure 1, for each molecular species (ATV, o-ATV, and p-ATV) and any possible H-atom donation—that is, for each of the three (ATV) or four (o-ATV, p-ATV) OH-groups and the NH-group (indicated for the molecular geometries presented in [22])—the results of the ATV-based species satisfy both theorems.

Table 8.
The enthalpies of reaction (in kcal/mol) characterizing the antioxidant activity of atorvastatin (ATV) and its ortho- and para-hydroxy metabolites (o-ATV, p-ATV) in methanolic phase [22] (and corrections reprinted [22]) satisfy the two theorems stated in this paper. The values of the difference between IP+PDE = PA+ETE and BDE, identical for all molecular species and positions of H-atom abstraction, are equal to the ionization of the H-atom in methanol computed at the same B3LYP/6-31+G(d,p) level of theory (cf. Table 4).
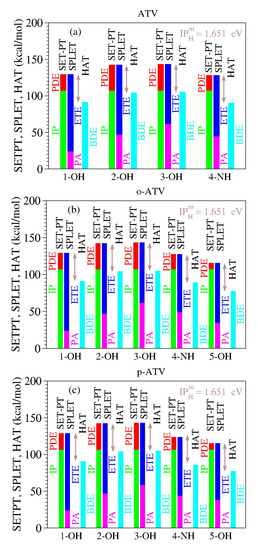
Figure 1.
The enthalpies of reaction for (a) atorvastatin (ATV) and its (b) ortho-hydroxy (o-ATV) and (c) para-hydroxy (p-ATV) metabolites [22] satisfy the two theorems of antioxidation discussed in this paper. See the main text for details.
3.5. Detailed Analysis of a Specific Case: Vitamin B3
Let us next examine in detail the case of vitamin B3 (C6H5NO2, InChI=1S/C6H5NO2/ c8-6(9)5-2-1-3-7-4-5/h1-4H,(H,8,9), CAS Registry Number: 59-67-6), whose optimized geometry is depicted in Figure 2. Vitamin B3 is one of the molecular species investigated in [23]. The analysis that follows shows that, as it should be in general, the antioxidant properties of vitamin B3 also obey the two theorems presented above.
Figure 2.
Optimized geometry of vitamin B3 (C6H5NO2). Figure generated using GABEDIT [56].
In our calculations for vitamin B3, we attempted to ensure consistency with our recent [22,48] and ongoing investigations on antioxidation, while also gaining insight into specific sources of the erroneous results reported in [23]. For the first reason, we used the B3LYP exchange-correlation functional, for which results for vitamin B3 are also presented in [23] (cf. Table 1 of the supplementary material of [23]).
Ambiguities arose regarding both the basis set—6-311++G(d,p) according to Section 3 but 6-311G**(≡6-311G(d,p)) according to Table 1 in the supplementary material of [23]— and the—unrestricted (UB3LYP) or spin-restricted open-shell (ROB3LYP)—method employed for radicals in [23]. (Unfortunately, our inquiry on these aspects to the authors of [23] continues to be pending.)
For the reasons delineated above, we computed the antioxidant descriptors of vitamin B3 using both methods (UB3LYP and ROB3LYP) and both basis sets (6-311++G(d,p) and 6-311G(d,p)). The results are presented in Table 9 and Table 10, and Figure 3. The inspection of Table 9 and Table 10 and Figure 3 reveals the clear differences between our estimates and those of [23], which are also shown. As is visible, both for the gaseous phase and for the aqueous phase our values do satisfy Theorems 1 and 2.

Table 9.
The enthalpies of reaction (in kJ/mol) that quantify the antioxidant activity of vitamin B3 computed for gaseous and aqueous phases using the methods indicated. Notice that there is no difference between unrestricted (UB3LYP) and restricted open-shell (ROB3LYP) methods in calculating the PA values, and for this reason the the latter are written in parentheses. Values claimed to be for the aqueous phase of [23] are also included, but some thereof seem rather to be for gas.

Table 10.
Combined enthalpies of reaction (in kJ/mol) for the three antioxidant mechanisms (HAT, SET-PT, and SPLET) for vitamin B3 in the gas and aqueous phase along with those extracted from [23]. Notice that our estimates satisfy both Theorems 1 and 2 while those of [23] do not.
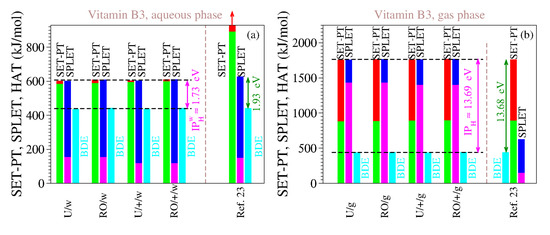
We also performed computations for the gas phase because the enormous values of IP and PDE of [23] (cf. Table 9) made us suspicious that, contrary to what [23] asserted, they were not computed for the aqueous phase but rather for the gaseous phase. It is, so far, an open question whether our assumption holds true or not, but the fact is that the IP and PDE of [23] are completely different from our IP and PDE in water, while being considerably closer to our estimates for the gas phase. This also holds true for all the other vitamins investigated in [23]; see Table 1.
Parenthetically (because this is not the primary aim of the present work), we can still mention a couple more incorrect statements in [23]. For example, the claim on page 5 of [23], that the first step of the SET-PT mechanism (i.e., Equation (2a)) is less energetically costly than the second SET-PT step (i.e., Equation (2b)), and another claim on page 6 that the production of the alkoxide anion in the first SPLET mechanism (i.e., Equation (3a)) requires more energy than that for the electron transfer from the alkoxide anion to the free radical (i.e., Equation (3b)). In reality, the inspection of the thermochemical data for the aqueous phase (which [23] considered) in Table 9 illustrates that just the opposite holds true (namely, and ).
3.6. Remark on the Dominant Antioxidant Mechanism
Theorem 1 makes it clear why the discussion on the competition between SET-PT and SPLET is incorrect in [23]. There, the former mechanism was ruled out due to the large values of (in fact, incorrectly computed, see Table 9), much larger than . In general, if this were the case, Theorem 1 would necessarily imply that , which means that the second step of SPLET would then act as a bottleneck for the SPLET pathway. To reiterate, discussing the competition SET-PT versus SPLET merely based on the enthalpies of reaction is impossible, simply because the combined enthalpies of the two pathways (SET-PT and SPLET) are strictly equal in all cases.
The claim made in [23] (even in the abstract) that HAT prevails is not substantiated by the values (even if they were correct) presented in that work. From the fact that , one can/should by no means conclude that HAT prevails over SPLET. This inequality holds in all cases (cf. Equation (9)).
On the other hand, as emphasized recently [22], a “small” value of (implicitly meaning a smaller than ) does not make SPLET a thermodynamically allowed pathway, per se. The relationship between and plays absolutely no role in the the first step of SPLET (proton loss). What matters in the first SPLET reaction is that the antioxidant’s PA be smaller than the PDE value of the neutralized free radical; see the discussion in [22]. Again, whether SPLET is allowed or not cannot be settled merely in terms of the antioxidant’s properties.
4. Conclusions
By presenting extensive data for the H-atom ionization potential obtained with frequently utilized functionals and basis sets (Table 3 and Table 4), we aimed to provide the reader with a toolkit useful for performing expedient sanity checks of published (or own) results on antioxidant thermochemistry relying on Theorems 1 and 2.
It was not our main purpose to provide an extensive documentation of errors in previous studies on free radical scavenging. By intentionally restricting ourselves to mention a very limited number of recent works [23,24,25] plagued by severe flaws, we primarily aimed to draw attention to the fact that such errors exist and, hence, that an overall word of caution is strongly recommended. Assisting the interested reader in quickly checking the (in)correctness of results on antioxidation reported in the previous literature on free radical scavenging is unfortunately a nontrivial utility of these theorems. We say “unfortunately” because a closer look at many publications may still be a source of numerous unpleasant surprises.
From a more general perspective, we believe that the two theorems formulated in this paper are important for several reasons. The most straightforward consequence is the clear demonstration that discriminating between SET-PT and SPLET—a “favorite” dilemma in the field of free radical scavenging—is impossible merely based on the reaction enthalpies characterizing the antioxidant. To this aim, letting alone aspects of kinetics—which are of potential, paramount importance—additional information on the thermochemical properties of the free radicals envisaged is indispensable.
Funding
In the initial stage, this research was funded by the German Research Foundation (DFG grant BA 1799/3-2). Computational support from the state of Baden-Württemberg through bwHPC and the German Research Foundation through grant no. INST 40/575-1 FUGG (bwUniCluster 2.0, bwForCluster/MLS&WISO 2.0/HELIX, and JUSTUS 2.0 cluster) is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the author upon reasonable request.
Conflicts of Interest
The author declares no conflict of interest.
Sample Availability
Not applicable.
References
- Sies, H. Oxidative Stress; Academic Press: Cambridge, MA, USA, 1985; pp. 1–501. [Google Scholar]
- Cadenas, E.; Sies, H. Oxidative stress: Excited oxygen species and enzyme activity. Adv. Enzym. Regul. 1985, 23, 217–237. [Google Scholar] [CrossRef]
- Sies, H. Biochemistry of Oxidative Stress. Angew. Chem. Int. Ed. 1986, 25, 1058–1071. [Google Scholar] [CrossRef]
- Sies, H. Oxidative stress: Oxidants and antioxidants. Exp. Physiol. 1997, 82, 291–295. [Google Scholar] [CrossRef] [PubMed]
- Sies, H. On the history of oxidative stress: Concept and some aspects of current development. Curr. Opin. Toxicol. 2018, 7, 122–126. [Google Scholar] [CrossRef]
- Knight, J.A. Diseases related to oxygen-derived free radicals. Ann. Clin. Lab. Sci. 1995, 25, 111–121. [Google Scholar]
- Pisoschi, A.M.; Pop, A. The role of antioxidants in the chemistry of oxidative stress: A review. Eur. J. Med. Chem. 2015, 97, 55–74. [Google Scholar] [CrossRef]
- Aruoma, O.I. Free radicals, oxidative stress, and antioxidants in human health and disease. J. Am. Oil Chem. Soc. 1998, 75, 199–212. [Google Scholar] [CrossRef]
- Moskovitz, J.; Yim, M.B.; Chock, P. Free Radicals and Disease. Arch. Biochem. Biophys. 2002, 397, 354–359. [Google Scholar] [CrossRef]
- Valko, M.; Leibfritz, D.; Moncol, J.; Cronin, M.T.; Mazur, M.; Telser, J. Free radicals and antioxidants in normal physiological functions and human disease. Int. J. Biochem. Cell Biol. 2007, 39, 44–84. [Google Scholar] [CrossRef]
- Pham-Huy, L.A.; He, H.; Pham-Huy, C. Free radicals, antioxidants in disease and health. Int. J. Biomed. Sci. IJBS 2008, 4, 89. [Google Scholar]
- Moon, J.K.; Shibamoto, T. Antioxidant Assays for Plant and Food Components. J. Agric. Food Chem. 2009, 57, 1655–1666. [Google Scholar] [CrossRef]
- Nimse, S.B.; Pal, D. Free radicals, natural antioxidants, and their reaction mechanisms. RSC Adv. 2015, 5, 27986–28006. [Google Scholar] [CrossRef]
- Lobo, V.; Patil, A.; Phatak, A.; Chandra, N. Free radicals, antioxidants and functional foods: Impact on human health. Pharmacogn. Rev. 2010, 4, 118–126. [Google Scholar] [CrossRef]
- Brewer, M. Natural Antioxidants: Sources, Compounds, Mechanisms of Action, and Potential Applications. Compr. Rev. Food Sci. Food Saf. 2011, 10, 221–247. [Google Scholar] [CrossRef]
- Neha, K.; Haider, M.R.; Pathak, A.; Yar, M.S. Medicinal prospects of antioxidants: A review. Eur. J. Med. Chem. 2019, 178, 687–704. [Google Scholar] [CrossRef]
- Galano, A.; Raul Alvarez-Idaboy, J. Computational strategies for predicting free radical scavengers’ protection against oxidative stress: Where are we and what might follow? Int. J. Quantum Chem. 2019, 119, e25665. [Google Scholar] [CrossRef]
- Nakanishi, I.; Kawashima, T.; Ohkubo, K.; Kanazawa, H.; Inami, K.; Mochizuki, M.; Fukuhara, K.; Okuda, H.; Ozawa, T.; Itoh, S.; et al. Electron-transfer mechanism in radical-scavenging reactions by a vitamin E model in a protic medium. Org. Biomol. Chem. 2005, 3, 626–629. [Google Scholar] [CrossRef]
- Musialik, M.; Litwinienko, G. Scavenging of DPPH• Radicals by Vitamin E Is Accelerated by Its Partial Ionization: The Role of Sequential Proton Loss Electron Transfer. Org. Lett. 2005, 7, 4951–4954. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Ji, H.F. How vitamin E scavenges DPPH radicals in polar protic media. New J. Chem. 2006, 30, 503–504. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, Y.; Li, Y.; Li, G.; Du, S.; Guo, H.; Yang, L.; Jiang, L.; Gao, H.; Song, Y. Molecularly Controlled Modulation of Conductance on Azobenzene Monolayer-Modified Silicon Surfaces. J. Phys. Chem. C 2008, 112, 8288–8293. [Google Scholar] [CrossRef]
- Bâldea, I. Why Ortho- and Para-Hydroxy Metabolites Can Scavenge Free Radicals That the Parent Atorvastatin Cannot? Important Pharmacologic Insight from Quantum Chemistry. Molecules 2022, 27, 5036, reprinted in arXiv arXiv:2208.07987. [Google Scholar] [CrossRef] [PubMed]
- Pandithavidana, D.R.; Jayawardana, S.B. Comparative Study of Antioxidant Potential of Selected Dietary Vitamins; Computational Insights. Molecules 2019, 24, 1646. [Google Scholar] [CrossRef] [PubMed]
- Rajan, V.K.; Hasna, C.K.; Muraleedharan, K. The natural food colorant Peonidin from cranberries as a potential radical scavenger—A DFT based mechanistic analysis. Food Chem. 2018, 262, 184–190. [Google Scholar] [CrossRef] [PubMed]
- Duque, L.; Guerrero, G.; Colorado, J.H.; Restrepo, J.A.; Velez, E. Theoretical Insight into mechanism of antioxidant capacity of atorvastatin and its o-hydroxy and p-hydroxy metabolites, using DFT methods. Comp Theor. Chem. 2022, 1214, 113758. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, J.F.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A Complete Basis Set Model Chemistry. II. Open-Shell Systems and the Total Energies of the First-Row Atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Bâldea, I. Long Carbon-Based Chains of Interstellar Medium Can Have a Triplet Ground State. Why Is This Important for Astrochemistry? ACS Earth Space Chem. 2019, 3, 863–872. [Google Scholar] [CrossRef]
- Bâldea, I. Alternation of Singlet and Triplet States in Carbon-Based Chain Molecules and Its Astrochemical Implications: Results of an Extensive Theoretical Study. Adv. Theor. Simul. 2019, 2, 1900084. [Google Scholar] [CrossRef]
- Bâldea, I. HCnH- Anion Chains with n≤8 are Nonlinear and Their Permanent Dipole Makes Them Potential Candidates for Astronomical Observation. Molecules 2022, 27, 3100. [Google Scholar] [CrossRef]
- Bâldea, I. Comprehensive Quantum Chemical Characterization of the Astrochemically Relevant HCnH Chain Family. An Attempt to Aid Astronomical Observations. Adv. Theor. Simul. 2022, 5, 2200244. [Google Scholar] [CrossRef]
- Burton, G.W.; Doba, T.; Gabe, E.; Hughes, L.; Lee, F.L.; Prasad, L.; Ingold, K.U. Autoxidation of biological molecules. 4. Maximizing the antioxidant activity of phenols. J. Am. Chem. Soc. 1985, 107, 7053–7065. [Google Scholar] [CrossRef]
- de Heer, M.I.; Mulder, P.; Korth, H.G.; Ingold, K.U.; Lusztyk, J. Hydrogen Atom Abstraction Kinetics from Intramolecularly Hydrogen Bonded Ubiquinol-0 and Other (Poly)methoxy Phenols. J. Am. Chem. Soc. 2000, 122, 2355–2360. [Google Scholar] [CrossRef]
- Mayer, I.; Salvador, P. Overlap populations, bond orders and valences for “fuzzy” atoms. Chem. Phys. Lett. 2004, 383, 368–375. [Google Scholar] [CrossRef]
- Jovanovic, S.V.; Steenken, S.; Tosic, M.; Marjanovic, B.; Simic, M.G. Flavonoids as Antioxidants. J. Am. Chem. Soc. 1994, 116, 4846–4851. [Google Scholar] [CrossRef]
- Jovanovic, S.V.; Steenken, S.; Hara, Y.; Simic, M.G. Reduction potentials of flavonoid and model phenoxyl radicals. Which ring in flavonoids is responsible for antioxidant activity? J. Chem. Soc. Perkin Trans. 2 1996, 11, 2497–2504. [Google Scholar] [CrossRef]
- Litwinienko, G.; Ingold, K.U. Abnormal Solvent Effects on Hydrogen Atom Abstractions. 1. The Reactions of Phenols with 2,2-Diphenyl-1-picrylhydrazyl (DPPH•) in Alcohols. J. Org. Chem. 2003, 68, 3433–3438. [Google Scholar] [CrossRef]
- Litwinienko, G.; Ingold, K.U. Abnormal Solvent Effects on Hydrogen Atom Abstraction. 2. Resolution of the Curcumin Antioxidant Controversy. The Role of Sequential Proton Loss Electron Transfer. J. Org. Chem. 2004, 69, 5888–5896. [Google Scholar] [CrossRef]
- Bâldea, I. Single-Molecule Junctions Based on Bipyridine: Impact of an Unusual Reorganization on the Charge Transport. J. Phys. Chem. C 2014, 118, 8676–8684. [Google Scholar] [CrossRef]
- Bâldea, I. A Quantum Chemical Study from a Molecular Transport Perspective: Ionization and Electron Attachment Energies for Species Often Used to Fabricate Single-Molecule Junctions. Faraday Discuss. 2014, 174, 37–56. [Google Scholar] [CrossRef]
- Bâldea, I. Critical analysis of radical scavenging properties of atorvastatin in methanol recently estimated via density functional theory. Comput. Theor. Chem. 2022, 1217, 113898. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Clarendon; Oxford University Press: Oxford, UK, 1989; p. 149. [Google Scholar]
- Jones, R.O.; Gunnarsson, O. The Density Functional Formalism, Its Applications and Prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Bâldea, I. Extending the Newns-Anderson Model to Allow Nanotransport Studies Through Molecules with Floppy Degrees of Freedom. Europhys. Lett. 2012, 99, 47002. [Google Scholar] [CrossRef]
- Bâldea, I.; Köppel, H.; Wenzel, W. (4,4′)-Bipyridine in Vacuo and in Solvents: A Quantum Chemical Study of a Prototypical Floppy Molecule From a Molecular Transport Perspective. Phys. Chem. Chem. Phys. 2013, 15, 1918–1928. [Google Scholar] [CrossRef]
- Bâldea, I. Demonstrating Why DFT-Calculations For Molecular Transport in Solvents Need Scissor Corrections. Electrochem. Commun. 2013, 36, 19–21. [Google Scholar] [CrossRef]
- Rimarcik, J.; Lukes, V.; Klein, E.; Ilcin, M. Study of the solvent effect on the enthalpies of homolytic and heterolytic N-H bond cleavage in p-phenylenediamine and tetracyano-p-phenylenediamine. J. Mol. Struct. THEOCHEM 2010, 952, 25–30. [Google Scholar] [CrossRef]
- Markovic, Z.; Tosovic, J.; Milenkovic, D.; Markovic, S. Revisiting the solvation enthalpies and free energies of the proton and electron in various solvents. Comput. Theor. Chem. 2016, 1077, 11–17. [Google Scholar] [CrossRef]
- Allouche, A.R. Gabedit: A Graphical User Interface For Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).