A Simplified Treatment for Efficiently Modeling the Spectral Signal of Vibronic Transitions: Application to Aqueous Indole
Abstract
1. Introduction
2. Theory
2.1. The Perturbed Vibronic Eigenstate
2.2. The Excitation and Emission Modeling
2.3. A Simplified Efficient Strategy to Evaluate the Vibrational Overlap
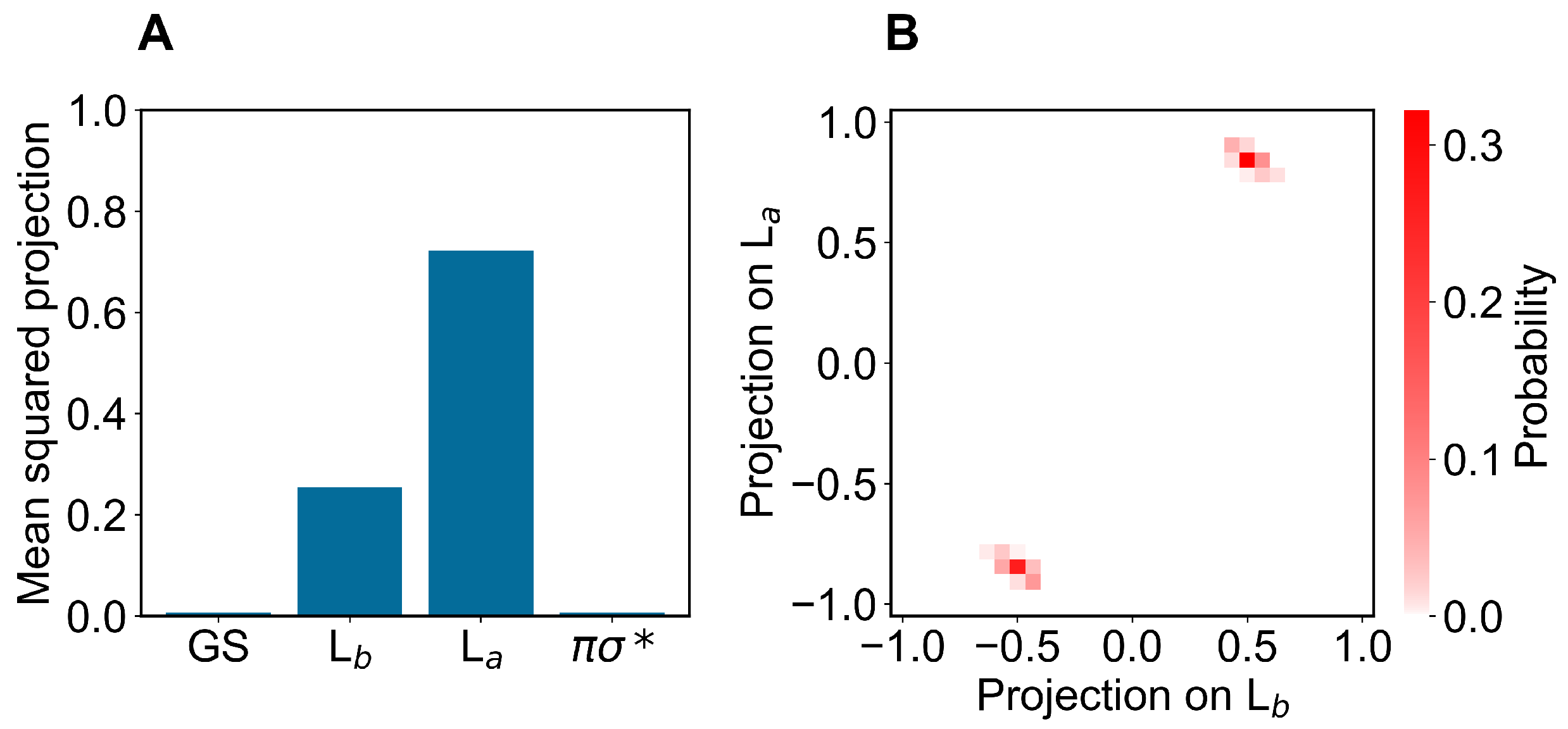
3. Application to Aqueous Indole
3.1. Computational Details
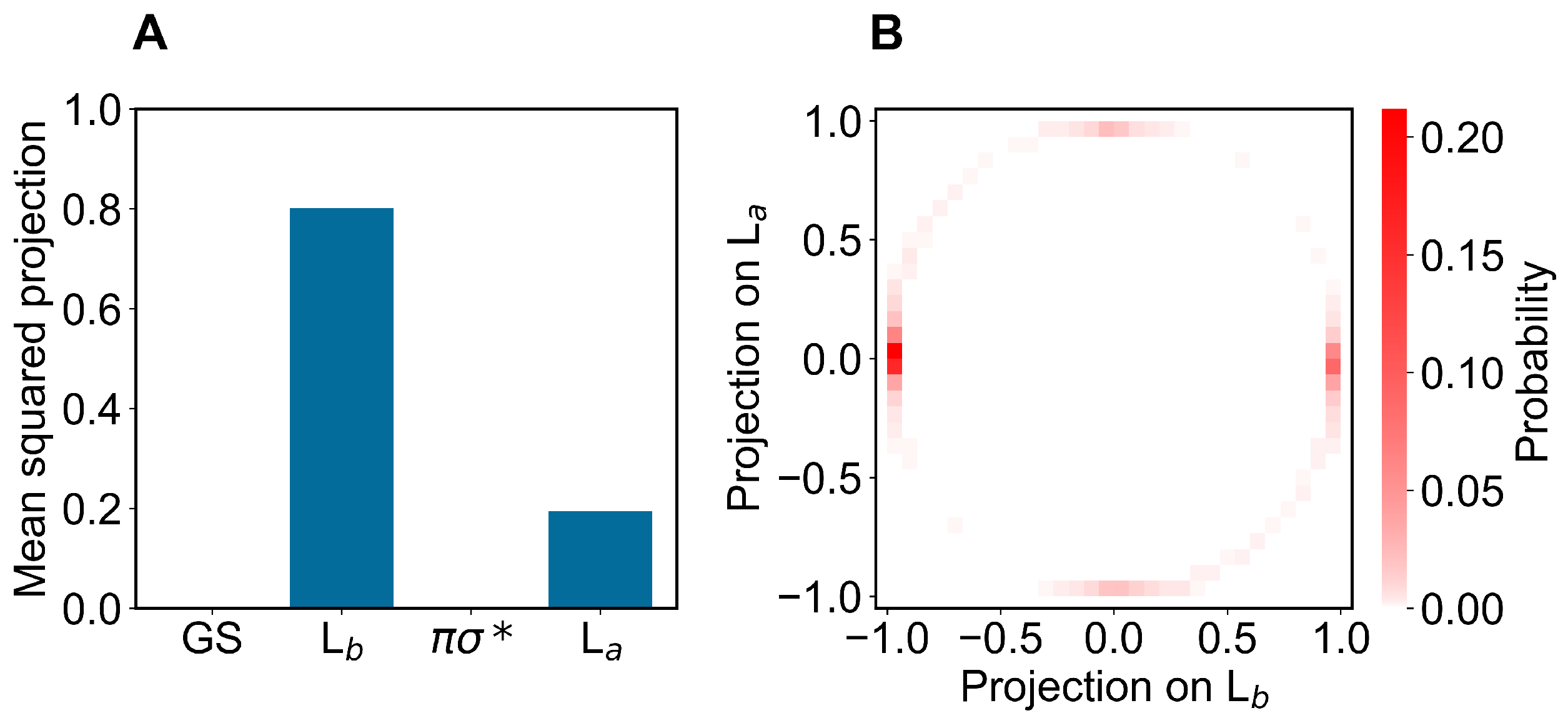
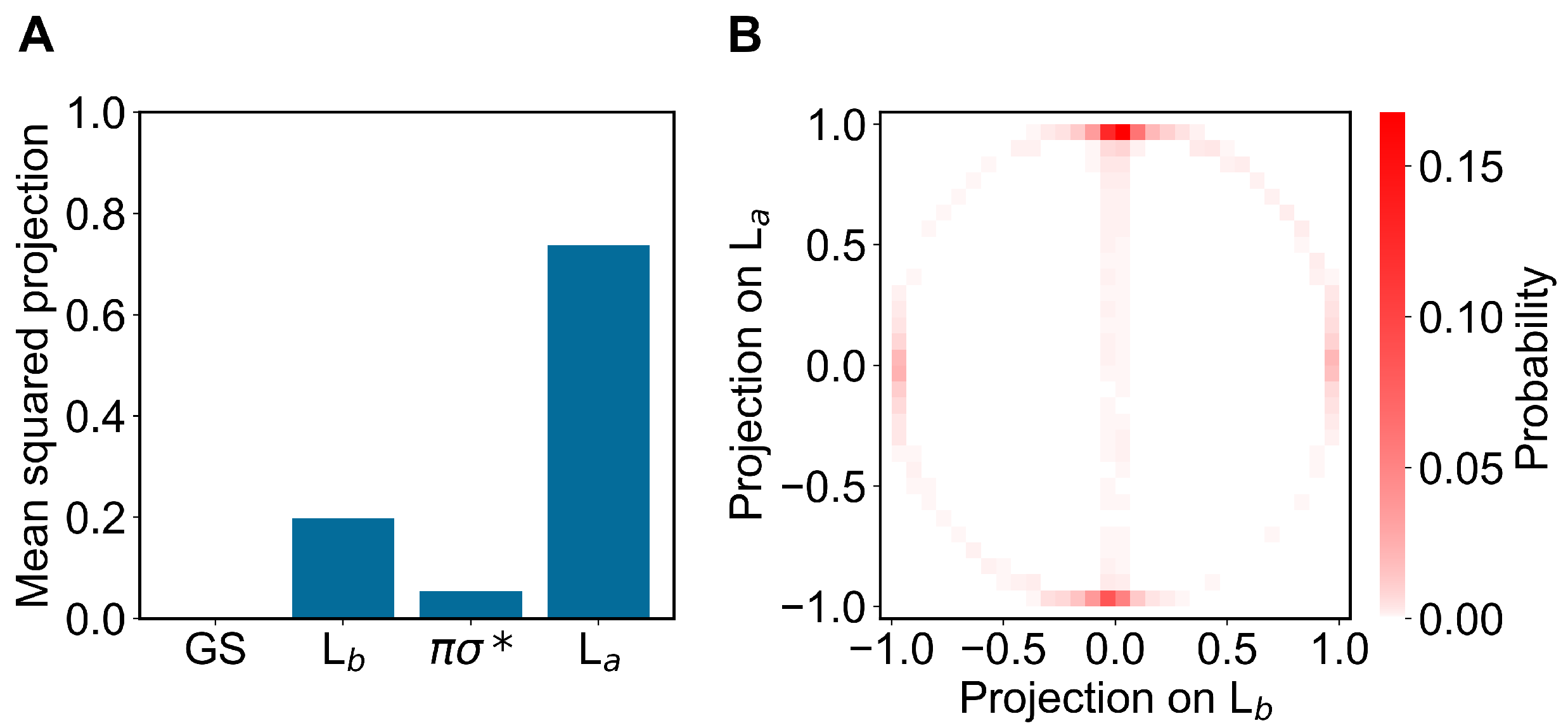
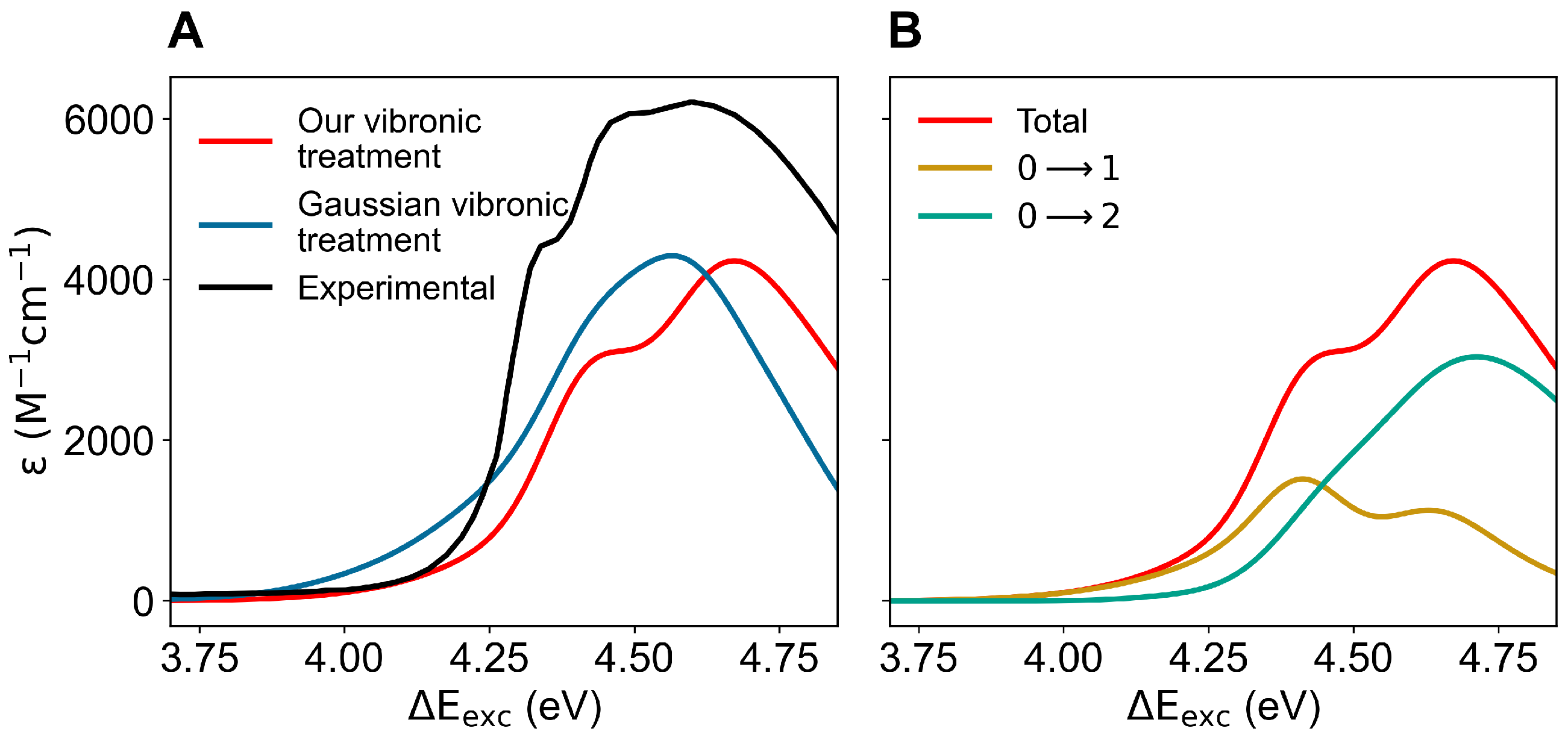
3.2. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Eftink, M. Fluorescence techniques for studying protein structure. Methods Biochem. Anal. 1991, 35, 127–205. [Google Scholar] [PubMed]
- Beechem, J.; Brand, L. Time-resolved fluorescence of proteins. Annu. Rev. Biochem. 1985, 54, 43–71. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kister, A.E. Protein Supersecondary Structures, 2nd ed.; Humana: New York, NY, USA, 2019. [Google Scholar]
- Burstein, E.; Vedenkina, N.; Ivkova, M. Fluorescence and the location of tryptophan residues in protein molecules. Photochem. Photobiol. 1973, 18, 263–279. [Google Scholar] [CrossRef] [PubMed]
- Reshetnyak, Y.K.; Burstein, E.A. Decomposition of Protein Tryptophan Fluorescence Spectra into Log-Normal Components. II. The Statistical Proof of Discreteness of Tryptophan Classes in Proteins. Biophys. J. 2001, 81, 1710–1734. [Google Scholar] [CrossRef] [PubMed]
- Callis, P.R.; Vivian, J.T.; Slater, L.S. Ab initio calculations of vibronic spectra for indole. Chem. Phys. Lett. 1995, 244, 53–58. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Roos, B.O. Theoretical Study of the Absorption and Emission Spectra of Indole in the Gas Phase and in a Solvent. J. Am. Chem. Soc. 1996, 118, 185–195. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Borin, A.C. A theoretical study of the emission spectra of indole and its analogs: Indene, benzimidazole, and 7-azaindole. Chem. Phys. 2000, 262, 267–283. [Google Scholar] [CrossRef]
- Brand, C.; Küpper, J.; Pratt, D.W.; Meerts, W.L.; Krügler, D.; Tatchen, J.; Schmitt, M. Vibronic coupling in indole: I. Theoretical description of the 1La–1Lb interaction and the electronic spectrum. Phys. Chem. Chem. Phys. 2010, 12, 4968–4979. [Google Scholar] [CrossRef]
- Giussani, A.; Merchán, M.; Roca-Sanjuán, D.; Lindh, R. Essential on the Photophysics and Photochemistry of the Indole Chromophore by Using a Totally Unconstrained Theoretical Approach. J. Chem. Theory Comput. 2011, 7, 4088–4096. [Google Scholar] [CrossRef]
- Arulmozhiraja, S.; Coote, M.L. 1L a and 1L b states of indole and azaindole: Is density functional theory inadequate? J. Chem. Theory Comput. 2012, 8, 575–584. [Google Scholar] [CrossRef] [PubMed]
- Brisker-Klaiman, D.; Dreuw, A. Explaining Level Inversion of the La and Lb States of Indole and Indole Derivatives in Polar Solvents. ChemPhysChem 2015, 16, 1695–1702. [Google Scholar] [CrossRef] [PubMed]
- Abou-Hatab, S.; Matsika, S. Theoretical Investigation of Positional Substitution and Solvent Effects on n-Cyanoindole Fluorescent Probes. J. Phys. Chem. B 2019, 123, 7424–7435. [Google Scholar] [CrossRef] [PubMed]
- Manian, A.; Shaw, R.A.; Lyskov, I.; Russo, S.P. The quantum chemical solvation of indole: Accounting for strong solute–solvent interactions using implicit/explicit models. Phys. Chem. Chem. Phys. 2022, 24, 3357–3369. [Google Scholar] [CrossRef] [PubMed]
- Santoro, F.; Lami, A.; Improta, R.; Bloino, J.; Barone, V. Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg–Teller effect: The Qx band of porphyrin as a case study. J. Chem. Phys. 2008, 128, 224311. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, J.; Ferrer, F.J.A.; Prampolini, G.; Santoro, F. Adiabatic-Molecular Dynamics Generalized Vertical Hessian Approach: A Mixed Quantum Classical Method To Compute Electronic Spectra of Flexible Molecules in the Condensed Phase. J. Chem. Theory Comput. 2020, 16, 1215–1231. [Google Scholar] [CrossRef] [PubMed]
- Mennucci, B.; Cappelli, C.; Guido, C.A.; Cammi, R.; Tomasi, J. Structures and Properties of Electronically Excited Chromophores in Solution from the Polarizable Continuum Model Coupled to the Time-Dependent Density Functional Theory. J. Phys. Chem. A 2009, 113, 3009–3020. [Google Scholar] [CrossRef]
- Marenich, A.; Cramer, C.J.; Truhlar, D.G. Electronic Absorption Spectra and Solvatochromic Shifts by the Vertical Excitation Model: Solvated Clusters and Molecular Dynamics Sampling. J. Phys. Chem. B 2015, 119, 958–967. [Google Scholar] [CrossRef]
- Zuehlsdorff, T.J.; Isborn, C.M. Modeling absorption spectra of molecules in solution. Int. J. Quant. Chem. 2019, 119, 25719. [Google Scholar] [CrossRef]
- Eilmes, A. Effect of Molecular Vibrations on the MD/QC-Simulated Absorption Spectra. Int. J. Quantum Chem. 2014, 114, 261–270. [Google Scholar] [CrossRef]
- Law, K.K.; Hassanali, A.A. The importance of nuclear quantum effects in spectral line broadening of optical spectra and electrostatic properties in aromatic chromophores. J. Chem. Phys. 2018, 148, 102331. [Google Scholar] [CrossRef]
- D’Abramo, M.; Aschi, M.; Amadei, A. Theoretical modeling of UV-Vis absorption and emission spectra in liquid state systems including vibrational and conformational effects: Explicit treatment of the vibronic transitions. J. Chem. Phys. 2014, 140, 164104. [Google Scholar] [CrossRef] [PubMed]
- Aschi, M.; Spezia, R.; Di Nola, A.; Amadei, A. A first-principles method to model perturbed electronic wavefunctions: The effect of an external homogeneous electric field. Chem. Phys. Lett. 2001, 344, 374–380. [Google Scholar] [CrossRef]
- Amadei, A.; D’Alessandro, M.; D’Abramo, M.; Aschi, M. Theoretical characterization of electronic states in interacting chemical systems. J. Chem. Phys. 2009, 130, 084109. [Google Scholar] [CrossRef] [PubMed]
- Zanetti-Polzi, L.; Del Galdo, S.; Daidone, I.; D’Abramo, M.; Barone, V.; Aschi, M.; Amadei, A. Extending the perturbed matrix method beyond the dipolar approximation: Comparison of different levels of theory. Phys. Chem. Chem. Phys. 2018, 20, 24369–24378. [Google Scholar] [CrossRef] [PubMed]
- D’Alessandro, M.; Aschi, M.; Mazzuca, C.; Palleschi, A.; Amadei, A. Theoretical modeling of UV-Vis absorption and emission spectra in liquid state systems including vibrational and conformational effects: The vertical transition approximation. J. Chem. Phys. 2013, 139, 114102. [Google Scholar] [CrossRef] [PubMed]
- Daidone, I.; Aschi, M.; Zanetti-Polzi, L.; Di Nola, A.; Amadei, A. On the origin of IR spectral changes upon protein folding. Chem. Phys. Lett. 2010, 488, 213–218. [Google Scholar] [CrossRef]
- Amadei, A.; Daidone, I.; Zanetti-Polzi, L.; Aschi, M. Modeling quantum vibrational excitations in condensed-phase molecular systems. Theor. Chem. Acc. 2011, 129, 31–43. [Google Scholar] [CrossRef]
- Chen, C.G.; Nardi, A.N.; Giustini, M.; D’Abramo, M. Absorption behavior of doxorubicin hydrochloride in visible region in different environments: A combined experimental and computational study. Phys. Chem. Chem. Phys. 2022, 24, 12027–12035. [Google Scholar] [CrossRef]
- Amadei, A.; Daidone, I.; Aschi, M. A general theoretical model for electron transfer reactions in complex systems. Phys. Chem. Chem. Phys. 2012, 14, 1360–1370. [Google Scholar] [CrossRef] [PubMed]
- Aschi, M.; D’Abramo, M.; Amadei, A. Photoinduced electron transfer in a dichromophoric peptide: A numerical experiment. Theor. Chem. Acc. 2016, 135, 132. [Google Scholar] [CrossRef]
- Piacente, G.; Amadei, A.; D’Abramo, M.; Daidone, I.; Aschi, M. Theoretical-computational modeling of photo-induced charge separation spectra and charge recombination kinetics in solution. Phys. Chem. Chem. Phys. 2014, 16, 20624–20638. [Google Scholar] [CrossRef]
- Zanetti-Polzi, L.; Aschi, M.; Amadei, A.; Daidone, I. Alternative Electron-Transfer Channels Ensure Ultrafast Deactivation of Light-Induced Excited States in Riboflavin Binding Protein. J. Phys. Chem. Lett. 2017, 8, 3321–3327. [Google Scholar] [CrossRef] [PubMed]
- Aschi, M.; Barone, V.; Carlotti, B.; Daidone, I.; Elisei, F.; Amadei, A. Photoexcitation and relaxation kinetics of molecular systems in solution: Towards a complete in silico model. Phys. Chem. Chem. Phys. 2016, 18, 28919–28931. [Google Scholar] [CrossRef] [PubMed]
- Del Galdo, S.; Aschi, M.; Amadei, A. IR spectroscopy of condensed phase systems: Can the environment induce vibrational mode coupling? Chem. Phys. Lett. 2021, 763, 138168. [Google Scholar] [CrossRef]
- Barone, V.; Bloino, J.; Biczysko, M.; Santoro, F. Fully Integrated Approach to Compute Vibrationally Resolved Optical Spectra: From Small Molecules to Macrosystems. J. Chem. Theory Comput. 2009, 5, 540–554. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Chem. Phys. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Del Galdo, S.; Marracino, P.; D’Abramo, M.; Amadei, A. In silico characterization of protein partial molecular volumes and hydration shells. Phys. Chem. Chem. Phys. 2015, 17, 31270–31277. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comp. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ψ, ϕ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comp. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M., Jr.; Kollman, P.A. Atomic charges derived from semiempirical methods. J. Comp. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1-2, 19–25. [Google Scholar] [CrossRef]
- Hilaire, M.R.; Mukherjee, D.; Troxler, T.; Gai, F. Solvent dependence of cyanoindole fluorescence lifetime. Chem. Phys. Lett. 2017, 685, 133–138. [Google Scholar] [CrossRef] [PubMed]
- Gallavotti, G. Elements of Mechanics; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.G.; Aschi, M.; D’Abramo, M.; Amadei, A. A Simplified Treatment for Efficiently Modeling the Spectral Signal of Vibronic Transitions: Application to Aqueous Indole. Molecules 2022, 27, 8135. https://doi.org/10.3390/molecules27238135
Chen CG, Aschi M, D’Abramo M, Amadei A. A Simplified Treatment for Efficiently Modeling the Spectral Signal of Vibronic Transitions: Application to Aqueous Indole. Molecules. 2022; 27(23):8135. https://doi.org/10.3390/molecules27238135
Chicago/Turabian StyleChen, Cheng Giuseppe, Massimiliano Aschi, Marco D’Abramo, and Andrea Amadei. 2022. "A Simplified Treatment for Efficiently Modeling the Spectral Signal of Vibronic Transitions: Application to Aqueous Indole" Molecules 27, no. 23: 8135. https://doi.org/10.3390/molecules27238135
APA StyleChen, C. G., Aschi, M., D’Abramo, M., & Amadei, A. (2022). A Simplified Treatment for Efficiently Modeling the Spectral Signal of Vibronic Transitions: Application to Aqueous Indole. Molecules, 27(23), 8135. https://doi.org/10.3390/molecules27238135





