Phase Transitions and Stabilities among Three Phases of Di-p-tolyl Disulfides
Abstract
:1. Introduction
2. Results and Discussion
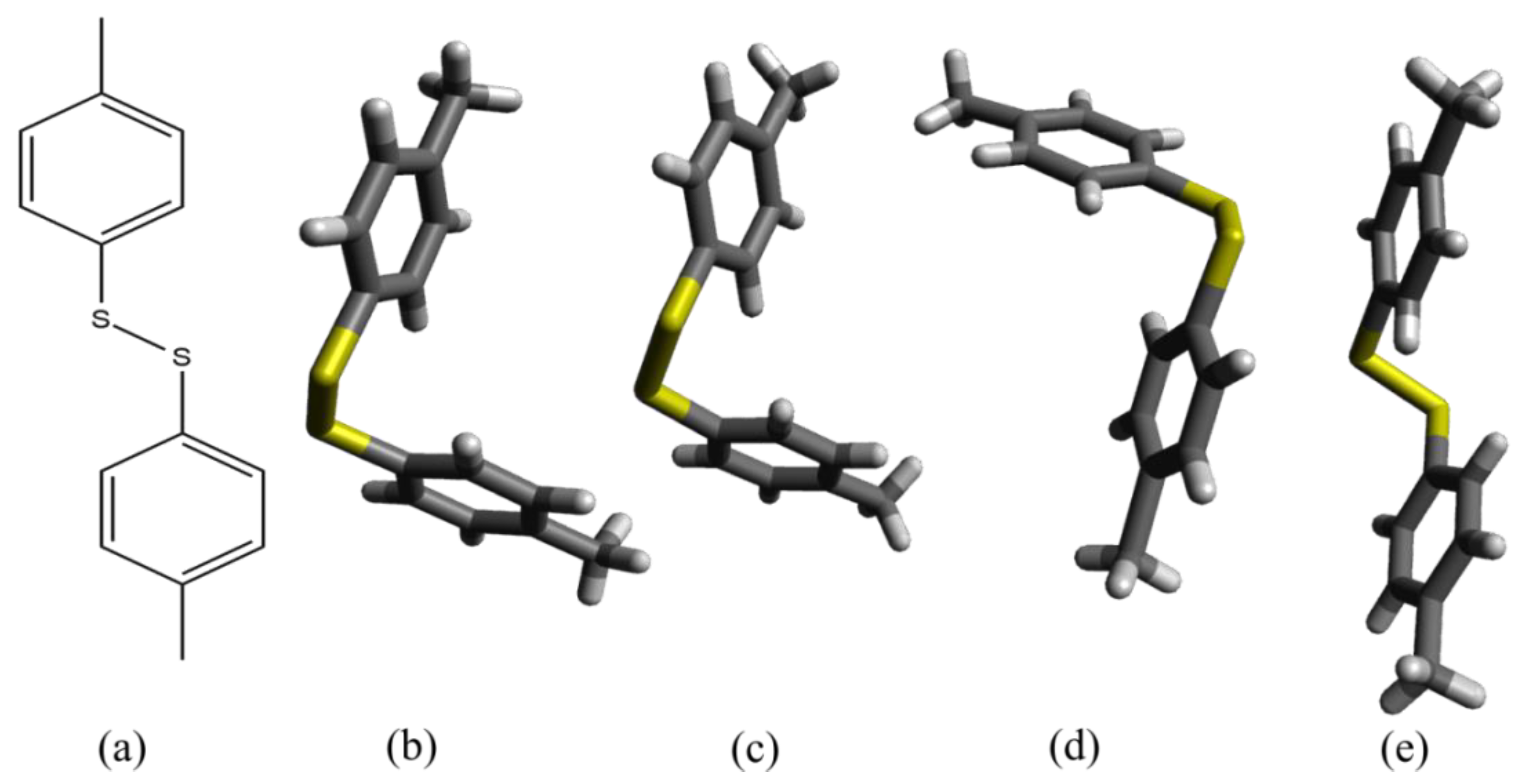
2.1. Crystal Structure Prediction
2.2. Pressure Dependence Volume
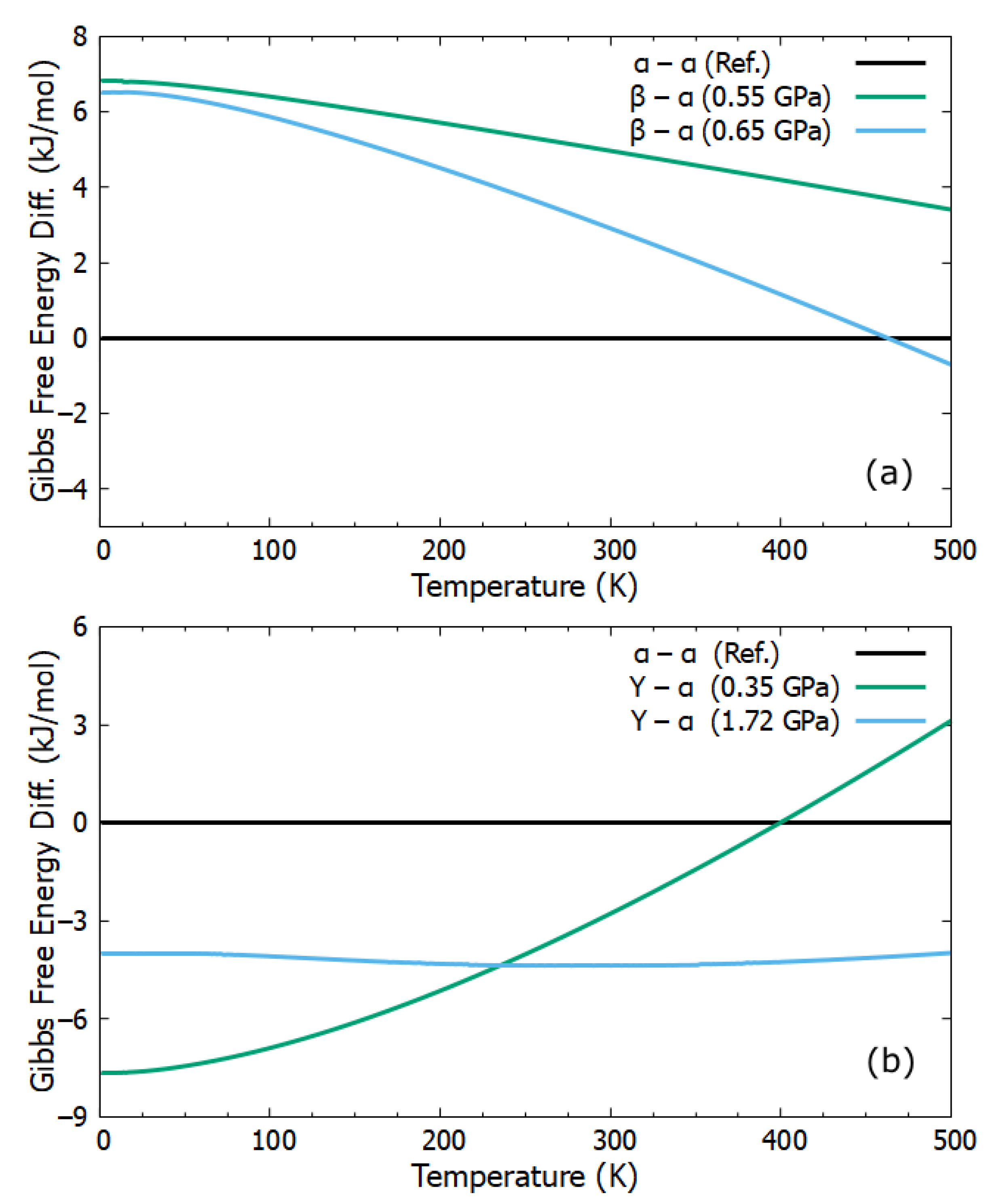
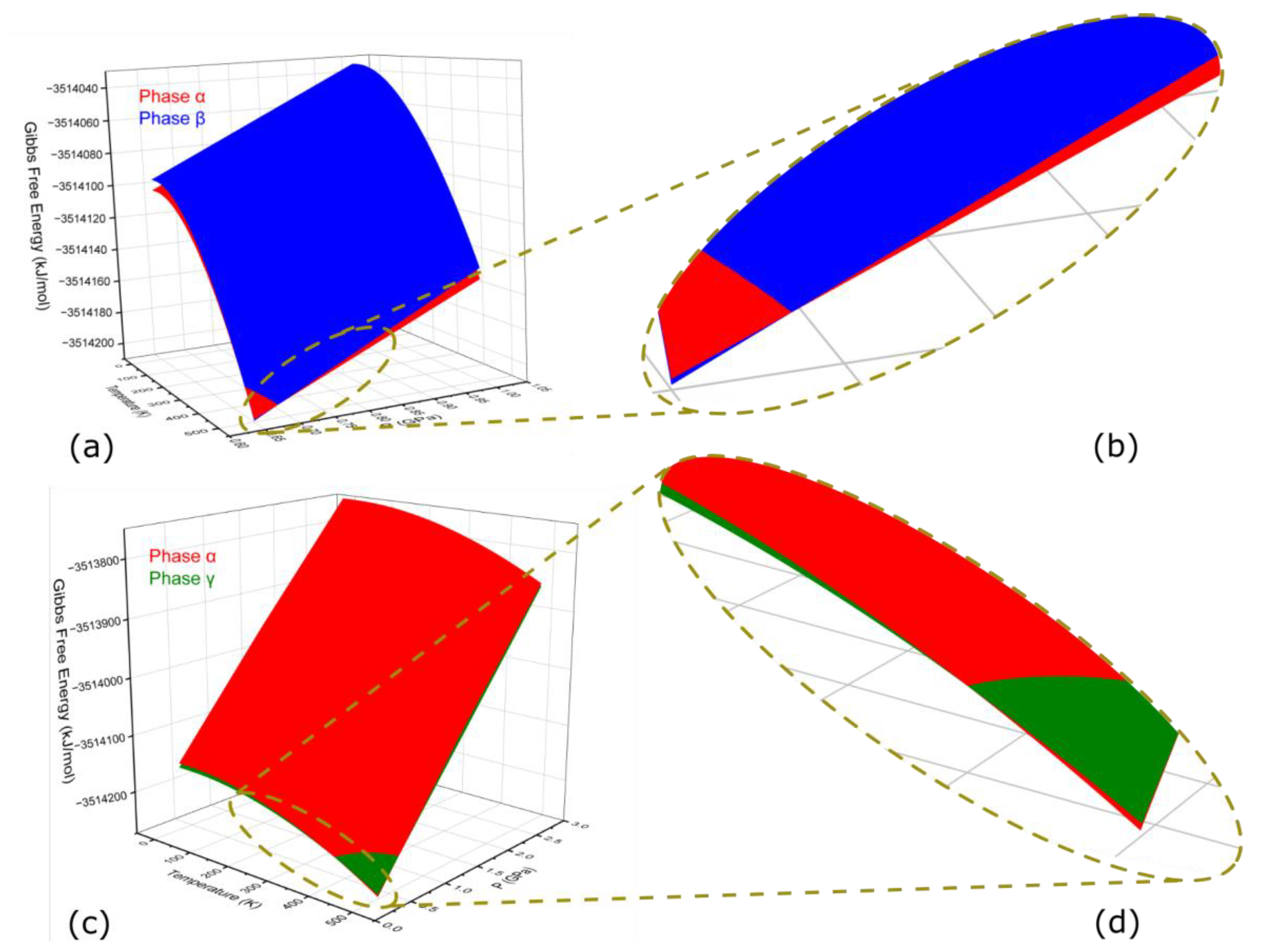
2.3. Gibbs Free Energy Difference
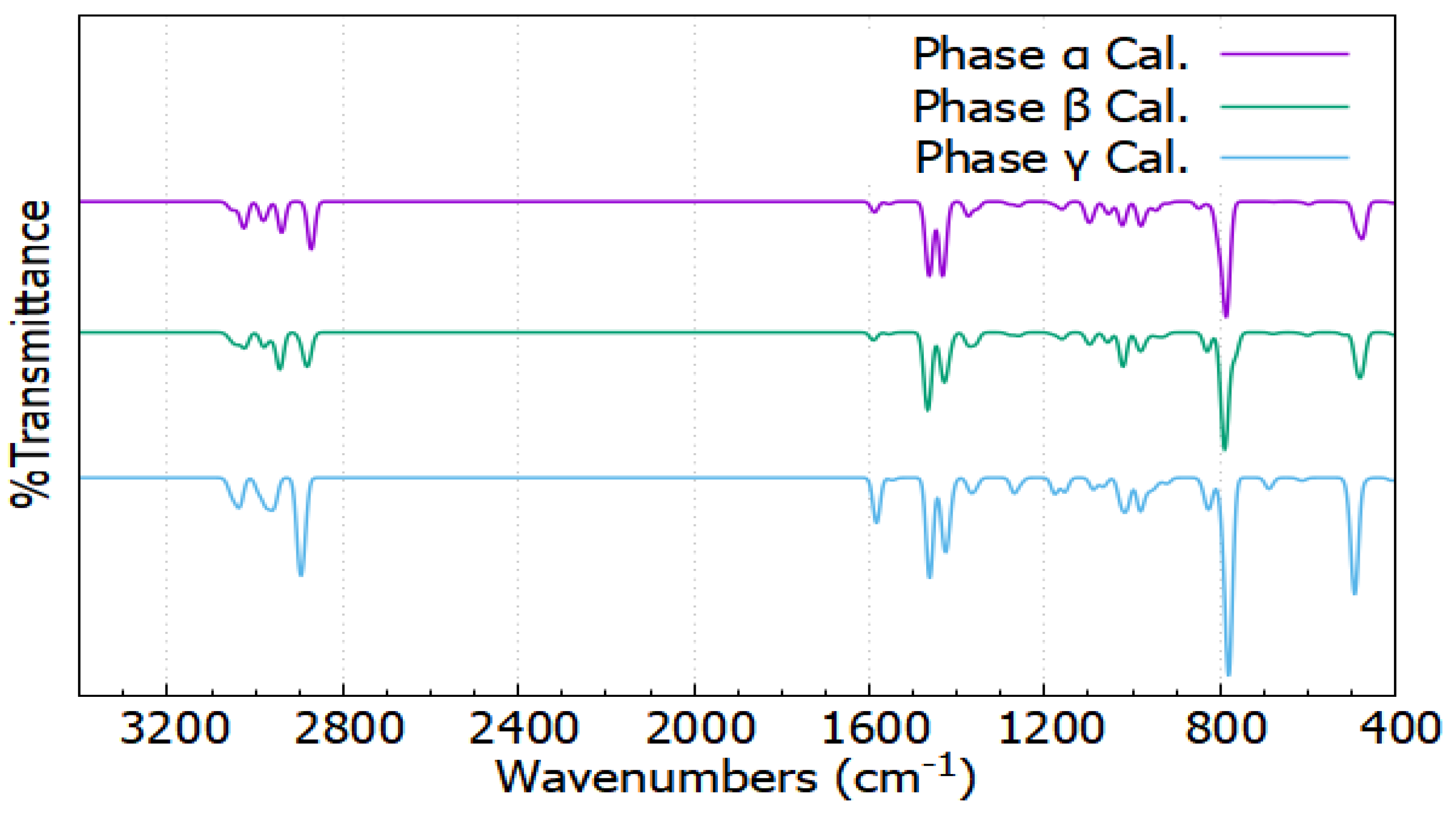
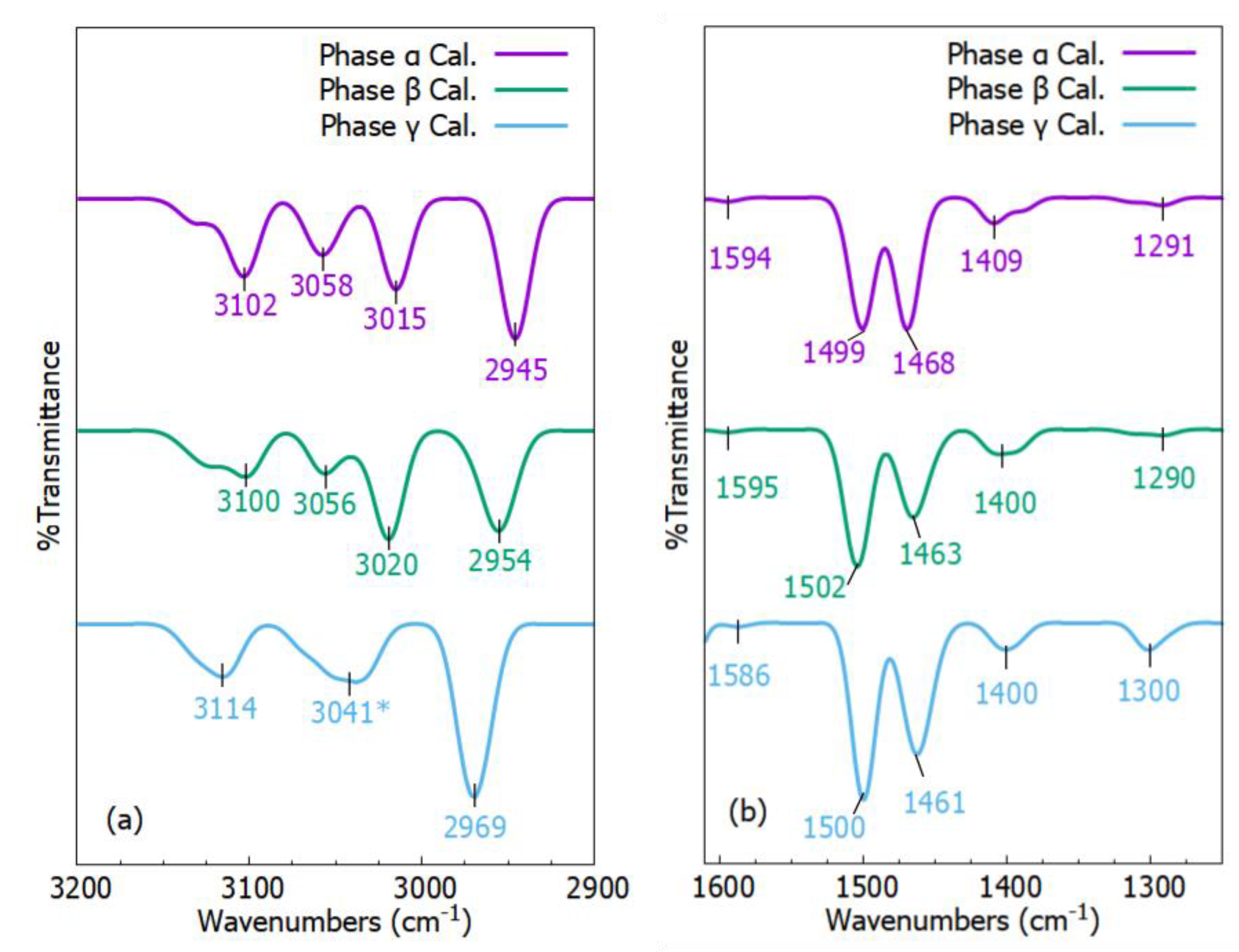
2.4. Vibrational Spectra
FT–IR Spectra
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Phase | P (GPa) | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | V (Å3) |
|---|---|---|---|---|---|---|---|---|
| α | Exp. atm | 7.593 | 5.713 | 14.722 | 90.00 | 94.76 | 90.00 | 636.417 |
| Cal. atm | 7.348 | 5.633 | 14.498 | 90.00 | 94.76 | 90.00 | 598.021 | |
| 0.25 | 7.212 | 5.59 | 14.411 | 90.00 | 94.76 | 90.00 | 578.977 | |
| 0.45 | 7.164 | 5.566 | 14.36 | 90.00 | 94.76 | 90.00 | 570.628 | |
| 0.65 | 7.081 | 5.565 | 14.253 | 90.00 | 94.76 | 90.00 | 559.713 | |
| 1 | 6.999 | 5.540 | 14.170 | 90.00 | 94.76 | 90.00 | 547.539 | |
| 1.52 | 6.950 | 5.493 | 14.147 | 90.00 | 94.76 | 90.00 | 538.218 | |
| 1.72 | 6.862 | 5.496 | 14.078 | 90.00 | 94.76 | 90.00 | 1355.29 | |
| 2.8 | 6.66 | 5.447 | 13.895 | 90.00 | 94.76 | 90.00 | 502.331 | |
| 4.5 | 6.488 | 5.368 | 13.644 | 90.00 | 94.76 | 90.00 | 473.549 | |
| 5.5 | 6.323 | 5.411 | 13.441 | 90.00 | 94.76 | 90.00 | 458.281 | |
| β | Exp. atm | 7.306 | 5.5093 | 14.0380 | 95.14 | 97.23 | 85.36 | 556.886 |
| Cal. atm | 7.541 | 5.662 | 14.245 | 95.14 | 97.23 | 85.36 | 599.465 | |
| 0.25 | 7.467 | 5.630 | 14.188 | 95.14 | 97.23 | 85.36 | 587.867 | |
| 0.45 | 7.421 | 5.600 | 14.146 | 95.14 | 97.23 | 85.36 | 579.411 | |
| 0.65 | 7.374 | 5.573 | 14.107 | 95.14 | 97.23 | 85.36 | 571.386 | |
| 1 | 7.310 | 5.534 | 14.052 | 95.14 | 97.23 | 85.36 | 560.270 | |
| 1.52 | 7.226 | 5.494 | 13.978 | 95.14 | 97.23 | 85.36 | 546.933 | |
| 1.72 | 7.198 | 5.479 | 13.953 | 95.14 | 97.23 | 85.36 | 542.355 | |
| 2.8 | 7.004 | 5.419 | 13.820 | 95.14 | 97.23 | 85.36 | 516.983 | |
| 4.5 | 6.757 | 5.403 | 13.641 | 95.14 | 97.23 | 85.36 | 490.837 | |
| 5.5 | 6.464 | 5.482 | 13.445 | 95.14 | 97.23 | 85.36 | 469.574 | |
| γ | Exp. atm | 15.260 | 5.962 | 14.615 | 90 | 115.56 | 90 | 599.75 |
| Cal. atm | 15.155 | 5.923 | 14.661 | 90 | 115.56 | 90 | 593.612 | |
| 0.25 | 15.117 | 5.888 | 14.619 | 90 | 115.56 | 90 | 586.938 | |
| 0.45 | 14.998 | 5.833 | 14.590 | 90 | 115.56 | 90 | 575.734 | |
| 1.52 | 14.787 | 5.714 | 14.390 | 90 | 115.56 | 90 | 548.432 | |
| 1.72 | 14.744 | 5.691 | 14.348 | 90 | 115.56 | 90 | 543.046 | |
| 2.8 | 14.475 | 5.639 | 14.172 | 90 | 115.56 | 90 | 521.787 |
References
- Forbes, E.S. The Load-Carrying Action of Organo-Sulphur Compounds—A Review. Wear 1970, 15, 87–96. [Google Scholar] [CrossRef]
- Koval’, I.V. Sulfides in Organic Synthesis. Application of Sulfides. Russ. Chem. Rev. 1994, 63, 147–168. [Google Scholar] [CrossRef]
- Adams, D.J.; Clark, J.H. Preparation of Trifluoromethyl Aryl Sulfides Using Silver(I) Trifluoromethanethiolate and an Inorganic Iodide. J. Org. Chem. 2000, 65, 1456–1460. [Google Scholar] [CrossRef]
- Khawula, T.N.Y.; Raju, K.; Franklyn, P.J.; Sigalas, I.; Ozoemena, K.I. Symmetric Pseudocapacitors Based on Molybdenum Disulfide (MoS2)-Modified Carbon Nanospheres: Correlating Physicochemistry and Synergistic Interaction on Energy Storage. J. Mater. Chem. A 2016, 4, 6411–6425. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Shao, Y.; Jiang, P.; Zhang, Q.; Hou, C.; Li, Y.; Wang, H. 1T-Molybdenum Disulfide/Reduced Graphene Oxide Hybrid Fibers as High Strength Fibrous Electrodes for Wearable Energy Storage. J. Mater. Chem. A 2019, 7, 3143–3149. [Google Scholar] [CrossRef]
- Yoo, H.D.; Li, Y.; Liang, Y.; Lan, Y.; Wang, F.; Yao, Y. Intercalation Pseudocapacitance of Exfoliated Molybdenum Disulfide for Ultrafast Energy Storage. Chem. Nano Mat. 2016, 2, 688–691. [Google Scholar] [CrossRef]
- Lei, W.; Xiao, J.-L.; Liu, H.-P.; Jia, Q.-L.; Zhang, H.-J. Tungsten Disulfide: Synthesis and Applications in Electrochemical Energy Storage and Conversion. Tungsten 2020, 2, 217–239. [Google Scholar] [CrossRef]
- Fan, Q.; Si, Y.; Guo, W.; Fu, Y. Insight into Chemical Reduction and Charge Storage Mechanism of 2,2′-Dipyridyl Disulfide toward Stable Lithium–Organic Battery. J. Phys. Chem. Lett. 2021, 12, 900–906. [Google Scholar] [CrossRef]
- Chu, TL and Chu, Shirley S and Schultz, N and Wang, C and Wu, CQ Solution-Grown Cadmium Sulfide Films for Photovoltaic Devices. J. Electrochem. Soc. 1992, 139, 2443. [CrossRef]
- Veerathangam, K.; Pandian, M.S.; Ramasamy, P. Size-Dependent Photovoltaic Performance of Cadmium Sulfide (CdS) Quantum Dots for Solar Cell Applications. J. Alloys Compd. 2018, 735, 202–208. [Google Scholar] [CrossRef]
- Barman, B.; Bangera, K.V.; Shivakumar, G.K. Effect of Substrate Temperature on the Suitability of Thermally Deposited Cadmium Sulfide Thin Films as Window Layer in Photovoltaic Cells. Superlattices Microstruct. 2018, 123, 374–381. [Google Scholar] [CrossRef]
- Mughal, M.A.; Sharma, R. Cadmium Sulfide-Buffered PV Systems: Assessing the Environmental, Health, and Economic Impacts. Ark. Acad. Sci. 2019, 73, 106–118. [Google Scholar] [CrossRef]
- Whittingham, M.S. Chemistry of Intercalation Compounds: Metal Guests in Chalcogenide Hosts. Prog. Solid State Chem. 1978, 12, 41–99. [Google Scholar] [CrossRef]
- Nazar, L.F.; Cuisinier, M.; Pang, Q. Lithium-Sulfur Batteries. MRS Bull. 2014, 39, 436–442. [Google Scholar] [CrossRef] [Green Version]
- Zuo, J.-H.; Gong, Y.-J. Applications of Transition-Metal Sulfides in the Cathodes of Lithium–Sulfur Batteries. Tungsten 2020, 2, 134–146. [Google Scholar] [CrossRef]
- Chen, H.; Li, W.; Liu, H.; Zhu, L. A Suitable Deposition Method of CdS for High Performance CdS-Sensitized ZnO Electrodes: Sequential Chemical Bath Deposition. Sol. Energy 2010, 84, 1201–1207. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, B.; Zhang, J.; Wang, T.; Liu, R.; Zhang, J.; Wang, X.; Wang, H. Synthesis and Photoelectrochemical Response of CdS Quantum Dot-Sensitized TiO2 Nanorod Array Photoelectrodes. Nanoscale Res. Lett. 2013, 8, 222. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Xie, Y.; Ali, G.; Yoo, S.H.; Cho, S.O. Improved Conversion Efficiency of Ag2S Quantum Dot-Sensitized Solar Cells Based on TiO2 Nanotubes with a ZnO Recombination Barrier Layer. Nanoscale Res. Lett. 2011, 6, 462. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Ma, Y.; Liu, J.; Mai, Y. Improving the Performance of Solid-State Quantum Dot-Sensitized Solar Cells Based on TiO 2 /CuInS 2 Photoelectrodes with Annealing Treatment. RSC Adv. 2016, 6, 92869–92873. [Google Scholar] [CrossRef]
- Mali, S.S.; Desai, S.K.; Kalagi, S.S.; Betty, C.A.; Bhosale, P.N.; Devan, R.S.; Ma, Y.-R.R.; Patil, P.S. PbS Quantum Dot Sensitized Anatase TiO2 Nanocorals for Quantum Dot-Sensitized Solar Cell Applications. Dalton Trans. 2012, 41, 6130. [Google Scholar] [CrossRef]
- Yoon, W.; Boercker, J.E.; Lumb, M.P.; Placencia, D.; Foos, E.E.; Tischler, J.G. Enhanced Open-Circuit Voltage of PbS Nanocrystal Quantum Dot Solar Cells. Sci. Rep. 2013, 3, 2225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, M.; Zuo, X.; Ma, X.; Xiao, X.; Yu, L.; Nan, J. Diphenyl Disulfide as a New Bifunctional Film-Forming Additive for High-Voltage LiCoO2/Graphite Battery Charged to 4.4 V. J. Power Sources 2016, 323, 29–36. [Google Scholar] [CrossRef]
- Zuo, X.; Zhao, M.; Ma, X.; Xiao, X.; Liu, J.; Nan, J. Effect of Diphenyl Disulfide as an Additive on the Electrochemical Performance of Li1.2Mn0.54Ni0.13Co0.13O2/Graphite Batteries at Elevated Temperature. Electrochim. Acta 2017, 245, 705–714. [Google Scholar] [CrossRef]
- Allum, K.G.; Forbes, E.S. The Load-Carrying Properties of Organic Sulphur Compounds, Part II, The Influence of Chemical Structure on the Antiwear Properties of Organic Disulphides. J. Inst. Pet 1967, 53, 174. [Google Scholar]
- Sobczak, S.; Katrusiak, A. Colossal Strain Release by Conformational Energy Up-Conversion in a Compressed Molecular Crystal. J. Phys. Chem. C 2017, 121, 2539–2545. [Google Scholar] [CrossRef]
- Shakhtshneider, T.P.; Boldyreva, E.V.; Vasilchenko, M.A.; Ahsbahs, H.; Uchtmann, H. Anisotropy of Crystal Structure Distortion in Organic Molecular Crystals of Drugs Induced by Hydrostatic Compression. J. Struct. Chem. 1999, 40, 892–898. [Google Scholar] [CrossRef]
- Tan, X.; Wang, K.; Li, S.; Yuan, H.; Yan, T.; Liu, J.; Yang, K.; Liu, B.; Zou, G.; Zou, B. Exploration of the Pyrazinamide Polymorphism at High Pressure. J. Phys. Chem. B 2012, 116, 14441–14450. [Google Scholar] [CrossRef]
- Fabbiani, F.P.A.; Buth, G.; Levendis, D.C.; Cruz-Cabeza, A.J. Pharmaceutical Hydrates under Ambient Conditions from High-Pressure Seeds: A Case Study of GABA Monohydrate. Chem. Commun. 2014, 50, 1817–1819. [Google Scholar] [CrossRef] [Green Version]
- Ostrowska, K.; Kropidłowska, M.; Katrusiak, A. High-Pressure Crystallization and Structural Transformations in Compressed R, S -Ibuprofen. Cryst. Growth Des. 2015, 15, 1512–1517. [Google Scholar] [CrossRef]
- Neumann, M.A.; van de Streek, J.; Fabbiani, F.P.A.; Hidber, P.; Grassmann, O. Combined Crystal Structure Prediction and High-Pressure Crystallization in Rational Pharmaceutical Polymorph Screening. Nat. Commun. 2015, 6, 7793. [Google Scholar] [CrossRef] [Green Version]
- Seryotkin, Y.V.; Drebushchak, T.N.; Boldyreva, E.V. A High-Pressure Polymorph of Chlorpropamide Formed on Hydrostatic Compression of the α-Form in Saturated Ethanol Solution. Acta Cryst. B Struct. Sci. Cryst. Eng. Mater. 2013, 69, 77–85. [Google Scholar] [CrossRef]
- Zakharov, B.A.; Goryainov, S.V.; Boldyreva, E.V. Unusual Seeding Effect in the Liquid-Assisted High-Pressure Polymorphism of Chlorpropamide. Cryst. Eng. Comm. 2016, 18, 5423–5428. [Google Scholar] [CrossRef] [Green Version]
- Kreisel, J.; Bouvier, P.; Maglione, M.; Dkhil, B.; Simon, A. High-Pressure Raman Investigation of the Pb-Free Relaxor BaTi0.65Zr0.35O3. Phys. Rev. B 2004, 69, 092104. [Google Scholar] [CrossRef]
- Nowicki, W.; Olejniczak, A.; Andrzejewski, M.; Katrusiak, A. Reverse sequence of transitions in prototypic relaxor 1,4-diazabicyclo[2.2.2]octane. Cryst. Eng. Comm. 2012, 14, 6428. [Google Scholar] [CrossRef]
- Bergantin, S.; Moret, M.; Buth, G.; Fabbiani, F.P.A. Pressure-Induced Conformational Change in Organic Semiconductors: Triggering a Reversible Phase Transition in Rubrene. J. Phys. Chem. C 2014, 118, 13476–13483. [Google Scholar] [CrossRef]
- Li, J.-Y.; Xu, Q.; Li, G.; Yin, Y.-X.; Wan, L.-J.; Guo, Y.-G. Research Progress Regarding Si-Based Anode Materials towards Practical Application in High Energy Density Li-Ion Batteries. Mater. Chem. Front. 2017, 1, 1691–1708. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-Performance Lithium Battery Anodes Using Silicon Nanowires. Nat. Nanotech 2008, 3, 31–35. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lee, J.-K.; Chung, S.-H.; Lee, H.-Y.; Lee, S.-M.; Baik, H.-K. Stress Effect on Cycle Properties of the Silicon Thin-Film Anode. J. Power Sources 2001, 97–98, 191–193. [Google Scholar] [CrossRef]
- Ali, I.; Tippabhotla, S.K.; Radchenko, I.; Al-Obeidi, A.; Stan, C.V.; Tamura, N.; Budiman, A.S. Probing Stress States in Silicon Nanowires During Electrochemical Lithiation Using In Situ Synchrotron X-Ray Microdiffraction. Front. Energy Res. 2018, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Liu, W.; Kim, Y.; Cho, J. Nanostructured Transition Metal Sulfides for Lithium Ion Batteries: Progress and Challenges. Nano Today 2014, 9, 604–630. [Google Scholar] [CrossRef]
- He, X.; Zhu, T.; Wang, X.; Liu, J.; Zhang, J.Z.H. Fragment Quantum Mechanical Calculation of Proteins and Its Applications. Acc. Chem. Res. 2014, 47, 2748–2757. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Qi, L.-W.; Zhang, J.Z.H.; He, X. Fragment Quantum Mechanical Method for Large-Sized Ion–Water Clusters. J. Chem. Theory Comput. 2017, 13, 2021–2034. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Ali, I.; Wang, Z.; Cai, J.; Wu, S.; Tang, J.; Zhang, L.; Ren, J.; Xiao, R.; Lu, Q.; et al. Machine Learning Accelerates Quantum Mechanics Predictions of Molecular Crystals. Phys. Rep. 2021, 934, 1–71. [Google Scholar] [CrossRef]
- Hao, X.; Liu, J.; Ali, I.; Luo, H.; Han, Y.; Hu, W.; Liu, J.; He, X.; Li, J. Ab Initio Determination of Crystal Stability of Di-p-Tolyl Disulfide. Sci. Rep. 2021, 11, 7076. [Google Scholar] [CrossRef]
- Luo, H.; Hao, X.; Gong, Y.; Zhou, J.; He, X.; Li, J. Rational Crystal Polymorph Design of Olanzapine. Cryst. Growth Des. 2019, 19, 2388–2395. [Google Scholar] [CrossRef]
- Tang, J.; Han, Y.; Ali, I.; Luo, H.; Nowak, A.; Li, J. Stability and Phase Transition Investigation of Olanzapine Polymorphs. Chem. Phys. Lett. 2021, 767, 138384. [Google Scholar] [CrossRef]
- Luo, H.; Liu, J.; He, X.; Li, J. Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics. Crystals 2019, 9, 460. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.; Tang, J.; Han, Y.; Wei, Z.; Zhang, Y.; Li, J. A Solid-Solid Phase Transformation of Triclabendazole at High Pressures. Crystals 2022, 12, 300. [Google Scholar] [CrossRef]
- Li, J.; Sode, O.; Voth, G.A.; Hirata, S. A Solid–Solid Phase Transition in Carbon Dioxide at High Pressures and Intermediate Temperatures. Nat. Commun. 2013, 4, 2647. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.; Han, Y.; Ji, Q.; Zhang, Y.; Wei, Z.; Li, J. Solid–Solid Phase Transformation of Aspirin at High Pressures and Room Temperatures. J. Appl. Cryst. 2022, 55, 1247–1254. [Google Scholar] [CrossRef]
- Gupta, V.P. Vibrational Frequencies and Intensities. In Principles and Applications of Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-803478-1. [Google Scholar]
- Bunaciu, A.A.; Aboul-Enein, H.Y.; Fleschin, S. Application of Fourier Transform Infrared Spectrophotometry in Pharmaceutical Drugs Analysis. Appl. Spectrosc. Rev. 2010, 45, 206–219. [Google Scholar] [CrossRef]
- Bunaciu, A.A.; Aboul-Enein, H.Y.; Hoang, V.D. Vibrational Spectroscopy Used in Polymorphic Analysis. TrAC Trends Anal. Chem. 2015, 69, 14–22. [Google Scholar] [CrossRef]
- Wang, Z.; Song, R.; Chen, W.; Wang, J.; Wang, P.; Zhang, Z.; Zhang, X.; Wan, F. Vibrational Spectra and Molecular Vibrational Behaviors of Dibenzyl Disulfide, Dibenzyl Sulphide and Bibenzyl. Int. J. Mol. Sci. 2022, 23, 1958. [Google Scholar] [CrossRef] [PubMed]
- Jana, S. Spectroscopic Characterization of Disulfiram and Nicotinic Acid after Biofield Treatment. J. Anal. Bioanal. Tech. 2015, 6, 1000265. [Google Scholar] [CrossRef] [Green Version]
- Abu-Saied, M.A.; Elkady, G.M.; Elnaggar, E.M.; Abd-Elnaim, G.H.; Elerian, A.F. Zirconium phosphate based polyvinyl chloride to use as proton conducting membrane for dmfc application. Membranes 2017, 2, 4. [Google Scholar]
- Dennis, J.E., Jr.; Moré, J.J. Quasi-Newton Methods, Motivation and Theory. SIAM Rev. 1977, 19, 46–89. [Google Scholar] [CrossRef] [Green Version]
- Beran, G.J.O. Modeling Polymorphic Molecular Crystals with Electronic Structure Theory. Chem. Rev. 2016, 116, 5567–5613. [Google Scholar] [CrossRef]
- Head, J.D.; Zerner, M.C. A Broyden—Fletcher—Goldfarb—Shanno Optimization Procedure for Molecular Geometries. Chem. Phys. Lett. 1985, 122, 264–270. [Google Scholar] [CrossRef]
- Liu, J.; He, X. Accurate Prediction of Energetic Properties of Ionic Liquid Clusters Using a Fragment-Based Quantum Mechanical Method. Phys. Chem. Chem. Phys. 2017, 19, 20657–20666. [Google Scholar] [CrossRef]
- Liu, J.; He, X.; Zhang, J.Z.H.; Qi, L.-W. Hydrogen-Bond Structure Dynamics in Bulk Water: Insights from Ab Initio Simulations with Coupled Cluster Theory. Chem. Sci. 2018, 9, 2065–2073. [Google Scholar] [CrossRef]

| Parameters | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | V (Å3) |
|---|---|---|---|---|---|---|---|
| Exp [25]. Phase α | 7.593 | 5.713 | 14.722 | 90.00 | 94.76 | 90.00 | 636.417 |
| Cal. Phase α | 7.348 | 5.633 | 14.498 | 90.00 | 94.76 | 90.00 | 598.021 |
| Exp [25]. Phase β | 7.306 | 5.509 | 14.038 | 95.14 | 97.23 | 85.36 | 556.886 |
| Cal. Phase β | 7.541 | 5.662 | 14.245 | 95.14 | 97.23 | 85.36 | 599.465 |
| Exp [25]. Phase γ | 15.260 | 5.962 | 14.615 | 90.00 | 115.56 | 90.00 | 1199.544 |
| Cal. Phase γ | 15.155 | 5.923 | 14.661 | 90.00 | 115.56 | 90.00 | 1187.223 |
| Exp. | Cal. α | Cal. β | Cal. γ | Assignment | References |
|---|---|---|---|---|---|
| 617 | 612 | 614 | N/A | δ C-C | [54] |
| 658 | N/A | N/A | 626 | δo/δi C—H, υ C—S / S—S | [54,55] |
| 695 | 695 | 695 | 705 | δo C—H | [54] |
| 971 | 968 | N/A | 974 | δo C—H | [54] |
| 803 | 806 | 809 | 800 | δ C—C | [54] |
| 1001 | 1006 | 1006 | 1006 | δ C—C | [54] |
| 1028 | 1048 | 1047 | 1044 | υ C—C, δ C—C | [54] |
| 1068 | 1081 | 1083 | 1092 | δ C—H | [54] |
| 1139 | 1126 | 1126 | 1117 | δ C—H | [54] |
| 1181 | 1188 | 1188 | 1182 | υ C—H, δ C—H | [54] |
| 1291 | 1291 | 1290 | 1300 | υ C—C | [54] |
| 1452 | 1468 | 1463 | 1461 | δ C—H | [54] |
| 1494 | 1499 | 1502 | 1500 | δ C—H | [54] |
| 1596/1599 | 1594 | 1595 | 1588 | υ C=C, υ C—C | [54,55] |
| 2943 | 2945 | 2954 | 2969 | υ C—H | [56] |
| 3043 | 3015 | 3020 | 3041 | υ C—H | [54] |
| 3052 | 3058 | 3056 | N/A | υ C—H | [54] |
| 3083 | 3102 | 3100 | 3114 | υ C—H | [54] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Han, Y.; Li, J. Phase Transitions and Stabilities among Three Phases of Di-p-tolyl Disulfides. Molecules 2022, 27, 8342. https://doi.org/10.3390/molecules27238342
Ali I, Han Y, Li J. Phase Transitions and Stabilities among Three Phases of Di-p-tolyl Disulfides. Molecules. 2022; 27(23):8342. https://doi.org/10.3390/molecules27238342
Chicago/Turabian StyleAli, Imran, Yanqiang Han, and Jinjin Li. 2022. "Phase Transitions and Stabilities among Three Phases of Di-p-tolyl Disulfides" Molecules 27, no. 23: 8342. https://doi.org/10.3390/molecules27238342
APA StyleAli, I., Han, Y., & Li, J. (2022). Phase Transitions and Stabilities among Three Phases of Di-p-tolyl Disulfides. Molecules, 27(23), 8342. https://doi.org/10.3390/molecules27238342








