Adsorption Equilibrium and Mechanism and of Water Molecule on the Surfaces of Molybdenite (MoS2) Based on Kinetic Monte-Carlo Method
Abstract
:1. Introduction
2. Method
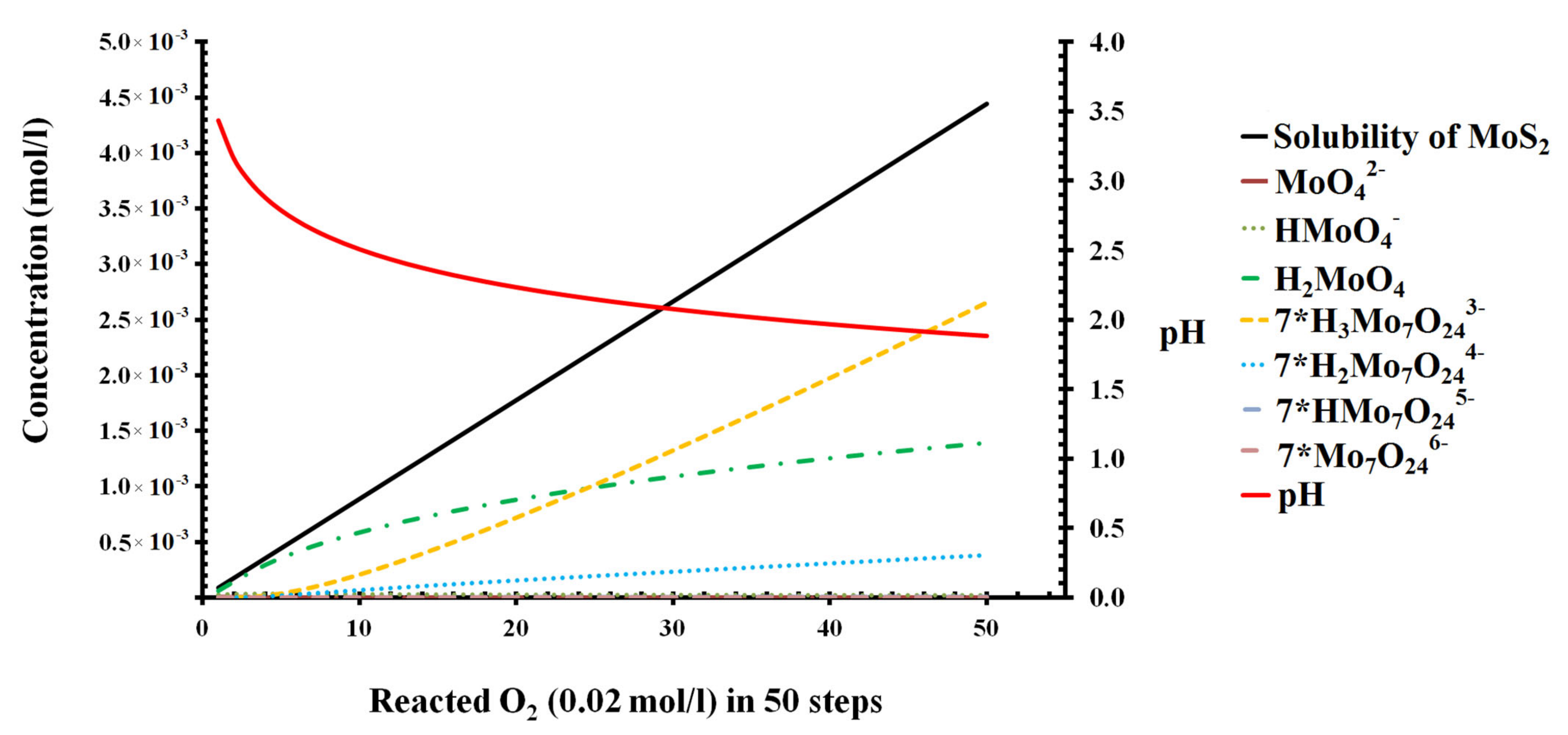
2.1. Thermodynamic Calculation of Eh-pH Diagrams and Reaction Forward Modeling
2.2. Molybdenite Crystal and Geometry Optimization
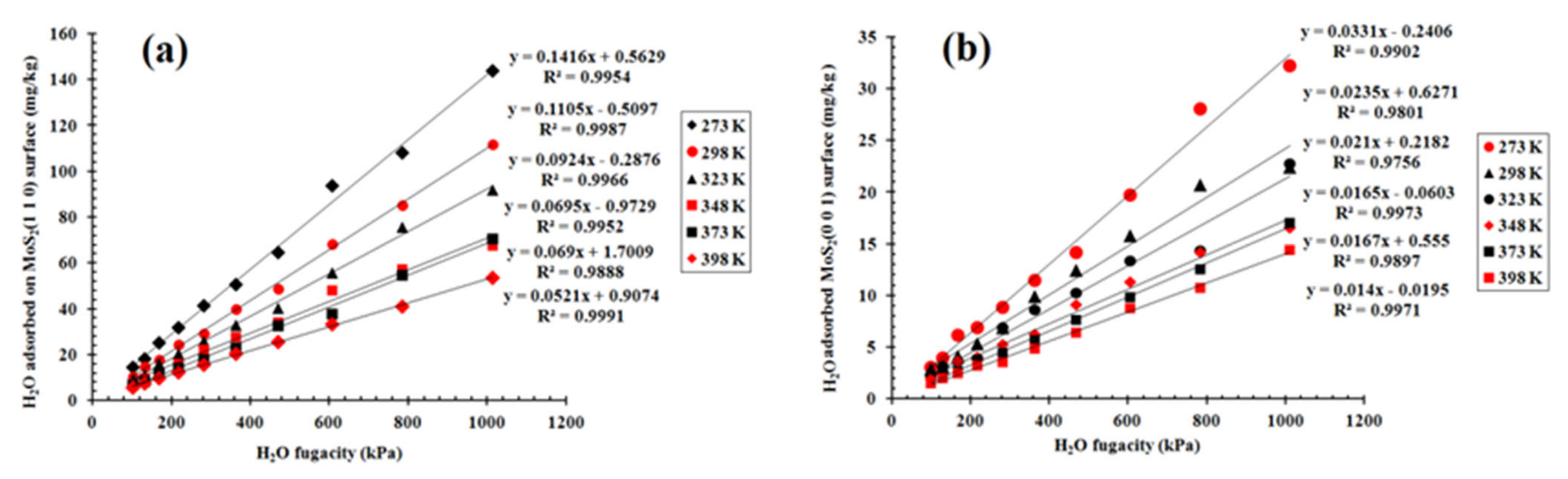
2.3. Sorption Isotherm
2.4. Kinetic Monte Carlo and Rate Coefficient Calculation
3. Results
3.1. Oxidation of Molybdenite Based on Thermodynamic Calculation
3.2. Sorption Isotherm of H2O on the (001) and (110) Surfaces
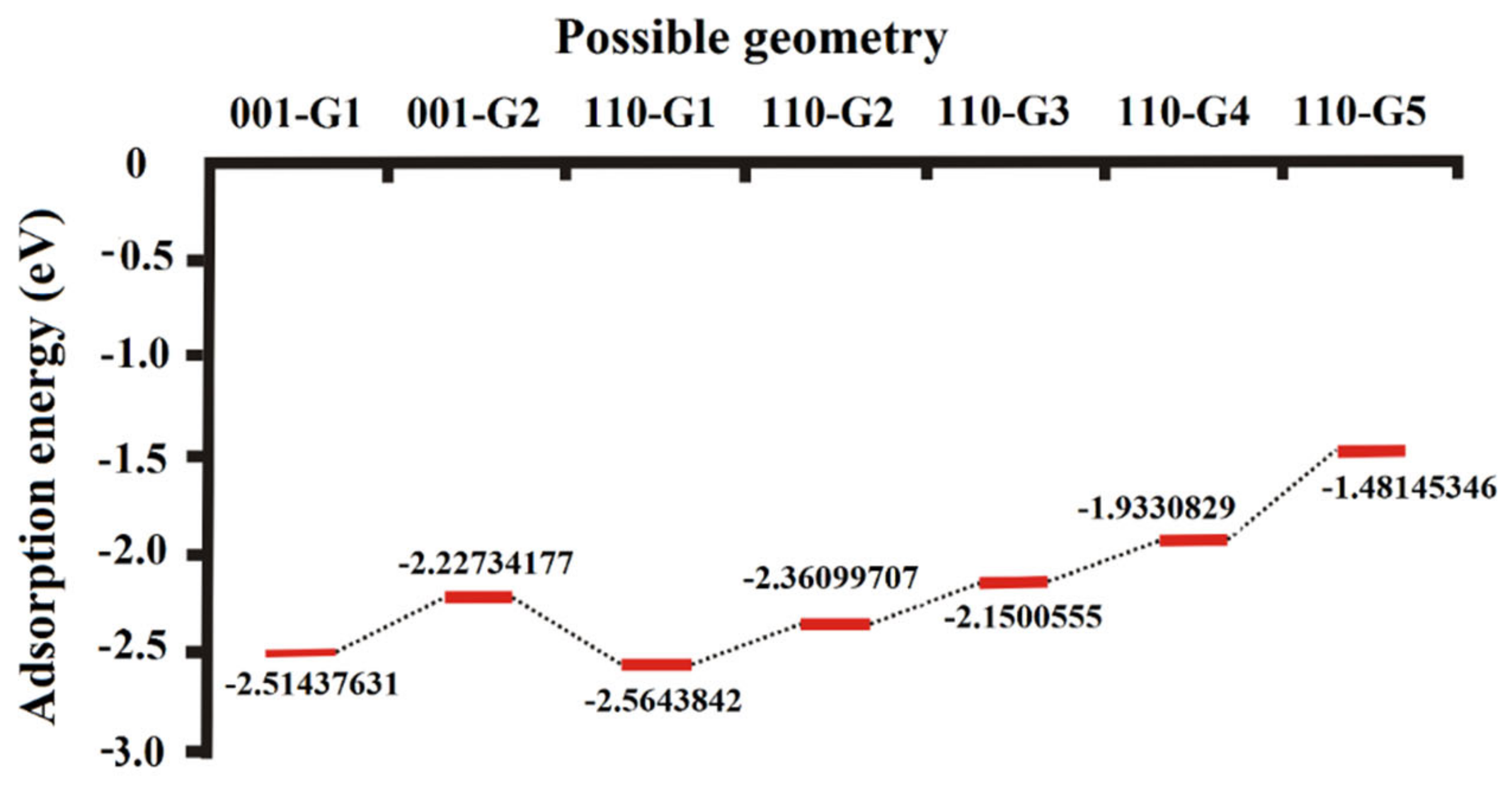
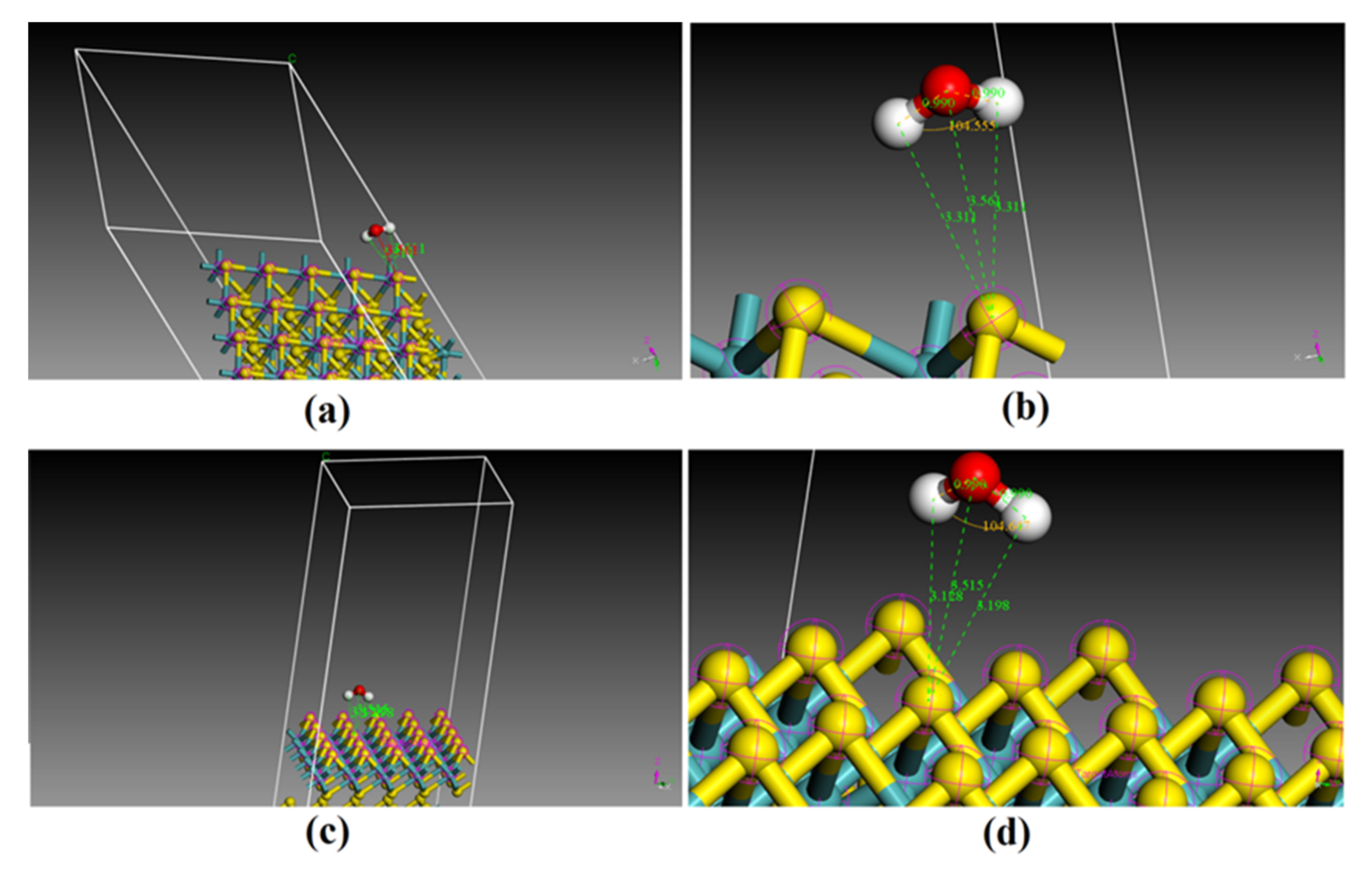
3.3. Adsorption Energy Derived from the Annealing Dynamics of H2O on the (001) and (110) Surfaces
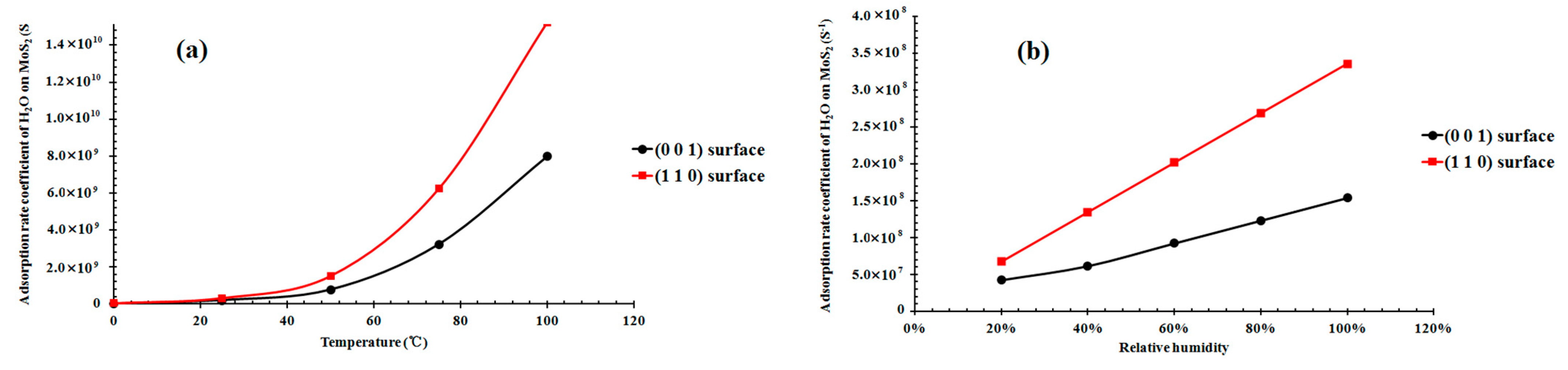
3.4. Adsorption Rate Coefficient of H2O on the (001) and (110) Surfaces as a Function of the Temperature and Humidity
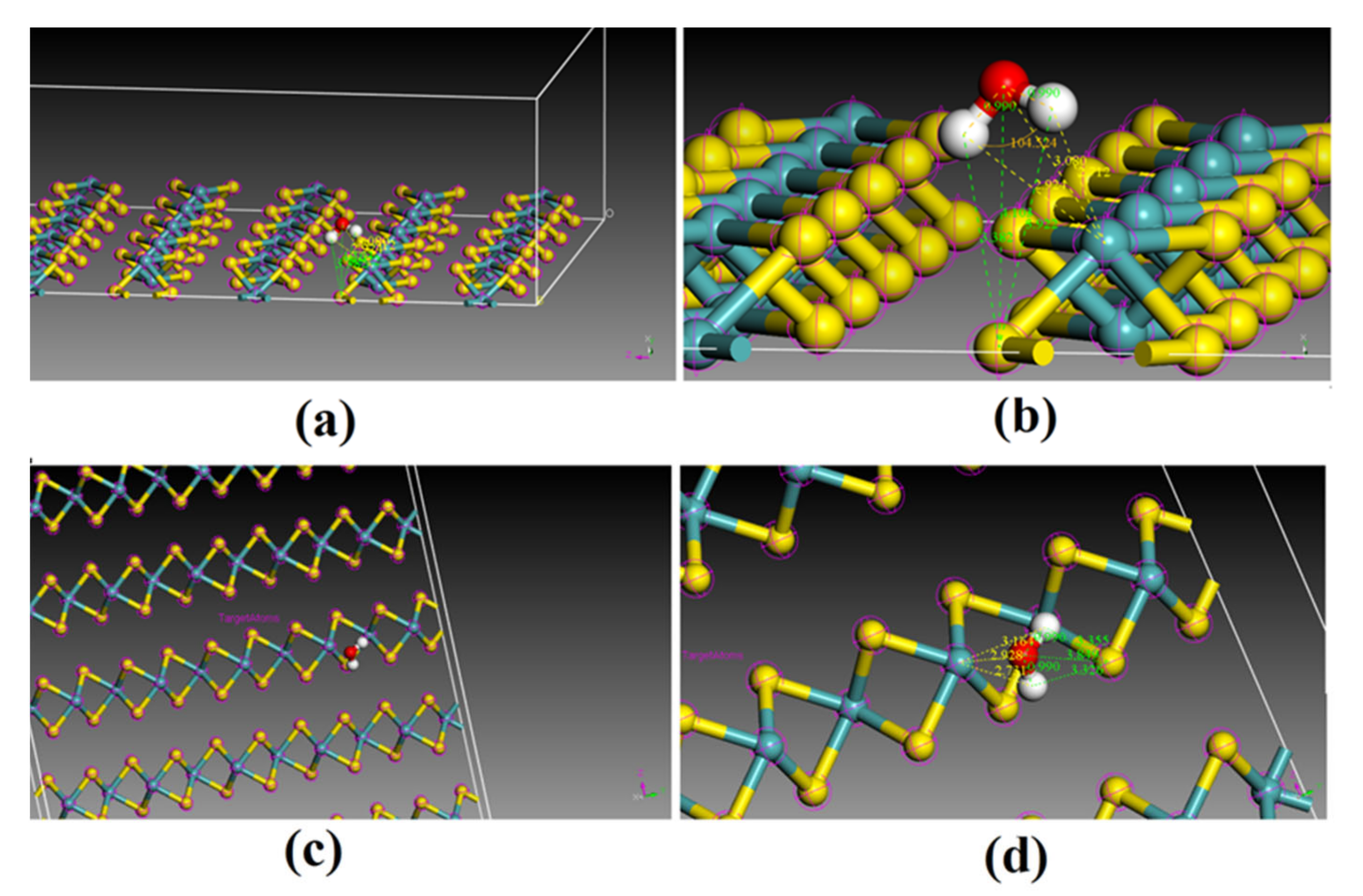
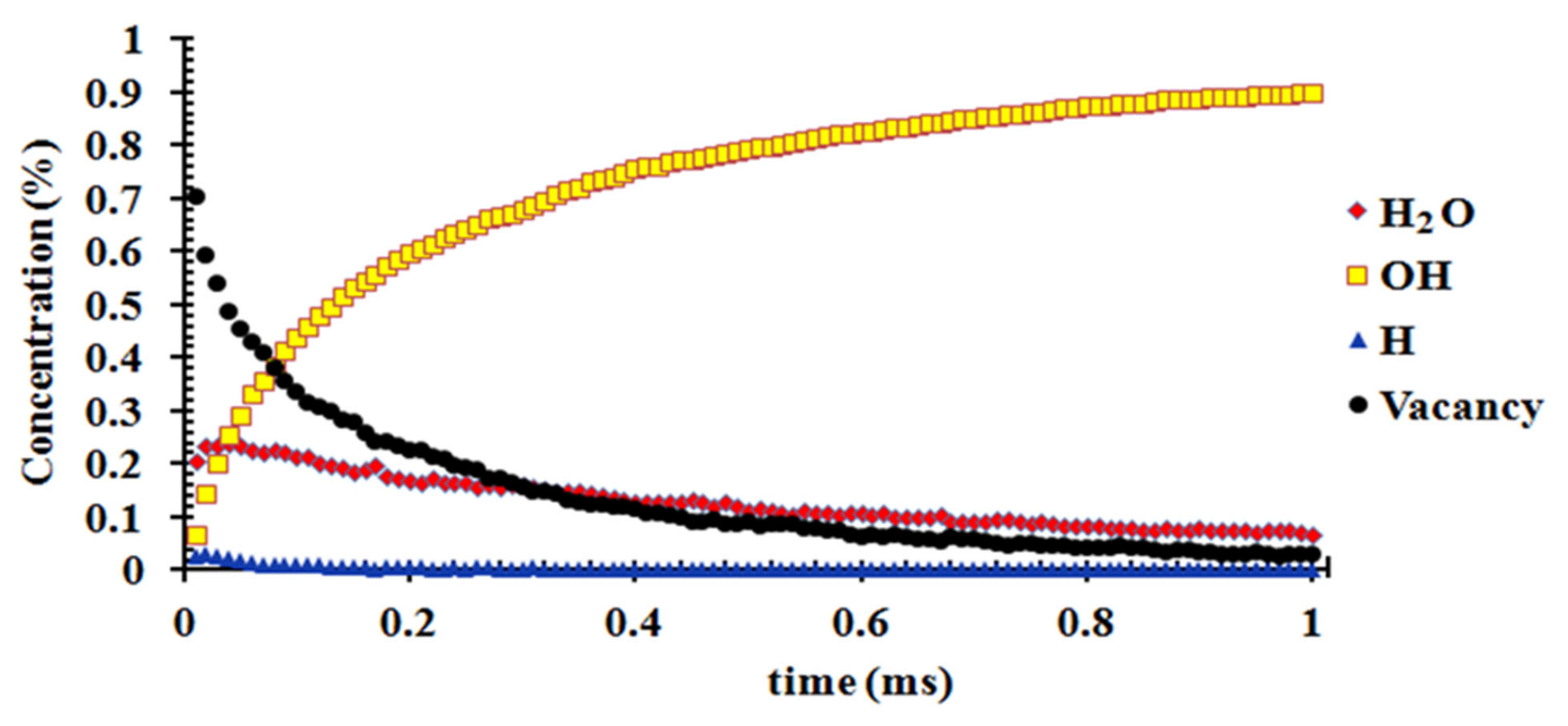
3.5. Kinetics of H2O Dissociative Adsorption on the (110) Surface
4. Discussion
4.1. Adsorption Capacity and Rate Comparison of H2O on the Different Surfaces of Molybdenite and Its Implications for the Mineral Reactivity
4.2. Adsorption Mechanism of H2O on the Surfaces of Molybdenite
4.3. Kinetic Modeling of Dissociative Adsorption of H2O on the (110) Surface and Its Implication for the Weathering of Molybdenite in the Surface Environment
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| KMC | Kinetic Monte Carlo |
| XPS | X-ray photoelectron spectroscopy |
| AFM | Atomic force microscopy |
| DFT | Density functional theory |
| SIMS | Secondary ion mass spectroscopy |
| GPW | Gaussian-Plane Wave |
| PBE | Perdew–Burke–Eenzerhof |
| LDA | Local-density approximation |
| PW91 | Perdew-Wang, 1991 |
| UFF | Universal force field |
References
- Gardner, C.B.; Carey, A.E.; Lyons, W.B.; Goldsmith, S.T.; McAdams, B.; Trierweiler, A.M. Molybdenum, vanadium, and uranium weathering in small mountainous rivers and rivers draining high-standing islands. Geochim. Cosmochim. Acta 2017, 219, 22–43. [Google Scholar] [CrossRef]
- Greaney, A.T.; Rudnick, R.L.; Gaschnig, R.M.; Whalen, J.B.; Luais, B.; Clemens, J.D. Geochemistry of molybdenum in the continental crust. Geochim. Cosmochim. Acta 2018, 238, 36–54. [Google Scholar] [CrossRef] [Green Version]
- Mendel, R.R. Biology of the molybdenum cofactor. J. Exp. Bot. 2007, 58, 2289–2296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwarz, G.; Mendel, R.R.; Ribbe, M.W. Molybdenum cofactors, enzymes and pathways. Nature 2009, 460, 839. [Google Scholar] [CrossRef] [PubMed]
- Wedepohl, K.H. The composition of the continental crust. Geochim. Cosmochim. Acta 1995, 59, 1217–1232. [Google Scholar] [CrossRef]
- Hess, F.L. Molybdenum Deposits, A Short Review; Government Publishing Office: Washington, DC, USA, 1924.
- LeAnderson, P.J.; Schrader, E.L.; Brake, S.; Kaback, D.S. Behavior of molybdenum during weathering of the Ceresco Ridge porphyry molybdenite deposit, Climax, Colorado and a comparison with the Hollister deposit, North Carolina. Appl. Geochem. 1987, 2, 399–415. [Google Scholar] [CrossRef]
- Yamamoto, M.; Einstein, T.L.; Fuhrer, M.S.; Cullen, W.G. Anisotropic etching of atomically thin MoS2. J. Phys. Chem. C 2013, 117, 25643–25649. [Google Scholar] [CrossRef]
- Zhang, X.; Jia, F.; Yang, B.; Song, S. Oxidation of molybdenum disulfide sheet in water under in situ atomic force microscopy observation. J. Phys. Chem. C 2017, 121, 9938–9943. [Google Scholar] [CrossRef]
- Ross, S.; Sussman, A. Surface oxidation of molybdenum disulfide. J. Phys. Chem. 1955, 59, 889–892. [Google Scholar] [CrossRef]
- Buck, V. Preparation and properties of different types of sputtered MoS2 films. Wear 1987, 114, 263–274. [Google Scholar] [CrossRef]
- Raybaud, P.; Hafner, J.; Kresse, G.; Kasztelan, S.; Toulhoat, H. Ab initio study of the H2–H2S/MoS2 gas–solid interface: The nature of the catalytically active sites. J. Catal. 2000, 189, 129–146. [Google Scholar] [CrossRef]
- Ataca, C.; Ciraci, S. Dissociation of H2O at the vacancies of single-layer MoS2. Phys. Rev. B 2012, 85, 195410. [Google Scholar] [CrossRef]
- Ghuman, K.K.; Yadav, S.; Singh, C.V. Adsorption and dissociation of H2O on monolayered MoS2 edges: Energetics and mechanism from ab initio simulations. J. Phys. Chem. C 2015, 119, 6518–6529. [Google Scholar] [CrossRef]
- Kinniburgh, D.G.; Cooper, D.M. PhreePlot: Creating Graphical Output with PHREEQC; Centre for Ecology and Hydrology: Gwynedd, UK, 2011. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey Techniques and Methods: Denver, CO, USA, 2013. [Google Scholar]
- Raybaud, P.; Hafner, J.; Kresse, G.; Toulhoat, H. Ab initio density functional studies of transition-metal sulphides: II. Electronic structure. J. Phys. Condens. Matter 1997, 9, 11107. [Google Scholar] [CrossRef]
- Stotu, U.; Marnntall, T. Molybdenite polytypes in theory and occurrence. II. Some naturally-occurring polytypes of molybdenite. Am. Mineral. 1970, 55, 1857–1875. [Google Scholar]
- Luck, J.M.; Allègre, C.J. The study of molybdenites through the 187Re-187Os chronometer. Earth Planet. Sci. Lett. 1982, 61, 291–296. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, M.F.; Hu, R.; Shen, N.; Yuan, S.; Bi, X.; Du, A.; Qu, W. Precise molybdenite Re–Os and mica Ar–Ar dating of the Mesozoic Yaogangxian tungsten deposit, central Nanling district, South China. Miner. Depos. 2006, 41, 661–669. [Google Scholar] [CrossRef]
- Dickinson, R.G.; Pauling, L. The crystal structure of molybdenite. J. Am. Chem. Soc. 1923, 45, 1466–1471. [Google Scholar] [CrossRef]
- Bronsema, K.D.; De Boer, J.L.; Jellinek, F. On the structure of molybdenum diselenide and disulfide. Z. Für Anorg. Und Allg. Chem. 1986, 540, 15–17. [Google Scholar] [CrossRef]
- Zubavichus, Y.V.; Slovokhotov, Y.L.; Schilling, P.J.; Tittsworth, R.C.; Golub, A.S.; Protzenko, G.A.; Novikov, Y.N. X-ray absorption fine structure study of the atomic and electronic structure of molybdenum disulfide intercalation compounds with transition metals. Inorg. Chim. Acta 1998, 280, 211–218. [Google Scholar] [CrossRef]
- Karolewski, M.A.; Cavell, R.G. SIMS study of Cs/MoS2 (0001): II. Chemisorption of O2, H2O, HCOOH, CO2 and CS2. Surf. Sci. 1989, 219, 261–276. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Jansen, A.P.J. An Introduction to Kinetic Monte Carlo Simulations of Surface Reactions; Springer: Berlin, Germany, 2012. [Google Scholar]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Liang, T.; Sawyer, W.G.; Perry, S.S.; Sinnott, S.B.; Phillpot, S.R. Energetics of oxidation in MoS2 nanoparticles by density functional theory. J. Phys. Chem. C 2011, 115, 10606–10616. [Google Scholar] [CrossRef]
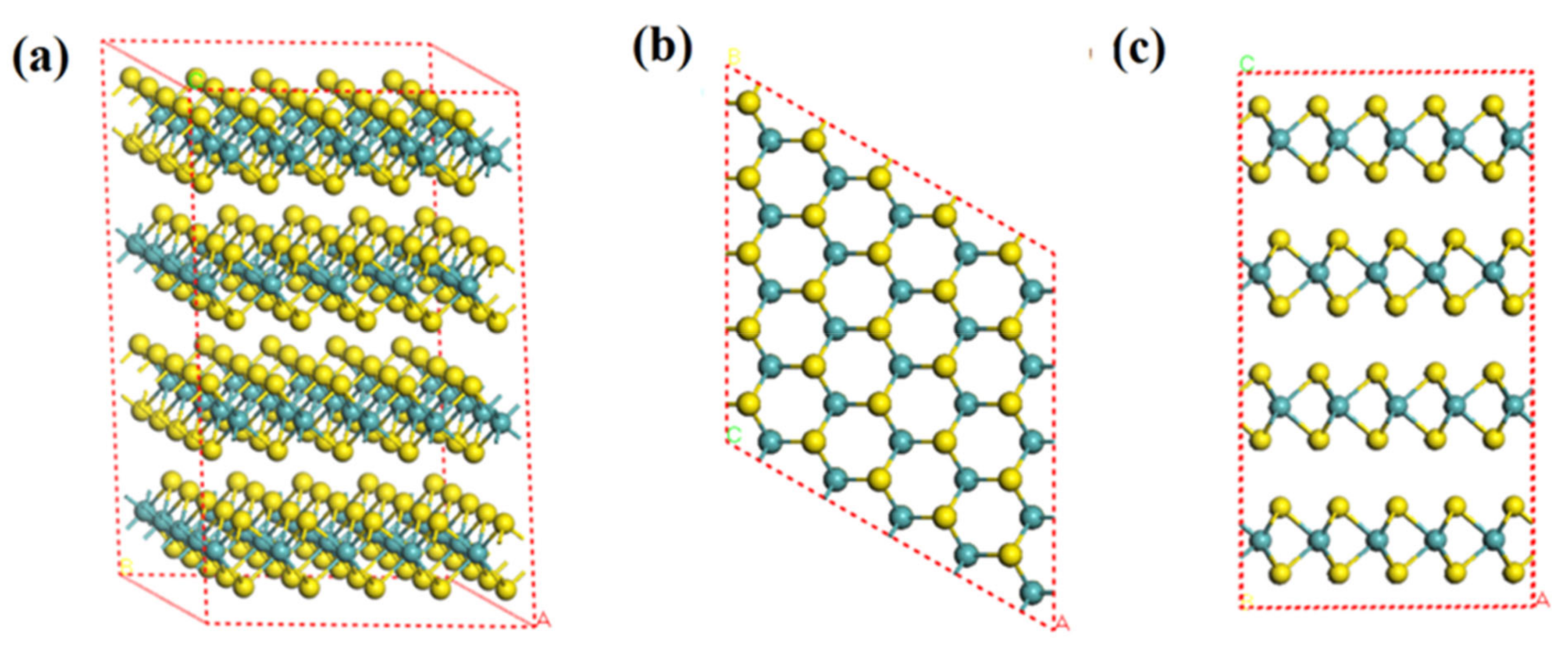




| Source | Lattice Constant—a (Å) | Lattice Constant—c (Å) | Mo-S Bond Length (Å) | S-S Bond Length (Å) | Band Gap (eV) |
|---|---|---|---|---|---|
| LDA | 3.136 | 12.052 | 2.381 | 3.110 | 0.74 |
| PBE | 3.168 | 12.616 | 2.407 | 3.128 | 1.102 |
| PW91 | 3.180 | 12.690 | 2.411 | 3.126 | 1.023 |
| Dickinson and Pauling, 1923 [21] | 3.15 | 12.3 | 1.29 | ||
| Swanson et al., 1955 | 3.16 | 12.295 | 1.29 | ||
| Bronsema et al., 1986 [22] | 3.16 | 12.296 | |||
| Zubavichus et al., 1998 [23] | 2.39 | 3.16 |
| T (°C) | Pvp (atm) | A-Site (Å2) | KH2O-ads (S−1) | |
|---|---|---|---|---|
| (001) | 0 | 0.006 | 3.23 | 2.97 × 107 |
| 25 | 0.0313 | 4.63 | 2.13 × 108 | |
| 50 | 0.1218 | 4.57 | 7.84 × 108 | |
| 75 | 0.3806 | 6.27 | 3.24 × 109 | |
| 100 | 1 | 6.09 | 7.98 × 109 | |
| (110) | 0 | 0.006 | 5.68 | 5.22 × 107 |
| 25 | 0.0313 | 7.31 | 3.35 × 108 | |
| 50 | 0.1218 | 8.92 | 1.53 × 109 | |
| 75 | 0.3806 | 12.10 | 6.25 × 109 | |
| 100 | 1 | 11.61 | 1.52 × 1010 |
| Reaction | Rate Coefficient (S−1) |
|---|---|
| MoS2 + H2O = MoS2-H2O | 4.84 ×107 |
| MoS2-H2O = MoS2 + H2O | 3.62 × 1010 |
| MoS2-H2O = MoS2-OH + H | 2.8 × 1010 |
| MoS2-OH + H = MoS2-H2O | 2.9 × 1011 |
| 2H-MoS2 = MoS2 + H2 | 2.38 × 108 |
| MoS2 + H2 = 2H-MoS2 | 1.20 × 108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Wang, X.; Zuo, Z.; Ni, S.; Dai, J.; Wang, D. Adsorption Equilibrium and Mechanism and of Water Molecule on the Surfaces of Molybdenite (MoS2) Based on Kinetic Monte-Carlo Method. Molecules 2022, 27, 8710. https://doi.org/10.3390/molecules27248710
Wang R, Wang X, Zuo Z, Ni S, Dai J, Wang D. Adsorption Equilibrium and Mechanism and of Water Molecule on the Surfaces of Molybdenite (MoS2) Based on Kinetic Monte-Carlo Method. Molecules. 2022; 27(24):8710. https://doi.org/10.3390/molecules27248710
Chicago/Turabian StyleWang, Ruilin, Xinyu Wang, Zhijun Zuo, Shijun Ni, Jie Dai, and Dewei Wang. 2022. "Adsorption Equilibrium and Mechanism and of Water Molecule on the Surfaces of Molybdenite (MoS2) Based on Kinetic Monte-Carlo Method" Molecules 27, no. 24: 8710. https://doi.org/10.3390/molecules27248710
APA StyleWang, R., Wang, X., Zuo, Z., Ni, S., Dai, J., & Wang, D. (2022). Adsorption Equilibrium and Mechanism and of Water Molecule on the Surfaces of Molybdenite (MoS2) Based on Kinetic Monte-Carlo Method. Molecules, 27(24), 8710. https://doi.org/10.3390/molecules27248710





