The Effects of Iron on In Silico Simulated Abiotic Reaction Networks
Abstract
:1. Introduction
2. Methods
2.1. Reaction Network Generation
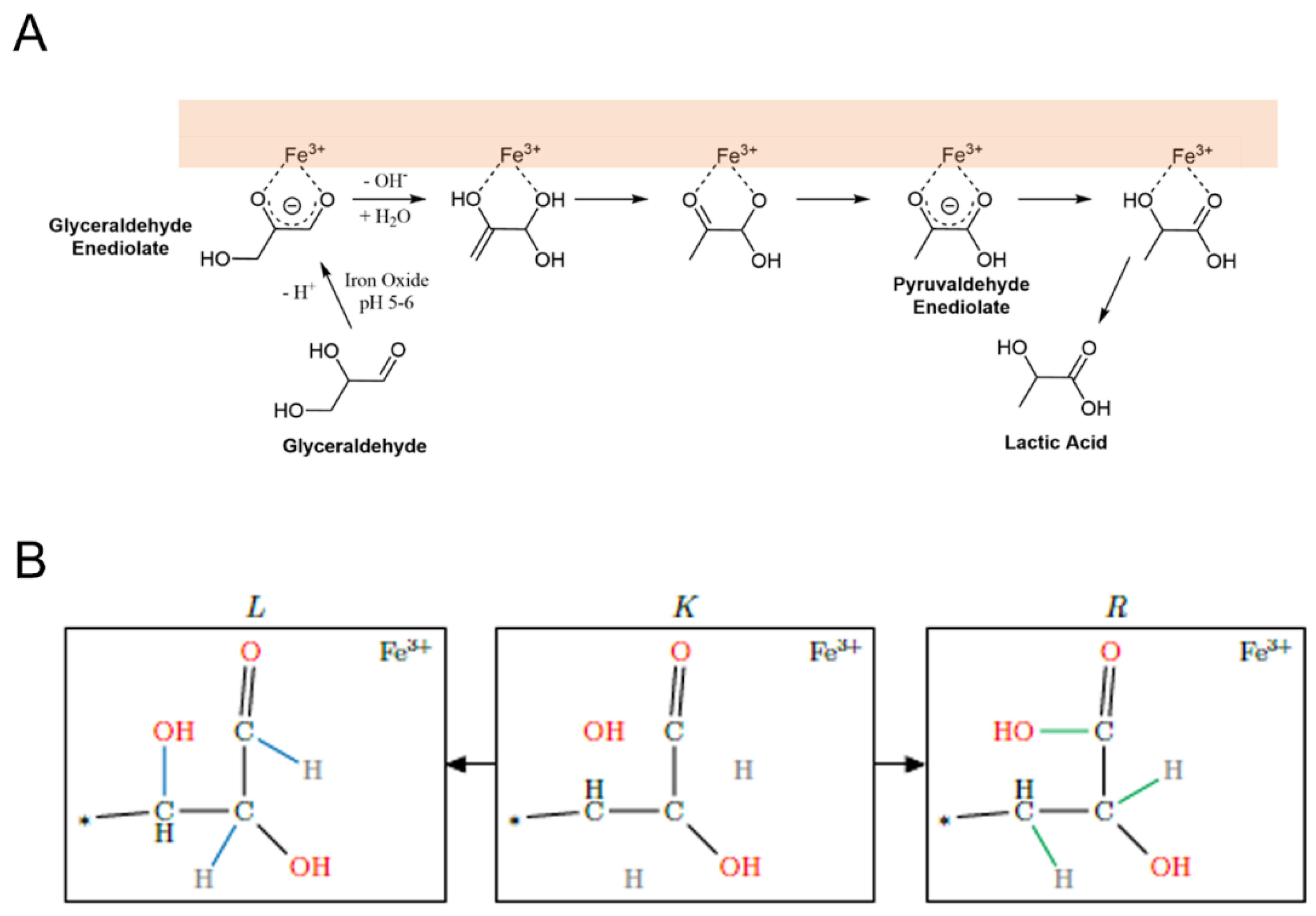
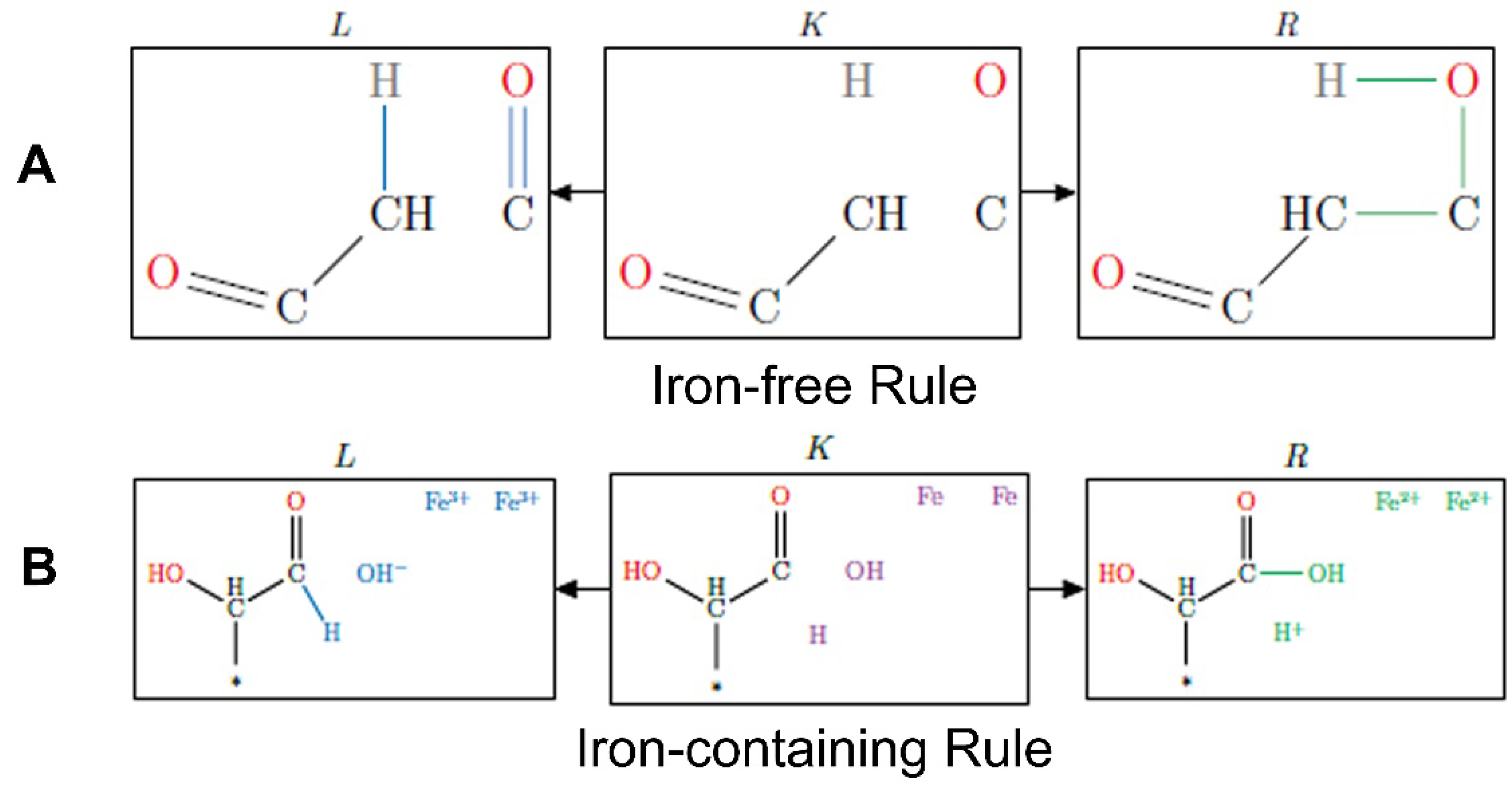
2.2. Reaction Mechanism Selection
2.3. Data Visualization
2.4. Reaction Network Exploration
- Formose Reaction Network
- HCHO + H2O
- HCHO + H2O + Fe2+ + Fe3+ + H+ + OH−
- Concentrated Pyruvic Acid Network
- Pyruvic Acid + H2O
- Pyruvic Acid + H2O + Fe2+ + Fe3+ + H+ + OH−
- Glucose Degradation Reaction Network
- Glucose + H2O
- Glucose + H2O + Fe2+ + Fe3+ + H+ + OH−
- Glucose-Glycine Maillard Reaction Network
- Glycine + Open Chain Glucose + H2O
- Glycine + Open Chain Glucose + H2O + Fe2+ + Fe3+ + H+ + OH−
3. Results and Discussion
3.1. Product Diversity
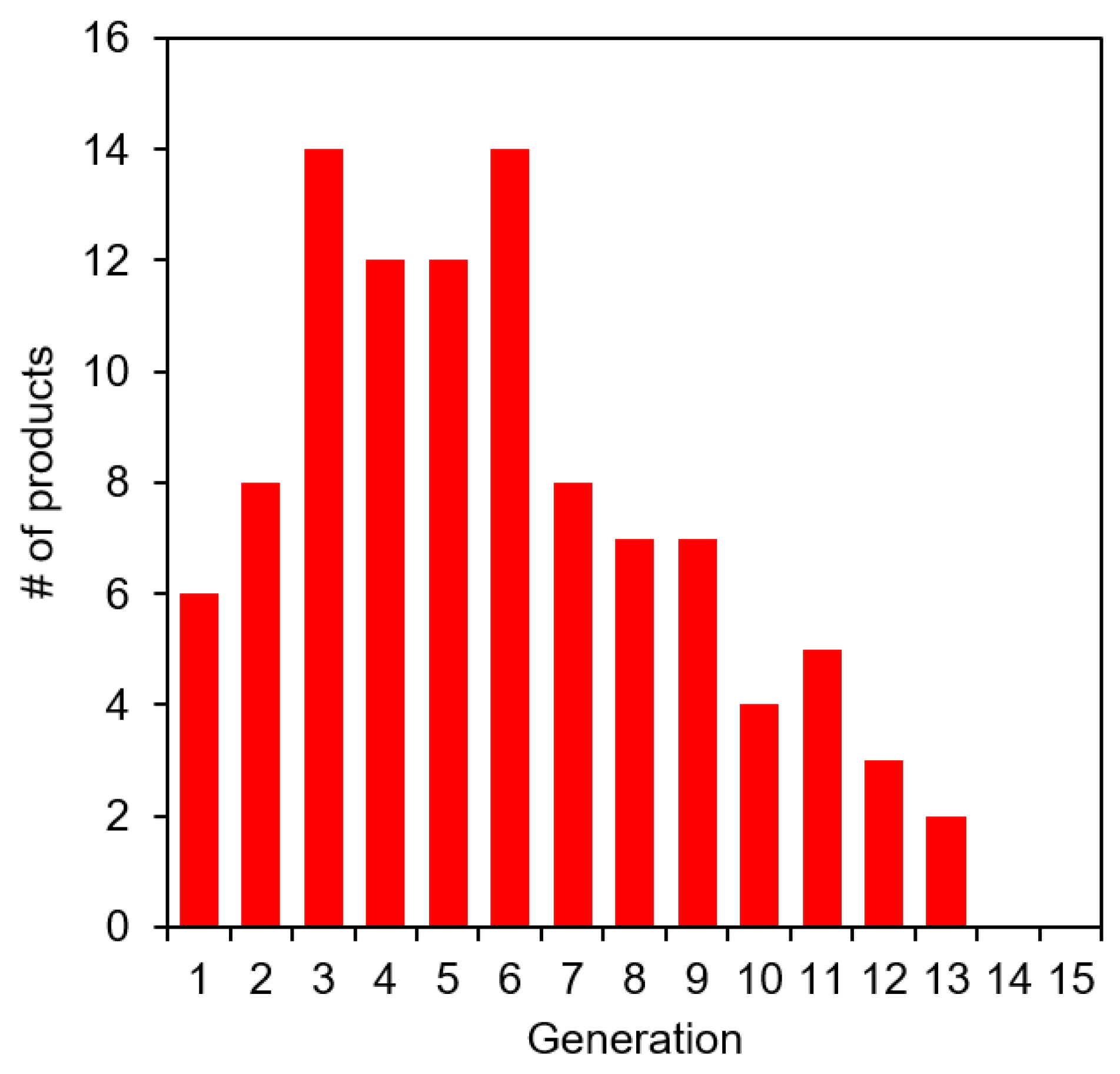
3.2. Reaction Diversity
3.3. Catalysis
3.4. Graph Metric Comparisons
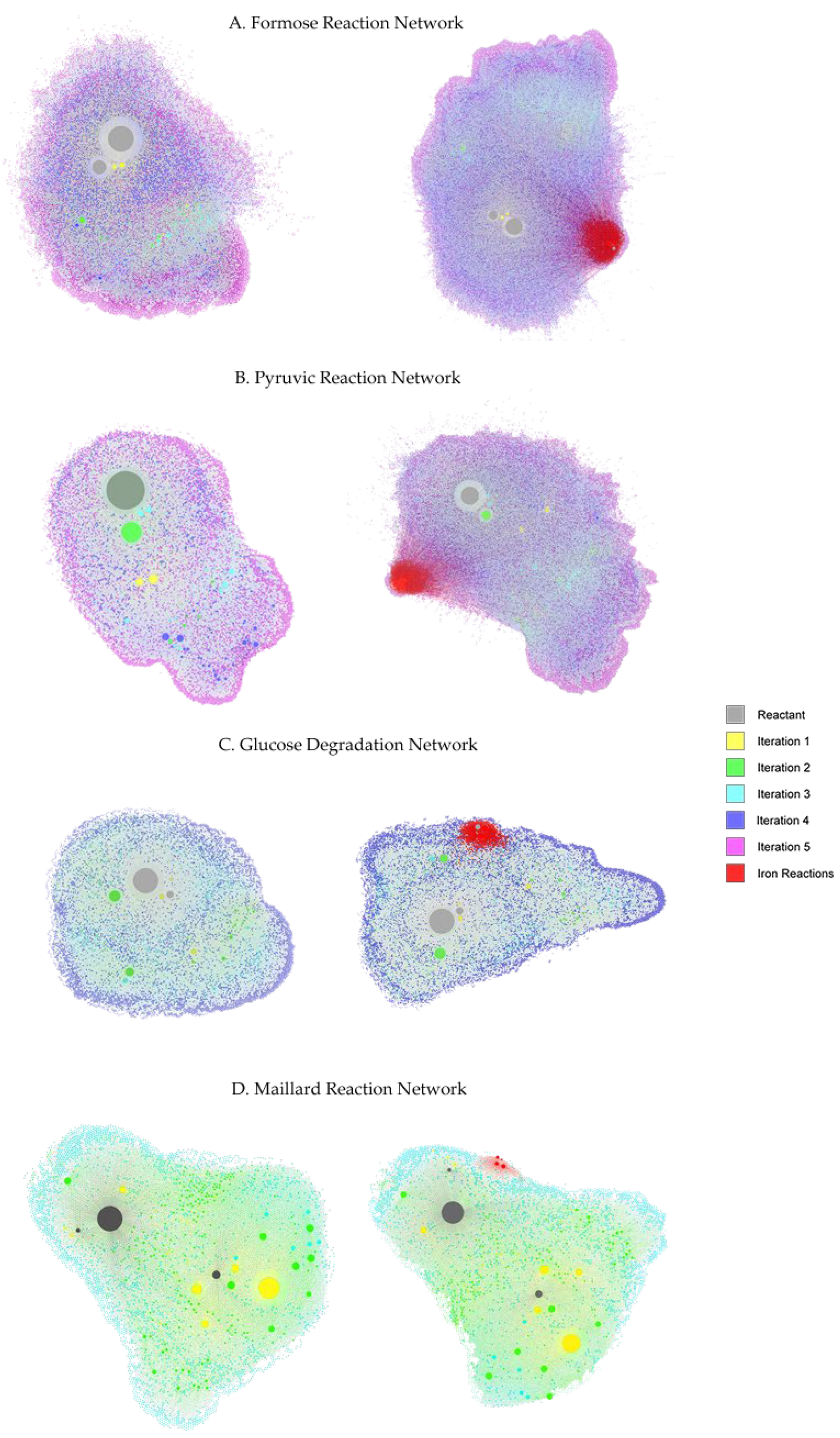
3.5. Gephi Visualization of the Networks
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morgan, J.W.; Anders, E. Chemical composition of Earth, Venus, and Mercury. Proc. Natl. Acad. Sci. USA 1980, 77, 6973–6977. [Google Scholar] [CrossRef] [Green Version]
- Frey, P.A.; Reed, G.H. The Ubiquity of Iron. ACS Chem. Biol. 2012, 7, 1477–1481. [Google Scholar] [CrossRef]
- Sobolev, D.; Roden, E.E. Evidence for Rapid Microscale Bacterial Redox Cycling of Iron in Circumneutral Environments. Antonie Van Leeuwenhoek 2002, 81, 587–597. [Google Scholar] [CrossRef]
- Fürstner, A. Iron Catalysis in Organic Synthesis: A Critical Assessment of What It Takes to Make This Base Metal a Multitasking Champion. ACS Cent. Sci. 2016, 2, 778–789. [Google Scholar] [CrossRef]
- Dhungana, S.; Crumbliss, A.L. Coordination Chemistry and Redox Processes in Siderophore-Mediated Iron Transport. Geomicrobiol. J. 2005, 22, 87–98. [Google Scholar] [CrossRef]
- Schumb, W.C.; Sherrill, M.S.; Sweetser, S.B. The Measurement of the Molal Ferric-Ferrous Electrode Potential. J. Am. Chem. Soc. 1937, 59, 2360–2365. [Google Scholar] [CrossRef]
- Adkins, H.; Elofson, R.M.; Rossow, A.G.; Robinson, C.C. The Oxidation Potentials of Aldehydes and Ketones. J. Am. Chem. Soc. 1949, 71, 3622–3629. [Google Scholar] [CrossRef]
- Stephens, P.J.; Jollie, D.R.; Warshel, A. Protein Control of Redox Potentials of Iron−Sulfur Proteins. Chem. Rev. 1996, 96, 2491–2514. [Google Scholar] [CrossRef]
- Barge, L.M.; Flores, E.; Baum, M.M.; VanderVelde, D.G.; Russell, M.J. Redox and pH gradients drive amino acid synthesis in iron oxyhydroxide mineral systems. Proc. Natl. Acad. Sci. USA 2019, 116, 4828–4833. [Google Scholar] [CrossRef] [Green Version]
- Wächtershäuser, G. Before enzymes and templates: Theory of surface metabolism. Microbiol. Rev. 1988, 52, 452–484. [Google Scholar] [CrossRef]
- Weber, A.L. Prebiotic sugar synthesis: Hexose and hydroxy acid synthesis from glyceraldehyde catalyzed by iron(III) hydroxide oxide. J. Mol. Evol. 1992, 35, 1–6. [Google Scholar] [CrossRef]
- Muchowska, K.B.; Varma, S.J.; Moran, J. Synthesis and breakdown of universal metabolic precursors promoted by iron. Nature 2019, 569, 104–107. [Google Scholar] [CrossRef]
- Kato, Y.; Watanabe, K.; Sato, Y. Effect of some metals on the Maillard reaction of ovalbumin. J. Agric. Food Chem. 1981, 29, 540–543. [Google Scholar] [CrossRef]
- Ferris, J.P.; Donner, D.B.; Lotz, W. Chemical evolution. IX. Mechanism of the oligomerization of hydrogen cyanide and its possible role in the origins of life. J. Am. Chem. Soc. 1972, 94, 6968–6974. [Google Scholar] [CrossRef]
- Breslow, R. On the mechanism of the formose reaction. Tetrahedron Lett. 1959, 1, 22–26. [Google Scholar] [CrossRef]
- Miller, S.L. A Production of Amino Acids Under Possible Primitive Earth Conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [Green Version]
- Parker, E.T.; Ii, H.J.C.; Bada, J.L.; Fernández, F.M. Quantitation of α-hydroxy acids in complex prebiotic mixtures via liquid chromatography/tandem mass spectrometry. Rapid Commun. Mass Spectrom. 2016, 30, 2043–2051. [Google Scholar] [CrossRef]
- Schmitt-Kopplin, P.; Gabelica, Z.; Gougeon, R.D.; Fekete, A.; Kanawati, B.; Harir, M.; Gebefuegi, I.; Eckel, G.; Hertkorn, N. High molecular diversity of extraterrestrial organic matter in Murchison meteorite revealed 40 years after its fall. Proc. Natl. Acad. Sci. USA 2010, 107, 2763–2768. [Google Scholar] [CrossRef] [Green Version]
- Pizzarello, S.; Shock, E. The Organic Composition of Carbonaceous Meteorites: The Evolutionary Story Ahead of Biochemistry. Cold Spring Harb. Perspect. Biol. 2010, 2, a002105. [Google Scholar] [CrossRef]
- Arya, A.; Ray, J.; Sharma, S.; Simbron, R.C.; Lozano, A.; Smith, H.B.; Andersen, J.L.; Chen, H.; Meringer, M.; Cleaves, H.J. An open source computational workflow for the discovery of autocatalytic networks in abiotic reactions. Chem. Sci. 2022, 13, 4838–4853. [Google Scholar] [CrossRef]
- Andersen, J.L.; Flamm, C.; Merkle, D.; Stadler, P.F. A Software Package for Chemically Inspired Graph Transformation. In Graph Transformation. ICGT 2016; Echahed, R., Minas, M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9761, pp. 73–88. [Google Scholar] [CrossRef] [Green Version]
- Schwall, K.; Zielenbach, K. SciFinder a New Generation of Research Tools. Chem. Innov. 2000, 30, 45–50. [Google Scholar]
- Plater, M.; Vassiliev, K. The Detection of Glycine from the Treatment of Glyoxylic Acid with iron(II) Sulfate and Ammonia in Water. J. Chem. Res. 2011, 35, 129–132. [Google Scholar] [CrossRef]
- Glor, P.R. The Mechanism of Iron (III) Oxidation of Glucose and Related Compounds. Ph.D. Thesis, The Institute of Paper Chemistry, Atlanta, GA, USA, 1968. [Google Scholar]
- Nealson, K.H. The limits of life on Earth and searching for life on Mars. J. Geophys. Res. Earth Surf. 1997, 102, 23675–23686. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 51–56. [Google Scholar]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An Open Source Software for Exploring and Manipulating Networks. In Proceedings of the International AAAI Conference on Web and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 3, pp. 361–362. [Google Scholar]
- Hazen, R.M.; Deamer, D.W. Hydrothermal Reactions of Pyruvic Acid: Synthesis, Selection, and Self-Assembly of Amphiphilic Molecules. Orig. Life Evol. Biosph. 2006, 37, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.Y.; Montgomery, R. Alkaline degradation of glucose: Effect of initial concentration of reactants. Carbohydr. Res. 1996, 280, 27–45. [Google Scholar] [CrossRef]
- Martins, S.I.; Jongen, W.M.; van Boekel, M.A. A review of Maillard reaction in food and implications to kinetic modelling. Trends Food Sci. Technol. 2000, 11, 364–373. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Frenkel-Pinter, M.; Rajaei, V.; Glass, J.B.; Hud, N.V.; Williams, L.D. Water and Life: The Medium is the Message. J. Mol. Evol. 2021, 89, 2–11. [Google Scholar] [CrossRef]
- Decker, P.; Schweer, H.; Pohlamnn, R. Bioids: X. Identification of formose sugars, presumable prebiotic metabolites, using capillary gas chromatography/gas chromatography—Mass spectrometry of n-butoxime trifluoroacetates on OV-225. J. Chromatogr. A 1982, 244, 281–291. [Google Scholar] [CrossRef]

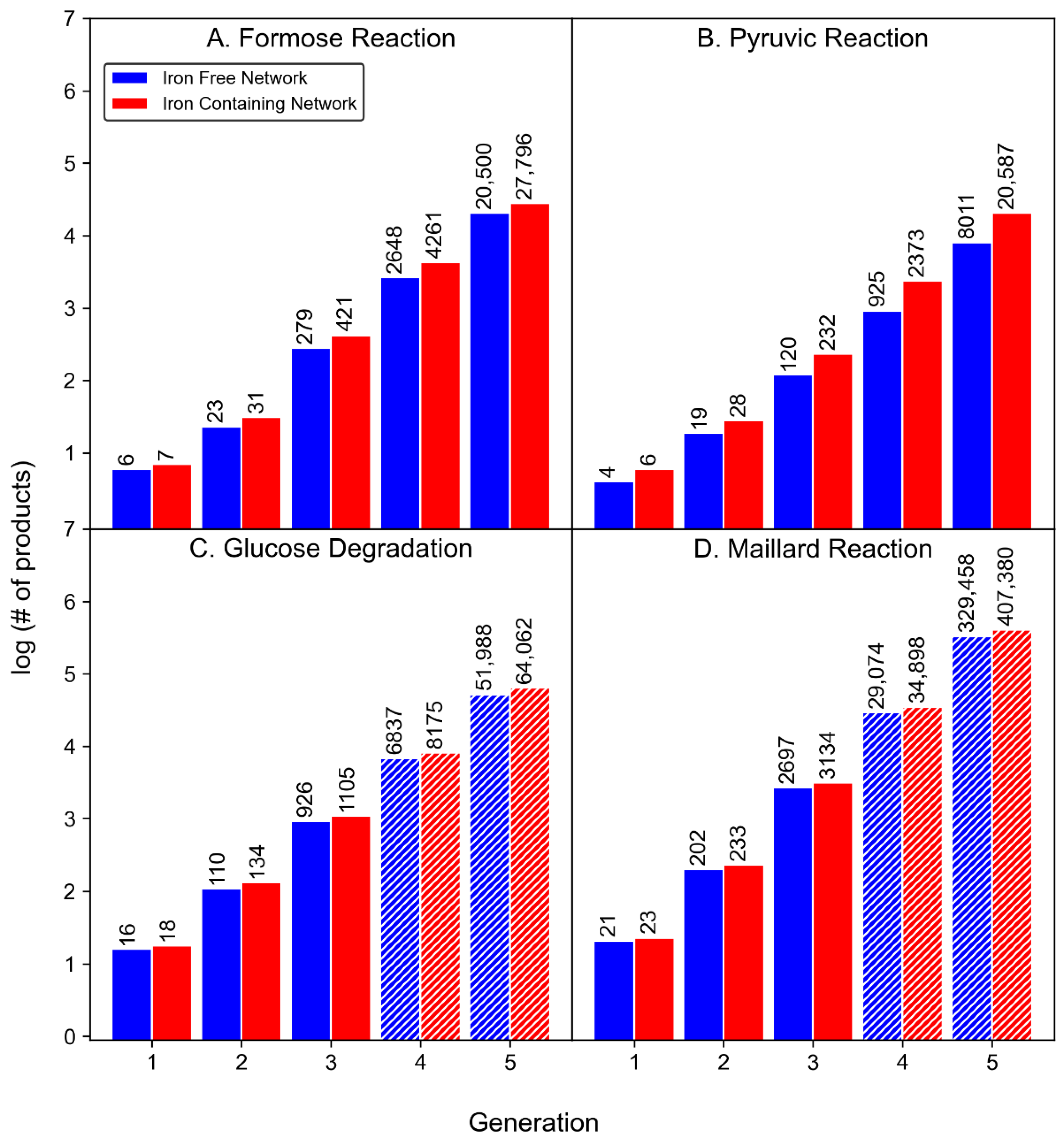


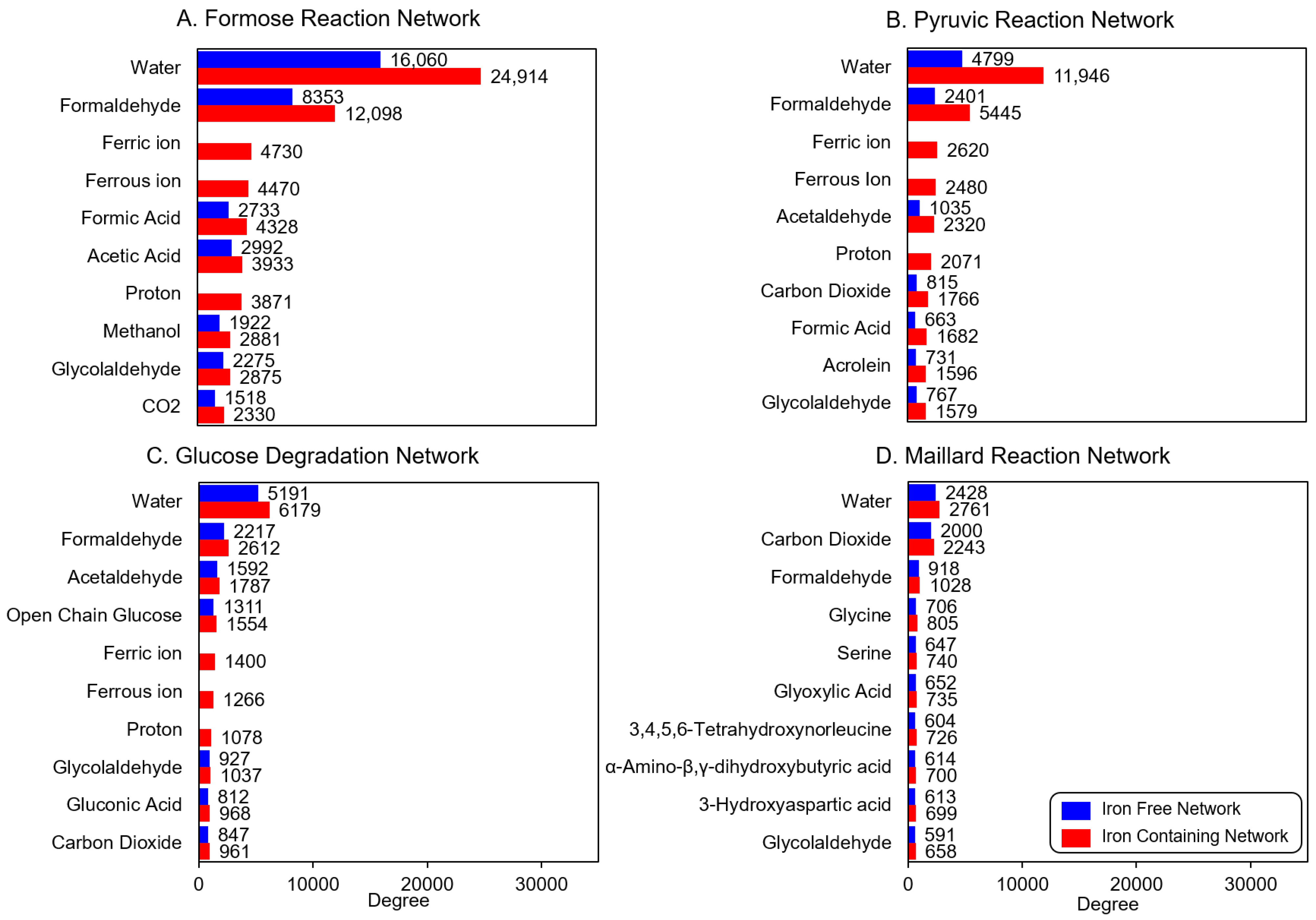
| Reaction | # of Iterations | Iron-Free Network | Iron-Containing Network |
|---|---|---|---|
| Formose Reaction | 5 | 23,459 | 32,523 |
| Pyruvic Acid Reaction | 5 | 9081 | 23,232 |
| Glucose Degradation Reaction | 4 | 7891 | 9438 |
| Glucose-Glycine Maillard Reaction | 3 | 2923 | 3417 |
| Reaction | # of Iterations | Iron-Free Network | Iron-Containing Network |
|---|---|---|---|
| Formose Reaction | 5 | 54,525 | 81,049 |
| Pyruvic Acid Reaction | 5 | 17,446 | 45,367 |
| Glucose Degradation Reaction | 4 | 19,271 | 23,661 |
| Glucose-Glycine Maillard Reaction | 3 | 8856 | 10,460 |
| Reaction Name | Iron-Free Network | Iron-Containing Network | % Change |
|---|---|---|---|
| 12 | 54 | 350% |
| 5 | 17 | 240% |
| 78 | 187 | 140% |
| 398 | 946 | 138% |
| 221 | 520 | 135% |
| 227 | 527 | 132% |
| 82 | 190 | 132% |
| 106 | 222 | 109% |
| 365 | 670 | 84% |
| 326 | 592 | 82% |
| 1830 | 3189 | 74% |
| 242 | 417 | 72% |
| 348 | 586 | 68% |
| 2482 | 4082 | 64% |
| 2731 | 4326 | 58% |
| 135 | 211 | 56% |
| 1884 | 2936 | 56% |
| 3756 | 5849 | 56% |
| 3825 | 5926 | 55% |
| 1500 | 2320 | 55% |
| 1691 | 2545 | 51% |
| 599 | 896 | 50% |
| 1623 | 2384 | 47% |
| 3966 | 5758 | 45% |
| 522 | 753 | 44% |
| 52 | 75 | 44% |
| 5494 | 7576 | 38% |
| 1731 | 2359 | 36% |
| 4327 | 5508 | 27% |
| 5228 | 6484 | 24% |
| 8739 | 10,579 | 21% |
| 0 | 2365 | - |
| 0 | 187 | - |
| 0 | 636 | - |
| 0 | 183 | - |
| 0 | 412 | - |
| 0 | 251 | - |
| 0 | 566 | - |
| 0 | 130 | - |
| Network | Reaction | Iron-Free Network | Iron-Containing Network | % Change |
|---|---|---|---|---|
| Pyruvic Reaction | Ring Closure 7 membered O, O | 40 | 194 | 385% |
| Hemiacetal Formation for 7 membered rings | 87 | 321 | 269% | |
| Ring Closure 6 membered O, O | 170 | 543 | 219% | |
| Hemiacetal Formation for 6 membered rings | 297 | 925 | 211% | |
| Michael Addition, Inverse | 318 | 979 | 208% | |
| Glucose Degradation Reaction | β-γ Unsaturated Acid Decarboxylation | 2 | 6 | 200% |
| α-β Unsaturated Acid Decarboxylation | 3 | 8 | 167% | |
| α-Keto Acid Decarboxylation | 11 | 19 | 73% | |
| Ring Closure 7 membered O, O | 29 | 49 | 69% | |
| Benzilic Acid Rearrangement, Inverse | 65 | 103 | 58% | |
| Glucose-Glycine Maillard Reaction | Strecker Degradation Dicarbonyl, C, H, C, H | 52 | 88 | 69% |
| Strecker Degradation Dicarbonyl, C, H, H, C | 52 | 88 | 69% | |
| Strecker Degradation Dicarbonyl, H, H, C, H | 13 | 22 | 69% | |
| Strecker Degradation Dicarbonyl, H, H, H, C | 13 | 22 | 69% | |
| Amide Formation Hydrolysis, C | 9 | 15 | 67% |
| CRN | # Generations | # Catalyzed Compounds | % Catalyzed |
|---|---|---|---|
| Formose Reaction | 5 | 1634 | 7% |
| Pyruvic Reaction | 5 | 765 | 8.4% |
| Glucose Degradation Reaction | 4 | 231 | 3% |
| Glucose-Glycine Maillard Reaction | 3 | 33 | 1.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahi, S.R.; Cleaves, H.J., II. The Effects of Iron on In Silico Simulated Abiotic Reaction Networks. Molecules 2022, 27, 8870. https://doi.org/10.3390/molecules27248870
Shahi SR, Cleaves HJ II. The Effects of Iron on In Silico Simulated Abiotic Reaction Networks. Molecules. 2022; 27(24):8870. https://doi.org/10.3390/molecules27248870
Chicago/Turabian StyleShahi, Sahil Rajiv, and H. James Cleaves, II. 2022. "The Effects of Iron on In Silico Simulated Abiotic Reaction Networks" Molecules 27, no. 24: 8870. https://doi.org/10.3390/molecules27248870
APA StyleShahi, S. R., & Cleaves, H. J., II. (2022). The Effects of Iron on In Silico Simulated Abiotic Reaction Networks. Molecules, 27(24), 8870. https://doi.org/10.3390/molecules27248870






