HeH+ under Spatial Confinement
Abstract
:1. Introduction
2. Methodology
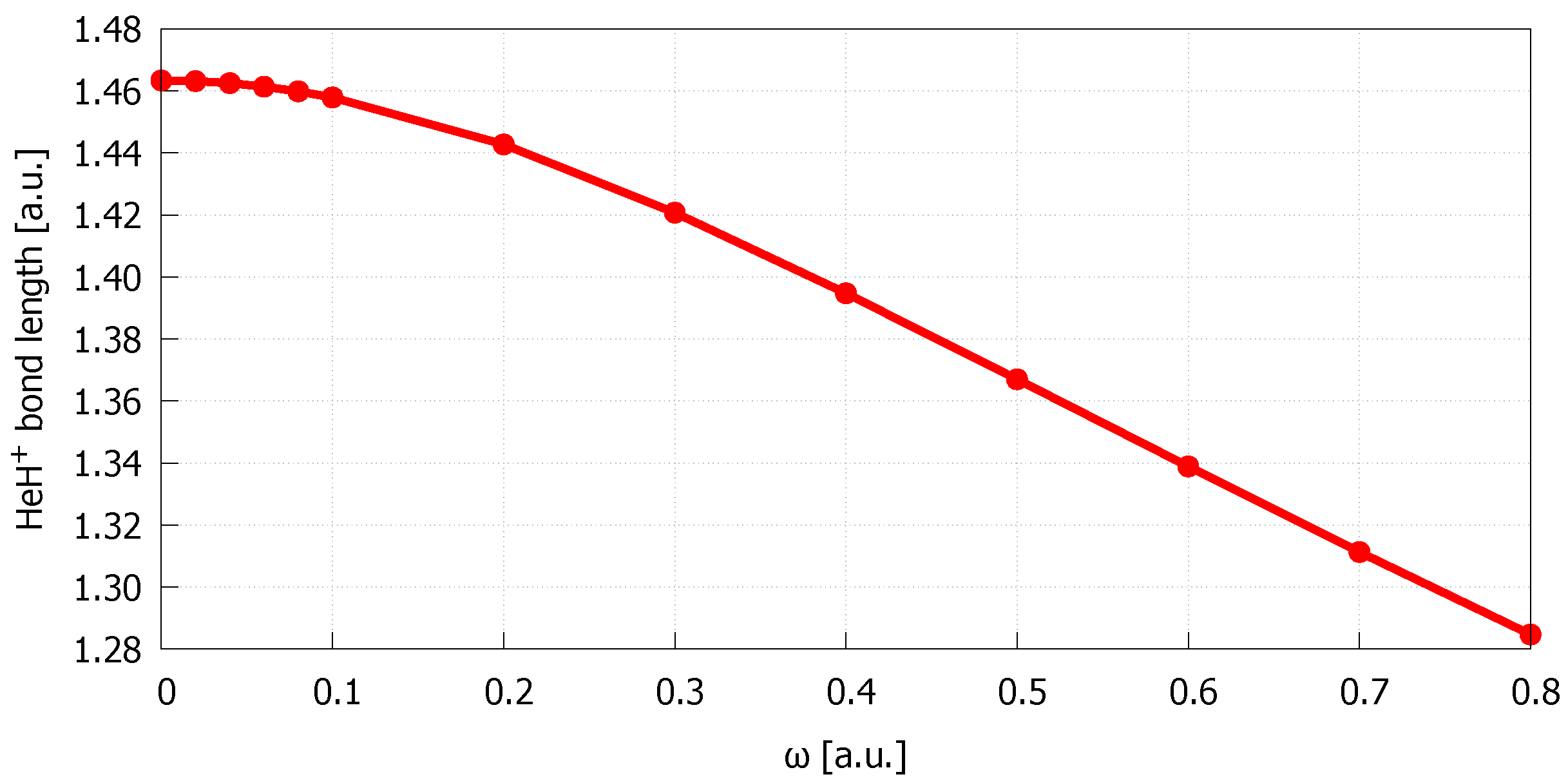
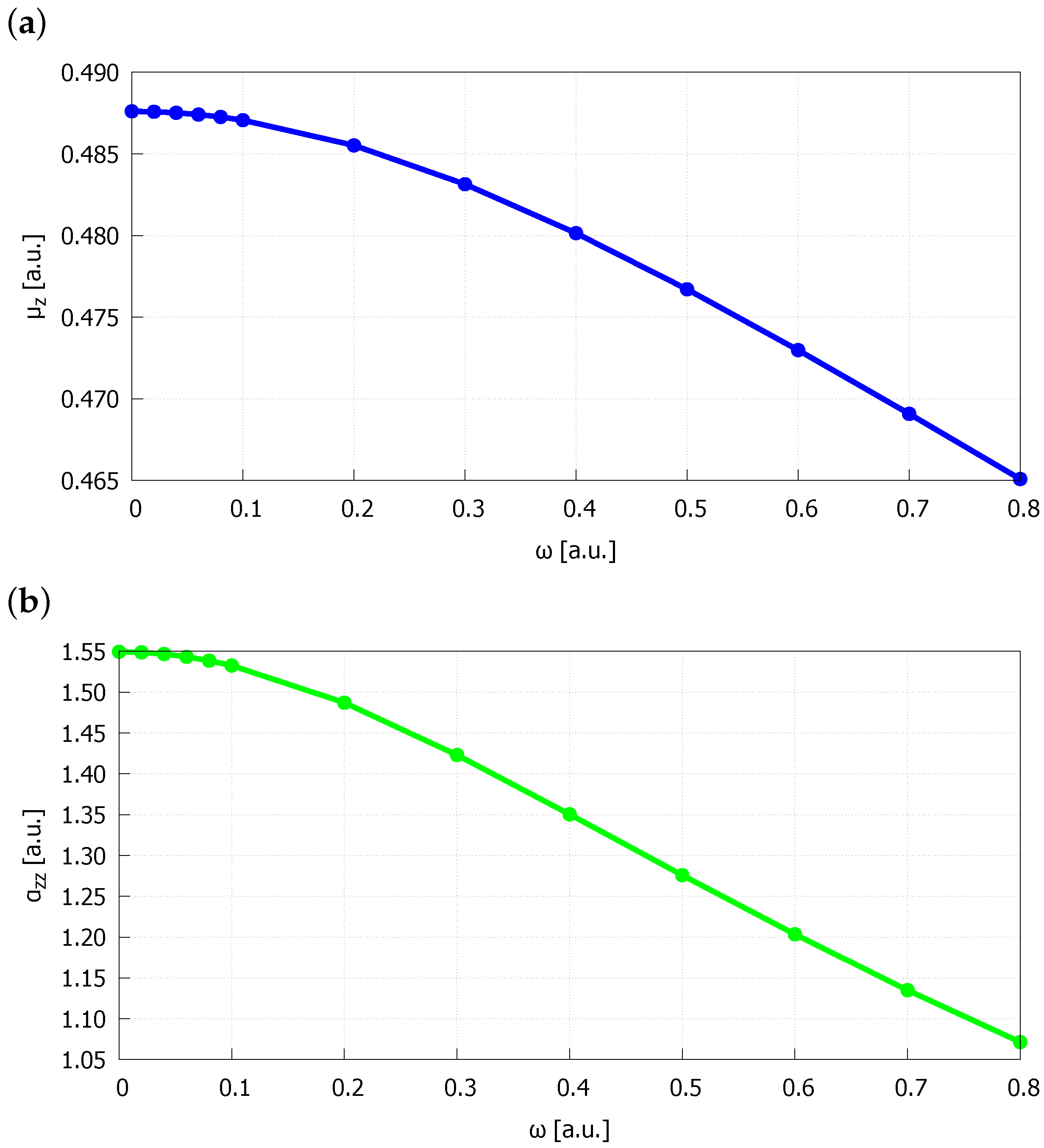
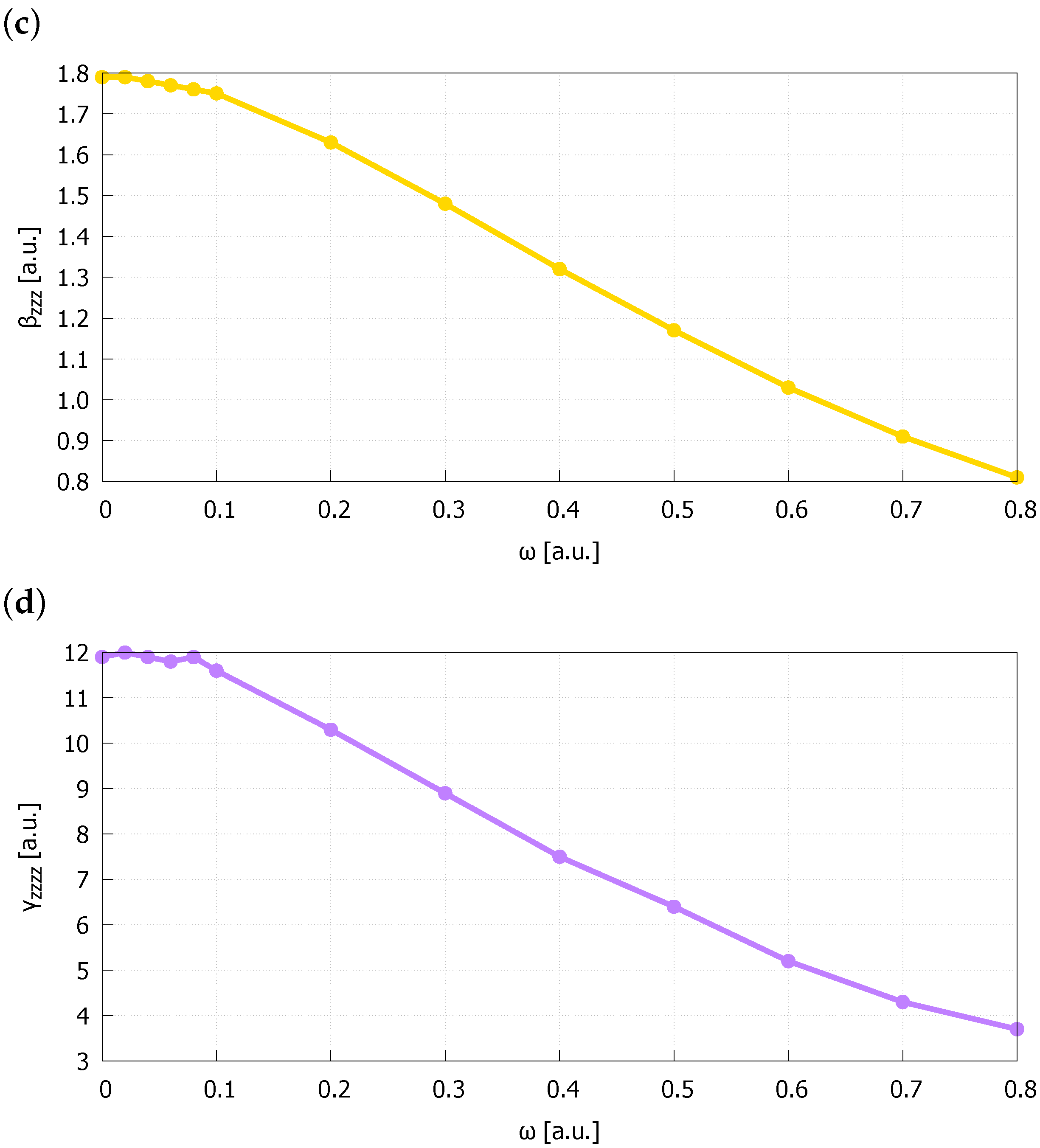
3. Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hogness, T.R.; Lunn, E.G. The Ionization of Hydrogen by Electron Impact as Interpreted by Positive Ray Analysis. Phys. Rev. 1925, 26, 44–55. [Google Scholar] [CrossRef]
- Drabowski, I.; Herzberg, G. The predicted infrared spectrum of HeH+ and its possible astrophysical importance. Ann. N. Y. Acad. Sci. 1977, 38, 14–25. [Google Scholar]
- Black, J.H. Molecules in planetary nebulae. Astrophys. J. 1978, 222, 125–131. [Google Scholar] [CrossRef]
- Flower, D.R.; Roueff, E. On the formation and destruction of HeH+ in gaseous nebulae and the associated infra-red emission line spectrum. Astron. Astrophys. 1979, 72, 361–366. [Google Scholar]
- Roberge, W.; Dalgarno, A. The formation and destruction of HeH+ in astrophysical plasmas. Astrophys. J. 1982, 255, 489–496. [Google Scholar] [CrossRef]
- Güsten, R.; Wiesemeyer, H.; Neufeld, D.; Menten, K.M.; Graf, U.U.; Jacobs, K.; Klein, B.; Ricken, O.; Risacher, C.; Stutzki, J. Astrophysical detection of the helium hydride ion HeH+. Nature 2019, 568, 357–359. [Google Scholar] [CrossRef] [Green Version]
- Harris, F.E. Potential Curve for HeH+. J. Chem. Phys. 1966, 44, 3636. [Google Scholar] [CrossRef]
- Stewart, R.F.; Watson, D.K.; Dalgarno, A. Variational time-dependent Hartree-Fock calculations. III. Potential curves for two-electron molecular systems. J. Chem. Phys. 1976, 65, 2104. [Google Scholar] [CrossRef]
- Bishop, D.M.; Cheung, L.M. Dynamic dipole polarizability of H2 and HeH+. J. Chem. Phys. 1980, 72, 5125. [Google Scholar] [CrossRef]
- Bishop, D.M.; Cheung, L.M. Dynamic dipole polarizability of HeH+. J. Chem. Phys. 1982, 76, 2492. [Google Scholar] [CrossRef]
- Pavanello, M.; Bubin, S.; Molski, M.; Adamowicz, L. Non-Born-Oppenheimer calculations of the pure vibrational spectrum of HeH+. J. Chem. Phys. 2005, 123, 104306. [Google Scholar] [CrossRef] [Green Version]
- Pachucki, K. Born-Oppenheimer potential for HeH+. Phys. Rev. A 2012, 85, 042511. [Google Scholar] [CrossRef]
- Tiihonen, J.; Kylanp, I.; Ranta, T.T. General polarizability and hyperpolarizability estimators for the path-integral Monte Carlo method. Phys. Rev. A 2016, 94, 1–8. [Google Scholar] [CrossRef]
- Yue, L.; Wustelt, P.; Sayler, A.M.; Oppermann, F.; Lein, M.; Paulus, G.G.; Gräfe, S. Strong-field polarizability-enhanced dissociative ionization. Phys. Rev. A 2018, 98, 043418. [Google Scholar] [CrossRef] [Green Version]
- Ayouz, M.; Kokoouline, V. Cross Sections and Rate Coefficients for Rovibrational Excitation of HeH+ Isotopologues by Electron Impact. Atoms 2019, 7, 67. [Google Scholar] [CrossRef] [Green Version]
- Giri, K.; Mishra, B.K.; Sathyamurthy, N. Disruptive influence of the host cage C60 on the guest He-H+ bond and bonding in H3+. J. Indian Chem. Soc. 2021, 98, 100101. [Google Scholar] [CrossRef]
- Montgomery, W.; Watson, J.S.; Sephton, M.A. An organic cosmo-barometer: Distinct pressure and temperature effects for methyl substituted polycyclic aromatic hydrocarbons. Astrophys. J. 2014, 784, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Jaskólski, W. Confined many-electron systems. Phys. Rep. 1996, 27, 1. [Google Scholar] [CrossRef]
- Bielińska-Wąż, D.; Karwowski, J.; Diercksen, G.H.F. Spectra of confined two-electron atoms. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 1987. [Google Scholar] [CrossRef]
- Buchachenko, A.L. Compressed Atoms. J. Phys. Chem. B 2001, 105, 5839–5846. [Google Scholar] [CrossRef]
- Sen, K.D.; Garza, J.; Vargas, R.; Aquino, N. Static dipole polarizability of shell-confined hydrogen atom. Phys. Lett. A 2002, 295, 299. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Sarkar, U. Chemical reactivity of the confined atoms. Chem. Phys. Lett. 2003, 372, 805. [Google Scholar] [CrossRef]
- Lo, J.M.H.; Klobukowski, M.; Diercksen, G.H.F. Low-Lying Excited States of the Hydrogen Molecule in Cylindrical Harmonic Confinement. In Advances in Quantum Chemistry; Sabin, J.R., Ed.; Academic Press: Waltham, MA, USA, 2005; Volume 48. [Google Scholar]
- Sabin, J.R.; Brändas, E.; Cruz, S.A. (Eds.) Advances in Quantum Chemistry: Theory of Confined Quantum Systems; Academic Press: Waltham, MA, USA, 2009; Volume 57–58. [Google Scholar]
- Sen, K.D. (Ed.) Electronic Structure of Quantum Confined Atoms and Molecules; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Rahm, M.; Cammi, R.; Ashcroft, N.W.; Hoffmann, R. Squeezing All Elements in the Periodic Table: Electron Configuration and Electronegativity of the Atoms under Compression. J. Am. Chem. Soc. 2019, 141, 10253–10271. [Google Scholar] [CrossRef] [PubMed]
- Cammi, R.; Rahm, M.; Hoffmann, R.; Ashcroft, N.W. Varying Electronic Configurations in Compressed Atoms: From the Role of the Spatial Extension of Atomic Orbitals to the Change of Electronic Configuration as an Isobaric Transformation. J. Chem. Theory Comput. 2020, 16, 5047–5056. [Google Scholar] [CrossRef]
- Bartkowiak, W.; Chołuj, M.; Kozłowska, J. Effect of confinement on the optical response properties of molecules. In Chemical Reactivity in Confined Systems: Theory, Modelling and Applications; Chattaraj, P.K., Chakraborty, D., Eds.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Bartkowiak, W.; Strasburger, K. Linear and nonlinear electric properties of spatially confined LiH molecule, studied with the finite field method. J. Mol. Struc.-Theochem. 2010, 960, 93. [Google Scholar] [CrossRef]
- Bielińska-Wąż, D.; Diercksen, G.H.F.; Klobukowski, M. Quantum chemistry of confined systems: Structure and vibronic spectra of a confined hydrogen molecule. Chem. Phys. Lett. 2001, 349, 215. [Google Scholar] [CrossRef]
- Borgoo, A.; Tozer, D.J.; Geerlings, P.; Proft, F.D. Influence of confinement on atomic and molecular reactivity indicators in DFT. Phys. Chem. Chem. Phys. 2008, 10, 1406. [Google Scholar] [CrossRef]
- Borgoo, A.; Tozer, D.J.; Geerlings, P.; Proft, F.D. Confinement effects on excitation energies and regioselectivity as probed by the Fukui function and the molecular electrostatic potential. Phys. Chem. Chem. Phys. 2009, 11, 2862. [Google Scholar] [CrossRef]
- Kozłowska, J.; Zaleśny, R.; Bartkowiak, W. On the nonlinear electrical properties of molecules in confined spaces—From cylindrical harmonic potential to carbon nanotube cages. Chem. Phys. 2014, 428, 19. [Google Scholar] [CrossRef]
- Cammi, R.; Verdolino, V.; Mennucci, B.; Tomasi, J. Towards the elaboration of a QM method to describe molecular solutes under the effect of a very high pressure. Chem. Phys. 2008, 344, 135. [Google Scholar] [CrossRef]
- Cammi, R.; Cappelli, C.; Mennucci, B.; Tomasi, J. Calculation and analysis of the harmonic vibrational frequencies in molecules at extreme pressure: Methodology and diborane as a test case. J. Chem. Phys. 2012, 137, 154112. [Google Scholar] [CrossRef] [PubMed]
- Holka, F.; Neogrády, P.; Kellö, V.; Urban, M.; Diercksen, G.H.F. Polarizabilities of confined two-electron systems: The 2-electron quantum dot, the hydrogen anion, the helium atom and the lithium cation. Mol. Phys. 2005, 103, 2747. [Google Scholar] [CrossRef]
- Góra, R.W.; Zaleśny, R.; Kozłowska, J.; Naciążek, P.; Roztoczyńska, A.; Strasburger, K.; Bartkowiak, W. Electric dipole (hyper)polarizabilities of spatially confined LiH molecule. J. Chem. Phys. 2012, 137, 094307. [Google Scholar] [CrossRef] [PubMed]
- Lo, J.M.H.; Klobukowski, M. Computational studies of one-electron properties of lithium hydride in confinement. Chem. Phys. 2006, 328, 132. [Google Scholar] [CrossRef]
- Zaleśny, R.; Góra, R.W.; Luis, J.M.; Bartkowiak, W. On the particular importance of vibrational contributions to the static electrical properties of model linear molecules under spatial confinement. Phys. Chem. Chem. Phys. 2015, 17, 21782. [Google Scholar] [CrossRef] [Green Version]
- Kozłowska, J.; Roztoczyńska, A.; Bartkowiak, W. About diverse behavior of the molecular electric properties upon spatial confinement. Chem. Phys. 2015, 456, 98. [Google Scholar] [CrossRef]
- Zaleśny, R.; Chołuj, M.; Kozłowska, J.; Bartkowiak, W.; Luis, J.M. Vibrational nonlinear optical properties of spatially confined weakly bound complexes. Phys. Chem. Chem. Phys. 2017, 19, 24276. [Google Scholar] [CrossRef] [Green Version]
- Chołuj, M.; Bartkowiak, W. Electric properties of molecules confined by the spherical harmonic potential. Int. J. Quantum Chem. 2019, 119, 1–8. [Google Scholar] [CrossRef]
- Chołuj, M.; Bartkowiak, W. Ground-state dipole moment of the spatially confined carbon monoxide and boron fluoride molecules. Chem. Phys. Lett. 2016, 663, 84. [Google Scholar] [CrossRef]
- Chołuj, M.; Bartkowiak, W.; Naciazek, P.; Strasburger, K. On the calculations of the static electronic dipole (hyper)polarizability for the free and spatially confined H−. J. Chem. Phys. 2017, 146, 1–6. [Google Scholar] [CrossRef]
- Chołuj, M.; Kozłowska, J.; Bartkowiak, W. Benchmarking DFT methods on linear and nonlinear electric properties of spatially confined molecules. Int. J. Quantum Chem. 2018, 118, 1–15. [Google Scholar] [CrossRef]
- Kozłowska, J.; Chołuj, M.; Zaleśny, R.; Bartkowiak, W. Two-photon absorption of the spatially confined LiH molecule. Phys. Chem. Chem. Phys. 2017, 19, 7568. [Google Scholar] [CrossRef] [PubMed]
- Chołuj, M.; Luis, J.M.; Bartkowiak, W.; Zaleśny, R. Infrared spectra of hydrogen-bonded molecular complexes under spatial confinement. Front. Chem. 2022, 9, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Luis, J.M.; Duran, M.; Andrès, J.L.; Champagne, B.; Kirtman, B. Finite field treatment of vibrational polarizabilities and hyperpolarizabilities: On the role of the Eckart conditions, their implementation, and their use in characterizing key vibrations. J. Chem. Phys. 1999, 111, 875. [Google Scholar] [CrossRef] [Green Version]
- Medved, M.; Stachovà, M.; Jacquemin, D.; Andrè, J.M.; Perpeté, E.A. A generalized Romberg differentiation procedure for calculation of hyperpolarizabilities. J. Mol. Struc.-Theochem. 2007, 847, 39. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zaleśny, R.; Góra, R.W.; Kozłowska, J.; Luis, M.J.; Ågren, H.; Bartkowiak, W. Resonant and Nonresonant Hyperpolarizabilities of Spatially Confined Molecules: A Case Study of Cyanoacetylene. J. Chem. Theory Comput. 2013, 9, 3463. [Google Scholar] [CrossRef]
- Roztoczyńska, A.; Kozłowska, J.; Lipkowski, P.; Bartkowiak, W. Does the spatial confinement influence the electric properties and cooperative effects of the hydrogen bonded systems? HCN chains as a case study. Chem. Phys. Lett. 2014, 608, 264. [Google Scholar] [CrossRef]
- Lipkowski, P.; Kozłowska, J.; Roztoczyńska, A.; Bartkowiak, W. Hydrogen-bonded complexes upon spatial confinement: Structural and energetic aspects. Phys. Chem. Chem. Phys. 2014, 16, 1430. [Google Scholar] [CrossRef]
- Kozłowska, J.; Bartkowiak, W. The effect of spatial confinement on the noble-gas HArF molecule: Structure and electric properties. Chem. Phys. 2014, 441, 83. [Google Scholar] [CrossRef]
| Basis Set | Bond Length [au] | Error [%] |
|---|---|---|
| aug-cc-pVDZ | 1.486696 | 1.600 |
| aug-cc-pVTZ | 1.466689 | 0.233 |
| aug-cc-pVQZ | 1.464062 | 0.053 |
| aug-cc-pV5Z | 1.463513 | 0.016 |
| aug-cc-pV6Z | 1.463369 | 0.006 |
| d-aug-cc-pVDZ | 1.486466 | 1.584 |
| d-aug-cc-pVTZ | 1.466693 | 0.233 |
| d-aug-cc-pVQZ | 1.464062 | 0.053 |
| d-aug-cc-pV5Z | 1.463512 | 0.016 |
| d-aug-cc-pV6Z | 1.463377 | 0.006 |
| t-aug-cc-pVDZ | 1.486432 | 1.582 |
| t-aug-cc-pVTZ | 1.466704 | 0.234 |
| t-aug-cc-pVQZ | 1.464068 | 0.054 |
| t-aug-cc-pV5Z | 1.463509 | 0.015 |
| t-aug-cc-pV6Z | 1.463358 | 0.005 |
| q-aug-cc-pVDZ | 1.486418 | 1.581 |
| q-aug-cc-pVTZ | 1.466706 | 0.234 |
| q-aug-cc-pVQZ | 1.464068 | 0.054 |
| q-aug-cc-pV5Z | 1.463512 | 0.016 |
| 5-aug-cc-pVDZ | 1.486415 | 1.581 |
| 5-aug-cc-pVTZ | 1.466706 | 0.234 |
| 5-aug-cc-pVQZ | 1.464068 | 0.054 |
| Bond Length | |||||
|---|---|---|---|---|---|
| 0.00 | 1.463369 | 0.487606 | 1.54943 | 1.79 | 11.9 |
| 0.02 | 1.463145 | 0.487584 | 1.54874 | 1.79 | 12.0 |
| 0.04 | 1.462483 | 0.487519 | 1.54669 | 1.78 | 11.9 |
| 0.06 | 1.461369 | 0.487411 | 1.54328 | 1.77 | 11.8 |
| 0.08 | 1.459846 | 0.487260 | 1.53859 | 1.76 | 11.9 |
| 0.10 | 1.457895 | 0.487067 | 1.53266 | 1.75 | 11.6 |
| 0.20 | 1.442737 | 0.485523 | 1.48709 | 1.63 | 10.3 |
| 0.30 | 1.420718 | 0.483147 | 1.42306 | 1.48 | 8.9 |
| 0.40 | 1.394746 | 0.480146 | 1.35040 | 1.32 | 7.5 |
| 0.50 | 1.367002 | 0.476706 | 1.27587 | 1.17 | 6.4 |
| 0.60 | 1.338911 | 0.472980 | 1.20339 | 1.03 | 5.2 |
| 0.70 | 1.311323 | 0.469080 | 1.13495 | 0.91 | 4.3 |
| 0.80 | 1.284713 | 0.465084 | 1.07136 | 0.81 | 3.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chołuj, M.; Lipkowski, P.; Bartkowiak, W. HeH+ under Spatial Confinement. Molecules 2022, 27, 8997. https://doi.org/10.3390/molecules27248997
Chołuj M, Lipkowski P, Bartkowiak W. HeH+ under Spatial Confinement. Molecules. 2022; 27(24):8997. https://doi.org/10.3390/molecules27248997
Chicago/Turabian StyleChołuj, Marta, Paweł Lipkowski, and Wojciech Bartkowiak. 2022. "HeH+ under Spatial Confinement" Molecules 27, no. 24: 8997. https://doi.org/10.3390/molecules27248997
APA StyleChołuj, M., Lipkowski, P., & Bartkowiak, W. (2022). HeH+ under Spatial Confinement. Molecules, 27(24), 8997. https://doi.org/10.3390/molecules27248997





