Next Article in Journal
The Potential Role of Fisetin, a Flavonoid in Cancer Prevention and Treatment
Next Article in Special Issue
Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations
Previous Article in Journal
LC-MS/MS-Based Metabolomic Profiling of Constituents from Glochidion velutinum and Its Activity against Cancer Cell Lines
Previous Article in Special Issue
Regulating the Electronic Structure of Freestanding Graphene on SiC by Ge/Sn Intercalation: A Theoretical Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 27
Issue 24
10.3390/molecules27249014
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Density Functional Theory Study of the Point Defects on KDP (100) and (101) Surfaces

by
Xiaoji Zhao
1,
Yanlu Li
1,* and
Xian Zhao
1,2,*
1
State Key Lab of Crystal Materials, Institute of Crystal Materials, Shandong University, Jinan 250100, China
2
Center for Optics Research and Engineering of Shandong University, Shandong University, Qingdao 266237, China
*
Authors to whom correspondence should be addressed.
Molecules 2022, 27(24), 9014; https://doi.org/10.3390/molecules27249014
Submission received: 29 November 2022 / Revised: 11 December 2022 / Accepted: 13 December 2022 / Published: 17 December 2022
(This article belongs to the Special Issue Applications of Density Functional Theory in Crystalline Materials)
Browse Figures
Review Reports Versions Notes

Abstract

:
Surface defects are usually associated with the formation of other forms of expansion defects in crystals, which have an impact on the crystals’ growth quality and optical properties. Thereby, the structure, stability, and electronic structure of the hydrogen and oxygen vacancy defects (VH and VO) on the (100) and (101) growth surfaces of KDP crystals were studied by using density functional theory. The effects of acidic and alkaline environments on the structure and properties of surface defects were also discussed. It has been found that the considered vacancy defects have different properties on the (100) and (101) surfaces, especially those that have been reported in the bulk KDP crystals. The (100) surface has a strong tolerance for surface VH and VO defects, while the VO defect causes a large lattice relaxation on the (101) surface and introduces a deep defect level in the band gap, which damages the optical properties of KDP crystals. In addition, the results show that the acidic environment is conducive to the repair of the VH defects on the surface and can eliminate the defect states introduced by the surface VO defects, which is conducive to improving the quality of the crystal surface and reducing the defect density. Our study opens up a new way to understand the structure and properties of surface defects in KDP crystals, which are different from the bulk phase, and also provides a theoretical basis for experimentally regulating the surface defects in KDP crystals through an acidic environment.

1. Introduction

Potassium dihydrogen phosphate (KH2PO4, KDP) crystal is the only nonlinear optical crystal material that can be used in inertial confinement nuclear fusion devices [1,2,3,4,5,6,7] because of its excellent nonlinear optical properties, high laser-damage threshold, wide light-transmission range, and ability to grow a large-sized single crystal. However, there is a certain gap between the actual nonlinear optical properties and the laser-damage threshold of KDP crystals in practical applications and for theoretical values. Numerous studies have shown that intrinsic point defects significantly influence the optical properties of KDP crystals. For example, Guillet et al. pointed out that the stress field caused by dislocation or the growth-sector boundary increases the concentration of intrinsic defects, which leads to a reduction in the laser-damage threshold [8]. The first-principles calculation results pointed out that hydrogen and oxygen defects may cause additional optical absorption and reduce the laser-damage threshold of KDP [9,10,11,12,13]. Sui et al. found that point defects such as hydrogen vacancy (VH), oxygen vacancy (VO), etc., can not only introduce defect states in the band gap but also cause large structural deformation and local lattice stress near the defect sites, which can reduce the optical performance of KDP crystals [14,15].
It should be noticed that apart from point defects in the crystals, the defects of KDP surfaces also affect the optical properties of KDP crystals. For example, by combining spectral detection and theoretical calculation, Ding et al. found that the intrinsic defects introduced by lateral cracks in the surface structure of KDP crystals have a serious effect on the laser-damage threshold of the crystals [16]. Since the surface is more active than the bulk crystal, electrons close to the defect state and surface state can be excited to high energy levels by absorbing laser energy. Moreover, when the laser-excited electrons relax to the ground state, they release energy through lattice phonons, which greatly reduces the structural stability of the KDP crystals and causes laser damage [17,18,19,20,21]. On the other hand, since the growth of KDP crystals occurs at the solid–liquid interface, and the growth environment cannot always be ideal and uniform, a large number of defects can be easily formed on the growth surfaces of KDP crystals [22,23]. Defects on the surfaces can extend into the KDP crystals as the surface layer grows further, creating large defects that may act as the origin point of the laser damage. Therefore, it is of great importance to investigate the formation and basic properties of the point defects on the growth surfaces of KDP crystals.
The KDP crystal belongs to the tetragonal crystal system with the space group of I 4 ¯ 2d (CCDC number: 2144930). The PO4 tetrahedron is the basic structural unit of the KDP crystal. These tetrahedrons are connected through hydrogen bonds and form the three-dimensional skeleton of the KDP crystal. K+ ions are arranged orderly in the three-dimensional skeletal system composed of PO4 tetrahedrons [24,25,26]. The growth surfaces of KDP crystals are (100) and (101), which correspond to the cylindrical and pyramidal surfaces, respectively. The (100) surface is a mixed layer of K ions and PO4 tetrahedra, while the (101) surface is a layer that exposes the K ions [27,28]. In the process of crystal growth, growth factors such as temperature, impurities, supersaturation, pH value, etc., can influence the growth quality of KDP crystals, including the formation of defects [29,30,31,32,33]. In particular, the pH value of the growth solution has been reported as an important factor affecting the growth quality and optical properties of KDP crystals [34,35,36]. For example, it has been reported that the growth quality of both the (100) and (101) surfaces of KDP crystals can be significantly improved by increasing the pH value from 3.5 to 5 [36]. Sun et al. found that increasing the pH value can increase the size and decrease the density of the scattering particles in KDP crystals, which is one of the main sources of optical loss and even crystal destruction under strong laser irradiation [37]. Although some research has been completed, the fundamental issues of point defects on KDP crystals’ surfaces are still unclear and need in-depth investigation.
In this work, we carried out density functional theory (DFT) calculations to study the local structural distortion and related electronic properties caused by VH and VO defects on the (100) and (101) surfaces of KDP crystals. Furthermore, by adsorbing H+ and OH− on the surfaces, we can simulate the acid and alkali growth environments of KDP crystals and explore the influence of these different growth environments on the formation and electronic structures of the VH and VO defects on the crystals’ surfaces. It has been found that the vacancy defects are preferable to be formed on the surfaces rather than in the bulk KDP crystal. VH and VO defects are found to have different electronic structures on the (100) and (101) surfaces, which is also different from the phenomenon in the bulk KDP crystal [14,15]. In the bulk KDP crystal, both VH and VO defects could introduce a defect level in the band gap. On the other hand, the acidic environment is found to be conducive to the repair of VH defects on KDP crystals’ surfaces, while the alkaline environment leads to more defects. Our results have produced new insights into the formation and electronic structures of the surface vacancy defects in KDP crystals. We also provide a theoretical basis for using pH value to regulate the formation and properties of point defects in KDP crystals.

2. Computational Details

The DFT calculations were performed by using the Vienna Ab initio Simulation Package (VASP) [38,39] with the projector-augmented-wave (PAW) formalism [40]. The H 1s1, O 2s22p4, P 3s23p3, and K 4s1 states were treated as valence electrons. The generalized gradient approximation (GGA) functional of Perdew Bourke Ernzerhof (PBE) [41] was used to describe the electron-exchange–correlation interactions. The electronic wave functions were expanded in plane waves using a cutoff energy of 500 eV. The force and energy convergence criteria of structural relaxation were set to be 0.02 eV/Å and 10−5 eV/atom, respectively. After the convergence tests, a Monkhorst-Pack k-point grid [42] of 3 × 3 × 1 was used to sample the Brillouin zone for structural optimization, and a denser grid of 7 × 7 × 1 was used for the electronic structure calculations.
According to the experimentally reported growth faces of KDP crystals [27,28], we constructed the (100) and (101) surface models by cutting four KDP molecule layers from a bulk 2 × 2 × 2 tetragonal supercell. A 15 Å vacuum layer was added perpendicular to both the (100) and (101) surfaces, to reduce the interaction between the neighboring periodic images. The surface VH and VO models were constructed by moving a hydrogen or oxygen atom from its original site. All the possible defect sites on the surface and sub-surface were considered, and only the defect with the lowest formation energy was chosen for the structural and property analysis. We simulated the charged defects by setting the total number of electrons and adding electrons or holes to the background of the whole system. Herein, we considered 0 and −1 charge states for the VH defect and 0, +1, and +2 charge states for the VO defect. The acid and alkali growth environments were simulated by placing H+ and OH− ions at about 1.5 Å above the optimized surfaces. In order to better investigate the effect of the acid and alkali growth environments on the intrinsic point defects on the surfaces, we mainly considered the adsorption of H+ and OH− near the defect sites of the surfaces. During the structural optimization, the bottom-most KDP molecule layer was fixed, and the top three KDP molecule layers were allowed to fully relax.
The relative stability of these defects can be determined by comparing their defect formation energies. The calculation formula is as follows [43,44,45,46]:
E f ( X q ) = E t o t a l ( X q ) − E t o t a l ( s u r f a c e ) + ∑ i n i μ i + q ( E f + E v + Δ V )
where Etotal (Xq) and Etotal (surface) are the total energies of the surface with and without the defect X, respectively. q represents the charge of the defect. ni represents the number of atoms of species i that are added or removed when the defect is created, and μi are the corresponding chemical potentials. Ef is the Fermi level of the bulk valence-band maximum Ev, and ΔV is a correction term that aligns the reference potential in the surface with the defect, with respect to the surface without the defect. We calculated the chemical potential of the required elements by referring to the work of Sui [25], namely that the chemical potential of H and O were taken as half of the energies of H2 and O2, and the chemical potentials of P and K were calculated according to the formation enthalpies of their stable compounds P2O5 and K2O. The obtained chemical potential of H, O, P, and K are −3.39, −4.47, −7.39, and −3.63 eV, respectively.

3. Results and Discussion

3.1. Stability and Structures of the Point Defects on the KDP Surfaces

Firstly, we constructed the most stable structures of the (100) and (101) surfaces, which correspond to the cylindrical and pyramidal surfaces of the KDP crystals, respectively, according to the exposed surface atoms reported by previous experiments [27,28], as can be seen in Figure 1. The calculated surface energies of the (100) and (101) surfaces are 0.0321 eV/Å2 and 0.0327 eV/Å2, respectively. The slightly higher surface energy of the (101) surface indicates a faster growth rate and a higher activity than the (100) surface. This is consistent with the experimental result: the growth rate of the pyramidal surface is higher than that of the cylindrical surface [27,47]. We can also infer from the calculated surface energies that the (101) surface has a stronger adsorption capacity for ions and small molecules.
Since VH and VO defects have been reported as the main defects in KDP crystals and also have a significant influence on the optical properties, we then focused on the structures and electronic structures of these two point defects on the surfaces of KDP crystals. The selected sites to construct the VH and VO defect models are shown in Figure 1, in which they reflect the different locations and coordination environments at the surface, subsurface, and interior of the surface models. We compared the difficulty of forming VH and VO defects at different sites on the (100) and (101) surfaces and in the bulk KDP crystal by calculating their defect formation energies, as seen in Table 1. It can be seen that the formation energies of both the VH and VO defects on both the (100) and (101) surfaces are more than 1 eV lower than those in the bulk KDP. This indicates that these vacancy defects are preferable to be formed on the surfaces rather than in the bulk. Meanwhile, their formation energy on the (101) surface is about 0.3 eV lower than that on the (100) surface, which indicates that the structure and properties of the (101) surface are more sensitive and susceptible to intrinsic defects. It should be noted that the VH defect prefers to form at the outermost surface site on both the (100) and (101) surfaces, while the VO defect shows different stable sites on the different surfaces of KDP crystals. For the (100) surface, the VO defect prefers to form at the surface site connected to the other PO4 group by the hydrogen bond. For the (101) surface, the formation energy of the VO defect at the inner site is 1.27 eV lower than that at the surface sites, indicating that the VO defects formed inside the crystal are extremely stable. In this case, the structure and properties of the (101) surface are mainly influenced by the VH defect instead of the VO defect. By comparing the formation energies, we selected Hsurf and Osub on the (100) surface and Hsurf and Oin on the (101) surface as the VH and VO defect sites for the following studies.
In order to further understand the impact of surface vacancy defects on the surface structures, we compared the local lattice distortion caused by the neutral and charged VH and VO defects on the (100) and (101) surfaces of KDP crystals in Figure 2. The change in the related bond lengths and bond angles are listed in Table 2. For the (100) surface, the removal of a surface hydrogen atom leads to two oxygen atoms that were initially connected through this hydrogen atom (O-H…O hydrogen bond) moving away from each other, and, thus, the distance between O1 and O2 increases by 1.82 Å (Figure 2b). At the same time, the two PO4 tetrahedra connected by this hydrogen atom distort with the bond angle ∠O2P2O3 increasing by about 8°. The influence of an electron captured by the neutral VH defect on the structure can be neglected (Figure 2c). For the VO defect, the adjacent hydrogen atom falls into the original vacancy defect, which leads to the movement of the hydrogen atom into the adjacent hydrogen bonds toward the PO4 tetrahedron. The bond length of H-O2 is, thus, shortened by 0.12 Å (Figure 2d). The effect of a one and two electron loss from the neutral VO defect on the structure can also be neglected (Figure 2e,f).
For the (101) surface, the surface VH defect has little influence on the local structure of the adjacent PO4 groups. In contrast, the VO defect in the inner layer leads to serious lattice distortion of PO3, because the VO defect shortens the P-O2 bond and increases the angle of ∠O2PO3, especially for the VO2+ defect. When the neutral VO0 loses one electron to form VO+, the hydrogen atom that was originally attached to the vacancy O atom becomes attached to the adjacent PO4 tetrahedron, instead of occupying the vacancy site like in the case of the (100) surface, due to the electrostatic repulsive force. A similar phenomenon has also been observed in the case of VO2+. The increase in electrostatic repulsion after the loss of two electrons moves the hydrogen atom farther away from the P atom in PO3. As a result, the H-P distance increases by 0.43 Å compared with the structure of VO+. However, the loss of two electrons causes a serious distortion in the structure of PO3. For instance, the O1-O2 distance increases by 0.05 Å, the P-O2 distance decreases by 0.05 Å, and the bond angle ∠O2PO3 increases by ~12°, compared with the structure of VO0.
Through the above analysis, it can be concluded that both the VH and VO defects have relatively local influences on the structure of the (100) surface and do not cause significant surface reconstruction. However, the VO defect on the (101) surface is mainly formed in the deep layers of the surface and, thus, causes a large degree and range of lattice distortion on the surface. Especially as the VO charge states increase from 0 to +2, the VO defect shows an increasing effect on the lattice distortion of the surface structure. We, thus, speculate that the VO defect will also have a great impact on the electronic structure of the (101) surface.

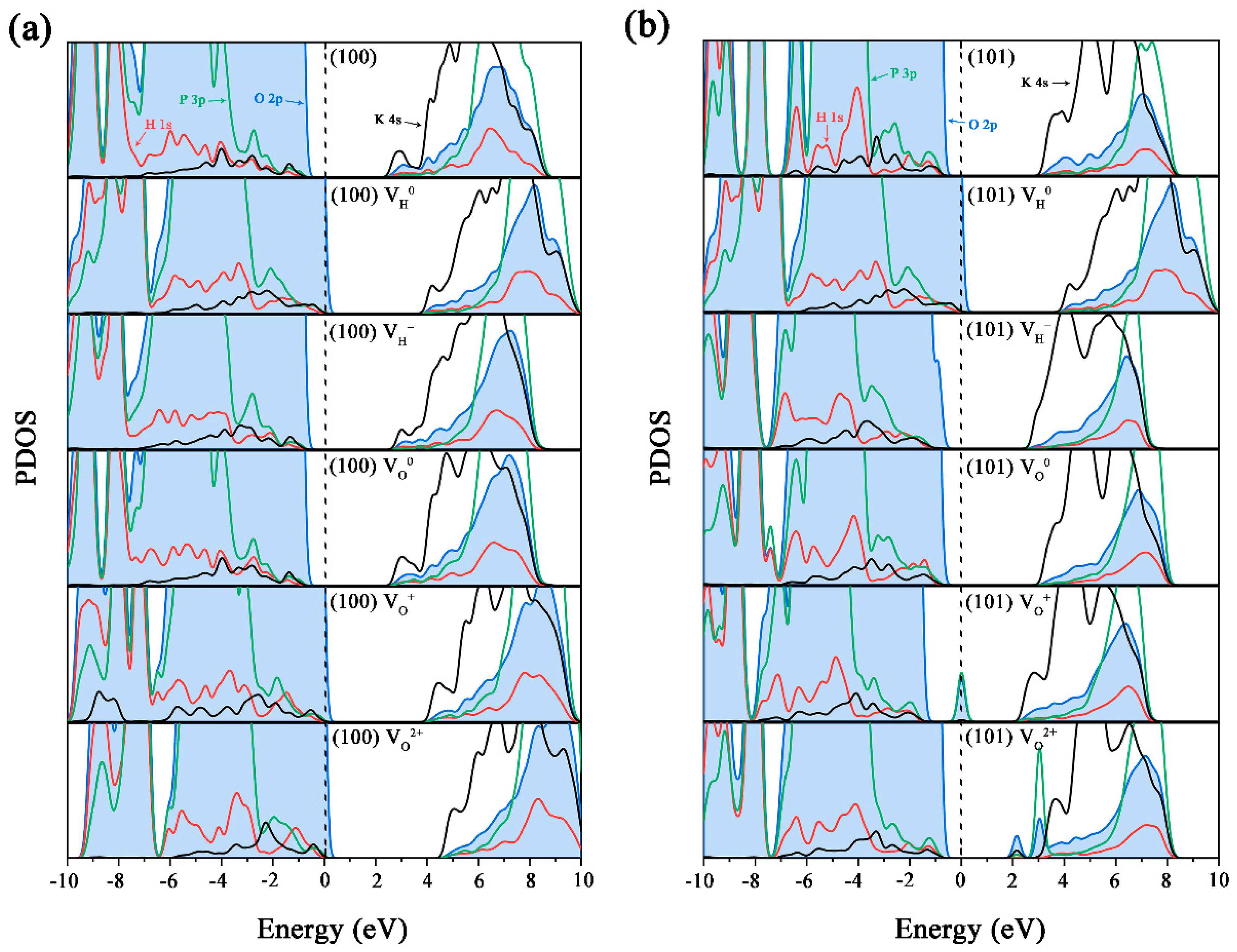
3.2. Electronic Structures of KDP Surfaces with Vacancy Defects

To confirm our suspicions, we calculated the partial density of states (PDOS) of the (100) and (101) surfaces with different charged VH and VO defects, as shown in Figure 3. For both the (100) and (101) surfaces, the valence band maximum (VBM) is mainly contributed by the O 2p states, while the conduction band minimum (CBM) is mainly contributed by the K 4s states. However, the contribution of the K 4s states to the CBM of the (101) surface is much stronger than that of the (100) surface because the (101) surface is exposed by the K+ ions. When a VH0 is formed on the (100) surface, a defect state is introduced near the VBM, and the charge disperses in the nearby O atoms. When VH0 gains one electron, the Fermi energy level shifts slightly upward, without a significant change in the contribution from the electron states. The VH on the (101) surface shows a similar influence on the VBM, but changes the contribution of the K 4s states to the CBM. Since the absence of a H atom leads to the transfer of the surrounding electrons to the defect site and a weakening of the charge transfer between the surface group and the K+ ions, the VH0 on the (101) surface reduces the contribution of the K electronic states to the CBM. When VH0 captures an electron to form VH−, the charge balance is restored, and the contribution of K+ ions at the CBM is significantly enhanced. This indicates that when the concentration of VH is high enough, the electrostatic force of the K+ ion layer on the (101) surface is weakened. When the surface adsorbs the growth groups, reaching the equilibrium state is not favorable and, thus, affects the microscopic growth process.
The generation of VO usually creates a donor level below the CBM in the bulk [13], but no donor level can be observed in the band structure of VO on the (100) surface (Figure 3a). This is because after forming a VO on the (100) surface, the neighboring H atom moves to the VO site to form a stable H-PO3 configuration, which causes two additional electrons to be transferred to the H atom. When VO+ and VO2+ defects are formed, the lost electrons are distributed over the surface instead of being localized around the vacancy site. Therefore, the charged VO defects do not introduce any defect levels in the band gap. In general, surface VO defects can be immediately filled with H atoms, thereby reducing the effect of defects on the structure and electronic structure of the (100) surface. Therefore, the acidic environment may be more conducive to eliminate the defect state of VO defects and maintain the good optical characteristics of the (100) surface.
The structure and electronic structure of the VO0 on the (101) surface are similar to those on the (100) surface due to the filling of the vacancy site by the neighboring H atom. However, when the VO0 loses one electron, the H atom leaves the VO site and forms a H-O chemical bond with its nearest neighboring O atom. Therefore, a normal VO defect can be observed (Figure 2k), which can introduce a deep and half-filled defect level in the band gap (Figure 3b). This defect level is composed by the 3p states of the adjacent P atom and the 2p states of the adjacent O atom. When the VO+ loses one more electron, this defect level moves below the CBM. In addition, another defect level at 2.2 eV can also be observed from the PDOS figure for the VO2+ on the (101) surface, which mainly comes from the 2p states of the three O atoms of the surface PO3 group. The deep defect levels introduced by VO+ and VO2+ defects can introduce additional optical absorption that damage the optical performance of KDP crystals. On the other hand, the VO defect forms in the inner layer of the (101) surface, so it is difficult to repair it in the process of crystal growth, and it is easy to enter the interior of a crystal with the stability of the growth layer and the process of the crystal’s growth. Therefore, the VO defect becomes the initial point of defect extension in the crystal and the prone point of laser damage, which has an adverse effect on the optical absorption and laser-damage properties of KDP crystals.

3.3. Effects of Acidic Environment on the Defective Surface of KDP Crystals

We simulated the effect of an acidic environment on the crystal surface by adsorbing H+ and compared the structural change of the perfect surfaces and defective surfaces, as shown in Figure 4. It has been found that the adsorption energies of H+ on the (100) and (101) surfaces are −0.43 eV and −1.08 eV, respectively. This indicates that the H+ is adsorbed on the (100) surface by very weak physisorption. This can be confirmed by the isolated charge distribution around the H+ (Figure 4a) and the fact that H+ is as far as 3.011 Å from the (100) surface. In order to further analyze the interaction between the adsorbed H+ and the surface, we plotted the PDOS of the adsorbed ions and their adjacent surface atoms in Figure 5a. Previous studies have found that if the adsorbed particles and the surface are bonded together, the PDOS of the bonded atoms will have the same resonance peaks [48,49]. As shown in Figure 5a, there is no resonance peak between H+ and the nearest atoms on the (100) surface, indicating that the H+ is not bonded to the surface. On the other hand, the much lower adsorption energy of the H+ on the (101) surfaces indicates that the adsorption of H+ on the (101) surface is quite stable. This is because H+ is connected to the outermost O atom on the (101) surface by a weak H-O bond. This can be judged by the charge distribution along the H-O bond (Figure 4d), by the bond length (1.674 Å) between the typical H-O bond length (0.96 Å), and by the hydrogen bond length (2.55 Å). The interaction between H and O has been proven to have a significant impact on the molecular arrangement and characteristics of materials [50]. This phenomenon can also be verified by the overlapped resonance peaks between the H ls states and O 2p states over a wide range, as shown in Figure 5a.
When the (100) surface contains a VH, the adsorbed H+ falls into the VH site, and the defect is repaired. According to Figure 5a, there are resonance peaks between the H+ adsorbed to the surface and the O atoms on both adjacent sides, indicating that H+ and O atoms form chemical bonds connecting the two PO4 tetrahedrons. This is consistent with the significant decrease in the adsorption energy of H+ on the defective surface (−4.87 eV). Therefore, the PDOSs of the H+ adsorbed (100) surface with and without VH are almost exactly the same (Figure 5b). For the surface containing the VO, the reduced H+ adsorption energy, with respect to that on the perfect surface and the overlapped resonance peaks shown in Figure 5a, all indicate that the surface VO defect promotes the interaction between the adsorbed H+ and the surface defect. It is interesting to note that the H that fell into the VO site combines with the adsorbed H+ and forms H2. Then, a Vo defect is formed at the (100) surface, and the H2 molecule is adsorbed at 1.23 Å above the defective surface. Therefore, a defect state of VO can be clearly observed near the VBM from the PDOS in Figure 5b. It should be noted that the formation of the H2 molecule represents an extreme situation, because we are examining the surface under vacuum conditions. In real experimental conditions, a KDP crystal’s growth surface is exposed to the solvent environment, and the water molecules, K+ ions, and growth groups in the solvent weaken the interaction between the surface H atom and the adsorbed H+ ions, making it difficult to form a real H2 molecule. However, our study shows that because the surface H atom and adsorbed H+ ion tend to attract each other and form a stable chemical bond, the acidic environment makes the VO defect on the (100) surface more stable, thereby damaging the optical properties of KDP crystals.
For the adsorption of H+ on the defective (101) surface, it can be seen from Figure 4e that the adsorbed H+ also restores the VH on the (101) surface, resulting in a serious reduction in the H+ adsorption energy, with respect to that on the perfect surface. This phenomenon is similar to that on the (100) surface, which can be verified by the resonance peaks at the same position and with similar intensity from the PDOSs of the H+ adsorption on the (100) and (101) surfaces with VH, as shown in Figure 5a. For the H+ adsorption on the (101) surface with a neutral VO, Figure 4f shows that the H+ connects with the O atom in the outer layer with slight deformation, and the PO4 tetrahedra at the adsorption position reaches the outermost layer of the crystal instead of K+. The PDOS in Figure 5a shows many overlapped resonance peaks, indicating the hybridization between the H ls and O 2p states and the bonding interaction between the adsorbed H+ and O atoms on the surface. Although H+ interacts with the (101) surface, H+ adsorption has little effect on the electronic structure of the (101) surface with a VO defect (Figure 5b). It is interesting that when the H+ adsorbs on the (101) surface with a charged VO defect (VO+ and VO2+), the VO site is filled by the adjacent H atom to form the stable H-PO3 configuration, as it occurs on the (100) surface. Therefore, the defect levels introduced by the charged VO defects can be eliminated (Figure 5b). From the above analysis, we can see that an acidic environment can repair the surface VH defects on both the (100) and (101) surfaces and can also eliminate the defect states in the band gap of the (101) surface induced by the VO defect. Therefore, the acidic environment plays a positive role in improving the surface quality and the optical properties of KDP crystals.

3.4. Effects of Alkaline Environment on the Defective Surface of KDP Crystals

By adsorbing OH− on the (100) and (101) surfaces, we investigated the influence of an alkaline environment on the structures and electronic structures of the VH and VO defects on KDP crystals’ surfaces. As shown in Figure 6, the adsorption energies of OH− on the (100) and (101) surfaces are −1.08 eV and −1.37 eV, respectively. From the moderate adsorption energy values for H+ on the (100) and (101) surfaces, we can make a preliminary inference that OH− is chemically adsorbed on the (101) surface. From Figure 6a, we can see that the OH− binds with the exposed H atom on the surface and forms a water molecule. The generated H2O molecule is adsorbed on the (100) surface and connects to the surface through a hydrogen bond. This phenomenon can be verified by the calculated PDOS in Figure 7a, where the resonance peaks of O on the OH− and the surface H atom overlap at about −7.5 eV, indicating the chemical interaction between the OH− and the H atom on the (100) surface. This phenomenon is consistent with the result of Zhang [51]. It can be seen from Figure 6a that a serious charge transfer occurs between the H2O molecule and the (100) surface, which greatly reduces the adsorption energy to −3.02 eV [52]. Therefore, the alkaline environment causes the (100) surface to lose H atoms and then destroy the surface structure to form VH defects. For the adsorption of OH− on the (101) surface, since there is no exposed H atom in the outermost layer, the OH− adsorbs near the surface O atoms with a H-O bond length of 1.941 Å. The adsorption of OH− has a slight influence on the structure and energy of the (101) surface. By comparison, it can be seen that OH− has a greater impact on the (100) surface than the (101) surface. This is consistent with experiments that grew high-quality KDP crystals in a weakly acidic environment.
When OH− adsorbs on the (100) surface with a VH defect, OH− also combines with the outmost H atom to form a H2O molecule and then adsorbs on the crystal surface (Figure 6b). Due to the attractive force from the VH, the distance between the H2O molecule and the surface slightly increases by 0.13 Å. Since the adsorbed H2O molecule has little influence on the structure and electron distribution of VH, the OH− adsorption has little influence on the electronic structure of the (100) surface with a VH defect (Figure 7b). In contrast, when OH− is adsorbed on the (100) surface with a VO defect, OH− is far away from the surface with a distance of 3.689 Å, indicating that there is no interaction between the OH− and the surface. This can also be verified by the PDOS in Figure 7a, which shows that the O atom in OH− and the H atom on the surface have no overlapped resonance peaks. Therefore, the OH− adsorption has little influence on the electronic structure of the (100) surface with a VO defect.
For the (101) surface with a VH defect, the adsorbed OH− could insert into the VH site, leading to an obvious charge transfer between the OH− and the adjacent O atom. This can be seen from the calculated charge distribution in Figure 6e and can be verified by the many overlapped resonance peaks over a wide energy range in Figure 7a. Due to the charge transfer, the surface K+ contributes more electrons, and the contribution of their electronic states at the CBM is, thus, enhanced. The effect of OH− adsorption on the structure and electronic structure of the (101) surface with a VO defect is similar to that of the (100) surface. Both the calculated charge distribution in Figure 6f and the PDOS in Figure 7a verify that there is almost no charge transfer between OH− and the surface. Therefore, the adsorption energy (−0.78 eV) is as high as that on the (100) surface. On the other hand, the introduced defect states of the charged VO defects in the band gap of the (101) surface cannot be eliminated because of the very weak interaction between OH− and the surface. Therefore, the alkaline environment cannot improve the electronic structure of the defective surfaces, but it leads to more VH defects on the surface, which is not conducive to the improvement of the surface quality and properties.

4. Conclusions

In summary, we investigated the structure, stability, and electronic structure of hydrogen and oxygen vacancy defects (VH and VO) on the (100) and (101) surfaces of KDP crystals using density functional theory. The effects of acidic and alkaline environments on the structure and properties of these defects were also studied. The results show that both VH and VO defects are more likely to be formed on the crystals’ surface than in the bulk phase. The effect of a VH defect on the electronic structures of the (100) and (101) surfaces is almost negligible, while a VO defect on the different surfaces shows different sites and electronic structure characteristics compared with that in the bulk KDP. Different from the donor energy level introduced by a VO defect in the bulk KDP, a VO defect on the (100) surface does not introduce any defect level and can maintain the good optical properties of the crystal. However, a VO defect on the (101) surface tends to be formed in the deep layer and introduce deep defect states, resulting in extra optical absorption and a reduction in the optical properties of KDP crystals. In addition, an acidic environment is conducive to the repair of surface VH and can eliminate the defect states introduced by the surface VO defects, which is conducive for improving the quality of the crystals’ surface and reducing the defect density. An alkaline environment leads to the formation of more VH defects, which should be avoided. Our study can provide theoretical guidance for the experimental optimization of the crystal-growth parameters needed to improve the quality of KDP crystals.

Author Contributions

Investigation, data curation, visualization, writing—original draft preparation, X.Z. (Xiaoji Zhao); investigation, writing—review and editing, funding acquisition, Y.L.; writing—review and editing, supervision, X.Z. (Xian Zhao). All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2020ZD35), the Young Scholars Program of Shandong University (Grant No. 2018WLJH65), and the Young Talents Cultivation Project of the State Key Laboratory of Crystal Materials.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This work was carried out at the National Supercomputer Center in Tianjin, and the calculations were performed on TianHe-1(A). This work was supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2020ZD35), the Young Scholars Program of Shandong University (Grant No. 2018WLJH65), and the Young Talents Cultivation Project of the State Key Laboratory of Crystal Materials. The authors would also like to express their gratitude to EditSprings (https://www.editsprings.cn (accessed on 12 December 2022)) for the expert linguistic services provided.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rashkovich, L.N. KDP-Family Single Crystals. Published under the Adam Hilger Imprint by IOP Publishing Ltd. 1991. Available online: https://www.amazon.co.uk/KDP-Family-Single-Crystals-Optoelectronics/dp/0750301058 (accessed on 17 November 2022).
  2. De Yoreo, J.J.; Burnham, A.K.; Whitman, P.K. Developing KH2PO4 and KD2PO4 crystals for the world’s most powerful laser. Int. Mater. Rev. 2002, 47, 113–152. [Google Scholar] [CrossRef]
  3. Nikogosyan, D. Nonlinear Optical Crystals: A Complete Survey; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  4. Yin, H.W.; Li, M.W.; Zhou, C.; Song, J. KDP single crystal growth via three-dimensional motion growth method. Cryst. Res. Technol. 2016, 51, 491–497. [Google Scholar] [CrossRef]
  5. Chen, D.Y.; Wang, B.; Wang, H.; Zhu, X.Y.; Xu, Z.Y.; Zhao, Y.N.; Wang, S.H.; Ni, K.Z.; Zheng, L.L.; Zhang, H.; et al. Rapid growth of a long-seed KDP crystal. High Power Laser Sci. Eng. 2020, 8, 5. [Google Scholar] [CrossRef] [Green Version]
  6. Zhang, Y.; Fan, Q.C.; Gao, W.; Wang, C.; Ji, F. Novel abrasive-free jet polishing for Bulk single-crystal KDP with a low viscosity microemulsion. Sci. Rep. 2022, 12, 8346. [Google Scholar] [CrossRef]
  7. Cheng, Z.P.; Gao, H.; Liu, Z.Y.; Guo, D.M. Investigation of the trajectory uniformity in water dissolution ultraprecision continuous polishing of large-sized KDP crystal. Int. J. Extreme Manuf. 2020, 2, 045101. [Google Scholar] [CrossRef]
  8. Guillet, F.; Bertussi, B.; Surmin, A.; Duchateau, G. Effect of stress on laser damage and its relation with precursor defects in KDP/DKDP. In Proceedings of the 43rd Annual Laser Damage Symposium on Optical Materials for High Power Lasers, Natl Inst Stand & Technol, Boulder, CO, USA, 18–21 September 2011; Spie-Int Soc Optical Engineering: Boulder, CO, USA, 2011. [Google Scholar]
  9. Liu, C.S.; Kioussis, N.; Demos, S.G.; Radousky, H.B. Electron- or hole-assisted reactions of H defects in hydrogen-bonded KDP. Phys. Rev. Lett. 2003, 91, 015505. [Google Scholar] [CrossRef]
  10. Liu, C.S.; Hou, C.J.; Kioussis, N.; Demos, S.G.; Radousky, H.B. Electronic structure calculations of an oxygen vacancy in KH2PO4. Phys. Rev. B 2005, 72, 134110. [Google Scholar] [CrossRef]
  11. Liu, C.S.; Zhang, Q.; Kioussis, N.; Demos, S.G.; Radousky, H.B. Electronic structure calculations of intrinsic and extrinsic hydrogen point defects in KH2PO4. Phys. Rev. B 2003, 68, 224107. [Google Scholar] [CrossRef]
  12. Wang, K.P.; Fang, C.S.; Zhang, J.X.; Liu, C.S.; Boughton, R.I.; Wang, S.L.; Zhao, X. First-principles study of interstitial oxygen in potassium dihydrogen phosphate crystals. Phys. Rev. B 2005, 72, 184105. [Google Scholar] [CrossRef]
  13. Hu, Y.; Zhu, Z.; Xiao, J.M.; Shao, H.Z.; Zhao, L.; Xu, M.; Zhuang, J. Atomic scale study of stress-induced misaligned subsurface layers in KDP crystals. Sci. Rep. 2019, 9, 10399. [Google Scholar] [CrossRef]
  14. Sui, T.T.; Lian, Y.F.; Xu, M.X.; Zhang, L.S.; Li, Y.L.; Zhao, X.; Xu, X.G.; Sun, X. Comparison of hydrogen vacancies in KDP and ADP crystals: A combination of density functional theory calculations and experiment. Phys. Chem. Chem. Phys. 2019, 21, 6186–6197. [Google Scholar] [CrossRef] [PubMed]
  15. Sui, T.T.; Wei, L.N.; Cao, X.Z.; Xu, M.X.; Zhang, L.S.; Zhao, X.; Chen, Z.X.; Li, Y.L.; Xu, X.G.; Sun, X. Comparison of oxygen vacancy and interstitial oxygen in KDP and ADP crystals from density functional theory calculations. Comput. Mater. Sci. 2020, 182, 109783. [Google Scholar] [CrossRef]
  16. Ding, W.Y.; Cheng, J.; Zhao, L.J.; Wang, Z.H.; Yang, H.; Liu, Z.C.; Xu, Q.; Wang, J.; Geng, F.; Chen, M.J. Determination of intrinsic defects of functional KDP crystals with flawed surfaces and their effect on the optical properties. Nanoscale 2022, 14, 10041–10050. [Google Scholar] [CrossRef] [PubMed]
  17. Miller, A.M.; Soustov, L.V. Absorption in and laser damage to KDP and DKDP crystals. Sov. J. Quantum Electron. 1989, 19, 39–45. [Google Scholar] [CrossRef]
  18. Ogorodnikov, I.N.; Pustovarov, V.A.; Shul’gin, B.V.; Kuanyshev, V.T.; Satybaldieva, M.K. Low-temperature time-resolved vacuum ultraviolet luminescent spectroscopy of KH2PO4 crystals with defects. Opt. Spectrosc. 2001, 91, 224–231. [Google Scholar] [CrossRef]
  19. Ogorodnikov, I.N.; Kirm, M.; Pustovarov, V.A.; Cheremnykh, V.S. Low-temperature time-resolved vacuum ultraviolet spectroscopy of self-trapped excitons in KH2PO4 crystals. Opt. Spectrosc. 2003, 95, 385–389. [Google Scholar] [CrossRef]
  20. Koketai, T.; Tagayeva, B.; Tussupbekova, A.; Mussenova, E. A mechanism of formation of radicals in crystal KDP (KH2PO4). In Proceedings of the 17th International Conference on Luminescence and Optical Spectroscopy of Condensed Matter (ICL), Univ Wroclaw, Fac Law, Adm & Econ, Wroclaw, Poland, 13–18 July 2014; Elsevier Science Bv: Wroclaw, Poland, 2014; pp. 101–105. [Google Scholar]
  21. Wang, Y.; Shao, J.D.; Hu, G.H.; Liu, X.F.; Zhao, Y.N.; Zhu, M.P. Effects of molecular vibration on the formation of transient defects during high-power UV laser excitation. Opt. Laser Technol. 2021, 135, 106681. [Google Scholar] [CrossRef]
  22. Ogorodnikov, I.N.; Yakovlev, V.Y.; Shul’gin, B.V.; Satybaldieva, M.K. Transient optical absorption of hole polarons in ADP (NH4H2PO4) and KDP (KH2PO4) crystals. Phys. Solid State 2002, 44, 880–887. [Google Scholar] [CrossRef]
  23. Huang, J.; Wu, Z.Q.; Wang, F.R.; Liu, H.J.; Sun, L.X.; Zhou, X.Y.; Ye, X.; Deng, Q.H.; Jiang, X.D.; Zheng, W.G.; et al. Initial damage and damage growth of KDP crystals induced by 355 nm pulse laser. Cryst. Res. Technol. 2018, 53, 1700269. [Google Scholar] [CrossRef]
  24. Wei, L.N.; Li, Y.; Jiang, X.Y.; Wu, P.C.; Zhao, X.; Zhang, L.S.; Liu, B.A.; Chai, X.X.; Xu, M.X.; Sun, X.; et al. Electron paramagnetic resonance spectroscopy and first-principles calculations of Cr3+ doped KDP crystals. CrystEngComm 2022, 24, 4948–4954. [Google Scholar] [CrossRef]
  25. Sui, T.T.; Wei, L.N.; Lian, Y.F.; Xu, M.X.; Zhang, L.S.; Li, Y.L.; Zhao, X.; Xu, X.G.; Sun, X. Structural stress and extra optical absorption induced by the intrinsic cation defects in KDP and ADP crystals: A theoretical study. CrystEngComm 2020, 22, 1962–1969. [Google Scholar] [CrossRef]
  26. Xu, D.L.; Xue, D.F. Chemical bond analysis of the crystal growth of KDP and ADP. J. Cryst. Growth 2006, 286, 108–113. [Google Scholar] [CrossRef]
  27. de Vries, S.A.; Goedtkindt, P.; Bennett, S.L.; Huisman, W.J.; Zwanenburg, M.J.; Smilgies, D.M.; De Yoreo, J.J.; van Enckevort, W.J.P.; Bennema, P.; Vlieg, E. Surface atomic structure of KDP crystals in aqueous solution: An explanation of the growth shape. Phys. Rev. Lett. 1998, 80, 2229–2232. [Google Scholar] [CrossRef]
  28. de Vries, S.A.; Goedtkindt, P.; Huisman, W.J.; Zwanenburg, M.J.; Feidenhans’l, R.; Bennett, S.L.; Smilgies, D.M.; Stierle, A.; De Yoreo, J.J.; van Enckevort, W.J.P.; et al. X-ray diffraction studies of potassium dihydrogen phosphate (KDP) crystal surfaces. J. Cryst. Growth 1999, 205, 202–214. [Google Scholar] [CrossRef]
  29. Liu, G.; Wang, S.; Gu, Q.; Ding, J.; Sun, Y.; Liu, W.; Zhu, S.; Liu, L. Numerical simulation of temperature field and velocity field of KDP crystal grown by traditional method. J. Synth. Cryst. 2013, 42, 1261–1266. [Google Scholar]
  30. Zhu, S.J.; Wang, S.L.; Ding, J.X.; Liu, G.X.; Wang, D.L.; Liu, L.; Li, W.D.; Huang, P.P.; Gu, Q.T.; Xu, X.G. Rapid growth and optical studies of KDP crystals with organic additives. J. Cryst. Growth 2014, 402, 48–52. [Google Scholar] [CrossRef]
  31. Liu, F.F.; Lisong, Z.; Yu, G.W.; Sun, X. Effect of pH value on the growth morphology of KH2PO4 crystal grown in defined crystallographic direction. Cryst. Res. Technol. 2015, 50, 164–170. [Google Scholar] [CrossRef]
  32. Li, W.D.; Li, Y.; Wang, S.L.; Cheng, W.Y. The relationship between the laser damaged threshold and step velocity in different supersaturation regions. RSC Adv. 2018, 8, 36453–36458. [Google Scholar] [CrossRef] [Green Version]
  33. Li, Y.; Li, W.D.; Zhang, X.M.; Wang, D.; Wang, S.L.; Liu, G.X. Influence of supersaturation on step evolution behavior of high concentration Fe3+ poisoned KDP crystal. J. Cryst. Growth 2020, 533, 125483. [Google Scholar] [CrossRef]
  34. Zhong, D.-G.; Teng, B.; Zhang, G.-H.; Li, X.-B.; Lu, X.-D. Influence of pH on solubility and solution stability of KDP crystal. J Synth. Cryst. 2006, 35, 1209–1213. [Google Scholar]
  35. Badrouj, M.; Malekfar, R. The pH effects on the growth rate of KDP (KH2PO4) crystal by investigating Raman active lattice modes. J. Raman Spectrosc. 2007, 38, 1089–1096. [Google Scholar] [CrossRef]
  36. Min, C.; Mingwei, L.I.; Dong, F.U.; Hang, S.H.I.; Jiangtao, Y.U. KDP crystal growth in differing pH value. J. Chongqing Univ. Nat. Sci. Ed. 2008, 31, 809–814. [Google Scholar]
  37. Sun, X.; Xu, X.; Wang, Z.; Chen, H.; Li, Y.; Shao, Z.; Gao, Z.; Fang, C. Growth Condition on the Scatter Particles in KDP Crystal. Plezoelectrics Acoustooptics 2002, 24, 303–305. [Google Scholar]
  38. Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  39. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  40. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  41. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
  42. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  43. Kohan, A.F.; Ceder, G.; Morgan, D.; Van de Walle, C.G. First-principles study of native point defects in ZnO. Phys. Rev. B 2000, 61, 15019–15027. [Google Scholar] [CrossRef] [Green Version]
  44. He, J.; Behera, R.K.; Finnis, M.W.; Li, X.; Dickey, E.C.; Phillpot, S.R.; Sinnott, S.B. Prediction of high-temperature point defect formation in TiO2 from combined ab initio and thermodynamic calculations. Acta Mater. 2007, 55, 4325–4337. [Google Scholar] [CrossRef]
  45. Yamada, N.; Tanida, Y.; Murata, H.; Kondo, T.; Yoshida, S. Wide-Range-Tunable p-Type Conductivity of Transparent CuI1-xBrxAlloy. Adv. Funct. Mater. 2020, 30, 2003096. [Google Scholar] [CrossRef]
  46. Woo, Y.W.; Li, Z.; Jung, Y.-K.; Park, J.-S.; Walsh, A. Inhomogeneous Defect Distribution in Mixed-Polytype Metal Halide Perovskites. ACS Energy Lett. 2022, 8, 356–360. [Google Scholar] [CrossRef]
  47. Ren, X.; Xu, D.L.; Xue, D.F. Crystal growth of KDP, ADP, and KADP. J. Cryst. Growth 2008, 310, 2005–2009. [Google Scholar] [CrossRef]
  48. Lv, L.; He, X.B.; Wang, J.S.; Ruan, Y.J.; Ouyang, S.X.; Yuan, H.; Zhang, T.R. Charge localization to optimize reactant adsorption on KCu7S4/CuO interfacial structure toward selective CO2 electroreduction. Appl. Catal. B-Environ. 2021, 298, 120531. [Google Scholar] [CrossRef]
  49. Wang, W.H.; Shen, Y.Q.; Wang, X.O.; Zhou, Z.X.; Fei, W.D. Adsorption of water on the KNTN (001) surface: A density functional theory study. Appl. Surf. Sci. 2014, 298, 102–108. [Google Scholar] [CrossRef]
  50. Alam, M.W.; Farhan, M.; Souayeh, B.; Aamir, M.; Khan, M.S. Synthesis, Crystal Structure, Density Functional Theory (DFT) Calculations and Molecular Orbital Calculations of 4-Bromoanilinium Perchlorate Single Crystal. Crystals 2021, 11, 1070. [Google Scholar] [CrossRef]
  51. Zhang, L.; Wu, Y.L.; Liu, Y.; Li, H. DFT study of single water molecule adsorption on the (100) and (101) surfaces of KH2PO4. RSC Adv. 2017, 7, 26170–26178. [Google Scholar] [CrossRef] [Green Version]
  52. Lin, L.; Shi, Z.G.; Huang, J.T.; Wang, P.T.; Yu, W.Y.; He, C.Z.; Zhang, Z.Y. Molecular adsorption properties of CH4 with noble metals doped onto oxygen vacancy defect of anatase TiO2 (101) surface: First-principles calculations. Appl. Surf. Sci. 2020, 514, 145900. [Google Scholar] [CrossRef]
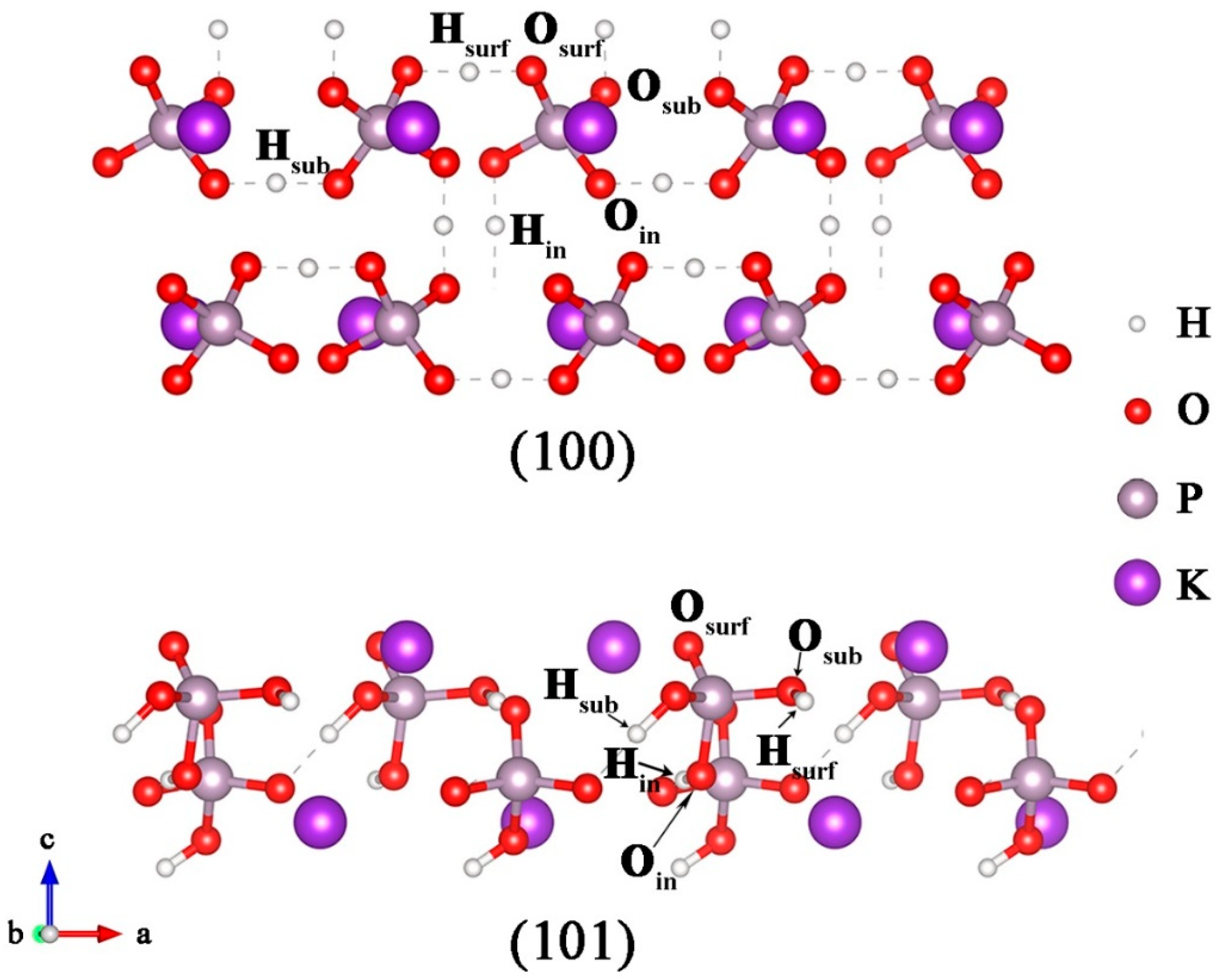
Molecules 27 09014 g001 550
Figure 1. Structures of KDP (100) and (101) surfaces with two-molecule layers. The possible vacancy sites are labeled in the figures.
Figure 1. Structures of KDP (100) and (101) surfaces with two-molecule layers. The possible vacancy sites are labeled in the figures.
Molecules 27 09014 g001
Molecules 27 09014 g002 550
Figure 2. (a) Structure of the (100) surface of KDP crystals, local lattice distortions of neutral and charged VH (b,c) and VO (d–f) defects on the (100) surface of KDP crystals, (g) structure of the (101) surface, and local lattice distortions of neutral and charged VH (h,i) and VO (j–l) defects on the (101) surface of KDP crystals. The dotted circles mark the position of the vacancy defects.
Figure 2. (a) Structure of the (100) surface of KDP crystals, local lattice distortions of neutral and charged VH (b,c) and VO (d–f) defects on the (100) surface of KDP crystals, (g) structure of the (101) surface, and local lattice distortions of neutral and charged VH (h,i) and VO (j–l) defects on the (101) surface of KDP crystals. The dotted circles mark the position of the vacancy defects.
Molecules 27 09014 g002
Molecules 27 09014 g003 550
Figure 3. Partial density of states of the VH and VO defects on the (100) (a) and (101) (b) surfaces, respectively.
Figure 3. Partial density of states of the VH and VO defects on the (100) (a) and (101) (b) surfaces, respectively.
Molecules 27 09014 g003
Molecules 27 09014 g004 550
Figure 4. Local and overall structures as well as the charge-density difference maps of H+ adsorbed on (100) and (101) surfaces. (a) Perfect (100) surface; (b) (100) surface with a VH defect; (c) (100) surface with a VO defect; (d) perfect (101) surface; (e) (101) surface with a VH defect; (f) (101) surface with a VO defect. Yellow and blue regions represent electron accumulation and depletion, respectively. The corresponding adsorption energy is listed at the top of each figure.
Figure 4. Local and overall structures as well as the charge-density difference maps of H+ adsorbed on (100) and (101) surfaces. (a) Perfect (100) surface; (b) (100) surface with a VH defect; (c) (100) surface with a VO defect; (d) perfect (101) surface; (e) (101) surface with a VH defect; (f) (101) surface with a VO defect. Yellow and blue regions represent electron accumulation and depletion, respectively. The corresponding adsorption energy is listed at the top of each figure.
Molecules 27 09014 g004
Molecules 27 09014 g005 550
Figure 5. (a) Partial density of states of the adsorbed H+ ions and the adjacent surface atoms on the (100) and (101) surfaces; (b) partial density of states of the H+ adsorbed (100) and (101) surfaces with VH and VO defects.
Figure 5. (a) Partial density of states of the adsorbed H+ ions and the adjacent surface atoms on the (100) and (101) surfaces; (b) partial density of states of the H+ adsorbed (100) and (101) surfaces with VH and VO defects.
Molecules 27 09014 g005
Molecules 27 09014 g006 550
Figure 6. Local and overall structures as well as the charge-density difference maps of OH− adsorbed on (100) and (101) surfaces. (a) Perfect (100) surface; (b) (100) surface with a VH defect; (c) (100) surface with a VO defect; (d) perfect (101) surface; (e) (101) surface with a VH defect; (f) (101) surface with a VO defect. Yellow and blue regions represent electron accumulation and depletion, respectively. The corresponding adsorption energy is listed at the top of each figure.
Figure 6. Local and overall structures as well as the charge-density difference maps of OH− adsorbed on (100) and (101) surfaces. (a) Perfect (100) surface; (b) (100) surface with a VH defect; (c) (100) surface with a VO defect; (d) perfect (101) surface; (e) (101) surface with a VH defect; (f) (101) surface with a VO defect. Yellow and blue regions represent electron accumulation and depletion, respectively. The corresponding adsorption energy is listed at the top of each figure.
Molecules 27 09014 g006
Molecules 27 09014 g007 550
Figure 7. (a) Partial density of states of the adsorbed OH− ions and the adjacent surface atoms on the (100) and (101) surfaces; (b) partial density of states of the OH− adsorbed (100) and (101) surfaces with VH and VO defects.
Figure 7. (a) Partial density of states of the adsorbed OH− ions and the adjacent surface atoms on the (100) and (101) surfaces; (b) partial density of states of the OH− adsorbed (100) and (101) surfaces with VH and VO defects.
Molecules 27 09014 g007
Table
Table 1. Comparison of the formation energies (eV) of VH and VO defects on the surfaces and in the bulk KDP crystal.
Table 1. Comparison of the formation energies (eV) of VH and VO defects on the surfaces and in the bulk KDP crystal.
DefectVHVO
PositionHsurf HsubHinOsurf OsubOin
(100) surface1.832.101.894.163.404.18
(101) surface1.652.042.004.344.343.07
KDP bulk 2.84 4.48
Table
Table 2. Bond lengths and bond angles between atoms adjacent to the vacancy defects on the KDP crystals’ surfaces.
Table 2. Bond lengths and bond angles between atoms adjacent to the vacancy defects on the KDP crystals’ surfaces.
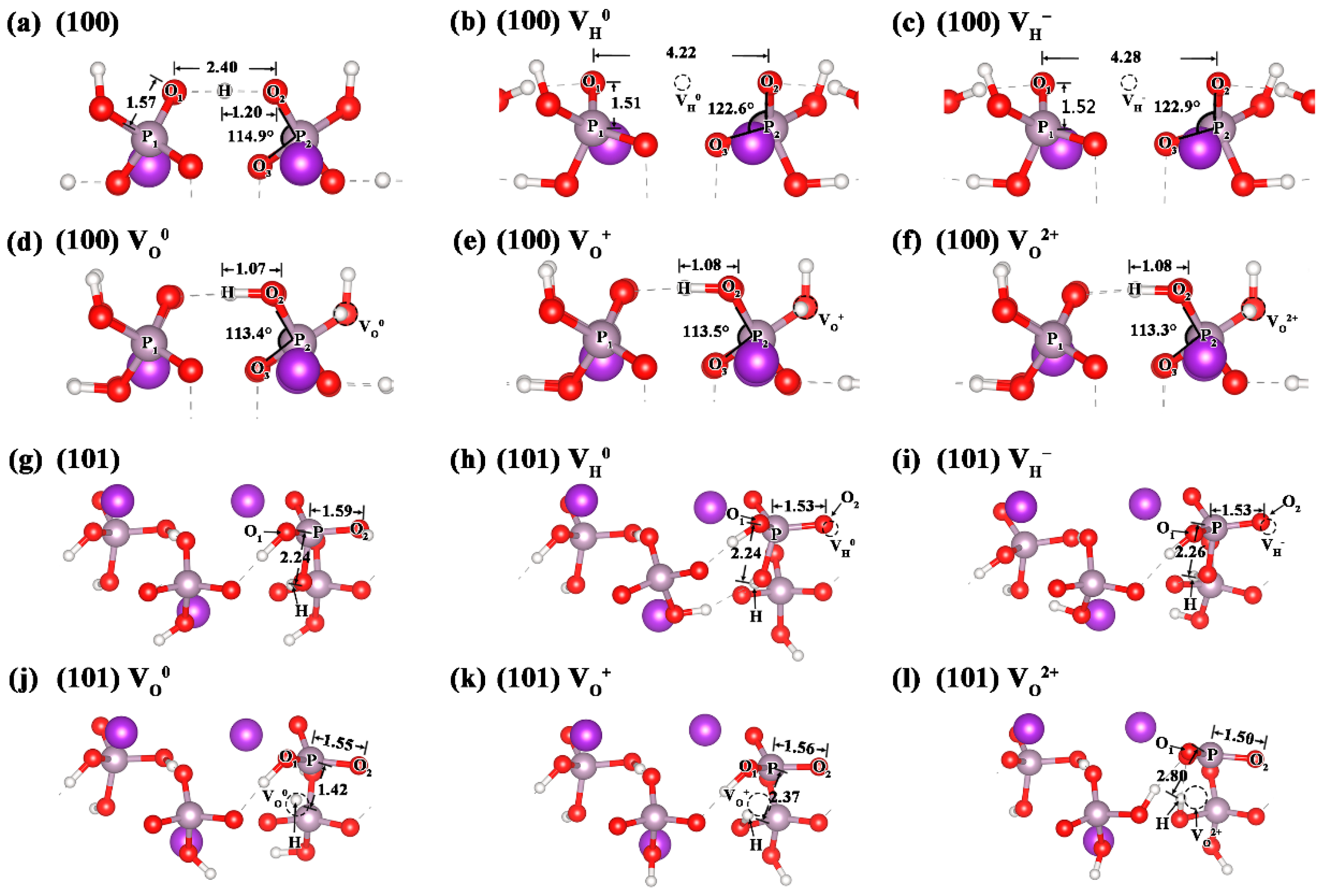
Bond Length (Å)Bond Angle
bondH-O2O1-O2P1-O1O2-P2-O3
(100) 1.202.401.57114.9°
(100), VH0-4.221.51122.6°
(100), VH−-4.281.52122.9°
(100), VO01.07--113.4°
(100), VO+1.08--113.5°
(100), VO2+1.08--113.3°
bondH-PO1-O2P-O2O2-P-O3
(101)2.242.501.59104.2°
(101), VH02.242.481.53105.5°
(101), VH−2.262.501.53105.2°
(101), VO01.422.531.55106.7°
(101), VO+2.372.531.56106.5°
(101), VO2+2.802.581.50118.9°
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhao, X.; Li, Y.; Zhao, X. Density Functional Theory Study of the Point Defects on KDP (100) and (101) Surfaces. Molecules 2022, 27, 9014. https://doi.org/10.3390/molecules27249014

AMA Style

Zhao X, Li Y, Zhao X. Density Functional Theory Study of the Point Defects on KDP (100) and (101) Surfaces. Molecules. 2022; 27(24):9014. https://doi.org/10.3390/molecules27249014

Chicago/Turabian Style

Zhao, Xiaoji, Yanlu Li, and Xian Zhao. 2022. "Density Functional Theory Study of the Point Defects on KDP (100) and (101) Surfaces" Molecules 27, no. 24: 9014. https://doi.org/10.3390/molecules27249014

APA Style

Zhao, X., Li, Y., & Zhao, X. (2022). Density Functional Theory Study of the Point Defects on KDP (100) and (101) Surfaces. Molecules, 27(24), 9014. https://doi.org/10.3390/molecules27249014

Article Metrics

Back to TopTop