Best-Practice Aspects of Quantum-Computer Calculations: A Case Study of the Hydrogen Molecule
Abstract
:1. Introduction
2. Results
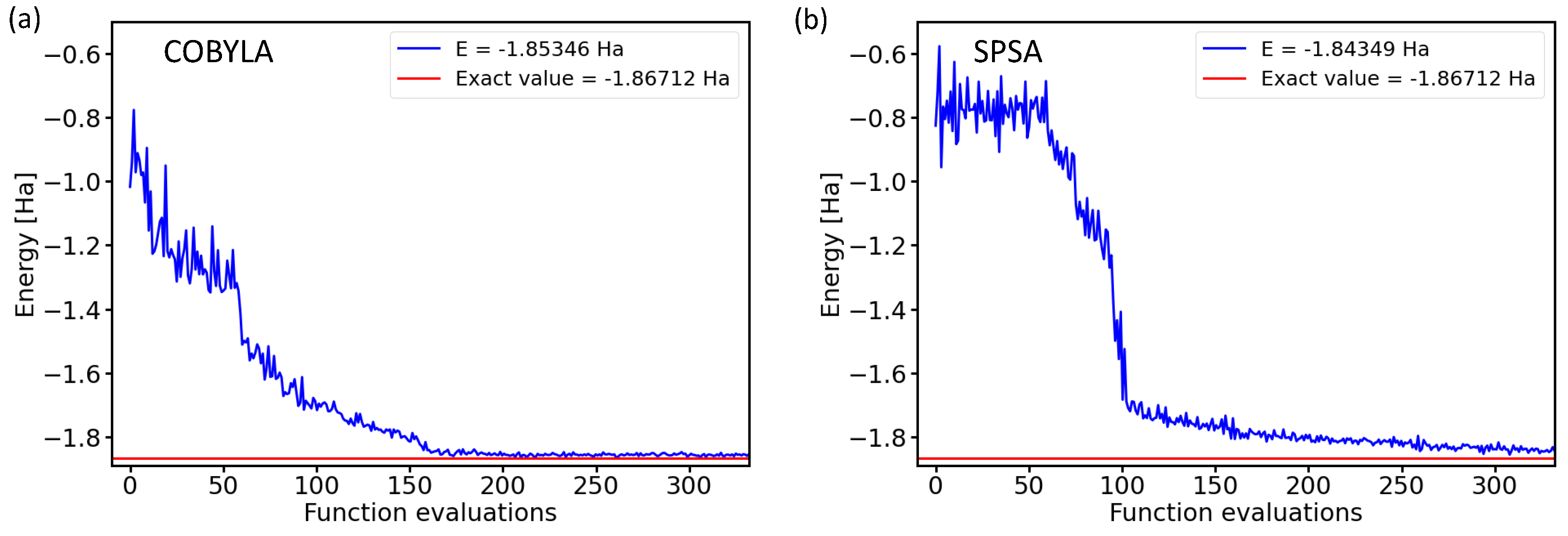
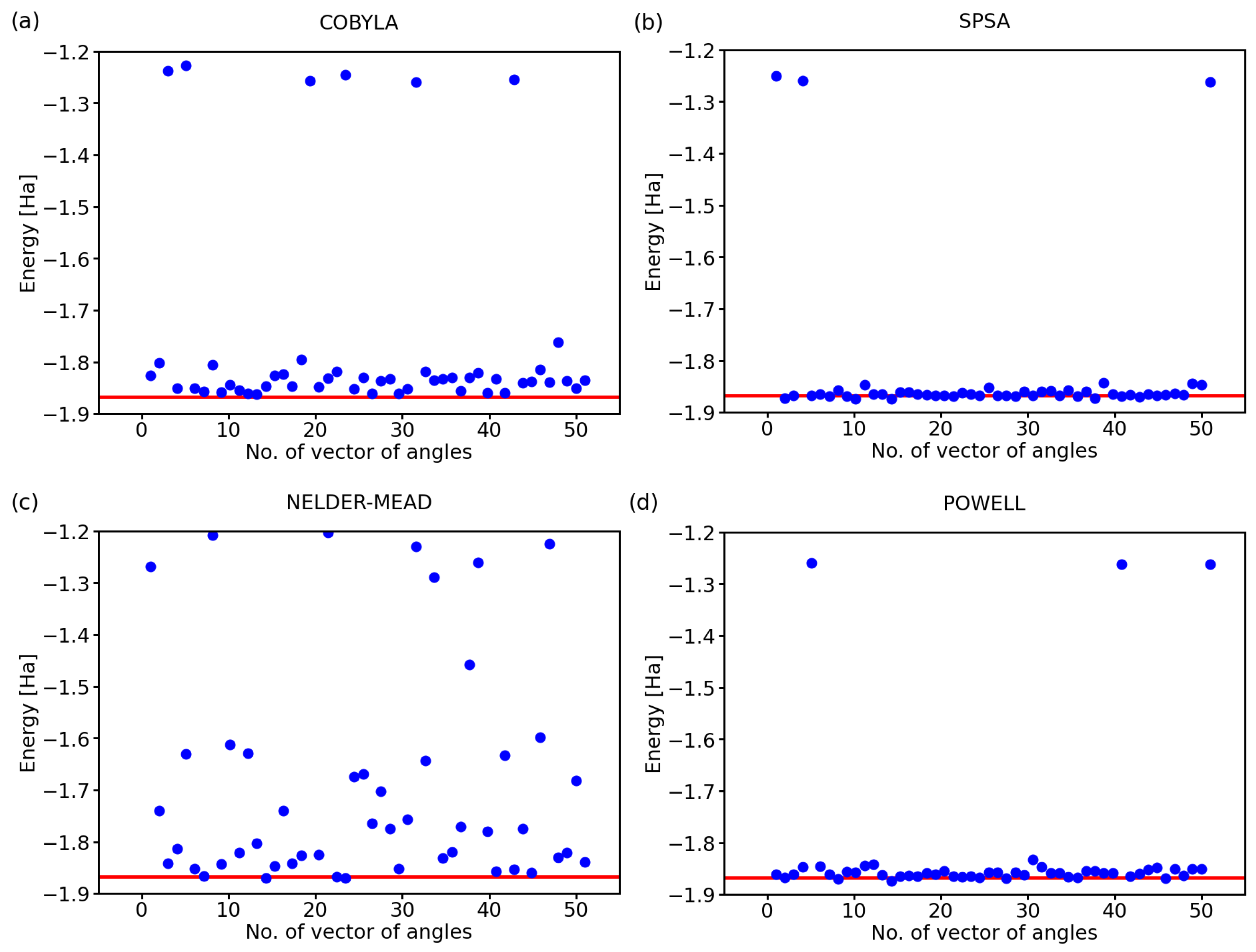
2.1. Performance of Various Optimization Methods
2.2. Impact of the Variational Form
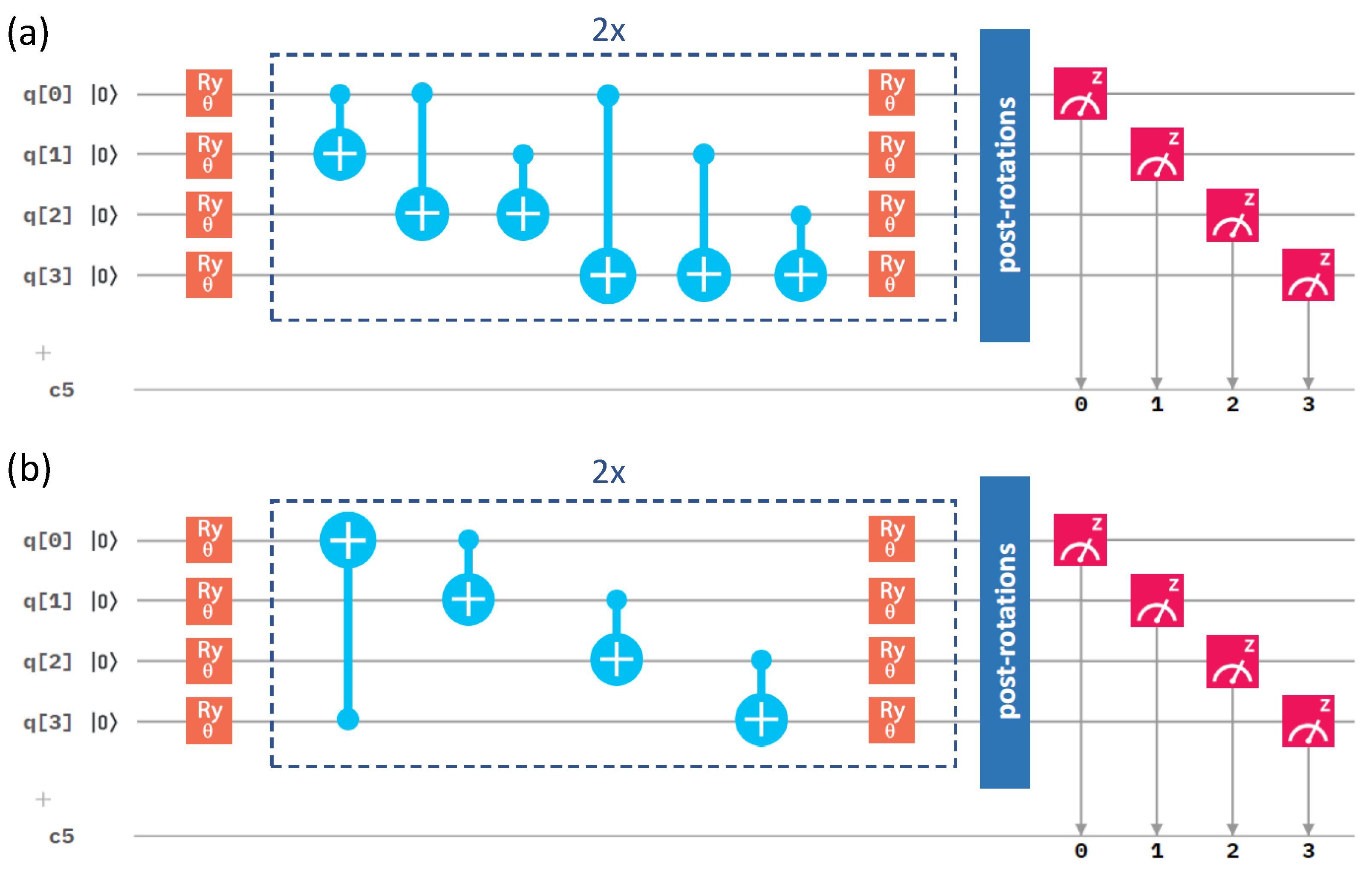
2.3. Influence of the Details of the Entangling Layers
2.4. Analysis of the Probabilities of the Basis States
2.5. Simulations of Noisy Runs
2.6. Experiments on Real Quantum Processors
3. Discussion
4. Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.; Romero, J.; Aspuru-Guzik, A. Potential of quantum computing for drug discovery. IBM J. Res. Dev. 2018, 62, 6:1–6:20. [Google Scholar] [CrossRef]
- Polsterová, S.; Friák, M.; Všianská, M.; Šob, M. Quantum-Mechanical Assessment of the Energetics of Silver Decahedron Nanoparticles. Nanomaterials 2020, 10, 767. [Google Scholar] [CrossRef] [Green Version]
- Lordi, V.; Nichol, J. dvances and opportunities in materials science for scalable quantum computing. MRS Bull. 2021, 46, 589–595. [Google Scholar] [CrossRef]
- Miceli, R.; McGuigan, M. Effective matrix model for nuclear physics on a quantum computer. In Proceedings of the New York Scientific Data Summit (NYSDS), New York, NY, USA, 12–14 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Di Matteo, O.; McCoy, A.; Gysbers, P.; Miyagi, T.; Woloshyn, R.M.; Navrátil, P. Improving Hamiltonian encodings with the Gray code. Phys. Rev. A 2021, 103, 042405. [Google Scholar] [CrossRef]
- Feynman, R. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed.; Cambridge University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.S.; Deng, Y.H.; Qin, J.; Wang, H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Wu, D.; Gong, S.Q.; Su, H.; et al. Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light. Phys. Rev. Lett. 2021, 127, 180502. [Google Scholar] [CrossRef]
- Friesner, R.A. Ab initio quantum chemistry: Methodology and applications. Proc. Natl. Acad. Sci. USA 2005, 102, 6648–6653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helgaker, T.; Klopper, W.; Tew, D.P. Quantitative quantum chemistry. Mol. Phys. 2008, 106, 2107–2143. [Google Scholar] [CrossRef]
- Cremer, D. Møller–Plesset perturbation theory: From small molecule methods to methods for thousands of atoms. WIREs Comput. Mol. Sci. 2011, 1, 509–530. [Google Scholar] [CrossRef]
- Lyakh, D.I.; Musiał, M.; Lotrich, V.F.; Bartlett, R.J. Multireference Nature of Chemistry: The Coupled-Cluster View. Chem. Rev. 2012, 112, 182–243. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- O’Malley, P.J.J.; Babbush, R.; Kivlichan, I.D.; Romero, J.; McClean, J.R.; Barends, R.; Kelly, J.; Roushan, P.; Tranter, A.; Ding, N.; et al. Scalable Quantum Simulation of Molecular Energies. Phys. Rev. X 2016, 6, 031007. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 15003. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Powell, M.J.D. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J.P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar] [CrossRef]
- Spall, J.C. Multivariate Stochastic Approximation Using a Simultaneous Perturbation Gradient Approximation. IEEE Trans. Autom. Control 1992, 37, 332–341. [Google Scholar] [CrossRef] [Green Version]
- Spall, J. Implementation of the simultaneous perturbation algorithm for stochastic optimization. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 817–823. [Google Scholar] [CrossRef]
- Spall, J.C. An Overview of the Simultaneous Perturbation Method for Efficient Optimization. Johns Hopkins Apl Tech. Dig. 1998, 19, 482–492. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Powell, M.J.D. The NEWUOA software for unconstrained optimization without derivatives. In Large-Scale Nonlinear Optimization; Di Pillo, G., Roma, M., Eds.; Springer: Boston, MA, USA, 2006; pp. 255–297. [Google Scholar] [CrossRef]
- Sachdeva, V.; Freimuth, D.M.; Mueller, C. Evaluating the Jaccard–Tanimoto Index on Multi-core Architectures. In International Conference on Computational Science, Proceedings of the 9th International Conference Baton Rouge, LA, USA, 25–27 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 944–953. [Google Scholar]
- Willett, P. Similarity-based virtual screening using 2D fingerprints. Drug Discov. Today 2006, 11, 1046–1053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murata, T. Machine discovery based on the co-occurence of references in search engine. In International Conference on Discovery Science, Proceedings of the Second International Conference, DS’99, Tokyo, Japan, 6–8 December 1999; Arikawa, S., Furukawa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1721, pp. 220–229. [Google Scholar]
- Mild, A.; Reutterer, T. Collaborative Filtering Methods for Binary Market Basket Data Analysis. In Proceedings of the 6th International Computer Science Conference, AMT 2001, Hong Kong, China, 18–20 December 2001; pp. 302–313. [Google Scholar]
- Liben-Nowell, D.; Kleinberg, J. The link prediction problem for social networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, New Orleans, LA, USA, 3–8 November 2003; pp. 302–313. [Google Scholar]
- Jaccard, P. The Distribution of the Flora in the Alpine Zone.1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Tanimoto, T.T. An Elementary Mathematical Theory of Classification and Prediction; Internal IBM Technical Report; McGraw-Hill: New York, NY, USA, 1958; p. 8. [Google Scholar]
- Bloch, F. Generalized theory of relaxation. Phys. Rev. 1957, 105, 1206–1222. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Kandala, A.; Temme, K.; Córcoles, A.D.; Mezzacapo, A.; Chow, J.M.; Gambetta, J.M. Error mitigation extends the computational reach of a noisy quantum processor. Nature 2019, 567, 491–495. [Google Scholar] [CrossRef] [Green Version]
- Endo, S.; Benjamin, S.C.; Li, Y. Practical Quantum Error Mitigation for Near-Future Applications. Phys. Rev. X 2018, 8, 031027. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z. Quantum Error Mitigation using Symmetry Expansion. Quantum 2021, 5, 548. [Google Scholar] [CrossRef]
- Suchsland, P.; Tacchino, F.; Fischer, M.H.; Neupert, T.; Barkoutsos, P.K.; Tavernelli, I. Algorithmic Error Mitigation Scheme for Current Quantum Processors. Quantum 2021, 5, 492. [Google Scholar] [CrossRef]
- Bravyi, S.; Sheldon, S.; Kandala, A.; Mckay, D.C.; Gambetta, J.M. Mitigating measurement errors in multiqubit experiments. Phys. Rev. A 2021, 103. [Google Scholar] [CrossRef]
- Geller, M.R.; Sun, M. Toward efficient correction of multiqubit measurement errors: Pair correlation method. Quantum Sci. Technol. 2021, 6, 025009. [Google Scholar] [CrossRef]
- Bravyi, S.; Gambetta, J.M.; Mezzacapo, A.; Temme, K. Tapering off qubits to simulate fermionic Hamiltonians. arXiv 2017, arXiv:1701.08213. [Google Scholar]
- Bravyi, S.; Kitaev, A. Fermionic quantum computation. Ann. Phys. 2002, 298, 210–226. [Google Scholar] [CrossRef] [Green Version]
- Jordan, P.; Wigner, E. Über das Paulische Äquivalenzverbot. Z. Phys. 1928, 47, 631–651. [Google Scholar] [CrossRef]
- VQE Tutorial. Available online: https://pennylane.ai/qml/demos/tutorial_vqe.html (accessed on 1 November 2021).
- Miháliková, I. Implementation of the Variational Quantum Eigensolver. 2021. Available online: https://github.com/imihalik/VQE_H2 (accessed on 4 January 2021).
- Qiskit’s Chemistry Module. Available online: https://qiskit.org/documentation/apidoc/qiskit_chemistry.html (accessed on 4 January 2021).
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.; Aspuru-Guzik, A.; O’Brien, J. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tilly, J.; Chen, H.; Cao, S.; Picozzi, D.; Setia, K.; Li, Y.; Grant, E.; Wossnig, L.; Rungger, I.; Booth, G.H.; et al. The Variational Quantum Eigensolver: A review of methods and best practices. arXiv 2021, arXiv:2111.05176. [Google Scholar]
- Rayleigh, J. In finding the correction for the open end of an organ-pipe. Phil. Trans. 1870, 161, 77. [Google Scholar]
- Ritz, W. Über eine neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik. J. Reine Angew. Math. 1909, 135, 1–61. [Google Scholar] [CrossRef]
- Arfken, G.; Weber, H. Rayleigh-Ritz variational technique. In Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985; pp. 957–961. ISBN 9781483277820. [Google Scholar]
- Miháliková, I.; Pivoluska, M.; Plesch, M.; Friák, M.; Nagaj, D.; Šob, M. The Cost of Improving the Precision of the Variational Quantum Eigensolver for Quantum Chemistry. arXiv 2021, arXiv:2111.04965. [Google Scholar] [CrossRef]
- IBM Quantum. Available online: https://quantum-computing.ibm.com/ (accessed on 4 January 2021).








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miháliková, I.; Friák, M.; Pivoluska, M.; Plesch, M.; Saip, M.; Šob, M. Best-Practice Aspects of Quantum-Computer Calculations: A Case Study of the Hydrogen Molecule. Molecules 2022, 27, 597. https://doi.org/10.3390/molecules27030597
Miháliková I, Friák M, Pivoluska M, Plesch M, Saip M, Šob M. Best-Practice Aspects of Quantum-Computer Calculations: A Case Study of the Hydrogen Molecule. Molecules. 2022; 27(3):597. https://doi.org/10.3390/molecules27030597
Chicago/Turabian StyleMiháliková, Ivana, Martin Friák, Matej Pivoluska, Martin Plesch, Martin Saip, and Mojmír Šob. 2022. "Best-Practice Aspects of Quantum-Computer Calculations: A Case Study of the Hydrogen Molecule" Molecules 27, no. 3: 597. https://doi.org/10.3390/molecules27030597
APA StyleMiháliková, I., Friák, M., Pivoluska, M., Plesch, M., Saip, M., & Šob, M. (2022). Best-Practice Aspects of Quantum-Computer Calculations: A Case Study of the Hydrogen Molecule. Molecules, 27(3), 597. https://doi.org/10.3390/molecules27030597






