Polycation–Polyanion Architecture of the Intermetallic Compound Mg3−xGa1+xIr
Abstract
:1. Introduction
2. Experimental and Computational Details
3. Results and Discussion
3.1. Crystal Structure Determination
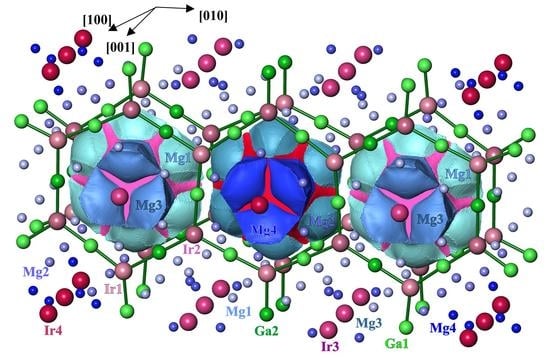
3.2. Crystal Structure Description
3.3. Band Structure and Properties
3.4. Chemical Bonding
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Pauling, L. Unsolved problems of structural chemistry. Special Collections & Archives Research Center, OSU Libraries, Oregon State University, LP Speeches, Box 1947s.7. Chem. Eng. News 1947, 25, 2970–2974. [Google Scholar]
- Grin, Y. Crystal Structure and Bonding in Intermetallic Compounds. In Comprehensive Inorganic Chemistry II; Elsevier: Oxford, UK, 2013; pp. 359–373. [Google Scholar]
- Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
- Miller, G.J.; Schmidt, M.W.; Wang, F.; You, T.-S. Quantitative Advances in the Zintl-Klemm Formalism. In Zintl-Phases and Recent Developments; Fässler, T.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–56. [Google Scholar]
- Grin, Y.; Savin, A.; Silvi, B. The ELF perspective of chemical bonding. In The Chemical Bond: Chemical Bonding Across the Periodic Table; Wiley-VCH: Weinheim, Germany, 2014; Volume 1, pp. 345–382. [Google Scholar]
- Amon, A.; Ormeci, A.; Bobnar, M.; Akselrud, L.; Avdeev, M.; Gumeniuk, R.; Burkhardt, U.; Prots, Y.; Hennig, C.; Leithe-Jasper, A.; et al. Cluster Formation in the Superconducting Complex Intermetallic Compound Be21Pt5. Acc. Chem. Res. 2018, 51, 214–222. [Google Scholar] [CrossRef] [Green Version]
- Freccero, R.; Hübner, J.-M.; Prots, Y.; Schnelle, W.; Schmidt, M.; Wagner, F.R.; Schwarz, U.; Grin, Y. “Excess” electrons in LuGe. Angew. Chem. Int. Ed. 2021, 60, 6457–6461. [Google Scholar] [CrossRef]
- Kotsch, M.; Prots, Y.; Ormeci, A.; Senyshyn, A.; Kohout, M.; Grin, Y. Bell-like [Ga5] clusters in Sr3Li5Ga5: Synthesis, crystal structure and bonding analysis. Z. Anorg. Allg. Chem. 2021, 647, 1–8. [Google Scholar]
- Alekseeva, A.M.; Abakumov, A.M.; Chizhov, P.S.; Leithe-Jasper, A.; Schnelle, W.; Prots, Y.; Hadermann, J.; Antipov, E.V.; Grin, Y. Ternary Magnesium Rhodium Boride Mg2Rh1−xB6+2x with a Modified Y2RhB6-Type Crystal Structure. Inorg. Chem. 2007, 46, 7378–7386. [Google Scholar] [CrossRef]
- Alekseeva, A.M.; Abakumov, A.M.; Leither-Jasper, A.; Schnelle, W.; Prots, Y.; Van Tendeloo, G.; Antipov, E.V.; Grin, Y. Spatial Separation of Covalent, Ionic, and Metallic Interactions in Mg11Rh18B8 and Mg3Rh5B3. Chem. Eur. J. 2013, 19, 17860–17870. [Google Scholar] [CrossRef] [PubMed]
- Alekseeva, A.M.; Leithe-Jasper, A.; Prots, Y.; Schnelle, W.; Ormeci, A.; Antipov, E.V.; Grin, Y. Superconducting non-centrosymmetric boride Mg10Ir19B16: Crystal structure and chemical bonding. Chem. Met. Alloys 2014, 7, 74–84. [Google Scholar] [CrossRef]
- Alekseeva, A.M.; Abakumov, A.M.; Leithe-Jasper, A.; Schnelle, W.; Prots, Y.; Hadermann, J.; Van Tendeloo, G.; Antipov, E.V.; Grin, Y. Mg1−xRhB: A New Boridometallide with 2D Polyanion. Z. Anorg. Allg. Chem. 2005, 631, 1047–1054. [Google Scholar] [CrossRef]
- Jiménez, A.M.B.; Burkhardt, U.; Cardoso-Gil, R.; Höfer, K.; Altendorf, S.G.; Schlögl, R.; Grin, Y.; Antonyshyn, I. Hf2B2Ir5: A Self-optimizing Catalyst in the Oxygen Evolution Reaction. ACS Appl. Energy Mat. 2020, 3, 11042–11052. [Google Scholar] [CrossRef]
- Blessing, R.H. An empirical correction for absorption anisotropy. Acta Crystallogr. 1995, A51, 33–38. [Google Scholar] [CrossRef]
- Parthé, E.; Gelato, L. The standardization of inorganic crystal-structure data. Acta Crystallogr. 1984, A40, 169–183. [Google Scholar] [CrossRef]
- Gelato, L.M.; Parthé, E. STRUCTURE TIDY—A computer program to standardize crystal structure data. J. Appl. Crystallogr. 1987, 20, 139–143. [Google Scholar] [CrossRef]
- Akselrud, L.; Grin, Y. WinCSD: Software package for crystallographic calculations (Version 4). J. Appl. Crystallogr. 2014, 47, 803–805. [Google Scholar] [CrossRef]
- Jepsen, O.; Burkhardt, A.; Andersen, O.K. The Program TB-LMTO-ASA; Version 4; Max-Planck-Institut für Festkörperforschung: Stuttgart, Germany, 1999. [Google Scholar]
- Kohout, M.; Wagner, F.R. Modified Version Lmto47e of the Stuttgart TB-LMTO-ASA Code; Max-Planck-Institut für Chemische Physik fester Stoffe: Dresden, Germany, 2016. [Google Scholar]
- Barth, U.; Hedin, L. A local exchange-correlation potential for the spin polarized case. I. J. Phys. C 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
- Koepernik, K.; Eschrig, H. Full-potential non-orthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 1999, 59, 1743–1757. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Kohout, M. A measure of electron localizability. Int. J. Quantum Chem. 2004, 97, 651–658. [Google Scholar] [CrossRef]
- Wagner, F.R.; Bezugly, V.; Kohout, M.; Grin, Y. Charge decomposition analysis of the electron localizability indicator: A bridge between the orbital and direct space representation of the chemical bond. Chem. Eur. J. 2007, 13, 5724–5741. [Google Scholar] [CrossRef]
- Kohout, M.; Wagner, F.R.; Grin, Y. Atomic shells from the electron localizability in momentum space. Int. J. Quantum Chem. 2006, 106, 1499–1507. [Google Scholar] [CrossRef]
- Kohout, M. Bonding indicators from electron pair density functionals. Faraday Discuss. 2007, 135, 43–54. [Google Scholar] [CrossRef]
- Ormeci, A.; Rosner, H.; Wagner, F.R.; Kohout, M.; Grin, Y. Electron Localization Function in Full-Potential Representation for Crystalline Materials. J. Phys. Chem. A 2006, 110, 1100–1105. [Google Scholar] [CrossRef] [PubMed]
- Kohout, M. DGrid Versions 4.6–5. 2018–2021. Available online: https://openbase.com/js/dgrid/versions (accessed on 21 December 2021).
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Fedorchuk, A.O.; Prots, Y.; Grin, Y. Crystal structures of europium magnesium gallium, EuMgxGa4−x, and europium lithium gallium, EuLixGa4−x (x ≤ 0.5). Z. Kristallogr. NCS 2005, 220, 317–318. [Google Scholar] [CrossRef]
- Emsley, J. Die Elemente; De Gruyter: Berlin, Germany; New York, NY, USA, 1994. [Google Scholar]
- Pauling, L. The Nature of the Chemical Bond; Cornel University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Donohue, J. The Structure of the Elements; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Amon, A.; Svanidze, E.; Ormeci, A.; König, M.; Kasinathan, D.; Takegami, D.; Prots, Y.; Liao, Y.-F.; Tsuei, K.-D.; Tjeng, L.H.; et al. Interplay of Atomic Interactions in the Intermetallic Semiconductor Be5Pt. Angew. Chem. Int. Ed. 2019, 58, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Grin, Y.; Armbrüster, M.; Baranov, A.I.; Finzel, K.; Kohout, M.; Ormeci, A.; Rosner, H.; Wagner, F.R. Atomic interactions in the intermetallic catalyst GaPd. Mol. Phys. 2016, 114, 1250–1259. [Google Scholar] [CrossRef]






| Composition | Mg2.944Ga1.056Ir |
|---|---|
| Space group | P63/mcm (no. 193) |
| Pearson symbol | hP90 |
| Formula units per unit cell, Z | 18 |
| Lattice parameters a | |
| a/Å | 14.4970 (3) |
| c/Å | 8.8638 (3) |
| V/Å3 | 1613.3 (1) |
| Calc. density/g cm−1 | 9.00 |
| Crystal shape | prism-like |
| Crystal size/mm3 | 0.030 × 0.030 × 0.125 |
| Diffraction system | RIGAKU AFC7 |
| Detector | Mercury CCD |
| Radiation, λ/Å | MoKα, 0.71073 |
| Scan; step/degree; N (images) | φ, ω, 0.6; 500 |
| Maximal 2θ/degree | 63.0 |
| Range in h, k, l | −21 ≤ h ≤ 16 |
| −20 ≤ k ≤ 20 | |
| −12 ≤ l ≤ 12 | |
| Absorption correction | multi-scan |
| T (max)/T (min) | 3.60 |
| Absorption coefficient/mm−1 | 47.9 |
| N (hkl) measured | 13000 |
| N (hkl) unique | 961 |
| R (int), | 0.061 |
| N (hkl) observed | 918 |
| Observation criteria | F (hkl) > 4σ (F) |
| Refined parameters | 49 |
| R (F) GOF | 0.027 1.04 |
| Residual peaks/e Å−3 | −1.90/1.45 |
| Atom | Site | x | y | z | Ueq |
|---|---|---|---|---|---|
| Mg1 | 24l | 0.1245 (2) | 0.4566 (2) | 0.0241 (3) | 0.0152 (8) |
| Mg2 | 12k | 0.2101 (3) | 0 | 0.5261 (4) | 0.0151 (11) |
| Mg3 * | 12j | 0.3391 (3) | 0.5577 (3) | ¼ | 0.0122 (10) |
| Mg4 * | 6g | 0.1118 (3) | 0 | ¼ | 0.0139 (13) |
| Ir1 | 6g | 0.31683 (4) | 0 | ¼ | 0.0082 (2) |
| Ir2 | 6g | 0.65164 (4) | 0 | ¼ | 0.0091 (2) |
| Ir3 | 4d | ⅓ | ⅔ | 0 | 0.0098 (2) |
| Ir4 | 2b | 0 | 0 | 0 | 0.0109 (2) |
| Ga1 | 12j | 0.17485 (9) | 0.33560 (9) | ¼ | 0.0127 (4) |
| Ga2 | 6g | 0.4863 (1) | 0 | ¼ | 0.0112 (4) |
| Atoms | d, Å | Atoms | d, Å | ||
|---|---|---|---|---|---|
| Mg1 – | 1Ir1 | 2.778 (3) | Mg4 – | 2Ir4 | 2.746 (1) |
| 1Mg3 | 2.812 (3) | 2Mg4 | 2.808 (3) | ||
| 1Ga2 | 2.869 (3) | 2Mg2 | 2.831 (3) | ||
| 1Ir2 | 2.965 (2) | 2Ga1 | 2.954 (2) | ||
| 1Ga1 | 2.983 (3) | 1Ir1 | 2.972 (2) | ||
| 1Mg1 | 3.039 (4) | 4Mg2 | 3.302 (3) | ||
| 1Ir3 | 3.043 (3) | ||||
| 1Mg1 | 3.092 (4) | Ir1 – | 2Ga1 | 2.410 (1) | |
| 1Mg1 | 3.127 (4) | 1Ga2 | 2.456 (1) | ||
| 1Mg2 | 3.127 (4) | 4Mg1 | 2.778 (3) | ||
| 1Ga1 | 3.190 (3) | 2Mg2 | 2.895 (3) | ||
| 1Mg3 | 3.256 (4) | 1Mg4 | 2.972 (2) | ||
| 1Mg3 | 3.358 (4) | ||||
| 1Ga2 | 3.368 (3) | Ir2 – | 1Ga2 | 2.398 (1) | |
| 2Ga1 | 2.428 (1) | ||||
| Mg2 – | 1Ir2 | 2.821 (3) | 2Mg2 | 2.821 (3) | |
| 1Mg4 | 2.831 (3) | 4Mg1 | 2.965 (3) | ||
| 1Ir1 | 2.895 (3) | 2Mg3 | 3.104 (4) | ||
| 2Ga2 | 2.905 (3) | ||||
| 1Ir1 | 3.054 (2) | Ir3 – | 6Mg3 | 2.747 (2) | |
| 2Mg2 | 3.080 (3) | 6Mg1 | 3.043 (3) | ||
| 2Mg1 | 3.127 (3) | ||||
| 2Mg4 | 3.302 (3) | Ir4 – | 6Mg4 | 2.746 (1) | |
| 2Ga1 | 3.333 (3) | 6Mg2 | 3.054 (2) | ||
| Mg3 – | 2Ir3 | 2.747 (2) | Ga1 – | 1Ir1 | 2.410 (1) |
| 2Mg3 | 2.812 (5) | 1Ir2 | 2.428 (1) | ||
| 2Mg1 | 2.812 (3) | 1Mg3 | 2.893 (4) | ||
| 1Ga1 | 2.893 (4) | 2Mg2 | 2.905 (3) | ||
| 1Ga2 | 2.903 (4) | 1Mg4 | 2.954 (2) | ||
| 1Ir2 | 3.104 (4) | 2Mg1 | 2.983 (3) | ||
| 2Mg1 | 3.256 (4) | 2Mg1 | 3.190 (3) | ||
| 2Mg1 | 3.358 (4) | 2Mg2 | 3.333 (3) | ||
| Ga2 – | 1Ir2 | 2.398 (1) | |||
| 1Ir1 | 2.456 (1) | ||||
| 4Mg1 | 2.869 (3) | ||||
| 2Mg3 | 2.903 (4) | ||||
| 4Mg1 | 3.368 (3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sichevych, O.; Prots, Y.; Schnelle, W.; Wagner, F.R.; Grin, Y. Polycation–Polyanion Architecture of the Intermetallic Compound Mg3−xGa1+xIr. Molecules 2022, 27, 659. https://doi.org/10.3390/molecules27030659
Sichevych O, Prots Y, Schnelle W, Wagner FR, Grin Y. Polycation–Polyanion Architecture of the Intermetallic Compound Mg3−xGa1+xIr. Molecules. 2022; 27(3):659. https://doi.org/10.3390/molecules27030659
Chicago/Turabian StyleSichevych, Olga, Yurii Prots, Walter Schnelle, Frank R. Wagner, and Yuri Grin. 2022. "Polycation–Polyanion Architecture of the Intermetallic Compound Mg3−xGa1+xIr" Molecules 27, no. 3: 659. https://doi.org/10.3390/molecules27030659
APA StyleSichevych, O., Prots, Y., Schnelle, W., Wagner, F. R., & Grin, Y. (2022). Polycation–Polyanion Architecture of the Intermetallic Compound Mg3−xGa1+xIr. Molecules, 27(3), 659. https://doi.org/10.3390/molecules27030659