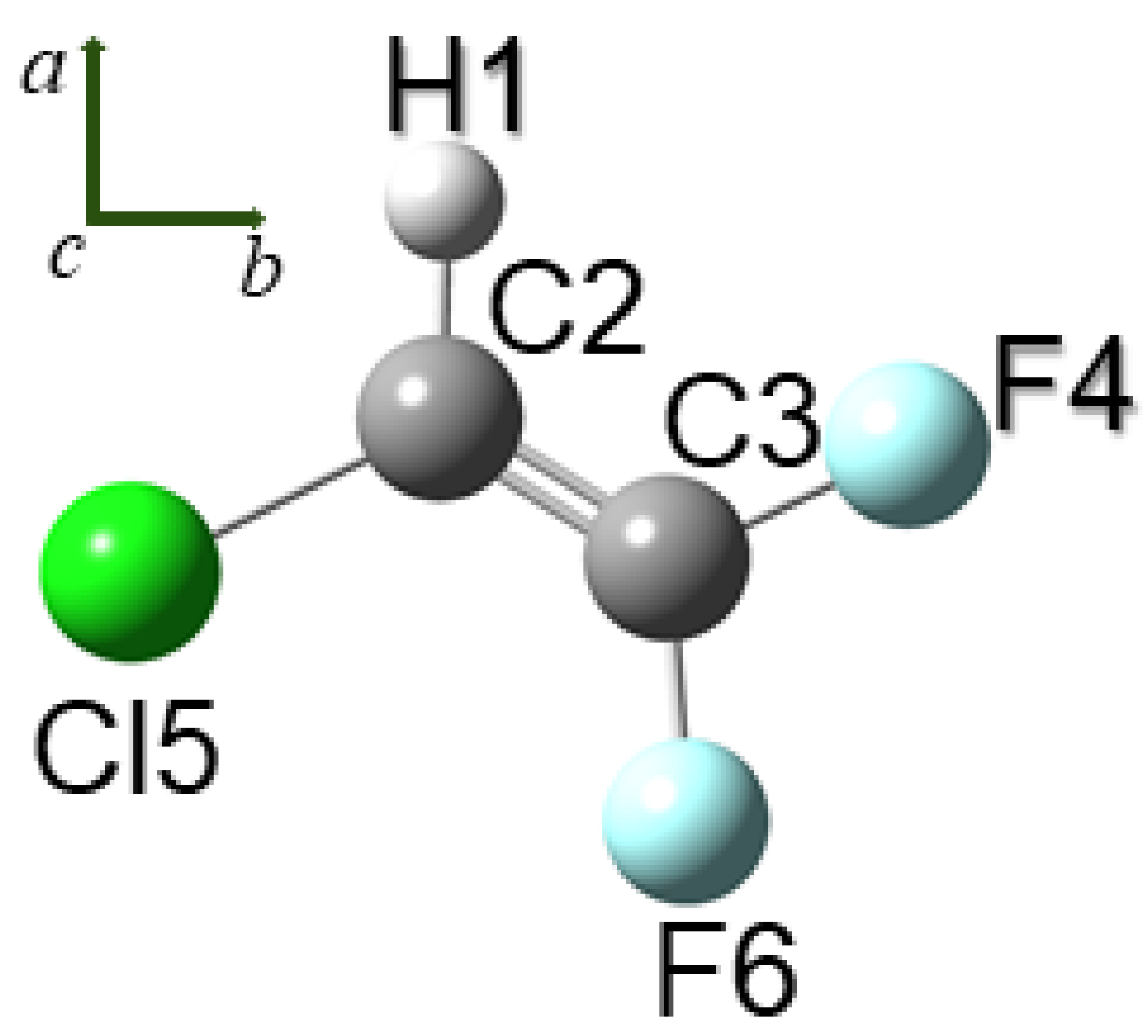
R1122 is a planar near-prolate molecule, with asymmetry parameter
, belonging to the
symmetry point group. The
a and
b principal axes of inertia define the molecular plane, whereas the
c axis is perpendicular to it, as illustrated in
Figure 1. It possesses 12 normal modes of vibration that, in terms of the symmetry species, can be classified as
;
vibrations give rise to hybrid
bands, whereas vibrations of
symmetry produce
c-type absorptions.
In the following equilibrium, geometries and rotational properties are discussed first, and then the attention is moved to the vibrational harmonic force field. Subsequently, anharmonic effects are introduced, and the issuing theoretical predictions used to drive the interpretation of the IR spectra are experimentally recorded. This subsection also deals with a description of the main absorption bands and the measurement of integrated absorption cross sections over the 400–6500 cm spectral range.
3.1. Equilibrium Geometry and Ro-Vibrational Spectroscopy
The fundamental prerequisite for obtaining reliable predictions of spectroscopic parameters that are accurate enough to drive the interpretation of experimental spectra is an accurate molecular geometry, in particular, for what concerns rotational spectroscopy. Although the ground-state rotational constants of six isotopologues of ClHC=CF
have been experimentally determined [
34], to the best of our knowledge, only an effective vibrationally averaged structure (namely the so-called
structure) has been proposed, with no attempt to derive the equilibrium geometry. In this respect, it is well known that the semi-experimental (SE) approach is the best method for obtaining accurate equilibrium structures for non-trivial (i.e., two- or three atom-) molecules in the gas-phase [
71]. The method makes use of vibrational contributions evaluated theoretically,
, to correct the experimentally derived rotational constants, usually those of the ground-vibrational state
(
being the principal axis of inertia), and obtain the so-called SE equilibrium rotational constants,
, of a set of isotopologues [
72]:
For each isotopologue, vibrational corrections
can be computed in the framework of VPT2 [
61,
62,
63]. A non-linear least-squares fitting procedure is then employed to invert the set of SE equilibrium rotational constants to the molecular structural parameters, thus returning the SE equilibrium geometry.
To obtained the SE equilibrium geometry of R1122, the ground-state rotational constants measured for
ClHC=CF
,
ClHC=CF
, ClH
C=CF
, ClHC=
CF
,
ClDC=CF
and
ClDC=CF
[
34] and the corresponding vibrational corrections computed at the rev-DSDPBEP86/jun-cc-pV(T+
d)Z level of theory have been fed into the MSR software [
73], which has been used for structural refinement. The lack of isotopic substitutions on F atoms, which prevents a reliable determination of the structural parameters involving them, can be overcome by using two strategies: the non-determinable parameters can be constrained to an accurate theoretical value or, alternatively, one can resort to the use of the predicate observations method, which uses estimates of structural parameters as additional input data [
74]. In addition to being more flexible with respect to treating theoretical parameters as rigid constraints, it should lead to more precise results [
75,
76]. In the present work, this second method has been adopted with predicates for the C3−F4 and C3−F6 bond lengths and C2C3F4 and C2C3F6 angles taken from the CCSD(T)/CBS+CV gradient scheme results. The final fit converged to the SE equilibrium geometry reported in
Table 1, with a root mean square deviation of
u Å
. All of the structural parameters are well determined, with maximum standard deviations of 1.1 mÅ for bond lengths and around 0.1° for angles, although, for the C3C2H1 angle, the 95% confidence interval represents a safer estimate of its accuracy.
Indeed, the same table also lists the equilibrium geometry of R1122 obtained from the CCSD(T)/CBS+CV and ChS composite methods and at the CCSD(T)/cc-pV5Z level of theory. The two composite schemes are in perfect agreement with the SE equilibrium geometry, with the largest deviation being 0.9 mÅ and 1.6 mÅ for bond lengths at the CCSD(T)/CBS+CV and ChS level, respectively, and within 0.1° for bond angles. The only exception is the C3C2H1 angle, which is 0.5° lower accordingly to the theoretical predictions. The equilibrium geometry obtained by using the large cc-pV5Z basis set is also in agreement with the SE structure, even though larger deviations than those for composite methods can be noted. A strikingly accurate equilibrium geometry is obtained by augmenting the PW6B95 and rev-DSDPBEP86 results through the nano-LEGO approach [
76]. In fact, whereas for the bare functionals, differences as large as 6–7 mÅ are obtained, as can be seen in
Table S1 of the Supplementary Materials (SM), the nano-LEGO procedure lowers the deviations to 1.2 mÅ, thus reaching the same accuracy as the CCSD(T)-based composite methods but at a far lower computational cost. Concerning valence angles, the deviations obtained for the C3C2Cl angle at the DFT level are somewhat larger than those stemming from CCSD(T)-based approaches, but this is due to the lack of the nano-LEGO parameterization for this angle. By comparing the SE geometrical parameters with the theoretical counterparts obtained by the different methods, it can be speculated that the SE value of the C3C2H1 angle may be overestimated by about 0.5°. A possible explanation may be related to the imprecision of the rotational constants experimentally determined for the deuterated species, that, in turn, affects the fitting procedure used for the structural refinement.
Moving from the equilibrium geometries, the corresponding equilibrium rotational constants have been derived and, then, by augmenting them through vibrational corrections at the DFT level, ground state rotational constants have been obtained. The rotational constants of
ClHC=CF
are compared to the available experimental results in
Table 2 together with quartic centrifugal distortion parameters (data refer to the Watson’s A-reduction Hamiltonian in the
representation) and nuclear quadrupolar coupling constants. The high accuracy obtained in the equilibrium geometry is mirrored in the predicted ground state rotational constants, which reproduce the experimental values with a mean absolute percentage error (MAPE) around 0.06% when the composite schemes are considered. The same accuracy is reached by the nano-LEGO corrected rev-DSDPBEP86 functional, which significantly improves the results delivered by the bare functional (MAPE
), as can be appreciated from
Table S2 of the Supplementary Materials. A sensible improvement is also noted by comparing PW6B95+nano-LEGO (MAPE
) with the corresponding non-augmented counterpart (MAPE
), which, in any case, overshoots the accuracy of the rotational constants obtained at the B3LYP/SNSD level of theory (MAPE
, see
Table S2 of Supplementary Materials). In passing, it is interesting to note that both the CCSD(T)/CBS+CV and ChS composite methods, and also the nano-LEGO augmented functionals, yield predictions that are more accurate than the computationally demanding CCSD(T)/cc-pV5Z level of theory, which reproduces the experimental outcomes with a MAPE of around 0.4%. Furthermore, by comparing the experimental data [
33,
34] with the theoretical counterparts, it is noted that the values obtained in ref. [
33] appear to be more accurate than those in ref. [
34], which is also coherent with their superior precision, probably because, in the former investigation, the effects of centrifugal distortion have been described up to terms depending on the sixth power of the angular momentum operators, whereas, in the latter, the rotational Hamiltonian has been truncated at the quartic terms. A good agreement can also be reported between the experimental and theoretical quartic centrifugal distortion constants obtained from the ChS, which, on average, achieve the same accuracy (MAPE
) as the CCSD(T)/cc-pV5Z computations, but with a significantly lower computational cost. The only notable difference between the two is the maximum deviation, which amounts to −4.6% and 1.8% for the ChS and CCSD(T)/cc-pV5Z, respectively. The rev-DSDPBEP86 and PW6B95 show slightly larger errors, the MAPE being around 2% and 4% in line with previous benchmark studies [
54,
55,
57].
Sextic centrifugal distortion constants have been computed, and are listed in
Table 3, where the comparison with the available experimental data [
33] is also given, again referring to the Watson’s A-reduction Hamiltonian in the
representation. As can be seen, the theoretical results obtained at the different levels of theory employed are in good overall agreement, with only the PW6B95 seeming to yield slightly larger values for the
and
centrifugal distortion parameters. Comparing the computed vales of
,
and
with the experimental counterparts, a general good agreement can be noted, even though, according to the expected accuracy of the calculations [
46,
77], the relative deviations between 10 and 15% suggest that the rotational spectra of this molecule may deserve additional investigations, with the aim of extending the analysis toward higher rotational quantum numbers (
J in particular). This should lead to the determination of the missing sextic centrifugal distortion parameters, which, in turn, can also affect the values of the remaining ones. In addition, or alternatively, a fit constraining the not-yet-determined parameters to the theoretical values should be performed. This may avoid the determinable sextic centrifugal distortion constants being biased in the attempt to account for the centrifugal distortions effects described by the missing parameters. In this regard, the values obtained from the HYB-1 and HYB-2 force fields are suggested for the purpose: the former has been obtained by using the CCSD(T)/CBS+CV geometry, ChS harmonic frequencies (see next subsection) and rev-DSDPBEP86/jun-cc-pV(T+
d)Z cubic force constants; the latter has been derived by mixing the CCSD(T)/cc-pV5Z geometry and harmonic force field with CCSD(T)/cc-pVTZ cubic force constants. For the sake of completeness, the rotational spectroscopic parameters of the
ClHC=CF
,
ClHC=
CF
,
ClH
C=CF
,
ClDC=CF
and
ClDC=CF
isotopic species, obtained at different levels of theory, can be found in
Tables S3–S7 of the Supplementary Materials.
Before concluding this subsection, the
(
k and
representing the vibrational normal mode and principal axis of inertia, respectively) ro-vibrational interaction constants and the
Coriolis coupling parameters (in absolute value), which are relevant for further ro-vibrational spectroscopic high-resolution spectroscopic investigations, are listed in
Table 4 and
Table 5, respectively. Concerning the Coriolis resonance, it should be recalled that R1122 vibrational levels belonging to the same symmetry species can interact through
c-type Coriolis interactions, whereas levels of different symmetries can be coupled by both
a- and
b-type Coriolis interactions. By using the
values, vibrational contributions to rotational constants have been worked out and employed to correct the equilibrium rotational constants corresponding to the SE structure, thus obtaining the rotational constants of the singly excited fundamental vibrational levels reported in
Table 6.
3.2. Harmonic Force Field
Harmonic wavenumbers of ClHC=CF
fundamental vibrations are listed in
Table 7, together with the description of the vibrational normal modes based on total energy distribution (TED) values (%) obtained in terms of the internal coordinates defined in the lower part of the same table. For each normal mode, the TED analysis has been carried out in terms of a set of internal coordinates and using the quadratic force constants obtained at the fc-CCSD(T) level of theory. Intensities computed within the double-harmonic approximation are also reported, with the ChS harmonic intensity of the normal mode
i,
computed according to the following expression:
where the first term on the r.h.s. is the harmonic intensity at the CCSD(T)/cc-pV(T+
d)Z level, whereas the second and the third terms account for the enlargement of the basis set and the contribution from the correlation of core electrons, respectively. The former is obtained as the difference between MP2 values computed with the cc-pV(Q+
d)Z and cc-pV(T+
d)Z basis sets, whereas the latter is the difference between intensities calculated at the MP2/cc-pwCVTZ level by correlating all and only valence electrons. While representing an empirical approximation, the reliability of this approach has been shown to provide reliable predictions [
59]. As can be seen, both the frequencies and intensities obtained at the CCSD(T)/cc-pV5Z and ChS levels are in very good agreement. Indeed, the composite approach, while mostly relying on MP2 computations, reproduces the CCSD(T)/cc-pV5Z results with an average accuracy of only 2 cm
and a maximum difference of 5 cm
reported for the
and
vibrations. Concerning harmonic intensities, the two methods agree on average within 0.7 km mol
, with the largest difference of 3.8 km mol
observed for the
vibration, that, given the strong intensity of this vibration, in relative terms, corresponds to only the 3%.
Table 7 also lists the harmonic wavenumbers and intensities of R1122 computed at the rev-DSDPBEP86/jun-cc-pV(T+
d)Z and PW6B95/jul-cc-pV(D+
d)Z levels of theory, whereas results from B2PLYP/jun-cc-pV(T+
d)Z and B3LYP/SNSD computations can be found in
Tables S8 and S9 of the Supplementary Materials, respectively. Both rev-DSDPBEP86 and PW6B95 confirm their reliability for computing vibrational properties [
55]; in particular, CCSD(T)/cc-pV5Z harmonic frequencies are reproduced with a MAD of only 4.2 cm
by the rev-DSDPBEP86 double-hybrid functional and 12.8 cm
by the PW6B95 hybrid functional, whereas, for harmonic intensities, the MADs amount to 2.1 and 4.4 km mol
, respectively. As can be seen by looking at the results reported in
Table 7, the TEDs of the
,
,
and
normal modes show significant contributions from bending and/or stretching involving the chlorine atom; therefore, the corresponding instances of
Cl isotopologue splitting should be visible in the experimental spectra.
3.3. Vibrational Spectroscopy beyond the Double-Harmonic Approximation
In order to obtain theoretical predictions that are usable for the quantitative interpretation of experimentally recorded spectra, both mechanical and electrical anharmonicity need to be considered in the calculations. For the purpose, fundamental vibrational frequencies and IR intensities computed beyond the double-harmonic approximation are reported in
Table 8, together with the experimentally measured wavenumbers (for a graphical comparison between the theory and experiment, see
Figure S1 of the Supplementary Materials), and in
Table 9, respectively. While a detailed interpretation of the experimental spectra is deferred to the next subsection, here, a comparison among the theoretical outcomes obtained at the different levels of theory is given, pointing out both their accuracy with respect to the experiment and the most important aspects required for the spectral interpretation.
Table 8 reports the predictions according to four different hybrid force fields: in the CC5Z:rDSD and CC5Z:PW6 ones, the harmonic properties from CCSD(T)/cc-pV5Z computations have been mixed with anharmonic contributions evaluated by using the rev-DSDPBEP86 and PW6B95 functionals, respectively; ChS:rDSD and ChS:PW6 are the similar counterparts, but are obtained using harmonic frequencies and IR intesities at the ChS level. In addition, the table also collects the predictions from full rev-DSDPBEP86/jun-cc-pV(T+
d)Z and PW6B95/jul-cc-pV(D+
d)Z computations, whereas B2PLYP and B3LYP results can be found in the
Supplementary Tables S8 and S9, respectively. The different hybrid force fields yield very similar results for the fundamental vibrational frequencies and, in general, they agree within a few wavenumbers. This is particularly important for the
,
and
fundamentals, for which accurate and reliable theoretical predictions become important for the assignment of overtones and combination bands, due to the lack of experimental observations. Indeed, the
vibration is predicted to occur at quite low wavenumbers, in a region that is difficult to access experimentally, whereas the
and
vibrations, both having an intensity of around 0.5 km mol
at the anharmonic level, produce absorptions that are too weak to be directly detected, even if the
frequency has been estimated from the measurement of difference bands (vide infra). Both the highest levels of theory used in the present work, i.e., CC5Z:rDSD and ChS:DSD, place
,
and
at 195, 580 and 235 cm
, respectively, and these values have been used for assisting the spectral interpretation (vide infra). Before moving to the interpretation of the R1122 vibrational signatures, it is interesting to note that the
vibration is involved in a Fermi resonance of type 2 with the
combination, which is predicted to be particularly strong at the ChS:rDSD level of theory due to the closeness of their deperturbed vibrational energies. In fact, while this interaction is of a weaker magnitude at the other levels of theory employed, it is described by the following matrix by the ChS:rDSD hybrid force field:
| | | |
| 1333.1 | −7.2 |
| −7.2 | 1334.4 |
whose eigenvalues and eigenvectors are, respectively:
| 2326 | 1341 |
| |
| |
As a matter of fact, the and levels are mixed to the same extent in the perturbed states, thus making an assignment in terms of unperturbed level labels meaningless. Given this caveat, the interpretation of the experimental spectrum remains unaffected and independent of the model hybrid calculation.
3.4. Interpreting Experiments: Vibrational Analysis and Absorption Cross Sections
The vibrational analysis was performed on the gas-phase spectra measured in the range of 400–6500 cm
. The first step was the assignment of all of the strongest fundamentals, which was carried out on the spectra obtained at lower pressures; then, the weaker absorption features (mainly due to overtone and combination bands) were identified in the spectra obtained at higher pressures. A survey spectrum of the overall region investigated is reported in
Figure 2.
Table 8 lists all of the assigned fundamentals, together with the corresponding predicted values obtained at different levels of theory; in the same way,
Table 9 reports the corresponding predicted anharmonic intensities. Finally,
Table 10 comprises all of the vibrational assignments carried out in the present work, together with the corresponding predicted values, whereas the anharmonic constants
derived from the assigned bands are reported in
Table S12 of the Supplementary Materials, where, for completeness, the full list of theoretical values obtained from the CC5Z:rDSD hybrid force field is also given. For the sake of comparison, the measured fundamental frequencies of R1122 are juxtaposed with those of similar halogenated ethenes (H
C=CHCl [
78], H
C=CHF [
79]
cis- and
trans- ClHC=CHF [
80], ClFC=CF
[
25]) in
Table S13 of the Supplementary Materials.
On the basis of quantum chemical calculations, the
and
fundamentals are expected to be around 195 and 235 cm
, respectively. Even though, for the latter one, the transition frequency has been experimentally confirmed by the observation of the
–
difference band, the recording of their spectra may require a dedicated investigation through, e.g., the use of synchrotron radiation facilities [
81,
82]. Furthermore, at room temperature, the two lowest-lying vibrational levels
and
present a relative population of approximately 39% and 32%, respectively, with respect to the ground vibrational state. For this reason, the absorptions due to hot bands contribute significantly to the room temperature IR spectra, even if, at the resolutions employed in the present work, they usually overlap and are covered by the stronger envelopes of the cold bands. If, on the one hand, their assignment can be attempted by recording spectra at higher resolutions (e.g., 0.1 cm
or better), on the other, the spectral congestion stemming from hot band absorptions can make high-resolution investigations challenging, thus requiring cold spectra [
83].
3.4.1. 400–800 cm Spectral Region
This spectral region is dominated by the strong absorption (with a predicted intensity in the range of 34–36 km mol
; see
Table 9) due to the
band (
symmetry), located at 751.1 cm
, being in good agreement with the calculated anharmonic values (obtained at different levels of theory) listed in
Table 8. In addition, there are also two weaker fundamentals of
symmetry (
and
) with a computed intensity (at the CC5Z:rDSD level of theory) of 3.13 and 1.43 km mol
, respectively; concerning the position of
, there is a very good agreement between its experimental value (at 431.8 cm
) and the predicted ones, which are in the range of 430–432 cm
. Moving to higher wavenumbers, it is worthwhile to note that the stronger
, located at 578.0 cm
, completely obscures the signals coming from the very weak
, predicted in the range of 580–594 cm
and with a computed intensity lower than 1 km mol
. Focusing on the position of
, all of the theoretical methods listed in
Table 8 (with the exception of the PW6B95 hybrid) led to predicted values having an absolute error that is not greater than one wavenumber. Besides, it is worthwhile to note that, even if on the basis of the TED analysis (see
Table 7), we could expect to see the instances of the
Cl isotopologue splitting for both of these two fundamentals (i.e.,
and
), only for
are these features clearly visible in the spectra (the signals are located at 578.0 and 577.4 cm
, respectively), whereas, in the case of
, they were not discernible (due to the predominant B-type envelope of this band). The agreement between the experimentally determined and the predicted positions for all of the bands assigned in this spectral region can be considered as very remarkable (the MAD is only 1.9 and 1.4 cm
at the CC5Z:rDSD and ChS:rDSD levels of theory, respectively; see the data listed in
Table 10). Finally, it is worthwhile to note that, using the
–
located at 736.2 cm
, it is possible to predict the position of
, thus obtaining a value of 235.3 cm
, which is in very good agreement with the ab initio data of 235 and 236 cm
yielded by the CC5Z:rDSD and ChS:rDSD levels of theory, respectively (see
Table 8).
3.4.2. 800–1800 cm Spectral Region
As expected by the analysis of the data reported in
Table 9, in this spectral region, the key features (which characterize the spectra measured at lower pressures) are the strong absorptions due to the
(at 971.5 cm
),
(at 1200 cm
),
(at 1341.7 cm
) and
(at 1747.5 cm
) fundamentals (all having
symmetry), which have computed intensities, at the CC5Z:rDSD level of theory, in the range of 84–142 km mol
. Located at lower wavenumbers, there is the much weaker
band (centered at 844.9 cm
, with a predicted intensity lower than 9 km mol
). The
and
fundamentals show distinct absorption features (located at 971.5/970.2 and 844.9/841.8 cm
, respectively) due to the presence of both the
Cl isotopologues, thus being in line with the predictions made on the basis of the corresponding TED analysis (as reported in
Table 7). Looking at the theoretical data, what is remarkable is the agreement between the CC5Z:rDSD predictions and the corresponding experimental values of these bands (the greatest error is less than two wavenumbers). The spectra recorded at increasing pressures allowed for the identification of several signals assigned to two-quanta combinations (for example,
+
,
+
,
+
,
+
and so on), as well as to overtone bands (2
, 2
and 2
). Even in this spectral region, the comparison between the measured positions of the assigned bands (fundamentals and many two-quanta transitions) and the predicted values (listed in
Table 10) points out the overall very good performance of the calculations carried out at the CC5Z:rDSD level of theory: the corresponding MAD is less than 2 cm
, whereas the computed data at the ChS:rDSD level of theory has a MAD of 2.5 cm
.
3.4.3. 1800–3200 cm Spectral Region
In the range of 1800–3200 cm
, only the
fundamental (
symmetry, located at 3135.9 cm
) is clearly visible in the spectra recorded at low pressures (as expected by looking at the corresponding calculated intensity, 12.07 km mol
at the CC5Z:rDSD level of theory; see
Table 9). Increasing the sample pressure allowed us to identify and assign the signals coming from the 2
(at 1939.8 cm
), 2
(at 2394.7 cm
) and 2
(at 2663.7 cm
) overtones, as well as several absorptions due to binary combinations mainly involving
or
(such as
+
,
+
,
+
,
+
,
+
,
+
). Looking at the comparison between the experimental and the predicted values (as reported in
Table 10) the overall agreement is still very good, with the MAD being around 3.5 cm
for both the CC5Z:rDSD and ChS:rDSD levels of theory.
3.4.4. 3200–6500 cm Spectral Region
The analysis of the signals falling in the last spectral region (3200–6500 cm) was carried out by using the spectra measured at a high sample pressure, and several two- and three-quanta combination bands (mainly involving ) were assigned. Besides them, the high-wavenumber side of this region is characterized by the 2 overtone (at 6150.1 cm) and the nearby + + band. Due to the presence of absorptions involving only two- and (some) three-quanta transitions, this spectral region can be considered as more challenging for the theoretical predictions than the former ones; regardless, the overall agreement reached at the CC5Z:rDSD level of theory is very good, with the MAD being only 4.1 cm, whereas, in this spectral region, the ChS:rDSD predictions present a larger MAD of 9 cm. Despite this, the computed anharmonic frequencies and intensities are accurate enough to lead to an unambiguous assignment of the observed spectral features.
Using the positions of the fundamentals as benchmark data to assess the performances of the different anharmonic force fields employed in the present work, the results reported in
Table 8 point out the excellent accuracy of CC5Z:rDSD; the MAD is only 1.4 cm
, and all of the bands are predicted with errors that are generally within a few wavenumbers (the largest absolute deviation is smaller than 4 cm
). For comparison, all of the other composite schemes yielded slightly larger MAD values, even if their predictions can still be considered as more than satisfactory; regardless, they all led to bigger deviations of up to around 8 cm
for some bands. The very remarkable accuracy offered by the CC5Z:rDSD method is further confirmed by taking into account the whole set of assigned transitions (thus including many overtone and combination bands, and, in some cases, up to three quanta; see
Table 10); the overall MAD is less than 3 cm
, and most of the deviations are generally lower than 6 cm
. For comparison, the predictions obtained at the ChS:rDSD level of theory have an overall MAD of 4.4 cm
.
3.4.5. Absorption Cross Sections and Integrated Band Intensities
In the present work, the determination of the absorption cross section spectra of R1122 was carried out by using the medium resolution spectra and following the procedure described in detail elsewhere (see, for example, ref. [
84] and references therein). Briefly speaking, the method is based on the least-squares fitting the point-by-point absorbance value, A(
) measured at each wavenumber,
, versus the corresponding sample concentration, and always using N
as an inert buffer gas. The slope that is thus obtained at each wavenumber,
(
), gives the absorbance cross section per molecule (cm
molecule
); in the same way, the point-by-point error estimate is also obtained (as a statistical uncertainty). It is worthwhile to note that this procedure avoids the distortion due to saturation effects and, at the same time, leads to a better signal-to-noise ratio for the weaker signals; besides, we demonstrated that it produces data in very good agreement with the ones yielded by the line-shape analyses carried out on high-resolution measurements (see, for example, refs. [
85,
86,
87,
88]).
The cross-section spectrum of the overall region investigated is reported in
Figure 3a, where it is also compared with the theoretical stick spectrum obtained from hybrid CC5Z:rDSD computations (panel b of the same Figure). As can be seen, the match between the measured and theoretical wavenumbers and relative intensities is very pleasant. In making the comparison, it should be stressed that, whereas the stick spectrum refers to anharmonic IR intensities, the experimental trace represents the cross section spectrum, which yields band intensities upon integrating over a given spectral interval, as explained above. Indeed,
Table 11 lists the experimental integrated absorption cross sections (cm molecule
) together with the corresponding theoretical predictions obtained at both the CC5Z:rDSD and ChS:rDSD levels of theory.
In the spectral range of 400–900 cm the band is the most intense absorption; its measured integrated intensity, 5.531(34) × 10 cm molecule, clearly overcomes the other fundamentals falling in this region ( has a value of 1.605(10) × 10 cm molecule, whereas and have cross-sections of 6.503(80) and 2.33(27) × 10 cm molecule, respectively).
The strongest absorptions (accounting for more than 68% of the overall integrated band intensities) are localized in the region of 900–1900 cm
, and they are due to the
,
,
and
fundamentals, which is as expected since all of their descriptions involve a significant fraction of C-F stretchings (see the corresponding TED% in terms of internal coordinates reported in
Table 7). Their individual integrated intensities range from 1.8 to 2.7 × 10
cm molecule
, and their overall sum is equal to 8.50 × 10
cm molecule
. At this point, it is worthwhile to note that the overall cross section of R1122 in the atmospheric window (900–1400 cm
) can be considered as rather large (around 5.9 × 10
cm molecule
), in line with that of other similar halogenated ethenes (for comparison, ClFC=CH
has an integrated value of almost 4.5 × 10
cm molecule
; see [
23], whereas that of ClFC=CF
is around 9.3 × 10
cm molecule
, see [
25]).
The fundamental, with an integrated intensity of almost 2.14 × 10 cm molecule, clearly dominates the region around 3000 cm. The other absorptions, falling at higher wavenumbers, i.e., in the range of 3440–6500 cm, are mainly due to overtone and combination bands, and their overall integrated cross section is around 4 × 10 cm molecule.
Concerning the comparison between the experimental data and the corresponding computed values, the data reported in
Table 11 highlight the very good overall performance of both the CC5Z:rDSD and ChS:rDSD levels of theory in reproducing the most intense absorptions (i.e., the ones falling in the region of 900–1900 cm
), with the average absolute errors being not greater than 6%. The predicted intensities for the weaker features (such as the combination and overtone bands) show larger deviations (in line with the trends seen in previous investigations; see, for example, ref. [
84] and references therein), but the average absolute error, considering the whole data set of integrated cross-sections up to 6300 cm
, is less than 3.5 × 10
cm molecule
(i.e., around 8% of the value of the overall integrated intensity).
By using the obtained cross section spectrum within the narrowband model of Ref. [
89], the radiative forcing (RF) of R1122 has been estimated to be 0.098 W m
ppbv
. Even if we are aware that this approach is not well suited for short-lived molecules and therefore this determined value should be considered as just an estimate of the actual RF, we note that the data thus computed are in good agreement with the ones obtained using a more sophisticated model on a similar halogenated olefin (e.g.,
trans-1-chloro- 3,3,3-trifluoropropylene, see [
37]). As pointed out in the introduction, for the atmospheric lifetime of R1122, a reasonable guess of the upper value should be in the range of 10–30 days (see also [
90]), thus leading to an estimated GWP between 1.5 and 4.5 on a 100-year time horizon, and between 6 and 18 on a 20-year time horizon.