New Insights into the (A)Synchronicity of Diels–Alder Reactions: A Theoretical Study Based on the Reaction Force Analysis and Atomic Resolution of Energy Derivatives
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Dataset
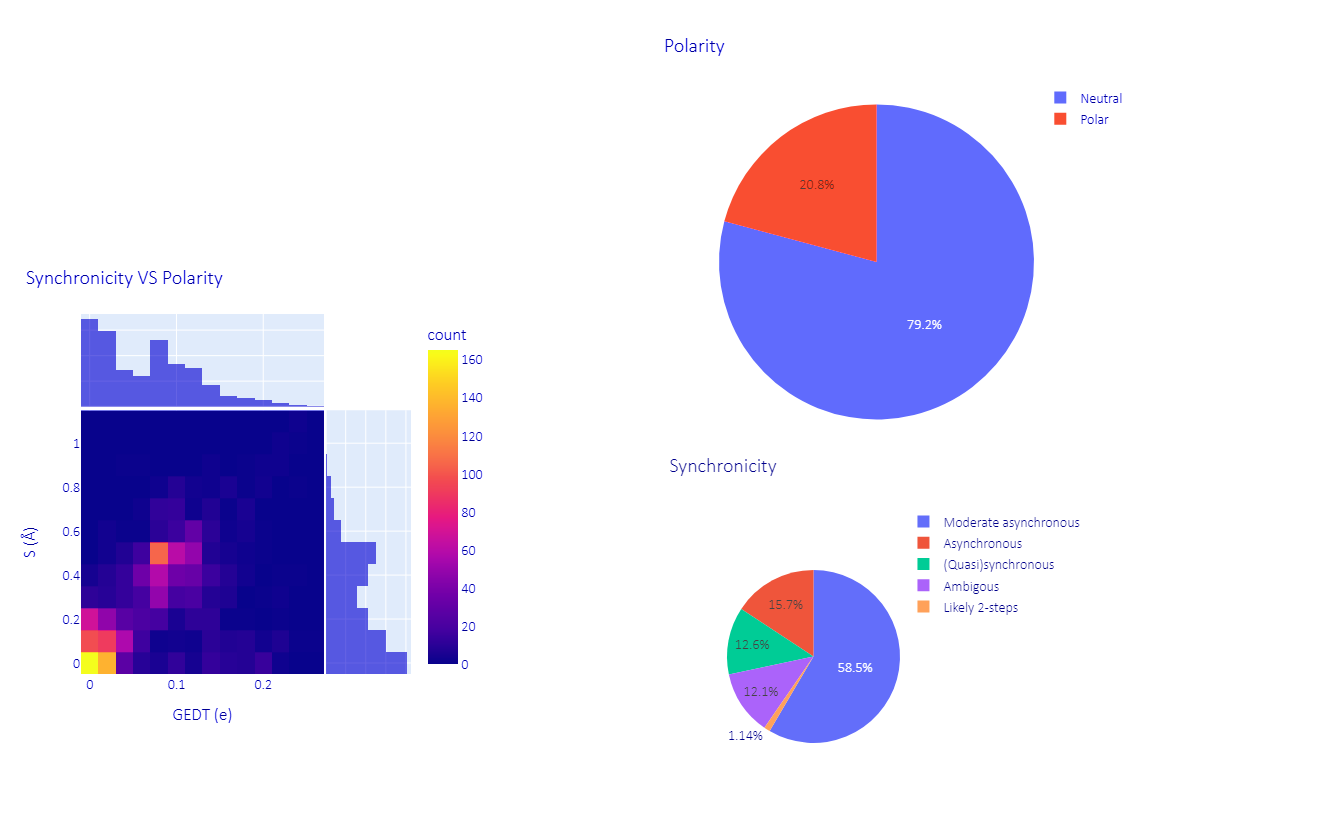
2.1.1. Heterogeneity
2.1.2. Polarity
2.1.3. (A)Synchronicity
2.2. Reaction Force Analysis
2.2.1. Potential Energy
2.2.2. Reaction Force and Reaction Force Constant Profiles
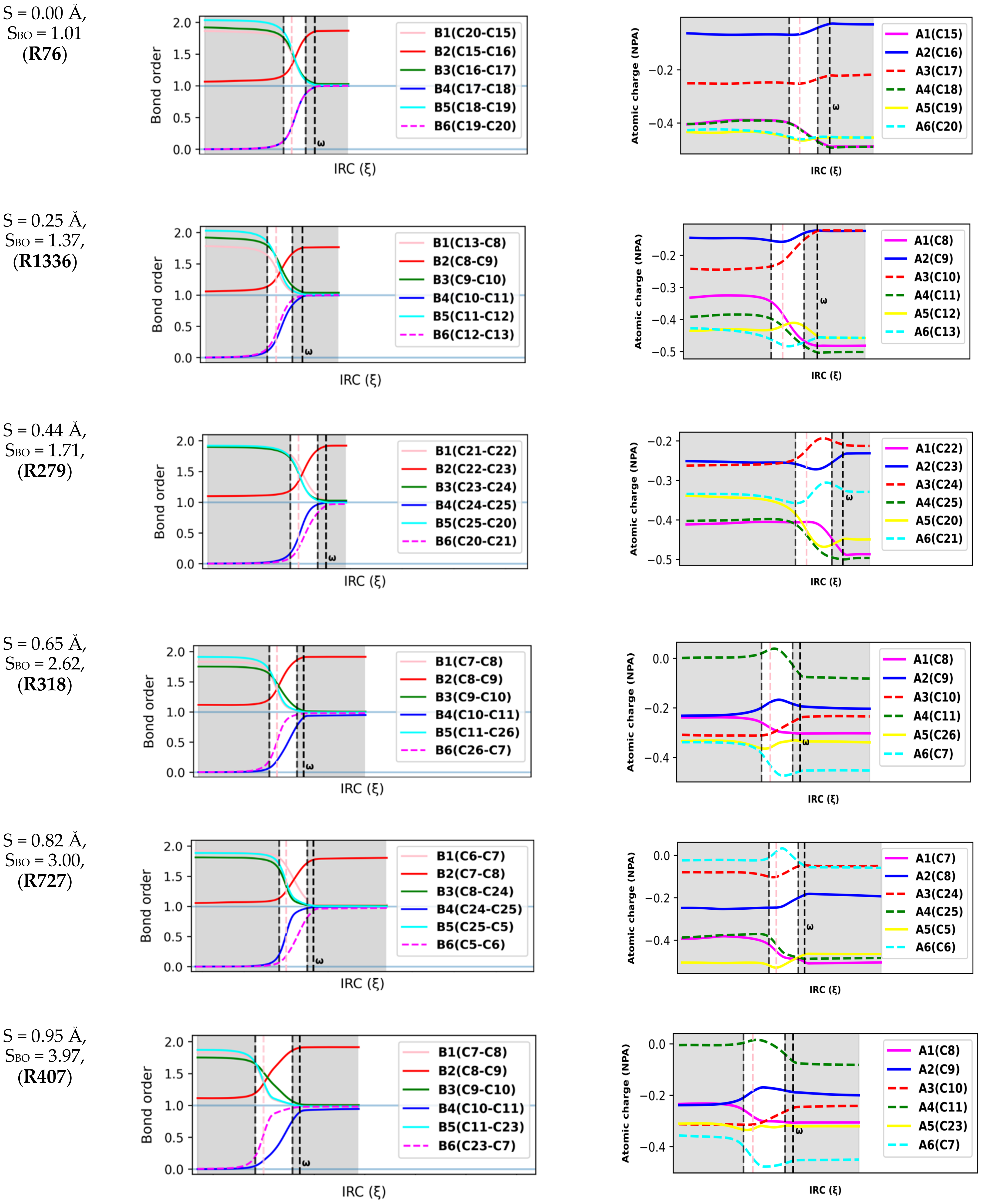
2.3. Natural Population Analysis
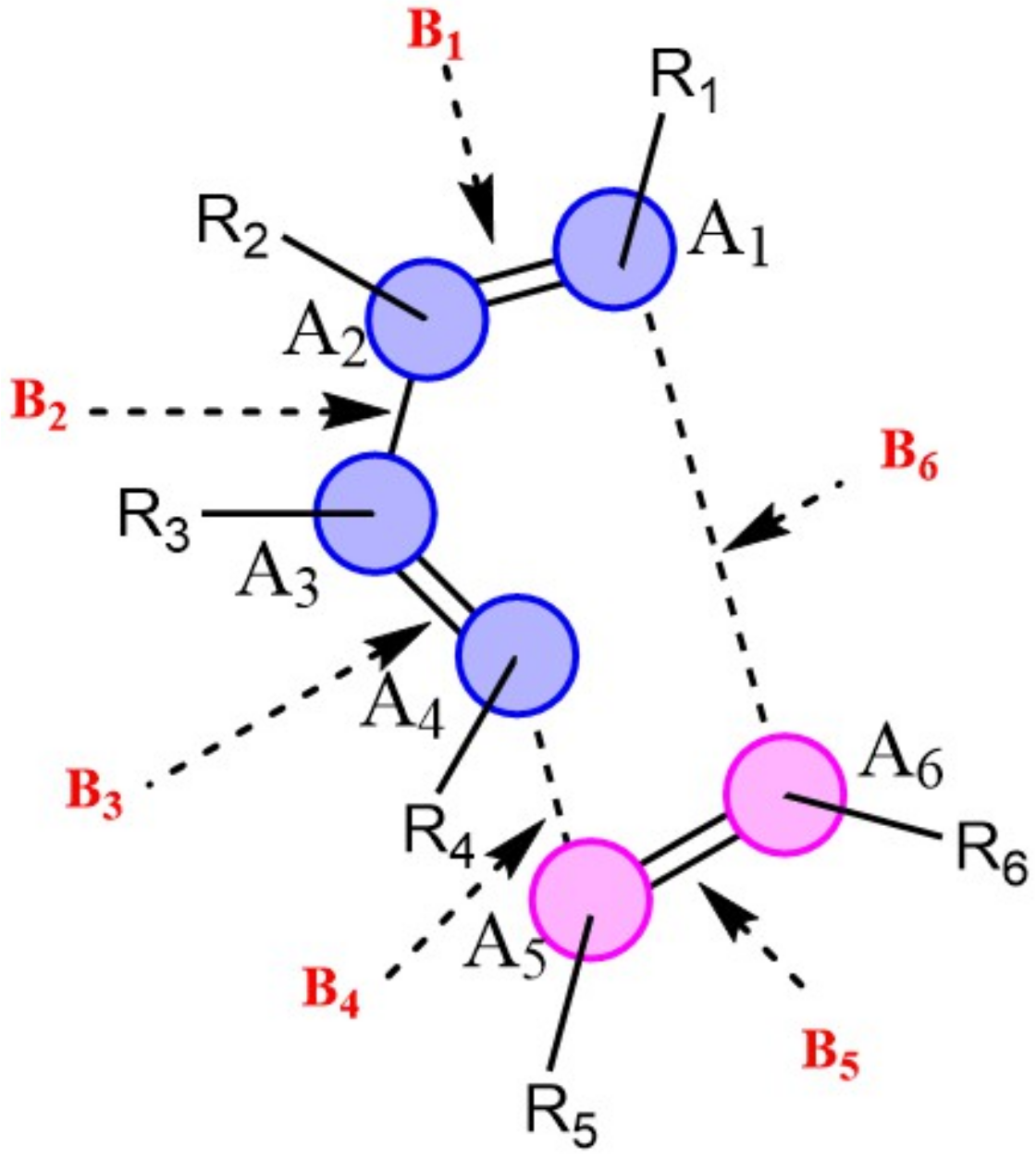
2.4. Atomic Resolution of Energy Derivatives
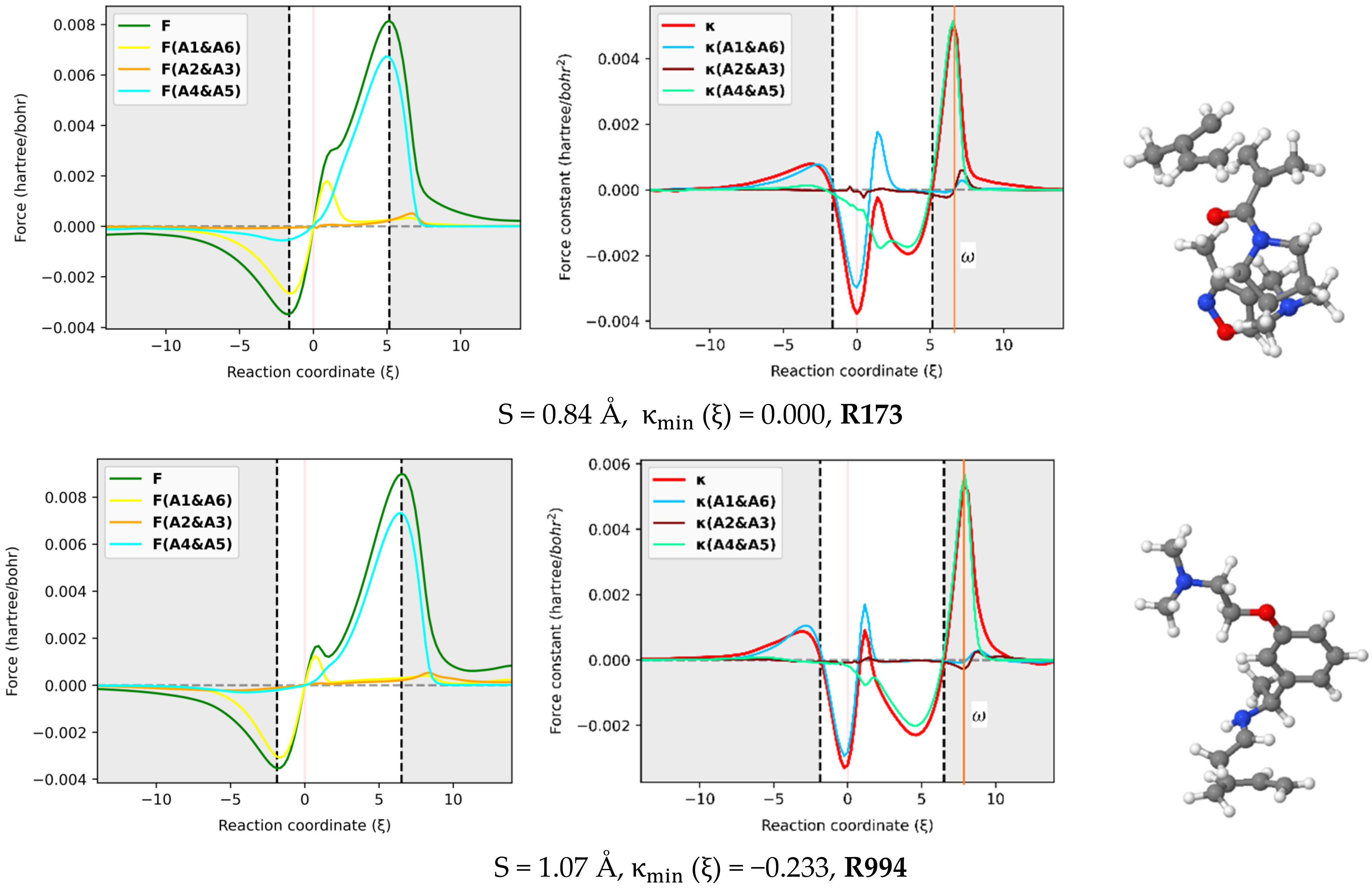
2.4.1. Reaction Force Decomposition
2.4.2. Reaction Force Constant Decomposition
2.5. On the Validity and Limitations of Our Conclusions
3. Methodology
3.1. Theoretical Background
3.1.1. Reaction Force Analysis
3.1.2. Atomic Resolution of Energy Derivatives
3.2. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Barriault, L.; Thomas, J.D.O.; Cle, R. Highly Stereoselective Hydroxy-Directed Diels-Alder Reaction and tertiary allylic magnesium alkoxide alcohol functionality and activated dienophiles such as. J. Org. Chem. 2003, 68, 2317–2323. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.G.; Hill, R.K. Stereochemistry of the Diels-Alder reaction. Chem. Rev. 1961, 61, 537–562. [Google Scholar] [CrossRef]
- Diels, O.; Alder, K. Synthesen in der hydroaromatischen Reihe. Justus Liebigs Ann. Chem. 1928, 460, 98–122. [Google Scholar] [CrossRef]
- Nicolaou, K.C.; Snyder, S.A.; Montagnon, T.; Vassilikogiannakis, G. The Diels-Alder reaction in total synthesis. Angew. Chemie Int. Ed. 2002, 41, 1668–1698. [Google Scholar] [CrossRef]
- Kinsman, A.C.; Kerr, M.A. The Total Synthesis of (+)-Hapalindole Q by an Organomediated Diels-Alder Reaction. J. Am. Chem. Soc. 2003, 125, 14120–14125. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.H.; Green, N.J.; Xu, S.Z. Application of the aza-Diels-Alder reaction in the synthesis of natural products. Org. Biomol. Chem. 2017, 15, 3105–3129. [Google Scholar] [CrossRef] [PubMed]
- Woodward, B.R.B.; Sondheimer, F.; Taub, D.; Heusler, K.; McLamore, W.M. Journal of the Chemical Society. J. Am. Chem. Soc. 1952, 74, 4223–4250. [Google Scholar] [CrossRef]
- Danishefsky, S.; Hirama, M.; Fritsch, N.; Clardy, J. Synthesis of Disodium Prephenate and Disodium Epiprephenate. Stereochemistry of Prephenic Acid and an Observation on the Base-Catalyzed Rearrangement of Prephenic Acid to /7-Hydroxyphenyllactic Acid. J. Amercican Chem. Soc. 1979, 101, 7013–7018. [Google Scholar] [CrossRef]
- Briou, B.; Améduri, B.; Boutevin, B. Trends in the Diels–Alder reaction in polymer chemistry. Chem. Soc. Rev. 2021, 50, 11055–11097. [Google Scholar] [CrossRef]
- Munirasu, S.; Albueme, J.; Boschetti-de-Fierro, A.; Abetz, V. Functionalization of carbon materials using the diels-alder reaction a. Macromol. Rapid Commun. 2010, 31, 574–579. [Google Scholar] [CrossRef] [Green Version]
- Gregoritza, M.; Brandl, F.P. The Diels-Alder reaction: A powerful tool for the design of drug delivery systems and biomaterials. Eur. J. Pharm. Biopharm. 2015, 97, 438–453. [Google Scholar] [CrossRef]
- Kittleson, A.R. Preparation and Some Properties of N—Trichloromethylthiotetrahydrophthalimide. Agric. food Chem. 1953, 1, 677–679. [Google Scholar] [CrossRef]
- Snow, R.A.; Cottrell, D.M.; Paquette, L.A. Demonstration and Analysis of Bridging Regioselectivity Operative during Di-pi-methane Photorearrangement of Ortho-Substituted Benzonorbornadienes and anti-7,8-Benzotricyclo[4.2.2.0]deca-3,7,9-trienes. J. Am. Chem. Soc. 1977, 13, 3734–3744. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Pierini, A.B. Mechanism of the Diels-Alder Reaction. Studies of the Addition of Maleic Anhydride to Furan and Methylfurans. J. Am. Chem. Soc. 1984, 106, 203–208. [Google Scholar] [CrossRef]
- Sakai, S. Theoretical analysis of concerted and stepwise mechanisms of the hetero-Diels-Alder reaction of butadiene with formaldehyde and thioformaldehyde. J. Mol. Struct. THEOCHEM 2003, 630, 177–185. [Google Scholar] [CrossRef]
- Steglenko, D.V.; Kletsky, M.E.; Kurbatov, S.V.; Tatarov, A.V.; Minkin, V.I.; Goumont, R.; Terrier, F. The stepwise Diels-Alder reaction of 4-nitrobenzodifuroxan with Danishefsky’s diene. Chem. A Eur. J. 2011, 17, 7592–7604. [Google Scholar] [CrossRef]
- Li, Y.; Houk, K.N. Diels-Alder Dimerization of 1,3-Butadiene: An ab Initio CASSCF Study of the Concerted and Stepwise Mechanisms and Butadiene–Ethylene Revisited. J. Am. Chem. Soc. 1993, 115, 7478–7485. [Google Scholar] [CrossRef]
- Dewar, M.J.S. Multibond Reactions Cannot Normally Be Synchronous. J. Am. Chem. Soc. 1984, 106, 209–219. [Google Scholar] [CrossRef]
- Nendel, M.; Tolbert, L.M.; Herring, L.E.; Islam, M.N.; Houk, K.N. Strained allenes as dienophiles in the Diels-Alder reaction: An experimental and computational study. J. Org. Chem. 1999, 64, 976–983. [Google Scholar] [CrossRef]
- Cossío, F.P.; Morao, I.; Jiao, H.; Von Ragué Schleyer, P. In-plane aromaticity in 1,3-dipolar cycloadditions. Solvent effects, selectivity, and nucleus-independent chemical shifts. J. Am. Chem. Soc. 1999, 121, 6737–6746. [Google Scholar] [CrossRef]
- Novikov, A.S.; Kuznetsov, M.L. Theoretical study of Re(IV) and Ru(II) bis-isocyanide complexes and their reactivity in cycloaddition reactions with nitrones. Inorganica Chim. Acta 2012, 380, 78–89. [Google Scholar] [CrossRef]
- Merino, P.; Chiacchio, M.A.; Legnani, L.; Delso, I.; Tejero, T. Introducing topology to assess the synchronicity of organic reactions. Dual reactivity of oximes with alkenes as a case study. Org. Chem. Front. 2017, 4, 1541–1554. [Google Scholar] [CrossRef]
- De Souza, M.A.F.; Ventura, E.; Do Monte, S.A.; Riveros, J.M.; Longo, R.L. Revisiting the concept of the (a)synchronicity of diels-alder reactions based on the dynamics of quasiclassical trajectories. J. Comput. Chem. 2016, 37, 701–711. [Google Scholar] [CrossRef]
- Loncharich, R.J.; Brown, F.K.; Houk, K.N. Transition Structures of the Diels-Alder Reaction of Butadiene with Acrolein. J. Org. Chem. 1989, 54, 1129–1134. [Google Scholar] [CrossRef]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Origin of the synchronicity in bond formation in polar Diels-Alder reactions: An ELF analysis of the reaction between cyclopentadiene and tetracyanoethylene. Org. Biomol. Chem. 2012, 10, 3841–3851. [Google Scholar] [CrossRef] [PubMed]
- Vermeeren, P.; Hamlin, T.A.; Bickelhaupt, F.M. Origin of Asynchronicity in Diels-Alder Reactions. Phys. Chem. Chem. Phys. 2021. [Google Scholar] [CrossRef] [PubMed]
- Yepes, D.; Donoso-Tauda, O.; Pérez, P.; Murray, J.S.; Politzer, P.; Jaque, P. The reaction force constant as an indicator of synchronicity/ nonsynchronicity in [4+2] cycloaddition processes. Phys. Chem. Chem. Phys. 2013, 15, 7311–7320. [Google Scholar] [CrossRef] [PubMed]
- Toro-Labbé, A.; Gutiérrez-Oliva, S.; Murray, J.S.; Politzer, P. The reaction force and the transition region of a reaction. J. Mol. Model. 2009, 15, 707–710. [Google Scholar] [CrossRef]
- Jedrzejewski, M.; Ordon, P.; Komorowski, L. Atomic Resolution for the Energy Derivatives on the Reaction Path. J. Phys. Chem. A 2016, 120, 3780–3787. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pantelides, S.T. Hellmann-Feynman theorem and the definition of forces in quantum time-dependent and transport problems. Phys. Rev. B Condens. Matter Mater. Phys. 2000, 61, 16207–16212. [Google Scholar] [CrossRef] [Green Version]
- Isamura, B.K.; Lobb, K. (Rhodes University, Makhanda, South Africa). AMADAR: A python-based package for large scale prediction of Diels-Alder transition state geometries and IRC path analysis. Unpublished work—under review.
- Domingo, L.R. Molecular electron density theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels-Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [Google Scholar] [CrossRef]
- Domingo, L.R.; Alder, N.; Diels, S.M.H.; Methodology, A. A Theoretical Study of the Molecular Mechanism of the Reaction between N, N-Dimethylmethyleneammonium Cation and Cyclopentadiene. J. Org. Chem. 2013, 66, 3211–3214. [Google Scholar] [CrossRef]
- Taylor, R.R.R.; Batey, R.A. A hetero Diels-Alder approach to the synthesis of chromans (3,4-dihydrobenzopyrans) using oxonium ion chemistry: The oxa-Povarov reaction. J. Org. Chem. 2013, 78, 1404–1420. [Google Scholar] [CrossRef]
- Yepes, D.; Murray, J.S.; Pérez, P.; Domingo, L.R.; Politzer, P.; Jaque, P. Complementarity of reaction force and electron localization function analyses of asynchronicity in bond formation in Diels-Alder reactions. Phys. Chem. Chem. Phys. 2014, 16, 6726–6734. [Google Scholar] [CrossRef]
- Politzer, P.; Burda, J.V.; Concha, M.C.; Lane, P.; Murray, J.S. Analysis of the reaction force for a gas phase S N2 process: CH 3Cl + H 2O → CH 3OH + HCl. J. Phys. Chem. A 2006, 110, 756–761. [Google Scholar] [CrossRef]
- Van Zeist, W.J.; Bickelhaupt, F.M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Yepes, D.; Jaque, P. Driving and retarding forces in a chemical reaction. J. Mol. Model. 2014, 20, 2351. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Jaque, P. Perspectives on the reaction force constant. J. Mol. Model. 2013, 19, 4111–4118. [Google Scholar] [CrossRef]
- Wakayama, H.; Sakai, S. Theoretical analysis of concerted and stepwise mechanisms of Diels-Alder reactions of butadiene with silaethylene and dislene. J. Phys. Chem. A 2007, 111, 13575–13582. [Google Scholar] [CrossRef]
- Burda, J.V.; Murray, J.S.; Toro-Labbé, A.; Gutiérrez-Oliva, S.; Politzer, P. Reaction force analysis of solvent effects in the addition of HCl to propene. J. Phys. Chem. A 2009, 113, 6500–6503. [Google Scholar] [CrossRef] [PubMed]
- Herrera, B.; Toro-Labbé, A. The role of reaction force and chemical potential in characterizing the mechanism of double proton transfer in the adenine-uracil complex. J. Phys. Chem. A 2007, 111, 5921–5926. [Google Scholar] [CrossRef] [PubMed]
- Hammoudan, I.; Chtita, S.; Riffi-Temsamani, D. QTAIM and IRC studies for the evaluation of activation energy on the C = P, C = N and C = O Diels-Alder reaction. Heliyon 2020, 6, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Zeeman, E.C. Catastrophe theory. Sci. Am. 1976, 234, 65–83. [Google Scholar] [CrossRef]
- Berski, S.; Andŕes, J.; Silvi, B.; Domingo, L.R. New findings on the Diels—Alder reactions. An analysis based on the bonding evolution theory. J. Phys. Chem. A 2006, 110, 13939–13947. [Google Scholar] [CrossRef]
- Dominikowska, J.; Jabłoński, M.; Palusiak, M. Feynman force components: Basis for a solution to the covalent: Vs. ionic dilemma. Phys. Chem. Chem. Phys. 2016, 18, 25022–25026. [Google Scholar] [CrossRef] [Green Version]
- Vermeeren, P.; Hamlin, T.A.; Fernández, I.; Bickelhaupt, F.M. How Lewis Acids Catalyze Diels–Alder Reactions. Angew. Chemie 2020, 132, 6260–6265. [Google Scholar] [CrossRef]
- Spezia, R.; Martínez-Nuñez, E.; Vazquez, S.; Hase, W.L. Theoretical and computational studies of non-equilibrium and non-statistical dynamics in the gas phase, in the condensed phase and at interfaces. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20170035. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.X.; Tremblay, M.; Hong, X.; Yang, Z.J. Entropic Path Sampling: Computational Protocol to Evaluate Entropic Profile along a Reaction Path. J. Phys. Chem. Lett. 2021, 12, 10713–10719. [Google Scholar] [CrossRef]
- Rincón, E.; Jaque, P.; Toro-Labbé, A. Reaction force analysis of the effect of Mg(II) on the 1,3 intramolecular hydrogen transfer in thymine. J. Phys. Chem. A 2006, 110, 9478–9485. [Google Scholar] [CrossRef]
- Toro-Labbé, A. Characterization of chemical reactions from the profiles of energy, chemical potential, and hardness. J. Phys. Chem. A 1999, 103, 4398–4403. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 365–368. [Google Scholar] [CrossRef]
- Inostroza-Rivera, R.; Herrera, B.; Toro-Labbé, A. Using the reaction force and the reaction electronic flux on the proton transfer of formamide derived systems. Phys. Chem. Chem. Phys. 2014, 16, 14489–14495. [Google Scholar] [CrossRef]
- Hargis, J.C.; Vöhringer-Martinez, E.; Woodcock, H.L.; Toro-Labbé, A.; Schaefer, H.F. Characterizing the mechanism of the double proton transfer in the formamide dimer. J. Phys. Chem. A 2011, 115, 2650–2657. [Google Scholar] [CrossRef]
- Labet, V.; Morell, C.; Toro-labbe, A. Theoretical Study of Cytosine Deamination from the Perspective of the Reaction Force Analysis. J. Phys. Chem. 2008, 112, 11487–11494. [Google Scholar] [CrossRef]
- Toro-Labbé, A.; Gutiérrez-Oliva, S.; Concha, M.C.; Murray, J.S.; Politzer, P. Analysis of two intramolecular proton transfer processes in terms of the reaction force. J. Chem. Phys. 2004, 121, 4570–4576. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C.; Klippenstein, S.J. Current Status of Transition-State Theory. J. Phys. Chem. 1996, 100, 12771–12800. [Google Scholar] [CrossRef]
- Zewail, A.H. Femtochemistry: Atomic-scale dynamics of the chemical bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
- Yepes, D.; Murray, J.S.; Politzer, P.; Jaque, P. The reaction force constant: An indicator of the synchronicity in double proton transfer reactions. Phys. Chem. Chem. Phys. 2012, 14, 11125–11134. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. The Hellmann-Feynman theorem: A perspective. J. Mol. Model. 2018, 24, 266. [Google Scholar] [CrossRef]
- Geerlings, P.; Fias, S.; Boisdenghien, Z.; De Proft, F. Conceptual DFT: Chemistry from the linear response function. Chem. Soc. Rev. 2014, 43, 4989–5008. [Google Scholar] [CrossRef]
- Komorowski, L.; Ordon, P. Vibrational softening of diatomic molecules. Theor. Chem. Acc. 2001, 105, 338–344. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling. Components 2011. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 (C.01). Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Irwin, J.J.; Shoichet, B.K. ZINC—A free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. [Google Scholar] [CrossRef] [Green Version]
- Casewit, C.J.; Colwell, K.S.; Rappé, A.K. Application of a Universal Force Field to Organic Molecules. J. Am. Chem. Soc. 1992, 114, 10035–10046. [Google Scholar] [CrossRef]
- Suleimanov, Y.V.; Green, W.H. Automated Discovery of Elementary Chemical Reaction Steps Using Freezing String and Berny Optimization Methods. J. Chem. Theory Comput. 2015, 11, 4248–4259. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- James, N.C.; Um, J.M.; Padias, A.B.; Hall, H.K.; Houk, K.N. Computational investigation of the competition between the concerted diels-alder reaction and formation of diradicals in reactions of acrylonitrile with nonpolar dienes. J. Org. Chem. 2013, 78, 6582–6592. [Google Scholar] [CrossRef] [Green Version]
- Dinadayalane, T.C.; Vijaya, R.; Smitha, A.; Sastry, G.N. Diels-Alder reactivity of butadiene and cyclic five-membered dienes ((CH)4X, X = CH2, SiH2, O, NH, PH, and S) with ethylene: A benchmark study. J. Phys. Chem. A 2002, 106, 1627–1633. [Google Scholar] [CrossRef]




| Reaction ID | GEDT(e) | S (Å) | Eact | Eact,1 | Eact,2 |
|---|---|---|---|---|---|
| R76 | 0.000 | 0.00 | 20.58 | 15.73 | 4.48 |
| R283 | 0.032 | 0.09 | 23.04 | 17.83 | 5.21 |
| R313 | 0.002 | 0.12 | 20.70 | 15.79 | 4.91 |
| R525 | 0.031 | 0.18 | 23.97 | 19.49 | 4.48 |
| R1336 | 0.051 | 0.25 | 16.64 | 12.30 | 4.34 |
| R568 | 0.011 | 0.27 | 22.79 | 18.03 | 4.76 |
| R359 | 0.107 | 0.37 | 21.69 | 16.56 | 5.13 |
| R725 | 0.112 | 0.38 | 20.74 | 15.62 | 5.12 |
| R1669 | 0.122 | 0.43 | 20.55 | 15.52 | 5.03 |
| R279 | 0.084 | 0.44 | 17.09 | 12.65 | 4.44 |
| R793 | 0.081 | 0.54 | 19.06 | 14.64 | 4.42 |
| R318 | 0.113 | 0.60 | 19.04 | 14.60 | 4.44 |
| R972 | 0.180 | 0.65 | 20.06 | 15.23 | 4.83 |
| R1453 | 0.089 | 0.76 | 23.73 | 18.87 | 4.86 |
| R1048 | 0.094 | 0.77 | 24.50 | 17.95 | 6.56 |
| R1439 | 0.128 | 0.80 | 19.02 | 14.28 | 4.74 |
| R727 | 0.153 | 0.82 | 21.38 | 16.48 | 4.10 |
| R407 | 0.138 | 0.95 | 19.65 | 14.80 | 4.85 |
| R1018 | 0.211 | 0.97 | 23.04 | 16.21 | 6.82 |
| R994 | 0.247 | 1.07 | 19.57 | 14.29 | 5.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isamura, B.K.; Lobb, K.A. New Insights into the (A)Synchronicity of Diels–Alder Reactions: A Theoretical Study Based on the Reaction Force Analysis and Atomic Resolution of Energy Derivatives. Molecules 2022, 27, 1546. https://doi.org/10.3390/molecules27051546
Isamura BK, Lobb KA. New Insights into the (A)Synchronicity of Diels–Alder Reactions: A Theoretical Study Based on the Reaction Force Analysis and Atomic Resolution of Energy Derivatives. Molecules. 2022; 27(5):1546. https://doi.org/10.3390/molecules27051546
Chicago/Turabian StyleIsamura, Bienfait Kabuyaya, and Kevin Alan Lobb. 2022. "New Insights into the (A)Synchronicity of Diels–Alder Reactions: A Theoretical Study Based on the Reaction Force Analysis and Atomic Resolution of Energy Derivatives" Molecules 27, no. 5: 1546. https://doi.org/10.3390/molecules27051546
APA StyleIsamura, B. K., & Lobb, K. A. (2022). New Insights into the (A)Synchronicity of Diels–Alder Reactions: A Theoretical Study Based on the Reaction Force Analysis and Atomic Resolution of Energy Derivatives. Molecules, 27(5), 1546. https://doi.org/10.3390/molecules27051546







