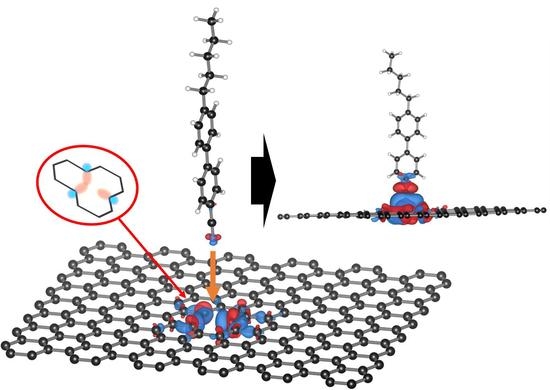
Insertion of the Liquid Crystal 5CB into Monovacancy Graphene
Abstract
:1. Introduction
2. Results and Discussion
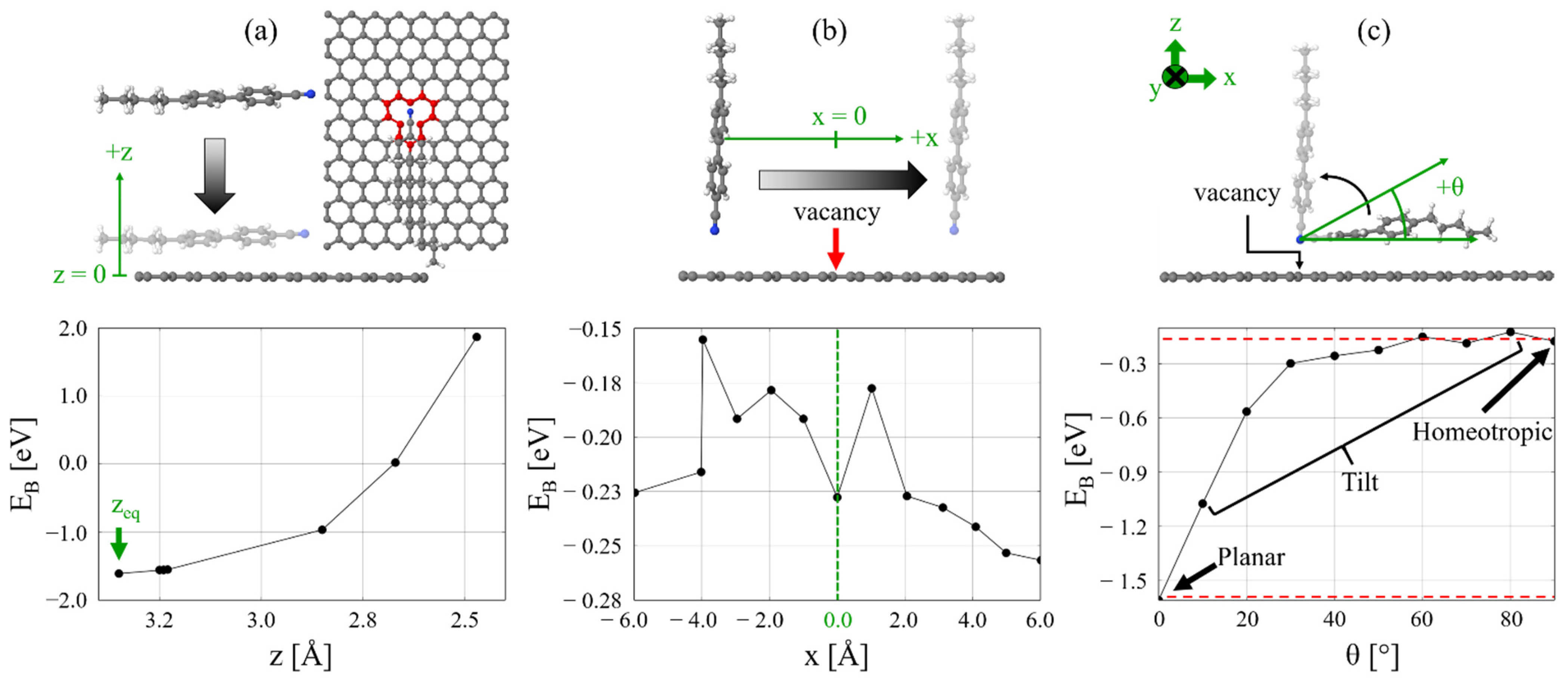
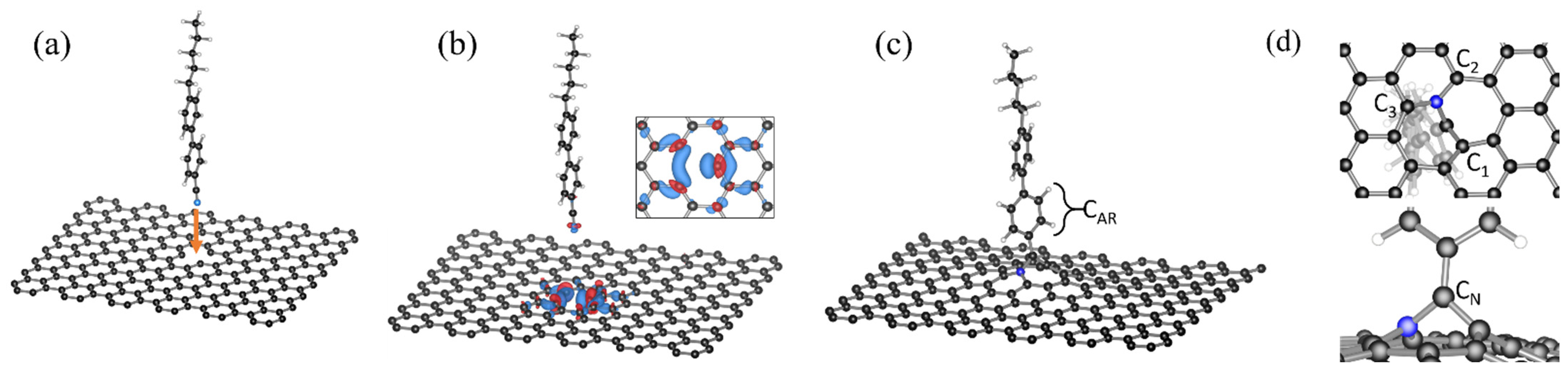
2.1. 5CB/MV-G Interaction
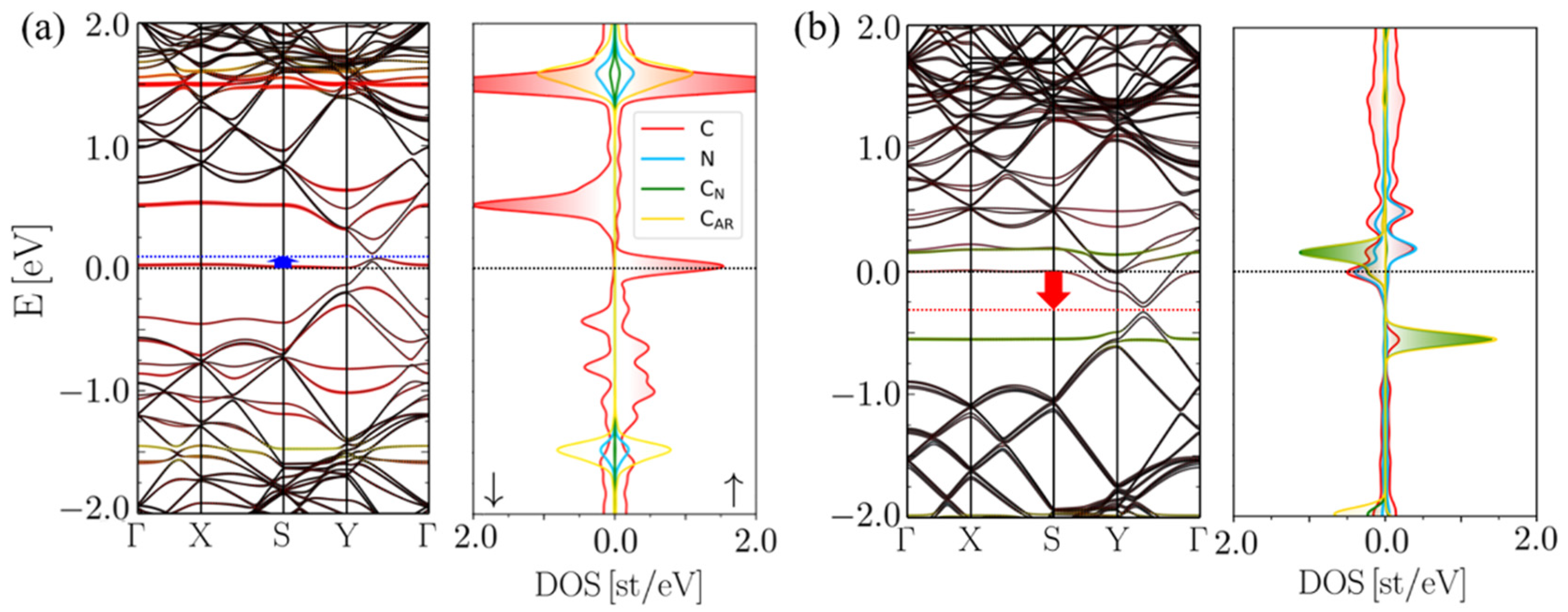
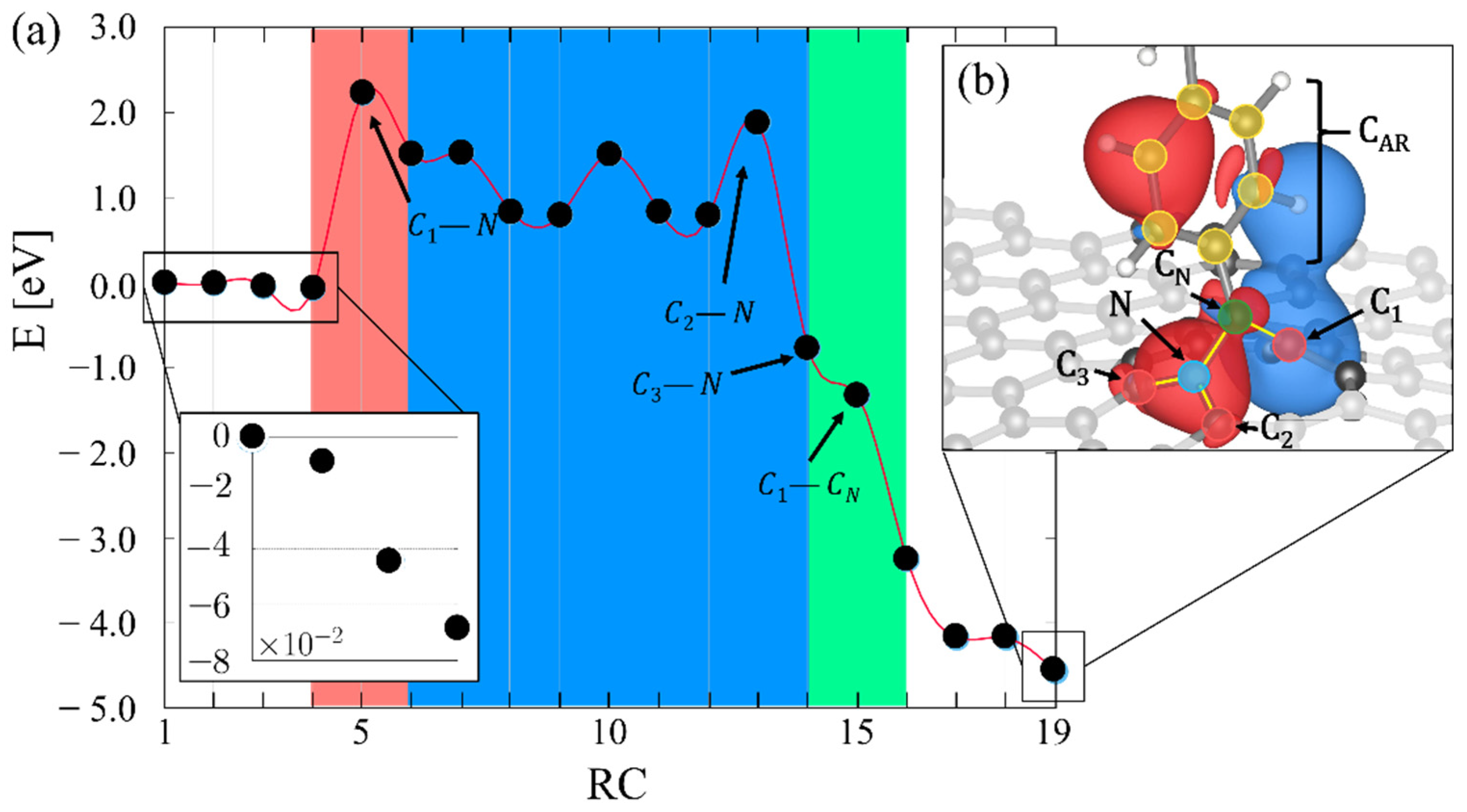
2.2. Insertion Reaction
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Yu, J.S.; Lev, B.; Jin, H.; Park, K.; Chae, D.H.; Kim, W.S.; Kim, J.H. Surface-induced transition of nematic liquid crystals on graphene/SiC substrate. EPL 2018, 124, 46004. [Google Scholar] [CrossRef]
- Yu, J.S.; Yun, J.E.; Kim, J.-H.H. Tilt angle change of nematic liquid crystal as a function of the number of graphite layers. Liq. Cryst. 2013, 40, 216–220. [Google Scholar] [CrossRef]
- Shen, T.Z.; Hong, S.H.; Lee, J.H.; Kang, S.G.; Lee, B.; Whang, D.; Song, J.K. Selectivity of Threefold Symmetry in Epitaxial Alignment of Liquid Crystal Molecules on Macroscale Single-Crystal Graphene. Adv. Mater. 2018, 30, 1802441. [Google Scholar] [CrossRef] [PubMed]
- Basu, R.; Lee, A. Ion trapping by the graphene electrode in a graphene-ITO hybrid liquid crystal cell. Appl. Phys. Lett. 2017, 111, 5–9. [Google Scholar] [CrossRef]
- Lim, Y.J.; Lee, B.H.; Kwon, Y.R.; Choi, Y.E.; Murali, G.; Lee, J.H.; Nguyen, V.L.; Lee, Y.H.; Lee, S.H. Monitoring defects on monolayer graphene using nematic liquid crystals. Opt. Express 2015, 23, 14162. [Google Scholar] [CrossRef]
- Son, J.-H.; Baeck, S.-J.; Park, M.-H.; Lee, J.-B.; Yang, C.-W.; Song, J.-K.; Zin, W.-C.; Ahn, J.-H. Detection of graphene domains and defects using liquid crystals. Nat. Commun. 2014, 5, 3484. [Google Scholar] [CrossRef] [Green Version]
- Woo Kim, D.; Ho Kim, Y.; Su Jeong, H.; Jung, H.-T. Direct visualization of large-area graphene domains and boundaries by optical birefringency. Nat. Nanotechnol. 2012, 7, 29–34. [Google Scholar] [CrossRef]
- Naqvi, B.A.; Shehzad, M.A.; Cha, J.; Min, K.-A.; Khan, M.F.; Hussain, S.; Seo, Y.; Hong, S.; Eom, J.; Jung, J. Visualizing Degradation of Black Phosphorus Using Liquid Crystals. Sci. Rep. 2018, 8, 12966. [Google Scholar] [CrossRef]
- Basu, R.; Kinnamon, D.; Spillmann, C.M.; Kolacz, J.; Frantz, J.A.; Myers, J.D. Graphene as an Alignment Layer and Electrode for Liquid Crystal Devices. U.S. Patent 10,564,505, 18 February 2020. [Google Scholar]
- Basu, R.; Shalov, S.A. Graphene as transmissive electrodes and aligning layers for liquid-crystal-based electro-optic devices. Phys. Rev. E 2017, 96, 012702. [Google Scholar] [CrossRef] [Green Version]
- Basu, R.; Garvey, A.; Kinnamon, D. Effects of graphene on electro-optic response and ion-transport in a nematic liquid crystal. J. Appl. Phys. 2015, 117, 074301. [Google Scholar] [CrossRef] [Green Version]
- Rummeli, M.H.; Ta, H.Q.; Mendes, R.G.; Gonzalez-Martinez, I.G.; Zhao, L.; Gao, J.; Fu, L.; Gemming, T.; Bachmatiuk, A.; Liu, Z. New Frontiers in Electron Beam–Driven Chemistry in and around Graphene. Adv. Mater. 2019, 31, 1800715. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xu, T.; Lu, J.; Sun, L.; Ni, Z. Defect Engineering in 2D Materials: Precise Manipulation and Improved Functionalities. Research 2019, 2019, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Z.; Carvalho, B.R.; Kahn, E.; Lv, R.; Rao, R.; Terrones, H.; Pimenta, M.A.; Terrones, M. Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 2016, 3, 022002. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef]
- Miró, P.; Audiffred, M.; Heine, T. An atlas of two-dimensional materials. Chem. Soc. Rev. 2014, 43, 6537–6554. [Google Scholar] [CrossRef]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Castro Neto, A.H. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef] [Green Version]
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef]
- Schwierz, F.; Pezoldt, J.; Granzner, R. Two-dimensional materials and their prospects in transistor electronics. Nanoscale 2015, 7, 8261–8283. [Google Scholar] [CrossRef] [Green Version]
- Deng, D.; Novoselov, K.S.; Fu, Q.; Zheng, N.; Tian, Z.; Bao, X. Catalysis with two-dimensional materials and their heterostructures. Nat. Nanotechnol. 2016, 11, 218–230. [Google Scholar] [CrossRef]
- Fu, Q.; Bao, X. Surface chemistry and catalysis confined under two-dimensional materials. Chem. Soc. Rev. 2017, 46, 1842–1874. [Google Scholar] [CrossRef] [PubMed]
- Chia, X.; Pumera, M. Characteristics and performance of two-dimensional materials for electrocatalysis. Nat. Catal. 2018, 1, 909–921. [Google Scholar] [CrossRef]
- Mendoza-Sánchez, B.; Gogotsi, Y. Synthesis of Two-Dimensional Materials for Capacitive Energy Storage. Adv. Mater. 2016, 28, 6104–6135. [Google Scholar] [CrossRef]
- Peng, L.; Zhu, Y.; Chen, D.; Ruoff, R.S.; Yu, G. Two-Dimensional Materials for Beyond-Lithium-Ion Batteries. Adv. Energy Mater. 2016, 6, 1600025. [Google Scholar] [CrossRef]
- Ren, Y.; Qiao, Z.; Niu, Q. Topological phases in two-dimensional materials: A review. Rep. Prog. Phys. 2016, 79, 066501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, A.Q.; Ye, X.G.; Yu, D.P.; Liao, Z.M. Topological Semimetal Nanostructures: From Properties to Topotronics. ACS Nano 2020, 14, 3755–3778. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Chang, H. Graphene and graphene-like two-dimensional materials in photodetection: Mechanisms and methodology. ACS Nano 2014, 8, 4133–4156. [Google Scholar] [CrossRef]
- Sun, Z.; Martinez, A.; Wang, F. Optical modulators with 2D layered materials. Nat. Photonics 2016, 10, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, Q.; Xia, F.; Wang, H. Two-dimensional materials for nanophotonics application. Nanophotonics 2015, 4, 128–142. [Google Scholar] [CrossRef]
- Mak, K.F.; Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 2016, 10, 216–226. [Google Scholar] [CrossRef]
- Schwartz, J.J.; Mendoza, A.M.; Wattanatorn, N.; Zhao, Y.; Nguyen, V.T.; Spokoyny, A.M.; Mirkin, C.A.; Baše, T.; Weiss, P.S. Surface dipole control of liquid crystal alignment. J. Am. Chem. Soc. 2016, 138, 5957–5967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dyck, O.; Zhang, L.; Yoon, M.; Swett, J.L.; Hensley, D.; Zhang, C.; Rack, P.D.; Fowlkes, J.D.; Lupini, A.R.; Jesse, S. Doping transition-metal atoms in graphene for atomic-scale tailoring of electronic, magnetic, and quantum topological properties. Carbon N. Y. 2021, 173, 205–214. [Google Scholar] [CrossRef]
- Shehzad, M.A.; Tien, D.H.; Iqbal, M.W.; Eom, J.; Park, J.H.; Hwang, C.; Seo, Y. Nematic Liquid Crystal on a Two Dimensional Hexagonal Lattice and its Application. Sci. Rep. 2015, 5, 13331. [Google Scholar] [CrossRef] [Green Version]
- Shehzad, M.A.; Lee, J.; Park, S.H.; Akhtar, I.; Khan, M.F.; Hussain, S.; Eom, J.; Jung, J.; Kim, G.; Hwang, C.; et al. Dynamics of liquid crystal on hexagonal lattice. 2D Mater. 2018, 5, 045021. [Google Scholar] [CrossRef] [Green Version]
- Fischer, S.A.; Kołacz, J.; Spillmann, C.M.; Gunlycke, D. Adsorption of the liquid crystal molecule 5CB on graphene. Phys. Rev. E 2018, 98, 052702. [Google Scholar] [CrossRef] [Green Version]
- Brown, P.A.; Fischer, S.A.; Kołacz, J.; Spillmann, C.; Gunlycke, D. Thermotropic liquid crystal (5CB) on two-dimensional materials. Phys. Rev. E 2019, 100, 62701. [Google Scholar] [CrossRef]
- Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related species. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Thrower, P.A. Chemistry & Physics of Carbon: Volume 25; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Wu, L.; Hu, S.; Yu, W.; Shen, S.; Li, T. Stabilizing mechanism of single-atom catalysts on a defective carbon surface. NPJ Comput. Mater. 2020, 6, 23. [Google Scholar] [CrossRef] [Green Version]
- Carr, L.D.; Lusk, M.T. Defect engineering: Graphene gets designer defects. Nat. Nanotechnol. 2010, 5, 316–317. [Google Scholar] [CrossRef]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From point defects in graphene to two-dimensional amorphous carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yazyev, O.V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef] [PubMed]
- Rasool, H.I.; Ophus, C.; Zettl, A. Atomic Defects in Two Dimensional Materials. Adv. Mater. 2015, 27, 5771–5777. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lv, R. Defect engineering of two-dimensional materials for efficient electrocatalysis. J. Mater. 2018, 4, 95–107. [Google Scholar] [CrossRef]
- Brown, P.A.; Xu, C.; Shuford, K.L. Periodic trends of pnictogen substitution into a graphene monovacancy: A first-principles investigation. Chem. Mater. 2014, 26, 5735–5744. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, C.; Li, Z.; Xie, Y. Vacancy Engineering for Tuning Electron and Phonon Structures of Two-Dimensional Materials. Adv. Energy Mater. 2016, 6, 1600436. [Google Scholar] [CrossRef]
- Xu, C.; Brown, P.A.; Lu, J.; Shuford, K.L. Electronic Properties of Halogen-Adsorbed Graphene. J. Phys. Chem. C 2015, 119, 17271–17277. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, L.; Du, A.; Gao, G.; Chen, J.; Yan, X.; Brown, C.L.; Yao, X. Defect Graphene as a Trifunctional Catalyst for Electrochemical Reactions. Adv. Mater. 2016, 28, 9532–9538. [Google Scholar] [CrossRef]
- Grasseschi, D.; Silva, W.C.; de Souza Paiva, R.; Starke, L.D.; do Nascimento, A.S. Surface coordination chemistry of graphene: Understanding the coordination of single transition metal atoms. Coord. Chem. Rev. 2020, 422, 213469. [Google Scholar] [CrossRef]
- Ding, Y.; Luo, S.; Ma, L.; An, J. Reductive Cleavage of Unactivated Carbon-Cyano Bonds under Ammonia-Free Birch Conditions. J. Org. Chem. 2019, 84, 15827–15833. [Google Scholar] [CrossRef] [PubMed]
- Thevenin, L.; Fliedel, C.; Fantin, M.; Ribelli, T.G.; Matyjaszewski, K.; Poli, R. Reductive Termination of Cyanoisopropyl Radicals by Copper(I) Complexes and Proton Donors: Organometallic Intermediates or Coupled Proton-Electron Transfer? Inorg. Chem. 2019, 58, 6445–6457. [Google Scholar] [CrossRef] [PubMed]
- Tsai, Y.J.; Kuo, C.L. Effect of Structural Disorders on the Li Storage Capacity of Graphene Nanomaterials: A First-Principles Study. ACS Appl. Mater. Interfaces 2020, 12, 22917–22929. [Google Scholar] [CrossRef] [PubMed]
- Robertson, A.W.; Do Lee, G.; He, K.; Yoon, E.; Kirkland, A.I.; Warner, J.H. The role of the bridging atom in stabilizing odd numbered graphene vacancies. Nano Lett. 2014, 14, 3972–3980. [Google Scholar] [CrossRef]
- Rodrigo, L.; Pou, P.; Pérez, R. Graphene monovacancies: Electronic and mechanical properties from large scale ab initio simulations. Carbon N. Y. 2016, 103, 200–208. [Google Scholar] [CrossRef]
- Jiang, Q.G.; Ao, Z.M.; Zheng, W.T.; Li, S.; Jiang, Q. Enhanced hydrogen sensing properties of graphene by introducing a mono-atom-vacancy. Phys. Chem. Chem. Phys. 2013, 15, 21016–21022. [Google Scholar] [CrossRef] [Green Version]
- Chigo Anota, E.; Escobedo-Morales, A.; Salazar Villanueva, M.; Vázquez-Cuchillo, O.; Rubio Rosas, E. On the influence of point defects on the structural and electronic properties of graphene-like sheets: A molecular simulation study. J. Mol. Model. 2013, 19, 839–846. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, F.; Gao, S.; He, L. Tunable magnetism of a single-carbon vacancy in graphene. Sci. Bull. 2020, 65, 194–200. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.C.; Zhang, Y.; Liu, F.C.; Ma, Y.; Feng, W.; Zhang, S.X.A. Dynamic nano-pulling effect of the boron-functionalized graphene monovacancy for molecule dissociation. J. Phys. D Appl. Phys. 2013, 46, 385302. [Google Scholar] [CrossRef]
- Yu, L.; Du, C.; Liu, X. Dy adsorption and penetration on defected graphene by first-principles calculations. Mater. Res. Express 2018, 5, 025022. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hafner, J. Materials simulations using VASP-a quantum perspective to materials science. Comput. Phys. Commun. 2007, 177, 6–13. [Google Scholar] [CrossRef]
- Hafner, J. Ab-Initio Simulations of Materials Using VASP: Density-Functional Theory and Beyond. J. Comput. Chem. 2008, 177, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paier, J.; Hirschl, R.; Marsman, M.; Kresse, G. The Perdew-Burke-Ernzerhof exchange-correlation functional applied to the G2-1 test set using a plane-wave basis set. J. Chem. Phys. 2005, 122, 234102. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Araki, T.; Serra, F.; Tanaka, H. Defect science and engineering of liquid crystals under geometrical frustration. Soft Matter 2013, 9, 8107–8120. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, P.A.; Kołacz, J.; Fischer, S.A.; Spillmann, C.M.; Gunlycke, D. Insertion of the Liquid Crystal 5CB into Monovacancy Graphene. Molecules 2022, 27, 1664. https://doi.org/10.3390/molecules27051664
Brown PA, Kołacz J, Fischer SA, Spillmann CM, Gunlycke D. Insertion of the Liquid Crystal 5CB into Monovacancy Graphene. Molecules. 2022; 27(5):1664. https://doi.org/10.3390/molecules27051664
Chicago/Turabian StyleBrown, Paul A., Jakub Kołacz, Sean A. Fischer, Christopher M. Spillmann, and Daniel Gunlycke. 2022. "Insertion of the Liquid Crystal 5CB into Monovacancy Graphene" Molecules 27, no. 5: 1664. https://doi.org/10.3390/molecules27051664
APA StyleBrown, P. A., Kołacz, J., Fischer, S. A., Spillmann, C. M., & Gunlycke, D. (2022). Insertion of the Liquid Crystal 5CB into Monovacancy Graphene. Molecules, 27(5), 1664. https://doi.org/10.3390/molecules27051664