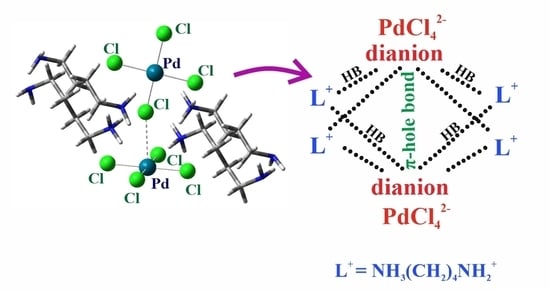
The Role of Hydrogen Bonds in Interactions between [PdCl4]2− Dianions in Crystal
Abstract
:1. Introduction
2. Computational Methods
3. Results
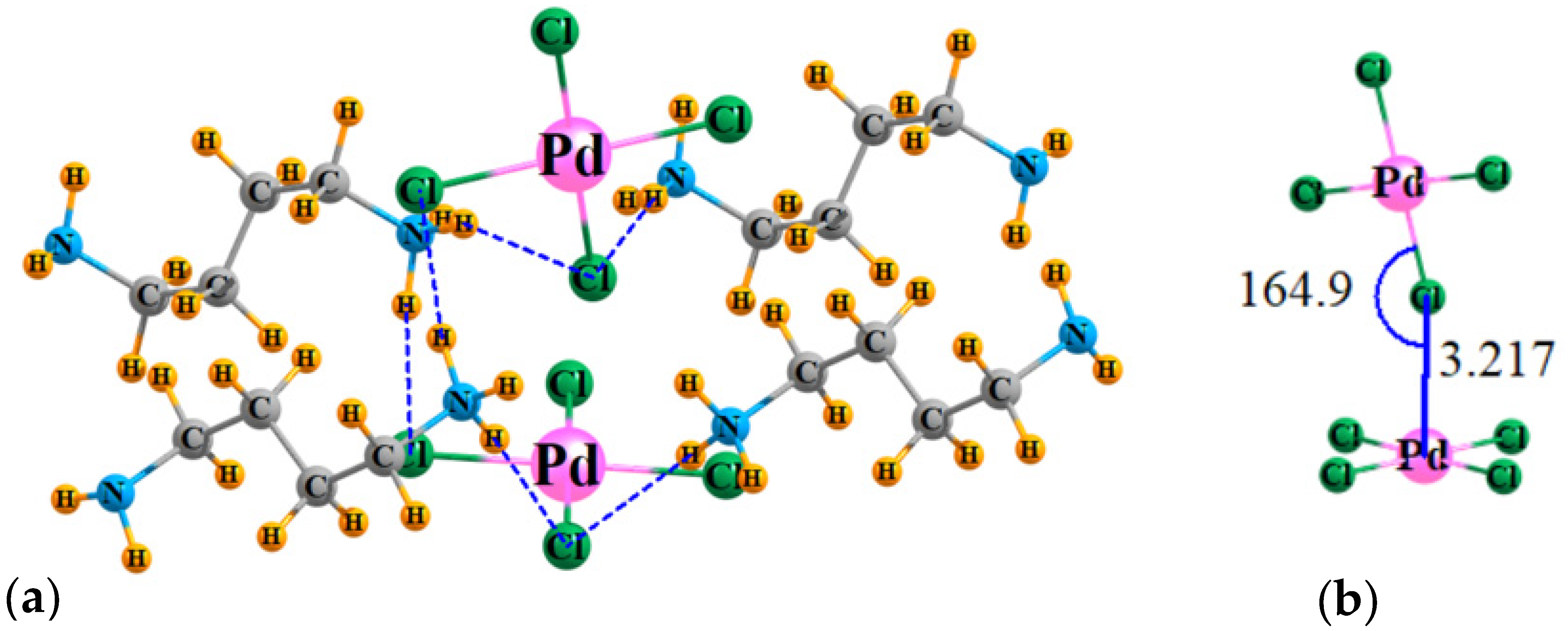
3.1. Direct Interactions between PdCl4 Units
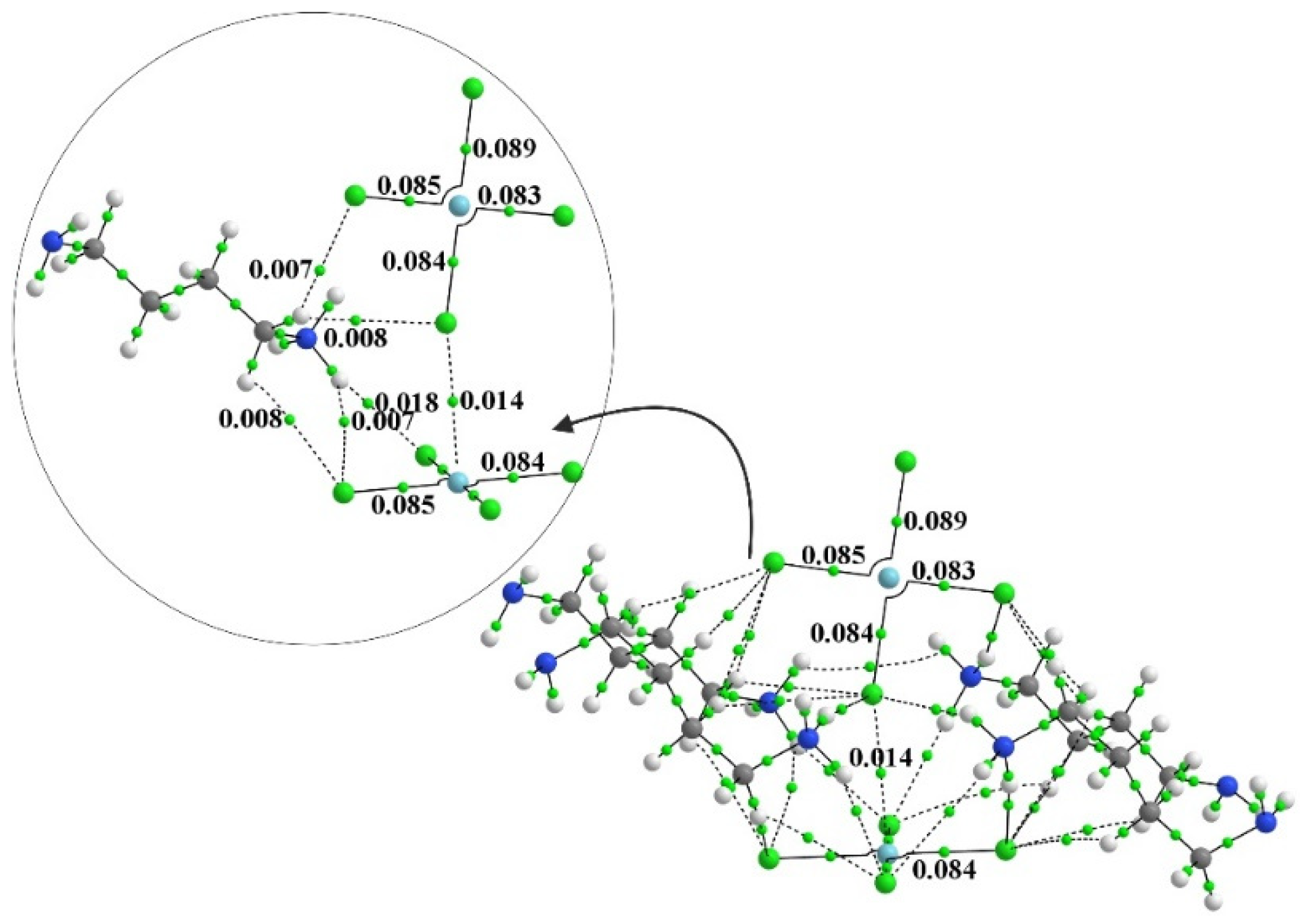
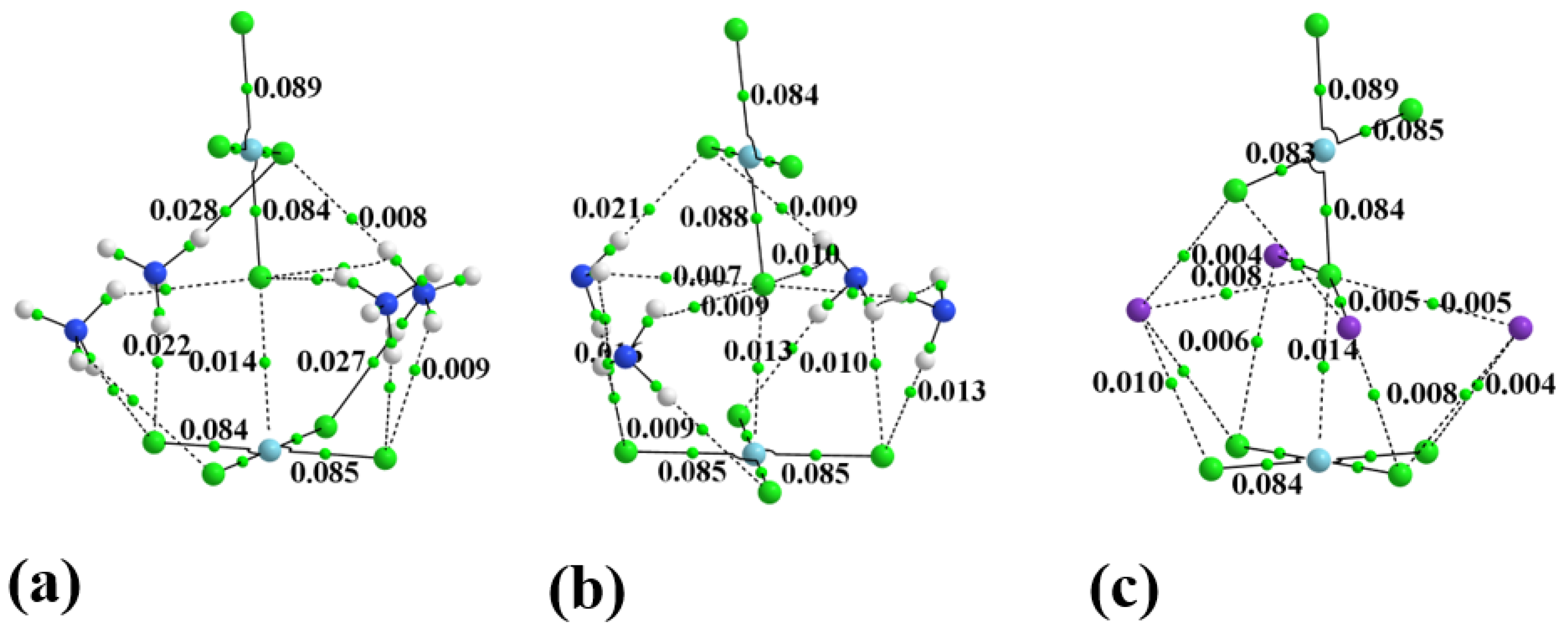
3.2. Secondary Interactions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Scheiner, S. The Hydrogen Bond: A Hundred Years and Counting. J. Indian Inst. Sci. 2020, 100, 61–76. [Google Scholar] [CrossRef]
- Latimer, W.M.; Rodebush, W.H. Polarity and ionization from the standpoint of the Lewis theory of valence. J. Am. Chem. Soc. 1920, 42, 1419–1433. [Google Scholar] [CrossRef] [Green Version]
- Scheiner, S. Forty years of progress in the study of the hydrogen bond. Struct. Chem. 2019, 30, 1119–1128. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen bonds and other interactions as a response to protect doublet/octet electron structure. J. Mol. Model. 2018, 24, 38. [Google Scholar] [CrossRef] [PubMed]
- Hobza, P.; Havlas, Z. Improper, blue-shifting hydrogen bond. Theor. Chem. Acc. 2002, 108, 325–334. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Pihko, P.M. Hydrogen Bonding in Organic Synthesis; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–383. [Google Scholar]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory; Oxford University Press: Oxford, UK, 2009; pp. 1–336. [Google Scholar]
- Espinosa, E.; Mata, I.; Alkorta, I.; Molins, E. Molecular structure and properties: Looking at hydrogen bonds. Acta Crystallogr. A-Found. Adv. 2007, 63, S37. [Google Scholar] [CrossRef] [Green Version]
- Jablonski, M.; Kaczmarek, A.; Sadlej, A.J. Estimates of the energy of intramolecular hydrogen bonds. J. Phys. Chem. A 2006, 110, 10890–10898. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bonding—New Insights; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond: In Structural Chemistry and Biology; International Union of Crystallography: Chester, UK, 2006. [Google Scholar]
- Zierkiewicz, W.; Jurecka, P.; Hobza, P. On differences between hydrogen bonding and improper blue-shifting hydrogen bonding. Chemphyschem 2005, 6, 609–617. [Google Scholar] [CrossRef]
- Metrangolo, P.; Neukirch, H.; Pilati, T.; Resnati, G. Halogen Bonding Based Recognition Processes: A World Parallel to Hydrogen Bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar] [CrossRef]
- Steiner, T. The hydrogen bond in the solid state. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Hobza, P.; Havlas, Z. Blue-Shifting Hydrogen Bonds. Chem. Rev. 2000, 100, 4253–4264. [Google Scholar] [CrossRef] [PubMed]
- Ghanty, T.K.; Staroverov, V.N.; Koren, P.R.; Davidson, E.R. Is the Hydrogen Bond in Water Dimer and Ice Covalent? J. Am. Chem. Soc. 2000, 122, 1210–1214. [Google Scholar] [CrossRef]
- Isaacs, E.D.; Shukla, A.; Platzman, P.M.; Hamann, D.R.; Barbiellini, B.; Tulk, C.A. Covalency of the Hydrogen Bond in Ice: A Direct X-ray Measurement. Phys. Rev. Lett. 1999, 82, 600–603. [Google Scholar] [CrossRef] [Green Version]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Etter, M.C. Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
- Zundel, G.; Sandorfy, C.; Schuster, P. The Hydrogen Bond: Recent Developments in Theory and Experiments; North-Holland: Amsterdam, The Natherland; Oxford, UK, 1976. [Google Scholar]
- Riley, K.E.; Hobza, P. Noncovalent interactions in biochemistry. Wires Comput. Mol. Sci. 2011, 1, 3–17. [Google Scholar] [CrossRef]
- Hobza, P.; Muller-Dethlefs, K. Non-Covalent Interactions: Theory and Experiment; Royal Society of Chemistry: London, UK, 2009. [Google Scholar]
- Juanes, M.; Saragi, R.T.; Caminati, W.; Lesarri, A. The Hydrogen Bond and Beyond: Perspectives for Rotational Investigations of Non-Covalent Interactions. Chem. A Eur. J. 2019, 25, 11402–11411. [Google Scholar] [CrossRef]
- Strekowski, L.; Wilson, B. Noncovalent interactions with DNA: An overview. Mutat. Res. Fundam. Mol. Mech. Mutagenesis 2007, 623, 3–13. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bond and Other Lewis Acid-Lewis Base Interactions as Preliminary Stages of Chemical Reactions. Molecules 2020, 25, 4668. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; da Silva, M.F.C.G. Noncovalent interactions in metal complex catalysis. Coordin. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
- Bhattacharyya, M.K.; Saha, U.; Dutta, D.; Frontera, A.; Verma, A.K.; Sharma, P.; Das, A. Unconventional DNA-relevant π-stacked hydrogen bonded arrays involving supramolecular guest benzoate dimers and cooperative anion–π/π–π/π–anion contacts in coordination compounds of Co(ii) and Zn(ii) phenanthroline: Experimental and theoretical studies. New J. Chem. 2020, 44, 4504–4518. [Google Scholar] [CrossRef]
- Newberry, R.W.; Raines, R.T. Secondary Forces in Protein Folding. ACS Chem. Biol. 2019, 14, 1677–1686. [Google Scholar] [CrossRef] [PubMed]
- Hennemann, M.; Murray, J.S.; Politzer, P.; Riley, K.E.; Clark, T. Polarization-induced sigma-holes and hydrogen bonding. J. Mol. Model. 2012, 18, 2461–2469. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Lane, P. sigma-hole bonding and hydrogen bonding: Competitive interactions. Int. J. Quantum Chem. 2007, 107, 3046–3052. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Oliva-Enrich, J.M. Hydrogen vs. Halogen Bonds in 1-Halo-Closo-Carboranes. Materials 2020, 13, 2163. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The sigma-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
- Murray, J.S.; Politzer, P. sigma-Holes and Si···N intramolecular interactions. J. Mol. Model. 2019, 25, 101. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. The π-hole revisited. Phys. Chem. Chem. Phys. 2021, 23, 16458–16468. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The sigma-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. sigma-holes and π-holes: Similarities and differences. J. Comput. Chem. 2018, 39, 464–471. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. sigma-Hole Bonding: A Physical Interpretation. Top Curr. Chem. 2015, 358, 19–42. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other sigma-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. sigma-Holes, pi-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef]
- Grabowski, S.J. Interactions Steering Arrangement of Molecules in Crystals. Crystals 2020, 10, 130. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Significance of hydrogen bonding and other noncovalent interactions in determining octahedral tilting in the CH3NH3PbI3 hybrid organic-inorganic halide perovskite solar cell semiconductor. Sci. Rep. 2019, 9, 50. [Google Scholar] [CrossRef] [Green Version]
- Riley, K.E.; Pitonak, M.; Cerny, J.; Hobza, P. On the Structure and Geometry of Biomolecular Binding Motifs (Hydrogen-Bonding, Stacking, X-H center dot center dot center dot pi): WFT and DFT Calculations. J. Chem. Theory Comput. 2010, 6, 66–80. [Google Scholar] [CrossRef]
- Takahashi, O.; Kohno, Y.; Nishio, M. Relevance of Weak Hydrogen Bonds in the Conformation of Organic Compounds and Bioconjugates: Evidence from Recent Experimental Data and High-Level ab Initio MO Calculations. Chem. Rev. 2010, 110, 6049–6076. [Google Scholar] [CrossRef]
- Rissanen, K. Weak Intermolecular Interactions in the Solid State. Croat. Chem. Acta 2010, 83, 341–347. [Google Scholar]
- Matczak-Jon, E.; Slepokura, K.; Zierkiewicz, W.; Kafarski, P.; Dabrowska, E. The role of hydrogen bonding in conformational stabilization of 3,5,6-and 3,5-substituted (pyridin-2-yl)aminomethane-1,1-diphosphonic acids and related (pyrimidin-2-yl) derivative. J. Mol. Struct. 2010, 980, 182–192. [Google Scholar] [CrossRef]
- Braga, D.; Grepioni, F.; Tedesco, E. X–H---π (X = O, N, C) Hydrogen bonds in organometallic crystals. Organometallics 1998, 17, 2669–2672. [Google Scholar] [CrossRef]
- Braga, D.; Grepioni, F. C-H center dot center dot center dot O hydrogen bonds in organometallic crystals. Intermol. Interact. 1998, 83–96. [Google Scholar]
- Resnati, G.; Scilabra, P.; Terraneo, G. Chalcogen Bonding in Crystal Engineering. Acta Cryst. 2019, 75, e488. [Google Scholar] [CrossRef]
- Maiti, M.; Thakurta, S.; Pilet, G.; Bauza, A.; Frontera, A. Two new hydrogen-bonded supramolecular dioxo-molybdenum(VI) complexes based on acetyl-hydrazone ligands: Synthesis, crystal structure and DFT studies. J. Mol. Struct. 2021, 1226, 129346. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Analysis of Halogen and Other sigma-Hole Bonds in Crystals. Crystals 2018, 8, 42. [Google Scholar] [CrossRef] [Green Version]
- Frontera, A.; Bauzá, A. On the importance of σ–hole interactions in crystal structures. Crystals 2021, 11, 1205. [Google Scholar] [CrossRef]
- Frontera, A.; Bauza, A. On the importance of pnictogen and chalcogen bonding interactions in supramolecular catalysis. Int. J. Mol. Sci. 2021, 22, 12550. [Google Scholar] [CrossRef]
- Priola, E.; Mahmoudi, G.; Andreo, J.; Frontera, A. Unprecedented [d9]Cu⋯[d10]Au coinage bonding interactions in {Cu(NH3)4[Au(CN)2]}+[Au(CN)2]−salt. Chem. Commun. 2021, 57, 7268–7271. [Google Scholar] [CrossRef]
- Gomila, R.M.; Bauza, A.; Mooibroek, T.J.; Frontera, A. π-Hole spodium bonding in tri-coordinated Hg(ii) complexes. Dalton Trans. 2021, 50, 7545–7553. [Google Scholar] [CrossRef]
- Daolio, A.; Pizzi, A.; Terraneo, G.; Frontera, A.; Resnati, G. Anion···Anion Interactions Involving σ-Holes of Perrhenate, Pertechnetate and Permanganate Anions. ChemPhysChem 2021, 22, 2281–2285. [Google Scholar] [CrossRef] [PubMed]
- Zierkiewicz, W.; Wysokinski, R.; Michalczyk, M.; Scheiner, S. On the Stability of Interactions between Pairs of Anions–Complexes of MCl3− (M=Be, Mg, Ca, Sr, Ba) with Pyridine and CN−. Chemphyschem 2020, 21, 870–877. [Google Scholar] [CrossRef] [PubMed]
- Wysokinski, R.; Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. How Many Pnicogen Bonds can be Formed to a Central Atom Simultaneously? J. Phys. Chem. A 2020, 124, 2046–2056. [Google Scholar] [CrossRef] [PubMed]
- Wysokinski, R.; Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Anion⋅⋅⋅Anion Attraction in Complexes of MCl3− (M=Zn, Cd, Hg) with CN−. Chemphyschem 2020, 21, 1119–1125. [Google Scholar] [CrossRef]
- Mo, O.; Montero-Campillo, M.M.; Yanez, M.; Alkorta, I.; Elguero, J. Are Anions of Cyclobutane Beryllium Derivatives Stabilized through Four-Center One-Electron Bonds? J. Phys. Chem. A 2020, 124, 1515–1521. [Google Scholar] [CrossRef]
- Miranda, M.O.; Duarte, D.J.R.; Alkorta, I. Anion-Anion Complexes Established between Aspartate Dimers. Chemphyschem 2020, 21, 1052–1059. [Google Scholar] [CrossRef]
- Azofra, L.M.; Elguero, J.; Alkorta, I. A Conceptual DFT Study of Phosphonate Dimers: Dianions Supported by H-Bonds. J. Phys. Chem. A 2020, 124, 2207–2214. [Google Scholar] [CrossRef]
- Azofra, L.M.; Elguero, J.; Alkorta, I. Stabilisation of dianion dimers trapped inside cyanostar macrocycles. Phys. Chem. Chem. Phys. 2020, 22, 11348–11353. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalczyk, M.; Maris, T.; Wysokiński, R.; Scheiner, S. Experimental and theoretical evidence of attractive interactions between dianions: [PdCl4]2−⋅⋅⋅[PdCl4]2−. Chem. Commun. 2021, 57, 13305–13308. [Google Scholar] [CrossRef]
- Wysokiński, R.; Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Anion⋅⋅⋅anion (MX3−)2 dimers (M = Zn, Cd, Hg; X = Cl, Br, I) in different environments. Phys. Chem. Chem. Phys. 2021, 23, 13853–13861. [Google Scholar] [CrossRef]
- Wysokinski, R.; Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Crystallographic and Theoretical Evidences of Anion⋅⋅⋅Anion Interaction. Chemphyschem 2021, 22, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Wysokinski, R.; Michalczyk, M.; Zierkiewicz, W.; Scheiner, S. Anion–anion and anion–neutral triel bonds. Phys. Chem. Chem. Phys. 2021, 23, 4818–4828. [Google Scholar] [CrossRef] [PubMed]
- Michalczyk, M.; Zierkiewicz, W.; Wysokinski, R.; Scheiner, S. Triel Bonds within Anion···Anion Complexes. Phys. Chem. Chem. Phys. 2021, 23, 25097–25106. [Google Scholar] [CrossRef] [PubMed]
- Grabarz, A.; Michalczyk, M.; Zierkiewicz, W.; Scheiner, S. Anion-Anion Interactions in Aerogen-Bonded Complexes. Influence of Solvent Environment. Molecules 2021, 26, 2116. [Google Scholar] [CrossRef]
- Quiñonero, D.; Alkorta, I.; Elguero, J. Metastable dianions and dications. ChemPhysChem 2020, 21, 1597–1607. [Google Scholar] [CrossRef]
- Niemann, T.; Stange, P.; Strate, A.; Ludwig, R. Like-likes-Like: Cooperative Hydrogen Bonding Overcomes Coulomb Repulsion in Cationic Clusters with Net Charges up to Q=+6e. Chemphyschem 2018, 19, 1691–1695. [Google Scholar] [CrossRef] [Green Version]
- Niemann, T.; Strate, A.; Ludwig, R.; Zeng, H.J.; Menges, F.S.; Johnson, M.A. Spectroscopic Evidence for an Attractive Cation-Cation Interaction in Hydroxy-Functionalized Ionic Liquids: A Hydrogen-Bonded Chainlike Trimer. Angew. Chem. Int. Edit. 2018, 57, 15364–15368. [Google Scholar] [CrossRef]
- Efimenko, I.A.; Churakov, A.V.; Ivanova, N.A.; Erofeeva, O.S.; Demina, L.I. Cationic–anionic palladium complexes: Effect of hydrogen bond character on their stability and biological activity. Russ. J. Inorg. Chem. 2017, 62, 1469–1478. [Google Scholar] [CrossRef]
- Chalanchi, S.M.; Alkorta, I.; Elguero, J.; Quinonero, D. Hydrogen Bond versus Halogen Bond in Cation-Cation Complexes: Effect of the Solvent. Chemphyschem 2017, 18, 3462–3468. [Google Scholar] [CrossRef]
- Wang, C.W.; Fu, Y.Z.; Zhang, L.N.; Danovich, D.; Shaik, S.; Mo, Y.R. Hydrogen- and Halogen-Bonds between Ions of like Charges: Are They Anti-Electrostatic in Nature? J. Comput. Chem. 2018, 39, 481–487. [Google Scholar] [CrossRef]
- Weinhold, F. Anti-Electrostatic Pi-Hole Bonding: How Covalency Conquers Coulombics. Molecules 2022, 27, 377. [Google Scholar] [CrossRef] [PubMed]
- Holthoff, J.M.; Weiss, R.; Rosokha, S.V.; Huber, S.M. “Anti-electrostatic” Halogen Bonding between Ions of Like Charge. Chem. A Eur. J. 2021, 27, 16530–16542. [Google Scholar] [CrossRef] [PubMed]
- Zapata, F.; Gonzalez, L.; Bastida, A.; Bautista, D.; Caballero, A. Formation of self-assembled supramolecular polymers by anti-electrostatic anion-anion and halogen bonding interactions. Chem. Commun. 2020, 56, 7084–7087. [Google Scholar] [CrossRef] [PubMed]
- Holthoff, J.M.; Engelage, E.; Weiss, R.; Huber, S.M. “Anti-Electrostatic” Halogen Bonding. Angew. Chem. Int. Ed. 2020, 59, 11150–11157. [Google Scholar] [CrossRef] [Green Version]
- Weinhold, F.; Klein, R.A. Anti-Electrostatic Hydrogen Bonds. Angew. Chem. Int. Ed. 2014, 53, 11214–11217. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Can Counter-Intuitive Halogen Bonding Be Coulombic? Chemphyschem 2021, 22, 1201–1207. [Google Scholar] [CrossRef]
- Maris, T.; Bravic, G.; Chanh, N.B.; Leger, J.M.; Bissey, J.C.; Villesuzanne, A.; Zouari, R.; Daoud, A. Structures and thermal behavior in the series of two-dimensional molecular composites NH3-(CH2)(4)-NH3 MCl(4) related to the nature of the metal M. Part 1: Crystal structures and phase transitions in the case M=Cu and Pd. J. Phys. Chem. Solids 1996, 57, 1963–1975. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm. J. Mol. Graph. Model. 2012, 38, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Bader, R. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Keith, A.T. AIMAll (Version 14.11.23); TK Gristmill Software: Overland Park, KS, USA, 2014. [Google Scholar]
- ADF2014, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2014.
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. Calculation of Small Molecular Interactions by Differences of Separate Total Energies—Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Boonseng, S.; Roffe, G.W.; Spencer, J.; Cox, H. The nature of the bonding in symmetrical pincer palladacycles. Dalton Trans. 2015, 44, 7570–7577. [Google Scholar] [CrossRef] [Green Version]
- Boonseng, S.; Roffe, G.W.; Jones, R.N.; Tizzard, G.J.; Coles, S.J.; Spencer, J.; Cox, H. The Trans Influence in Unsymmetrical Pincer Palladacycles: An Experimental and Computational Study. Inorganics 2016, 4, 25. [Google Scholar] [CrossRef] [Green Version]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X-H center dot center dot center dot F-Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Eint | EES | Vs,max | VS,min | Q c | |
|---|---|---|---|---|---|
| (PdCl4)2−2 | +212 | +218 | −371 | −387 | −2.00 |
| neutral | |||||
| +4 Ar | +209 | +206 | −184 | −202 | −2.00 |
| +4 NH3 | +182 | +173 | −172 | −194 | −1.96 |
| +4 L0,a | +157 | +159 | −162 | −185 | −1.92 |
| +4(PC)0,b | +182 | −2.00 | |||
| +1 | |||||
| +4 K+ | −97 | −94 | −58 | −75 | −1.91 |
| +4 NH4+ | −111 | −99 | −56 | −72 | −1.80 |
| +4 L+ | −101 | −94 | −53 | −70 | −1.82 |
| +4 (PC)+ | −98 | −2.00 | |||
| +2 | |||||
| +2 Ca2+ | −121 | −44 | −27 | −63 | −1.73 |
| +2 L2+ | −124 | −64 | −64 | −84 | −1.85 |
| +2 (PC)2+ | −108 | −2.00 |
| ρ, au | −½ V, kcal/mol | |||
|---|---|---|---|---|
| Pd···Cl | Σothers a | Pd···Cl | Σothers a | |
| (PdCl4)2−2 | 0.014 | - | 2.67 | - |
| neutral | ||||
| +4 Ar | 0.013 | 0.027 | 2.73 | 4.81 |
| +4 NH3 | 0.013 | 0.053 | 2.77 | 8.93 |
| +4 L0,a | 0.013 | 0.058 | 2.80 | 10.03 |
| +4(PC)0,b | 0.013 | - | 2.74 | - |
| +1 | ||||
| +4 K+ | 0.014 | 0.028 | 3.00 | 4.54 |
| +4 NH4+ | 0.014 | 0.066 | 3.01 | 10.79 |
| +4 L+ | 0.014 | 0.071 | 3.01 | 11.60 |
| +4 (PC)+ | 0.014 | - | 2.97 | - |
| +2 | ||||
| +2 Ca2+ | 0.014 | 0.012 | 2.89 | 1.69 |
| +2 L2+ | 0.014 | 0.033 | 2.84 | 5.90 |
| +2 (PC)2+ | 0.013 | - | 2.81 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wysokiński, R.; Zierkiewicz, W.; Michalczyk, M.; Maris, T.; Scheiner, S. The Role of Hydrogen Bonds in Interactions between [PdCl4]2− Dianions in Crystal. Molecules 2022, 27, 2144. https://doi.org/10.3390/molecules27072144
Wysokiński R, Zierkiewicz W, Michalczyk M, Maris T, Scheiner S. The Role of Hydrogen Bonds in Interactions between [PdCl4]2− Dianions in Crystal. Molecules. 2022; 27(7):2144. https://doi.org/10.3390/molecules27072144
Chicago/Turabian StyleWysokiński, Rafał, Wiktor Zierkiewicz, Mariusz Michalczyk, Thierry Maris, and Steve Scheiner. 2022. "The Role of Hydrogen Bonds in Interactions between [PdCl4]2− Dianions in Crystal" Molecules 27, no. 7: 2144. https://doi.org/10.3390/molecules27072144
APA StyleWysokiński, R., Zierkiewicz, W., Michalczyk, M., Maris, T., & Scheiner, S. (2022). The Role of Hydrogen Bonds in Interactions between [PdCl4]2− Dianions in Crystal. Molecules, 27(7), 2144. https://doi.org/10.3390/molecules27072144