Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation
Abstract
:1. Introduction
2. Materials and Methods
- by defining the key torsion angles to distinguish the main conformations,
- then by performing rigid scans to locate the extrema of the potential energy hyper-surface;
- by combining the minima of these rigid scans to preselect conformations;
- then by performing full geometry optimizations on the latter.
3. Results
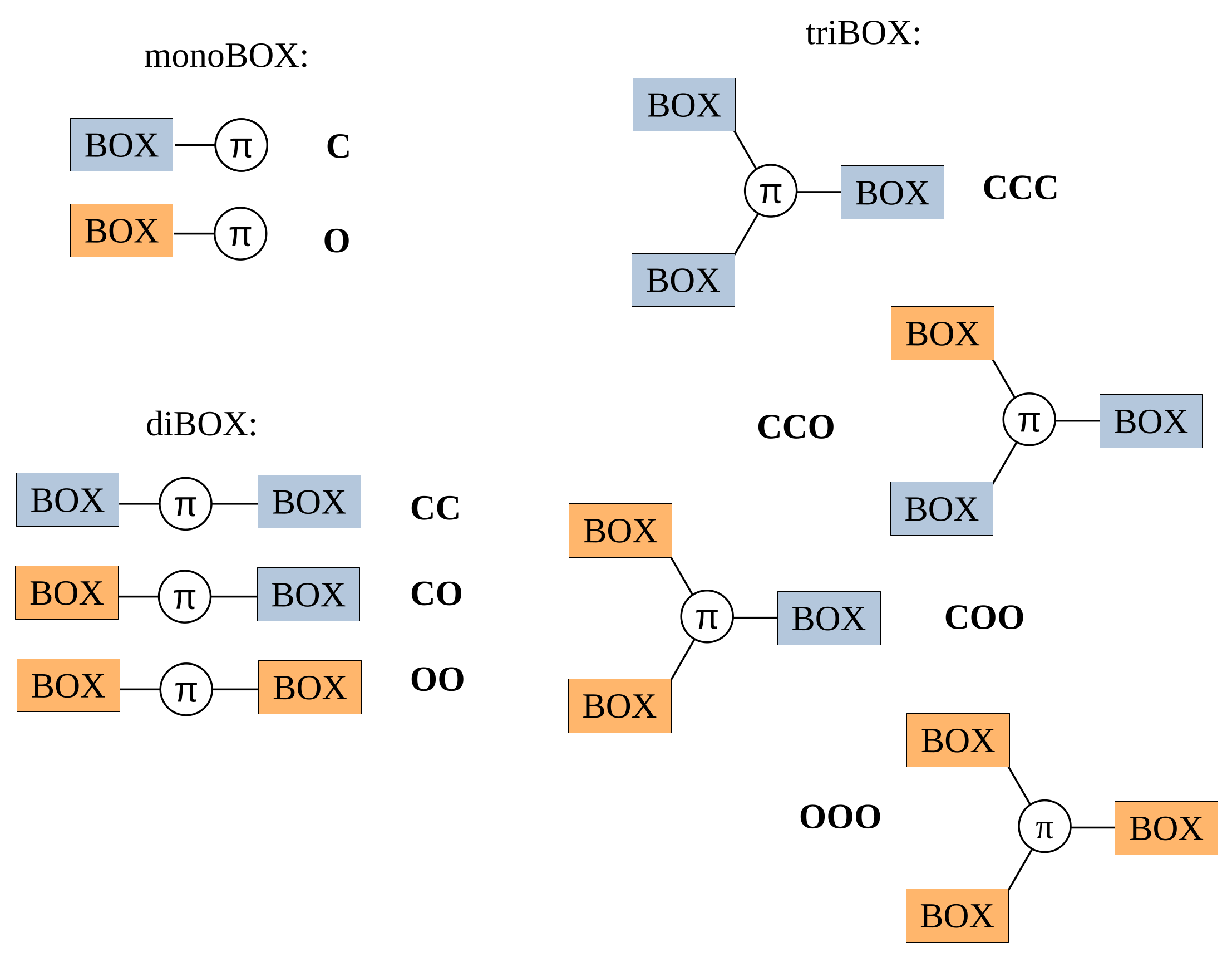
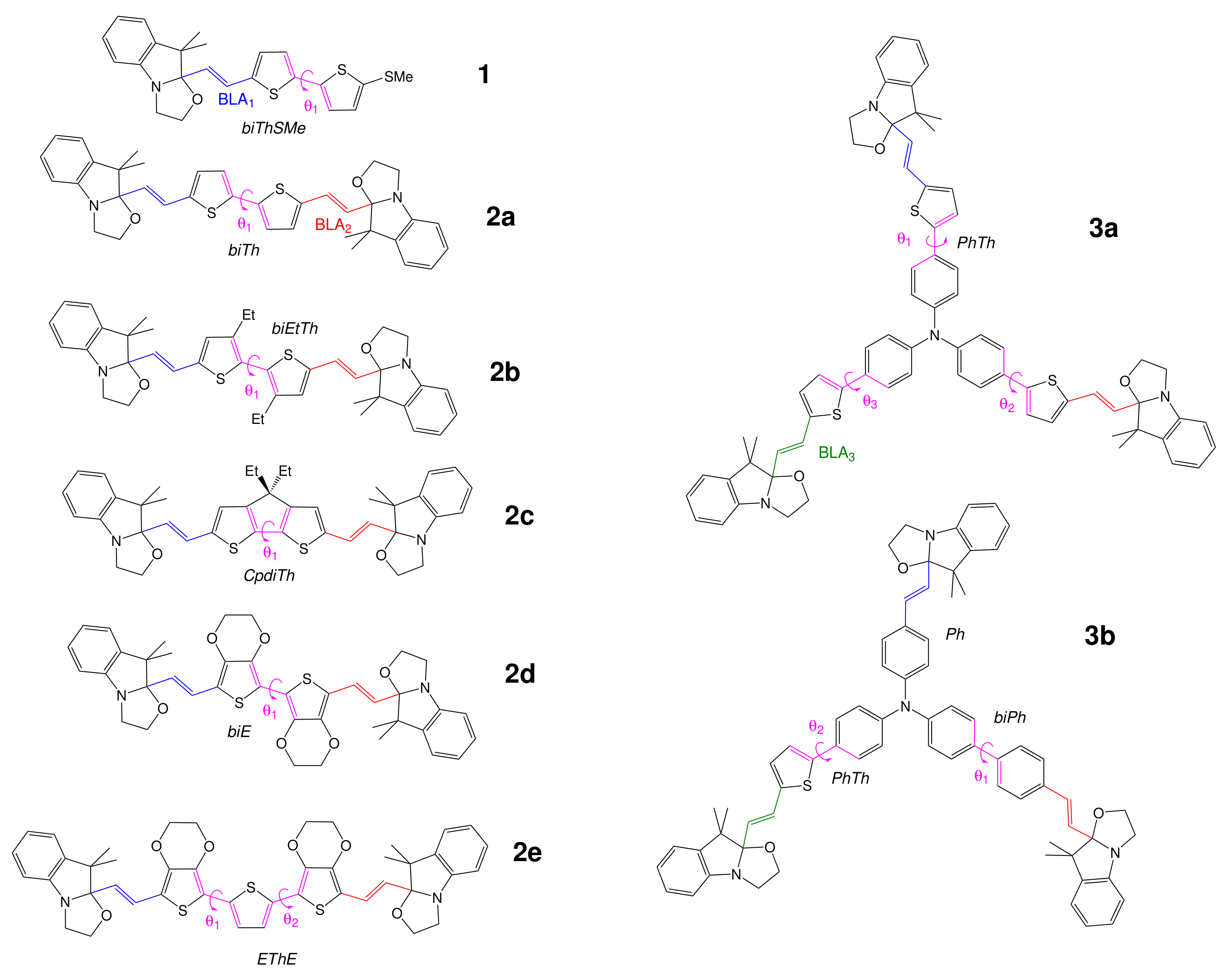
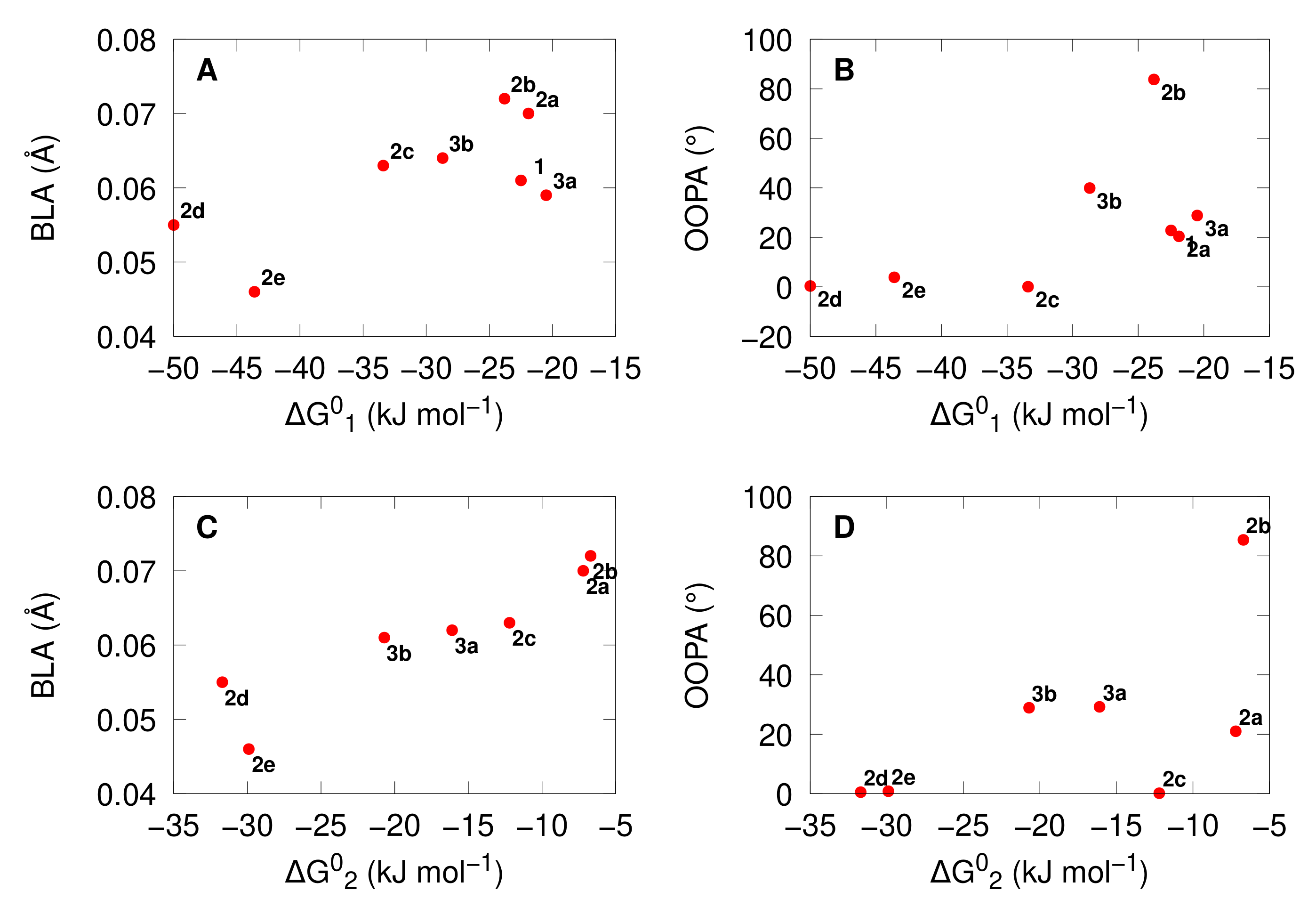
3.1. Structural Properties
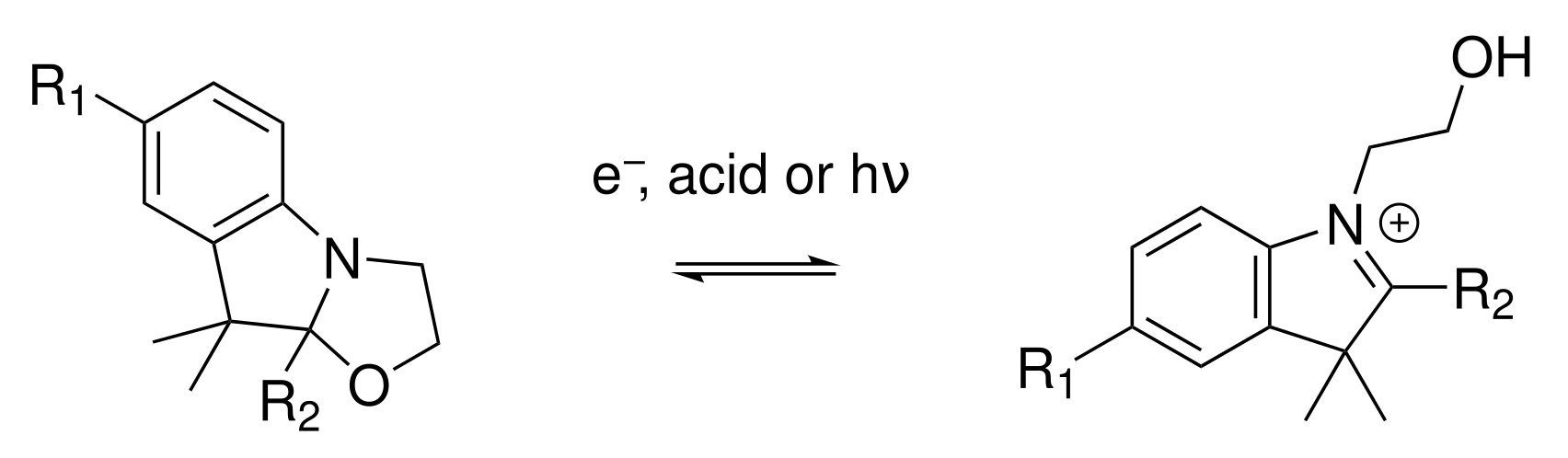
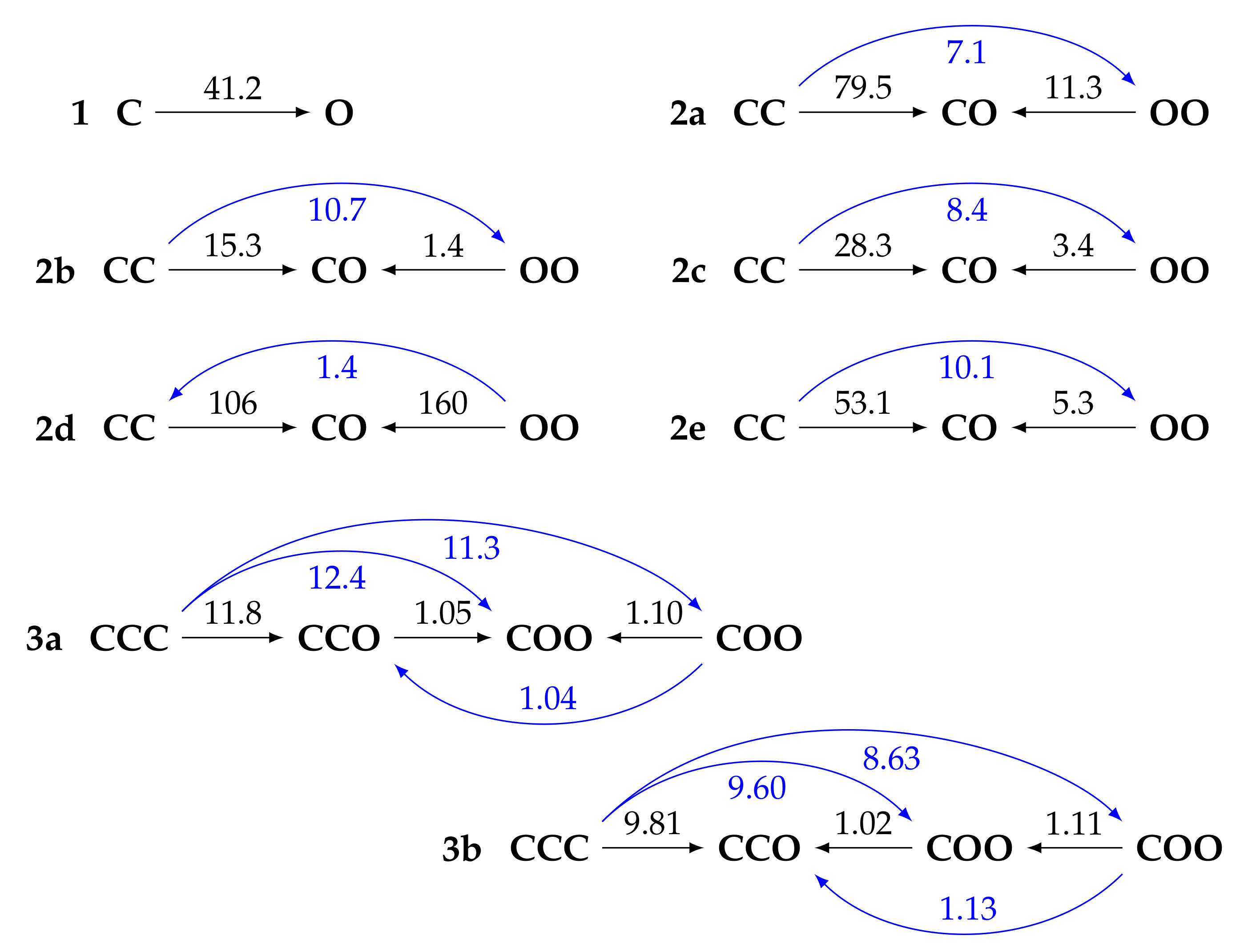
3.2. Acidochromic Properties
3.3. NLO Properties
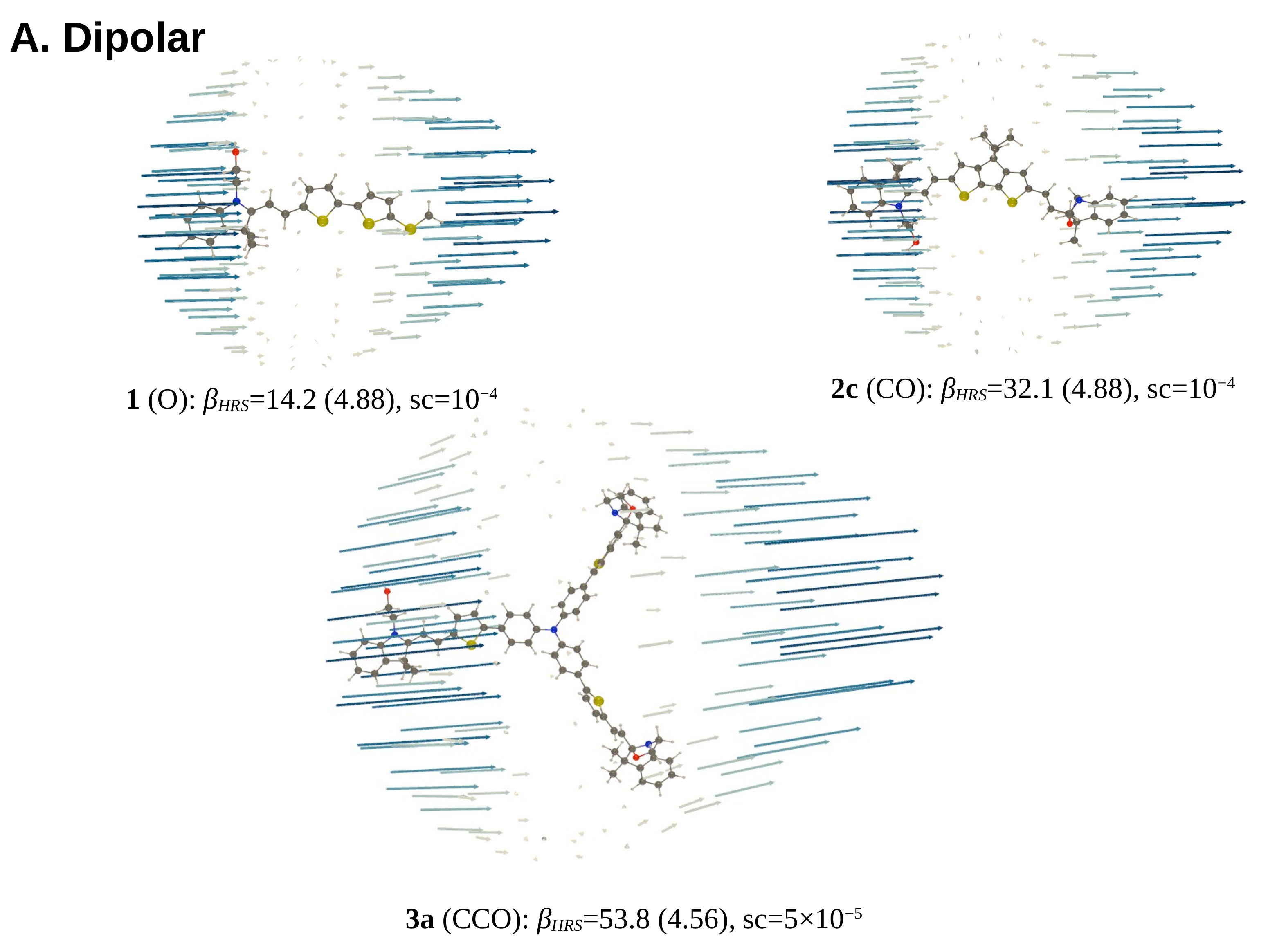
3.3.1. βHRS, Their Contrasts, and the DR
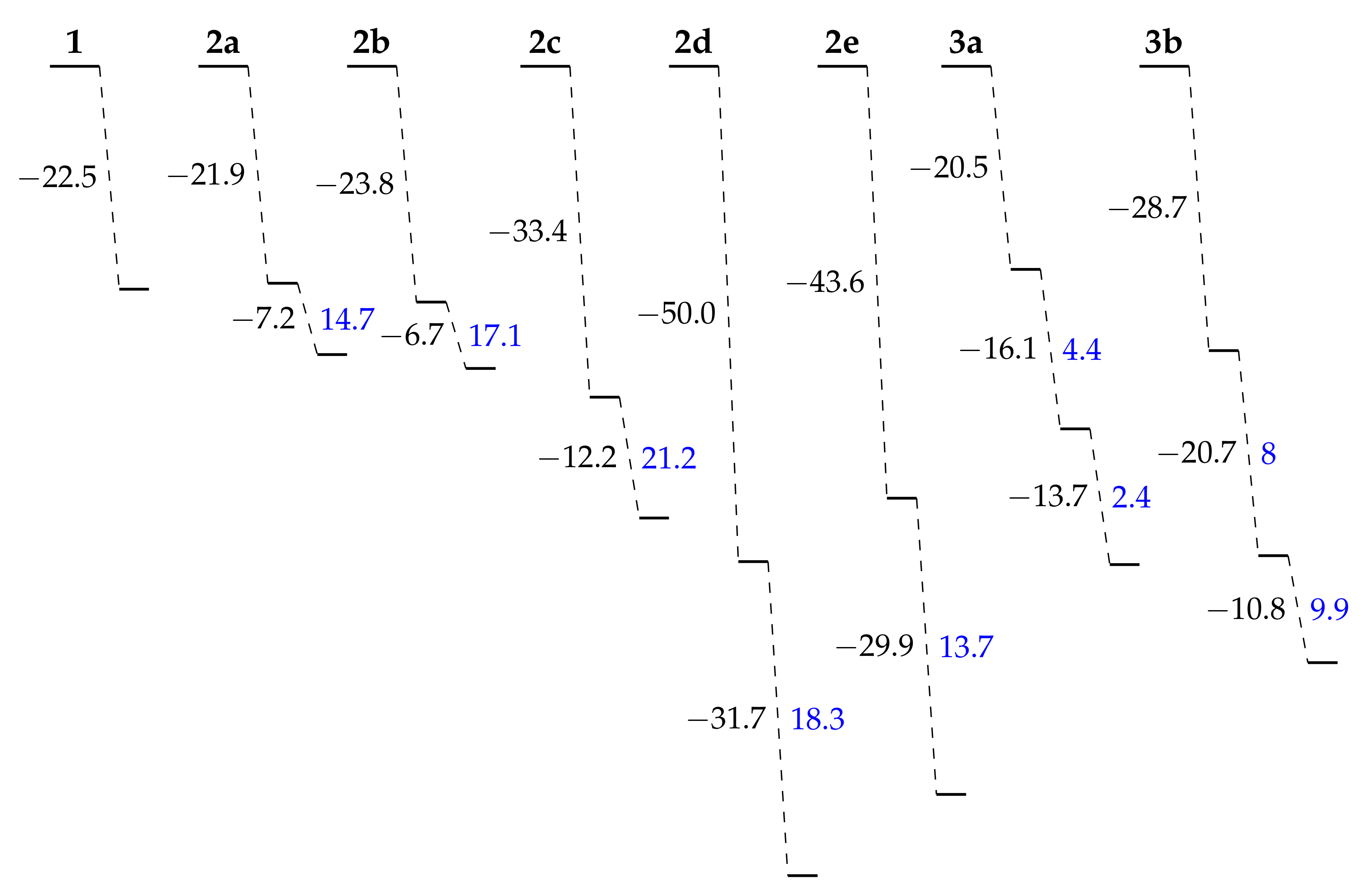
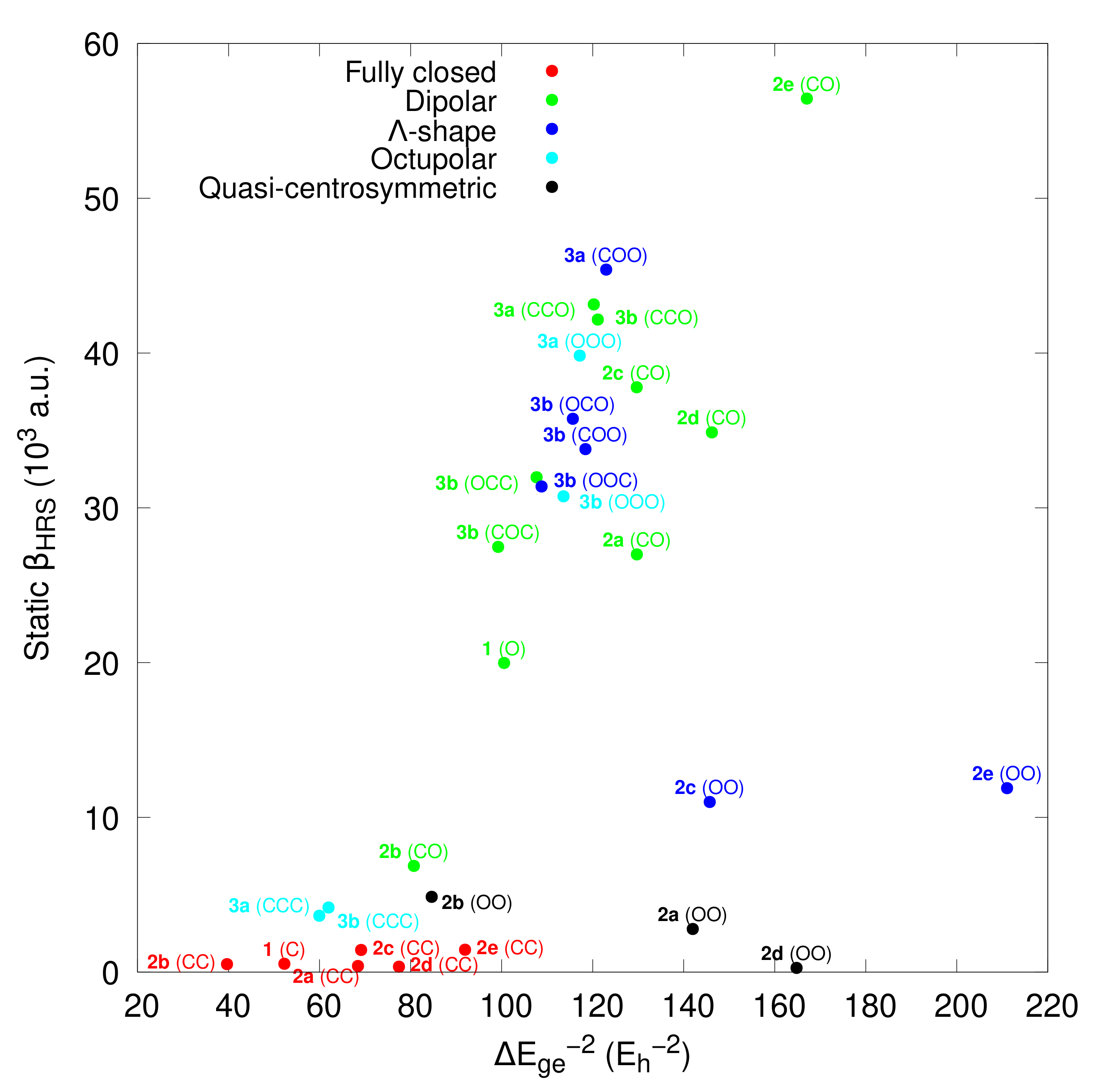
- For 1, opening the unique BOX gives rise to a push–pull π-conjugated NLOphore, of which the β response is much larger (from one to two orders of magnitude) than for the closed form;
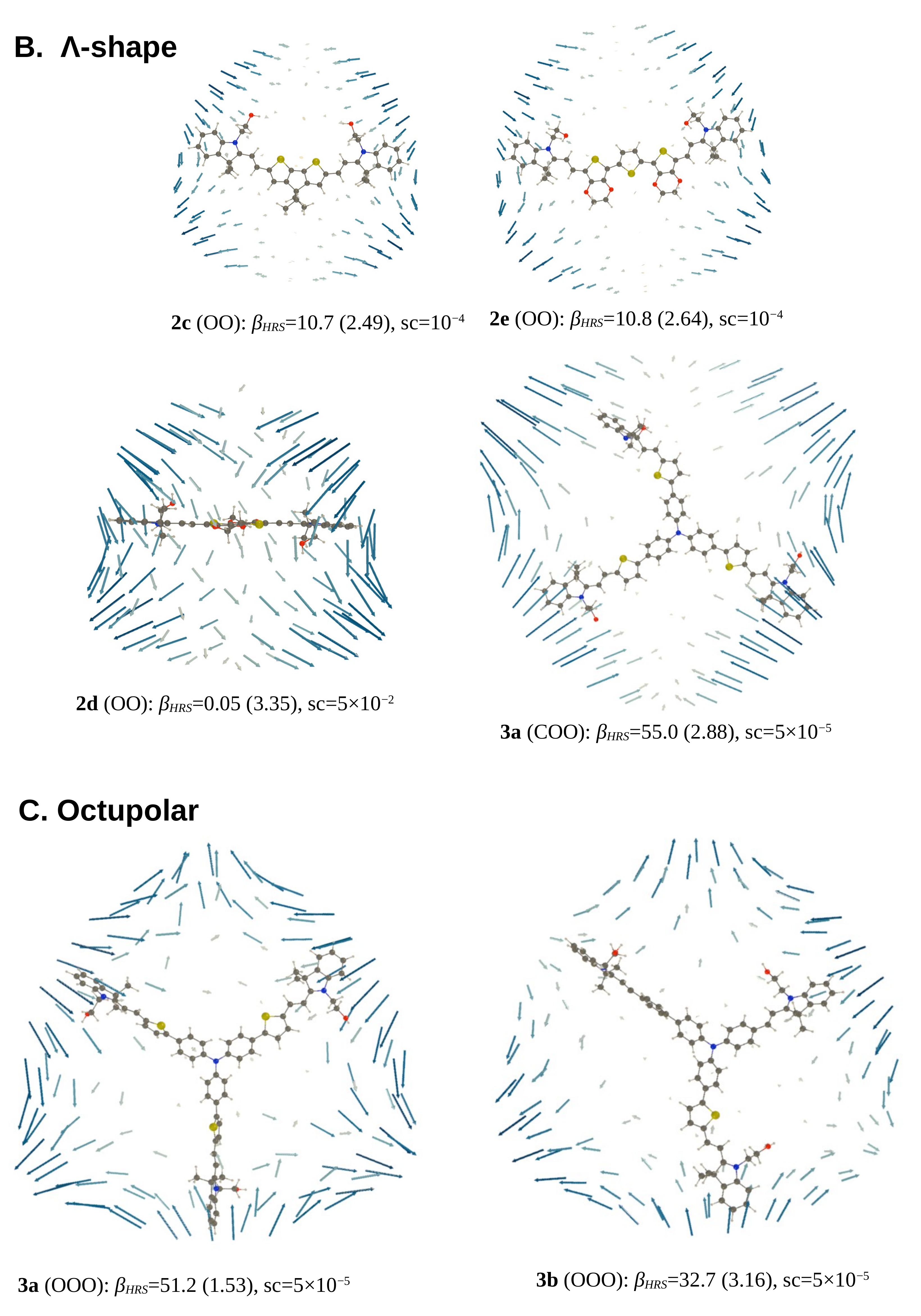
- For diBOX (2a–2e), the order is CC < OO < CO with, usually, large contrasts for the first opening reaction (Figure 6), while the second contrast depends much on the π-linker;
- For triBOX (3a, 3b), the βHRS of the open forms (CCO, COO, OOO) are similar, resulting in contrasts close to 1 for the second and third openings.
3.3.2. Unit Sphere Representations
3.3.3. Comparison with Experiments
3.3.4. Further Analysis
4. Conclusions and Outlooks
- The first opening leads to a drastic change of the NLO responses (at most, a tenfold increase of βHRS accompanied by an increase of the DR), driven by an enhancement of the push–pull π-conjugation.
- The following openings see either a decrease (diBOXs) or a modest variation (triBOX) of βHRS.
- Nevertheless, these second (and third) openings are also accompanied by a change of the depolarization ratio, which may help to differentiate between the forms.
- The opening mechanism upon protonation is sequential, and the trend of exergonicity is also in phase with the π-conjugation.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Feringa, B.L.; Browne, W.R. (Eds.) Molecular Switches, 2nd ed.; Completely Revised and Enlarged Edition; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Feringa, B.L.; van Delden, R.A.; Koumura, N.; Geertsema, E.M. Chiroptical Molecular Switches. Chem. Rev. 2000, 100, 1789–1816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raymo, F.M. Digital Processing and Communication with Molecular Switches. Adv. Mater. 2002, 14, 401–414. [Google Scholar] [CrossRef]
- Antonov, L. Tautomerism: Methods and Theories; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Andréasson, J.; Pischel, U. Molecules with a Sense of Logic: A Progress Report. Chem. Soc. Rev. 2015, 44, 1053–1069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hann, R.A.; Bloor, D. Organic Materials for Non-Linear Optics II; Royal Society of Chemistry: London, UK, 1991. [Google Scholar]
- Coe, B.J. Molecular Materials Possessing Switchable Quadratic Nonlinear Optical Properties. Chem. Eur. J. 1999, 5, 2464–2471. [Google Scholar] [CrossRef]
- Delaire, J.A.; Nakatani, K. Linear and Nonlinear Optical Properties of Photochromic Molecules and Materials. Chem. Rev. 2000, 100, 1817–1846. [Google Scholar] [CrossRef]
- Castet, F.; Rodriguez, V.; Pozzo, J.L.; Ducasse, L.; Plaquet, A.; Champagne, B. Design and Characterization of Molecular Nonlinear Optical Switches. Acc. Chem. Res. 2013, 46, 2656–2665. [Google Scholar] [CrossRef]
- Kariduraganavar, M.Y.; Doddamani, R.V.; Waddar, B.; Parne, S.R. Nonlinear Optical Responsive Molecular Switches. In Nonlinear Optics-From Solitons to Similaritons; Bakırtaş, İ., Antar, N., Eds.; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Torrent-Sucarrat, M.; Navarro, S.; Marcos, E.; Anglada, J.M.; Luis, J.M. Design of Hückel–Möbius Topological Switches with High Nonlinear Optical Properties. J. Phys. Chem. C 2017, 121, 19348–19357. [Google Scholar] [CrossRef] [Green Version]
- Avramopoulos, A.; Zaleśny, R.; Reis, H.; Papadopoulos, M.G. A Computational Strategy for the Design of Photochromic Derivatives Based on Diarylethene and Nickel Dithiolene with Large Contrast in Nonlinear Optical Properties. J. Phys. Chem. C 2020, 124, 4221–4241. [Google Scholar] [CrossRef]
- Garza, A.J.; Osman, O.I.; Wazzan, N.A.; Khan, S.B.; Scuseria, G.E.; Asiri, A.M. Photochromic and Nonlinear Optical Properties of Fulgides: A Density Functional Theory Study. Comput. Theor. Chem. 2013, 1022, 82–85. [Google Scholar] [CrossRef]
- Li, P.X.; Wang, M.S.; Zhang, M.J.; Lin, C.S.; Cai, L.Z.; Guo, S.P.; Guo, G.C. Electron-Transfer Photochromism To Switch Bulk Second-Order Nonlinear Optical Properties with High Contrast. Angew. Chem. Int. Ed. 2014, 53, 11529–11531. [Google Scholar] [CrossRef]
- Nishizawa, S.; Fihey, A.; Jacquemin, D.; Matsuda, K. Computational Investigation on the Switching Efficiency of Diarylethene: Comparison between the First Hyperpolarizability and Exchange Interaction. Chem. Phys. Lett. 2016, 659, 258–262. [Google Scholar] [CrossRef]
- Markey, K.; Krüger, M.; Seidler, T.; Reinsch, H.; Verbiest, T.; De Vos, D.E.; Champagne, B.; Stock, N.; van der Veen, M.A. Emergence of Nonlinear Optical Activity by Incorporation of a Linker Carrying the p-Nitroaniline Motif in MIL-53 Frameworks. J. Phys. Chem. C 2017, 121, 25509–25519. [Google Scholar] [CrossRef]
- Castet, F.; Gillet, A.; Bureš, F.; Plaquet, A.; Rodriguez, V.; Champagne, B. Second-Order Nonlinear Optical Properties of Λ -Shaped Pyrazine Derivatives. Dyes Pigment. 2021, 184, 108850. [Google Scholar] [CrossRef]
- Desmedt, E.; Woller, T.; Teunissen, J.L.; De Vleeschouwer, F.; Alonso, M. Fine-Tuning of Nonlinear Optical Contrasts of Hexaphyrin-Based Molecular Switches Using Inverse Design. Front. Chem. 2021, 9, 786036. [Google Scholar] [CrossRef]
- Karthika, C.; Das, P.; Samuelson, A. Electro-Switching of First Hyperpolarizability of Metallorganic Complexes via Ligand Reduction/Oxidation. Chem. Phys. Lett. 2021, 768, 138351. [Google Scholar] [CrossRef]
- Clays, K.; Persoons, A. Hyper-Rayleigh Scattering in Solution. Phys. Rev. Lett. 1991, 66, 2980–2983. [Google Scholar] [CrossRef]
- Hendrickx, E.; Clays, K.; Persoons, A. Hyper-Rayleigh Scattering in Isotropic Solution. Acc. Chem. Res. 1998, 31, 675–683. [Google Scholar] [CrossRef]
- Verbiest, T.; Clays, K.; Rodriguez, V. Second-Order Nonlinear Optical Characterization Techniques: An Introduction; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Finn, R.S.; Ward, J.F. Dc-Induced Optical Second-Harmonic Generation in the Inert Gases. Phys. Rev. Lett. 1971, 26, 285–289. [Google Scholar] [CrossRef]
- Levine, B.F.; Bethea, C.G. Second and Third Order Hyperpolarizabilities of Organic Molecules. J. Chem. Phys. 1975, 63, 2666–2682. [Google Scholar] [CrossRef]
- Kanis, D.R.; Ratner, M.A.; Marks, T.J. Design and Construction of Molecular Assemblies with Large Second-Order Optical Nonlinearities. Quantum Chemical Aspects. Chem. Rev. 1994, 94, 195–242. [Google Scholar] [CrossRef]
- Shelton, D.P.; Rice, J.E. Measurements and Calculations of the Hyperpolarizabilities of Atoms and Small Molecules in the Gas Phase. Chem. Rev. 1994, 94, 3–29. [Google Scholar] [CrossRef]
- Papadopoulos, M.G.; Sadlej, A.J.; Leszczynski, J. Non-Linear Optical Properties of Matter: From Molecules to Condensed Phases; Number 1 in Challenges and Advances in Computational Chemistry and Physics; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Champagne, B.; Beaujean, P.; de Wergifosse, M.; Cardenuto, M.H.; Liégeois, V.; Castet, F. Quantum Chemical Methods for Predicting and Interpreting Second-Order Nonlinear Optical Properties: From Small to Extended π-Conjugated Molecules. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2018; pp. 117–138. [Google Scholar] [CrossRef]
- Petkov, I.; Charra, F.; Nunzi, J.M.; Deligeorgiev, T. Photochemistry of 2-[(1,3,3-Trimethylindoline-2(1H)-Ylidene)Propen-1-Yl]-3,3-Dimethylindolino[1,2-b]-Oxazolidine in Solution. J. Photochem. Photobiol. A 1999, 128, 93–96. [Google Scholar] [CrossRef]
- Sanguinet, L.; Pozzo, J.L.; Rodriguez, V.; Adamietz, F.; Castet, F.; Ducasse, L.; Champagne, B. Acido- and Phototriggered NLO Properties Enhancement. J. Phys. Chem. B 2005, 109, 11139–11150. [Google Scholar] [CrossRef] [PubMed]
- Mançois, F.; Sanguinet, L.; Pozzo, J.L.; Guillaume, M.; Champagne, B.; Rodriguez, V.; Adamietz, F.; Ducasse, L.; Castet, F. Acido-Triggered Nonlinear Optical Switches: Benzazolo-oxazolidines. J. Phys. Chem. B 2007, 111, 9795–9802. [Google Scholar] [CrossRef]
- Sevez, G.; Gan, J.; Delbaere, S.; Vermeersch, G.; Sanguinet, L.; Levillain, E.; Pozzo, J.L. Photochromic Performance of a Dithienylethene–Indolinooxazolidine Hybrid. Photochem. Photobiol. Sci. 2010, 9, 131–135. [Google Scholar] [CrossRef]
- Bondu, F.; Hadji, R.; Szalóki, G.; Alévêque, O.; Sanguinet, L.; Pozzo, J.L.; Cavagnat, D.; Buffeteau, T.; Rodriguez, V. Huge Electro-/Photo-/Acidoinduced Second-Order Nonlinear Contrasts From Multiaddressable Indolinooxazolodine. J. Phys. Chem. B 2015, 119, 6758–6765. [Google Scholar] [CrossRef]
- Szalóki, G.; Alévêque, O.; Pozzo, J.L.; Hadji, R.; Levillain, E.; Sanguinet, L. Indolinooxazolidine: A Versatile Switchable Unit. J. Phys. Chem. B 2015, 119, 307–315. [Google Scholar] [CrossRef] [Green Version]
- Sanguinet, L.; Berthet, J.; Szalóki, G.; Alévêque, O.; Pozzo, J.L.; Delbaere, S. 13 Metastable States Arising from a Simple Multifunctional Unimolecular System. Dyes Pigment. 2017, 137, 490–498. [Google Scholar] [CrossRef] [Green Version]
- Aidibi, Y.; Guerrin, C.; Alévêque, O.; Leriche, P.; Delbaere, S.; Sanguinet, L. BT-2-BOX: An Assembly toward Multimodal and Multilevel Molecular System Simple as a Breeze. J. Phys. Chem. C 2019, 123, 11823–11832. [Google Scholar] [CrossRef]
- Guerrin, C.; Aidibi, Y.; Sanguinet, L.; Leriche, P.; Aloise, S.; Orio, M.; Delbaere, S. When Light and Acid Play Tic-Tac-Toe with a Nine-State Molecular Switch. J. Am. Chem. Soc. 2019, 141, 19151–19160. [Google Scholar] [CrossRef]
- Pielak, K.; Bondu, F.; Sanguinet, L.; Rodriguez, V.; Champagne, B.; Castet, F. Second-Order Nonlinear Optical Properties of Multiaddressable Indolinooxazolidine Derivatives: Joint Computational and Hyper-Rayleigh Scattering Investigations. J. Phys. Chem. C 2017, 121, 1851–1860. [Google Scholar] [CrossRef]
- Tonnelé, C.; Pielak, K.; Deviers, J.; Muccioli, L.; Champagne, B.; Castet, F. Nonlinear Optical Responses of Self-Assembled Monolayers Functionalized with Indolino–Oxazolidine Photoswitches. Phys. Chem. Chem. Phys. 2018, 20, 21590–21597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quertinmont, J.; Beaujean, P.; Stiennon, J.; Aidibi, Y.; Leriche, P.; Rodriguez, V.; Sanguinet, L.; Champagne, B. Combining Benzazolo-Oxazolidine Twins toward Multi-State Nonlinear Optical Switches. J. Phys. Chem. B 2021, 125, 3918–3931. [Google Scholar] [CrossRef] [PubMed]
- Aidibi, Y.; Beaujean, P.; Quertinmont, J.; Stiennon, J.; Hodée, M.; Leriche, P.; Berthet, J.; Delbaere, S.; Champagne, B.; Sanguinet, L. A Molecular Loaded Dice: When the π Conjugation Breaks the Statistical Addressability of an Octastate Multimodal Molecular Switch. Dyes Pigment. 2022, 202, 110270. [Google Scholar] [CrossRef]
- Brasselet, S.; Zyss, J. Multipolar Molecules and Multipolar Fields: Probing and Controlling the Tensorial Nature of Nonlinear Molecular Media. J. Opt. Soc. Am. B 1998, 15, 257. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom– Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Chai, J.D.; Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF Version of the PCM Solvation Method: An Overview of a New Method Addressed to Study Molecular Solutes at the QM Ab Initio Level. Comput. Theor. Chem. 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Quertinmont, J.; Champagne, B.; Castet, F.; Hidalgo Cardenuto, M. Explicit versus Implicit Solvation Effects on the First Hyperpolarizability of an Organic Biphotochrome. J. Phys. Chem. A 2015, 119, 5496–5503. [Google Scholar] [CrossRef]
- Liégeois, V. DrawMol. UNamur. Available online: https://www.unamur.be/drawmol (accessed on 21 April 2022).
- Bondu, F.; Quertinmont, J.; Rodriguez, V.; Pozzo, J.L.; Plaquet, A.; Champagne, B.; Castet, F. Second-Order Nonlinear Optical Properties of a Dithienylethene–Indolinooxazolidine Hybrid: A Joint Experimental and Theoretical Investigation. Chem. Eur. J. 2015, 21, 18749–18757. [Google Scholar] [CrossRef]
- Beaujean, P.; Bondu, F.; Plaquet, A.; Garcia-Amorós, J.; Cusido, J.; Raymo, F.M.; Castet, F.; Rodriguez, V.; Champagne, B. Oxazines: A New Class of Second-Order Nonlinear Optical Switches. J. Am. Chem. Soc. 2016, 138, 5052–5062. [Google Scholar] [CrossRef]
- Bouquiaux, C.; Tonnelé, C.; Castet, F.; Champagne, B. Second-Order Nonlinear Optical Properties of an Amphiphilic Dye Embedded in a Lipid Bilayer. A Combined Molecular Dynamics–Quantum Chemistry Study. J. Phys. Chem. B 2020, 124, 2101–2109. [Google Scholar] [CrossRef]
- Grabarz, A.M.; Ośmiałowski, B. Benchmarking Density Functional Approximations for Excited-State Properties of Fluorescent Dyes. Molecules 2021, 26, 7434. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yang, M.; Champagne, B. Large Off-Diagonal Contribution to the Second-Order Optical Nonlinearities of Λ-Shaped Molecules. J. Phys. Chem. A 2003, 107, 3942–3951. [Google Scholar] [CrossRef]
- Orr, B.; Ward, J. Perturbation Theory of the Non-Linear Optical Polarization of an Isolated System. Mol. Phys. 1971, 20, 513–526. [Google Scholar] [CrossRef]
- Oudar, J.L.; Chemla, D.S. Hyperpolarizabilities of the Nitroanilines and Their Relations to the Excited State Dipole Moment. J. Chem. Phys. 1977, 66, 2664–2668. [Google Scholar] [CrossRef]
- Alam, M.M.; Beerepoot, M.T.P.; Ruud, K. A Generalized Few-State Model for the First Hyperpolarizability. J. Chem. Phys. 2020, 152, 244106. [Google Scholar] [CrossRef]
- Cho, M.; Kim, H.S.; Jeon, S.J. An Elementary Description of Nonlinear Optical Properties of Octupolar Molecules: Four-state Model for Guanidinium-Type Molecules. J. Chem. Phys. 1998, 108, 7114–7120. [Google Scholar] [CrossRef]
- Beaujean, P.; Champagne, B. Unraveling the Symmetry Effects on the Second-Order Nonlinear Optical Responses of Molecular Switches: The Case of Ruthenium Complexes. Inorg. Chem. 2022, 61, 1928–1940. [Google Scholar] [CrossRef]
- Otero, N.; Karamanis, P.; Mandado, M. A New Method to Analyze and Understand Molecular Linear and Nonlinear Optical Responses via Field-Induced Functions: A Straightforward Alternative to Sum-over-States (SOS) Analysis. Phys. Chem. Chem. Phys. 2019, 21, 6274–6286. [Google Scholar] [CrossRef]
- De Wergifosse, M.; Grimme, S. A Unified Strategy for the Chemically Intuitive Interpretation of Molecular Optical Response Properties. J. Chem. Theory Comput. 2020, 16, 7709–7720. [Google Scholar] [CrossRef]
| Form | BLA1 | BLA2 | BLA3 | ||||
|---|---|---|---|---|---|---|---|
| 1 (biThSMe) | C | 0.148 | — | — | 29.5 | — | — |
| O | 0.061 | — | — | 22.8 | — | — | |
| 2a (biTh) | CC | 0.147 | 0.147 | — | 25.5 | — | — |
| CO | 0.148 | 0.060 | — | 20.4 | — | — | |
| OO | 0.071 | 0.070 | — | 21.0 | — | — | |
| 2b (biEtTh) | CC | 0.148 | 0.148 | — | 88.9 | — | — |
| CO | 0.148 | 0.068 | — | 83.8 | — | — | |
| OO | 0.073 | 0.072 | — | 85.4 | — | — | |
| 2c (Cpdith) | CC | 0.145 | 0.145 | — | 0.05 | — | — |
| CO | 0.147 | 0.042 | — | 0.04 | — | — | |
| OO | 0.063 | 0.063 | — | 0.15 | — | — | |
| 2d (biE) | CC | 0.142 | 0.142 | — | 0.99 | — | — |
| CO | 0.143 | 0.037 | — | 0.36 | — | — | |
| OO | 0.055 | 0.055 | — | 0.51 | — | — | |
| 2e (EThE) | CC | 0.142 | 0.142 | — | 3.3 | 8.8 | — |
| CO | 0.143 | 0.042 | — | 3.8 | 2.3 | — | |
| OO | 0.046 | 0.046 | — | 0.8 | 5.3 | — | |
| 3a (PhTh) | CCC | 0.147 | 0.147 | 0.147 | 31.2 | 30.7 | 31.3 |
| CCO | 0.147 | 0.147 | 0.059 | 31.9 | 30.5 | 28.8 | |
| COO | 0.147 | 0.061 | 0.061 | 31.2 | 29.2 | 28.7 | |
| OOO | 0.062 | 0.062 | 0.062 | 28.9 | 30.2 | 29.7 | |
| 3b | Ph(C)-BiPh(C)-PhTh(C) | 0.156 | 0.157 | 0.147 | 39.4 | 31.7 | — |
| Ph(C)-BiPh(C)-PhTh(O) | 0.157 | 0.157 | 0.056 | 39.9 | 26.6 | — | |
| Ph(C)-BiPh(O)-PhTh(C) | 0.156 | 0.085 | 0.147 | 37.4 | 31.2 | — | |
| Ph(O)-BiPh(C)-PhTh(C) | 0.064 | 0.157 | 0.147 | 39.9 | 31.0 | — | |
| Ph(C)-BiPh(O)-PhTh(O) | 0.157 | 0.086 | 0.058 | 39.2 | 28.9 | — | |
| Ph(O)-BiPh(C)-PhTh(O) | 0.069 | 0.157 | 0.061 | 39.8 | 31.0 | — | |
| Ph(O)-BiPh(O)-PhTh(C) | 0.067 | 0.087 | 0.147 | 35.7 | 28.6 | — | |
| Ph(O)-BiPh(O)-PhTh(O) | 0.070 | 0.087 | 0.062 | 39.2 | 29.6 | — |
| Form | Static | 1907 nm | 1300 nm | 1064 nm | |
|---|---|---|---|---|---|
| 1 | C | 0.5 (3.78) | 0.4 (3.67) | 0.5 (3.71) | 0.6 (3.71) |
| O | 20.0 (4.82) | 16.7 (4.89) | 29.9 (4.94) | 77.3 (4.97) | |
| 2a | CC | 0.4 (4.01) | 0.3 (3.86) | 0.4 (3.91) | 0.5 (3.96) |
| CO | 27.0 (4.81) | 26.1 (4.90) | 50.8 (4.95) | 148.5 (4.98) | |
| OO | 2.8 (2.33) | 2.3 (2.43) | 4.2 (2.57) | 14.4 (2.31) | |
| 2b | CC | 0.5 (5.11) | 0.4 (3.99) | 0.4 (4.04) | 0.5 (4.07) |
| CO | 6.9 (4.48) | 6.1 (4.61) | 8.9 (4.74) | 14.4 (4.87) | |
| OO | 4.9 (2.43) | 4.2 (2.47) | 6.1 (2.54) | 9.5 (2.62) | |
| 2c | CC | 1.4 (3.30) | 1.2 (3.08) | 1.5 (3.12) | 1.9 (3.13) |
| CO | 37.8 (4.79) | 32.9 (4.88) | 74.6 (4.96) | 666.6 (5.02) | |
| OO | 11.0 (2.44) | 9.7 (2.58) | 22.6 (2.54) | 92.5 (1.09) | |
| 2d | CC | 0.4 (4.02) | 0.3 (3.79) | 0.4 (3.95) | 0.5 (4.12) |
| CO | 34.9 (4.83) | 32.1 (4.91) | 75.7 (4.96) | 1009.0 (4.94) | |
| OO | 0.3 (3.75) | 0.2 (3.23) | 0.5 (2.82) | 2.7 (2.85) | |
| 2e | CC | 1.4 (5.15) | 1.1 (5.09) | 1.6 (5.07) | 2.5 (4.62) |
| CO | 56.4 (4.92) | 61.1 (4.97) | 174.2 (4.98) | 1523.2 (4.93) | |
| OO | 11.9 (2.66) | 11.6 (2.65) | 33.7 (2.72) | 55.5 (0.20) | |
| 3a | CCC | 4.2 (1.72) | 4.4 (1.64) | 6.0 (1.61) | 8.6 (1.59) |
| CCO | 43.1 (4.47) | 52.5 (4.54) | 114.9 (4.74) | 528.1 (4.96) | |
| COO | 45.4 (2.92) | 55.2 (2.91) | 116.2 (3.07) | 514.4 (2.94) | |
| OOO | 39.8 (1.52) | 50.3 (1.47) | 105.7 (1.46) | 410.4 (1.46) | |
| 3b | CCC | 3.6 (1.64) | 3.8 (1.63) | 5.0 (1.65) | 7.0 (1.68) |
| CCO | 35.6 (4.65) | 37.3 (4.70) | 76.7 (4.82) | 281.9 (4.93) | |
| COO | 35.2 (3.22) | 36.5 (3.15) | 68.8 (3.28) | 203.5 (3.20) | |
| OOO | 30.7 (3.24) | 32.8 (3.16) | 62.4 (3.37) | 179.2 (3.84) |
| Form | Static | 1907 nm | 1300 nm | 1064 nm |
|---|---|---|---|---|
| Ph(C)-BiPh(C)-PhTh(O) | 42.2 (4.66) | 48.3 (4.69) | 108.8 (4.83) | 502.4 (4.92) |
| Ph(C)-BiPh(O)-PhTh(C) | 27.5 (4.13) | 33.5 (4.31) | 62.5 (4.52) | 148.9 (4.75) |
| Ph(O)-BiPh(C)-PhTh(C) | 32.0 (4.67) | 30.8 (4.71) | 58.0 (4.82) | 154.6 (4.93) |
| Ph(C)-BiPh(O)-PhTh(O) | 33.8 (2.93) | 39.3 (2.92) | 83.6 (3.28) | 347.8 (3.98) |
| Ph(O)-BiPh(C)-PhTh(O) | 35.8 (3.23) | 36.9 (3.16) | 69.8 (3.27) | 206.6 (3.11) |
| Ph(O)-BiPh(O)-PhTh(C) | 31.4 (3.25) | 32.7 (3.16) | 58.2 (3.38) | 151.3 (3.85) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beaujean, P.; Sanguinet, L.; Rodriguez, V.; Castet, F.; Champagne, B. Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation. Molecules 2022, 27, 2770. https://doi.org/10.3390/molecules27092770
Beaujean P, Sanguinet L, Rodriguez V, Castet F, Champagne B. Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation. Molecules. 2022; 27(9):2770. https://doi.org/10.3390/molecules27092770
Chicago/Turabian StyleBeaujean, Pierre, Lionel Sanguinet, Vincent Rodriguez, Frédéric Castet, and Benoît Champagne. 2022. "Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation" Molecules 27, no. 9: 2770. https://doi.org/10.3390/molecules27092770
APA StyleBeaujean, P., Sanguinet, L., Rodriguez, V., Castet, F., & Champagne, B. (2022). Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation. Molecules, 27(9), 2770. https://doi.org/10.3390/molecules27092770







