Topological and Spectral Properties of Wavy Zigzag Nanoribbons
Abstract
1. Introduction
2. Computational Techniques
- Vertex Wiener =
- Edge Wiener
- Vertex-edge Wiener
- Vertex Szeged =
- Edge Szeged =
- Edge-vertex Szeged =
- Padmakar-Ivan
- Schultz
- Gutman
- Vertex Mostar =
- Edge Mostar =
3. Results and Discussion
3.1. Distance Based Descriptors
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
3.2. Degree Based Topological Descriptors
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
3.3. Numerical Values
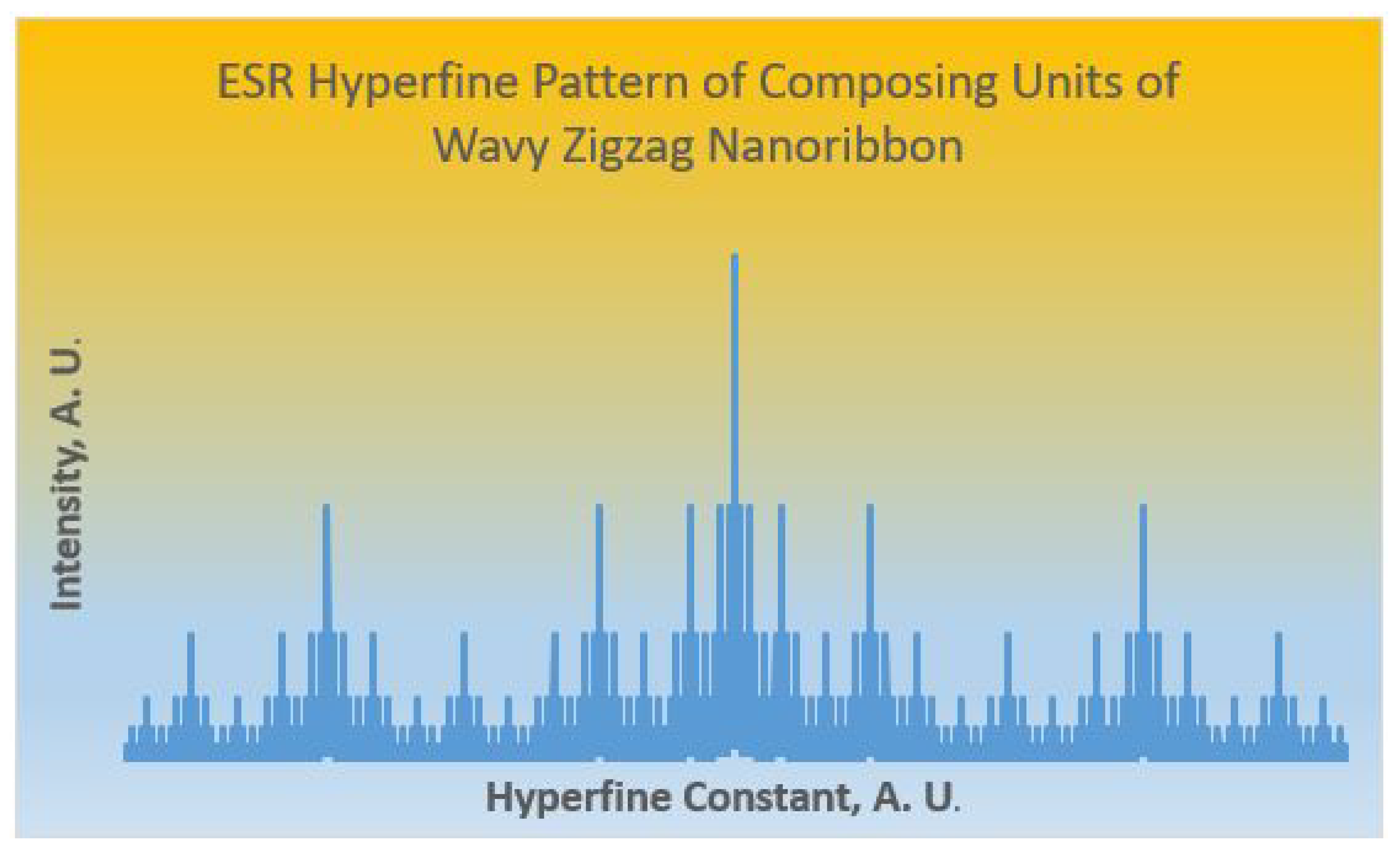
4. Applications to Stabilities and Spectroscopy of Wavy Zigzag Nanoribbons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, F.; Chen, J.; Hu, X.; He, F.; Bean, E.; Tsang, D.C.W.; Ok, Y.S.; Gao, B. Applications of carbonaceous adsorbents in the remediation of polycyclic aromatic hydrocarbon-contaminated sediments: A review. J. Clean. Prod. 2020, 225, 120263. [Google Scholar] [CrossRef]
- Gan, S.; Lau, E.V.; Ng, H.K. Remediation of soils contaminated with polycyclic aromatic hydrocarbons (PAHs). J. Hazard. Mater. 2009, 172, 532–549. [Google Scholar] [CrossRef] [PubMed]
- Bansal, V.; Kim, K.-H. Review of PAH contamination in food products and their health hazards. Environ. Int. 2015, 84, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Queiroz, R.N.; Prediger, P.; Vieira, M.G.A. Adsorption of polycyclic aromatic hydrocarbons from wastewater using graphene-based nanomaterials synthesized by conventional chemistry and green synthesis: A critical review. J. Hazard. Mater. 2022, 422, 126904. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Cao, Y.; Colella, N.S.; Liang, Y.; Brédas, J.-L.; Houk, K.N.; Briseno, A.L. Unconventional, chemically stable, and soluble two-dimensional angular polycyclic aromatic hydrocarbons: From molecular design to device applications. Acc. Chem. Res. 2015, 48, 500–509. [Google Scholar] [CrossRef]
- Aumaitre, C.; Morin, J.-F. Polycyclic aromatic hydrocarbons as potential building blocks for organic solar cells. Chem. Rec. 2019, 19, 1142–1154. [Google Scholar] [CrossRef]
- Shafy, H.I.A.; Mansour, M.S.M. A review on polycyclic aromatic hydrocarbons: Source, environmental impact, effect on human health and remediation. Egypt. J. Pet. 2016, 25, 107–123. [Google Scholar] [CrossRef]
- Menzie, C.A.; Potocki, B.B.; Santodonato, J. Exposure to carcinogenic PAHs in the environment. Environ. Sci. Technol. 1992, 26, 1278–1284. [Google Scholar] [CrossRef]
- Masih, J.; Singhvi, R.; Kumar, K.; Jain, V.K.; Taneja, A. Seasonal variation and sources of polycyclic aromatic hydrocarbons (PAHs) in indoor and outdoor air in a semi arid tract of northern india. Aerosol Air Qual. Res. 2012, 12, 515–525. [Google Scholar] [CrossRef]
- Srogi, K. Monitoring of environmental exposure to polycyclic aromatic hydrocarbons: A review. Environ. Chem. Lett. 2007, 5, 169–195. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Cui, G.; Bi, Z.; Zhang, R.; Liu, J.; Yu, X.; Li, Z. A comprehensive review on graphene-based anti-corrosive coatings. Chem. Eng. J. 2019, 373, 104–121. [Google Scholar] [CrossRef]
- Dhinakaran, V.; Stalin, B.; Sai, M.S.; Vairamuthu, J.; Marichamy, S. Recent developments of graphene composites for energy storage devices. Mater. Today Proc. 2021, 45, 1779–1782. [Google Scholar] [CrossRef]
- Hao, W.; Wang, Y.; Zhao, H.; Zhu, J.; Li, S. Strong dependence of the vertical charge carrier mobility on the π-π stacking distance in molecule/graphene heterojunctions. Phys. Chem. Chem. Phys. 2020, 22, 13802–13807. [Google Scholar] [CrossRef] [PubMed]
- Zhan, B.; Li, C.; Yang, J.; Jenkins, G.; Huang, W.; Dong, X. Graphene field-effect transistor and its application for electronic sensing. Small 2014, 10, 4042–4065. [Google Scholar] [CrossRef]
- Yoo, E.; Kim, J.; Hosono, E.; Zhou, H.-S.; Kudo, T.; Honma, I. Large reversible Li storage of graphene nanosheet families for use in rechargeable lithium ion batteries. Nano Lett. 2008, 8, 2277–2282. [Google Scholar] [CrossRef]
- Sharma, B.K.; Ahn, J.-H. Graphene based field effect transistors: Efforts made towards flexible electronics. Solid-State Electron. 2013, 89, 177–188. [Google Scholar] [CrossRef]
- Alabi, A.; Cseri, L.; Hajaj, A.A.; Szekely, G.; Budd, P.; Zou, L. Graphene-PSS/l-DOPA nanocomposite cation exchange membranes for electrodialysis desalination. Environ. Sci. Nano 2020, 7, 3108–3123. [Google Scholar] [CrossRef]
- Dash, B.S.; Jose, G.; Lu, Y.-J.; Chen, J.-P. Functionalized reduced graphene oxide as a versatile tool for cancer therapy. Int. J. Mol. Sci. 2021, 22, 2989. [Google Scholar] [CrossRef]
- Dong, X.; Fu, D.; Fang, W.; Shi, Y.; Chen, P.; Li, L.-J. Doping single-layer graphene with aromatic molecules. Small 2009, 5, 1422–1426. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H. Chemical preparation of graphene-based nanomaterials and their applications in chemical and biological sensors. Small 2011, 7, 2413–2427. [Google Scholar] [CrossRef] [PubMed]
- Seabra, A.B.; Paula, A.J.; Lima, R.D.; Alves, O.L.; Durán, N. Nanotoxicity of graphene and graphene oxide. Chem. Res. Toxicol. 2014, 27, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Narváez, E.M.; Pires, L.B.; Gálvez, A.Z.; Merkoçi, A. Graphene-based biosensors: Going simple. Adv. Mater. 2017, 29, 1604905. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, M.; Hashmi, M.S.J. Wonder material graphene: Properties, synthesis and practical applications. Adv. Mater. Process. Technol. 2018, 4, 573–602. [Google Scholar] [CrossRef]
- Kosynkin, D.V.; Higginbotham, A.L.; Sinitskii, A.; Lomeda, J.R.; Dimiev, A.; Price, B.K.; Tour, J.M. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons. Nature 2009, 458, 872–876. [Google Scholar] [CrossRef]
- Pincak, R.; Smotlacha, J.; Osipov, V.A. Electronic states of zigzag graphenenanoribbons with edges reconstructed with topological defects. Phys. B Condens. Matter. 2015, 475, 61–65. [Google Scholar] [CrossRef][Green Version]
- Damasceno, D.A.; Rajapakse, R.K.N.D.N.; Mesquita, E. Atomistic modelling of size-dependent mechanical properties and fracture of pristine and defective cove-edged graphene nanoribbons. Nanomaterials 2020, 10, 1422. [Google Scholar] [CrossRef]
- Jiang, D.-E.; Sumpter, B.G.; Dai, S. Unique chemical reactivity of a graphene nanoribbon’s zigzag edge. J. Chem. Phys. 2007, 126, 134701. [Google Scholar] [CrossRef]
- Okada, S.; Oshiyama, A. Magnetic ordering in hexagonally bonded sheets with first-row elements. Phys. Rev. Lett. 2001, 87, 146803. [Google Scholar] [CrossRef]
- Lee, H.; Son, Y.-W.; Park, N.; Han, S.; Yu, J. Magnetic ordering at the edges of graphitic fragments: Magnetic tail interactions between the edge-localized states. Phys. Rev. B 2005, 72, 174431. [Google Scholar] [CrossRef]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A.N.; et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 2006, 312, 1191–1196. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.; Song, Z.; Li, T.; Li, X.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.; Marchenkov, A.N.; Conrad, E.H.; First, P.N.; et al. Ultrathin epitaxial graphite: 2D Electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 2004, 108, 19912–19916. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Rizzo, D.J.; Veber, G.; Cao, T.; Bronner, C.; Chen, T.; Zhao, F.; Rodriguez, H.; Louie, S.G.; Crommie, M.F.; Fischer, F.R. Topological band engineering of graphene nanoribbons. Nature 2018, 560, 204–208. [Google Scholar] [CrossRef]
- Ruffieux, P.; Cai, J.; Plumb, N.C.; Patthey, L.; Prezzi, D.; Ferretti, A.; Molinari, E.; Feng, X.; Müllen, K.; Pignedoli, C.A.; et al. Electronic structure of atomically precise graphene nanoribbons. ACS Nano 2012, 6, 6930–6935. [Google Scholar] [CrossRef]
- Johnson, A.P.; Gangadharappa, H.V.; Pramod, K. Graphene nanoribbons: A promising nanomaterial for biomedical applications. J. Control. Release 2020, 325, 141–162. [Google Scholar] [CrossRef]
- Song, S.; Ng, P.W.; Edalatmanesh, S.; Solé, A.P.; Peng, X.; Kolorenč, J.; Sosnová, Z.; Stetsovych, O.; Su, J.; Li, J.; et al. Designer magnetic topological graphene nanoribbons. arXiv 2022, arXiv:2204.12880. [Google Scholar]
- Arockiaraj, M.; Clement, J.; Balasubramanian, K. Analytical expressions for topological properties of polycyclic benzenoid networks. J. Chemom. 2016, 30, 682–697. [Google Scholar] [CrossRef]
- Imran, M.; Baig, A.Q.; Ali, H. On molecular topological properties of hex-derived networks. J. Chemom. 2016, 30, 121–129. [Google Scholar] [CrossRef]
- Khadikar, P.V.; Karmarkar, S.; Agrawal, V.K. A novel PI index and its applications to QSPR/QSAR studies. J. Chem. Inf. Comput. Sci. 2001, 41, 934–949. [Google Scholar] [CrossRef] [PubMed]
- Khadikar, P.V.; Karmarkar, S.; Agrawal, V.K.; Singh, J.; Shrivastava, A.; Lukovits, I.; Diudea, M.V. Szeged index-Applications for drug modeling. Lett. Drug Des. Discov. 2005, 2, 606–624. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics: Vol. I: Alphabetical Listing/Vol. II: Appendices, References; Methods and Principles in Medical Chemistry; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Balasubramanian, K. Combinatorial enumeration of isomers of superaromatic polysubstituted cycloarenes and coronoid hydrocarbons with applications to NMR. J. Phys. Chem. A 2018, 122, 8243–8257. [Google Scholar] [CrossRef]
- Balasubramanian, K. Computational and Artificial Intelligence Techniques for Drug Discovery and Administration; Reference Module in Biomedical Sciences; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Aihara, J.-I. Topological resonance energy, bond resonance energy, and circuit resonance energy. J. Phys. Org. Chem. 2008, 21, 79–85. [Google Scholar] [CrossRef]
- Aihara, J.-I. Graph theory of ring-current diamagnetism. Bull. Chem. Soc. Jpn. 2018, 91, 274–303. [Google Scholar] [CrossRef]
- Dias, J.R. Valence-bond determination of diradical character of polycyclic aromatic hydrocarbons: From acenes to rectangular benzenoids. J. Phys. Chem. A 2013, 117, 4716–4725. [Google Scholar] [CrossRef]
- Aihara, J.-I.; Makino, M.; Ishida, T.; Dias, J.R. Analytical study of superaromaticity in cycloarenes and related coronoid hydrocarbons. J. Phys. Chem. A 2013, 117, 4688–4697. [Google Scholar] [CrossRef]
- Makino, M.; Dias, J.R.; Aihara, J.-I. Bond resonance energy verification of σ-aromaticity in cycloalkanes. J. Phys. Chem. A 2020, 124, 4549–4555. [Google Scholar] [CrossRef]
- Balasubramanian, K. Symmetry and combinatorial concepts for cyclopolyarenes, nanotubes and 2D-sheets: Enumerations, isomers, structures spectra & properties. Symmetry 2022, 14, 34. [Google Scholar]
- Dearden, J.C. The use of topological indices in QSAR and QSPR modeling. Adv. QSAR Model. 2017, 24, 57–88. [Google Scholar]
- Hayat, S.; Imran, M. Computation of topological indices of certain networks. Appl. Math. Comput. 2014, 240, 213–228. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Klavžar, S.; Mushtaq, S. Distance-based topological indices of nanosheets, nanotubes and nanotori of SiO2. J. Math. Chem. 2019, 57, 343–369. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Paul, D.; Klavžar, S.; Clement, J.; Tiggaa, S.; Balasubramanian, K. Relativistic distance based and bond additive topological descriptors of zeolite RHO materials. J. Mol. Struct. 2022, 1250, 131798. [Google Scholar] [CrossRef]
- Liu, J.-B.; Iqbal, H.; Shahzad, K. Topological properties of concealed non-kekulean benzenoid hydrocarbon. Polycycl. Aromat. Compd. 2022. [Google Scholar] [CrossRef]
- Adnan, M.; Bokhary, S.A.; Abbas, G.; Iqbal, T. Degree-based topological indices and QSPR analysis of antituberculosis drugs. J. Chem. 2022, 2022, 5748626. [Google Scholar] [CrossRef]
- Hayat, S.; Khan, S.; Imran, M. Quality testing of spectrum-based distance descriptors for polycyclic aromatic hydrocarbons with applications to carbon nanotubes and nanocones. Arabian J. Chem. 2021, 14, 102994. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Clement, J.; Paul, D.; Balasubramanian, K. Relativistic distance-based topological descriptors of Linde type A zeolites and their doped structures with very heavy elements. Mol. Phys. 2020, 119, e1798529. [Google Scholar] [CrossRef]
- Sarkar, P.; De, N.; Pal, A. On some topological indices and their importance in chemical sciences: A comparative study. Eur. Phys. J. Plus. 2022, 137, 195. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Klavžar, S.; Mushtaq, S.; Balasubramanian, K. Topological characterization of the full k-subdivision of a family of partial cubes and their applications to α-types of novel graphyne and graphdiyne materials. Polycycl. Aromat. Compd. 2021, 41, 1902–1924. [Google Scholar] [CrossRef]
- Huilgol, M.I.; Sriram, V.; Balasubramanian, K. Structure-activity relations for antiepileptic drugs through omega polynomials and topological indices. Mol. Phys. 2022, 120, e1987542. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, Y.; Li, Y.; Furtula, B. On relations between Sombor and other degree-based indices. J. Appl. Math. Comput. 2022, 68, 1–17. [Google Scholar] [CrossRef]
- Klavžar, S.; Gutman, I.; Mohar, B. Labeling of benzenoid systems which reflects the vertex-distance relation. J. Chem. Inf. Comput. Sci. 1995, 35, 590–593. [Google Scholar] [CrossRef]
- Klavžar, S. A bird’s eye view of the cut method and a survey of its recent applications in chemical graph theory. MATCH Commun. Math. Comput. Chem. 2008, 60, 255–274. [Google Scholar]
- Kavitha, S.R.J.; Abraham, J.; Arockiaraj, M.; Jency, J.; Balasubramanian, K. Topological characterization and graph entropies of tessellations of kekulene structures: Existence of isentropic structures and applications to thermochemistry, NMR and ESR. J. Phys. Chem. A 2021, 125, 8140–8158. [Google Scholar] [CrossRef]
- Abraham, J.; Arockiaraj, M.; Jency, J.; Kavitha, S.R.J.; Balasubramanian, K. Graph entropies, enumeration of circuits, walks and topological properties of three classes of isoreticular metal organic frameworks. J. Math. Chem. 2022, 60, 695–732. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Jency, J.; Abraham, J.; Kavitha, S.R.J.; Balasubramanian, K. Two-dimensional coronene fractal structures: Topological entropy measures, energetics, NMR and ESR spectroscopic patterns and existence of isentropic structures. Mol. Phys. 2022, 120, e2079568. [Google Scholar] [CrossRef]
- Bloom, G.S.; Kennedy, J.W.; Quintas, L.V. Some Problems Concerning Distance and Path Degree Sequences. In Graph Theory; Springer: Berlin/Heidelberg, Germany, 1983; pp. 179–190. [Google Scholar]
- Balasubramanian, K. Topochemie-2020-A computational package for computing topological indices, spectral polynomials, walks and distance degree sequences and combinatorial generators. J. Phys. Chem. A 2021, 125, 8140–8158. [Google Scholar]
- Balasubramanian, K. Operator and algebraic methods for NMR-spectroscopy. I. Generation of NMR Spin Species. J. Chem. Phys. 1983, 78, 6358–6368. [Google Scholar] [CrossRef]
- Henrdon, W.C. Resonance energies of aromatic hydrocarbons. Quantitative test of resonance theory. J. Am. Chem. Soc. 1973, 95, 2404–2406. [Google Scholar]
- Zdetsis, A.D.; Economou, E.N. Rationalizing and reconciling energy gaps and quantum confinement in narrow atomically precise armchair graphene nanoribbons. Carbon 2017, 116, 422–434. [Google Scholar] [CrossRef]
- El Abbassi, M.; Perrin, M.L.; Barin, G.B.; Sangtarash, S.; Overbeck, J.; Braun, O.; Lambert, C.J.; Sun, Q.; Prechtl, T.; Narita, A.; et al. Controlled quantum dot formation in atomically engineered graphene nanoribbon field-effect transistors. ACS Nano 2020, 14, 5754–5762. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Dai, S. Circumacenes versus periacenes: HOMO–LUMO gap and transition from nonmagnetic to magnetic ground state with size. Chem. Phys. Lett. 2008, 466, 72–75. [Google Scholar] [CrossRef]
- Chopra, S.; Maidich, L. Density functional theory based study of graphene nano-ribbons of various shapes and sizes. Quantum Matter 2014, 3, 559–563. [Google Scholar] [CrossRef]
- Kimouche, A.; Ervasti, M.M.; Drost, R.; Halonen, S.; Harju, A.; Joensuu, P.M.; Sainio, J.; Liljeroth, P. Ultra-narrow metallic armchair graphene nanoribbons. Nat. Commun. 2015, 6, 10177. [Google Scholar] [CrossRef] [PubMed]
- Patil, V.M.; Narkhede, R.R.; Masand, N.; Cheke, R.S.; Balasubramanian, K. Molecular insights into resveratrol and its analogs as SARS-CoV-2 (COVID-19) protease inhibitors. Coronaviruses 2021, 2, e130921189258. [Google Scholar] [CrossRef]
- Balasubramanian, K. CASSCF/CI calculations on Si4 and Si4+. Chem. Phys. Lett. 1987, 135, 283–287. [Google Scholar] [CrossRef]
- Zhang, D.; Qu, Z.; Liu, C.; Jiang, Y. Excitation energy calculation of conjugated hydrocarbons: A new Pariser–Parr–Pople model parameterization approaching CASPT2 accuracy. J. Chem. Phys. 2011, 134, 024114. [Google Scholar] [CrossRef] [PubMed]

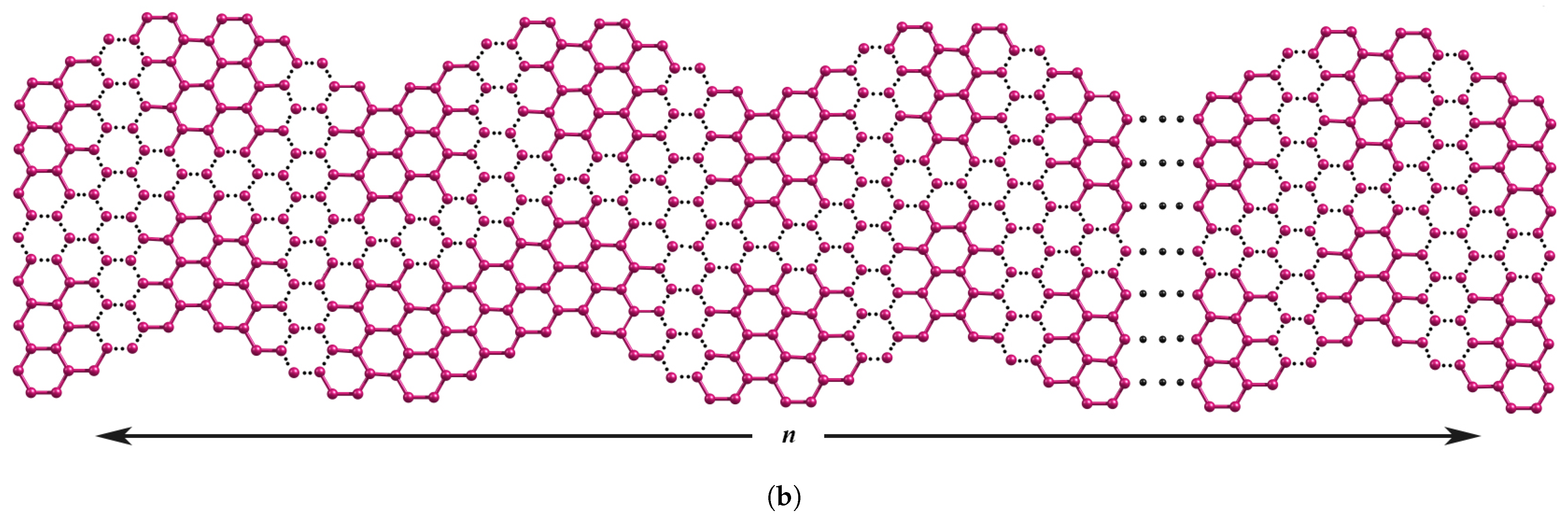

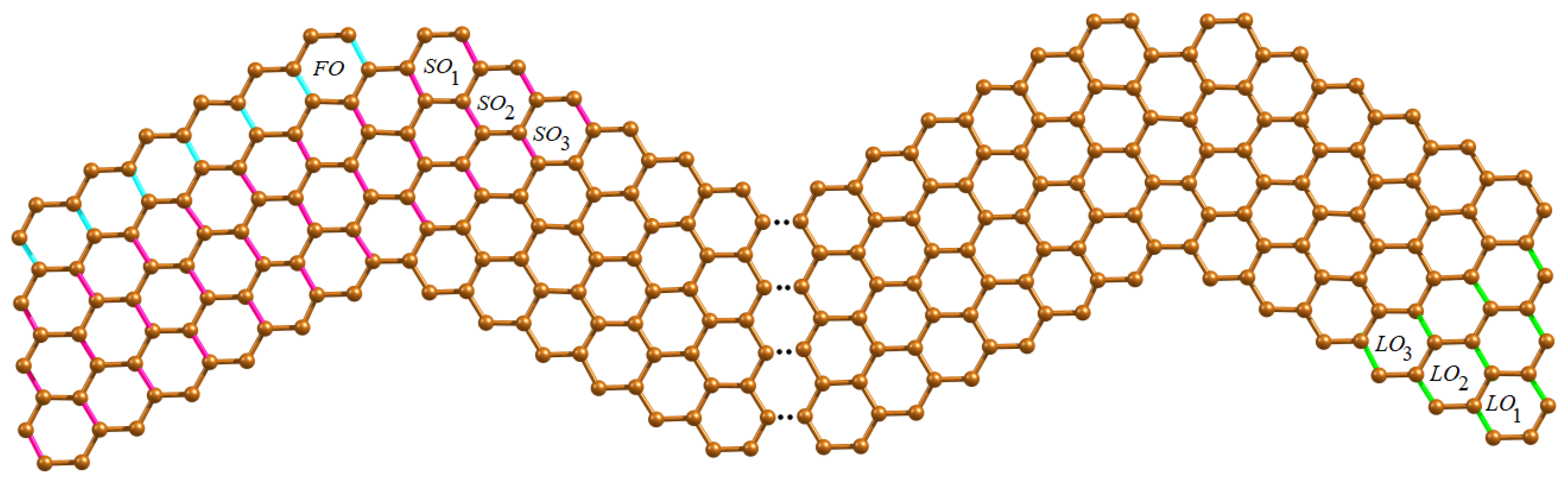

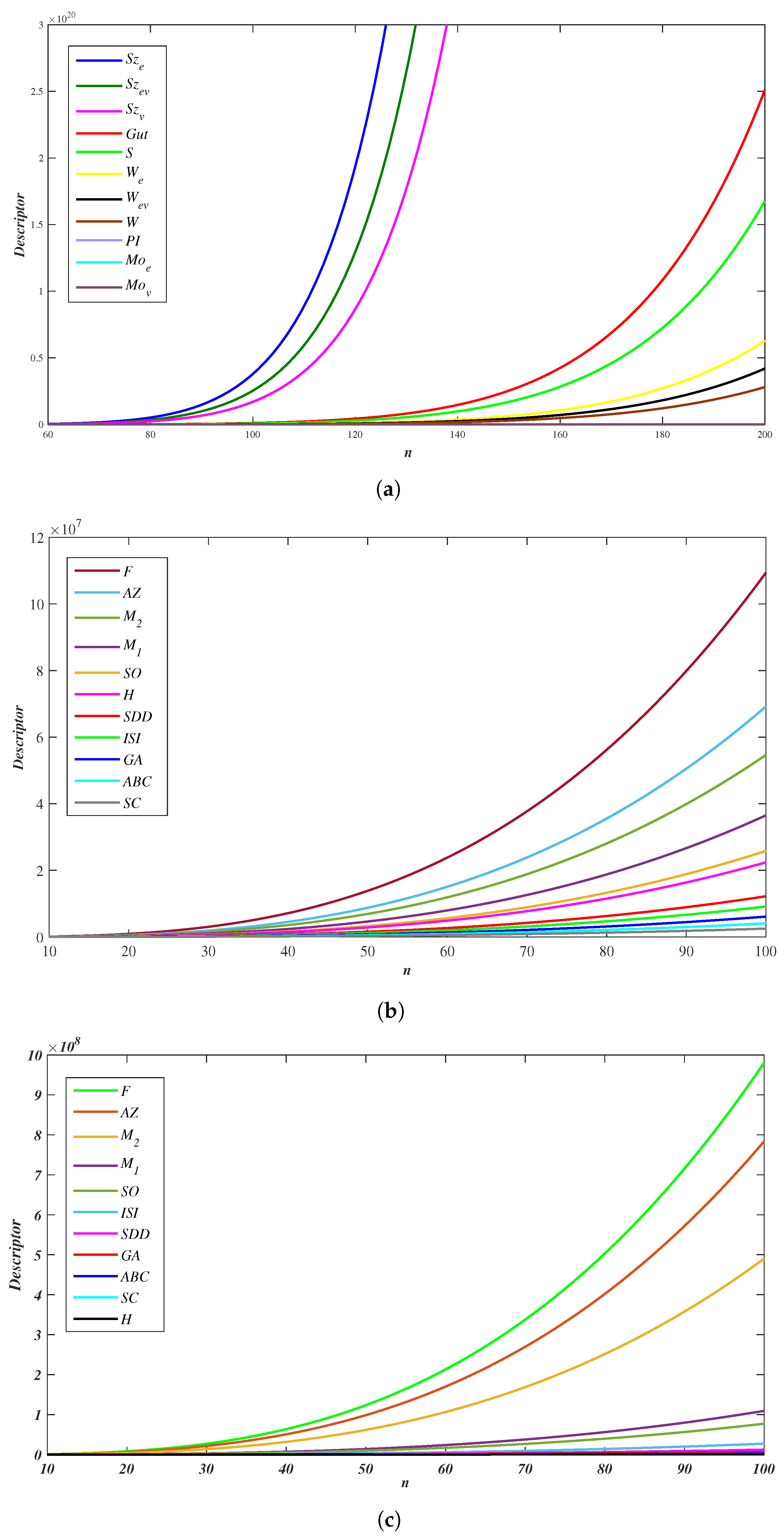
| Range | ||||
|---|---|---|---|---|
| r | ||||
| r |
| Range | ||||
|---|---|---|---|---|
| Bond | Bond Degree | Number of Apperance in |
|---|---|---|
| X−Y | WNR | |
| C−C | ||
| C−H | − |
| Bond | Bond Degree-sum | Number of Appearances in |
|---|---|---|
| X−Y | WNR | |
| C−C | 4 | |
| C−H | − |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| W | 198 | 16,988 | 265,090 | 1,995,080 | 9,900,014 | 37,435,172 | 116,825,002 | 315,961,424 | 764,827,734 | 1,694,512,428 | |
| W | 144 | 23,902 | 447,338 | 3,656,560 | 19,008,676 | 74,039,578 | 235,829,606 | 647,405,812 | 1,585,027,224 | 3,543,167,190 | |
| W | 171 | 20,185 | 344,512 | 2,701,379 | 13,719,069 | 52,648,697 | 165,987,706 | 452,283,443 | 1,101,041,295 | 2,450,306,985 | |
| Sz | 360 | 58,230 | 1,336,218 | 13,209,706 | 80,974,236 | 363,962,990 | 1,314,958,190 | 4,038,660,258 | 10,939,664,656 | 26,808,888,486 | |
| Sz | 252 | 81,660 | 2,249,918 | 24,170,052 | 155,271,436 | 719,090,380 | 2,652,165,798 | 8,269,315,796 | 22,657,699,020 | 56,027,704,284 | |
| Sz | 306 | 69,067 | 1,734,606 | 17,871,135 | 112,137,204 | 511,606,727 | 1,867,520,568 | 5,779,084,127 | 15,743,942,926 | 38,756,383,875 | |
| PI | 144 | 6428 | 57,744 | 279,244 | 961,536 | 2,665,804 | 6,354,848 | 13,550,044 | 26,514,224 | 48,460,476 | |
| S | 840 | 85,988 | 1,421,788 | 11,009,804 | 55,565,776 | 212,481,764 | 668,408,452 | 1,818,575,052 | 4,422,544,728 | 9,834,683,940 | |
| Gut | 889 | 108,760 | 1,906,145 | 15,188,508 | 77,966,465 | 301,507,160 | 956,059,001 | 2,616,774,636 | 6,393,217,769 | 14,269,710,136 | |
| Mo | 36 | 2476 | 21,416 | 100,956 | 342,076 | 938,156 | 2,219,136 | 4,704,316 | 9,163,796 | 16,688,556 | |
| Mo | 36 | 3250 | 29,268 | 140,902 | 483,740 | 1,338,706 | 3,187,580 | 6,791,478 | 13,282,292 | 24,267,090 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 436 | 1350 | 3016 | 5650 | 9468 | 14,686 | 21,520 | 30,186 | 40,900 | ||
| 65 | 582 | 1879 | 4280 | 8109 | 13,690 | 21,347 | 31,404 | 44,185 | 60,014 | ||
| 41.292 | 310.539 | 959.915 | 2142.156 | 4009.997 | 6716.172 | 10,413.417 | 15,254.467 | 21,392.057 | 28,978.922 | ||
| 9.152 | 56.446 | 165.720 | 360.975 | 666.211 | 1105.426 | 1702.622 | 2481.798 | 3466.955 | 4682.092 | ||
| 12.919 | 81.353 | 241.464 | 529.252 | 980.716 | 1631.858 | 2518.676 | 3677.171 | 5143.342 | 6953.190 | ||
| 107.391 | 784.844 | 2455.984 | 5530.875 | 10,419.578 | 17,532.156 | 27,278.672 | 40,069.1875 | 56,313.766 | 76422.469 | ||
| 6.197 | 34.824 | 103.634 | 224.322 | 412.587 | 683.125 | 1050.633 | 1529.808 | 2135.347 | 2881.947 | ||
| 14.3 | 107.4 | 333.7 | 747.2 | 1401.9 | 2351.8 | 3650.9 | 5353.2 | 7512.7 | 10,183.4 | ||
| F | 134 | 1196 | 3834 | 8696 | 16,430 | 27,684 | 43,106 | 63,344 | 89,046 | 12,0860 | |
| H | 43.67 | 303.34 | 905.67 | 1982.67 | 3666.33 | 6088.67 | 9381.67 | 13,677.33 | 19,107.67 | 25,804.67 | |
| 26.67 | 169.34 | 498.67 | 1086.67 | 2005.33 | 3326.67 | 5122.67 | 7465.33 | 10,426.67 | 14,078.67 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 130 | 1164 | 3758 | 8560 | 16,218 | 27,380 | 42,694 | 62,808 | 88,370 | 120,028 | ||
| 297 | 4238 | 14863 | 35,088 | 67,829 | 116,002 | 182,523 | 270,308 | 382,273 | 521,334 | ||
| 93.747 | 828.213 | 2666.904 | 6068.026 | 11,489.785 | 19,390.384 | 30,228.029 | 44,460.926 | 62,547.279 | 84,945.295 | ||
| 7.444 | 41.034 | 116.806 | 250.759 | 458.893 | 757.210 | 1161.709 | 1688.389 | 2353.250 | 3172.294 | ||
| 12.783 | 81.439 | 241.984 | 530.419 | 982.744 | 1634.959 | 2523.063 | 3683.058 | 5150.942 | 6962.716 | ||
| 296.352 | 6053.189 | 22,252.391 | 53,564.827 | 104,661.365 | 180,212.873 | 284,890.219 | 423,364.271 | 600,305.898 | 820,385.968 | ||
| 4.092 | 22.104 | 62.581 | 134.008 | 244.874 | 403.656 | 618.847 | 898.929 | 1252.389 | 1687.712 | ||
| 31.20 | 287.338 | 932.669 | 2129.192 | 4038.907 | 6823.815 | 10,645.914 | 15,667.207 | 22,049.691 | 29,955.368 | ||
| F | 658 | 8672 | 30,102 | 70,780 | 136,538 | 233,208 | 366,622 | 542,612 | 767,010 | 1,045,648 | |
| H | 2.576 | 12.048 | 32.538 | 68.045 | 122.569 | 200.111 | 304.669 | 440.245 | 610.837 | 820.447 | |
| 27.777 | 168.594 | 494.301 | 1076.896 | 1988.380 | 3300.753 | 5086.015 | 7416.166 | 10,363.205 | 13,999.134 | ||
| Strutures | C NMR Pattern | HOMO-LUMO Gap | Total -Electron Energy/Bond | -Electron Delocalization Energy/Bond | Resonance Energy/Bond |
|---|---|---|---|---|---|
| ZNR | 30 signals 1:1:...:1:1 | 0.132706 | 1.46369662 | 0.4636966 | 0.1123377 |
| ZNR | 38 signals 1:1:...:1:1 | 0.07387 | 1.468135457 | 0.46813546 | 0.1042822 |
| ZNR | 38 signals 1:1:...:1:1 | 0.048414 | 1.47682673 | 0.47682673 | 0.10325986 |
| ZNR | 46 signals 1:1:...:1:1 | 0.0184152 | 1.4854958 | 0.48549581 | 0.0953989 |
| ZNR | 58 signals 1:1:...:1:1 | 0.00701 | 1.49130572 | 0.49130572 | 0.09010814 |
| ZNR | 98 signals 1:1:...:1:1 | 0.000152 | 1.5096 | 0.5096296 | 0.0708 |
| WNR | 152 signals 1:1:...:1:1 | 0.000404 | 1.4854719 | 0.4854719 | 0.10200974 |
| WNR | 190 signals 1:1:...:1:1 | 0.00074 | 1.48667696 | 0.48667696 | 0.1018617 |
| WNR | 190 signals 1:1:...:1:1 | 0.0 | 1.50358001 | 0.5035800 | 0.1018617 |
| WNR | 228 signals 1:1:...:1:1 | 0.000014 | 1.4874809132 | 0.48748091 | 0.1017633 |
| WNR | 230 signals 1:1:...:1:1 | 0.0 | 1.51395311 | 0.5139531 | 0.0913716 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arockiaraj, M.; Fiona, J.C.; Kavitha, S.R.J.; Shalini, A.J.; Balasubramanian, K. Topological and Spectral Properties of Wavy Zigzag Nanoribbons. Molecules 2023, 28, 152. https://doi.org/10.3390/molecules28010152
Arockiaraj M, Fiona JC, Kavitha SRJ, Shalini AJ, Balasubramanian K. Topological and Spectral Properties of Wavy Zigzag Nanoribbons. Molecules. 2023; 28(1):152. https://doi.org/10.3390/molecules28010152
Chicago/Turabian StyleArockiaraj, Micheal, J. Celin Fiona, S. Ruth Julie Kavitha, Arul Jeya Shalini, and Krishnan Balasubramanian. 2023. "Topological and Spectral Properties of Wavy Zigzag Nanoribbons" Molecules 28, no. 1: 152. https://doi.org/10.3390/molecules28010152
APA StyleArockiaraj, M., Fiona, J. C., Kavitha, S. R. J., Shalini, A. J., & Balasubramanian, K. (2023). Topological and Spectral Properties of Wavy Zigzag Nanoribbons. Molecules, 28(1), 152. https://doi.org/10.3390/molecules28010152







