Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO4 Embedded in a Chain of Silicates
Abstract
:1. Introduction
2. Chain of Silicates
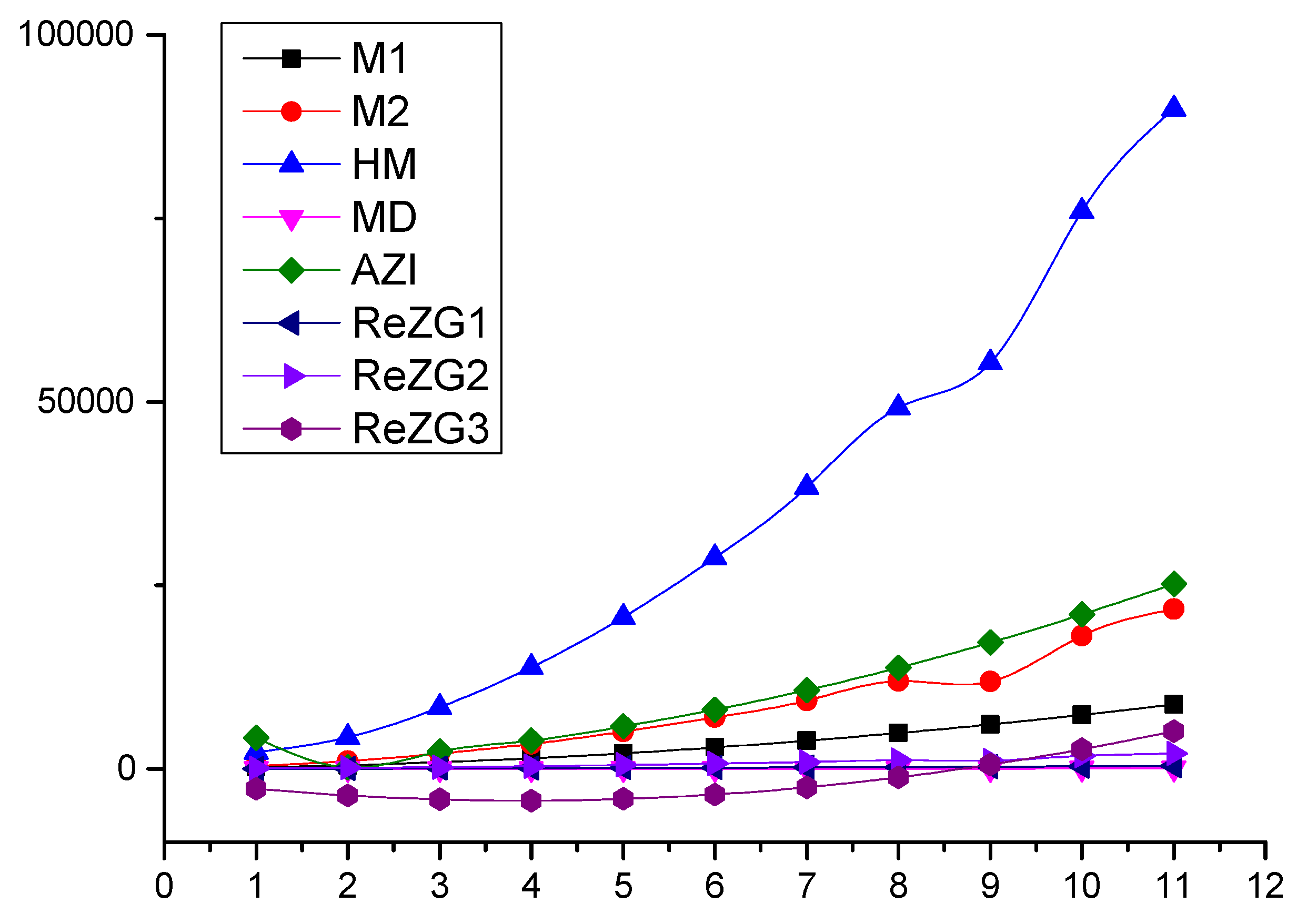
3. Zagreb Polynomials and Indices for 2,
Comparison
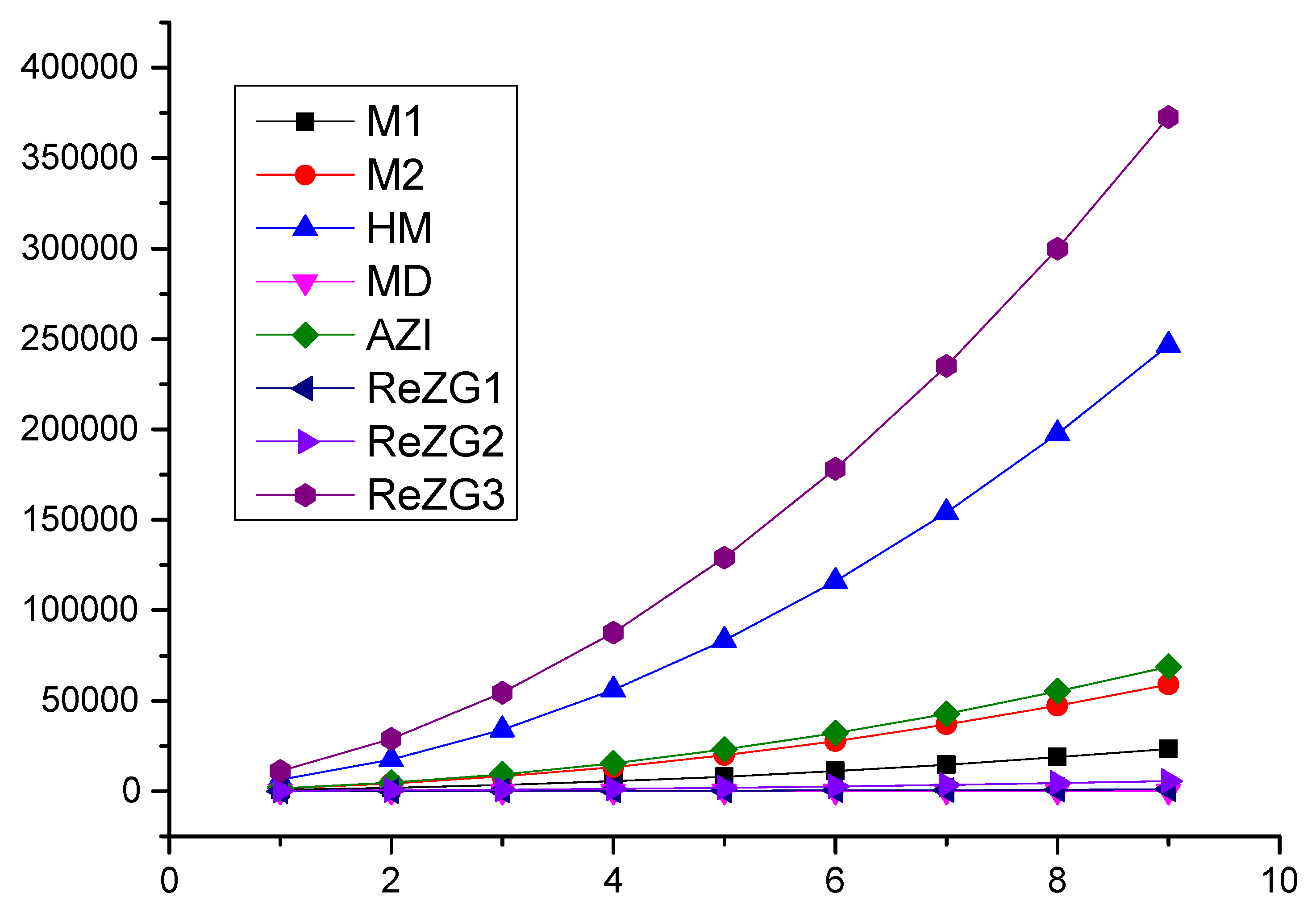
4. Zagreb Polynomials and Indices for and p Are Odd
Comparison
5. Conclusions
- Are Zagreb polynomials and Zagreb indices affected when both p and q are even or odd?
- The results will be interesting when .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Ghani, M.U.; Sultan, F.; Tag El Din, E.S.M.; Khan, A.R.; Liu, J.B.; Cancan, M. A Paradigmatic Approach to Find the Valency-Based K-Banhatti and Redefined Zagreb Entropy for Niobium Oxide and a Metal—Organic Framework. Molecules 2022, 27, 6975. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Ul Haq Bokhary, S.A.; Rehman, M.U.; Ali, U.; Mubeen, H.; Iqbal, Q.; Liu, J.B. Degree-Based Indices of Some Complex Networks. J. Math. 2021, 2021, 5531357. [Google Scholar] [CrossRef]
- Irfan, M.; Rehman, H.U.; Almusawa, H.; Rasheed, S.; Baloch, I.A. M-Polynomials and Topological Indices for Line Graphs of Chain Silicate Network and H-Naphtalenic Nanotubes. J. Math. 2021, 2021, 5551825. [Google Scholar] [CrossRef]
- Liu, J.B.; Zhang, T.; Hayat, S. The Calculations of Topological Indices on Certain Networks. J. Math. 2021, 2021, 6694394. [Google Scholar] [CrossRef]
- Li, Z.; Li, C.J. CuBr-catalyzed efficient alkynylation of sp3 C- H bonds adjacent to a nitrogen atom. J. Am. Chem. Soc. 2004, 126, 11810–11811. [Google Scholar] [CrossRef]
- Shi, L.; Xia, W. Photoredox functionalization of C–H bonds adjacent to a nitrogen atom. Chem. Soc. Rev. 2012, 41, 7687–7697. [Google Scholar] [CrossRef]
- Ashraful Alam, M.; Ghani, M.U.; Kamran, M.; Shazib Hameed, M.; Hussain Khan, R.; Baig, A. Degree-Based Entropy for a Non-Kekulean Benzenoid Graph. J. Math. 2022, 2022, 2288207. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, A.R.; Ghani, M.U.; Ghaffar, A.; Inc, M. Computation of zagreb polynomials and zagreb indices for benzenoid triangular & hourglass system. Polycycl. Aromat. Compd. 2022, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ghani, M.U.; Sultan, F.; Inc, M.; Cancan, M. Connecting SiO 4 in Silicate and Silicate Chain Networks to Compute Kulli Temperature Indices. Molecules 2022, 27, 7533. [Google Scholar] [CrossRef]
- Ghani, M.U.; Sultan, F.; El Sayed, M.; Cancan, M.; Ali, S. SiO4 characterization in a chain and C6 H6 embedded in a Non-kekulean structure for Kulli Temperature indices. Eur. PMC 2022. [Google Scholar] [CrossRef]
- Costa, P.; Evangelista, J.S.; Leal, I.; Miranda, P.C. Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR. Mathematics 2021, 9, 60. [Google Scholar]
- Mondal, S.; Dey, A.; De, N.; Pal, A. QSPR analysis of some novel neighbourhood degree-based topological descriptors. Complex Intell. Syst. 2021, 7, 977–996. [Google Scholar] [CrossRef]
- Al-Ahmadi, B.; Saleh, A.; Al-Shammakh, W. Downhill Zagreb Polynomials of Graphs. Res. Rev. Discret. Math. Struct. 2021, 7, 15–26. [Google Scholar]
- Zakharov, A.B.; Tsarenko, D.K.; Ivanov, V.V. Topological characteristics of iterated line graphs in the QSAR problem: A multigraph in the description of properties of unsaturated hydrocarbons. Struct. Chem. 2021, 32, 1629–1639. [Google Scholar] [CrossRef]
- Natarajan, V.; Kumar, P.N.; Ahmad, M.; Sharma, J.P.; Chaudhary, A.K.; Sharma, P.K. Effect of electron-phonon interaction and valence band edge shift for carrier-type reversal in layered ZnS/rGO nanocomposites. J. Colloid Interface Sci. 2021, 586, 39–46. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I. Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem 2004, 52, 3-1. [Google Scholar]
- Shirdel, G.; Rezapour, H.; Sayadi, A. The hyper-Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Vukičević, D.; Graovac, A. Valence connectivity versus Randić, Zagreb and modified Zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat. Chem. Acta 2004, 77, 501–508. [Google Scholar]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Ranjini, P.; Lokesha, V.; Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 2013, 1, 116–121. [Google Scholar]
- Ghani, M.U.; Kashif Maqbool, M.; George, R.; Ofem, A.E.; Cancan, M. Entropies Via Various Molecular Descriptors of Layer Structure of H3BO3. Mathematics 2022, 10, 4831. [Google Scholar] [CrossRef]
- Koubisy, M.; Shaaban, K.S.; Wahab, E.A.; Sayyed, M.; Mahmoud, K. Synthesis, structure, mechanical and radiation shielding features of 50SiO 2–(48+ X) Na 2 B 4 O 7–(2- X) MnO 2 glasses. Eur. Phys. J. Plus 2021, 136, 1–18. [Google Scholar] [CrossRef]
- Mandlimath, T.R.; Balaji, D.; Kumar, S.P. Synthesis, structural and thermal expansion investigation of La, Ce and Eu substituted Bi4 (SiO4) 3. Mater. Chem. Phys. 2021, 270, 124841. [Google Scholar] [CrossRef]
- Liebau, F. Structural Chemistry of Silicates: Structure, Bonding, and Classification; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]

| Type of Atom–Bond | |||
|---|---|---|---|
| Number of atom–bonds |
| p | q | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 198 | 396 | 2243 | 1.723 | 422.4811 | 13 | 46 | −2744 |
| 3 | 3 | 486 | 1071 | 4278 | 3.3055 | 182.6090 | 27 | 113.5 | −3646 |
| 4 | 4 | 900 | 2070 | 8392 | 5.388 | 2324.6907 | 46 | 211 | −4172 |
| 5 | 5 | 1440 | 3393 | 13,856 | 7.9722 | 3848.7256 | 70 | 338.5 | −4322 |
| 6 | 6 | 2106 | 5040 | 20,670 | 11.055 | 5754.7139 | 99 | 496 | −4096 |
| 7 | 7 | 2898 | 7011 | 28,834 | 14.6388 | 8042.6556 | 133 | 683.5 | −3494 |
| 8 | 8 | 3816 | 9306 | 38,348 | 18.7222 | 10,712.5607 | 172 | 901 | −2516 |
| 9 | 9 | 4860 | 11,925 | 49,212 | 23.3055 | 13,764.3992 | 216 | 1148.5 | −1162 |
| 10 | 10 | 6030 | 14,869 | 55,297 | 28.3888 | 17,198.2011 | 265 | 1426 | 568 |
| 11 | 11 | 7326 | 18,135 | 75,990 | 33.9722 | 21,013.9564 | 319 | 1738.5 | 2674 |
| 12 | 12 | 8748 | 21,726 | 89,904 | 40.0555 | 25,211.6651 | 378 | 2071 | 5156 |
| Type of Atom–Bond | |||
|---|---|---|---|
| Number of atom bonds |
| p,q | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3,4 | 661 | 1512 | 6426 | 4.1666 | 1690.6176 | 35 | 156 | 11,256 |
| 5,6 | 1746 | 4158 | 17,550 | 9.3333 | 4738.6876 | 83 | 411 | 28,884 |
| 7,8 | 3330 | 8100 | 34,074 | 16.5 | 9314.6712 | 151 | 786 | 54,384 |
| 9,10 | 5418 | 13,338 | 55,998 | 25.66 | 15,418.2684 | 239 | 1281 | 87,756 |
| 11,12 | 8010 | 19,872 | 83,322 | 36.83 | 23,049.7792 | 347 | 1896 | 129,000 |
| 13,14 | 11,106 | 27,702 | 116,044 | 50 | 32,209.1036 | 475 | 2631 | 178,116 |
| 15,16 | 14,706 | 36,828 | 154,170 | 65.16 | 42,896.2416 | 623 | 3486 | 235,104 |
| 17,18 | 18,810 | 47,250 | 197,694 | 82.33 | 55,111.1932 | 791 | 4461 | 299,964 |
| 19,20 | 23,418 | 58,968 | 246,618 | 101.5 | 68,853.9584 | 979 | 5556 | 372,696 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tag El Din, E.S.M.; Sultan, F.; Ghani, M.U.; Liu, J.-B.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Alhushaybari, A. Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO4 Embedded in a Chain of Silicates. Molecules 2023, 28, 201. https://doi.org/10.3390/molecules28010201
Tag El Din ESM, Sultan F, Ghani MU, Liu J-B, Dehraj S, Cancan M, Alharbi FM, Alhushaybari A. Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO4 Embedded in a Chain of Silicates. Molecules. 2023; 28(1):201. https://doi.org/10.3390/molecules28010201
Chicago/Turabian StyleTag El Din, El Sayed M., Faisal Sultan, Muhammad Usman Ghani, Jia-Bao Liu, Sanaullah Dehraj, Murat Cancan, Fahad M. Alharbi, and Abdullah Alhushaybari. 2023. "Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO4 Embedded in a Chain of Silicates" Molecules 28, no. 1: 201. https://doi.org/10.3390/molecules28010201






