Physical Mechanism of One-Photon Absorption, Two-Photon Absorption, and Electron Circular Dichroism of 1,3,5 Triazine Derivatives Based on Molecular Planarity
Abstract
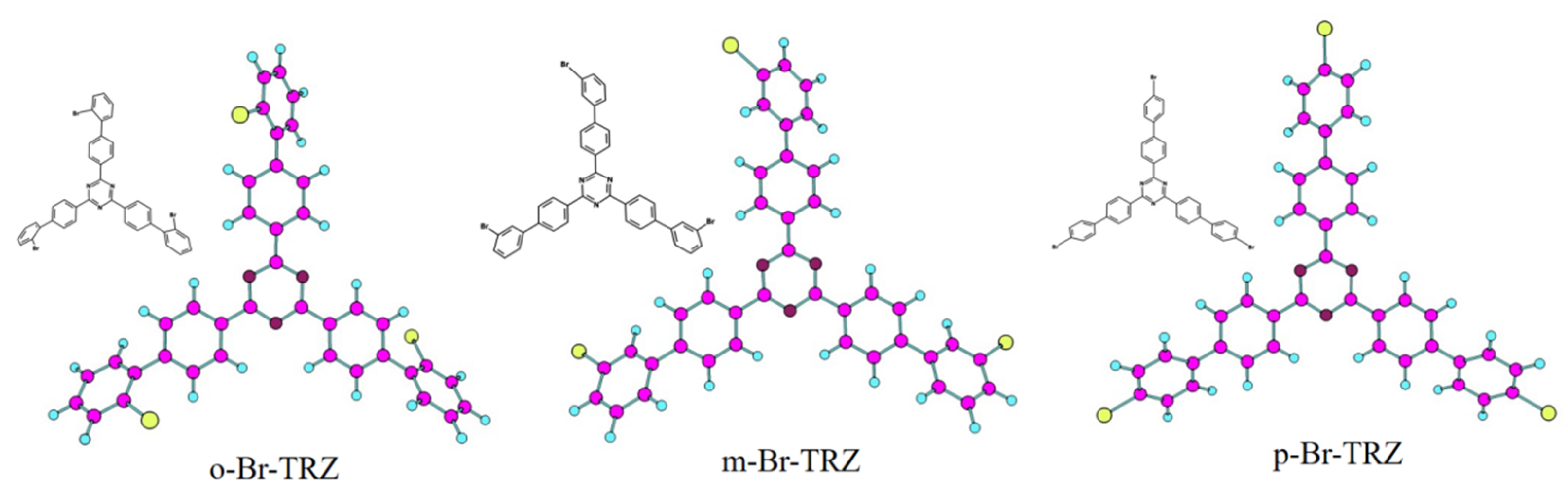
1. Introduction
2. Results
2.1. OPA
2.2. TPA
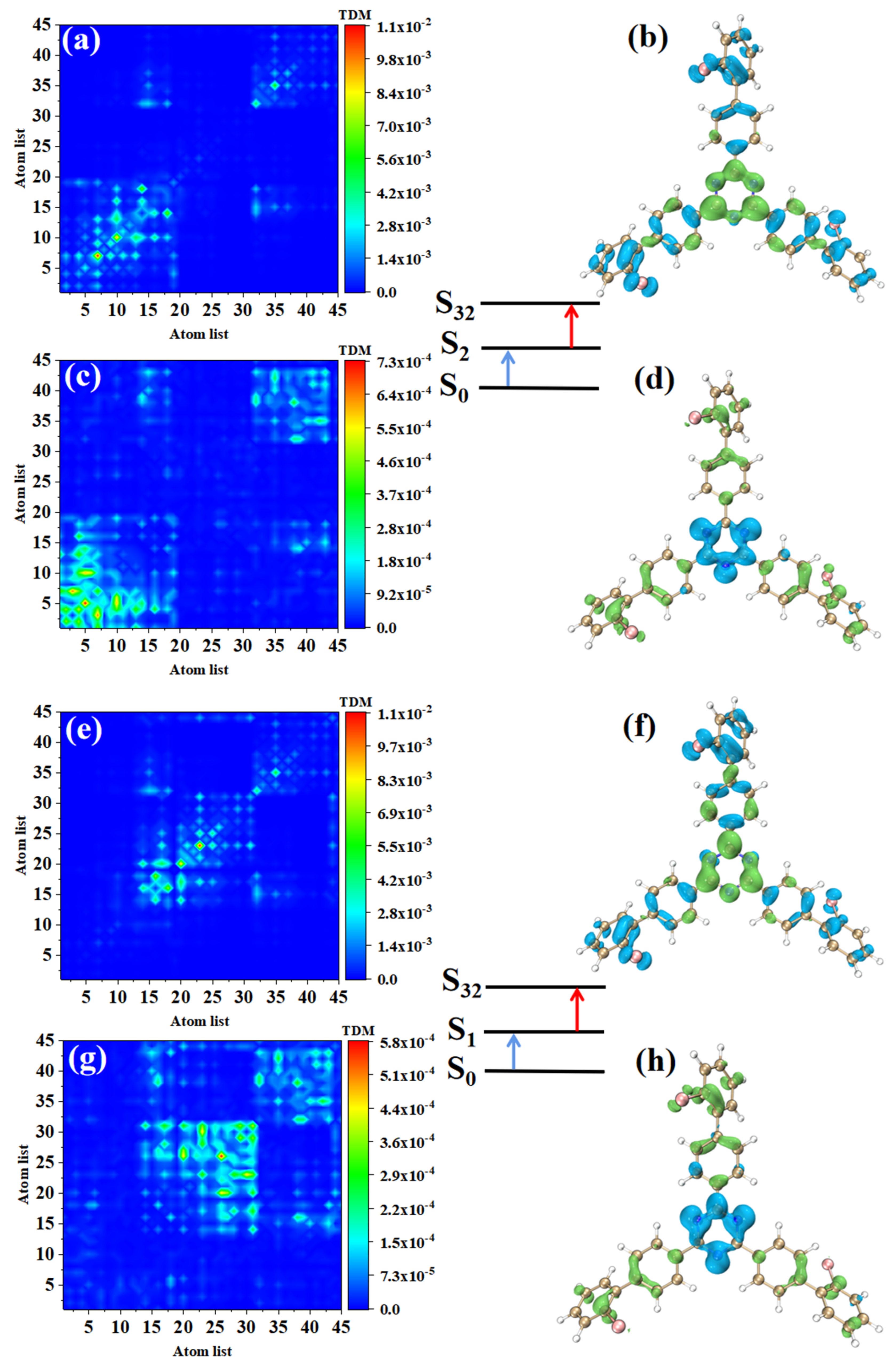
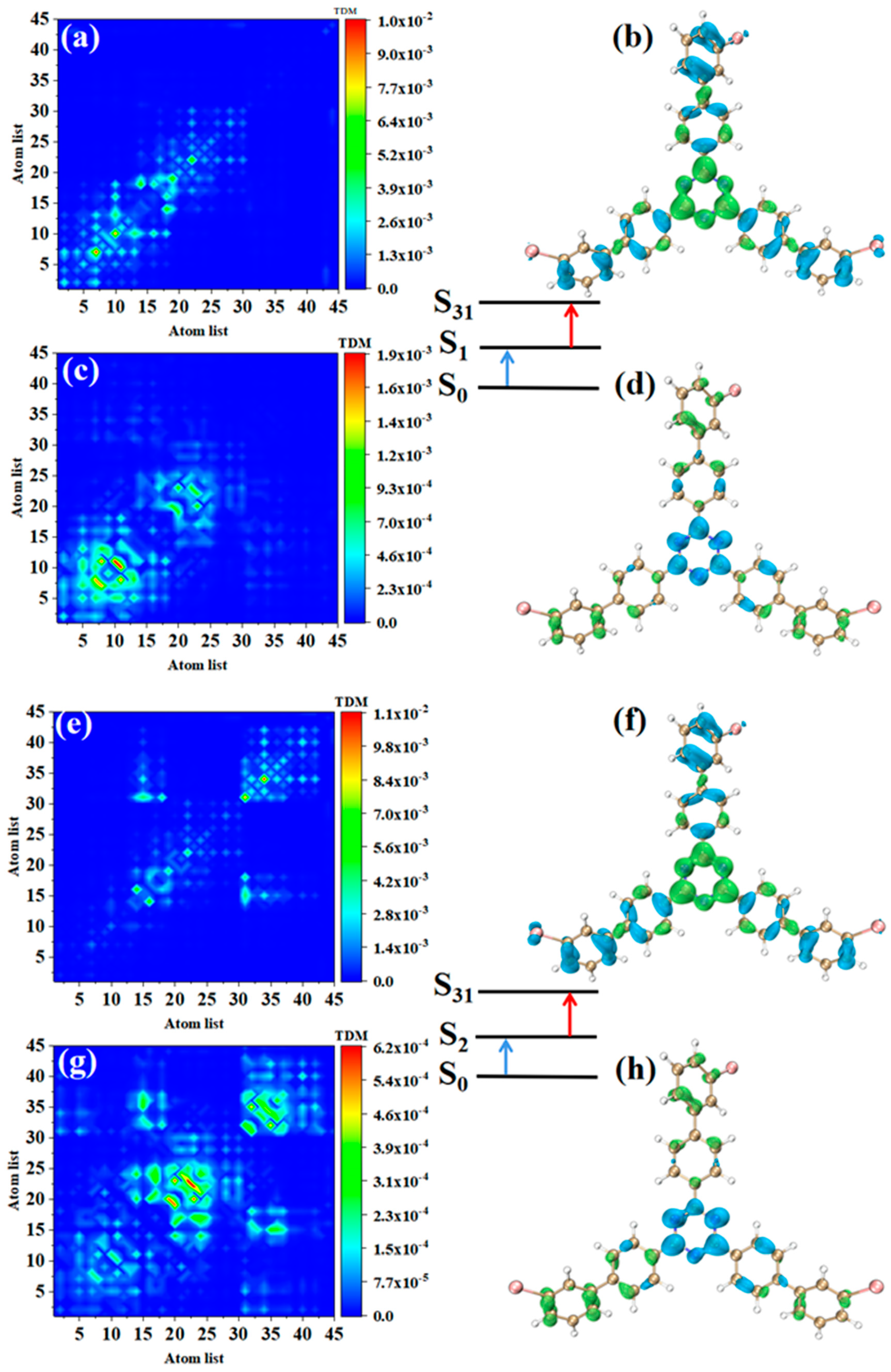
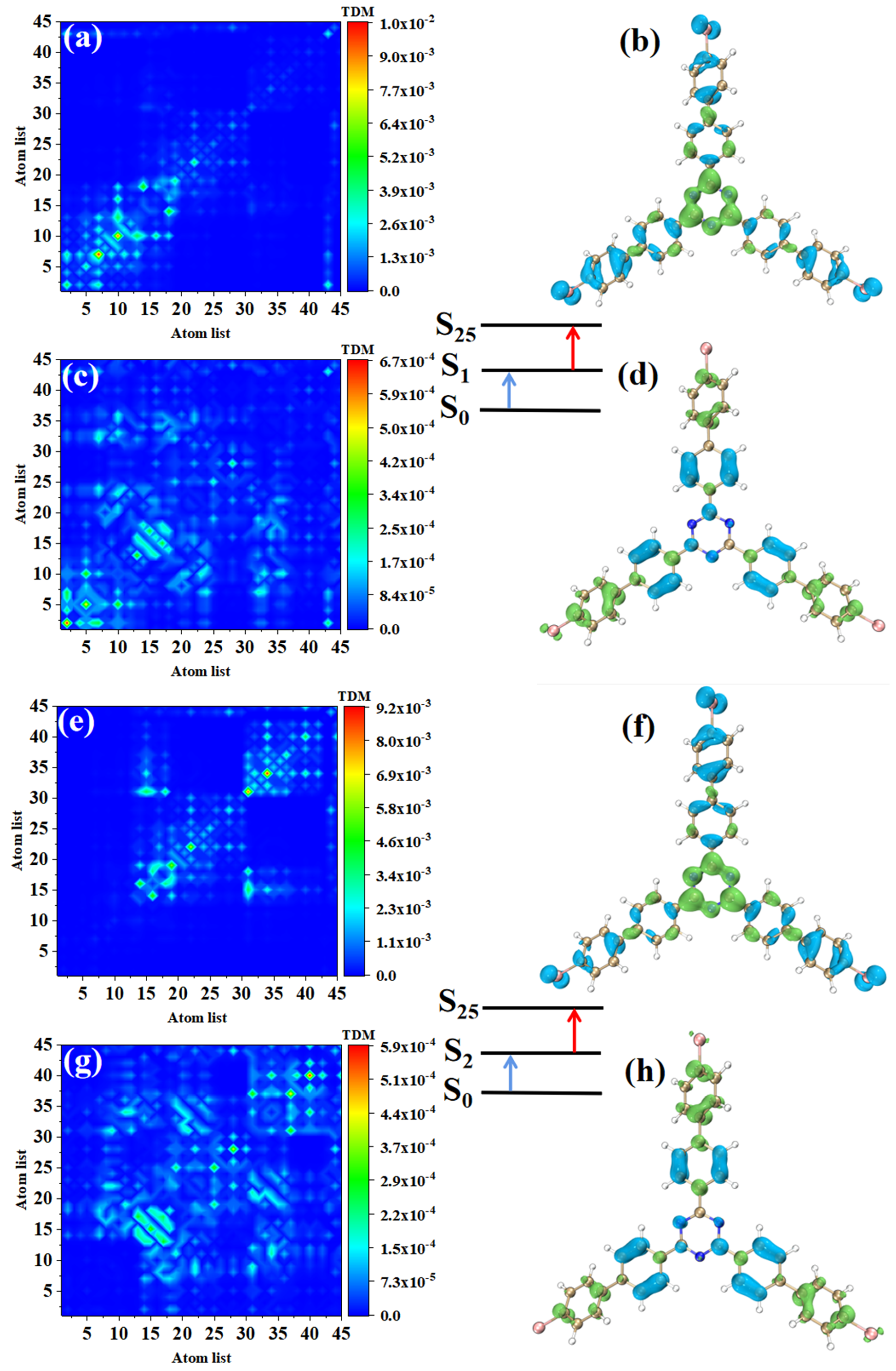
2.3. Transition Density Matrix (TDM) and Electron Hole Pair Density
3. Discussion
3.1. OPA Spectrum and TPA Spectrum
3.2. Electron Excitation Characteristics of OPA
3.3. Electron Excitation Characteristics of TPA
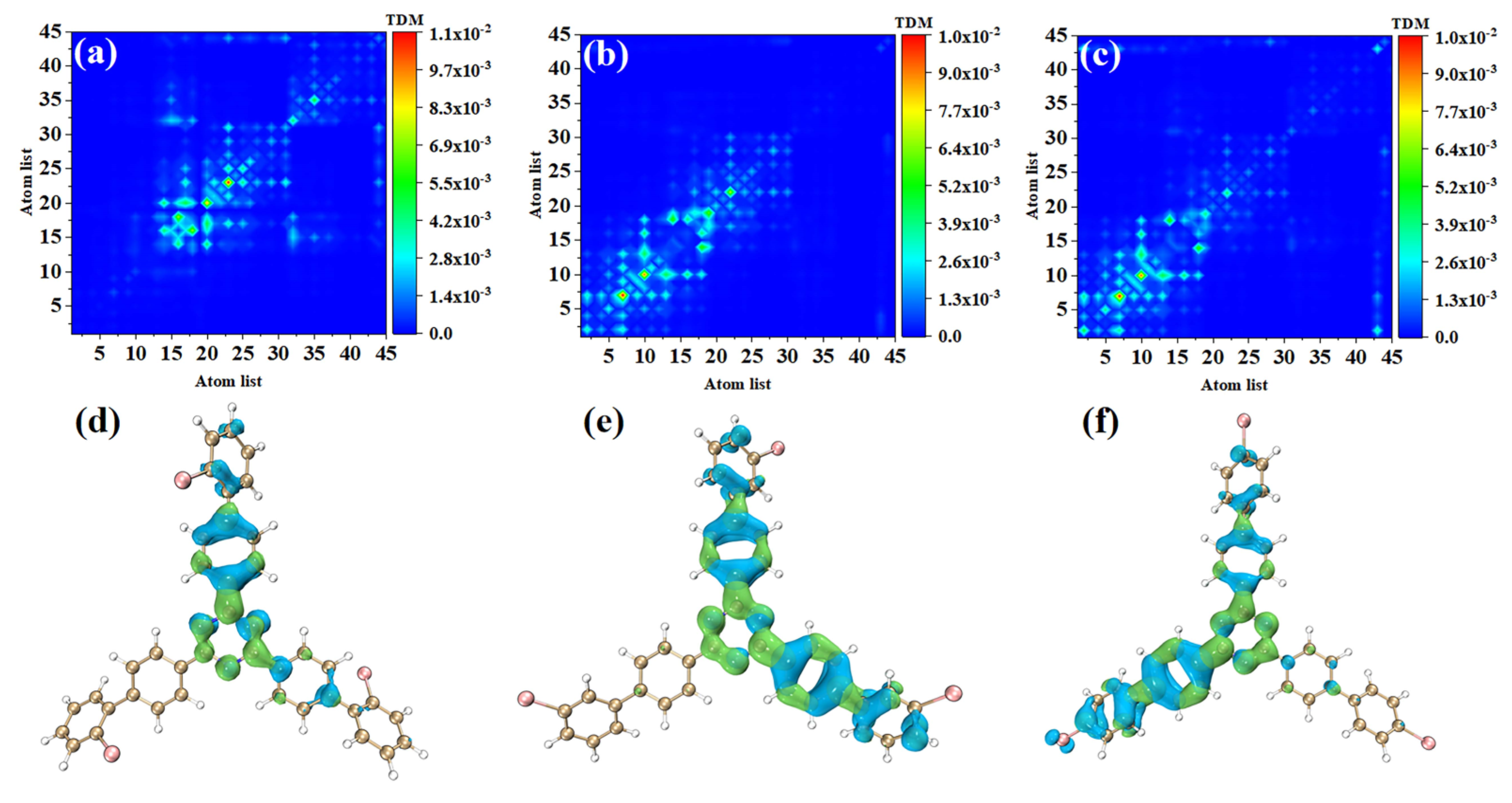
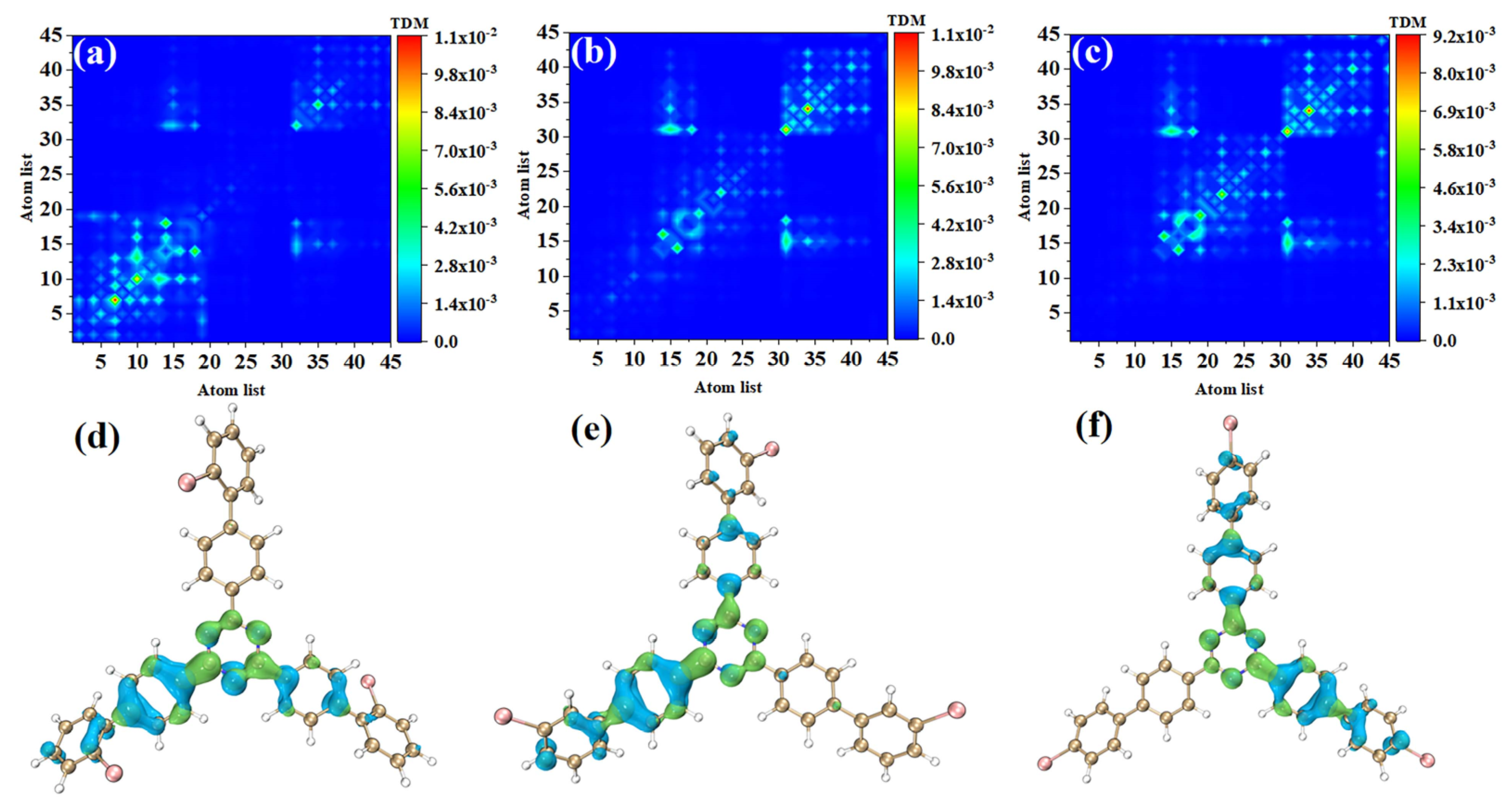
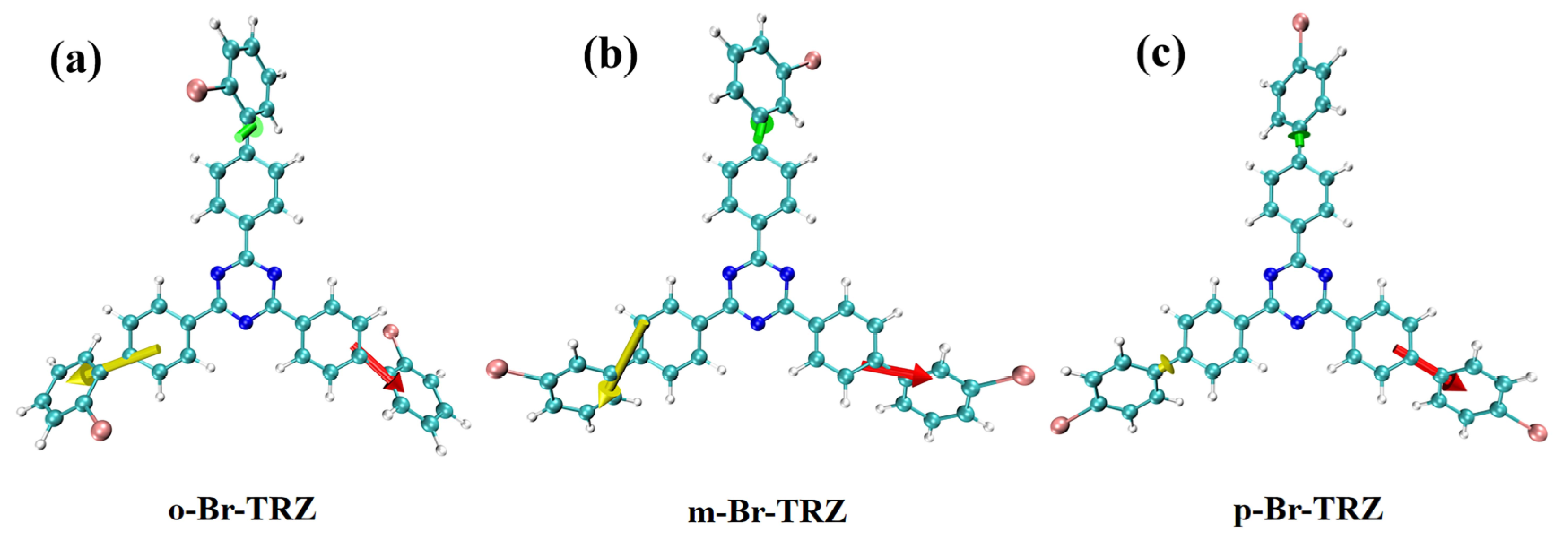
3.4. Transition Dipole Moment Analysis of Molecular Fragments
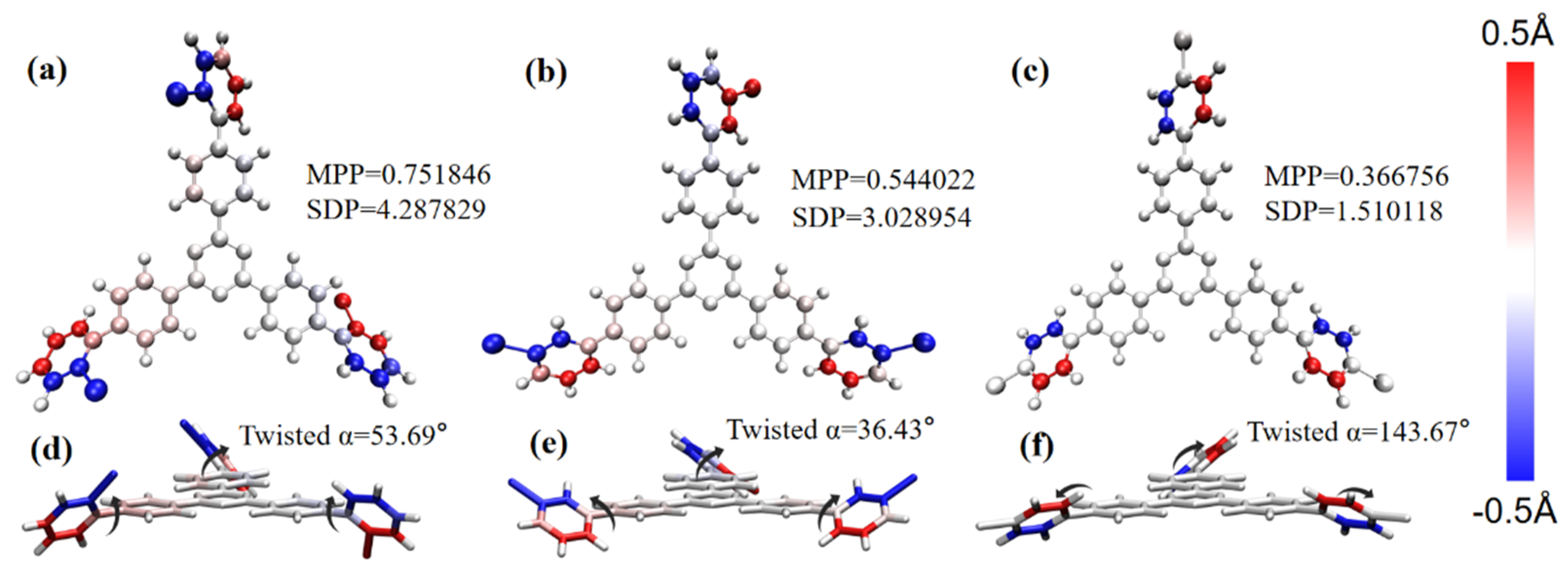
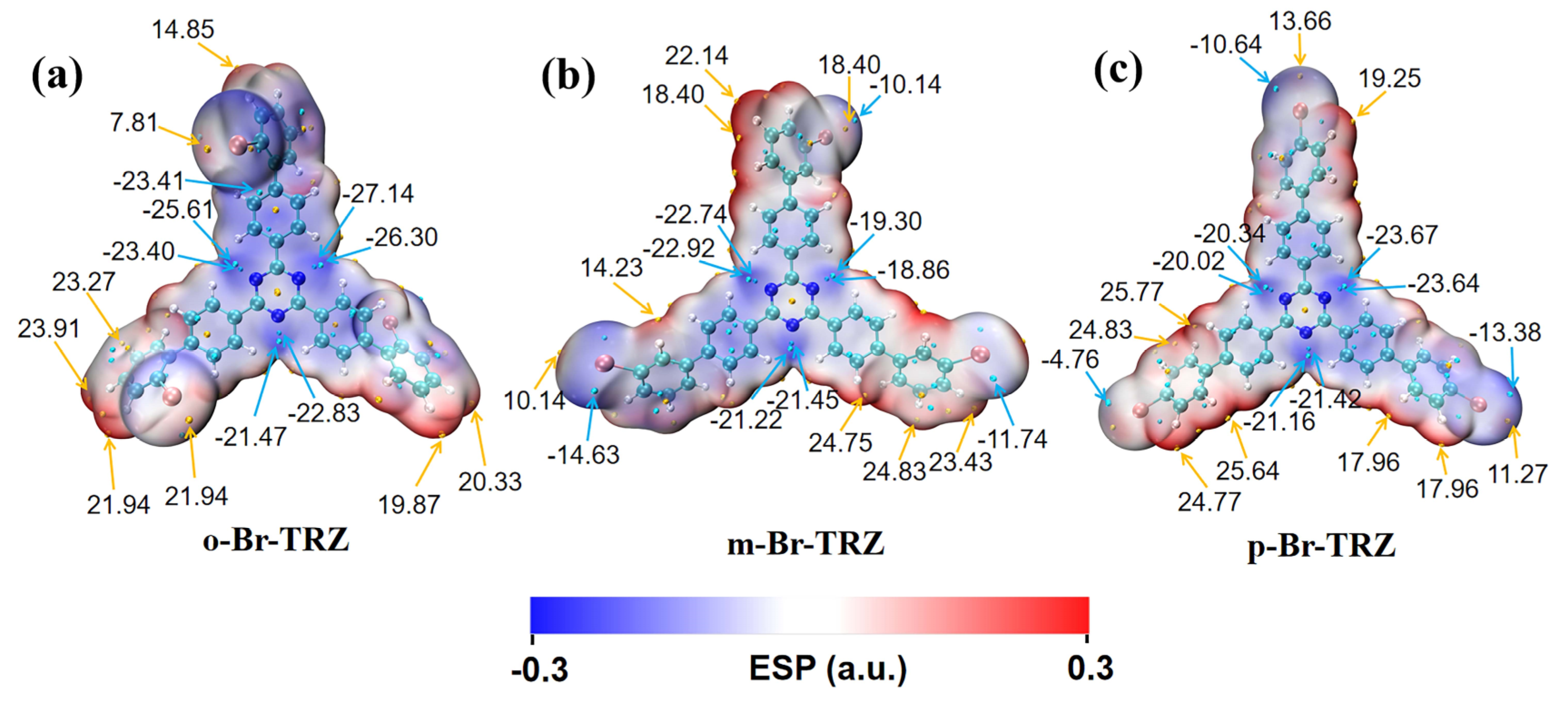
3.5. Electrostatic Potential Analysis of Molecular Surface
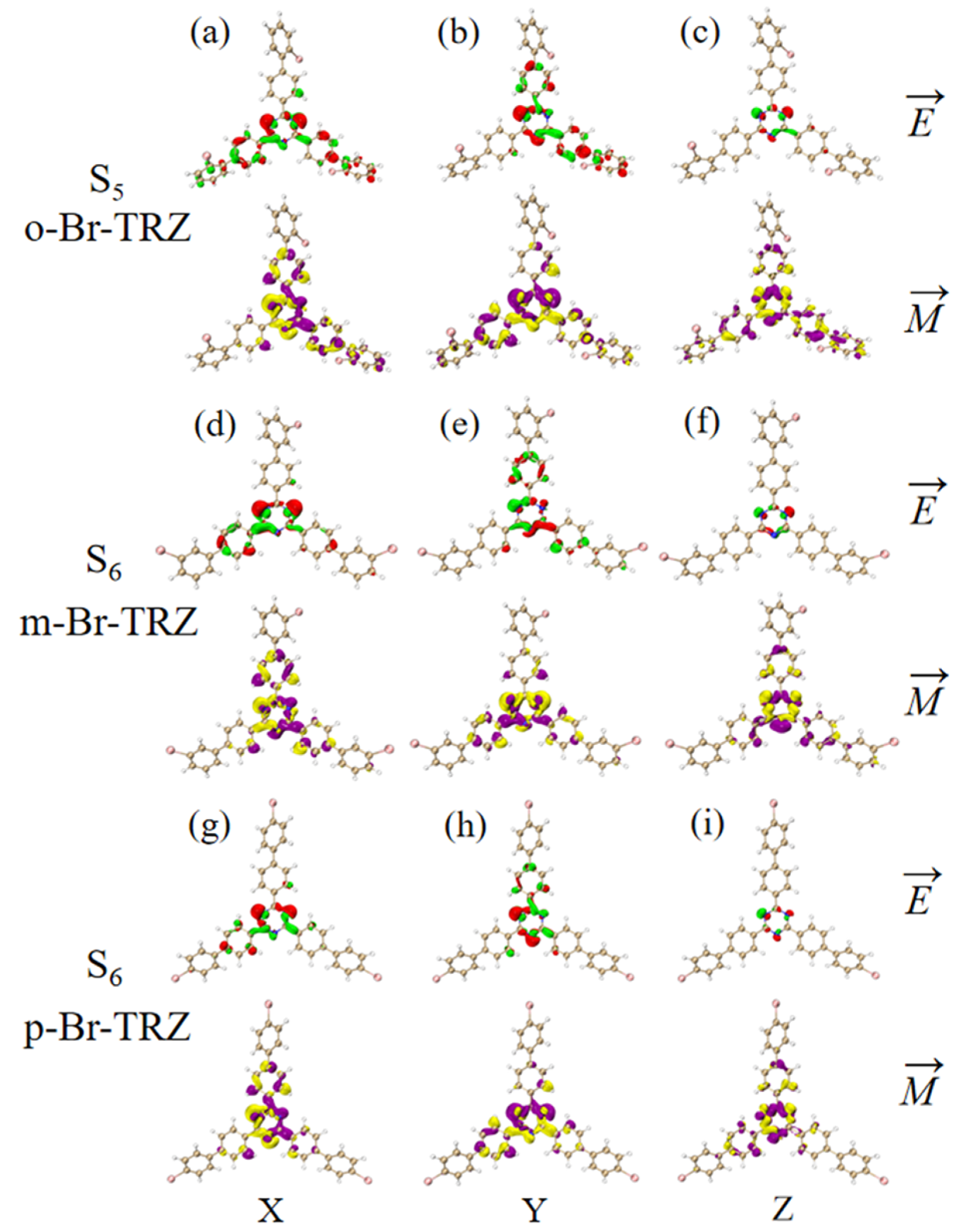
3.6. Electronic Circular Dichroism Spectra and Chiral Electromagnetic Interaction
4. Calculation Details
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Agrawal, G.P. Nonlinear fiber optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin/Heidelberg, Germany, 2000; pp. 195–211. [Google Scholar]
- Medishetty, R.; Zaręba, J.K.; Mayer, D.; Samoc, M.; Fischer, R.A. Nonlinear optical properties, upconversion and lasing in metal–organic frameworks. Chem. Soc. Rev. 2017, 46, 4976–5004. [Google Scholar] [CrossRef]
- Chai, Z.; Hu, X.; Wang, F.H.; Niu, X.X.; Xie, J.Y.; Gong, Q.H. Ultrafast all-optical switching. Adv. Opt. Mater. 2017, 5, 1600665. [Google Scholar] [CrossRef]
- Tripathi, S.K.; Kaur, R.; Kaur, J.; Sharma, M. Third-order nonlinear optical response of Ag–CdSe/PVA hybrid nanocomposite. Appl. Phys. A 2015, 120, 1047–1057. [Google Scholar] [CrossRef]
- Jeyaram, S.; Geethakrishnan, T. Third-order nonlinear optical properties of acid green 25 dye by Z-scan method. Opt. Laser Technol. 2017, 89, 179–185. [Google Scholar] [CrossRef]
- Petrosyan, A.M. Salts of l-histidine as nonlinear optical materials: A review. J. Cryst. Phys. Chem. 2010, 1, 33–56. [Google Scholar]
- Drobizhev, M.; Makarov, N.S.; Tillo, S.E.; Hughes, T.E.; Rebane, A. Two-photon absorption properties of fluorescent proteins. Nat. Methods 2011, 8, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Pawlicki, M.; Collins, H.A.; Denning, R.G.; Anderson, A.L. Two-photon absorption and the design of two-photon dyes. Angew. Chem. Int. Ed. 2009, 18, 3244–3266. [Google Scholar] [CrossRef]
- Dudek, M.; Tarnowicz-Staniak, N.; Deiana, M.; Poktadek, Z.; Samoc, M.; Matczyszyn, K. Two-photon absorption and two-photon-induced isomerization of azobenzene compounds. RSC Adv. 2020, 66, 40489–40507. [Google Scholar] [CrossRef]
- Yao, S.; Belfield, K.D. Two-photon fluorescent probes for bioimaging. Eur. J. Org. Chem. 2012, 17, 3199–3217. [Google Scholar] [CrossRef]
- Shen, Y.; Shuhendler, A.J.; Ye, D.; Xue, J.J.; Chen, H.Y. Two-photon excitation nanoparticles for photodynamic therapy. Chem. Soc. Rev. 2016, 24, 6725–6741. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Wang, B.; Yang, J.B.; He, N.N.; Qian, S.X.; Hua, J.L. Synthesis, Two-Photon Absorption and Optical Limiting Properties of Multi-branched Styryl Derivatives Based on 1,3,5-Triazine. Chem. Asian J. 2011, 1, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Mutoh, K.; Nakagawa, Y.; Sakamoto, A.; Kobayashi, Y.; Abe, J. Stepwise two-photon-gated photochemical reaction in photochromic [2.2] paracyclophane-bridged bis (imidazole dimer). J. Am. Chem. Soc. 2015, 17, 5674–5677. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.K.; Narayan, R.J. Two-photon polymerization for biological applications. Mater. Today 2017, 6, 314–322. [Google Scholar] [CrossRef]
- Albota, M.; Beljonne, D.; Brédas, J.L.; Ehrlich, J.E.; Fu, J.Y.; Heikal, A.A.; Hess, H.E.; Kogej, T.; Levin, M.D.; Marder, S.R.; et al. Design of organic molecules with large two-photon absorption cross-sections. Science 1998, 281, 1653–1656. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Shu, M.; Hu, J.; Zhu, S.Q.; Shi, H.; Zhu, H.J. Star-shaped D-π-A compounds with a 1,3,5-triazine core and N-aryl chromophore substituted fluorene arms: Synthesis, aggregation induced emission and two-photon absorption. Dye. Pigment. 2017, 137, 174–181. [Google Scholar] [CrossRef]
- Wanninger, S.; Lorenz, V.; Subhan, A.; Frank, T.E. Metal complexes of curcumin–synthetic strategies, structures and medicinal applications. Chem. Soc. Rev. 2015, 15, 4986–5002. [Google Scholar] [CrossRef]
- Zhou, H.; Zheng, Z.; Xu, G.; Yu, Z.P.; Yang, X.F.; Cheng, L.H.; Tian, X.H.; Kong, L.; Tian, Y.P. 1,3,5-Triazine-cored derivatives dyes containing triphenylamine based two-photon absorption: Synthesis, optical characterization and bioimaging. Dye. Pigment. 2012, 3, 570–582. [Google Scholar] [CrossRef]
- Li, Y.F.; Xie, X.; Gong, X.J.; Liu, M.L.; Chen, R.F.; Gao, D.Q.; Huang, W. Two bipolar blue-emitting fluorescent materials based on 1,3,5-triazine and peripheral pyrene for organic light-emitting diodes. Dye. Pigment. 2017, 145, 43–53. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Y.; Wang, Y.; Wang, G.Q.; Liu, D.J.; Hua, J.L. Ultrafast responses of multi-branched compounds based on 1,3,5-triazine: Investigation of the reason for enhanced two-photon absorption property. Appl. Phys. A 2017, 123, 516. [Google Scholar] [CrossRef]
- Tromayer, M.; Gruber, P.; Rosspeintner, A.; Ajami, A.; Husinsky, W.; Plasser, F.; Gonzalez, L.; Vauthey, E.; Ovsianikov, A.; Liska, R. Wavelength-optimized two-photon polymerization using initiators based on multipolar aminostyryl-1,3,5-triazines. Sci. Rep. 2018, 8, 17273. [Google Scholar] [CrossRef]
- Szlachcic, P.; Uchacz, T. Influence of fluorine on the photophysical, electrochemical properties and basicity of 1, 3-diphenylpyrazolo [3, 4-b] quinoline derivatives. J. Lumin. 2018, 194, 579–587. [Google Scholar] [CrossRef]
- Qiao, W.; Mu, X.; Zhou, Y.; Wang, J.G. Physical mechanism of the photoinduced charge transfer in multibranched compounds during one-and two-photon absorption. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 231, 118144. [Google Scholar] [CrossRef] [PubMed]
- Ohta, K.; Antonov, L.; Yamada, S. Theoretical study of the two-photon absorption properties of several asymmetrically substituted stilbenoid molecules. J. Chem. Phys. 2007, 127, 084504. [Google Scholar] [CrossRef] [PubMed]
- Zojer, E.; Buchacher, P.; Wudl, F.; Cornil, J.; Calbert, J.P.; Bredas, J.L.; Leising, G. Excited state localization in organic molecules consisting of conjugated and nonconjugated segments. J. Chem. Phys. 2000, 113, 10002–10012. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Chen, Q.X. An sp-hybridized all-carboatomic ring, cyclo [18] carbon: Bonding character, electron delocalization, and aromaticity. Carbon 2020, 165, 468–475. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Li, X. Gaussian 16, Revision A. 03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Warnke, I.; Furche, F. Circular dichroism: Electronic. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 150–166. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Physiol. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R. Adiabatic timedependent density functional methods for excited state properties. J. Chem. Phys. 2002, 117, 7433–7447. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAMB3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Mu, X.J.; Cai, K.S.; Wei, W.J.; Li, Y.E.; Wang, Z.; Wang, J.G. Dependence of UV–visible absorption characteristics on the migration distance and the hyperconjugation effect of a methine chain. J. Phys. Chem. C 2018, 122, 7831–7837. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Casida, M.E.; Salahub, D.R. Nuclear magnetic resonance shielding tensors calculated with a sum-over-states density functional perturbation theory. J. Am. Chem. Soc. 1994, 13, 5898–5908. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]



| Molecule | Excited States | Excited Energy (eV) | |||||
|---|---|---|---|---|---|---|---|
| o-Br-TRZ | S1 | 4.408 | 0.783 | 0.877 | −2.334 | 5.549 | −0.578 |
| S2 | 4.415 | 0.861 | 0.791 | −1.907 | 4.624 | −0.605 | |
| m-Br-TRZ | S1 | 4.288 | 0.913 | 0.796 | −1.535 | 4.902 | −0.597 |
| S2 | 4.293 | 0.866 | 0.798 | −2.834 | 4.911 | −0.641 | |
| p-Br-TRZ | S1 | 4.215 | 0.998 | 0.795 | −2.320 | 5.181 | −0.879 |
| S2 | 4.216 | 1.003 | 0.793 | −2.651 | 5.195 | −0.890 |
| Molecule | TPA States | Path | Transition Process | Integral Value (Debye) | TPA Cross-Section (GM) |
|---|---|---|---|---|---|
| o-Br-TRZ | S32 | S2 | 12.592 × 5.180 | 1.533 × 103 | |
| S1 | 12.213 × 4.223 | ||||
| m-Br-TRZ | S31 | S1 | 15.740 × 5.963 | 2.173 × 103 | |
| S2 | 16.296 × 2.967 | ||||
| p-Br-TRZ | S25 | S1 | 18.192 × 10.328 | 5.331 × 103 | |
| S2 | 18.223 × 10.283 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Shi, X.; Yang, F.; Zhang, X.; Dai, R.; Jia, Y.; Yan, N.; Li, S.; Wang, Z.; Liang, Z. Physical Mechanism of One-Photon Absorption, Two-Photon Absorption, and Electron Circular Dichroism of 1,3,5 Triazine Derivatives Based on Molecular Planarity. Molecules 2023, 28, 4700. https://doi.org/10.3390/molecules28124700
Chen X, Shi X, Yang F, Zhang X, Dai R, Jia Y, Yan N, Li S, Wang Z, Liang Z. Physical Mechanism of One-Photon Absorption, Two-Photon Absorption, and Electron Circular Dichroism of 1,3,5 Triazine Derivatives Based on Molecular Planarity. Molecules. 2023; 28(12):4700. https://doi.org/10.3390/molecules28124700
Chicago/Turabian StyleChen, Xiangtao, Xiaoyan Shi, Fuming Yang, Xiqing Zhang, Rui Dai, Yan Jia, Ningte Yan, Sixuan Li, Zihan Wang, and Zhongzhu Liang. 2023. "Physical Mechanism of One-Photon Absorption, Two-Photon Absorption, and Electron Circular Dichroism of 1,3,5 Triazine Derivatives Based on Molecular Planarity" Molecules 28, no. 12: 4700. https://doi.org/10.3390/molecules28124700
APA StyleChen, X., Shi, X., Yang, F., Zhang, X., Dai, R., Jia, Y., Yan, N., Li, S., Wang, Z., & Liang, Z. (2023). Physical Mechanism of One-Photon Absorption, Two-Photon Absorption, and Electron Circular Dichroism of 1,3,5 Triazine Derivatives Based on Molecular Planarity. Molecules, 28(12), 4700. https://doi.org/10.3390/molecules28124700








