Polymer Dynamics in Glycerol–Water Mixtures
Abstract
:1. Introduction
2. Results and Discussion
3. MGSE Method
4. Molecular Dynamics in Glycerol/Water Mixture
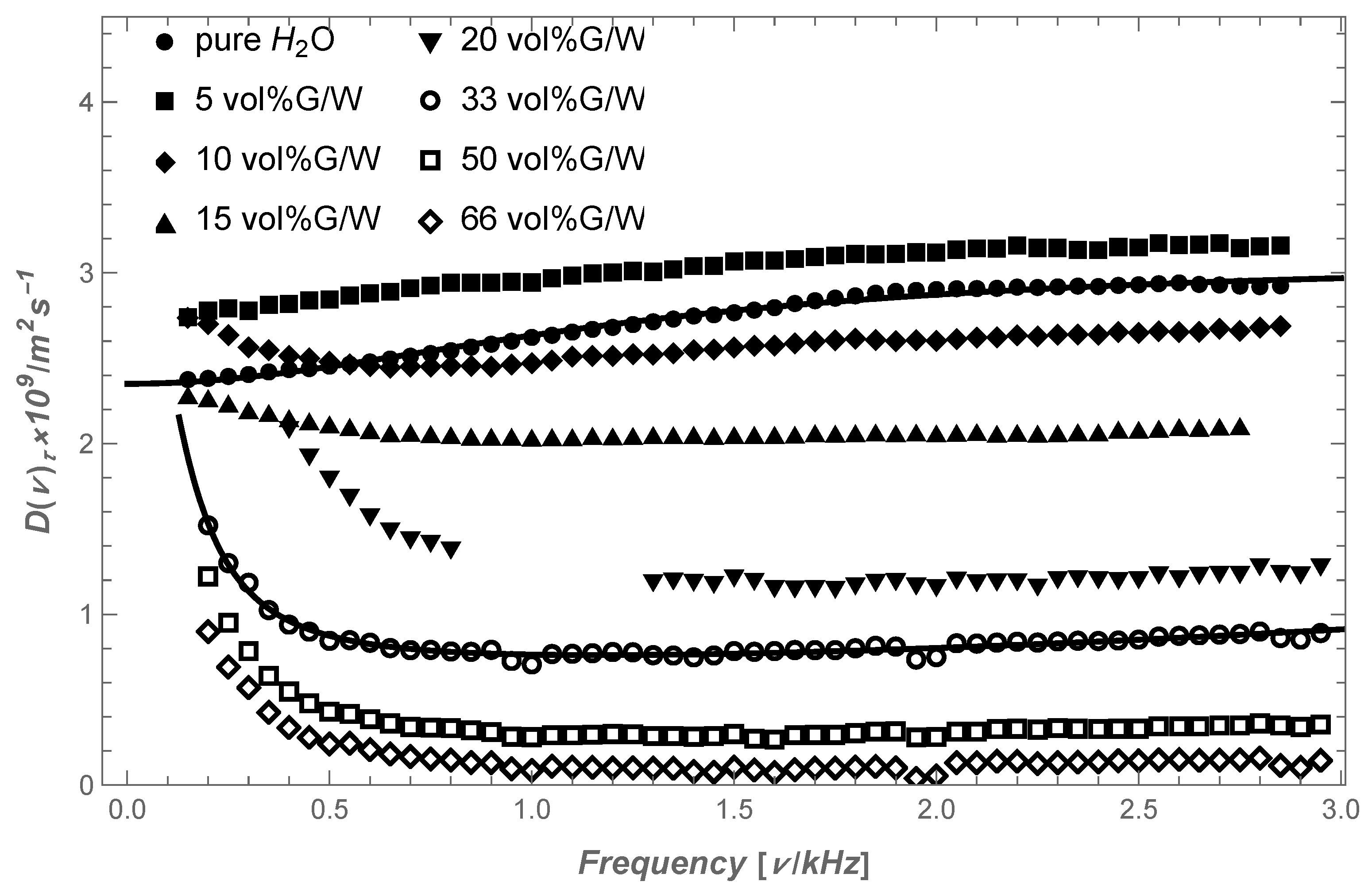
5. Dynamics of a Polymer in a Shear Rate Viscosity-Thickening Solvent
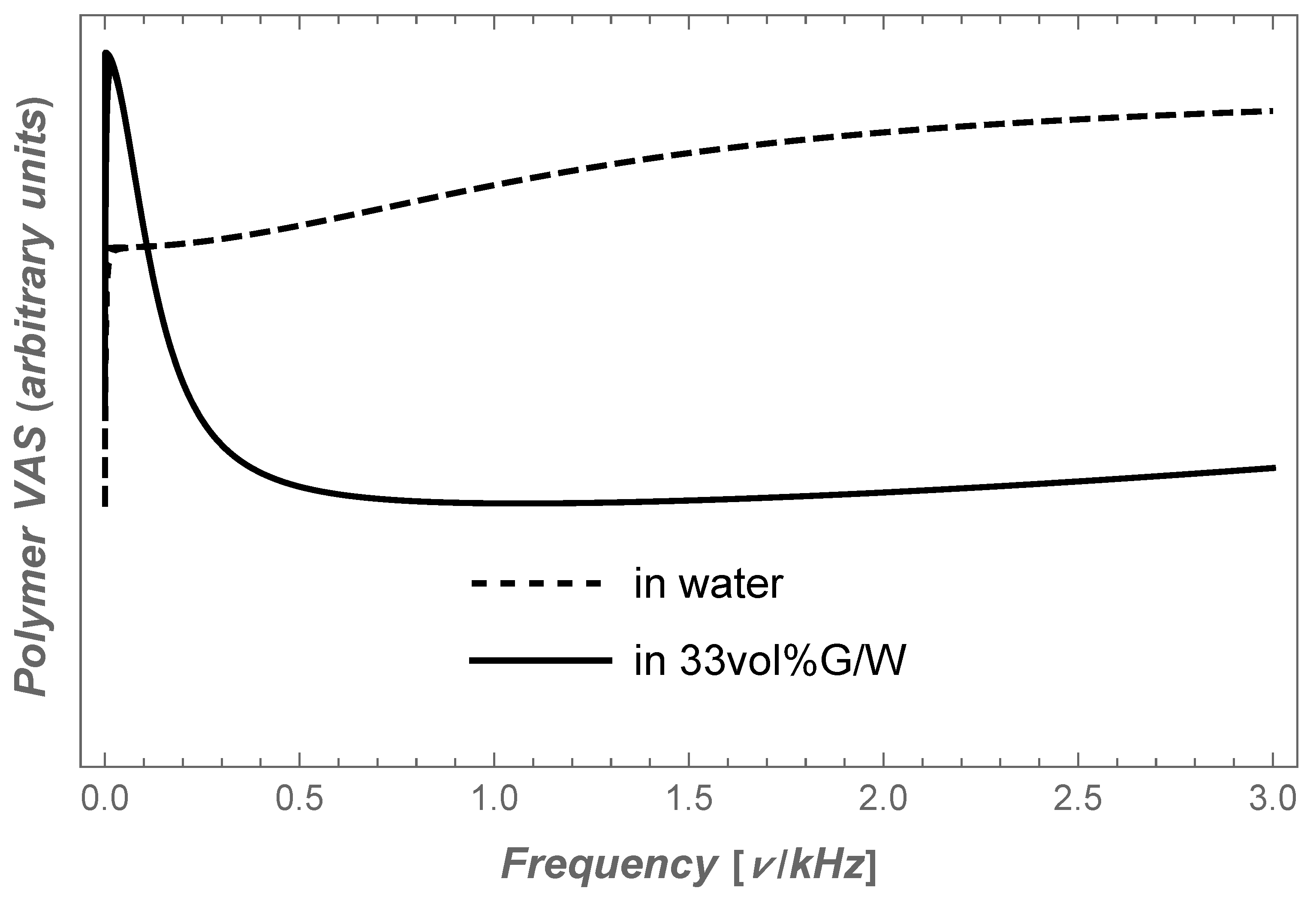
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- GhattyvenkataKrishnaa, P.K.; Carrib, G.A. Effect of glycerol–water binary mixtures on the structure and dynamics of protein solutions. J. Biomol. Struct. Dyn. 2014, 32, 424–437. [Google Scholar] [CrossRef]
- Marcus, Y. Some thermodynamic and structural aspects of mixtures of glycerol with water. Phys. Chem. Chem. Phys. 2000, 2, 4891–4896. [Google Scholar] [CrossRef]
- Hayashi, Y.; Puzenko, A.; Balin, I.; Ryabov, Y.E.; Feldman, Y.J. Relaxation Dynamics in Glycerol-Water Mixtures. 2. Mesoscopic Feature in Water Rich Mixtures. Phys. Chem. B 2005, 109, 9174–9177. [Google Scholar] [CrossRef]
- Puzenko, A.; Hayashi, Y.; Ryabov, Y.E.; Balin, I.; Feldman, Y.E.; Kaatze, U.; Behrends, R. Relaxation Dynamics in Glycerol-Water Mixtures: I. Glycerol-Rich Mixtures. Phys. Chem. B 2005, 109, 6031–6035. [Google Scholar] [CrossRef]
- Dashnau, J.L.; Nucci, N.V.; Sharp, K.A.; Vanderkooi, J.M. Hydrogen Bonding and the Cryoprotective Properties of Glycerol/Water Mixtures. J. Phys. Chem. B 2006, 110, 13670–13677. [Google Scholar] [CrossRef]
- Mendelovic, E.; Frost, L.R.; Kloprogge, T. Cryogenic Raman spectroscopy of glycerol. J. Raman Spectrosc. 2000, 31, 1121–1125. [Google Scholar] [CrossRef]
- Doess, A.; Paluch, M.; Sillescu, H.; Hinze, G. From Strong to Fragile Glass Formers: Secondary Relaxation in Polyalcohols. Phys. Rev. Lett. 2002, 88, 095701. [Google Scholar] [CrossRef]
- Mizuno, K.; Miyashita, Y.; Shindo, Y.; Ogawa, H. NMR and FT-IR Studies of Hydrogen Bonds in Ethanol-Water Mixtures. J. Phys. Chem. 1995, 99, 3225–3228. [Google Scholar] [CrossRef]
- D’Errico, G.; Ortona, O.; Capuano, F.; Vitagliano, V. Diffusion coefficients for the binary system glycerol + water at 25 °C. A velocity correlation study. J. Chem. Eng. Data 2004, 49, 1665–1670. [Google Scholar] [CrossRef]
- Waudby, C.A.; Launay, H.; Cabrita, L.D.; Christodoulou, J. Protein folding on the ribosome studied using NMR spectroscopy. Prog. NMR Spectrosc. 2013, 74, 57–75. [Google Scholar] [CrossRef] [Green Version]
- Zhuravleva, A.; Korzhnev, D.M. Protein folding by NMR. Prog. NMR Spectrosc. 2017, 100, 52–77. [Google Scholar] [CrossRef] [Green Version]
- Mills, R. Self-diffusion in Normal and Heavy Water in the Range 1–45°. J. Phys. Chem. 1973, 77, 685–688. [Google Scholar] [CrossRef]
- Nishijima, Y.; Oster, G. Diffusion in Glycerol-Water Mixture. Bull. Chem. Soc. Japan 1960, 33, 1649–1651. [Google Scholar] [CrossRef] [Green Version]
- Hahn, E.L. Spin-echoes. Phys. Rev. 1950, 80, 580–594. [Google Scholar] [CrossRef]
- Douglass, D.C. Self-diffusion and velocity correlation. J. Chem. Phys. 1961, 35, 81–90. [Google Scholar] [CrossRef]
- Callaghan, P.; Stepišnik, J. Advances in Magnetic and Optical Resonance; Chapter Generalised Analysis of Motion Using Magnetic Field Gradients; Warren, S., Ed.; Academic Press, Inc.: San Diego, CA, USA, 1996; Volume 19, pp. 326–389. [Google Scholar]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance. Phys. Rev. 1954, 94, 630–638. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Inst. 1958, 29, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Stepišnik, J. Analysis of NMR self-diffusion measurements by density matrix calculation. Phys. B 1981, 104, 350–364. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Non-equilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 1986. [Google Scholar]
- Chaikin, P.M.; Lubensky, T.C. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Požar, M.; Lovrinčevicč, B.; Zoranič, L.; Primorac, T.; Sokolič, F.; Perera, A. Micro-heterogeneity versus clustering in binary mixtures of ethanol with water or alkane. Phys. Chem. Chem. Phys. 2016, 18, 23971. [Google Scholar] [CrossRef] [Green Version]
- Fischer, H.E.; Barnes, A.C.; Salmon, P.S. Neutron and x-ray diffraction studies of liquids and glasses. Rep. Prog. Phys. 2006, 69, 233–299. [Google Scholar] [CrossRef]
- Chen, C.; Li, W.Z.; Song, Y.C.; Weng, L.D.; Zhang, N. Concentration dependence of water self-diffusion coefficients in dilute glycerol–water binary and glycerol–water–sodium chloride ternary solutions and the insights from hydrogen bonds. Mol. Phys. 2012, 110, 283–291. [Google Scholar] [CrossRef]
- Zimm, B.H. Dynamics of polymer molecules in dilute solution: Viscoelasticity, flow birefringence and dielectric loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Stepišnik, J.; Mattea, C.; Stapf, S.; Mohorič, A. Molecular velocity auto-correlations in glycerol/water mixtures studied by NMR MGSE method. Phys. A 2020, 553, 124171. [Google Scholar] [CrossRef]
- Stepišnik, J.; Mattea, C.; Stapf, S.; Mohorič, A. Molecular velocity auto-correlation of simple liquids observed by NMR MGSE method. Eur. Phys. J. B 2018, 91, 293. [Google Scholar] [CrossRef]
- Stepišnik, J.; Callaghan, P. The long time-tail of molecular velocity correlation in a confined fluid: Observation by modulated gradient spin echo NMR. Phys. B 2000, 292, 296–301. [Google Scholar] [CrossRef]
- Callaghan, P.T.; Codd, S.L. Flow coherence in a bead pack observed using frequency domain modulated gradient nuclear magnetic resonance. Phys. Fluids 2001, 13, 421–426. [Google Scholar] [CrossRef]
- Topgaard, D.; Malmborg, C.; Soederman, O. Restricted Self-Diffusion of Water in a Highly Concentrated W/O Emulsion Studied Using Modulated Gradient Spin-Echo NMR. J. Mag. Res. 2002, 156, 195–201. [Google Scholar] [CrossRef]
- Stepišnik, J.; Mohorič, A.; Mattea, C.; Stapf, S.; Serša, I. Velocity autocorrelation spectra in molten polymer measured by NMR modulated gradient spin-echo. EuroPhys. Lett. 2014, 106, 27007. [Google Scholar] [CrossRef]
- Alder, B.; Wainwright, T. Decay of the velocity autocorrelation function. Phys. Rev. A 1970, 1, 18–21. [Google Scholar] [CrossRef]
- Wang, M.C.; Ornstein, L.C. On the theory of the Brownian motion II. Rev. Mod. Phys. 1945, 17, 323–342. [Google Scholar] [CrossRef]
- Stanley, H.; Kumar, P.; Xu, L.; Yan, Z.; Mazza, M.; Buldyrev, S.; Chen, S.H.; Mallamace, F. The puzzling unsolved mysteries of liquid water: Some recent progress. Phys. A 2007, 386, 729–743. [Google Scholar] [CrossRef] [Green Version]
- Vnales, A.D.; Desposito, M.A. Anomalous diffusion: Exact solution of the generalized Langevin equation for harmonically bounded particle. Phys. Rev. E 2006, 73, 016111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Fluessigkeiten suspendierten Teilchen. Ann. Der Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- von Smoluchowski, M. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Ann. Der Phys. 1906, 326, 756–780. [Google Scholar] [CrossRef] [Green Version]
- Gadre, S.R.; Yeole, S.D.; Sahu, N. Quantum chemical investigations on molecular clusters. Chem. Rev. 2014, 114, 12132–12173. [Google Scholar] [CrossRef]
- Guo, J.H.; Luo, Y.; Augustsson, A.; Kashtanov, S.; Rubensson, J.; Shuh, D.K.; Agren, H.; Nordgren, J. Molecular structure of alcohol-water mixtures. Phys. Rev. Lett. 2003, 91, 157401. [Google Scholar] [CrossRef]
- Vaitheeswaran, S.; Yin, H.; Rasaiah, J.C.; Humme, G. Water clusters in nonpolar cavities. Proc. Natl. Acad. Sci. USA 2004, 101, 17002–17005. [Google Scholar] [CrossRef]
- Saykally, R.J.; Blake, G.A. Molecular interactions and hydrogen bond tunneling dynamics: Some new perspectives. Science 1993, 259, 1570–1575. [Google Scholar] [CrossRef]
- Jensen, M.H.; Gainaru, C.; Alba-Simionesco, C.; Hecksher, T.; Niss, K. Slow rheological mode in glycerol and glycerol-water mixtures. Phys. Chem. Chem. Phys. 2018, 20, 1716–1723. [Google Scholar] [CrossRef] [Green Version]
- Cheng, N.S. Formula for the Viscosity of a Glycerol-Water Mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, S.; Vasi, C.; Stanley, H.E. Some considerations on the transport properties of water-glycerol suspensions. J. Chem. Phys. 2016, 144, 014501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mori, H. Transport, collective Motion, and Brownian motion. Prog.Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef] [Green Version]
- Mason, T. Estimating the viscoelastic moduli of complex fluids using generalized Stokes-Einstein equation. Rheol. Acta 2000, 39, 371–378. [Google Scholar] [CrossRef]
- Cheng, R.R.; Hawk, A.T.; Makarov, D.E. Exploring the role of internal friction in the dynamics of unfolded proteins using simple polymer models. J. Chem. Phys. 2013, 138, 074112. [Google Scholar] [CrossRef] [PubMed]
- Rouse, P. A theory of the linear viscoelastic properties of dilute solutions of coiling polymer. J. Chem. Phys. 1953, 21, 1272–1279. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer system. J. Chem. Soc. Faraday Trans. 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R. Self-consistent theory of polydisperse entangled polymers: Linear viscoelasticity of binary blends. J. Chem. Phys. 1988, 89, 5291. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef] [Green Version]
- Perez-Aparicio, R.; Colmenero, J.; Alvarez, F.; Padding, J.T.; Briels, W.J. Chain dynamics of poly(ethylene-alt-propylene) melts by means of coarse-grained simulations based on atomistic molecular dynamics. J. Chem. Phys. 2010, 132, 0249045. [Google Scholar] [CrossRef]
- Stepišnik, J.; Mohorič, A.; Serša, I.; Lahajnar, G. Analysis of Polymer Dynamics by NMR Modulated Gradient Spin Echo. Macromol. Symp. 2011, 305, 55–62. [Google Scholar]
- Hagen, S.J. Solvent viscosity and friction in protein folding dynamics. Curr. Protein Pept. Sci. 2010, 11, 385–395. [Google Scholar] [CrossRef] [PubMed]
- Jacob, M.; Schindler, T.; Balbach, J.; Schmid, F.X. Diffusion control in an elementary protein folding reaction. Proc. Natl. Acad. Sci. USA 1997, 94, 5622–5627. [Google Scholar] [CrossRef] [PubMed]
- Gregory, R.B. The influence of glycerol on hydrogen isotope exchange in lysozyme. Biopolymers 1988, 27, 1699–1709. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zocchi, G. Viscoelastic Transition and Yield Strain of the Folded Protein. PLoS ONE 2011, 6, e28097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepišnik, J. Polymer Dynamics in Glycerol–Water Mixtures. Molecules 2023, 28, 5506. https://doi.org/10.3390/molecules28145506
Stepišnik J. Polymer Dynamics in Glycerol–Water Mixtures. Molecules. 2023; 28(14):5506. https://doi.org/10.3390/molecules28145506
Chicago/Turabian StyleStepišnik, Janez. 2023. "Polymer Dynamics in Glycerol–Water Mixtures" Molecules 28, no. 14: 5506. https://doi.org/10.3390/molecules28145506
APA StyleStepišnik, J. (2023). Polymer Dynamics in Glycerol–Water Mixtures. Molecules, 28(14), 5506. https://doi.org/10.3390/molecules28145506





