Development of Tailored Graphene Nanoparticles: Preparation, Sorting and Structure Assessment by Complementary Techniques
Abstract
:1. Introduction
2. Results and Discussion
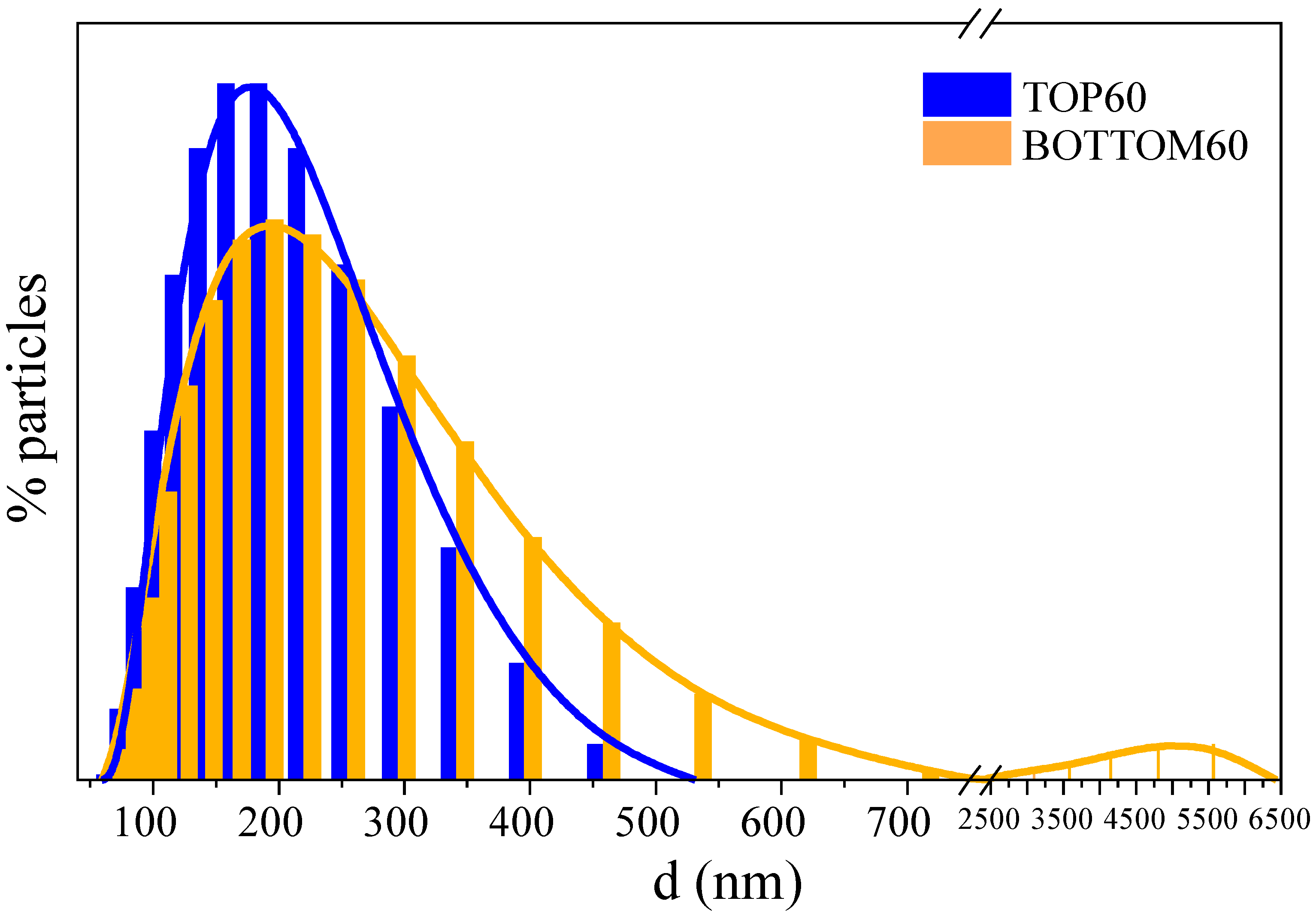
2.1. GNPs Size Distribution by DLS
- (a)
- In the case of isolated, thin GNPs floating in water, the aspect ratio of the individual layers of nanoparticles is high, so the “equivalent” sphere model cannot capture the right average size.
- (b)
- Graphene nanoparticles are hydrophobic and can form small clusters in water. For this reason, the estimated average diameter of the particles also takes into account the presence of clusters containing a few GNPs. Since the water dispersion is very stable, especially in the case of TOP60 GNPs, these clusters, if present, are small; namely, they do not reach the critical size for precipitation.
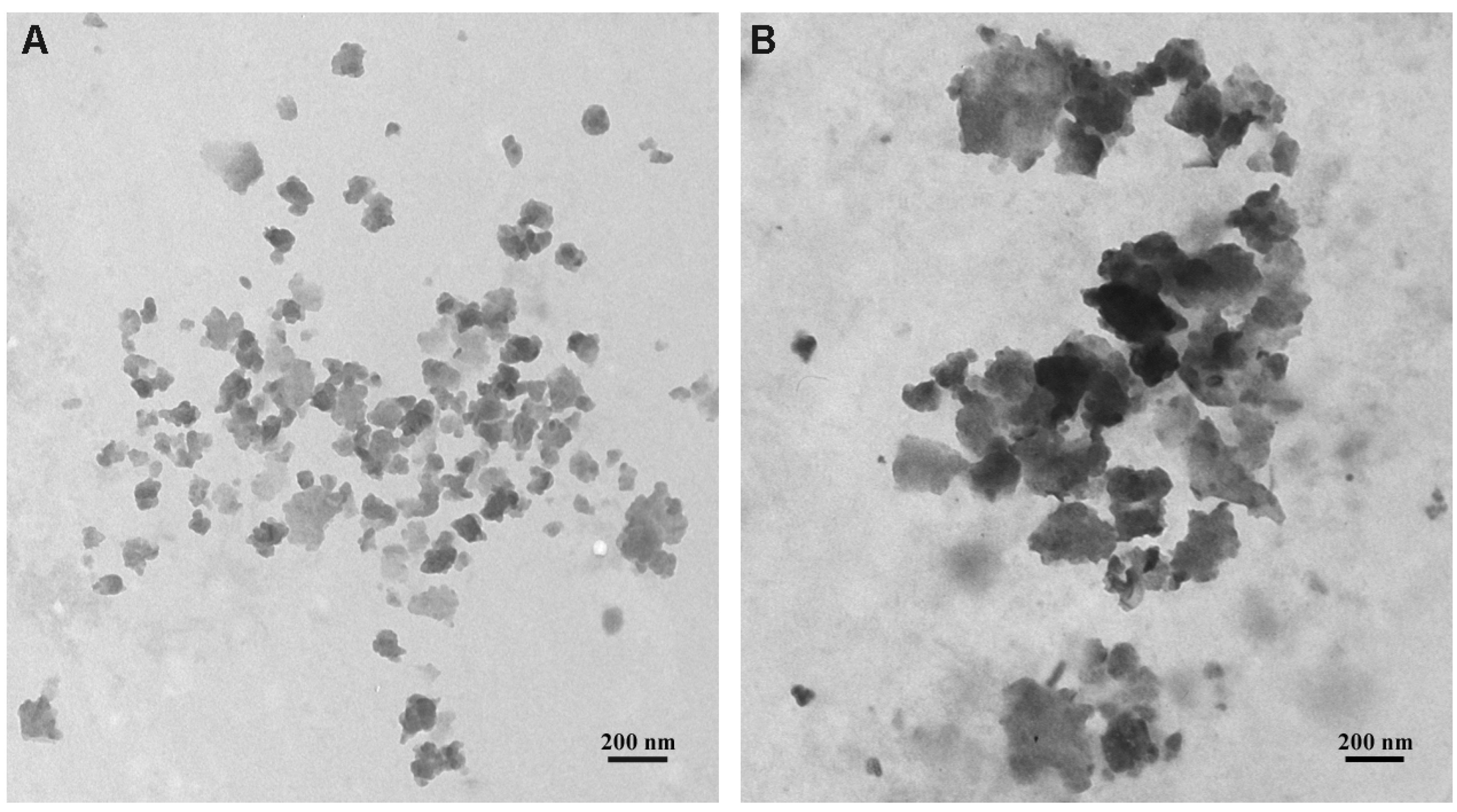
2.2. GNPs Size from TEM Images
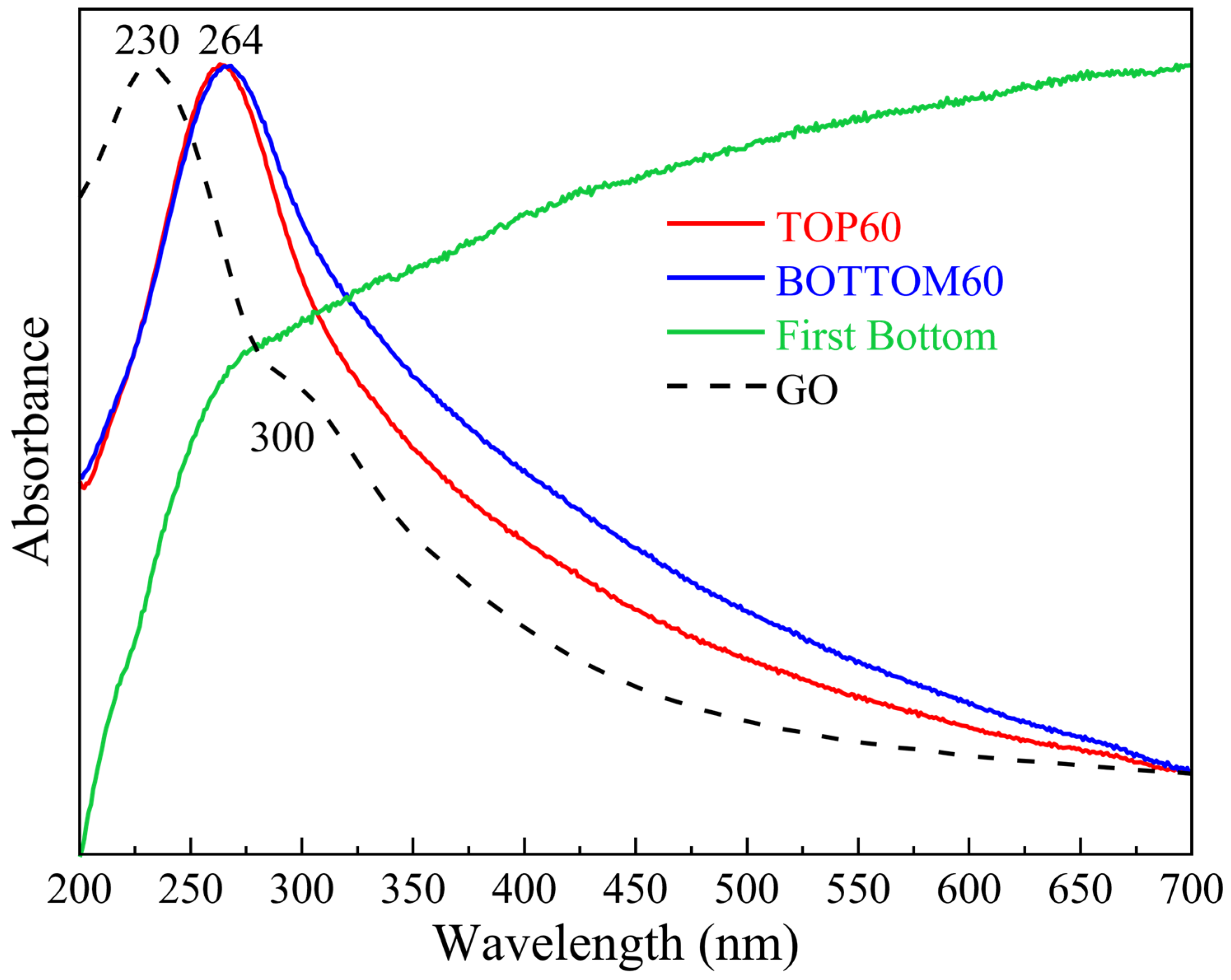
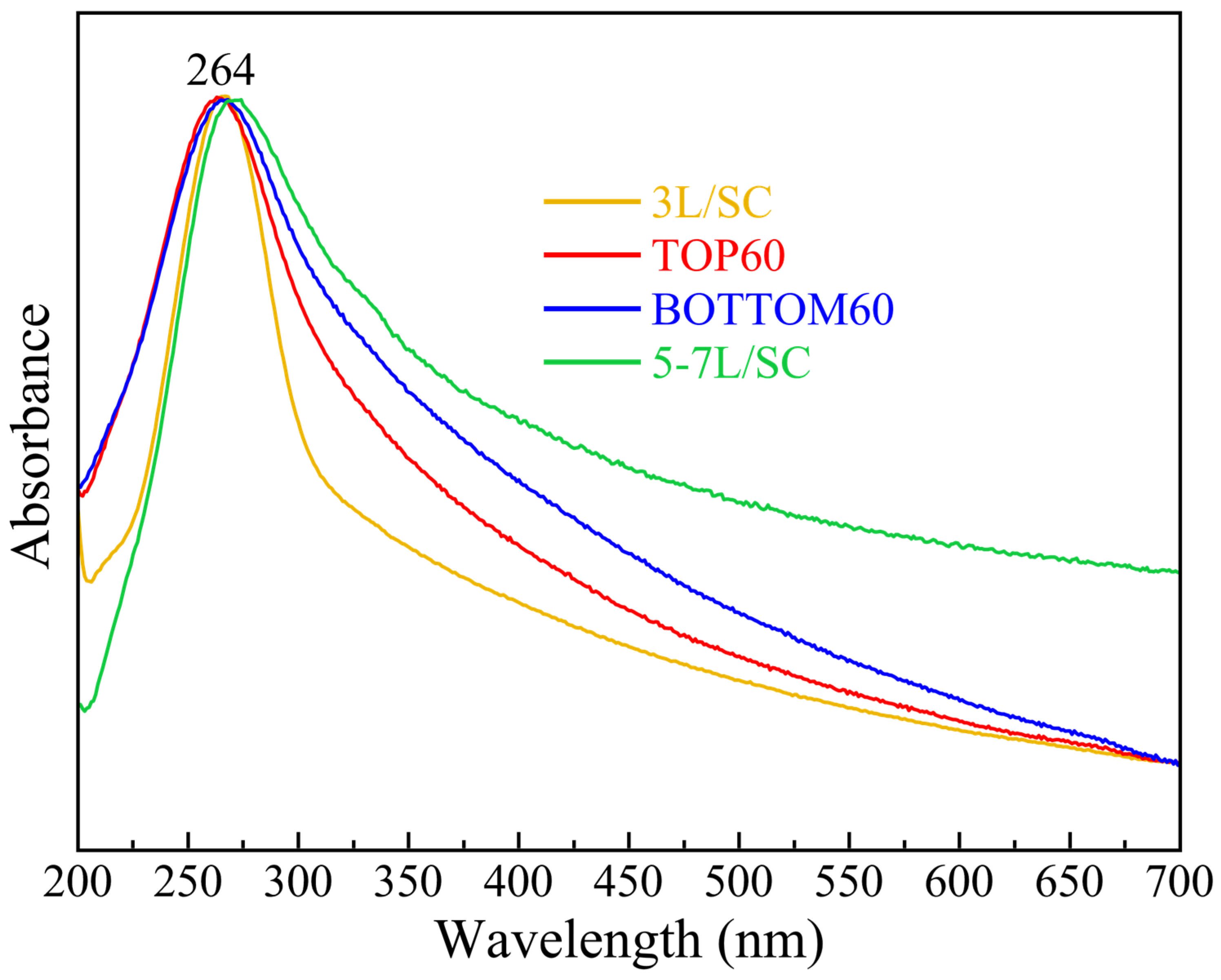
2.3. UV-Vis Extinction Spectra of GNPs
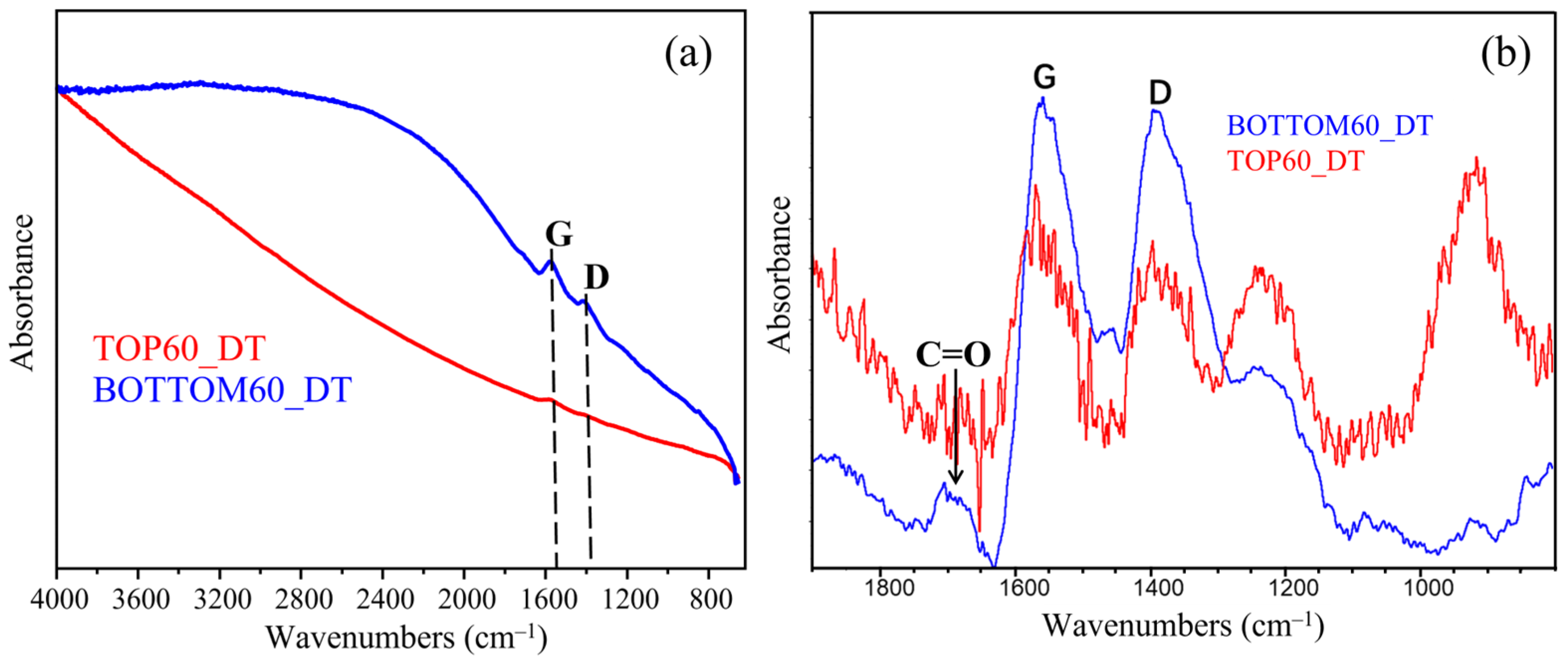
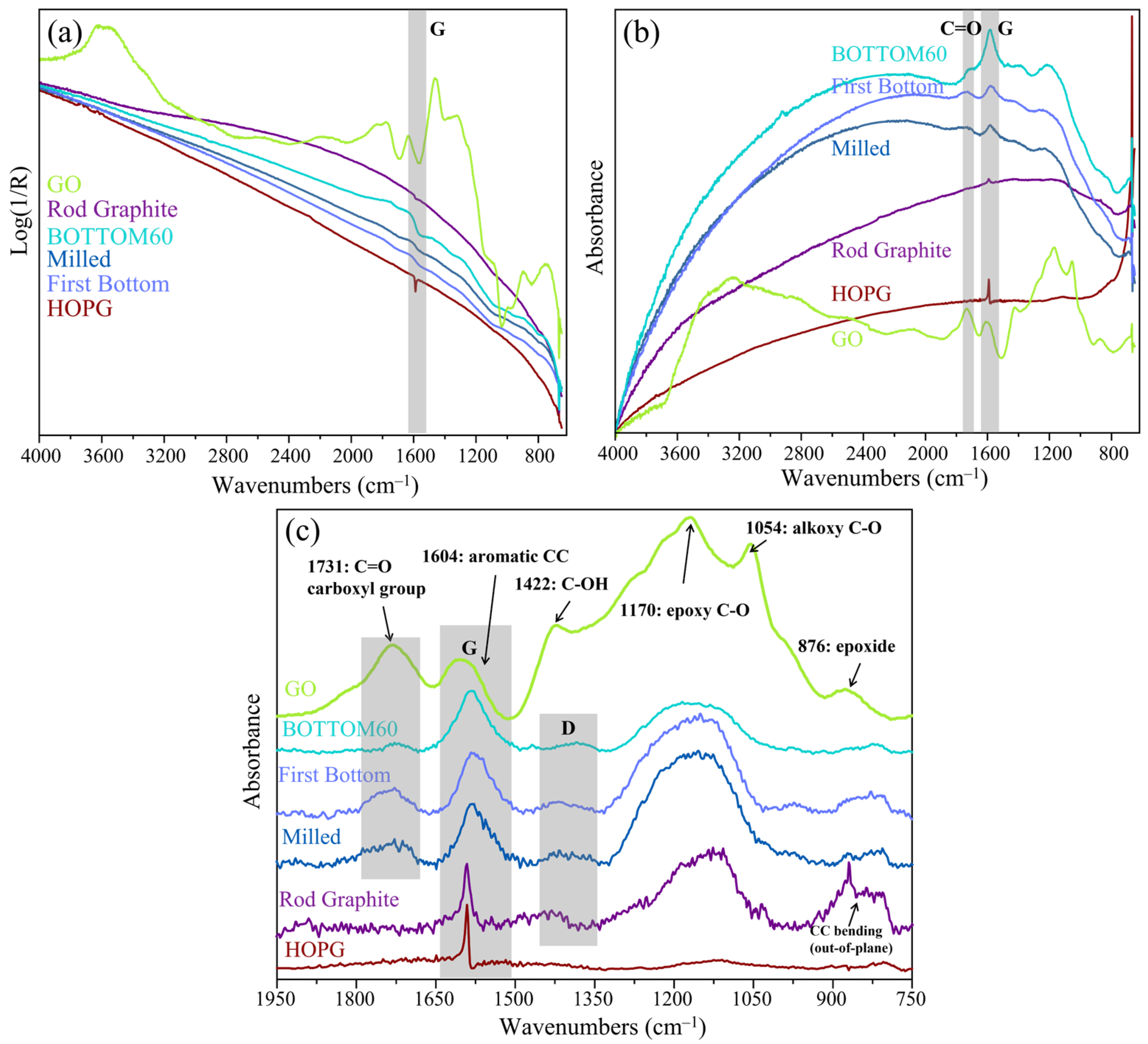
2.4. Infrared Absorption Spectra of GNPs
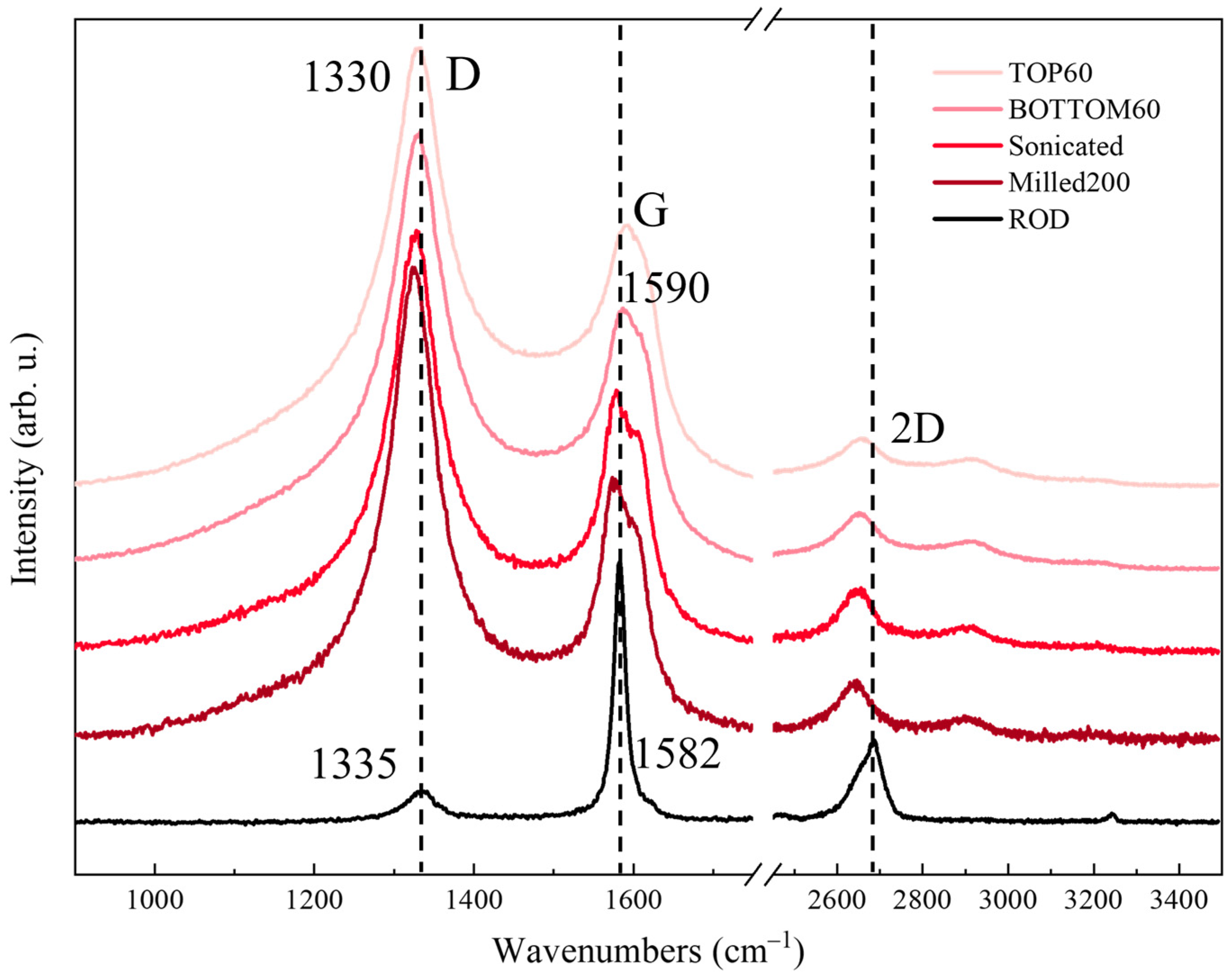
2.5. Raman Spectra of Graphene-Based Nanoparticles (GNPs)
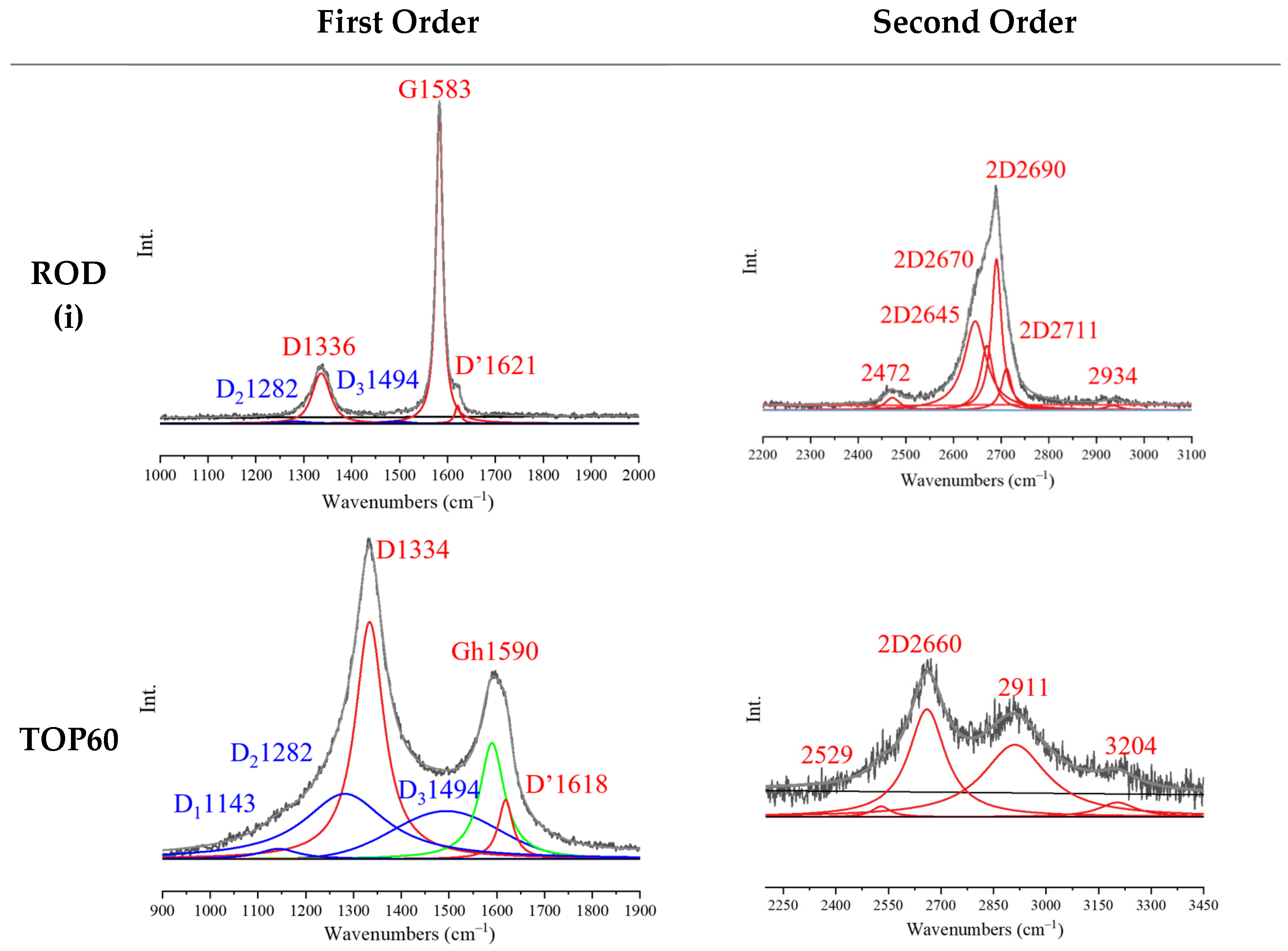
2.5.1. Raman Spectra of Graphite/Graphene and GNPs: General Features and Theoretical Background
2.5.2. Raman Spectra of Commercial 3L GNPs
2.5.3. Raman Spectra of TOP60 and BOTTOM60
- (a)
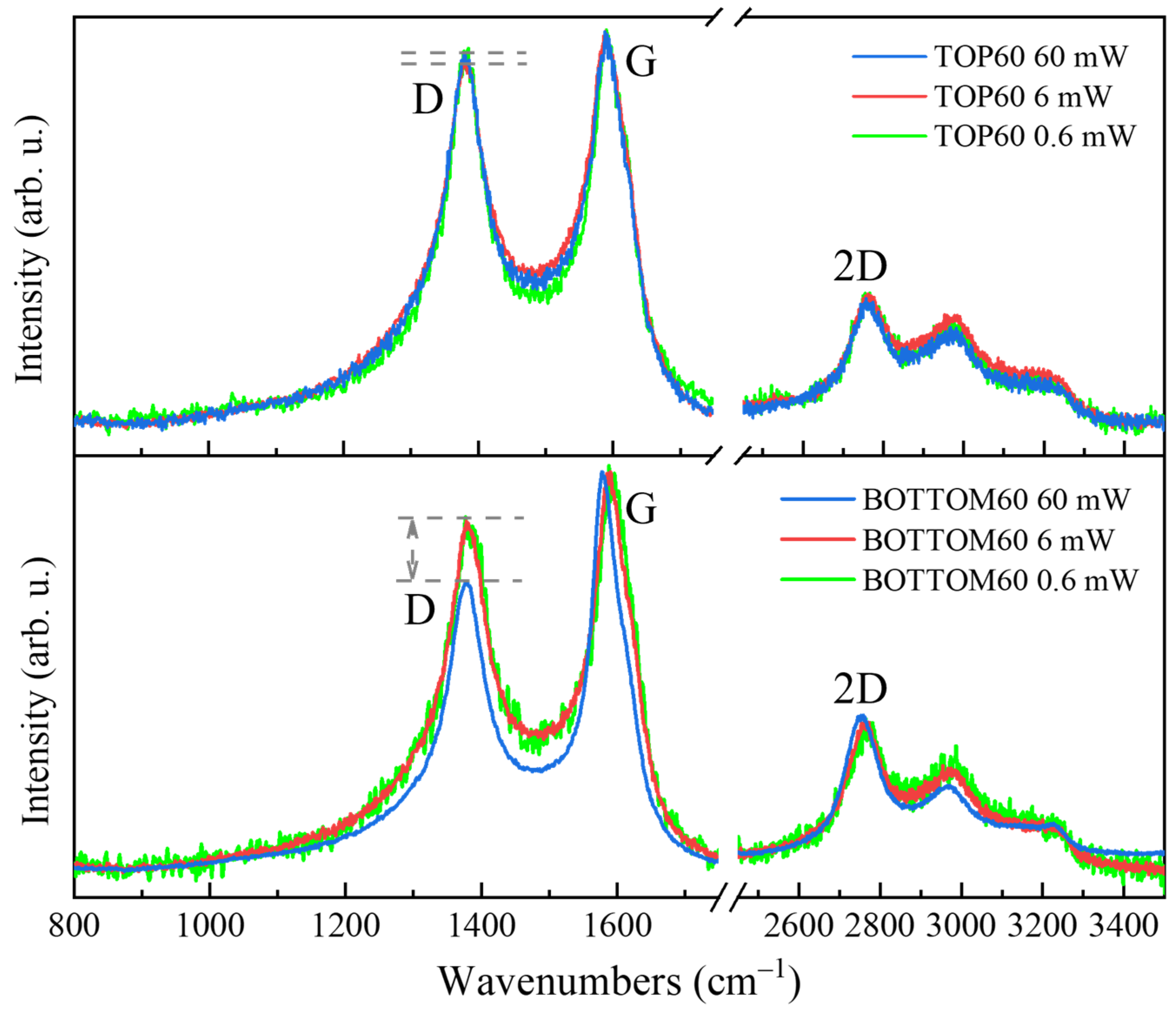
- The TOP60 and BOTTOM60 nanoparticles show quasi-superimposable Raman spectra, with strong D and D’ lines, as expected for small size (small <L>) particles. The G line is now a broad and symmetric peak at higher wavenumbers with respect to HOPG and ROD and coincident with the Gh component of 3L/SC. The similarity of the GNPs spectra confirms that the Raman analysis is sensitive to the drastic reduction in <L> to the scale of the tenths of nanometers, but it seems poorly sensitive to the differences in the average lateral size, which has been highlighted by other techniques. In addition, it does not provide specific information about GNPs thickness nor on the chemical functionalization of the edges, which is indeed more abundant for the BOTTOM60 samples, according to IR evidence. As will be illustrated in Section 2.5.5, a more detailed description can be reached only by means of quantitative analysis based on the curve fitting of multi-wavelength Raman spectra.
- (b)
- The D1, D2, and D3 bands rise, showing a higher intensity with respect to 3L/SC, thus suggesting the presence of additional disorder, probably associated with the local structure of the edges.
- (c)
- The highly symmetric shape of the 2D band demonstrates that the stacking in BOTTOM60 and TOP60 could be affected by turbostratic disorder.
- (d)
- We observe several transitions involving two vibrational quanta in addition to the 2D line, in particular of the strong G + D combination band, which is a typical molecular feature observed in the Raman spectra of polycyclic aromatic hydrocarbons, PAHs [67,68]. It can be taken as evidence that we are approaching the molecular regime. As already observed, this feature was clearly observable also for 3L/S and 3L/SC.
- (e)
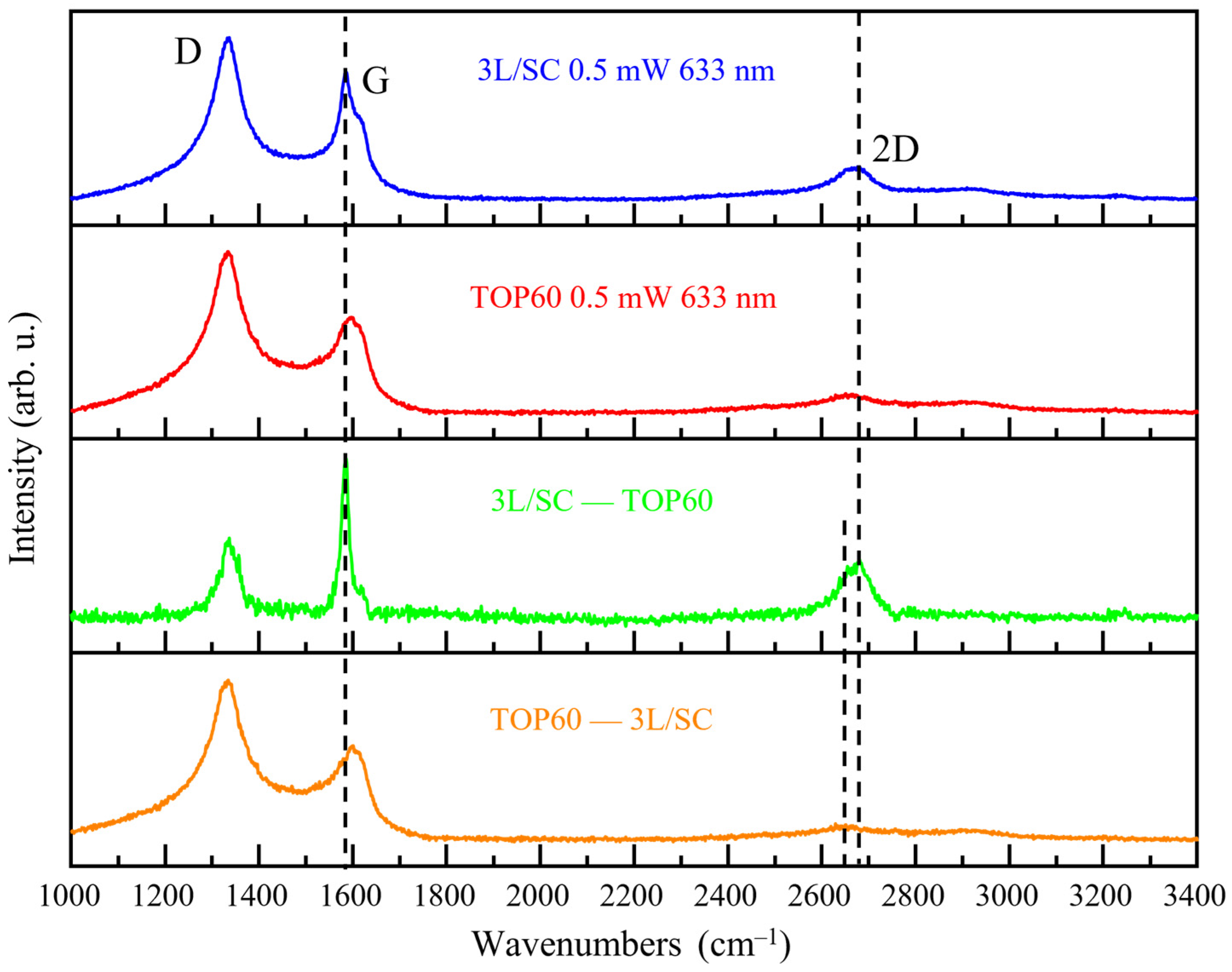
2.5.4. Raman Spectra of TOP60 vs. 3L/SC
2.5.5. Multi-Wavelength Raman Spectra
- (i)
- Overall, the Raman pattern and the parameters extracted by the fitting confirm that the degree of structural disorder, which is related to the particle size, is comparable for TOP60 and BOTTOM60. However, some differences can be appreciated by looking at the peaks’ intensity ratios ID/IG, which are reported in Table 5. The spectra recorded with laser wavelengths of 532 nm and 405 nm show that BOTTOM60 has lower ID/IG values than TOP60, and the same scenario results from an alternative measure of the disorder, namely from the ratio among areas of D and G components, AD/AG (Table 5). These data agree with the finding that TOP60 GNPs are smaller, meaning that the confinement effects associated with the presence of the edges are more effective. This evidence is further supported by the ID’/IG (and AD’/AG) values, which indicate a more important contribution from the vibrational modes localized on the GNPs edges in the case of TOP60. In this framework, it seems difficult to rationalize the apparent anomaly of the ID/IG values obtained at 633 nm excitation, which suggests the opposite trend, showing a smaller value (2.04) for TOP60, compared with ID/IG = 2.30 for BOTTOM60 (see Table 5). The analysis of ID/ID’, point (ii) below, offers an interpretation of it.
- (ii)
- The ID/ID’ parameter, which is often used to assess the relative amount of edges and other kinds of structural disorders, shows a rather systematic trend at each fixed excitation wavelength while passing from 3L/SC, TOP60 and BOTTOM60. For L/SC ID/D’, the values are 3.8 (633 nm), 4.3 (532 nm), and 5.2 (405 nm). These values are close to those reported in Table 5 for TOP60. A higher ID/ID’ value is always found for BOTTOM60 (see Table 5), thus suggesting that in the spectra of BOTTOM60, the contribution to the disorder due to the presence of edges is smaller. This finding explains the apparent anomaly of ID/IG at 633 nm (point i above). The large ID/IG value of BOTTOM60 could be ascribed to the presence of a structural/chemical disorder not associated with confinement by edges, which seems to be efficiently probed while exciting in the red.
- (iii)
- Different from the D component, the frequencies of the broad D1, D2, and D3 components turn out to be independent of the excitation energy. This behavior means that the D1, D2, and D3 components correspond to the Raman transitions not affected or scarcely affected by resonance: some of them can be ascribed to localized vibrations, which are not coupled with low-energy π electron transitions.
- (iv)
- Interestingly, the intensity of D1, D2, and D3 is scarcely affected by the kind of nanoparticles, and it shows a decreasing trend with the decreasing of the exciting laser wavelength. This finding confirms that the D1, D2, and D3 components can be ascribed to the localized vibrations of the disordered regions, possibly in the presence of carbon atoms in sp3 hybridization and/or to vibrations involving functional groups (C=O) on the GNPs edges.
- (v)
- GNPs show a D + G peak with an intensity comparable to that of the 2D line: this feature is indicative of the small size of the TOP60 and of BOTTOM60 GNPs since it is hardly observed in the case of large graphene sheets, while it is a remarkable feature in the second-order Raman spectra of large PAH molecules [67,68].
- (vi)
- The A2D/AG (or I2G/IG) values (Table 5) highlight some differences between TOP60 and BOTTOM60. While they are insensitive to the GNP type while exciting with the blue laser, I2G/IG shows an opposite trend for the Raman experiments using 633 nm (a higher value for BOTTOM60) and 532 nm excitations, where TOP60 shows the highest value. These trends are consistent with the tendency of the A2D/AG values. As already mentioned, 2D band intensity is often referred to as a parameter sensitive to the graphene layers’ stacking, but the observed trends confirm that the use of this parameter presents a delicate issue since it is affected by several factors, which in turn depend on the resonance phenomena.
2.5.6. GNP Structure Modifications upon the Photons Flux
3. Materials and Methods
3.1. Preparation Procedure of Graphene-Based Nanoparticles (GNPs)
3.1.1. Materials
3.1.2. GNPs Preparation
- Ball milling procedure: The ROD was weighed in quantities of 500 mg and inserted into a stainless-steel jar of 5 mL with 4 stainless-steel balls (ø7 mm) and ground for 200 min with a Retch Mixer Mill MM 400. The frequency oscillation of 30 Hz was set for preparing the samples.
- Sonication procedure: 80 mg of the ground graphite dispersed in 24 mL of sterile water was prepared for sonication. The sonication was performed at room temperature using an Ultrasonic Processor GEX750 with a flat-head tip at 450 W and 20 kHz. We performed sonication in steps of 20 s spaced out by 10 s at rest, for a total time of 5 min; at the end of the sonication, the temperature of the samples rose to 47.2 °C.
- Centrifugation procedure: After sonication, the samples were transferred to pre-cleaned vials of 8 mL for centrifugation. In order to avoid the contamination of the samples, the vials were cleaned with acetone and then with hydrogen peroxide (30%) and were washed several times with sterile water in order to remove all of the organic and inorganic contaminants. The first cycle of centrifugation was carried out using a Hettich EBA21 centrifuge at 5000 rpm for 10 min to remove the fraction of the larger and thicker graphitic particles and large clusters. Then, 90% of the supernatant was separated from the sediment and it was subjected to a second centrifugation cycle at 5000 rpm for 60 min. After the second centrifugation, the supernatant (TOP) of the GNPs was separated from the sediment (BOTTOM) of the GNPs by drawing 80% of the dispersion. In this way, two types of samples of GNPs were collected after the second centrifugation. These two samples were referred to as TOP60 and BOTTOM60, according to the second centrifugation time of 60 min.
3.2. Characterization of GNPs
3.2.1. Dynamic Light Scattering (DLS)
3.2.2. Transmission Electron Microscopy (TEM)
3.2.3. UV-Visible Extinction Spectroscopy
3.2.4. Infrared Spectroscopy
3.2.5. Raman Spectroscopy
4. Conclusions
- (i)
- The Raman characterization of GNPs assemblies requires careful sampling at different points of the specimen in order to check the homogeneity of the material and to verify if the irreversible structure rearrangement has been induced by photon flux.
- (ii)
- The use of empirical relationships to obtain structural information from Raman observables (e.g., Raman shifts, bands intensities) should be critically managed by means of a careful comparison of the spectral pattern with the Raman spectra of some reference materials.
- (iii)
- Raman spectra deconvolution is mandatory for GNPs. However, some guidelines/protocols have to be set before the spectra processing. Indeed, the parameters extracted after the curve fitting procedure must be analyzed in a comparative way, e.g., to establish quantitative trends and/or to discuss similarities/differences among samples. For this reason, the number and type of components for the fitting must be established on the ground of physical considerations.
- (iv)
- It is very important to verify that the trends obtained considering the parameters coming from the deconvolution (e.g., peaks frequencies or intensity ratios between individual components) are compatible with the qualitative trends which we can obtain by the direct comparison of the raw spectral data, before any mathematical processing.
- (v)
- When interpreting the spectra, it is essential to remember that the Raman response for a given GNPs material is due to the convolution of the responses of all the different “species” which are present in the sample. Even in the case of nanoparticles with a sharp distribution of sizes, the structural disorder can make each individual particle different from the others, e.g., because of a peculiar structure of the edges or because of the different kind of layer stacking. In this respect, the commercial sample 3L/SC showed a very intriguing behavior with a Raman response resulting as the weighted sum of a graphite-like spectrum and of a spectrum presenting disorder-related features similar to that of the TOP60 GNPs.
- (vi)
- The features described at point v. are further complicated by the occurrence of resonance phenomena: it can “select” the GNPs that better match the resonance condition because of their electronic structure. Moreover, a few peculiar vibrational modes of each individual GNP are selectively enhanced by resonance.
- (vii)
- The study of the second-order Raman spectrum proves to be rich in information. Particles smaller than 100 nm approach a regime in between a crystalline solid (with a partial disorder) and a very large molecule. However, a widely applicable metric allowing for the extraction of quantitative structural information from two quanta transitions is still lacking. Indeed, several entangled factors determine the pattern of the second-order Raman spectrum.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Small, J.P.; Amori, M.E.S.; Kim, P. Electric Field Modulation of Galvanomagnetic Properties of Mesoscopic Graphite. Phys. Rev. Lett. 2005, 94, 176803. [Google Scholar] [CrossRef] [Green Version]
- Potts, J.R.; Dreyer, D.R.; Bielawski, C.W.; Ruoff, R.S. Graphene-based polymer nanocomposites. Polymer 2011, 52, 5–25. [Google Scholar] [CrossRef] [Green Version]
- Schwierz, F. Graphene transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef]
- Eda, G.; Chhowalla, M. Chemically Derived Graphene Oxide: Towards Large-Area Thin-Film Electronics and Optoelectronics. Adv. Mater. 2010, 22, 2392–2415. [Google Scholar] [CrossRef]
- Shen, J.; Zhu, Y.; Yang, X.; Li, C. Graphene quantum dots: Emergent nanolights for bioimaging, sensors, catalysis and photovoltaic devices. Chem. Commun. 2012, 48, 3686–3699. [Google Scholar] [CrossRef]
- May, P.; Khan, U.; O’Neill, A.; Coleman, J.N. Approaching the theoretical limit for reinforcing polymers with graphene. J. Mater. Chem. 2012, 22, 1278–1282. [Google Scholar] [CrossRef]
- Geim, A.; Novoselov, K. The rise of graphene. In Nanosci. Technol. Collect. Rev. Nat. Journals; World Scientific: Singapore, 2010; pp. 11–19. [Google Scholar]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.; Potts, J.; Ruoff, R. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2010, 39, 228–240. [Google Scholar] [CrossRef]
- Wojtoniszaka, M.; Chena, X.; Kalenczuka, R.; Wajdab, A.; Łapczukb, J.; Kurzewskib, M.; Drozdzikb, M.; Chuc, P.; Borowiak-Palena, E. Synthesis, dispersion, and cytocompatibility of graphene oxide and reduced graphene oxide. Colloids Surf. B Biointerfaces 2012, 89, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, M. Cancer nanotechnology: Opportunities and challenges. Nat. Rev. Cancer 2005, 5, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Riehemann, K.; Schneider, S.W.; Luger, T.A.; Godin, B.; Ferrari, M.; Fuchs, H. Nanomedicine-Challenge and Perspectives. Angew. Chem. Int. Ed. 2009, 48, 872–897. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De, M.; Ghosh, P.S.; Rotello, V.M. Applications of Nanoparticles in Biology. Adv. Mater. 2008, 20, 4225–4241. [Google Scholar] [CrossRef] [Green Version]
- Barreto, J.; O’Malley, W.; Kubeil, M.; Graham, B.; Stephan, H.; Spiccia, L. Nanomaterials: Applications in cancer imaging and therapy. Adv. Mater. 2011, 23, H18–H40. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Nemanich, R.J.; Solin, S.A. First- and second-order Raman scattering from finite-size crystals of graphite. Phys. Rev. B 1979, 20, 392–401. [Google Scholar] [CrossRef]
- Castiglioni, C.; Tommasini, M.; Zerbi, G. Raman spectroscopy of polyconjugated molecules and materials: Confinement effect in one and two dimensions. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 2425–2459. [Google Scholar] [CrossRef]
- Castiglioni, C.; Negri, F.; Rigolio, M.; Zerbi, G. Raman activation in disordered graphites of the A1′ symmetry forbidden k≠0 phonon: The origin of the D line. J. Chem. Phys. 2001, 115, 3769–3778. [Google Scholar] [CrossRef]
- Castiglioni, C.; Mapelli, C.; Negri, F.; Zerbi, G. Origin of the D line in the Raman spectrum of graphite: A study based on Raman frequencies and intensities of polycyclic aromatic hydrocarbon molecules. J. Chem. Phys. 2001, 114, 963. [Google Scholar] [CrossRef]
- Yi, M.; Shen, Z. A review on mechanical exfoliation for the scalable production of graphene. J. Mater. Chem. A 2015, 3, 11700–11715. [Google Scholar] [CrossRef]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casiraghi, C.; Hartschuh, A.; Qian, H.; Piscanec, S.; Georgi, C.; Fasoli, A.; Novoselov, K.S.; Basko, D.M.; Ferrari, A.C. Raman Spectroscopy of Graphene Edges. Nano Lett. 2009, 9, 1433–1441. [Google Scholar] [CrossRef] [Green Version]
- Negri, F.; Castiglioni, C.; Tommasini, M.; Zerbi, G. A Computational Study of the Raman Spectra of Large Polycyclic Aromatic Hydrocarbons: Toward Molecularly Defined Subunits of Graphite. J. Phys. Chem. A 2002, 106, 3306–3317. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.C.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095–14107. [Google Scholar] [CrossRef] [Green Version]
- Rigolio, M.; Castiglioni, C.; Zerbi, G.; Negri, F. Density functional theory prediction of the vibrational spectra of polycyclic aromatic hydrocarbons: Effect of molecular symmetry and size on Raman intensities. J. Mol. Struct. 2001, 563, 79–87. [Google Scholar] [CrossRef]
- Mapelli, C.; Castiglioni, C.; Zerbi, G.; Müllen, K. Common force field for graphite and polycyclic aromatic hydrocarbons. Phys. Rev. B 1999, 60, 12710–12725. [Google Scholar] [CrossRef]
- Backes, C.; Paton, K.R.; Hanlon, D.; Yuan, S.; Katsnelson, M.I.; Houston, J.; Smith, R.J.; McCloskey, D.; Donegan, J.F.; Coleman, J.N. Spectroscopic metrics allow in situ measurement of mean size and thickness of liquid-exfoliated few-layer graphene nanosheets. Nanoscale 2016, 8, 4311–4323. [Google Scholar] [CrossRef]
- Backes, C.; Smith, R.J.; McEvoy, N.; Berner, N.; McCloskey, D.; Nerl, H.; O’Neill, A.; King, P.J.; Higgins, T.; Hanlon, D.; et al. Edge and confinement effects allow in situ measurement of size and thickness of liquid-exfoliated nanosheets. Nat. Commun. 2014, 5, 4576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khoshhesab, Z.M. Reflectance IR spectroscopy. Infrared Spectrosc. Sci. Eng. Technol. 2012, 11, 233–244. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Murata, R.; Inoue, K.-I.; Wang, L.; Ye, S.; Morita, A. Dispersion of Complex Refractive Indices for Intense Vibrational Bands. I. Quantitative Spectra. J. Phys. Chem. B 2021, 125, 9794–9803. [Google Scholar] [CrossRef] [PubMed]
- Jeon, I.-Y.; Shin, Y.-R.; Sohn, G.-J.; Choi, H.-J.; Bae, S.-Y.; Mahmood, J.; Jung, S.-M.; Seo, J.-M.; Kim, M.-J.; Chang, D.W.; et al. Edge-carboxylated graphene nanosheets via ball milling. Proc. Natl. Acad. Sci. USA 2012, 109, 5588–5593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeon, I.-Y.; Bae, S.-Y.; Seo, J.-M.; Baek, J.-B. Scalable Production of Edge-Functionalized Graphene Nanoplatelets via Mechanochemical Ball-Milling. Adv. Funct. Mater. 2015, 25, 6961–6975. [Google Scholar] [CrossRef]
- Berne, B.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Courier Corporation: North Chelmsford, MA, USA, 2000. [Google Scholar]
- Bhattacharjee, S. DLS and zeta potential—What they are and what they are not? J. Control. Release 2016, 235, 337–351. [Google Scholar] [CrossRef]
- Lotya, M.; Rakovich, A.; Donegan, J.; Coleman, J. Measuring the lateral size of liquid-exfoliated nanosheets with dynamic light scattering. Nanotechnology 2013, 24, 265703. [Google Scholar] [CrossRef]
- Zheng, T.; Bott, S.; Huo, Q. Techniques for Accurate Sizing of Gold Nanoparticles Using Dynamic Light Scattering with Particular Application to Chemical and Biological Sensing Based on Aggregate Formation. ACS Appl. Mater. Interfaces 2016, 8, 21585–21594. [Google Scholar] [CrossRef]
- Kravets, V.G.; Grigorenko, A.N.; Nair, R.R.; Blake, P.; Anissimova, S.; Novoselov, K.; Geim, A.K. Spectroscopic ellipsometry of graphene and an exciton-shifted van Hove peak in absorption. Phys. Rev. B 2010, 81, 155413. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; Shan, J.; Heinz, T.F. Seeing Many-Body Effects in Single- and Few-Layer Graphene: Observation of Two-Dimensional Saddle-Point Excitons. Phys. Rev. Lett. 2011, 106, 046401. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; Ju, L.; Wang, F.; Heinz, T.F. Optical spectroscopy of graphene: From the far infrared to the ultraviolet. Solid State Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
- Lai, Q.; Zhu, S.; Luo, X.; Zou, M.; Huang, S. Ultraviolet-visible spectroscopy of graphene oxides. AIP Adv. 2012, 2, 032146. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, G.-Y.; Yu, C.-H.; Xie, Y.; Xia, M.-Y.; Lu, B.-Y.; Fei, X.; Peng, Q. The UV absorption of graphene oxide is size-dependent: Possible calibration pitfalls. Mikrochim. Acta 2019, 186, 207. [Google Scholar] [CrossRef] [PubMed]
- Barbera, V.; Porta, A.; Brambilla, L.; Guerra, S.; Serafini, A.; Valerio, A.M.; Vitale, A.; Galimberti, M. Polyhydroxylated few layer graphene for the preparation of flexible conductive carbon paper. RSC Adv. 2016, 6, 87767–87777. [Google Scholar] [CrossRef]
- Centrone, A.; Brambilla, L.; Renouard, T.; Gherghel, L.; Mathis, C.; Müllen, K.; Zerbi, G. Structure of new carbonaceous materials: The role of vibrational spectroscopy. Carbon N. Y. 2005, 43, 1593–1609. [Google Scholar] [CrossRef]
- Dato, A.; Lee, Z.; Jeon, K.-J.; Erni, R.; Radmilovic, V.; Frenklachd, M. Clean and highly ordered graphene synthesized in the gas phase. Chem. Commun. 2009, 6095–6097. [Google Scholar] [CrossRef]
- Hontoria-Lucas, C.; Lopez-Peinado, A.J.; Lopez-Gonzalez, J.d.D.; Rojas-Cervantes, M.L.; Martin-Aranda, R.M. Study of oxygen-containing groups in a series of graphite oxides: Physical and chemical characterization. Carbon N. Y. 1995, 33, 1585–1592. [Google Scholar] [CrossRef]
- Sadeghi, H.; Dorranian, D. Influence of size and morphology on the optical properties of carbon nanostructures. J. Theor. Appl. Phys. 2016, 10, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Bhowmik, P.; Zhao, B.; Hamon, M.; Itkis, M.; Haddon, R. Determination of the acidic sites of purified single-walled carbon nanotubes by acid–base titration. Chem. Phys. Lett. 2001, 345, 25–28. [Google Scholar] [CrossRef]
- Zhang, Z.; Flaherty, D.W. Modified potentiometric titration method to distinguish and quantify oxygenated functional groups on carbon materials by pKa and chemical reactivity. Carbon N. Y. 2020, 166, 436–445. [Google Scholar] [CrossRef]
- Orth, E.; Ferreira, J.; Fonsaca, J.; Blaskievicz, S.; Domingues, S.; Dasgupta, A.; Terrones, M.; Zarbin, A. pKa determination of graphene-like materials: Validating cheical functionalization. J. Colloid Interface Sci. 2016, 467, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Tuinstra, F.; Koenig, J.L. Raman Spectrum of Graphite. J. Chem. Phys. 1970, 53, 1126–1130. [Google Scholar] [CrossRef] [Green Version]
- Escribano, R.; Sloan, J.; Siddique, N.; Sze, N.; Dudev, T. Raman spectroscopy of carbon-containing particles. Vib. Spectrosc. 2001, 26, 179–186. [Google Scholar] [CrossRef]
- Pócsik, I.; Hundhausen, M.; Koós, M.; Ley, L. Origin of the D peak in the Raman spectrum of microcrystalline graphite. J. Non-Cryst. Solids 1998, 227, 1083–1086. [Google Scholar] [CrossRef]
- Cançado, L.G.; Jorio, A.; Pimenta, M.A. Measuring the absolute Raman cross section of nanographites as a function of laser energy and crystallite size. Phys. Rev. B Condens. Matter 2007, 76, 064304. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Calizo, I.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Temperature Dependence of the Raman Spectra of Graphene and Graphene Multilayers. Nano Lett. 2007, 7, 2645–2649. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Raman Spectroscopy of Carbon Nanotubes in 1997 and 2007. J. Phys. Chem. C 2007, 111, 17887–17893. [Google Scholar] [CrossRef]
- Thomsen, C.; Reich, S. Double Resonant Raman Scattering in Graphite. Phys. Rev. Lett. 2000, 85, 5214–5217. [Google Scholar] [CrossRef] [Green Version]
- Eckmann, A.; Felten, A.; Mishchenko, A.; Britnell, L.; Krupke, R.; Novoselov, K.S.; Casiraghi, C. Probing the Nature of Defects in Graphene by Raman Spectroscopy. Nano Lett. 2012, 12, 3925–3930. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Pachter, R.; Mehmood, F.; Islam, A.; Maruyama, B.; Boeckl, J. A Raman spectroscopy signature for characterizing defective single-layer graphene: Defect-induced I (D)/I (D’) intensity ratio by theoretical analysis. Carbon N. Y. 2015, 90, 53–62. [Google Scholar] [CrossRef]
- Yoon, D.; Moon, H.; Cheong, H.; Choi, J.; Choi, J.; Park, B. Variations in the Raman Spectrum as a Function of the Number ofGraphene Layers. J. Korean Phys. Soc. 2009, 55, 1299–1303. [Google Scholar] [CrossRef]
- Maghsoumi, A.; Beser, U.; Feng, X.; Narita, A.; Müllen, K.; Castiglioni, C.; Tommasini, M. Raman spectroscopy of holey nanographene C216. J. Raman Spectrosc. 2021, 52, 2301–2316. [Google Scholar] [CrossRef]
- Maghsoumi, A.; Brambilla, L.; Castiglioni, C.; Müllen, K.; Tommasini, M. Overtone and combination features of G and D peaks in resonance Raman spectroscopy of the C78 H26 polycyclic aromatic hydrocarbon. J. Raman Spectrosc. 2015, 46, 757–764. [Google Scholar] [CrossRef]
- Girit, C.O.; Meyer, J.C.; Erni, R.; Rossell, M.D.; Kisielowski, C.; Yang, L.; Park, C.-H.; Crommie, M.F.; Cohen, M.L.; Louie, S.G.; et al. Graphene at the Edge: Stability and Dynamics. Science 2009, 323, 1705–1708. [Google Scholar] [CrossRef]
- Jia, X.; Hofmann, M.; Meunier, V.; Sumpter, B.G.; Campos-Delgado, J.; Romo-Herrera, J.M.; Son, H.; Hsieh, Y.-P.; Reina, A.; Kong, J.; et al. Controlled Formation of Sharp Zigzag and Armchair Edges in Graphitic Nanoribbons. Science 2009, 323, 1701–1705. [Google Scholar] [CrossRef]
- Sadezky, A.; Muckenhuber, H.; Grothe, H.; Niessner, R.; Pöschl, U. Raman Microspectroscopy of Soot and Related Carbonaceous Materials: Spectral Analysis and Structural Information. Carbon 2005, 43, 1731–1742. [Google Scholar] [CrossRef]
- Ivleva, N.; McKeon, U.; Niessner, R.; Pöschl, U. Raman Microspectroscopic Analysis of Size-Resolved Atmospheric Aerosol Particle Samples Collected with an Elpi: Soot, Humic-Like Substances, and Inorganic Compounds. Aerosol Sci. Technol. 2007, 41, 655–671. [Google Scholar] [CrossRef] [Green Version]
- Claramunt, S.; Varea, A.; Lopez-Diaz, D.; Velázquez, M.; Cornet, A.; Cirera, A. The importance of interbands on the interpretation of the Raman spectrum of graphene oxide. J. Phys. Chem. C. 2015, 119, 10123–10129. [Google Scholar] [CrossRef]




| Different Stages of Production | Abbreviation |
|---|---|
| After Ball Milling (60 min) | Milled60 |
| After Balling Milling (120 min) | Milled120 |
| After Balling Milling (180 min) | Milled180 |
| After Balling Milling (200 min) | Milled200 |
| After Sonication | Sonicated |
| Separation of supernatant after First Centrifugation (10 min) | First TOP |
| Separation of the sediment after First Centrifugation (10 min) | First BOTTOM |
| Separation of supernatant after Second Centrifugation (60 min) | TOP60 |
| Separation of the sediment after Second Centrifugation (60 min) | BOTTOM60 |
| Samples | ε550/εmax | <N> |
|---|---|---|
| TOP60 | 0.35 | 3.6 |
| BOTTOM60 | 0.54 | 5.7 |
| 3L/SC | 0.35 | 3.6 |
| 5–7L/SC | 0.50 | 6.2 |
| Samples | AC=O/AG |
|---|---|
| HOPG | - |
| Rod Graphite | - |
| Milled200 | 0.51 |
| First Bottom | 0.43 |
| BOTTOM60 | 0.11 |
| Sample | Peak Position (cm−1) | Intensity Ratio (*) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | G | Gh | D’ | D1 | D2 | D3 | 2D | ID/IG | ID’/IG | ID1/IG | ID2/IG | ID3/IG | I2D/IG | A2D/AG | |
| HOPG | - | 1582 [14] | - | - | - | - | - | 2688 2647 | - | - | - | - | - | 0.53 | 1.5 |
| ROD (i) | 1336 | 1583 [17] | - | 1621 | - | 1282 | 1494 | 2690 2670 2645 | 0.16 | 0.06 | - | 0.01 | 0.01 | 0.66 | 1.35 |
| ROD (ii) | 1334 | 1580 [24] | - | 1617 | 1143 | 1282 | 1494 | 2692 2670 2649 | 0.45 | 0.11 | 0.02 | 0.04 | 0.02 | 0.61 | 1.24 |
| 3L/P | 1336 | 1582 [19] | - | 1619 | - | - | - | 2687 2662 | 0.21 | 0.05 | - | - | - | 0.51 | 0.89 |
| 3L/S | 1336 | 1582 [19] | 1590 [49] | 1621 | 1143 | 1282 | 1494 | 2663 | 0.64 | 0.18 | 0.03 | 0.11 | 0.09 | 0.43 | 0.99 |
| 3L/SC | 1334 | 1582 [14] | 1590 [55] | 1620 | 1143 | 1282 | 1494 | 2666 | 1.66 | 0.44 | 0.07 | 0.44 | 0.31 | 0.27 | 0.6 |
| TOP60 | 1334 | - | 1590 [62] | 1618 | 1143 | 1282 | 1494 | 2660 | 2.04 | 0.51 | 0.09 | 0.56 | 0.41 | 0.21 | 0.43 |
| BOTTOM60 | 1332 | - | 1590 [65] | 1616 | 1143 | 1282 | 1494 | 2659 | 2.3 | 0.51 | 0.13 | 0.56 | 0.42 | 0.27 | 0.52 |
| ID/IG | AD/AG | ID’/IG | AD’/AG | I2D/IG | A2D/AG | ID/ID’ | ||
|---|---|---|---|---|---|---|---|---|
| 633 nm | TOP60 | 2.04 | 2.4 | 0.51 | 0.30 | 0.21 | 0.43 | 4.00 |
| BOTTOM 60 | 2.3 | 2.47 | 0.51 | 0.26 | 0.27 | 0.52 | 4.51 | |
| 532 nm | TOP60 | 1.69 | 2.09 | 0.41 | 0.19 | 0.18 | 0.37 | 4.12 |
| BOTTOM 60 | 1.42 | 1.78 | 0.28 | 0.09 | 0.13 | 0.2 | 5.07 | |
| 405 nm | TOP60 | 1.07 | 1.23 | 0.17 | 0.07 | 0.1 | 0.18 | 6.29 |
| BOTTOM 60 | 0.87 | 1.07 | 0.13 | 0.04 | 0.1 | 0.18 | 6.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Brambilla, L.; Sartori, P.; Moscheni, C.; Perrotta, C.; Zema, L.; Bertarelli, C.; Castiglioni, C. Development of Tailored Graphene Nanoparticles: Preparation, Sorting and Structure Assessment by Complementary Techniques. Molecules 2023, 28, 565. https://doi.org/10.3390/molecules28020565
Hu K, Brambilla L, Sartori P, Moscheni C, Perrotta C, Zema L, Bertarelli C, Castiglioni C. Development of Tailored Graphene Nanoparticles: Preparation, Sorting and Structure Assessment by Complementary Techniques. Molecules. 2023; 28(2):565. https://doi.org/10.3390/molecules28020565
Chicago/Turabian StyleHu, Kaiyue, Luigi Brambilla, Patrizia Sartori, Claudia Moscheni, Cristiana Perrotta, Lucia Zema, Chiara Bertarelli, and Chiara Castiglioni. 2023. "Development of Tailored Graphene Nanoparticles: Preparation, Sorting and Structure Assessment by Complementary Techniques" Molecules 28, no. 2: 565. https://doi.org/10.3390/molecules28020565
APA StyleHu, K., Brambilla, L., Sartori, P., Moscheni, C., Perrotta, C., Zema, L., Bertarelli, C., & Castiglioni, C. (2023). Development of Tailored Graphene Nanoparticles: Preparation, Sorting and Structure Assessment by Complementary Techniques. Molecules, 28(2), 565. https://doi.org/10.3390/molecules28020565









