Structural Analysis and Classification of Low-Molecular-Weight Hyaluronic Acid by Near-Infrared Spectroscopy: A Comparison between Traditional Machine Learning and Deep Learning
Abstract
1. Introduction
2. Results and Discussion
2.1. NMR and FTIR Spectrum Description
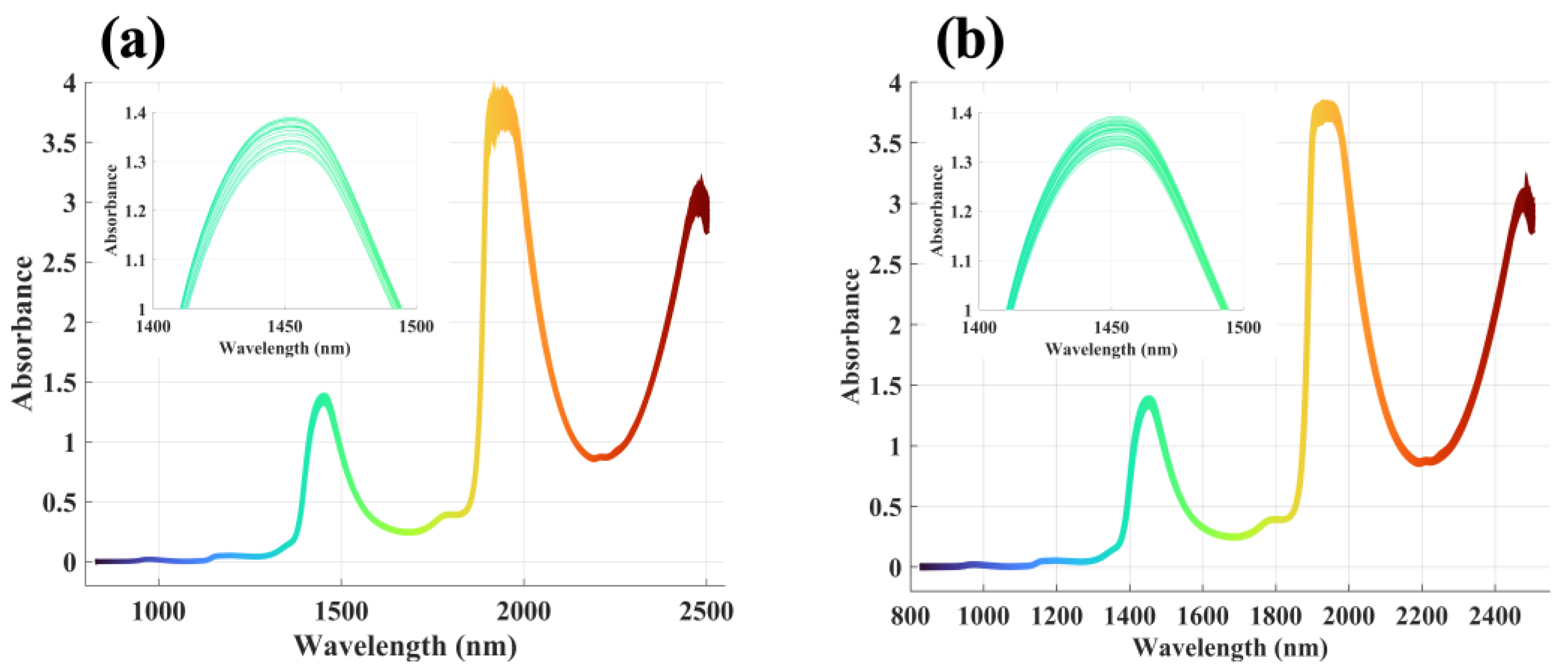
2.2. NIR Spectrum Description
2.3. Analysis of 2DCOS Synchronous and Asynchronous Spectra
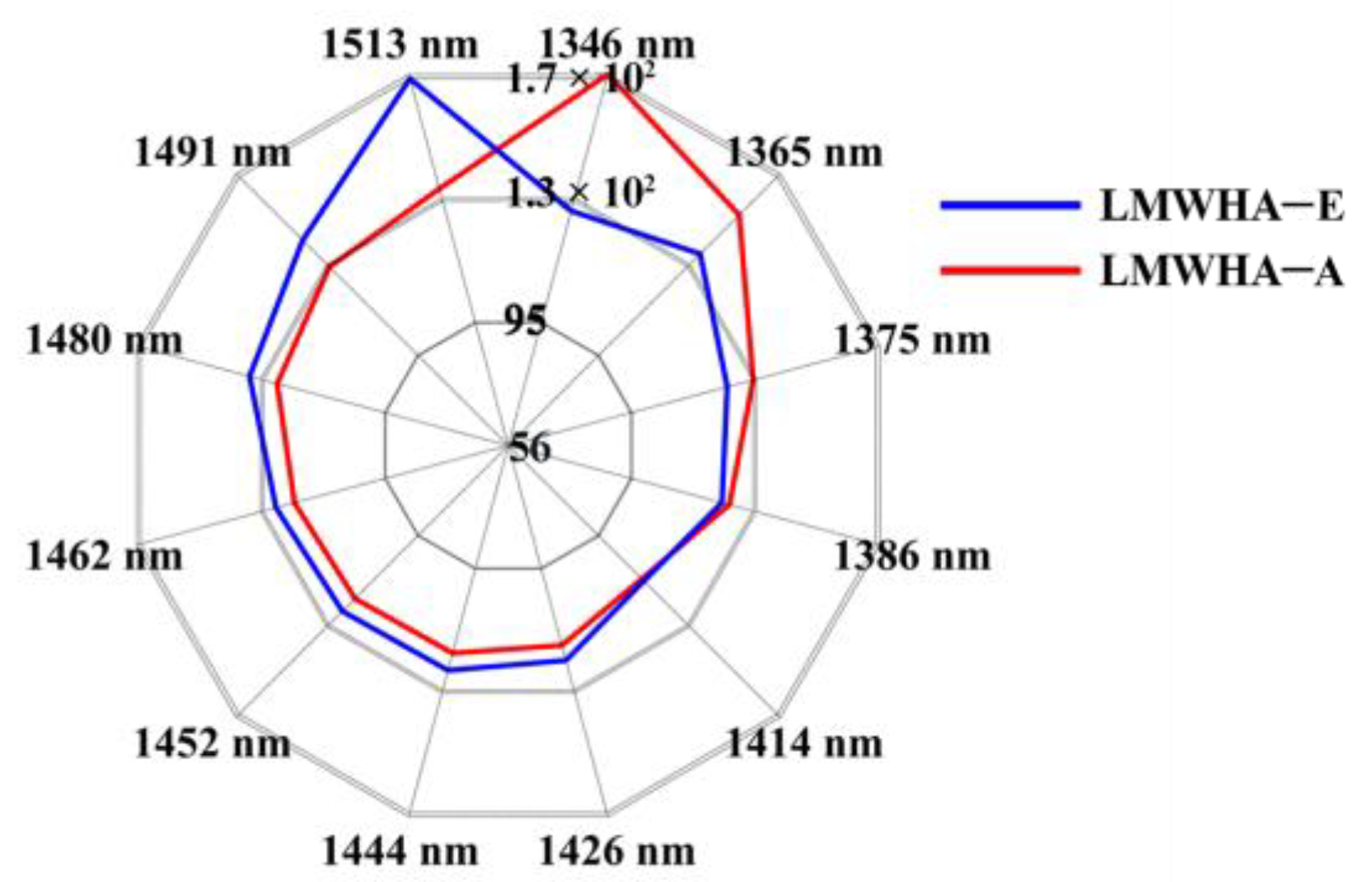
2.4. Aquaphotomics Analysis
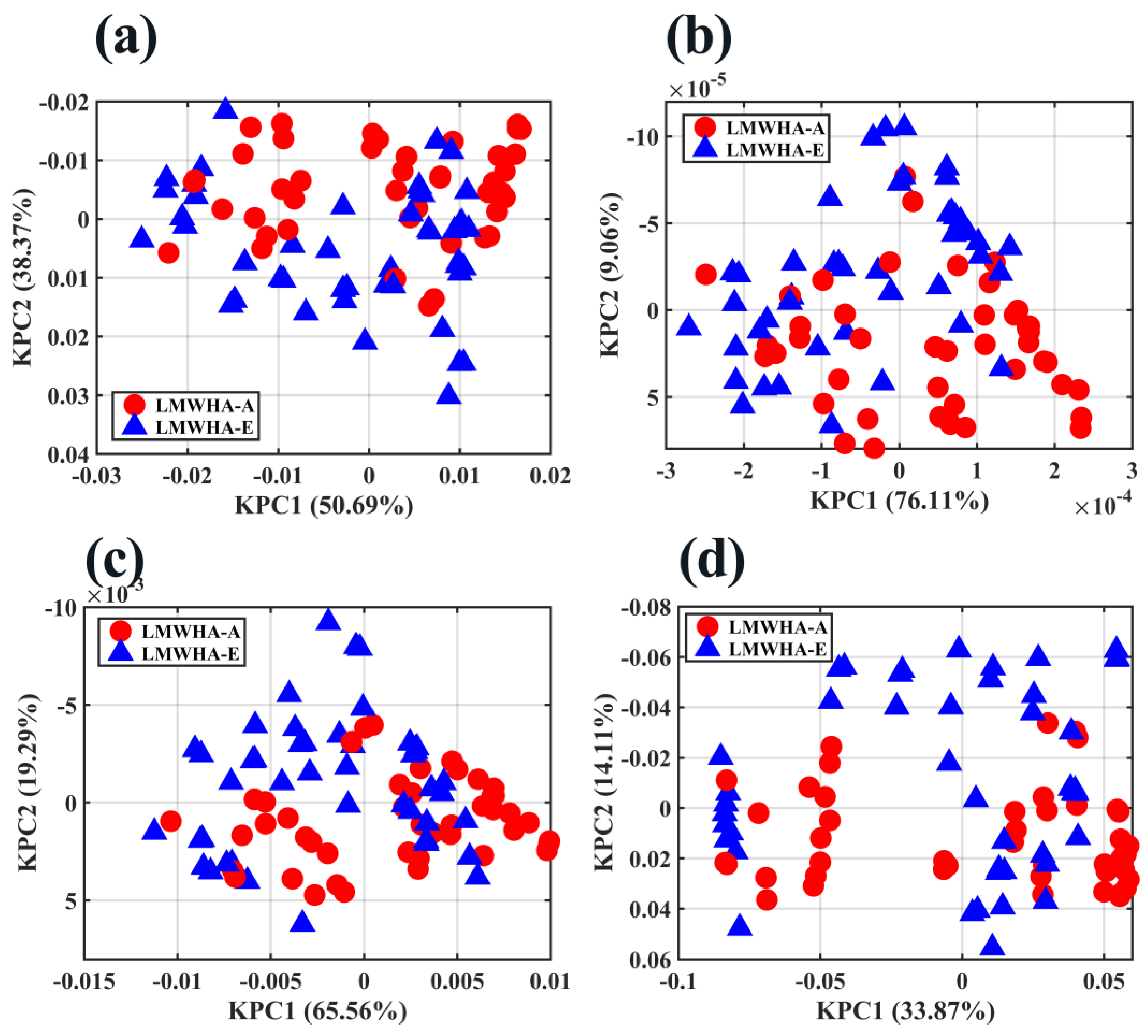
2.5. Sample Exploration by PCA, KPCA, and t-SNE
2.6. Sample Classification Based on Traditional Machine Learning Methods
2.6.1. PLS-DA
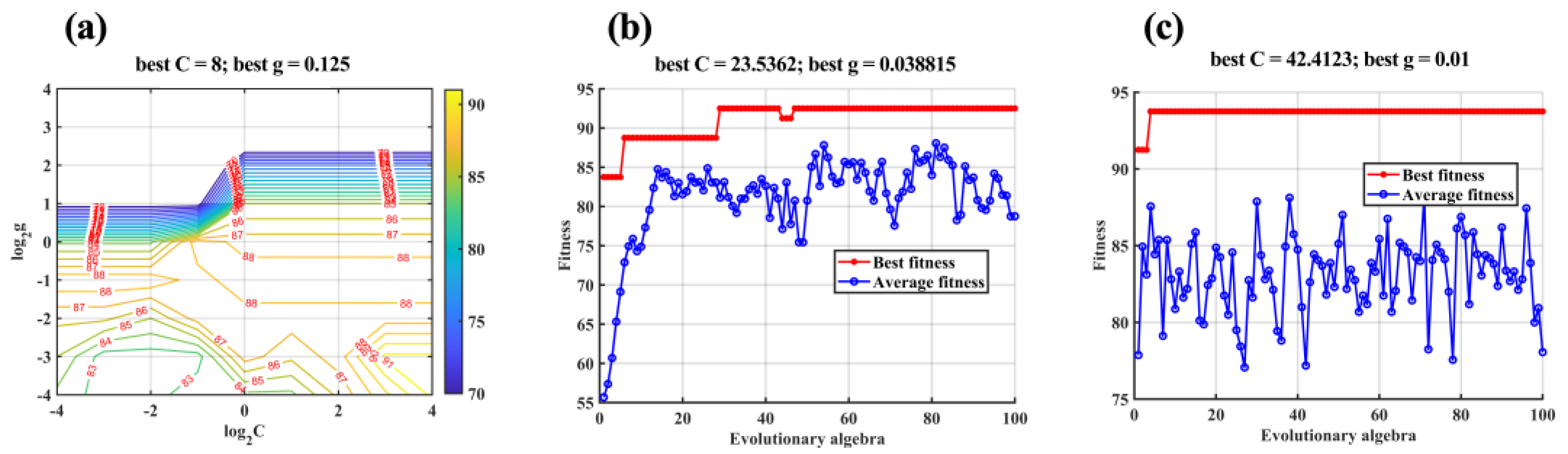
2.6.2. SVC and Optimized SVCs
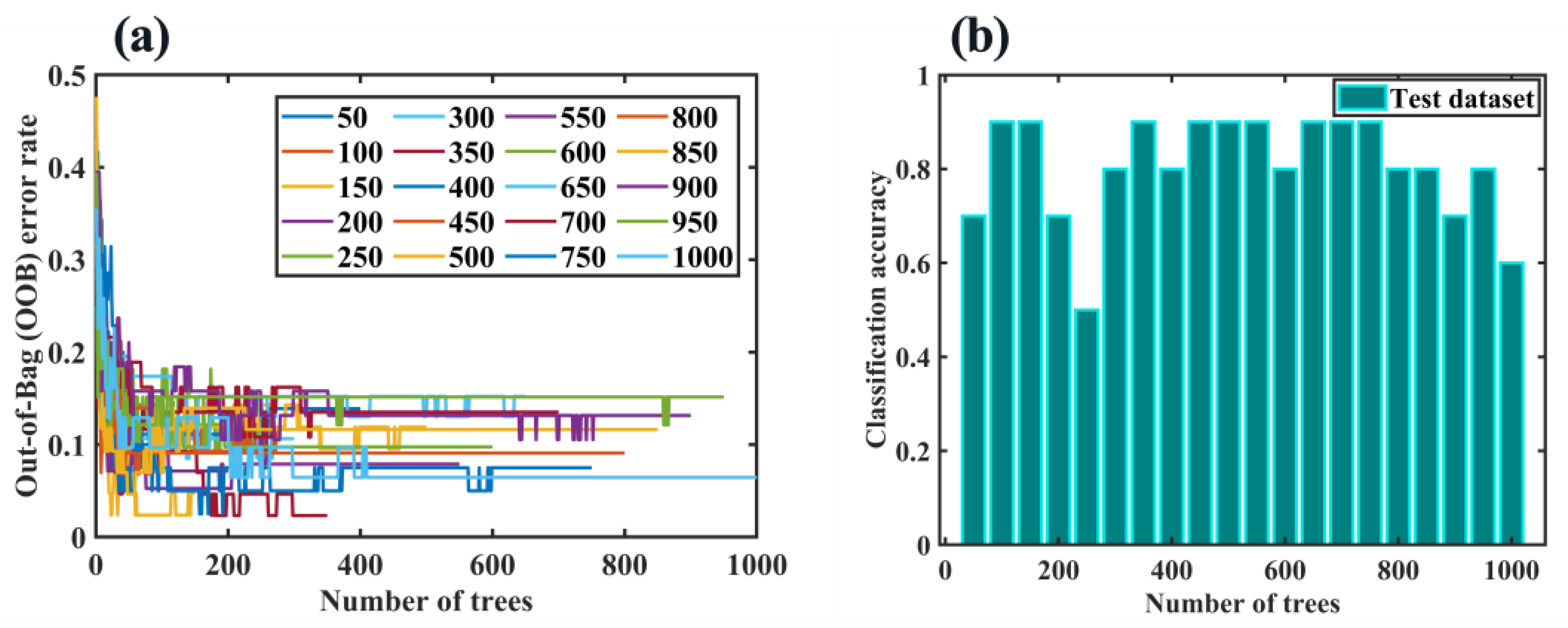
2.6.3. RF Algorithm
2.7. Sample Classification Based on Deep Learning Methods
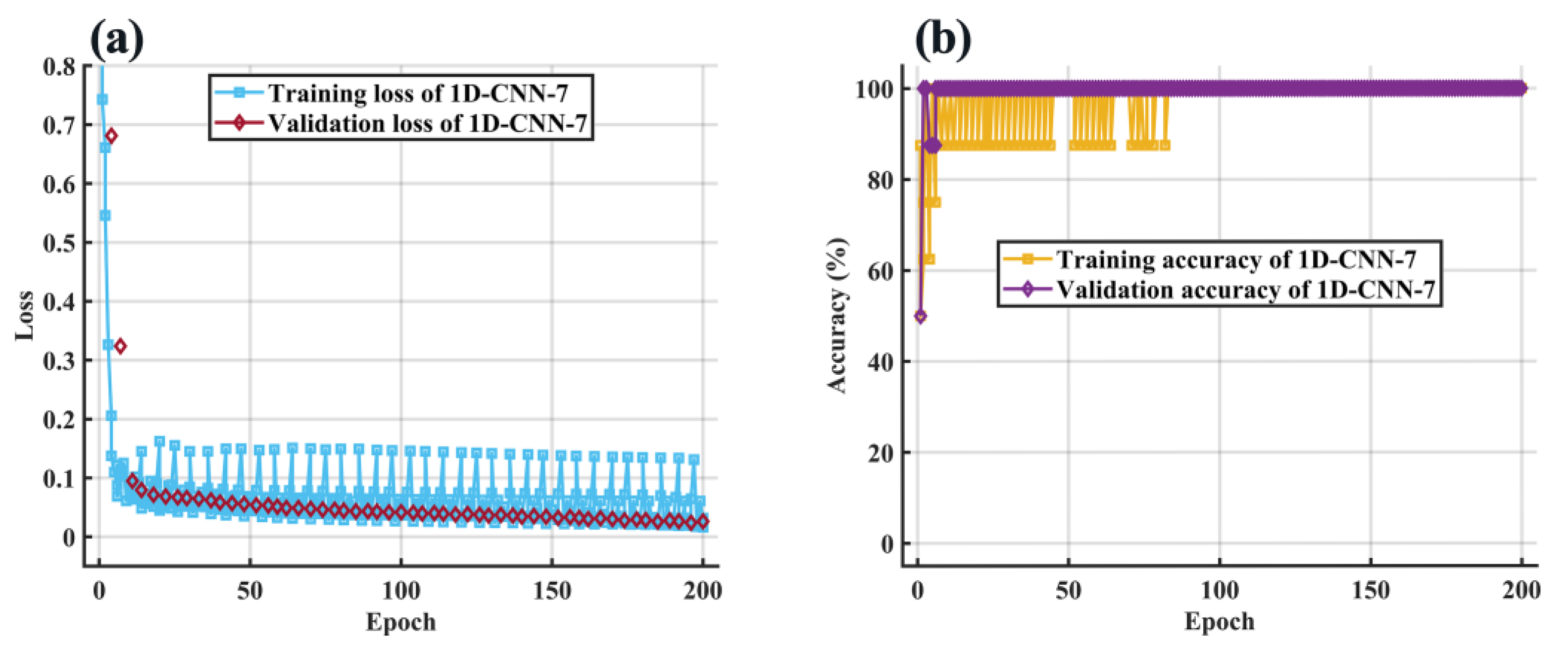
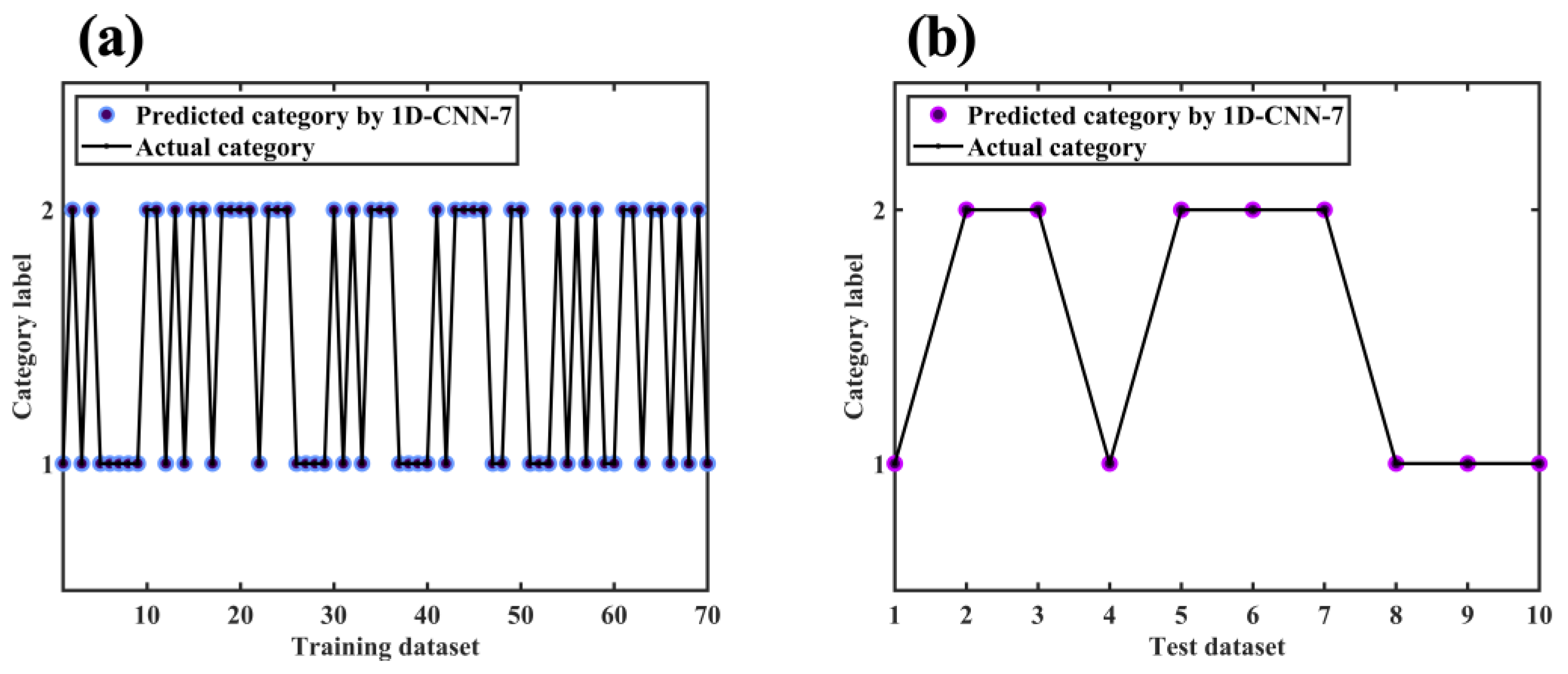
2.7.1. 1D-CNN
2.7.2. LSTM
3. Materials and Methods
3.1. Samples
3.2. NMR Spectral Data Acquisition and Processing
3.3. FTIR Spectral Data Acquisition
3.4. NIR Spectral Data Acquisition and Sample Set Division
3.5. NIR Spectral Preprocessing
3.6. 2DCOS Analysis
3.7. Aquaphotomics Analysis
3.8. Data Dimensionality Reduction
3.9. Sample Classification Based on Machine Learning Methods
3.10. Programming Language
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burdick, J.A.; Prestwich, G.D. Hyaluronic acid hydrogels for biomedical applications. Adv. Mater. 2011, 23, 41–56. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.C.; Lall, R.; Srivastava, A.; Sinha, A. Hyaluronic acid: Molecular mechanisms and therapeutic trajectory. Front. Vet. Sci. 2019, 6, 192–215. [Google Scholar] [CrossRef] [PubMed]
- Bayer, I.S. Hyaluronic acid and controlled release: A review. Molecules 2020, 25, 2649. [Google Scholar] [CrossRef]
- Chang, W.H.; Liu, P.Y.; Lin, M.H.; Lu, C.J.; Chou, H.Y.; Nian, C.Y.; Jiang, Y.T.; Hsu, Y.H. Applications of hyaluronic acid in ophthalmology and contact Lenses. Molecules 2021, 26, 2485. [Google Scholar] [CrossRef]
- Juncan, A.M.; Moisă, D.G.; Santini, A.; Morgovan, C.; Rus, L.L.; Vonica-Țincu, A.L.; Loghin, F. Advantages of hyaluronic acid and its combination with other bioactive ingredients in cosmeceuticals. Molecules 2021, 26, 4429. [Google Scholar] [CrossRef]
- Radrezza, S.; Aiello, G.; Baron, G.; Aldini, G.; Carini, M.; D’Amato, A. Integratomics of human dermal fibroblasts treated with low molecular weight hyaluronic acid. Molecules 2021, 26, 5096. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, Y.; Yang, H.; Qiu, P.; Cong, Z.; Zou, Y.; Song, L.; Guo, J.; Anastassiades, T.P. A low molecular weight hyaluronic acid derivative accelerates excisional wound healing by modulating pro-inflammation, promoting epithelialization and neovascularization, and remodeling collagen. Int. J. Mol. Sci. 2019, 20, 3722. [Google Scholar] [CrossRef]
- Lokeshwar, V.B.; Mirza, S.; Jordan, A. Targeting hyaluronic acid family for cancer chemoprevention and therapy. Adv. Cancer. Res. 2014, 123, 35–65. [Google Scholar] [CrossRef]
- Zamboni, F.; Vieira, S.; Reis, R.L.; Oliveira, J.M.; Collins, M.N. The potential of hyaluronic acid in immunoprotection and immunomodulation: Chemistry, processing and function. Prog. Nat. Sci. 2018, 97, 97–122. [Google Scholar] [CrossRef]
- Rayahin, J.E.; Buhrman, J.S.; Zhang, Y.; Koh, T.J.; Gemeinhart, R.A. High and low molecular weight hyaluronic acid differentially influence macrophage activation. ACS Biomater. Sci. Eng. 2015, 1, 481–493. [Google Scholar] [CrossRef]
- Schmidt, J.; Pilbauerova, N.; Soukup, T.; Suchankova-Kleplova, T.; Suchanek, J. Low molecular weight hyaluronic acid effect on dental pulp stem cells in vitro. Biomolecules 2020, 11, 22. [Google Scholar] [CrossRef]
- Valcarcel, J.; García, M.R.; Varela, U.R.; Vázquez, J.A. Hyaluronic acid of tailored molecular weight by enzymatic and acid depolymerization. Int. J. Biol. Macromol. 2020, 145, 788–794. [Google Scholar] [CrossRef]
- Pang, B.; Wang, H.; Huang, H.; Liao, L.; Wang, Y.; Wang, M.; Du, G.; Kang, Z. Enzymatic production of low-molecular-weight hyaluronan and its oligosaccharides: A review and prospects. J. Agric. Food Chem. 2022, 70, 14129–14139. [Google Scholar] [CrossRef] [PubMed]
- DeLorenzi, C. New high dose pulsed hyaluronidase protocol for hyaluronic acid filler vascular adverse events. Aesthet. Surg. J. 2017, 37, 814–825. [Google Scholar] [CrossRef] [PubMed]
- Beć, K.B.; Grabska, J.; Huck, C.W. Near-infrared spectroscopy in bio-applications. Molecules 2020, 25, 2948. [Google Scholar] [CrossRef] [PubMed]
- Beć, K.B.; Huck, C.W. Advances in near-infrared spectroscopy and related computational methods. Molecules 2019, 24, 4370. [Google Scholar] [CrossRef]
- Tian, W.; Chen, G.; Zhang, G.; Wang, D.; Tilley, M.; Li, Y. Rapid determination of total phenolic content of whole wheat flour using near-infrared spectroscopy and chemometrics. Food Chem. 2021, 344, 128633. [Google Scholar] [CrossRef] [PubMed]
- Amirvaresi, A.; Nikounezhad, N.; Amirahmadi, M.; Daraei, B.; Parastar, H. Comparison of near-infrared (NIR) and mid-infrared (MIR) spectroscopy based on chemometrics for saffron authentication and adulteration detection. Food Chem. 2021, 344, 128647. [Google Scholar] [CrossRef]
- Yang, J.; Xu, J.; Zhang, X.; Wu, C.; Lin, T.; Ying, Y. Deep learning for vibrational spectral analysis: Recent progress and a practical guide. Anal. Chim. Acta 2019, 1081, 6–17. [Google Scholar] [CrossRef]
- Lee, L.C.; Liong, C.Y.; Jemain, A.A. Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: A review of contemporary practice strategies and knowledge gaps. Analyst 2018, 143, 3526–3539. [Google Scholar] [CrossRef]
- Luo, X.; Wen, X.; Zhou, M.; Abusorrah, A.; Huang, L. Decision-tree-initialized dendritic neuron model for fast and accurate data classification. IEEE Trans. Neural Netw. Learn. 2022, 33, 4173–4183. [Google Scholar] [CrossRef] [PubMed]
- Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Saritas, M.M.; Yasar, A. Performance analysis of ANN and naive bayes classification algorithm for data classification. Int. J. Intell. Syst. 2019, 7, 88–91. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, Y.; Pan, Y. A new locally adaptive k-nearest neighbor algorithm based on discrimination class. Knowl. Based Syst. 2020, 204, 106185. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Greener, J.G.; Kandathil, S.M.; Moffat, L.; Jones, D.T. A guide to machine learning for biologists. Nat. Rev. Mol. Cell Biol. 2022, 23, 40–55. [Google Scholar] [CrossRef]
- Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Commun. ACM 2019, 63, 68–77. [Google Scholar] [CrossRef]
- Huang, W.; Liu, H.; Zhang, Y.; Mi, R.; Tong, C.; Xiao, W.; Shuai, B. Railway dangerous goods transportation system risk identification: Comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM. Appl. Soft Comput. 2021, 109, 107541. [Google Scholar] [CrossRef]
- Kaseb, Z.; Rahbar, M. Towards CFD-based optimization of urban wind conditions: Comparison of genetic algorithm, particle swarm optimization, and a hybrid algorithm. Sustain. Cities Soc. 2022, 77, 103565. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Zhang, L.; Gao, R.X.; Wu, D. Deep learning for smart manufacturing: Methods and applications. J. Manuf. Syst. 2018, 48, 144–156. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Lv, J. Automatically designing CNN architectures using the genetic algorithm for image classification. IEEE Trans. Cybern. 2020, 50, 3840–3854. [Google Scholar] [CrossRef]
- Banerjee, I.; Ling, Y.; Chen, M.C.; Hasan, S.A.; Langlotz, C.P.; Moradzadeh, N.; Chapman, B.; Amrhein, T.; Mong, D.; Rubin, D.L.; et al. Comparative effectiveness of convolutional neural network (CNN) and recurrent neural network (RNN) architectures for radiology text report classification. Artif. Intell. Med. 2019, 97, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Qin, J.; Hu, Y. Efficient degradation of high-molecular-weight hyaluronic acid by a combination of ultrasound, hydrogen peroxide, and copper ion. Molecules 2019, 24, 617. [Google Scholar] [CrossRef]
- Alkrad, J.A.; Mrestani, Y.; Stroehl, D.; Wartewig, S.; Neubert, R. Characterization of enzymatically digested hyaluronic acid using NMR, Raman, IR, and UV-Vis spectroscopies. J. Pharm. Biomed. Anal. 2003, 31, 545–550. [Google Scholar] [CrossRef]
- Mendes, M.; Cova, T.; Basso, J.; Ramos, M.L.; Vitorino, R.; Sousa, J.; Pais, A.; Vitorino, C. Hierarchical design of hyaluronic acid-peptide constructs for glioblastoma targeting: Combining insights from NMR and molecular dynamics simulations. J. Mol. Liq. 2020, 315, 113774. [Google Scholar] [CrossRef]
- Tokita, Y.; Okamoto, A. Hydrolytic degradation of hyaluronic acid. Polym. Degrad. Stab. 1995, 48, 269–273. [Google Scholar] [CrossRef]
- Buhren, B.A.; Schrumpf, H.; Hoff, N.-P.; Bölke, E.; Hilton, S.; Gerber, P.A. Hyaluronidase: From clinical applications to molecular and cellular mechanisms. Eur. J. Med. Res. 2016, 21, 5. [Google Scholar] [CrossRef]
- Bázár, G.; Romvári, R.; Szabó, A.; Somogyi, T.; Éles, V.; Tsenkova, R. NIR detection of honey adulteration reveals differences in water spectral pattern. Food Chem. 2016, 194, 873–880. [Google Scholar] [CrossRef]
- Kovacs, Z.; Bázár, G.; Oshima, M.; Shigeoka, S.; Tanaka, M.; Furukawa, A.; Nagai, A.; Osawa, M.; Itakura, Y.; Tsenkova, R. Water spectral pattern as holistic marker for water quality monitoring. Talanta 2016, 147, 598–608. [Google Scholar] [CrossRef]
- Dong, Q.; Guo, X.; Li, L.; Yu, C.; Nie, L.; Tian, W.; Zhang, H.; Huang, S.; Zang, H. Understanding hyaluronic acid induced variation of water structure by near-infrared spectroscopy. Sci. Rep. 2020, 10, 1387. [Google Scholar] [CrossRef] [PubMed]
- Noda, I. Two-dimensional infrared spectroscopy. J. Am. Chem. Soc. 1989, 111, 8116–8118. [Google Scholar] [CrossRef]
- Noda, I. Determination of two-dimensional correlation spectra using the Hilbert transform. Appl. Spectrosc. 2000, 54, 994–999. [Google Scholar] [CrossRef]
- Muncan, J.; Tsenkova, R. Aquaphotomics—From innovative knowledge to integrative platform in science and technology. Molecules 2019, 24, 2742. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Paul, D. PCA in high dimensions: An orientation. Proc. IEEE Inst. Electr. Electron. Eng. 2018, 106, 1277–1292. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-M.; Yoo, C.; Choi, S.W.; Vanrolleghem, P.A.; Lee, I.-B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. J. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Kobak, D.; Berens, P. The art of using t-SNE for single-cell transcriptomics. Nat. Commun. 2019, 10, 5416. [Google Scholar] [CrossRef]
- Hekmatmanesh, A.; Wu, H.; Jamaloo, F.; Li, M.; Handroos, H. A combination of CSP-based method with soft margin SVM classifier and generalized RBF kernel for imagery-based brain computer interface applications. Multimed. Tools. Appl. 2020, 79, 17521–17549. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, S.; Zhang, Z.; Jia, W. An improved grid search algorithm to optimize SVR for prediction. Soft Comput. 2021, 25, 5633–5644. [Google Scholar] [CrossRef]
- Soumaya, Z.; Taoufiq, B.D.; Benayad, N.; Yunus, K.; Abdelkrim, A. The detection of Parkinson disease using the genetic algorithm and SVM classifier. Appl. Acoust. 2021, 171, 107528. [Google Scholar] [CrossRef]
- Kour, V.P.; Arora, S. Particle swarm optimization based support vector machine (P-SVM) for the segmentation and classification of plants. IEEE Access 2019, 7, 29374–29385. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS-J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Chen, X.; Chai, Q.; Lin, N.; Li, X.; Wang, W. 1D convolutional neural network for the discrimination of aristolochic acids and their analogues based on near-infrared spectroscopy. Anal. Methods 2019, 11, 5118–5125. [Google Scholar] [CrossRef]
- Chai, Q.; Zeng, J.; Lin, D.; Li, X.; Huang, J.; Wang, W. Improved 1D convolutional neural network adapted to near-infrared spectroscopy for rapid discrimination of Anoectochilus roxburghii and its counterfeits. J. Pharm. Biomed. Anal. 2021, 199, 114035. [Google Scholar] [CrossRef]
- Shang, H.; Shang, L.; Wu, J.; Xu, Z.; Zhou, S.; Wang, Z.; Wang, H.; Yin, J. NIR spectroscopy combined with 1D-convolutional neural network for breast cancerization analysis and diagnosis. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 287, 121990. [Google Scholar] [CrossRef] [PubMed]
- Mishra, P.; Passos, D. Multi-output 1-dimensional convolutional neural networks for simultaneous prediction of different traits of fruit based on near-infrared spectroscopy. Postharvest Biol. Technol. 2022, 183, 111741. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Zheng, J.; Ma, L.; Wu, Y.; Ye, L.; Shen, F. Nonlinear dynamic soft sensor development with a supervised hybrid CNN-LSTM network for industrial processes. ACS Omega 2022, 7, 16653–16664. [Google Scholar] [CrossRef] [PubMed]
- Birim, S.; Kazancoglu, I.; Mangla, S.K.; Kahraman, A.; Kazancoglu, Y. The derived demand for advertising expenses and implications on sustainability: A comparative study using deep learning and traditional machine learning methods. Ann. Oper. Res. 2022, 1, 1–31. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Keun, H.C.; Beckonert, O.; Griffin, J.L.; Richter, C.; Moskau, D.; Lindon, J.C.; Nicholson, J.K. Cryogenic probe 13C NMR spectroscopy of urine for metabonomic studies. Anal. Chem. 2002, 74, 4588–4593. [Google Scholar] [CrossRef]
- Palmioli, A.; Alberici, D.; Ciaramelli, C.; Airoldi, C. Metabolomic profiling of beers: Combining 1H NMR spectroscopy and chemometric approaches to discriminate craft and industrial products. Food Chem. 2020, 327, 127025. [Google Scholar] [CrossRef]
- Waidyanatha, S.; Pierfelice, J.; Cristy, T.; Mutlu, E.; Burback, B.; Rider, C.V.; Ryan, K. A strategy for test article selection and phytochemical characterization of Echinacea purpurea extract for safety testing. Food Chem. Toxicol. 2020, 137, 111125. [Google Scholar] [CrossRef]
- Torniainen, J.; Afara, I.O.; Prakash, M.; Sarin, J.K.; Stenroth, L.; Töyräs, J. Open-source python module for automated preprocessing of near infrared spectroscopic data. Anal. Chim. Acta 2020, 1108, 1–9. [Google Scholar] [CrossRef]
- Sohn, S.I.; Oh, Y.J.; Pandian, S.; Lee, Y.H.; Zaukuu, J.L.Z.; Kang, H.J.; Ryu, T.H.; Cho, W.S.; Cho, Y.S.; Shin, E.K. Identification of Amaranthus species using visible-near-infrared (vis-NIR) spectroscopy and machine learning methods. Remote Sens. 2021, 13, 4149. [Google Scholar] [CrossRef]
- Mishra, P.; Lohumi, S. Improved prediction of protein content in wheat kernels with a fusion of scatter correction methods in NIR data modelling. Biosyst. Eng. 2021, 203, 93–97. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Zhang, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Cheng, H.; Liu, Y. Rapid identification of soil organic matter level via visible and near-infrared spectroscopy: Effects of two-dimensional correlation coefficient and extreme learning machine. Sci. Total Environ. 2018, 644, 1232–1243. [Google Scholar] [CrossRef]
- Noda, I. Recent advancement in the field of two-dimensional correlation spectroscopy. J. Mol. Struct. 2008, 883, 2–26. [Google Scholar] [CrossRef]
- Zanni, M.T.; Hochstrasser, R.M. Two-dimensional infrared spectroscopy: A promising new method for the time resolution of structures. Curr. Opin. Struct. Biol. 2001, 11, 516–522. [Google Scholar] [CrossRef]
- Le Sueur, A.L.; Horness, R.E.; Thielges, M.C. Applications of two-dimensional infrared spectroscopy. Analyst 2015, 140, 4336–4349. [Google Scholar] [CrossRef] [PubMed]
- Knopf-Marques, H.; Pravda, M.; Wolfova, L.; Velebny, V.; Schaaf, P.; Vrana, N.E.; Lavalle, P. Hyaluronic acid and its derivatives in coating and delivery systems: Applications in tissue engineering, regenerative medicine and immunomodulation. Adv. Healthc. Mater. 2016, 5, 2841–2855. [Google Scholar] [CrossRef] [PubMed]
- Tsenkova, R.; Munćan, J.; Pollner, B.; Kovacs, Z. Essentials of aquaphotomics and its chemometrics approaches. Front. Chem. 2018, 6, 363. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.L.; Billings, S.A. Feature subset selection and ranking for data dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 162–166. [Google Scholar] [CrossRef]
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58. [Google Scholar] [CrossRef]
- Al Rahhal, M.M.; Bazi, Y.; AlHichri, H.; Alajlan, N.; Melgani, F.; Yager, R.R. Deep learning approach for active classification of electrocardiogram signals. Inf. Sci. 2016, 345, 340–354. [Google Scholar] [CrossRef]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 2128. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Fan, E.; Wang, P. Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognit. Lett. 2021, 141, 61–67. [Google Scholar] [CrossRef]
- Luque, A.; Carrasco, A.; Martín, A.; de Las Heras, A. The impact of class imbalance in classification performance metrics based on the binary confusion matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]
- Deng, X.; Liu, Q.; Deng, Y.; Mahadevan, S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Inf. Sci. 2016, 340, 250–261. [Google Scholar] [CrossRef]
- Pepe, M.S.; Cai, T.; Longton, G. Combining predictors for classification using the area under the receiver operating characteristic curve. Biometrics 2006, 62, 221–229. [Google Scholar] [CrossRef]







| Method | Accuracy (%) | Precision (%) | Specificity (%) | Sensitivity/ Recall (%) | F1 Score | AUC |
|---|---|---|---|---|---|---|
| Training of SVC | 90 | 92.5 | 92.1 | 88.1 | 90.2 | 0.9706 |
| Training of GS−SVC | 100 | 100 | 100 | 100 | 100 | 1 |
| Training of GA−SVC | 98.8 | 97.5 | 97.6 | 100 | 98.7 | 0.9819 |
| Training of PSO−SVC | 93.8 | 95 | 94.9 | 92.7 | 93.8 | 0.9750 |
| Test of SVC | 70 | 60 | 66.3 | 75 | 66.7 | 0.6400 |
| Test of GS−SVC | 80 | 80 | 80 | 80 | 80 | 0.8000 |
| Test of GA−SVC | 90 | 100 | 100 | 83.3 | 90.9 | 0.9600 |
| Test of PSO−SVC | 80 | 60 | 71.4 | 100 | 75 | 0.8000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Zang, L.; Nie, L.; Li, L.; Zhong, L.; Guo, X.; Huang, S.; Zang, H. Structural Analysis and Classification of Low-Molecular-Weight Hyaluronic Acid by Near-Infrared Spectroscopy: A Comparison between Traditional Machine Learning and Deep Learning. Molecules 2023, 28, 809. https://doi.org/10.3390/molecules28020809
Tian W, Zang L, Nie L, Li L, Zhong L, Guo X, Huang S, Zang H. Structural Analysis and Classification of Low-Molecular-Weight Hyaluronic Acid by Near-Infrared Spectroscopy: A Comparison between Traditional Machine Learning and Deep Learning. Molecules. 2023; 28(2):809. https://doi.org/10.3390/molecules28020809
Chicago/Turabian StyleTian, Weilu, Lixuan Zang, Lei Nie, Lian Li, Liang Zhong, Xueping Guo, Siling Huang, and Hengchang Zang. 2023. "Structural Analysis and Classification of Low-Molecular-Weight Hyaluronic Acid by Near-Infrared Spectroscopy: A Comparison between Traditional Machine Learning and Deep Learning" Molecules 28, no. 2: 809. https://doi.org/10.3390/molecules28020809
APA StyleTian, W., Zang, L., Nie, L., Li, L., Zhong, L., Guo, X., Huang, S., & Zang, H. (2023). Structural Analysis and Classification of Low-Molecular-Weight Hyaluronic Acid by Near-Infrared Spectroscopy: A Comparison between Traditional Machine Learning and Deep Learning. Molecules, 28(2), 809. https://doi.org/10.3390/molecules28020809





