Abstract
Multifunctional materials with a coexistence of proton conduction properties, single–molecule magnet (SMM) behaviors and magneto–optical Faraday effects have rarely been reported. Herein, a new pair of Cu(II)–Dy(III) enantiomers, [DyCu2(RR/SS–H2L)2(H2O)4(NO3)2]·(NO3)·(H2O) (R–1 and S–1) (H4L = [RR/SS] –N,N′–bis [3–hydroxysalicylidene] –1,2–cyclohexanediamine), has been designed and prepared using homochiral Schiff–base ligands. R–1 and S–1 contain linear Cu(II)–Dy(III)–Cu(II) trinuclear units and possess 1D stacking channels within their supramolecular networks. R–1 and S–1 display chiral optical activity and strong magneto–optical Faraday effects. Moreover, R–1 shows a zero–field SMM behavior. In addition, R–1 demonstrates humidity– and temperature–dependent proton conductivity with optimal values of 1.34 × 10−4 S·cm−1 under 50 °C and 98% relative humidity (RH), which is related to a 1D extended H–bonded chain constructed by water molecules, nitrate and phenol groups of the RR–H2L ligand.
1. Introduction
Current interest in multifunctional materials with two or more properties in the same matter have been vigorously pursued in chemistry, physics and material science [,,,] because multifunctionality can simply coexist [], interact when one function affects the other [,] or act in synergy resulting in new functions [,], so as to realize efficient, flexible and smart applications. Multifunctional magnets that combine optimized magnetic properties with additional functions are a class of important examples of such interactions or synergies. For instance, chiral magnets are of special interest not only because interactions between chirality and magnetism can cause some intriguing properties, such as multiferroics [], but also because new physical phenomena could be observed in such optically active magnets stemming from the synergy between chirality and magnetism, such as magneto–chiral dichroisms (MChD) [,] and magneto–optical Faraday effects []. In addition, proton–conductive magnets have lately gained heightened attention because they could be widely used in electrical and magnetic fields [,,,], and the coexistence of proton conduction and magnetism is predicted to produce a new property, called spinprotonics [,]. In pursuit of advanced multifunctional magnets, tri– or more functional magnets, such as chiral proton–conductive magnets, have also appeared []. Nevertheless, such multifunctional magnets with chirality and proton conduction are quite rare because simultaneously integrating these functions into a single material is still a daunting challenge.
Single molecule magnets (SMMs), as one of the major breakthroughs in magnetic research in the past three decades, possess a slow relaxation of magnetization that is similar to memory effects observed in magnetic nanoparticles, offering promising application prospects in the next generation of quantum computing, spintronics and high–density data storage [,]. To date, a considerable number of d– [,,], d–f [,] and pure f–block [,,] metal complexes showing SMM behaviors have been reported. Within this field, lanthanide ions, especially the Dy3+ ion, are the most sought–after spin centers because of their ground–state spin and large magnetic anisotropy [,]. The magnetic anisotropy of the Dy(III) ion in SMMs arises from spin–orbit coupling and an axial crystal field []. For example, high–performance SMMs are Dy(III)–containing metal–inorganic complexes displaying slow magnetic relaxation behavior with record magnetic blocking temperatures [,] or high–energy barriers []. However, these molecules usually suffer from the fast quantum tunneling of magnetization (QTM) in zero field, limiting the relaxation time [,]. Previous achievements demonstrated that intramolecular magnetic exchange in SMMs can powerfully suppress QTM to obtain high working temperatures []. Therefore, the construction of mixed 3d–4f SMMs is desirable because such systems combine the large magnetic anisotropy of lanthanide and the strong magnetic couplings of 3d spin centers.
Recently, multifunctional SMMs have been pursued with particular interest because introducing additional properties can provide deep investigations into magnetic behavior [] to achieve their applications as soon as possible. For instance, luminescent SMMs, with an interplay between magnetic anisotropy and luminescence, are observed on the basis of the electronic structure of 4f metal ions [], and many electrical–conducting [,], chiral [], proton–conductive SMMs [] have been prepared. In pursuit of advanced multifunctional materials, a few tri– or more functional SMMs have also appeared []. Among them, chiral proton–conductive SMMs have attracted much attention as they have promising applications in electrical and magnetic fields and can provide an excellent platform to explore synergies among different functions (e.g., magnetism and chirality, proton conduction and magnetism). Surprisingly, chiral proton–conductive SMMs with magneto–optical Faraday effects are scarce, to the best of our knowledge, only one such related work has been achieved [].
In addition to spin center, the selection of organic ligands is important to achieve chiral proton–conducting SMMs. In this paper, the R– and S– amine–phenol ligands, (RR/SS)–N,N′–bis(3–hydroxysalicylidene)–1,2–cyclohexanediamine (H4L), are chosen as organic ligands on the basis of the following considerations: (1) according to numerous previously reported works, the Schiff–base ligands are beneficial for the formation of low dimensional 3d–4f complexes showing SMM behavior [,,]; (2) chiral ligands are prone to induce the structures to crystallize in enantiomeric forms that can lead to new functions, such as MChD and strong magneto–optical Faraday effects in magnetic molecules; and (3) the ligand with four phenol –OH groups is an excellent H–bonding acceptor and donor that favors the formation of rich H–bonding networks in materials, which is constructive for a proton conductor. Herein, a new pair of Cu(II)–Dy(III) enantiomers, [DyCu2(RR/SS–H2L)2(H2O)4(NO3)2]·(NO3)·(H2O) (R–1 and S–1), is successfully obtained, which contain linear Cu2Dy trimers. Due to the enantiomeric structures of R–1 and S–1, the magnetism and proton conductivity of the two isomers are expected to be the same, therefore, only the magnetic and proton–conducting properties of R–1 were studied. R–1 shows the zero–field SMM behavior and moderate proton conductivity of 1.34 × 10−4 S·cm−1 under 50 °C and 98% RH.
2. Results and Discussion
2.1. X–ray Single–Crystal Structure Determination
Suitable single crystals of R–1 and S–1 were used to collect the diffraction data on a Bruker APEX–II CCD and Rigaku CCD diffractometer equipped with graphite–monochromated Mo–Kα radiation (λ = 0.71073 Å) at 293 K, respectively. The raw intensity dates were reduced and collected through the SAINT software 1996 []. The olex2 solve structure solution program and the ShelXL–2015 refinement package were applied to solve the two structures [,]. The difference Fourier map was used to locate non–hydrogen atoms. Hydrogen atoms were placed in their calculated positions geometrically and refined based on the riding model. No higher space group could be found by the PLATON software from the IUcr website (http://www.iucr.org/ (accessed on 2 November 2023)) []. Pertinent crystal data, structure refinement results and selected bond lengths and bond angles of R–1 and S–1 were all displayed in Table S1 and Table S2 in the ESI, respectively.
2.2. Crystal Structural Descriptions of R–1
Single–crystal X–ray diffraction results show that R–1 and S–1 are isomorphous (Figure 1) and crystallized in a monoclinic system with the space group of C2. Therefore, R–1 is selected as an example to explain the crystal structure. As depicted in Figure S1, the asymmetric unit contains two half–occupied Dy(III) ions, two independent Cu(II) ions, two bideprotonated organic ligands RR–H2L2−, three NO3− anions, four coordinated molecules and one lattice water molecule. The Dy1 ion is coordinated by eight phenolate oxygen atoms (i.e., O1, O2, O3, O4, O1B, O2B, O3B and O4B) from two RR–H2L2− ligands and one coordinated water molecule (O1W). Based on the SHAPE analysis [], the coordinated environment of Dy1 exhibits a capped square antiprism with a continuous shape measurement value of 2.294 (Table S3 and Figure S3a). The Dy2 ion is also nine–coordinated by eight phenolate oxygen atoms and one coordinated water molecule (O5, O6, O7, O8, O5A, O6A, O7A, O8A and O3W) to a similar coordination geometry as the capped square antiprism (Figure S3b). The bond lengths of Dy–O are within the range of 2.311(5)–2.556(7) Å, which are similar to those of Dy–O based complexes [,]. Cu1 is pseudo–six coordinated by two phenol O atoms, two nitrogen atoms from one RR–H2L2− ligand, an oxygen atom from a nitrate anion and an oxygen atom from a coordinated water molecule, forming a strongly distorted octahedral–coordinated environment (Figure S3c). Notably, one of the “axial” bond lengths (Cu1–O13 = 2.934(4) Å) is substantially longer than the equatorial and another “axial” distances (1.890(5)–1.954(1) Å), which are attributed to the Jahn–Teller distortion and closely resemble other copper(II)–oxygen–based complexes [,,]. Moreover, the distorted octahedron configuration of Cu2 ion is similar to that of the Cu1 ion (Figure S3d). Interestingly, the RR–H2L2– adopts a sexadentate ligand with μ2–κO1:κO2:κO3:κO4:κN1:κN2 coordination mode, and two phenol groups are deprotonated, resulting in a RR–H2L2– deprotonation type. As shown in Figure 1, two RR–H2L2− ligands bridge one Dy(III) ion and two Cu(II) ions to form trinuclear Cu1–Dy1–Cu1B and Cu2–Dy2–Cu2B units, in which the Cu(II) ions and the Dy(III) ion are arranged in an almost linear manner with Cu(II)–Dy(II)–Cu(II) angles of 174.046(23)° and 172.975(24)°, respectively.
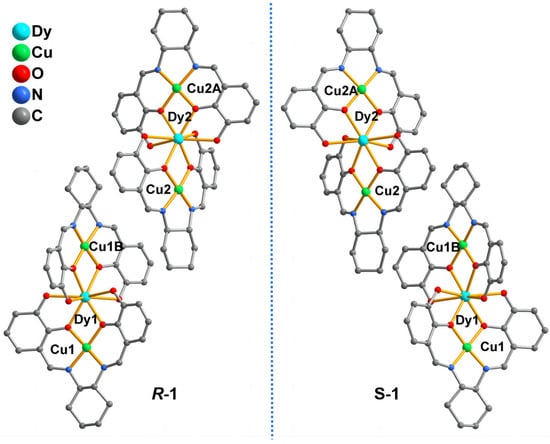
Figure 1.
The enantiomeric structures of R–1 and S–1. The coordinated water molecules, coordinated nitrate oxygen atoms and the H atoms are omitted for clarity. Symmetric code: B: 1 − x, y, 2 − z.
As displayed in Figure S4, these adjacent Cu1–Dy1–Cu1B and Cu2–Dy2–Cu2B trimers are alternately connected by hydrogen bonds constructed with coordinated water molecules, nitrate anions and phenol groups of the RR–H2L2− ligand (O1−H1···O12, O1−H1···O13, O1W–H1WA···O12, O1W−H1WB···O12, O2W−H2WA···O14, O4−H4···O5W) forming 1D supermolecular chains. These 1D supermolecular chains are further formed by hydrogen bonds constructed with coordinated water molecules and nitrate anions (O2W−H2WB···O15, O4W−H4WA···O16) forming a 2D supermolecular layer along the bc plane (Figure S5). The NO3− counteranions are located in the accessible voids of R–1 (Figure S5). Notably, a 1D extensive H–bonding chain is formed by water molecules, nitrate anions and phenol groups of the RR–H2L2− ligand (O1W−H1WA···O12, O1−H1···O12, O1−H1···O2, O4−H4···O2, O4−H4···O5W, O5W−5WB···O15, O2W−H2WB···O15, O2W−H4···O3, O1W−H4···O3) (Figure 2).
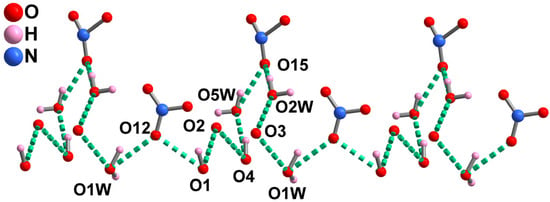
Figure 2.
The 1D H–bonding chain and the potential proton transport pathway of R–1.
2.3. Thermal Stability
As depicted in Figure S6a, the X–ray diffraction patterns of enantiomers R–1 and S–1 are basically in accordance with the simulated patterns, demonstrating that the samples are pure phases. TGA curves show that enantiomers R–1 and S–1 have similar thermal behaviors. Therefore, the description is performed only for R–1, Figure S7 shows that 5.70% of the weight loss before 109 °C is attributed to the release of one lattice water molecule and three coordinated water molecules (calcd. 5.76%). The second weight loss of 14.92% at temperatures up to 297 °C results from the release of three nitrate anions (calcd. 14.88%). Then, the decomposition of the framework occurs until 800 °C. The high thermal stability is key in a promising proton conductor. Thus, the crystal sample of R–1 is heated to 30 °C, 50 °C, 70 °C, 90 °C and 110 °C in air for 24 h; their measured PXRD patterns still match the simulated one (Figure S6b), indicating that R–1 has excellent thermal stability.
2.4. Circular Dichroism (CD) and Magnetic Circular Dichroism (MCD)
The UV–vis and CD spectra of R–1 and S–1 are obtained to investigate their optical activities. As shown in Figure S9, the UV–vis spectra of R–1 and S–1 in CH3CN solution are almost identical, and the strong peaks at 274 nm in the UV region can be attributed to the π–π* transition of the aromatic benzene rings of H4L ligands. The peak around 352 nm is ascribed to π–π* conjugated interplays between benzene rings and the carbon–nitrogen double bond []. The CD spectra of R–1 and S–1 in MeCN solutions have an excellent mirror image relationship in the 200–700 nm range, revealing their enantiomeric natures (Figure S8). Moreover, the peak positions of CD spectra are roughly consistent with those in the UV spectra. CD spectra show two cotton peaks around 220 and 244 nm, and a peak around 288 nm, which can be assigned to exciton coupling for π–π* transitions of aromatic groups []; additionally, the CD peak at 374 nm is derived from the n–π* transition of azomethine chromophore []. The weak peak at 580 nm belongs to the d–d transition of the transition metal Cu(II) (Figure 3a) [].
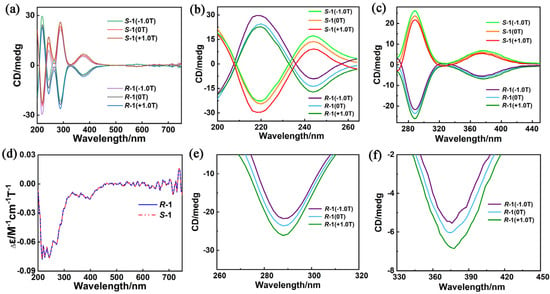
Figure 3.
CD spectra of R−1 and S−1 in CH3CN solution (c = 1.6 × 10−5 molL−1; H = 0 and ±1.0 T; optical path = 1 mm) in the range of (a) 200–750 nm; and partially enlarged view of (b) 200–265 nm, (c) 265–450 nm and (d) MCD spectra of enantiomers R–1 and S–1 in a CH3CN solution (c = 1.6 × 10−5 molL−1) at room temperature; and partially enlarged view of CD spectra of (e) R–1 and (f) R–1 in the range of 260–450 nm.
Their CD spectra under external magnetic fields (±1.0 T) and direct current (dc) fields are measured to study the magneto–optical properties of R–1 and S–1 at room temperature more clearly. Positive (+1.0 T, NS) and reverse (−1.0 T, SN) magnetic fields are parallel and antiparallel, respectively, to the polarized light. Figure 3a shows that the CD signals of R–1 and S–1 exhibit a negative effect under the positive magnetic field (+1.0 T, NS) without changing the position and shape of the peak. By contrast, the negative magnetic field (−1.0 T, SN) shows a positive effect on CD signals. Notably, the CD signal intensities of R–1 under +1.0 T and S–1 under −1.0 T are higher than that of CD signals without magnetic field (0 T). As depicted in Figure 3d, pure MCD signals are obtained in accordance with the formula MCD = [CD(+1.0T) − CD(−1.0T)]/2 to further study the magneto–optical properties of R–1 and S–1 []. Strong MCD signals of R–1 and S–1 are detected at 220, 243 and 382 nm (Figure 3b,e), which are ascribed to the large orbital angular momentum of aromatic π–conjugated systems of the H4L ligands and excitonic coupling of chromophores []. Remarkably, the |gmax(MCD)| values of R–1 and S–1 at room temperature are 0.435 T−1 and 0.433 T−1, respectively (Figure S10), which are large values and comparable with those of previously reported molecular complexes [,], indicating strong magneto–optical Faraday effects.
2.5. Magnetic Properties
The direct current (dc) magnetic susceptibility has been carried out on polycrystalline samples of R–1 in the temperature range of 2–300 K, under an applied magnetic field of 1000 Oe (Figure S11a). At room temperature, the χMT molar value is 15.55 cm3Kmol−1 at 300 K, which is slightly larger than the theoretical value for two CuII ions (S = 1/2, g = 2, and C = 0.75 cm3Kmol−1) and one DyIII ion (S = 5/2, L = 5, 6H15/2, g = 4/3, and C = 14.18 cm3Kmol−1) []. With decreasing temperature, χMT gradually increases within the range of 75–300 K and then quickly rises to a maximum value of 20.78 cm3Kmol−1 at 6 K. After further cooling, the χMT value of R–1 decreases to 19.44 cm3Kmol−1 at 2 K. This behavior may be due to the presence of ferromagnetic Cu–Dy coupling or/and the progressive depopulation of DyIII stark sublevels [,]. The field dependence of magnetization (M vs. H) for R–1 is measured in the temperature range of 2–5 K (Figure S11b). For complex R–1, the M value reaches 8.67 Nβ at 2 K, which is lower than the theoretical saturation value of 12 Nβ [,]. Furthermore, the unsaturated magnetization and the nonsuperimposition of the M vs. H/T curves suggests the existence of an isolated ground state and/or magnetic anisotropy in the system for compounds []. The temperature dependence of the alternating current (ac) magnetic susceptibility measurement was determined to explore the magnetization dynamics of R–1 in depth. As shown in Figure 4, under a zero–dc field with an oscillation of 2.5 Oe, the plots of in–phase (χ′) and out–of–phase (χ″) signals show temperature dependence in the frequency range of 50–1399 Hz, revealing characteristic magnet relaxation of SMMs []. The ln(τ)–T−1 plot, which is based on the χ″–ν curves (Figure S12) was fitted using the Arrhenius law, −ln(τ) = −ln(τ0) + Ueff/kBT, affording an effective energy barrier of 14.60 K and a pre–exponential factor (τ0) of 7.74 × 10−6 s for R–1 (Figure S13a). The energy barrier of R–1 is comparable with that of the complex ([Dy{hfac}3][Cu{hfac}2]2{3,5–bPy–Ph–Nit}{H2O}])n·nC7H16 (hfac− = hexafluoroacetylacetonate, 3,5–bPy–Ph–Nit = 2–[3,5–bis(3–pyridyl)–phenyl]–4,4,5,5–tetramethylimidazoline–1–oxyl–3–oxide, Ueff = 17.80 K) [], and the τ0 value of R–1 is in accordance with the expected τ0 values (i.e., 10−6–10−11) for SMMs []. The Cole–Cole diagrams (χ″ vs. χ′) of R–1 show semicircular shapes between 2.0–4.1 K. The width distribution of relaxation time (α) was fitted with the CC–Fit (Figure S13b), which uses the generalized Debye model, giving α values of 0.14–0.19 (Table S5). The small α values indicate a relatively narrow distribution for a single relaxation process.
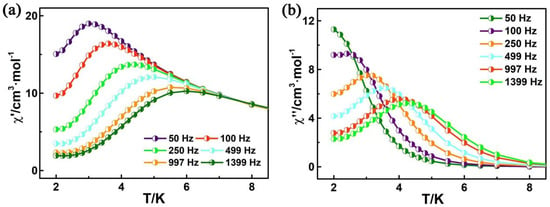
Figure 4.
Temperature dependence of the in−phase (a) and out−of−phase (b) components of the ac magnetic susceptibility for R–1 in zero–dc fields with an oscillation of 2.5 Oe.
2.6. Proton Conduction
In recent years, coordination complexes (CPs), as a new class of proton–conducting materials that can be used in fuel cells, smart grids and information processing devices [,], have been highlighted because of their low cost, moderate operating temperature, functionalizable pores and tunable structures. In particular, their crystalline features offer excellent opportunities for revealing the structure–activity relationship, such as proton transfer pathways, which is conducive to designing improvements to proton conductive materials [,]. Previous reports showed that designable H–bonding networks for proton transport pathways are crucial in a low–temperature proton conductor. Therefore, the 1D extended H–binding chain in R–1 and S–1 can act as an excellent proton transport pathway, and the relatively high water absorption and high thermal properties of R–1 make its good proton conductivity property to be explored. Ac impedance measurement was carried out using a compacted pellet over a frequency domain of 107–1 Hz. As illustrated in Figure 5a, all Nyquist plots present one semicircle at high frequencies with an inclined tail at low frequencies, indicative of a typical feature of proton migration [,]. The humidity–dependent proton conductivities of R–1 are measured under 60%–100% RH at a fixed temperature to evaluate the effect of humidity on conductivity (Figure 5b). At 60% RH and 25 °C, the conductivity of R–1 is nearly negligible (1.18 × 10−9 S·cm−1), which increases by nearly four orders of magnitude with increasing RH and evaluated to be 7.44 × 10−5 S·cm−1 at 100% RH (Table S6). For R–1, the increasing trend of proton conductivities manifest that guest water molecules play a remarkable role in promoting the proton migration in accordance with most water–assisted Ln–CPs [,]. At fixed RH, the proton conductivity values of R–1 increase along with increasing temperatures. Temperature–dependent conductivities are explored to further determine the proton conduction mechanism. At 100% RH, the conductivity of R–1 increases from 7.44 × 10−5 S·cm−1 to the optimal value of 1.34 × 10−4 S·cm−1 (under 50 °C) as the temperature increases (Figure 5c and Table S7). The optimal value (1.34 × 10−4 S·cm−1) is comparable to those of some reported Ln–MOFs, namely, (APP)4[BiAgI8]·H2O (APP = 4–aminopiperidine, 2.09 × 10−4 S·cm−1 at 95 °C and 90% RH) [], LnL(H2O)3·2H2O (L = N–phenyl–N′–phenyl bicycle [,,]oct–7–ene–2,3,5,6– tetracarboxdiimide tetracarboxylic acid; 1.33 × 10−5, 75 °C, and 97% RH) [] and Ce(H5L)(H2O)4 (L = 1,2,4,5–tetrakis(phosphonomethyl)benzene, 1.2 × 10−4, 85 °C and 95% RH) []. As illustrated in Figure 5d, the activation energy (Ea) is calculated to be 0.22 eV by fitting to the Arrhenius equation σT = σ0exp(Ea/kT) [], illustrating that the possible pathway of proton migration for R–1 follows the Grotthus mechanism (Ea = 0.1–0.4 eV) rather than the vehicle mechanism (Ea = 0.5–0.9 eV). The Grotthus mechanism, a typical hopping mechanism, occurs in the process of proton transfer among hydrogen–bond networks [,,,]; while the vehicle mechanism is mediated by protons transferred by the diffusion of “movable carriers” (e.g., HS−, OH−, H2O, and H3O+) [,,]. On the basis of the structural analysis, in R–1, the 1–D extended H–bonding chain constructed by water molecules, nitrate anions and phenol groups of the RR–L2− ligand is conducive to high proton conductivity (1.34 × 10−4 S·cm−1). Remarkably, the optimal proton conductivity of the R–1 is two orders of magnitude higher than that of the reported chiral proton–conductive SMMs with the magneto–optical Faraday effect (Table S8). Moreover, the well–matched PXRD patterns of R–1 before and after water conductivity measurements show no change, confirming that the sample is stable during proton conduction measurements (Figure S6a).
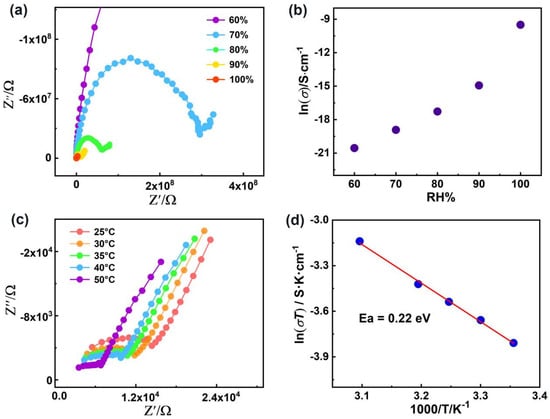
Figure 5.
(a) Nyquist plot for R−1 at 25 °C under different RH levels; (b) plot of proton conductivity for R−1 vs. RH at 25 °C; (c) Nyquist plot for R−1 at different temperatures under 100% RH; (d) Plots of ln(σT) vs. 1000/T for R−1 under 100% RH.
3. Experimental Section
All chemistry regents were purchased from commercial suppliers and used without further purification. The H4L ligand (Figure S2) was synthesized according to the literature [].
3.1. Materials and Instruments
Elemental analysis (C, H, and N) was measured with an Elementar Vario EL III microanalyzer. IR spectra were recorded in the 400–4000 cm−1 region using KBr pellets and a Nicolet Magna 750 FT–IR spectrophotometer. PXRD patterns were measured on a Bruker ADVANCE D8θ −2θ diffractometer equipped with Cu–Kα radiation (λ = 1.54057 Å). TG analysis of R–1 was performed on a NETZSCH STA2500 thermal instrument with heating rates of 10 °C min−1 under N2 atmosphere from 25 °C to 800 °C. The circular dichroism (CD) spectra were acquired by using a Chirascan ACD spectrometer. The MCD spectra were measured using a Chirascan ACD spectrometer equipped with a permanent magnet (+1.0 T or −1.0 T). Magnetic susceptibilities were carried out on a Quantum Design MPMS–XL5 (SQUID) magnetometer. Proton conductivity measurements were measured on a Solartron 1260 impedance/gain–phase analyzer with a quasi–four–electrode AC impedance technique to study the proton mobility in conditions of different temperatures and humidities. The microcrystalline sample was pressed into a pellet with thickness of 0.71 mm and diameter of 2.5 mm. The resistance values of the sample were obtained from the Debye semicircle on the Nyquist plot. The conductivity was calculated using the equation σ = L/(RS), σ (S·cm−1) means the conductivity, L (cm) is the thickness, R (Ω) is the resistance and S (cm2) is cross–sectional the area.
3.2. Syntheses of R–1 and S–1
A mixture of RR–H4L (0.2 mmol) and Cu(Ac)2·6H2O (0.2 mmol) in CH3OH/CHCl3 (v/v = 1:1) was stirred for 15 min. Then Dy(NO3)3·6H2O (0.1 mmol) was added and the mixture continuously stirred for another 15 min. After filtration, the filtrate was crystallized at room temperature by evaporation without disturbation. After two weeks, dark purple columnar crystals R–1 were obtained and washed several times with CHCl3. The yield was 45–50% (based on Dy). Complex S–1 was prepared using the same procedure as the synthesis of R–1 but SS–H4L was used instead of RR–H4L. Anal. Calcd for R–1 (C40H44Cu2DyN7O21, %): C, 38.42; H, 3.55; N, 7.84%; Found (%): C, 38.56; H, 3.57; N, 7.80%. FT–IR peaks (KBr, cm−1) for R–1: 423w, 523w, 562w, 648w, 743w, 869w, 1022w, 1209s, 1253s, 1304s, 1383vs, 1467s, 1628vs, 2862m, 2939m, 3404m; for S–1: 422w, 525w, 568w, 661w, 744m, 872w, 1021w, 1084w, 1209s, 1248s, 1304s, 1383vs, 1467vs, 1622vs, 2864m, 2937m, 3397m.
4. Conclusions
In this work, a new pair of enantiomers containing trinuclear DyCu2 linear units, [DyCu2(RR/SS–H2L)2(H2O)4(NO3)2]·(NO3)·(H2O) (R–1 and S–1) (H4L = [RR/SS]–N,N′–bis [3–hydroxysalicylidene]–1,2–cyclohexanediamine), were rationally designed and successfully prepared. R–1 shows zero–field SMM behavior, strong magneto–optical Faraday effects and moderate proton conductivity (1.34 × 10−4 S·cm−1 under 50 °C under 100% RH) originating from a 1D H–bonded chain built by water molecules, nitrate and phenol groups of the RR–H2L ligand. Furthermore, this study demonstrates that chiral hydroxysalicylic ligands are good ligands for preparing homochiral 3d–4f molecule–based materials with multifunctionalities including SMM behavior, proton conductivity and magneto–optical coupling.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28227506/s1. Table S1. Crystal data for R–1 and S–1. Table S2. Selected bond lengths (Å) and angles (o) for R–1 and S–1. Table S3. Summary of SHAPE analysis for R–1. Table S4. H-bonding length and angle table for R–1. Figure S1. The asymmetric unit of R–1 with 40% thermal ellipsoids. Symmetry codes: A: x, 1−y, −z. The H atoms are omitted for clarity. Figure S2. The structure of the H4L ligand. Figure S3. The coordinated geometry of Dy1, Cu1, and Cu2. Figure S4. The 1-D supramolecular chain of R–1 connected through hydrogen bonds along the bc plane (green dashed line). Figure S5. The 2-D supramolecular layer of R–1 connected through hydrogen bonds along the ab plane (green dashed line). Figure S6. (a) PXRD patterns of the simulated one, as-synthesized R–1 and S–1 and after proton conduction of R–1. (b) PXRD patterns of R–1 after heated at different temperature for 24 h. Figure S7. The TGA plot of R–1 andS–1. Figure S8. CD spectra of enantiomers R–1 andS–1 in a CH3CN solution (c = 0.02 g·L−1) at room temperature. Figure S9. UV spectra of enantiomers R–1 andS–1 in CH3CN solution (c = 0.02 g·L−1) at room temperature. Figure S10. (a) χMT vs T plots for R–1 at 1000 Oe. (b) Field-dependent magnetization for R–1. Figure S11. Plot of ln(τ) versus T−1 for R–1, the red solid line is fitted with the Arrhenius law. Figure S12. The χ″-ν curves for R–1. Figure S13. (a) Plot of ln(τ) versus T−1 for R–1, the red solid line is fitted with the Arrhenius law. (b) Cole–Cole plots of R–1 under zero dc field (the yellow solid line represents the least-squares fitting by using CC-FIT software). Table S5. Linear combination of two modified Debye model fitting parameters from 2.0 to 4.1 K at Hdc = 0 Oe. Table S6. The proton conductivity of R–1 at 25 °C under variable relative humidity (RH). Table S7. The proton conductivity of R–1 at 100 % RH under variable temperature (°C). Table S8. Comparison of the properties of proton conduction, single molecule magnet (SMM) and magneto-optical Faraday effect of R–1 with that of the complexes based on chiral Schiff ligands.
Author Contributions
Conceptualization, S.-D.Z. and Y.-L.Z.; methodology, H.-R.W., Y.-B.L. and C.-M.L.; validation, S.-J.L. and C.-M.L.; investigation, S.-Y.Z., B.S., Y.L. and F.L.; writing—original draft preparation, S.-D.Z.; writing—review and editing, Y.-B.L. and C.-M.L.; project administration, S.-D.Z. and Y.-B.L.; funding acquisition, Y.-B.L. and C.-M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NSF of China (21661005, 22271289 and 22161002), the NSF of Jiangxi Provincial Education Department (GJJ211416 and GJJ2201223).
Data Availability Statement
X–ray crystallographic data file in CIF format, IR spectra, H–bonding length and angle, selected bond distances and angles, Summary of SHAPE analysis or R–1 and S–1. The asymmetric unit, 1D supramolecular chain, 2D supramolecular layer of R–1. The structure of the H4L ligand. The PXRD patterns, TGA plot, CD spectra, UV spectra, corresponding gMCD values (MCD) of enantiomers R–1 and S–1. The χMT vs T plot, ln(τ) vs T−1 plot and field–dependent magnetization for R–1. Linear combination of two modified Debye model fitting parameters. The proton conductivity of R–1 under different RHs and temperatures. CCDC number: R–1 for 2195312 and S–1 for 2195311.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rikken, J.L.J.A.; Raupach, E. Observation of magneto–chiral dichroism. Nature 1997, 390, 493–494. [Google Scholar] [CrossRef]
- Barron, L.D. Chirality, magnetism and light. Nature 2000, 405, 895–896. [Google Scholar] [CrossRef]
- Kirchon, A.; Feng, L.; Drake, H.F.; Joseph, E.A.; Zhou, H.C. From fundamentals to applications: A toolbox for robust and multifunctional MOF materials. Chem. Soc. Rev. 2018, 47, 8611–8638. [Google Scholar] [CrossRef]
- Liu, C.M.; Xiong, R.G.; Zhang, D.Q.; Zhu, D.B. Nanoscale Homochiral C3–Symmetric Mixed–Valence Manganese Cluster Complexes with Both Ferromagnetic and Ferroelectric Properties. J. Am. Chem. Soc. 2010, 132, 4044–4045. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Chen, W.C.; Li, Z.J.; Zhang, J.F.; Zhao, W.J.; Feng, Y.; Tang, B.Z.; Lee, C.S. Manipulation of Molecular Aggregation States to Realize Polymorphism, AIE, MCL, and TADF in a Single Molecule. Angew. Chem. Int. Ed. 2018, 57, 12473–12477. [Google Scholar] [CrossRef]
- Train, C.R.; Gheorghe, R.; Krstic, V.; Chamoreau, L.; Ovnesyan, N.S.; Rikken, G.L.J.A.; Gruselle, M.; Verdaguer, M. Strong magneto–chiral dichroism in enantiopure chiral ferromagnets. Nat. Mater. 2008, 7, 729–734. [Google Scholar] [CrossRef]
- Wang, H.Y.; Ge, J.Y.; Hua, C.; Jiao, C.Q.; Wu, Y.; Leong, C.F.; D’Alessandro, D.M.; Liu, T.; Zuo, J.L. Photo– and Electronically Switchable Spin–Crossover Iron(II) Metal–Organic Frameworks Based on a Tetrathiafulvalene Ligan. Angew. Chem. Int. Ed. 2017, 56, 5465–5470. [Google Scholar] [CrossRef]
- Ou Yang, J.; Crassous, J. Chiral multifunctional molecules based on organometallic helicenes: Recent advances. Coord. Chem. Rev. 2018, 376, 533–547. [Google Scholar] [CrossRef]
- Yang, J.G.; Li, K.; Wang, J.; Sun, S.S.; Chi, W.J.; Wang, C.; Chang, X.Y.; Zou, C.; To, W.P.; Li, M.D.; et al. Controlling Metallophilic Interactions in Chiral Au(I) Double Salts towards Excitation Wavelength–Tunable Circularly Polarized Luminescence. Angew. Chem. Int. Ed. 2020, 59, 6915–6922. [Google Scholar] [CrossRef]
- Long, J.; Ivanov, M.S.; Khomchenko, V.A.; Mamontova, E.; Thibaud, J.M.; Rouquette, J.; Beaudhuin, M.; Granier, D.; Ferreira, R.A.S.; Carlos, L.D.; et al. Room temperature magnetoelectric coupling in a molecular ferroelectric ytterbium(III) complex. Science 2020, 367, 671–676. [Google Scholar] [CrossRef]
- Atzori, M.; Breslavetz, I.; Paillot, K.; Inoue, K.; Rikken, G.L.J.A.; Train, C. A Chiral, Prussian Blue Analogue Pushes Magneto–Chiral Dichroism Limits. J. Am. Chem. Soc. 2019, 141, 20022–20025. [Google Scholar] [CrossRef]
- Atzori, M.; Santanni, F.; Breslavetz, I.; Paillot, K.; Caneschi, A.; Rikken, G.L.J.A.; Sessoli, R.; Train, C. Magnetic Anisotropy Drives Magnetochiral Dichroism in a Chiral Molecular Helix Probed with Visible Light. J. Am. Chem. Soc. 2020, 142, 13908–13916. [Google Scholar] [CrossRef]
- Liu, C.M.; Sun, R.; Wang, B.W.; Wu, F.; Hao, X.; Shen, Z. Homochiral Ferromagnetic Coupling Dy2 Single–Molecule Magnetswith Strong Magneto–Optical Faraday Effects at Room Temperature. Inorg. Chem. 2021, 60, 12039–12048. [Google Scholar] [CrossRef]
- Lim, D.W.; Kitagawa, H. Proton Transport in Metal–Organic Frameworks. Chem. Rev. 2020, 120, 8416–8467. [Google Scholar] [CrossRef]
- Ye, Y.X.; Gong, L.S.; Xiang, S.C.; Zhang, Z.J.; Chen, B.L. Metal–Organic Frameworks as a Versatile Platform for Proton Conductors. Adv. Mater. 2020, 32, 1907090. [Google Scholar] [CrossRef]
- Han, B.X.; Jiang, Y.F.; Sun, X.R.; Li, Z.F.; Li, G. Proton conductive N–heterocyclic metal–organic frameworks. Coord. Chem. Rev. 2021, 432, 213754. [Google Scholar] [CrossRef]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Sadakiyo, M.; Ōkawa, H.; Shigematsu, A.; Ohba, M.; Yamada, T.; Kitagawa, H. Promotion of Low–Humidity Proton Conduction by Controlling Hydrophilicity in Layered Metal–Organic Frameworks. J. Am. Chem. Soc. 2012, 134, 5472–5745. [Google Scholar] [CrossRef]
- Okawa, H.; Sadakiyo, M.; Yamada, T.; Maesato, M.; Ohba, M.; Kitagawa, H. Proton–Conductive Magnetic Metal–Organic Frameworks, {NR3(CH2COOH)}[MaIIMbIII(ox)3]: Effect of Carboxyl Residue upon Proton Conduction. J. Am. Chem. Soc. 2013, 135, 2256–2262. [Google Scholar] [CrossRef]
- Pardo, E.; Train, C.; Gontard, G.; Boubekeur, K.; Fabelo, O.; Liu, H.B.; Dkhil, B.; Lloret, F.; Nakagawa, K.; Tokoro, H.; et al. High Proton Conduction in a Chiral Ferromagnetic Metal–Organic Quartz–like Framework. J. Am. Chem. Soc. 2011, 133, 15328–15331. [Google Scholar] [CrossRef]
- Bill, E. Single–molecule magnets: Iron lines up. Nat. Chem. 2013, 5, 556–557. [Google Scholar] [CrossRef]
- Katie, R.M.; Stefan, G.M.; Wayne, W.L.J.; Stosh, A.K.; David, K.S.; Tolek, T.; Jeffrey, R.L. Influence of Pyrazolate vs N-Heterocyclic Carbene Ligands on the Slow Magnetic Relaxation of Homoleptic Trischelate Lanthanide(III) and Uranium(III) Complexes. J. Am. Chem. Soc. 2014, 16, 6056–6068. [Google Scholar]
- Abbas, P.; Quinn, K.; Alexandropoulos, D.I.; Damjanović, M.; Wernsdorfer, W.; Escuer, A.; Mayans, J.; Orcid, M.P.; Stamatatos, T.C. Transition Metal Single–Molecule Magnets: A {Mn31} Nanosized Cluster with a Large Energy Barrier of ~60 K and Magnetic Hysteresis at ~5 K. J. Am. Chem. Soc. 2017, 139, 15644–15647. [Google Scholar] [CrossRef]
- Chakarawet, K.; Bunting, P.C.; Long, J.R. Large Anisotropy Barrier in a Tetranuclear Single–Molecule Magnet Featuring Low–Coordinate Cobalt Centers. J. Am. Chem. Soc. 2018, 140, 2058–2061. [Google Scholar] [CrossRef]
- Ibrahim, M.; Lan, D.Y.H.; Bassil, B.S.; Xiang, Y.X.; Suchopar, A.; Powell, A.K.; Kortz, U. Hexadecacobalt(II)–Containing Polyoxometalate–Based Single–Molecule Magnet. Angew. Chem. Int. Ed. 2011, 50, 4708–4711. [Google Scholar] [CrossRef]
- Osa, S.; Kido, T.; Matsumoto, N.; Re, N.; Pochaba, A.; Mrozinski, J. A Tetranuclear 3d−4f Single Molecule Magnet:[CuIILTbIII(hfac)2]2. J. Am. Chem. Soc. 2004, 126, 420–421. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Jena, H.S.; Konar, S. Co3Gd4 Cage as Magnetic Refrigerant and Co3Dy3 Cage Showing Slow Relaxation of Magnetisation. Molecules 2022, 27, 1130. [Google Scholar] [CrossRef]
- Meng, Y.S.; Xu, L.; Xiong, J.; Yuan, Q.; Liu, T.; Wang, B.W.; Gao, S. Low–Coordinate Single–Ion Magnets by Intercalation of Lanthanides into a Phenol Matrix. Angew. Chem. Int. Ed. 2018, 57, 4673–4676. [Google Scholar] [CrossRef]
- Benmansour, S.; Hernández–Paredes, A.; Bayona–Andrés, M.; Gómez–García, C.J. Slow Relaxation of the Magnetization in Anilato–Based Dy(III) 2D Lattices. Molecules 2021, 26, 1190. [Google Scholar] [CrossRef]
- Chen, Y.C.; Liu, J.L.; Ungur, L.; Liu, J.; Li, Q.W.; Wang, L.F.; Ni, Z.P.; Chibotaru, L.F.; Chen, X.M.; Tong, M.L. Symmetry–Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single–Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef]
- Wang, Y.X.; Ma, Y.; Chai, Y.; Shi, W.; Sun, Y.; Cheng, P. Observation of Magnetodielectric Effect in a Dysprosium–Based Single–Molecule Magnet. J. Am. Chem. Soc. 2018, 140, 7795–7798. [Google Scholar] [CrossRef]
- Kazin, P.E.; Zykin, M.A.; Utochnikova, V.V.; Magdysyuk, O.V.; Vasiliev, A.V.; Zubavichus, Y.V.; Schnelle, W.; Felser, C.; Jansen, M. “Isolated” DyO+ Embedded in a Ceramic Apatite Matrix Featuring Single–Molecule Magnet Behavior with a High Energy Barrier for Magnetization Relaxation. Angew. Chem. Int. Ed. 2017, 56, 13416–13420. [Google Scholar] [CrossRef]
- Harriman, K.L.M.; Brosmer, J.L.; Ungur, L.; Diaconescu, P.L.; Murugesu, M. Pursuit of Record Breaking Energy Barriers: A Study of Magnetic Axiality in Diamide Ligated DyIII Single–Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 1420–1423. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single–molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, Y.C.; Liu, J.L.; Vieru, V.; Ungur, L.; Jia, J.H.; Chibotaru, L.F.; Lan, Y.H.; Wernsdorfer, W.; Gao, S.; et al. A Stable Pentagonal–Bipyramidal Dy(III) Single–Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.S.; Jiang, S.D.; Wang, B.W.; Gao, S. Understanding the Magnetic Anisotropy toward Single–Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef]
- Ding, Y.S.; Chilton, N.F.; Winpenny, R.; Zheng, Y.Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near–Perfect Pentagonal Bipyramidal Dysprosium(III) Single–Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, Y.N.; Tang, J.K. Recent advances in dysprosium–based single molecule magnets: Structural overview and synthetic strategies. Coord. Chem. Rev. 2013, 257, 1728–1763. [Google Scholar] [CrossRef]
- Marin, R.; Brunet, G.; Murugesu, M. Shining new light on multifunctional lanthanide single–molecule magnets. Angew. Chem. Int. Ed. 2021, 60, 1728–1746. [Google Scholar] [CrossRef]
- El Rez, B.; Liu, J.W.; Bereau, V.; Duhayon, C.; Horino, Y.; Suzuki, T.; Coolen, L.; Sutter, J.P. Concomitant emergence of circularly polarized luminescence and single–molecule magnet behavior in chiral–at–metal Dy complex. Inorg. Chem. Front. 2020, 7, 4527–4534. [Google Scholar] [CrossRef]
- Sato, T.; Breedlove, B.K.; Yamashita, M.; Katoh, K. Electro–Conductive Single–Molecule Magnet Composed of a Dysprosium(III)–Phthalocyaninato Double–Decker Complex with Magnetoresistance. Angew. Chem. Int. Ed. 2021, 60, 21179–21183. [Google Scholar] [CrossRef]
- Shen, Y.B.; Cosquer, G.; Zhang, H.T.; Breedlove, B.K.; Cui, M.X.; Yamashita, M. 4f–π Molecular Hybrid Exhibiting Rich Conductive Phases and Slow Relaxation of Magnetization. J. Am. Chem. Soc. 2021, 143, 9543–9550. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Zhao, C.; Feng, T.T.; Liu, X.D.; Ying, X.; Li, X.L.; Zhang, Y.Q.; Tang, J.K. Air–Stable Chiral Single–Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K. J. Am. Chem. Soc. 2021, 143, 10077–10082. [Google Scholar] [CrossRef]
- Qin, L.; Yu, Y.Z.; Liao, P.Q.; Xue, W.; Zheng, Z.P.; Chen, X.M.; Zheng, Y.Z.A. “Molecular Water Pipe”: A Giant Tubular Cluster {Dy72} Exhibits Fast Proton Transport and Slow Magnetic Relaxation. Adv. Mater. 2016, 28, 10772–10779. [Google Scholar] [CrossRef]
- Rouquette, J.; Jerome, L.; Marc, T.J.; Rute, F.A.S.; Bruno, D.; Luis, C.D.; Veaceslav, V.; Liviu, C.F.; Leszek, K.; Julien, H.; et al. A High–Temperature Molecular Ferroelectric Zn/Dy Complex Exhibiting Single–Ion–Magnet Behavior and Lanthanide Luminescence. Angew. Chem. Int. Ed. 2015, 127, 2264–2268. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhu, S.D.; Lu, Y.B.; Hao, X.; Wen, H.R. Homochiral Cu6Dy3 single–molecule magnets displaying proton conduction and a strong magneto–optical Faraday effect. Inorg. Chem. Front. 2023, 10, 3714–3722. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhang, D.Q.; Hao, X.; Zhu, D.B. Assembly of chiral 3d–4f wheel–like cluster complexes with achiral ligands: Single–molecule magnetic behavior and magnetocaloric effect. Inorg. Chem. Front. 2020, 7, 3340–3351. [Google Scholar] [CrossRef]
- Kotrle, K.; Nemec, I.; Moncol, J.; Čižmár, E.; Herchel, R. 3d–4f magnetic exchange interactions and anisotropy in a series of heterobimetallic vanadium(IV)–lanthanide(III) Schiff base complexes. Dalton Trans. 2021, 50, 13883–13893. [Google Scholar] [CrossRef]
- Bhanja, A.; Schulze, M.; Herchel, R.; Pineda, E.M.; Wernsdorfer, W.; Ray, D. Selective Coordination of Self–Assembled Hexanuclear [Ni4Ln2] and [Ni2Mn2Ln2] (Ln = DyIII, TbIII, and HoIII) Complexes: Stepwise Synthesis, Structures, and Magnetic Properties. Inorg. Chem. 2020, 59, 17929–17944. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SADABS: Program for Empirical Absorption Correction of Area Detector Data; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
- CrystalClear. Software User’s Guide for the Rigaku R–Axis, and Mercury and Jupiter CCD Automated X−ray Imaging System; Version 1.35; Rigaku Molecular Structure Corporation: Akishima, Japan, 2008. [Google Scholar]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Cryst. 2009, D65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE, version 2.1; Electronic Structure Group, Universitat de Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Litvinova, Y.M.; Gayfulin, Y.M.; Leusen, J.; Samsonenko, D.G.; Lazarenko, V.A.; Zubavichus, Y.V.; Kogerler, P.; Mironov, Y.V. Metal–organic frameworks based on polynuclear lanthanide complexes and octahedral rhenium clusters. Inorg. Chem. Front. 2019, 6, 1518–1526. [Google Scholar] [CrossRef]
- Canaj, A.B.; Dey, S.; Mart, E.R.; Wilson, C.; Rajaraman, G.; Murrie, M. Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single–Ion Magnets. Angew. Chem. Int. Ed. 2019, 58, 14146–14151. [Google Scholar] [CrossRef]
- Jabeur, W.; Msalmi, R.; Korb, M.; Mosconi, E.; Tozri, A.; Althubiti, N.A.; Naili, H. Optical and magnetic characterization of one–dimensional Cu(II)–based perovskite: A high UV–Vis–NIR absorber. J. Mater. Chem. C 2021, 9, 17158–17166. [Google Scholar] [CrossRef]
- Portillo Moreno, O.; Portillo Araiza, O.R.; Chavez Portillo, M.; Carranza Tellez, V.; Vicencio Garrido, M.A. Jahn–Teller effect analysis at coordination complex [Cu(NH3)4]2+ ion, growth by green synthesis in CuS nanocrystals. Optik 2022, 251, 168470. [Google Scholar] [CrossRef]
- Wen, H.R.; Bao, J.; Liu, S.J.; Liu, C.M.; Zhang, C.W.; Tang, Y.Z. Temperature–controlled polymorphism of chiral CuII–LnIII dinuclear complexes exhibiting slow magnetic relaxation. Dalton Trans. 2015, 44, 11191–11201. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wu, G.; Xu, H.; Wang, X.; Long, L.S.; Kong, X.J.; Zheng, L.S. Magnetooptical Properties of Chiral [Co2Ln] Clusters. Inorg. Chem. 2020, 59, 193–197. [Google Scholar] [CrossRef]
- Cai, G.; Bozhkova, N.; Odingo, J.; Berova, N.; Nakanishi, K. Circular dichroism exciton chirality method. New red–shifted chromophores for hydroxyl groups. J. Am. Chem. Soc. 1993, 115, 7192–7198. [Google Scholar] [CrossRef]
- Seo, M.S.; Sun, D.; Kim, H. Stereoselective Chiral Recognition of Amino Alcohols with 2,2′–Dihydroxybenzil. J. Org. Chem. 2017, 82, 6586–6591. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, S.; Wang, H.; Dou, J.; Jiang, J. Magneto–chiral dichroism in chiral mixed (phthalocyaninato)(porphyrinato) rare earth triple–decker SMMs. Inorg. Chem. Front. 2014, 1, 167–171. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Segawa, H.; Ishii, K. Magneto–Chiral Dichroism of Organic Compounds. Angew. Chem. Int. Ed. 2011, 50, 9133–9136. [Google Scholar] [CrossRef] [PubMed]
- Kitagawa, Y.; Wada, S.; Yanagisawa, K.; Nakanishi, T.; Fushimi, K.; Hasegawa, Y. Molecular Design Guidelines for Large Magnetic Circular Dichroism Intensities in Lanthanide Complexes. ChemPhysChem 2016, 17, 845–849. [Google Scholar] [CrossRef]
- Huang, X.D.; Xu, Y.; Fan, K.; Bao, S.S.; Kurmoo, M.; Zheng, L.M. Reversible SC–SC Transformation involving [4 + 4] Cycloaddition of Anthracene: A Single–Ion to Single–Molecule Magnet and Yellow–Green to Blue–White Emission. Angew. Chem. Int. Ed. 2018, 57, 8577–8581. [Google Scholar] [CrossRef] [PubMed]
- Latendresse, T.P.; Bhuvanesh, N.S.; Nippe, M. Hard Single–Molecule Magnet Behavior by a Linear Trinuclear Lanthanide–[1]Metallocenophane Complex. J. Am. Chem. Soc. 2017, 139, 14877–14880. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhang, D.Q.; Zhu, D.B. Fine Tuning the Energy Barrier of Molecular Nanomagnets via Lattice Solvent Molecules. Sci. Rep. 2017, 7, 15483. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.L.; Zou, H.H.; Zhang, Z.; Sun, W.Y.; Liang, F.P. Two types of Cu–Ln Heterometallic Coordination Polymers with 2–Hydroxyisophthalate: Syntheses, Structures and Magnetic Properties. Cryst. Growth Des. 2015, 15, 2883–2890. [Google Scholar] [CrossRef]
- Fatila, E.M.; Rouzieres, M.; Jennings, M.C.; Lough, A.J.; Clerac, R.; Preuss, K.E. Fine–Tuning the Single–Molecule Magnet Properties of a [Dy(III)–Radical](2) Pair. J. Am. Chem. Soc. 2013, 135, 9596–9599. [Google Scholar] [CrossRef]
- Ma, Y.J.; Hu, J.X.; Han, S.D.; Li, J.H.; Wang, G.M. Manipulating On/Off Single–Molecule Magnet Behavior in a Dy(III)–Based Photochromic Complex. J. Am. Chem. Soc. 2020, 142, 2682–2689. [Google Scholar] [CrossRef]
- Sun, J.; Sun, Z.; Wang, K.; Xi, L.; Ma, Y.; Li, L.C. Slow relaxation of magnetization in unprecedented Cu–Ln–Rad hetero–tri–spin chains constructed from multidentate nitronyl nitroxide. J. Mater. Chem. C 2019, 7, 9057–9064. [Google Scholar] [CrossRef]
- Ling, B.K.; Zhai, Y.Q.; Jin, P.B.; Ding, H.F.; Zhang, X.F.; Lv, Y.; Fu, Z.D.; Deng, J.W.; Schulze, M.; Wernsdorfer, W.; et al. Suppression of zero–field quantum tunneling of magnetization by a fluorido bridge for a “very hard” 3d–4f single–molecule magnet. Matter 2022, 5, 3485–3498. [Google Scholar] [CrossRef]
- Yao, Z.Z.; Pan, L.; Liu, L.Z.; Zhang, J.D.; Lin, Q.J.; Ye, Y.X.; Zhang, Z.J.; Xiang, S.C.; Chen, B.L. Simultaneous implementation of resistive switching and rectifying effects in a metal–organic framework with switched hydrogen bond pathway. Sci. Adv. 2019, 5, eaaw4515. [Google Scholar] [CrossRef]
- Afzal, J.; Fu, Y.; Luan, T.X.; Su, Z.; Li, P.Z. Highly Effective Proton–Conduction Matrix–Mixed Membrane Derived from an –SO3H Functionalized Polyamide. Molecules 2022, 27, 4110. [Google Scholar] [CrossRef]
- Zhu, S.-D.; Hu, J.-J.; Dong, L.; Wen, H.-R.; Liu, S.-J.; Lu, Y.-B.; Liu, C.-M. Multifunctional Zn(II)–Yb(III) complex enantiomers showing second–harmonic generation, near–infrared luminescence, single–molecule magnet behaviour and proton conduction. J. Mater. Chem. C 2020, 8, 16032–16041. [Google Scholar] [CrossRef]
- Kallem, P.; Drobek, M.; Julbe, A.; Vriezekolk, E.J.; Mallada, R.; Pina, M.P. Hierarchical Porous Polybenzimidazole Microsieves: An Efficient Architecture for Anhydrous Proton Transport via Polyionic Liquids. ACS Appl. Mater. Interfaces 2017, 9, 14844–14857. [Google Scholar] [CrossRef]
- Umeyama, D.; Horike, S.; Inukai, M.; Takura, T.; Kitagawa, S. Inherent Proton Conduction in a 2D Coordination Framework. J. Am. Chem. Soc. 2012, 134, 12780–12785. [Google Scholar] [CrossRef]
- Zhou, H.Q.; Zheng, S.-L.; Wu, C.-M.; Ye, X.-H.; Liao, W.-M.; He, J. Structure, Luminescent Sensing and Proton Conduction of a Boiling–Water–Stable Zn(II) Metal–Organic Framework. Molecules 2021, 26, 5044. [Google Scholar] [CrossRef]
- Kim, S.; Joarder, B.; Hurd, J.; Zhang, J.; Dawson, K.W.; Gelfand, B.S.; Wong, N.E.; Shimizu, G.K.H. Achieving Superprotonic Conduction in Metal–Organic Frameworks through Iterative Design Advances. J. Am. Chem. Soc. 2018, 140, 1077–1082. [Google Scholar] [CrossRef]
- Zhang, F.M.; Dong, L.Z.; Qin, J.S.; Guan, W.; Liu, J.; Li, S.L.; Lu, M.; Lan, Y.Q.; Su, Z.M.; Zhou, H.C. Effect of Imidazole Arrangements on Proton–Conductivity in Metal–Organic Frameworks. J. Am. Chem. Soc. 2017, 139, 6183–6189. [Google Scholar] [CrossRef]
- Lassoued, M.S.; Bi, L.Y.; Wu, Z.X.; Zhou, G.J.; Zheng, Y.Z. Piperidine–induced Switching of the direct band gaps of Ag(I)/Bi(III) bimetallic iodide double perovskites. J. Mater. Chem. C 2020, 8, 5349–5354. [Google Scholar] [CrossRef]
- Zhu, M.; Hao, Z.M.; Song, X.Z.; Meng, X.; Zhao, S.N.; Song, S.Y.; Zhang, H.J. A New Type of Double–Chain Based 3D Lanthanide(III) Metal–Organic Framework Demonstrating Proton Conduction and Tunable Emission. Chem. Commun. 2014, 50, 1912–1914. [Google Scholar] [CrossRef]
- Wong, N.E.; Ramaswamy, P.; Lee, A.S.; Gelfand, B.S.; Bladek, K.J.; Taylor, J.M.; Spasyuk, D.M.; Shimizu, G.K.H. Tuning Intrinsic and Extrinsic Proton Conduction in Metal–Organic Frameworks by the Lanthanide Contraction. J. Am. Chem. Soc. 2017, 139, 14676–14683. [Google Scholar] [CrossRef]
- Li, S.J.; Zhao, Y.; Knoll, S.; Liu, R.J.; Li, G.; Peng, Q.P.; Qiu, P.T.; He, D.F.; Streb, C.; Chen, X.N. High Proton–Conductivity in Covalently Linked Polyoxometalate–Organoboronic Acid–Polymers. Angew. Chem. Int. Ed. 2021, 60, 16953–16957. [Google Scholar] [CrossRef]
- Wang, S.; Wahiduzzaman, M.; Davis, L.; Tissot, A.; Shepard, W.; Marrot, J.; Martineau–Corcos, C.; Hamdane, D.; Maurin, G.; Devautour–Vinot, S.; et al. A Robust Zirconium Amino Acid Metal–Organic Framework for Proton Conduction. Nat. Commun. 2018, 9, 4937. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, T.; Aonuma, T.; Tamaki, T.; Ohashi, H.; Ushiyama, H.; Yamashitac, K.; Yamaguchi, T. The proton conduction mechanism in a material consisting of packed acids. Chem. Sci. 2014, 5, 4878–4887. [Google Scholar] [CrossRef]
- Qin, Y.; Gao, T.L.; Xie, W.P.; Li, Z.F.; Li, G. Ultrahigh Proton Conduction in Two Highly Stable Ferrocenyl Carboxylate Frameworks. ACS Appl. Mater. Interfaces 2019, 11, 31018–31027. [Google Scholar] [CrossRef]
- Lu, Y.-B.; Huang, J.; Liao, Y.-Q.; Lin, X.-L.; Huang, S.-Y.; Liu, C.-M.; Wen, H.-R.; Liu, S.-J.; Wang, F.-Y.; Zhu, S.-D. Multifunctional Dinuclear Dy–Based Coordination Complex Showing Visible Photoluminescence, Single–Molecule Magnet Behavior, and Proton Conduction. Inorg. Chem. 2022, 61, 18545–18553. [Google Scholar] [CrossRef]
- Zhu, S.-D.; Dong, L.; Hu, J.-J.; Wen, H.-R.; Lu, Y.-B.; Deng, W.-H.; Liu, C.-M.; Liu, S.-J.; Xu, G.; Fu, Z.-H. A proton conductor showing an indication of single–ion magnet behavior based on a mononuclear Dy(iii) complex. J. Mater. Chem. C 2021, 9, 481–488. [Google Scholar] [CrossRef]
- Liang, X.Q.; Zhang, F.; Feng, W.; Zou, X.Q.; Zhao, C.J.; Na, H.; Liu, C.; Sun, F.X.; Zhu, G.S. From metal–organic framework (MOF) to MOF–polymer composite membrane: Enhancement of low–humidity proton conductivity. Chem. Sci. 2013, 4, 983–992. [Google Scholar] [CrossRef]
- Pili, S.; Argent, S.P.; Morris, C.G.; Rought, P.; Garcia–Sakai, V.; Silverwood, I.P.; Easun, T.L.; Li, M.; Warren, M.R.; Murray, C.A.; et al. Proton Conduction in a Phosphonate–Based Metal–Organic Framework Mediated by Intrinsic “Free Diffusion inside a Sphere”. J. Am. Chem. Soc. 2016, 138, 6352–6355. [Google Scholar] [CrossRef]
- Markus, A.; Ingo, J.; Susanne, K.; Patrick, W.; Birgit, W.; Roland, F. Dicatechol–diimines: Easily accessible ligands for the self–assembly of dinuclear triple–stranded helicates. Dalton Trans. 2004, 1, 37–43. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).