The Sticking of N2 on W(100) Surface: An Improvement in the Description of the Adsorption Dynamics Further Reconciling Theory and Experiment
Abstract
:1. Introduction
2. Results and Discussion
2.1. The ILJ Long-Range Potential of N and N2 Interacting with W(100)
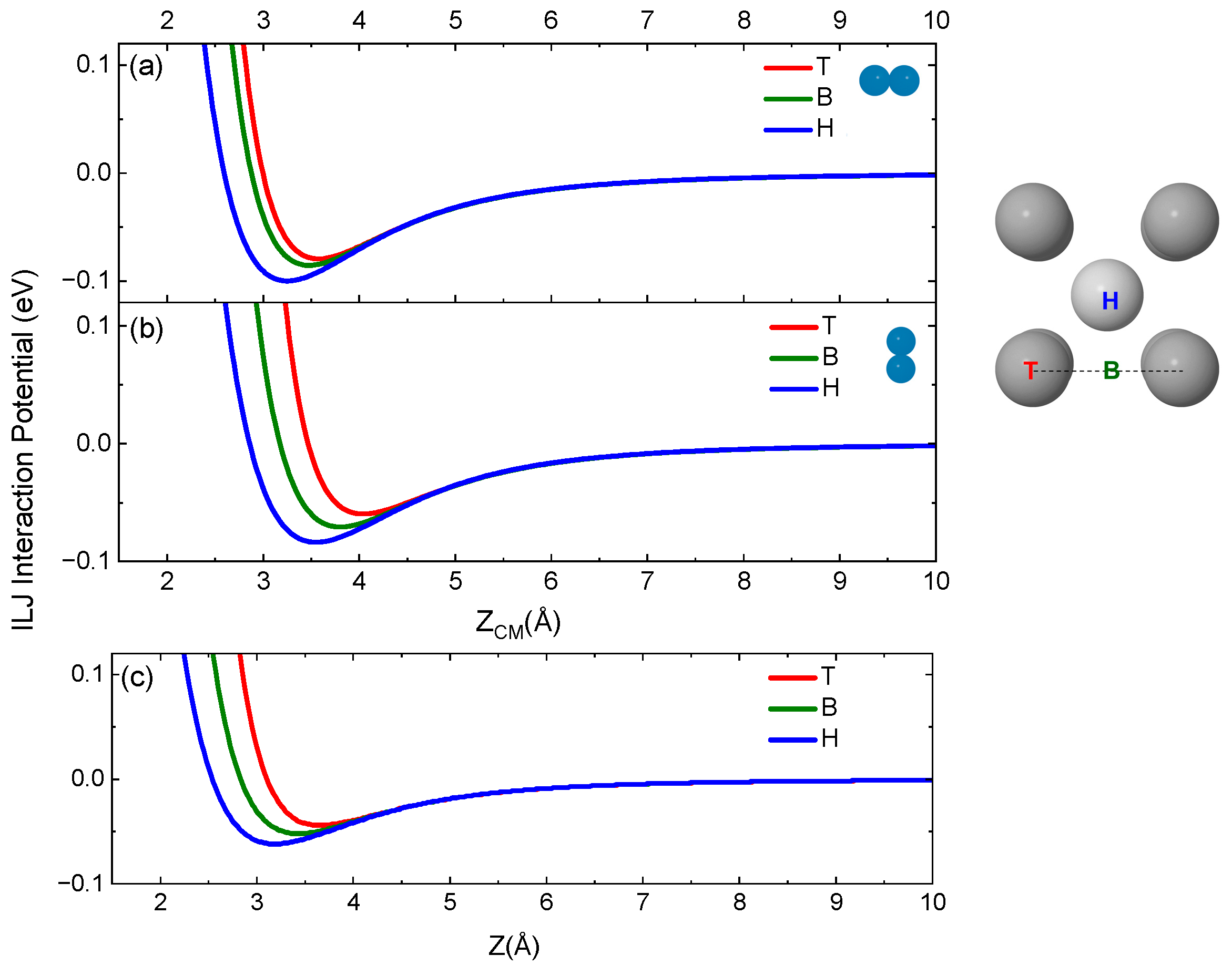
2.2. Potential Energy Surface Determination
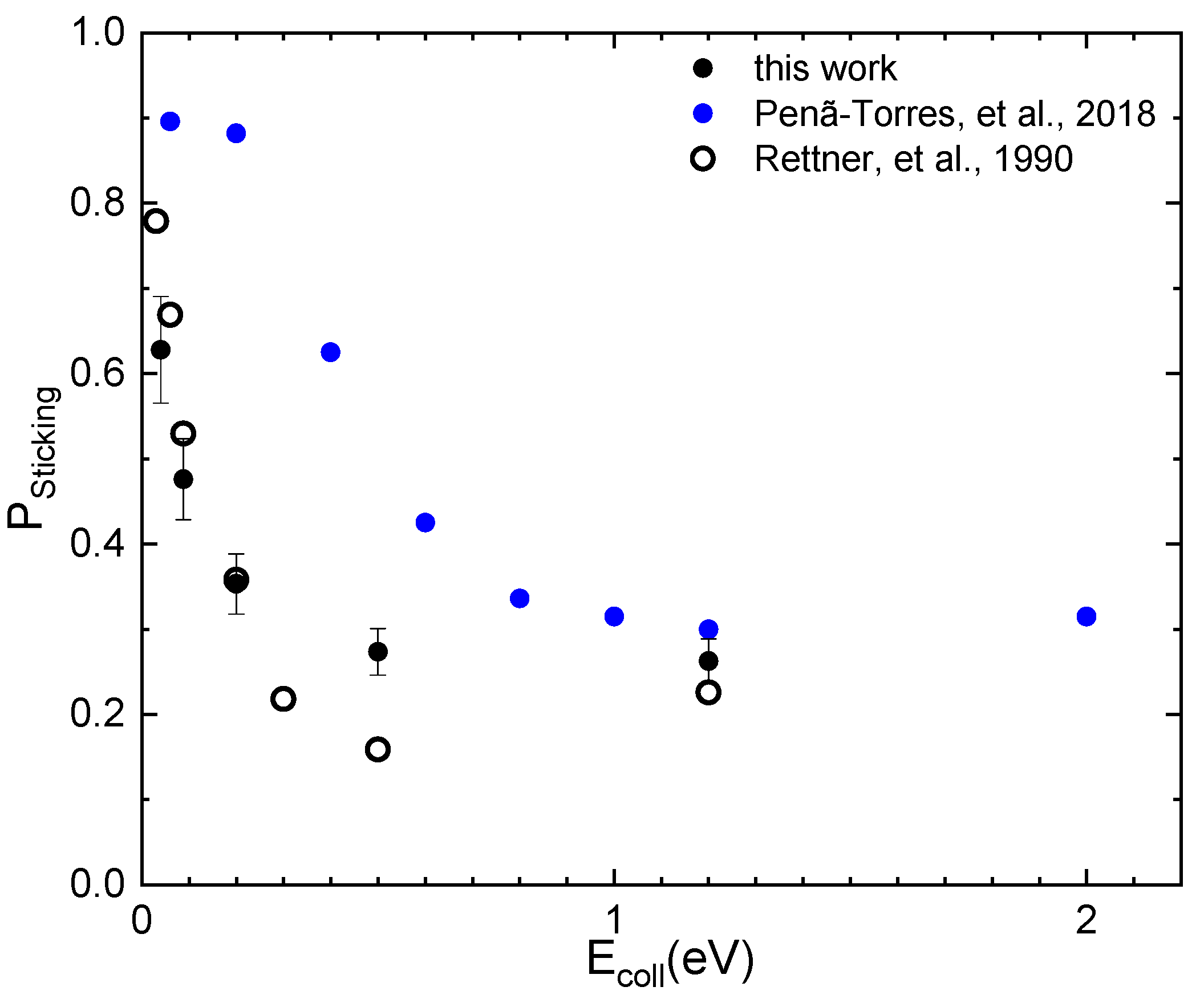
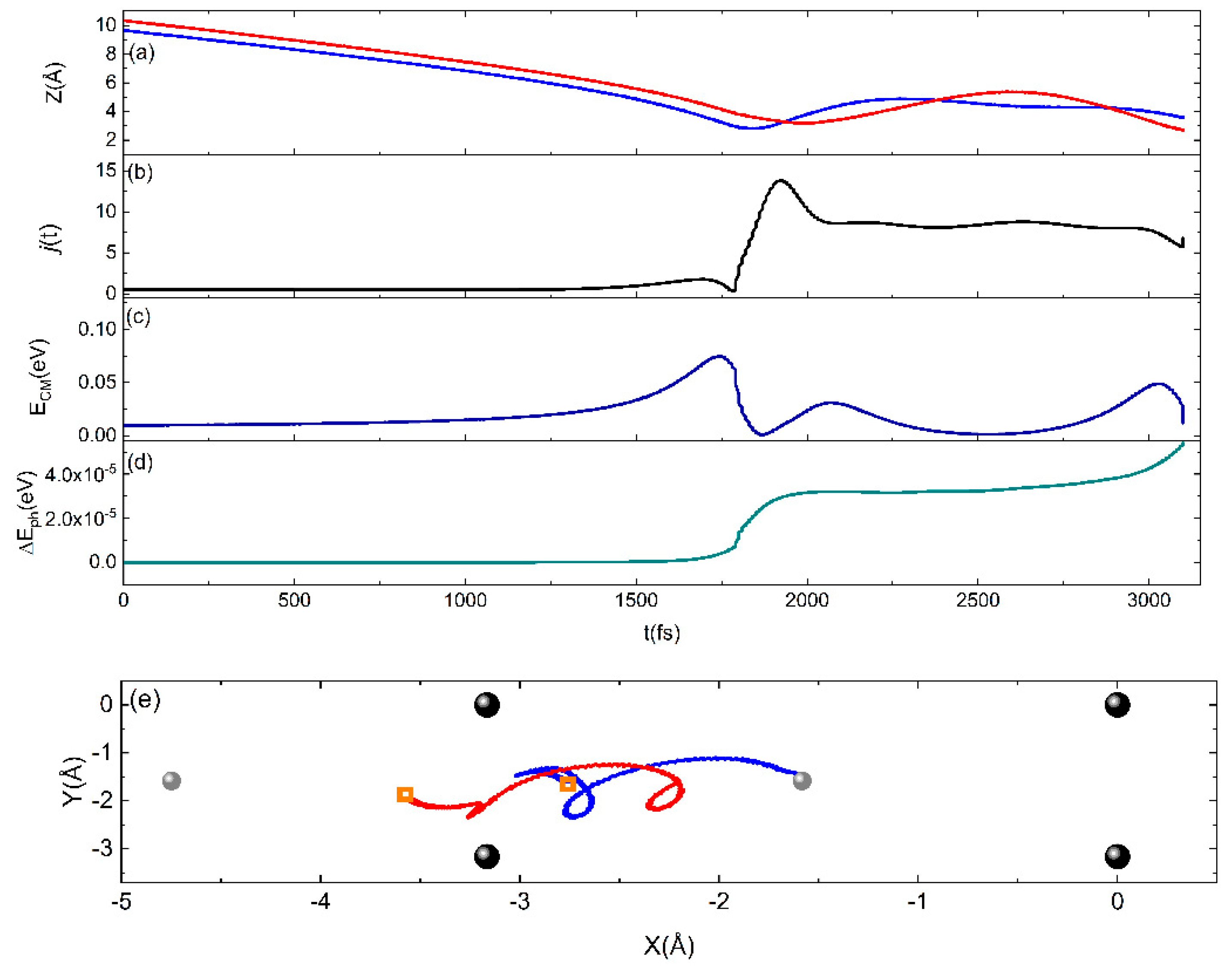
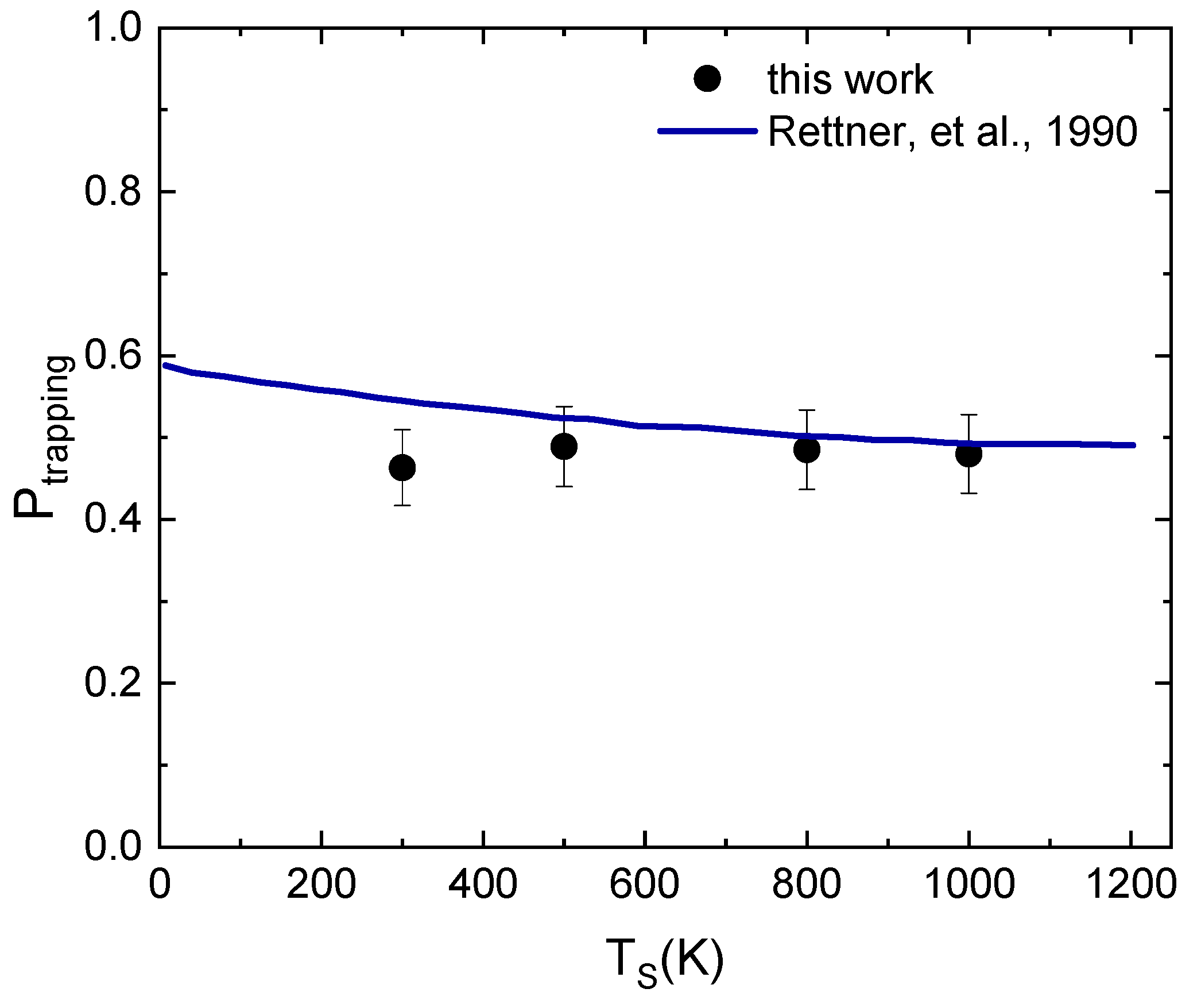
2.3. The Sticking Probability for N2 Interacting on W(100)
3. Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dɡbrowski, A. Adsorption-from theory to practice. Adv. Colloid Interface Sci. 2001, 93, 135–224. [Google Scholar] [CrossRef]
- Ptushinskiĭ, Y.G. Low-temperature adsorption of gases on metal surfaces. Low Temp. Phys. 2004, 30, 1–26. [Google Scholar] [CrossRef]
- Groß, A. Adsorption on Surfaces in Theoretical Surface Science—A Microscopic Perspective; Springer: Berlin/Heidelberg, Germany, 2009; pp. 101–160. [Google Scholar]
- Hammer, B.; Norskov, J.K. Theoretical Surface Science and Catalysis—Calculations and Concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar]
- Gao, W.; Chen, Y.; Li, B.; Liu, S.-P.; Liu, X.; Jiang, Q. Determining the adsorption energies of small molecules with the intrinsic properties of adsorbates and substrates. Nat. Commun. 2020, 11, 1196. [Google Scholar] [CrossRef]
- Allouche, A. First principles calculations on nitrogen reactivity on tungsten surfaces. J. Phys. Condens. Matter 2016, 28, 015001. [Google Scholar] [CrossRef]
- Penã-Torres, A.; Busnengo, H.F.; Juaristi, J.I.; Larregaray, P.; Crespos, C. Dynamics of N2 sticking on W(100): The decisive role of van der Waals interactions. Phys. Chem. Chem. Phys. 2018, 20, 19326–19331. [Google Scholar] [CrossRef]
- Peña-Torres, A.; Busnengo, H.F.; Juaristi, J.I.; Larregaray, P.; Crespos, C. Energy Dissipation Effects on the Adsorption Dynamics of N2 on W(100). J. Phys. Chem. C 2019, 123, 2900–2910. [Google Scholar] [CrossRef]
- Rettner, C.T.; Stein, H.; Schweizer, E.K. Effect of collision energy and incidence angle on the precursor-mediated dissociative chemisorption of N2 on W(100). J. Chem. Phys. 1988, 89, 3337–3341. [Google Scholar] [CrossRef]
- Rettner, C.T.; Schweizer, E.K.; Stein, H. Dynamics of the chemisorption of N2 on W(100): Precursor-mediated and activated dissociation. J. Chem. Phys. 1990, 93, 1442–1454. [Google Scholar] [CrossRef]
- Rettner, C.T.; Schweizer, E.K.; Stein, H.; Auerbach, D.J. Role of Surface Temperature in the Precursor-Mediated Dissociative Chemisorption of N2 on W(100). Phys. Rev. Lett. 1988, 61, 986–989. [Google Scholar] [CrossRef]
- Auerbach, D.J.; Pfnur, H.E.; Rettner, C.T.; Schlaegel, J.E.; Lee, J.; Madix, R.J. Kinetic energy and angular dependence of activated dissociative adsorption of N2 on W(110): Observed insensitivity to incidence angle. J. Chem. Phys. 1984, 81, 2515–2516. [Google Scholar] [CrossRef]
- Pfnur, H.E.; Rettner, C.T.; Lee, J.; Madix, R.J.; Auerbach, D.J. Dynamics of the activated dissociative chemisorption of N2 on W(110): A molecular beam study. J. Chem. Phys. 1986, 85, 7452–7466. [Google Scholar] [CrossRef]
- Ertl, G.; Thiele, N. XPS studies with ammonia synthesis catalysts. Appl. Surf. Sci. 1979, 3, 99–112. [Google Scholar] [CrossRef]
- Volpilhac, G.; Salin, A. Dissociative adsorption of N2 on the W(100) surface. Surf. Sci. 2004, 556, 129–144. [Google Scholar] [CrossRef]
- Hafner, J.; Kresse, G. The Vienna ab-initio simulation program VASP: An efficient and versatile tool for studying the structural, dynamic and electronic properties of materials. In Properties of Complex Inorganic Solids; Gonis, A., Meike, A., Turchi, P.E.A., Eds.; Springer: Boston, MA, USA, 1997; pp. 69–82. [Google Scholar] [CrossRef]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard-Jones model: A simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489–5503. [Google Scholar] [CrossRef] [PubMed]
- Rutigliano, M.; Pirani, F. The role of long-range interactions on the selectivity of gaseous molecule-surface scattering. Chem. Phys. Lett. 2021, 770, 138444. [Google Scholar] [CrossRef]
- Billing, G.D. Dynamics of Molecule Surface Interactions, 1st ed.; John-Wiley & Sons: New York, NY, USA, 2000; pp. 112–141. [Google Scholar]
- Rutigliano, M.; Pirani, F. Scattering of N2 Molecules from Silica Surfaces: Effect of Polymorph and Surface Temperature. Molecules 2022, 27, 7445. [Google Scholar] [CrossRef]
- Rutigliano, M.; Pirani, F. Selectivity and Stereodynamics Effects in the Scattering of Nitrogen Molecules from a Graphite Surface. J. Phys. Chem. C 2020, 124, 10470–10482. [Google Scholar] [CrossRef]
- Cambi, R.; Cappelletti, D.; Liuti, G.; Pirani, F. Generalized correlations in terms of polarizability for van der Waals interaction potential parameter calculations. J. Chem. Phys. 1991, 95, 1852–1861. [Google Scholar] [CrossRef]
- Vidali, G.; Ihm, G.; Kim, H.-Y.; Cole, M.W. Potentials of physical adsorption. Surf. Scie. Reports 1991, 12, 133–181. [Google Scholar] [CrossRef]
- Olney, T.N.; Cann, N.M.; Cooper, G.; Brion, C.E. Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum-rules. Chem. Phys. 1997, 223, 59–98. [Google Scholar] [CrossRef]
- Werner, H.-J.; Meyer, W. Finite perturbation calculations for the static dipole polarizabilities of the first-row atoms. Phys. Rev. A 1976, 13, 13–16. [Google Scholar] [CrossRef]
- Ibarguen, C.; Larregaray, P.; Peña-Torres, A.; Crespos, C. Inelastic Scattering of N2 off W(001): Reconciling Experiment and Theory at Low Collision Energies. J. Phys. Chem. C 2018, 122, 28856–28861. [Google Scholar] [CrossRef]
- Ibarguen Becerra, C.; Crespos, C.; Galparsoro, O.; Larregaray, P. Atomic scattering of H and N on W(100): Effect of lattice vibration and electronic excitations on the dynamics. Surf. Sci. 2020, 701, 121678. [Google Scholar] [CrossRef]
- Rutigliano, M.; Pirani, F. Surface processes involving nitrogen molecules and atoms on silica surface at low temperature: The role of energy exchanges. Plasma Sources Sci. Technol. 2022, 31, 094006. [Google Scholar] [CrossRef]
- Andersson, S.; Harris, J. Trapping of molecular hydrogen at surfaces via translational-rotational energy conversion. Phys. Rev. B 1983, 27, 9–14. [Google Scholar] [CrossRef]
- Beutl, M.; Rendulic, K.D.; Castro, G.R. Does the rotational state of a molecule influence trapping in a precursor? An investigation of N2/W(100),CO/FeSi(100) and O2/Ni(111). Surf. Sci. 1997, 385, 97–106. [Google Scholar] [CrossRef]
- Beutl, M.; Riedler, M.; Rendulic, K.D. Strong rotational effects in the adsorption dynamics of H2/Pd(111): Evidence for dynamical steering. Chem. Phys. Lett. 1995, 247, 249–252. [Google Scholar] [CrossRef]
- Kay, M.; Darling, G.R.; Holloway, S.; White, J.A.; Bird, D.M. Steering effects in non-activated adsorption. Chem. Phys. Lett. 1995, 245, 311–318. [Google Scholar] [CrossRef]
- Gross, A.; Wilke, S.; Scheffler, M. Six-dimensional quantum dynamics of adsorption and desorption of H2 at Pd(100) no need for a molecular precursor adsorption state. Surf. Sci. 1996, 357–358, 614–618. [Google Scholar] [CrossRef]
- Rutigliano, M.; Cacciatore, M. Eley–Rideal recombination of hydrogen atoms on a tungsten surface. Phys. Chem. Chem. Phys. 2011, 13, 7475–7484. [Google Scholar] [CrossRef] [PubMed]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure: IV. In Constants of Diatomic Molecules; Van Nostrand Reinhold Company: New York, NY, USA, 1979; pp. 412–413. [Google Scholar]
- Muckerman, J.T. Monte Carlo Calculations of Energy Partitioning and Isotope Effects in Reactions of Fluorine Atoms with H2, HD, and D2. J. Chem. Phys. 1971, 54, 1155–1164. [Google Scholar] [CrossRef]
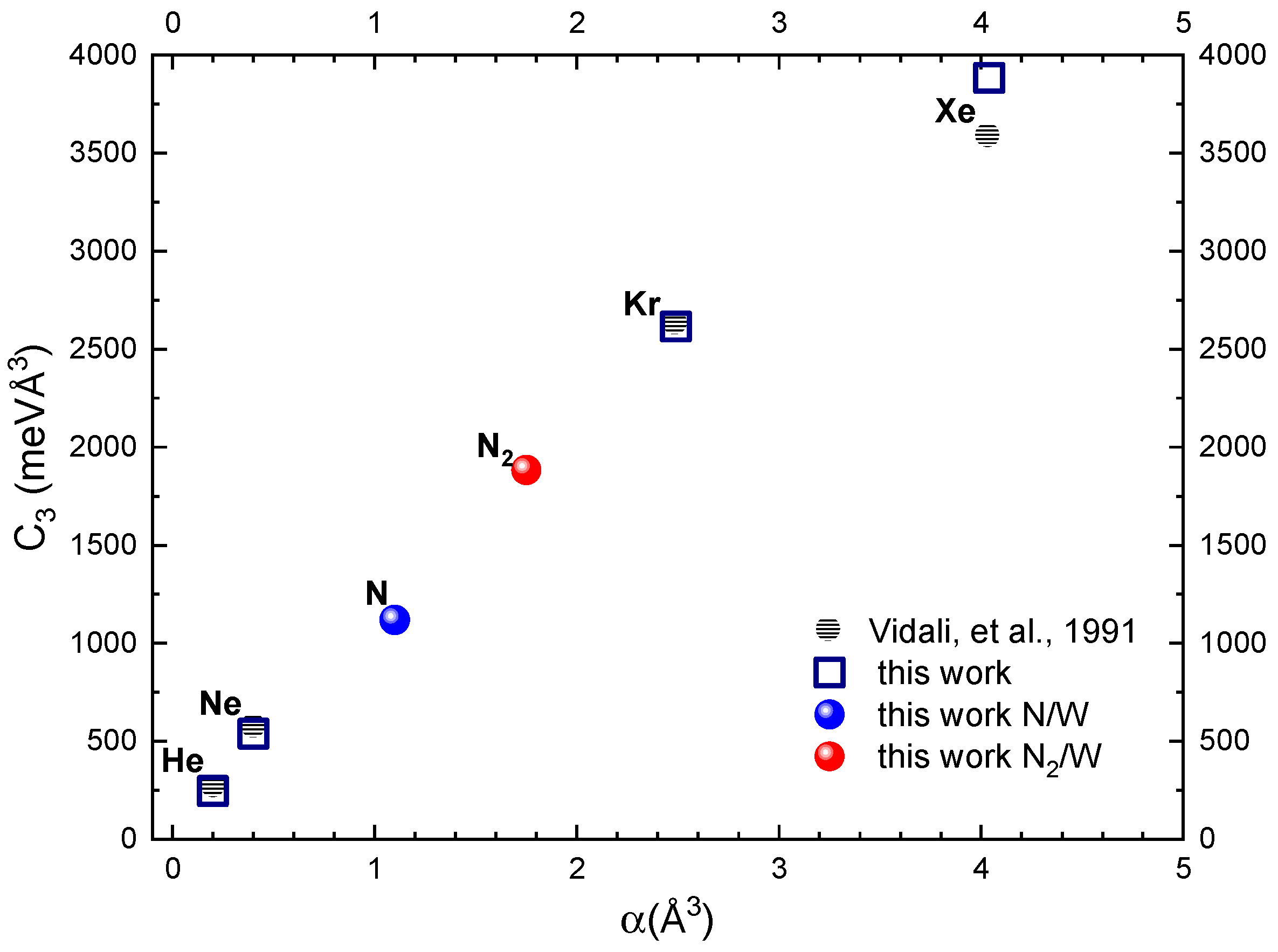

| Interaction | ε(meV) | (Å) | β | (meV Å6) | (meV Å3) |
|---|---|---|---|---|---|
| N(N2)–W | 6.23 | 4.07 | 6.3 | 28,452 | 941.5 |
| N–W | 7.40 | 4.07 | 7.0 | 33,635 | 1119 |
| Site | (eV) | (Å−1) | (Å) | (eV) | (Å) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | A | B | A | B | |
| T | 0.693 | −0.675 | 1.16 | 3.59 | 2.54 | −0.01 | 0.0079 | −0.0079 | 2.95 | 0.07 |
| B | 0.390 | −0.155 | 1.25 | 1.1 | 2.89 | −0.63 | 0.0065 | −0.0057 | 2.72 | −0.03 |
| Site | (eV) | (Å−1) | (Å) | (eV) | (Å) |
|---|---|---|---|---|---|
| T | 3.845 | 1.45 | 1.97 | 0.014 | 2.88 |
| B | 2.35 | 1.75 | 2.08 | 0.0051 | 2.95 |
| H | 1.69 | 1.50 | 2.42 | 0.018 | 2.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rutigliano, M.; Pirani, F. The Sticking of N2 on W(100) Surface: An Improvement in the Description of the Adsorption Dynamics Further Reconciling Theory and Experiment. Molecules 2023, 28, 7546. https://doi.org/10.3390/molecules28227546
Rutigliano M, Pirani F. The Sticking of N2 on W(100) Surface: An Improvement in the Description of the Adsorption Dynamics Further Reconciling Theory and Experiment. Molecules. 2023; 28(22):7546. https://doi.org/10.3390/molecules28227546
Chicago/Turabian StyleRutigliano, Maria, and Fernando Pirani. 2023. "The Sticking of N2 on W(100) Surface: An Improvement in the Description of the Adsorption Dynamics Further Reconciling Theory and Experiment" Molecules 28, no. 22: 7546. https://doi.org/10.3390/molecules28227546
APA StyleRutigliano, M., & Pirani, F. (2023). The Sticking of N2 on W(100) Surface: An Improvement in the Description of the Adsorption Dynamics Further Reconciling Theory and Experiment. Molecules, 28(22), 7546. https://doi.org/10.3390/molecules28227546







