Diffusion-Controlled Reactions: An Overview
Abstract
:1. Introduction
2. The Role of Diffusive Transport
3. Imperfect Surface Reactions
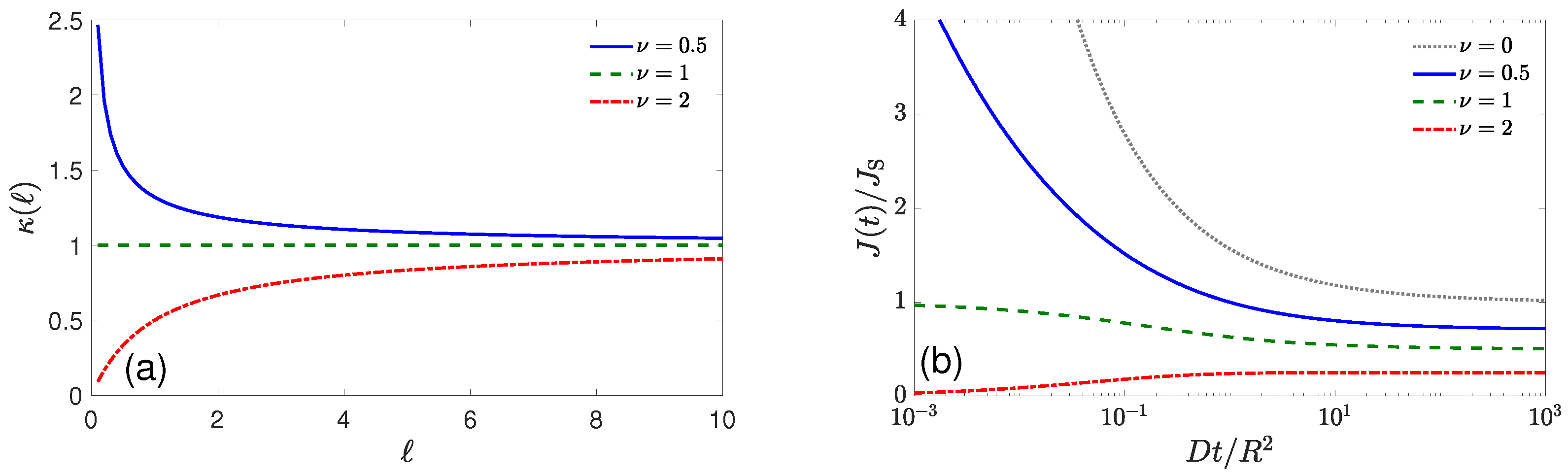
4. Various Extensions
5. Beyond the Conventional Framework
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Murrey, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Volpert, V. Elliptic Partial Differential Equations. Vol. 2. Reaction-Diffusion Equations; Monographs in Mathematics, 104; Springer: Basel, Switzerland, 2014. [Google Scholar]
- von Smoluchowski, M. Versuch einer Mathematischen Theorie der Koagulations Kinetic Kolloider Lousungen. Z. Phys. Chem. 1918, 92U, 129–168. [Google Scholar] [CrossRef]
- North, A.M. Diffusion-controlled reactions. Q. Rev. Chem. Soc. 1966, 20, 421–440. [Google Scholar] [CrossRef]
- Wilemski, G.; Fixman, M. General theory of diffusion-controlled reactions. J. Chem. Phys. 1973, 58, 4009–4019. [Google Scholar] [CrossRef]
- Calef, D.F.; Deutch, J.M. Diffusion-Controlled Reactions. Ann. Rev. Phys. Chem. 1983, 34, 493–524. [Google Scholar] [CrossRef]
- Berg, O.G.; von Hippel, P.H. Diffusion-Controlled Macromolecular Interactions. Ann. Rev. Biophys. Biophys. Chem. 1985, 14, 131–160. [Google Scholar] [CrossRef]
- Rice, S. Diffusion-Limited Reactions; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Bressloff, P.C.; Newby, J.M. Stochastic models of intracellular transport. Rev. Mod. Phys. 2013, 85, 135–196. [Google Scholar] [CrossRef]
- Lindenberg, K.; Metzler, R.; Oshanin, G. (Eds.) Chemical Kinetics: Beyond the Textbook; World Scientific: Hackensack, NJ, USA, 2019. [Google Scholar]
- Witten, T.A., Jr.; Sander, L.M. Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Lauffenburger, D.A.; Linderman, J. Receptors: Models for Binding, Trafficking, and Signaling; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Küchler, A.; Yoshimoto, M.; Luginbühl, S.; Mavelli, F.; Walde, P. Enzymatic reactions in confined environments. Nat. Nanotechnol. 2016, 11, 409–420. [Google Scholar] [CrossRef]
- Hill, T.L. Effect of rotation on the diffusion-controlled rate of ligand-protein association. Proc. Natl. Acad. Sci. USA 1975, 72, 4918–4922. [Google Scholar] [CrossRef]
- Zwanzig, R. Diffusion controlled ligand binding to spheres partially covered by receptors: An effective medium treatment. Proc. Nat. Acad. Sci. USA 1990, 87, 5856–5857. [Google Scholar] [CrossRef]
- Held, M.; Metzner, P.; Prinz, J.-H.; Noé, F. Mechanisms of Protein-Ligand Association and Its Modulation by Protein Mutations. Biophys. J. 2011, 100, 701–710. [Google Scholar] [CrossRef] [PubMed]
- Sano, H.; Tachiya, M. Partially diffusion-controlled recombination. J. Chem. Phys. 1979, 71, 1276–1282. [Google Scholar] [CrossRef]
- Agmon, N.; Pines, E.; Huppert, D. Geminate recombination in proton-transfer reactions. II. Comparison of diffusional and kinetic schemes. J. Chem. Phys. 1988, 88, 5631–5638. [Google Scholar] [CrossRef]
- Sano, H.; Tachiya, M. Theory of diffusion-controlled reactions on spherical surfaces and its application to reactions on micellar surfaces. J. Chem. Phys. 1981, 75, 2870–2878. [Google Scholar] [CrossRef]
- Brownstein, K.R.; Tarr, C.E. Importance of Classical Diffusion in NMR Studies of Water in Biological Cells. Phys. Rev. A 1979, 19, 2446–2453. [Google Scholar] [CrossRef]
- Grebenkov, D.S. NMR Survey of Reflected Brownian Motion. Rev. Mod. Phys. 2007, 79, 1077–1137. [Google Scholar] [CrossRef]
- Richter, P.H.; Eigen, M. Diffusion controlled reaction rates in spheroidal geometry application to repressor-operator. association and membrane bound enzymes. Biophys. Chem. 1974, 2, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Berg, O.G.; Winter, R.B.; von Hippel, P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids: 1. Models and theory. Biochemistry 1981, 20, 6929–6948. [Google Scholar] [CrossRef]
- Sheinman, M.; Bénichou, O.; Kafri, Y.; Voituriez, R. Classes of fast and specific search mechanisms for proteins on DNA. Rep. Prog. Phys. 2012, 75, 026601. [Google Scholar] [CrossRef] [PubMed]
- Golestanian, R. Anomalous Diffusion of Symmetric and Asymmetric Active Colloids. Phys. Rev. Lett. 2009, 102, 188305. [Google Scholar] [CrossRef]
- Oshanin, G.; Popescu, M.N.; Dietrich, S. Active colloids in the context of chemical kinetics. J. Phys. A Math. Theor. 2017, 50, 134001. [Google Scholar] [CrossRef]
- Traytak, S.D.; Grebenkov, D.S. Diffusion-influenced reaction rates for active ’sphere-prolate spheroid’ pairs and Janus dimers. J. Chem. Phys. 2018, 148, 024107. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. The Pathway for Oxygen. Structure and Function in the Mammalian Respiratory System; Harvard University Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Sapoval, B.; Filoche, M.; Weibel, E. Smaller is better - but not too small: A physical scale for the design of the mammalian pulmonary acinus. Proc. Natl. Acad. Sci. USA 2002, 99, 10411–10416. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S.; Filoche, M.; Sapoval, B.; Felici, M. Diffusion-reaction in Branched Structures: Theory and Application to the Lung Acinus. Phys. Rev. Lett. 2005, 94, 050602. [Google Scholar] [CrossRef] [PubMed]
- Collins, F.C.; Kimball, G.E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949, 4, 425–437. [Google Scholar] [CrossRef]
- Bénichou, O.; Chevalier, C.; Klafter, J.; Meyer, B.; Voituriez, R. Geometry-controlled kinetics. Nat. Chem. 2010, 2, 472–477. [Google Scholar] [CrossRef]
- Bénichou, O.; Voituriez, R. From first-passage times of random walks in confinement to geometry-controlled kinetics. Phys. Rep. 2014, 539, 225–284. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Imperfect Diffusion-Controlled Reactions. In Chemical Kinetics: Beyond the Textbook; Lindenberg, K., Metzler, R., Oshanin, G., Eds.; World Scientific: Hackensack, NJ, USA, 2019; pp. 191–219. [Google Scholar]
- Blender, R.; Dieterich, W.; Kirchhoff, T.; Sapoval, B. Impedance of Fractal Interfaces. J. Phys. A Math. Gen. 1990, 23, 1225–1232. [Google Scholar] [CrossRef]
- Coppens, M.-O. The effect of fractal surface roughness on diffusion and reaction in porous catalysts: From fundamentals to practical applications. Cat. Today 1999, 53, 225–243. [Google Scholar] [CrossRef]
- Filoche, M.; Sapoval, B. Transfer Across Random versus Deterministic Fractal Interfaces. Phys. Rev. Lett. 2000, 84, 5776–5779. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; Araujo, S.D.; Filoche, M.; Sapoval, B. Screening Effects in Flow through Rough Channels. Phys. Rev. Lett. 2007, 98, 194101. [Google Scholar] [CrossRef]
- Serov, A.S.; Salafia, C.; Grebenkov, D.S.; Filoche, M. The Role of Morphology in Mathematical Models of Placental Gas Exchange. J. Appl. Physiol. 2016, 120, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Galanti, M.; Fanelli, D.; Traytak, S.D.; Piazza, F. Theory of diffusion-influenced reactions in complex geometries. Phys. Chem. Chem. Phys. 2016, 18, 15950–15954. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S.; Traytak, S.D. Semi-analytical computation of Laplacian Green functions in three-dimensional domains with disconnected spherical boundaries. J. Comput. Phys. 2019, 379, 91–117. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Diffusion toward non-overlapping partially reactive spherical traps: Fresh insights onto classic problems. J. Chem. Phys. 2020, 152, 244108. [Google Scholar] [CrossRef]
- Nguyen, B.-T.; Grebenkov, D.S. A Spectral Approach to Survival Probability in Porous Media. J. Stat. Phys. 2010, 141, 532–554. [Google Scholar] [CrossRef]
- Piazza, F. The physics of boundary conditions in reaction-diffusion problems. J. Chem. Phys. 2022, 157, 234110. [Google Scholar] [CrossRef]
- Weiss, G.H. Overview of theoretical models for reaction rates. J. Stat. Phys. 1986, 42, 3–36. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Grebenkov, D.S.; Filoche, M.; Sapoval, B. Spectral Properties of the Brownian Self-Transport Operator. Eur. Phys. J. B 2003, 36, 221–231. [Google Scholar] [CrossRef]
- Bressloff, P.C. Stochastic switching in biology: From genotype to phenotype. J. Phys. A Math. Theor. 2017, 50, 133001. [Google Scholar] [CrossRef]
- Cortés, J.; Le, D.T.; Iehl, R.; Siméon, T. Simulating ligand-induced conformational changes in proteins using a mechanical disassembly method. Phys. Chem. Chem. Phys. 2010, 12, 8268–8276. [Google Scholar] [CrossRef]
- Lüking, M.; Elf, J.; Levy, Y. Conformational Change of Transcription Factors from Search to Specific Binding: A lac Repressor Case Study. J. Phys. Chem. B 2022, 126, 9971–9984. [Google Scholar] [CrossRef]
- Galanti, M.; Fanelli, D.; Piazza, F. Conformation-controlled binding kinetics of antibodies. Sci. Rep. 2016, 6, 18976. [Google Scholar] [CrossRef]
- Reva, M.; DiGregorio, D.A.; Grebenkov, D.S. A first-passage approach to diffusion-influenced reversible binding: Insights into nanoscale signaling at the presynapse. Sci. Rep. 2021, 11, 5377. [Google Scholar] [CrossRef]
- Bénichou, O.; Moreau, M.; Oshanin, G. Kinetics of stochastically gated diffusion-limited reactions and geometry of random walk trajectories. Phys. Rev. E 2000, 61, 3388–3406. [Google Scholar] [CrossRef] [PubMed]
- Reingruber, J.; Holcman, D. Gated Narrow Escape Time for Molecular Signaling. Phys. Rev. Lett. 2009, 103, 148102. [Google Scholar] [CrossRef] [PubMed]
- Lawley, S.D.; Keener, J.P. A new derivation of Robin boundary conditions through homogenization of a stochastically switching boundary. SIAM J. Appl. Dyn. Syst. 2015, 14, 1845–1867. [Google Scholar] [CrossRef]
- Zhou, H.-X.; Zwanzig, R. A rate process with an entropy barrier. J. Chem. Phys. 1991, 94, 6147–6152. [Google Scholar] [CrossRef]
- Reguera, D.; Schmid, G.; Burada, P.S.; Rubí, J.-M.; Reimann, P.; Hänggi, P. Entropic Transport: Kinetics, Scaling, and Control Mechanisms. Phys. Rev. Lett. 2006, 96, 130603. [Google Scholar] [CrossRef]
- Chapman, S.J.; Erban, R.; Isaacson, S. Reactive boundary conditions as limits of interaction potentials for Brownian and Langevin dynamics. SIAM J. Appl. Math. 2016, 76, 368–390. [Google Scholar] [CrossRef]
- Berg, H.C.; Purcell, E.M. Physics of chemoreception. Biophys. J. 1977, 20, 193–219. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Makhnovskii, Y.A.; Monine, M.I.; Zitserman, V.Y.; Shvartsman, S.Y. Boundary homogenization for trapping by patchy surfaces. J. Chem. Phys. 2004, 121, 11390–11394. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Monine, M.I.; Muratov, C.B.; Shvartsman, S.Y. Homogenization of boundary conditions for surfaces with regular arrays of traps. J. Chem. Phys. 2006, 124, 036103. [Google Scholar] [CrossRef]
- Muratov, C.B.; Shvartsman, S.Y. Boundary homogenization for periodic arrays of absorbers. Multiscale Model. Simul. 2008, 7, 44–61. [Google Scholar] [CrossRef]
- Bernoff, A.; Lindsay, A.; Schmidt, D. Boundary homogenization and capture time distributions of semipermeable membranes with periodic patterns of reactive sites. Multiscale Model. Simul. 2018, 16, 1411–1447. [Google Scholar] [CrossRef]
- Punia, B.; Chaudhury, S.; Kolomeisky, A.B. Understanding the Reaction Dynamics on Heterogeneous Catalysts Using a Simple Stochastic Approach. J. Phys. Chem. Lett. 2021, 12, 11802–11810. [Google Scholar] [CrossRef]
- Sapoval, B. General Formulation of Laplacian Transfer Across Irregular Surfaces. Phys. Rev. Lett. 1994, 73, 3314–3316. [Google Scholar] [CrossRef] [PubMed]
- Sapoval, B. Transport Across Irregular Interfaces: Fractal Electrodes, Membranes and Catalysts. In Fractals and Disordered Systems; Bunde, A., Havlin, S., Eds.; Springer: Berlin, Germany, 1996; pp. 233–261. [Google Scholar]
- Grebenkov, D.S.; Filoche, M.; Sapoval, B. Mathematical Basis for a General Theory of Laplacian Transport towards Irregular Interfaces. Phys. Rev. E 2006, 73, 021103. [Google Scholar] [CrossRef] [PubMed]
- Powles, J.G.; Mallett, M.J.D.; Rickayzen, G.; Evans, W.A.B. Exact analytic solutions for diffusion impeded by an infinite array of partially permeable barriers. Proc. R. Soc. Lond. A 1992, 436, 391–403. [Google Scholar]
- Bressloff, P.C.; Earnshaw, B.A.; Ward, M.J. Diffusion of protein receptors on a cylindrical dendritic membrane with partially absorbing traps. SIAM J. Appl. Math. 2008, 68, 1223–1246. [Google Scholar] [CrossRef]
- Grebenkov, D.S.; Oshanin, G. Diffusive escape through a narrow opening: New insights into a classic problem. Phys. Chem. Chem. Phys. 2017, 19, 2723–2739. [Google Scholar] [CrossRef]
- Guérin, T.; Dolgushev, M.; Bénichou, O.; Voituriez, R. Universal kinetics of imperfect reactions in confinement. Commun. Chem. 2021, 4, 157. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences; Springer: Berlin, Germany, 1985. [Google Scholar]
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications, 3rd ed.; Springer: Berlin, Germany, 1996. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Schuss, Z. Brownian Dynamics at Boundaries and Interfaces in Physics, Chemistry and Biology; Springer: New York, NY, USA, 2013. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Krapf, D.; Metzler, R. Strange interfacial molecular dynamics. Phys. Today 2019, 72, 48–54. [Google Scholar] [CrossRef]
- Chubynsky, M.V.; Slater, G.W. Diffusing Diffusivity: A Model for Anomalous, yet Brownian, Diffusion. Phys. Rev. Lett. 2014, 113, 098302. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Seno, F.; Metzler, R.; Sokolov, I.M. Brownian yet Non-Gaussian Diffusion: From Superstatistics to Subordination of Diffusing Diffusivities. Phys. Rev. X 2017, 7, 021002. [Google Scholar] [CrossRef]
- Lanoiselée, Y.; Moutal, N.; Grebenkov, D.S. Diffusion-limited reactions in dynamic heterogeneous media. Nat. Commun. 2018, 9, 4398. [Google Scholar] [CrossRef]
- Grebenkov, D.S. A unifying approach to first-passage time distributions in diffusing diffusivity and switching diffusion models. J. Phys. A Math. Theor. 2019, 52, 174001. [Google Scholar] [CrossRef]
- Yuste, S.B.; Abad, E.; Lindenberg, K. Exploration and Trapping of Mortal Random Walkers. Phys. Rev. Lett. 2013, 110, 220603. [Google Scholar] [CrossRef] [PubMed]
- Meerson, B.; Redner, S. Mortality, Redundancy, and Diversity in Stochastic Search. Phys. Rev. Lett. 2015, 114, 198101. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S.; Rupprecht, J.-F. The escape problem for mortal walkers. J. Chem. Phys. 2017, 146, 084106. [Google Scholar] [CrossRef]
- Turing, A. The Chemical Basis of Morphogenesis. Phil. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Milo, R.; Rhillips, R. Cell Biology by the Numbers; Garland Science: New York, NY, USA, 2015. [Google Scholar]
- Redner, S. A Guide to First Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Metzler, R.; Oshanin, G.; Redner, S. (Eds.) First-Passage Phenomena and Their Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Yu, J.; Xiao, J.; Ren, X.; Lao, K.; Xie, X.S. Probing Gene Expression in Live Cells, One Protein Molecule at a Time. Science 2006, 311, 1600–1603. [Google Scholar] [CrossRef] [PubMed]
- Raj, A.; van Oudenaarden, A. Nature, Nurture, or Chance: Stochastic Gene Expression and Its Consequences. Cell 2008, 135, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.S.; Choi, P.J.; Li, G.-W.; Lee, N.K.; Lia, G. Single-Molecule Approach to Molecular Biology in Living Bacterial Cells. Annu. Rev. Biophys. 2008, 37, 417–444. [Google Scholar] [CrossRef]
- Li, G.-W.; Xie, X.S. Central dogma at the single-molecule level in living cells. Nature 2011, 475, 308–315. [Google Scholar] [CrossRef]
- Kastantin, M.; Walder, R.; Schwartz, D.K. Identifying Mechanisms of Interfacial Dynamics Using Single-Molecule Tracking. Langmuir 2012, 28, 12443–12456. [Google Scholar] [CrossRef]
- Wang, D.; Wu, H.; Schwartz, D.K. Three-Dimensional Tracking of Interfacial Hopping Diffusion. Phys. Rev. Lett. 2017, 119, 268001. [Google Scholar] [CrossRef] [PubMed]
- Norregaard, K.; Metzler, R.; Ritter, C.M.; Berg-Sørensen, K.; Oddershede, L.B. Manipulation and Motion of Organelles and Single Molecules in Living Cells. Chem. Rev. 2017, 117, 4342–4374. [Google Scholar] [CrossRef]
- Sungkaworn, T.; Jobin, M.-L.; Burnecki, K.; Weron, A.; Lohse, M.-J.; Calebiro, D. Single-molecule imaging reveals receptor-G protein interactions at cell surface hot spots. Nature 2017, 550, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S.; Metzler, R.; Oshanin, G. Strong defocusing of molecular reaction times results from an interplay of geometry and reaction control. Commun. Chem. 2018, 1, 96. [Google Scholar] [CrossRef]
- Grebenkov, D.S.; Metzler, R.; Oshanin, G. Towards a full quantitative description of single-molecule reaction kinetics in biological cells. Phys. Chem. Chem. Phys. 2018, 20, 16393–16401. [Google Scholar] [CrossRef]
- Elf, J.; Barkefors, I. Single-molecule kinetics in living cells. Ann. Rev. Biochem. 2019, 88, 635–659. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Spectral theory of imperfect diffusion-controlled reactions on heterogeneous catalytic surfaces. J. Chem. Phys. 2019, 151, 104108. [Google Scholar] [CrossRef]
- Goodrich, F.C. Random walk with semi-adsorbing barrier. J. Chem. Phys. 1954, 22, 588–594. [Google Scholar] [CrossRef]
- Mysels, K.J. Diffusion-controlled adsorption kinetics. General solution and some applications. J. Phys. Chem. 1982, 86, 4648–4651. [Google Scholar] [CrossRef]
- Agmon, N. Diffusion with back reaction. J. Chem. Phys. 1984, 81, 2811–2817. [Google Scholar] [CrossRef]
- Agmon, N.; Weiss, G.H. Theory of non-Markovian reversible dissociation reactions. J. Chem. Phys. 1989, 91, 6937–6942. [Google Scholar] [CrossRef]
- Agmon, N.; Szabo, A. Theory of reversible diffusion-influenced reactions. J. Chem. Phys. 1990, 92, 5270–5284. [Google Scholar] [CrossRef]
- Kim, H.; Shin, K.J. Exact solution of the reversible diffusion-influenced reaction for an isolated pair in three dimensions. Phys. Rev. Lett. 1999, 82, 1578–1581. [Google Scholar] [CrossRef]
- Prüstel, T.; Tachiya, M. Reversible diffusion-influenced reactions of an isolated pair on some two dimensional surfaces. J. Chem. Phys. 2013, 139, 194103. [Google Scholar] [CrossRef] [PubMed]
- Scher, Y.; Lauber Bonomo, O.; Pal, A.; Reuveni, S. Microscopic theory of adsorption kinetics. J. Chem. Phys. 2023, 158, 094107. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S. Diffusion-controlled reactions with non-Markovian binding/unbinding kinetics. J. Chem. Phys. 2023, 158, 214111. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Zaid, I.M.; Lomholt, M.; Sokolov, I.M.; Metzler, R. Bulk-mediated surface diffusion along a cylinder: Propagators and crossovers. Phys. Rev. E 2009, 79, 040105. [Google Scholar] [CrossRef]
- Bénichou, O.; Grebenkov, D.S.; Levitz, P.E.; Loverdo, C.; Voituriez, R. Optimal Reaction Time for Surface-Mediated Diffusion. Phys. Rev. Lett. 2010, 105, 150606. [Google Scholar] [CrossRef]
- Bénichou, O.; Grebenkov, D.S.; Levitz, P.E.; Loverdo, C.; Voituriez, R. Mean first-passage time of surface-mediated diffusion in spherical domains. J. Stat. Phys. 2011, 142, 657–685. [Google Scholar] [CrossRef]
- Rojo, F.; Budde, C.E. Enhanced diffusion through surface excursion: A master-equation approach to the narrow-escape-time problem. Phys. Rev. E 2011, 84, 021117. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Zaid, I.M.; Lomholt, M.A.; Sokolov, I.M.; Metzler, R. Effective surface motion on a reactive cylinder of particles that perform intermittent bulk diffusion. J. Chem. Phys. 2011, 134, 204116. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Zaid, I.M.; Lomholt, M.; Sokolov, I.M.; Metzler, R. Bulk-mediated diffusion on a planar surface: Full solution. Phys. Rev. E 2012, 86, 041101. [Google Scholar] [CrossRef]
- Rupprecht, J.-F.; Bénichou, O.; Grebenkov, D.S.; Voituriez, R. Exact mean exit time for surface-mediated diffusion. Phys. Rev. E 2012, 86, 041135. [Google Scholar] [CrossRef]
- Rupprecht, J.-F.; Bénichou, O.; Grebenkov, D.S.; Voituriez, R. Kinetics of active surface-mediated diffusion in spherically symmetric domains. J. Stat. Phys. 2012, 147, 891–918. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Dagdug, L.; Bezrukov, S.M. A new approach to the problem of bulk-mediated surface diffusion. J. Chem. Phys. 2015, 143, 084103. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Dagdug, L.; Bezrukov, S.M. Bulk-mediated surface transport in the presence of bias. J. Chem. Phys. 2017, 147, 014103. [Google Scholar] [CrossRef] [PubMed]
- Bénichou, O.; Loverdo, C.; Moreau, M.; Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 2011, 83, 81–129. [Google Scholar] [CrossRef]
- Filoche, M.; Sapoval, B.; Andrade, J.S., Jr. Deactivation Dynamics of Rough Catalytic Surfaces. AIChE 2005, 51, 998–1008. [Google Scholar] [CrossRef]
- Filoche, M.; Grebenkov, D.S.; Andrade, A.S., Jr.; Sapoval, B. Passivation of irregular surfaces accessed by diffusion. Proc. Natl. Acad. Sci. USA 2008, 105, 7636–7640. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Paradigm Shift in Diffusion-Mediated Surface Phenomena. Phys. Rev. Lett. 2020, 125, 078102. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Residence times and other functionals of reflected Brownian motion. Phys. Rev. E 2007, 76, 041139. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Probability distribution of the boundary local time of reflected Brownian motion in Euclidean domains. Phys. Rev. E 2019, 100, 062110. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Joint distribution of multiple boundary local times and related first-passage time problems with multiple targets. J. Stat. Mech. 2020, 103205. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Surface Hopping Propagator: An Alternative Approach to Diffusion-Influenced Reactions. Phys. Rev. E 2020, 102, 032125. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Statistics of boundary encounters by a particle diffusing outside a compact planar domain. J. Phys. A Math. Theor. 2021, 54, 015003. [Google Scholar] [CrossRef]
- Bressloff, P.C. Narrow capture problem: An encounter-based approach to partially reactive targets. Phys. Rev. E 2022, 105, 034141. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S. Statistics of diffusive encounters with a small target: Three complementary approaches. J. Stat. Mech. 2022, 083205. [Google Scholar] [CrossRef]
- Levitin, M.; Mangoubi, D.; Polterovich, I. Topics in Spectral Geometry. Preliminary Version. Available online: https://bookstore.ams.org/view?ProductCode=GSM/237 (accessed on 29 May 2023).
- Grebenkov, D.S. An encounter-based approach for restricted diffusion with a gradient drift. J. Phys. A Math. Theor. 2022, 55, 045203. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with Stochastic Resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A Math. Theor. 2020, 53, 193001. [Google Scholar] [CrossRef]
- Bressloff, P.C. Diffusion-mediated surface reactions and stochastic resetting. J. Phys. A Math. Theor. 2022, 55, 275002. [Google Scholar] [CrossRef]
- Benkhadaj, Z.; Grebenkov, D.S. Encounter-based approach to diffusion with resetting. Phys. Rev. E 2022, 106, 044121. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Depletion of Resources by a Population of Diffusing Species. Phys. Rev. E 2022, 105, 054402. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S. Encounter-based approach to the escape problem. Phys. Rev. E 2023, 107, 044105. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C. A probabilistic model of diffusion through a semipermeable barrier. Proc. R. Soc. A 2022, 478, 20220615. [Google Scholar] [CrossRef]
- Bressloff, P.C. Renewal equation for single-particle diffusion through a semipermeable interface. Phys. Rev. E. 2023, 107, 014110. [Google Scholar] [CrossRef]
- Bressloff, P.C. Renewal equations for single-particle diffusion in multilayered media. SIAM J. Appl. Math. 2023, 83, 1518–1545. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grebenkov, D.S. Diffusion-Controlled Reactions: An Overview. Molecules 2023, 28, 7570. https://doi.org/10.3390/molecules28227570
Grebenkov DS. Diffusion-Controlled Reactions: An Overview. Molecules. 2023; 28(22):7570. https://doi.org/10.3390/molecules28227570
Chicago/Turabian StyleGrebenkov, Denis S. 2023. "Diffusion-Controlled Reactions: An Overview" Molecules 28, no. 22: 7570. https://doi.org/10.3390/molecules28227570
APA StyleGrebenkov, D. S. (2023). Diffusion-Controlled Reactions: An Overview. Molecules, 28(22), 7570. https://doi.org/10.3390/molecules28227570





