Accelerating Kinetics with Time-Reversal Path Sampling
Abstract
:1. Introduction
2. Theoretical Results
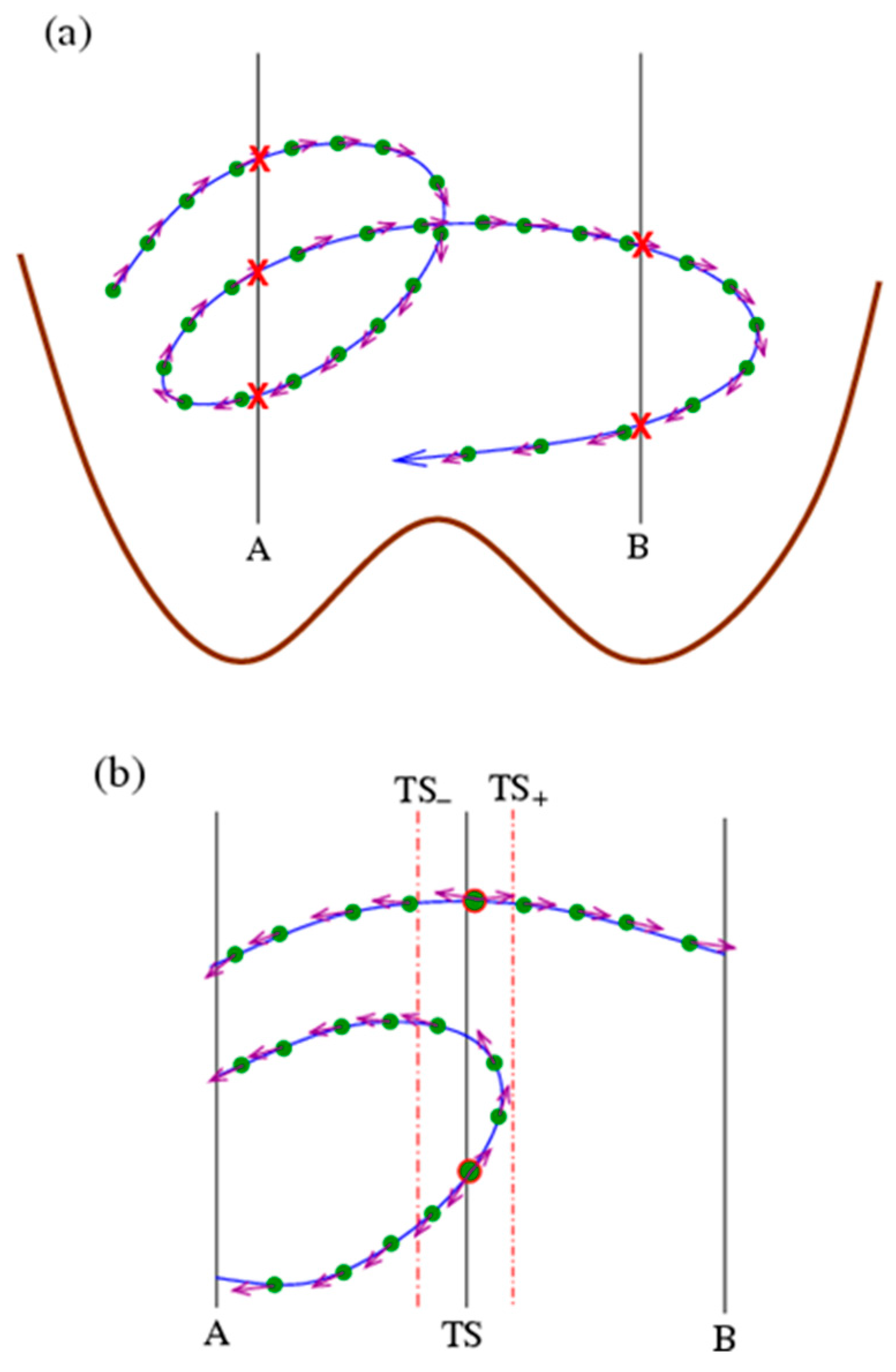
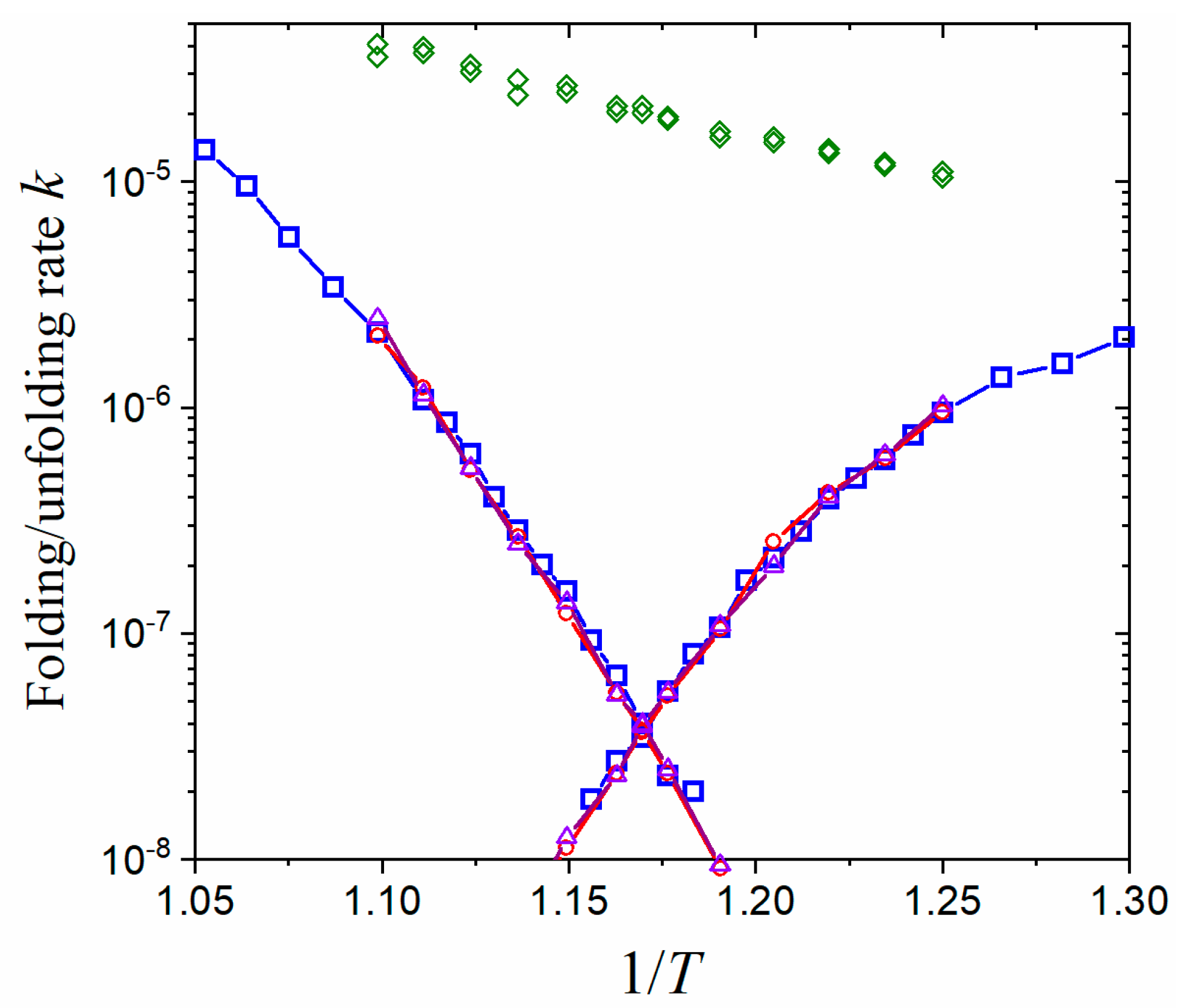
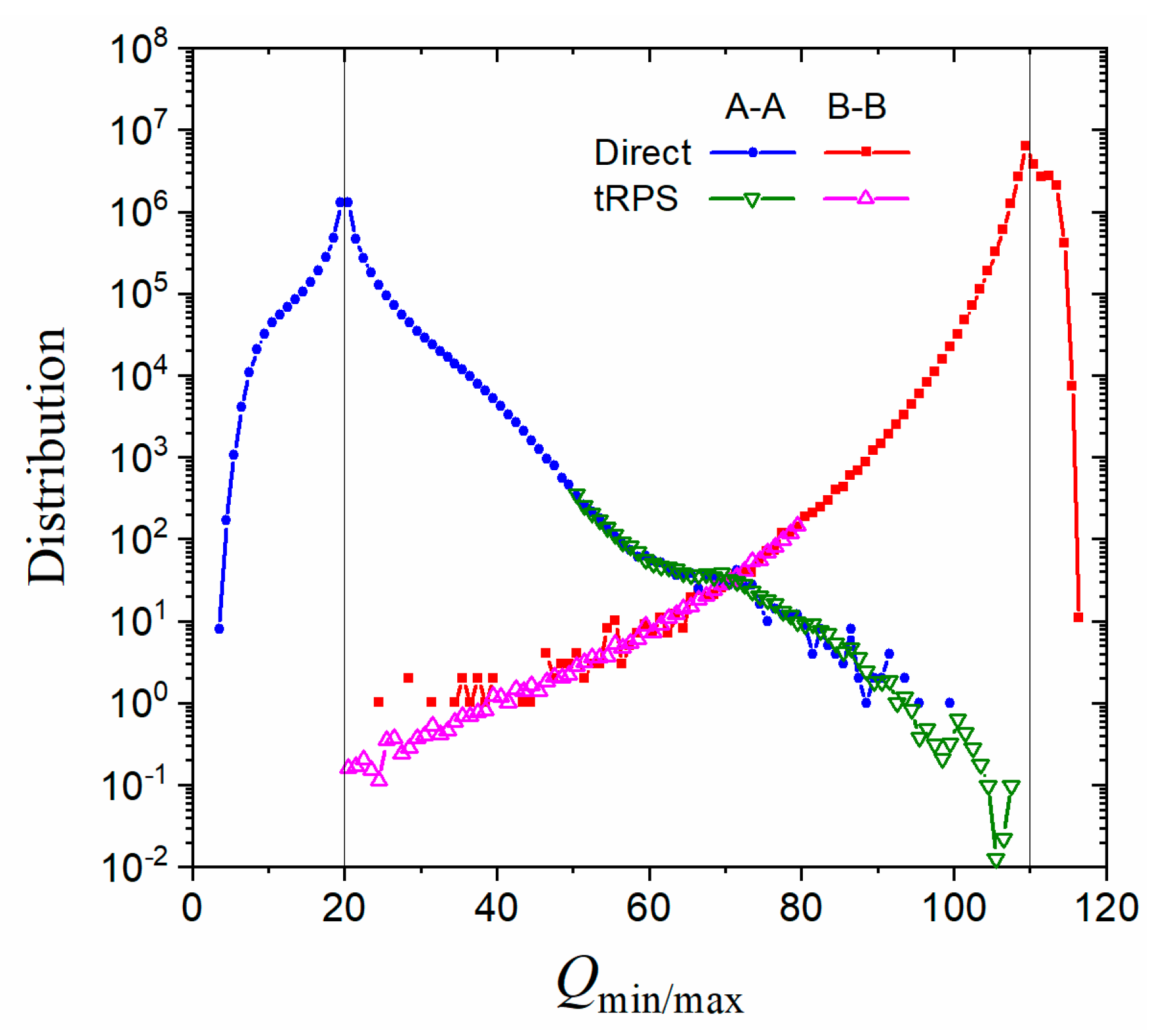
3. Numerical Results
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.I.; Shao, Q.; Zhang, J.; Yang, L.J.; Gao, Y.Q. Enhanced sampling in molecular dynamics. J. Chem. Phys. 2019, 151, 070902. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.M.; Valleau, J.P. Non-physical sampling distributions in Monte-Carlo free-energy estimation—Umbrella sampling. J. Comp. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Swendsen, R.H. New Monte-Carlo technique for studying phase-transitions. Phys. Rev. Lett. 1988, 61, 2635–2638. [Google Scholar] [CrossRef] [PubMed]
- Ferrenberg, A.M.; Swendsen, R.H. Optimized Monte-Carlo data-analysis. Phys. Rev. Lett. 1989, 63, 1195–1198. [Google Scholar] [CrossRef] [PubMed]
- Swendsen, R.H.; Wang, J.S. Replica Monte-Carlo simulation of spin-glasses. Phys. Rev. Lett. 1986, 57, 2607–2609. [Google Scholar] [CrossRef] [PubMed]
- Marinari, E.; Parisi, G. Simulated tempering—A new Monte-Carlo scheme. Europhys. Lett. 1992, 19, 451–458. [Google Scholar] [CrossRef]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jap. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
- Gao, Y.Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed]
- Stecher, T.; Bernstein, N.; Csanyi, G. Free energy surface reconstruction from umbrella samples using gaussian process regression. J. Chem. Theory Comput. 2014, 10, 4079–4097. [Google Scholar] [CrossRef] [PubMed]
- Sultan, M.M.; Wayment-Steele, H.K.; Pande, V.S. Transferable neural networks for enhanced sampling of protein dynamics. J. Chem. Theory Comput. 2018, 14, 1887–1894. [Google Scholar] [CrossRef] [PubMed]
- Bonati, L.; Zhang, Y.Y.; Parrinello, M. Neural networks-based variationally enhanced sampling. Proc. Natl. Acad. Sci. USA 2019, 116, 17641–17647. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wang, Y.; Chang, J.; Zhang, L.; Wang, H.; E, W. Efficient sampling of high-dimensional free energy landscapes using adaptive reinforced dynamics. Nat. Comput. Sci. 2022, 2, 20–29. [Google Scholar] [CrossRef]
- Chong, B.; Yang, Y.G.; Wang, Z.L.; Xing, H.; Liu, Z.R. Reinforcement learning to boost molecular docking upon protein conformational ensemble. Phys. Chem. Chem. Phys. 2021, 23, 6800–6806. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Onsager, L.; Machlup, S. Fluctuations and irreversible processes. Phys. Rev. 1953, 91, 1505–1512. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Zhang, Z.; Chan, H.S. Transition paths, diffusive processes, and preequilibria of protein folding. Proc. Natl. Acad. Sci. USA 2012, 109, 20919–20924. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Swenson, D.W.H. Transition path sampling as Markov chain Monte Carlo of trajectories: Recent algorithms, software, applications, and future outlook. Adv. Theory Simul. 2021, 4, 2000237. [Google Scholar] [CrossRef]
- Dellago, C.; Bolhuis, P.G.; Csajka, F.S.; Chandler, D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108, 1964–1977. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Dellago, C.; Bolhuis, P.G.; Geissler, P.L. Transition path sampling. In Advances in Chemical Physics; Prigogine, I., Rice, S.A., Eds.; LIDSEN Publishing Inc.: Auburn, OH, USA, 2002; Volume 123, pp. 1–78. [Google Scholar]
- van Erp, T.S.; Moroni, D.; Bolhuis, P.G. A novel path sampling method for the calculation of rate constants. J. Chem. Phys. 2003, 118, 7762–7774. [Google Scholar] [CrossRef]
- Cabriolu, R.; Refsnes, K.M.S.; Bolhuis, P.G.; van Erp, T.S. Foundations and latest advances in replica exchange transition interface sampling. J. Chem. Phys. 2017, 147, 152722. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.J.; Warren, P.B.; ten Wolde, P.R. Sampling rare switching events in biochemical networks. Phys. Rev. Lett. 2005, 94, 018104. [Google Scholar] [CrossRef]
- Allen, R.J.; Frenkel, D.; ten Wolde, P.R. Simulating rare events in equilibrium or nonequilibrium stochastic systems. J. Chem. Phys. 2006, 124, 024102. [Google Scholar] [CrossRef]
- Hummer, G. From transition paths to transition states and rate coefficients. J. Chem. Phys. 2004, 120, 516–523. [Google Scholar] [CrossRef]
- Best, R.B.; Hummer, G. Reaction coordinates and rates from transition paths. Proc. Natl. Acad. Sci. USA 2005, 102, 6732–6737. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Okazaki, K.-I.; Hummer, G. Transition path sampling of rare events by shooting from the top. J. Chem. Phys. 2017, 147, 152716. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Brotzakis, Z.F.; Vendruscolo, M. A maximum caliber approach for continuum path ensembles. Europ. Phys. J. B 2021, 94, 188. [Google Scholar] [CrossRef]
- Voter, A.F. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 1997, 78, 3908–3911. [Google Scholar] [CrossRef]
- Voter, A.F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665–4677. [Google Scholar] [CrossRef]
- Badasyan, A.; Liu, Z.R.; Chan, H.S. Probing possible downhill folding: Native contact topology likely places a significant constraint on the folding cooperativity of proteins with similar to 40 residues. J. Mol. Biol. 2008, 384, 512–530. [Google Scholar] [CrossRef]
- Metzner, P.; Schutte, C.; Vanden-Eijnden, E. Transition path theory for markov jump processes. Multiscale Model. Simul. 2009, 7, 1192–1219. [Google Scholar] [CrossRef]
- Chandler, D. Statistical-mechanics of isomerization dynamics in liquids and transition-state approximation. J. Chem. Phys. 1978, 68, 2959–2970. [Google Scholar] [CrossRef]
- Hanggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory—50 years after Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Peters, B.; Trout, B.L. Obtaining reaction coordinates by likelihood maximization. J. Chem. Phys. 2006, 125, 054108. [Google Scholar] [CrossRef]
- Menzl, G.; Singraber, A.; Dellago, C. S-shooting: A Bennett-Chandler-like method for the computation of rate constants from committor trajectories. Faraday Discuss. 2016, 195, 345–364. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Simmerling, C.; Dill, K. Protein modeling: Protein storytelling through physics. Science 2020, 370, 1056. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Jackson, S.E.; Fersht, A.R. Folding of chymotrypsin inhibitor-2. 1. Evidence for a 2-state transition. Biochemistry 1991, 30, 10428–10435. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937–953. [Google Scholar] [CrossRef] [PubMed]
- Kaya, H.; Chan, H.S. Solvation effects and driving forces for protein thermodynamic and kinetic cooperativity: How adequate is native-centric topological modeling? J. Mol. Biol. 2003, 326, 911–931. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.S.; McHale, K.; Louis, J.M.; Eaton, W.A. Single-molecule fluorescence experiments determine protein folding transition path times. Science 2012, 335, 981–984. [Google Scholar] [CrossRef]
- Wallin, S.; Chan, H.S. Conformational entropic barriers in topology-dependent protein folding: Perspectives from a simple native-centric polymer model. J. Phys.-Condes. Matter 2006, 18, S307–S328. [Google Scholar] [CrossRef]
- Liu, Z.R.; Chan, H.S. Solvation and desolvation effects in protein folding: Native flexibility, kinetic cooperativity and enthalpic barriers under isostability conditions. Phys. Biol. 2005, 2, S75–S85. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Thirumalai, D. Kinetics of protein-folding—Nucleation mechanism, time scales, and pathways. Biopolymers 1995, 36, 83–102. [Google Scholar] [CrossRef]
- van Erp, T.S. Reaction rate calculation by parallel path swapping. Phys. Rev. Lett. 2007, 98, 268301. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z. Accelerating Kinetics with Time-Reversal Path Sampling. Molecules 2023, 28, 8147. https://doi.org/10.3390/molecules28248147
Liu Z. Accelerating Kinetics with Time-Reversal Path Sampling. Molecules. 2023; 28(24):8147. https://doi.org/10.3390/molecules28248147
Chicago/Turabian StyleLiu, Zhirong. 2023. "Accelerating Kinetics with Time-Reversal Path Sampling" Molecules 28, no. 24: 8147. https://doi.org/10.3390/molecules28248147
APA StyleLiu, Z. (2023). Accelerating Kinetics with Time-Reversal Path Sampling. Molecules, 28(24), 8147. https://doi.org/10.3390/molecules28248147






