Revealing Internal Rotation and 14N Nuclear Quadrupole Coupling in the Atmospheric Pollutant 4-Methyl-2-nitrophenol: Interplay of Microwave Spectroscopy and Quantum Chemical Calculations
Abstract
:1. Introduction
2. Results
2.1. Computational
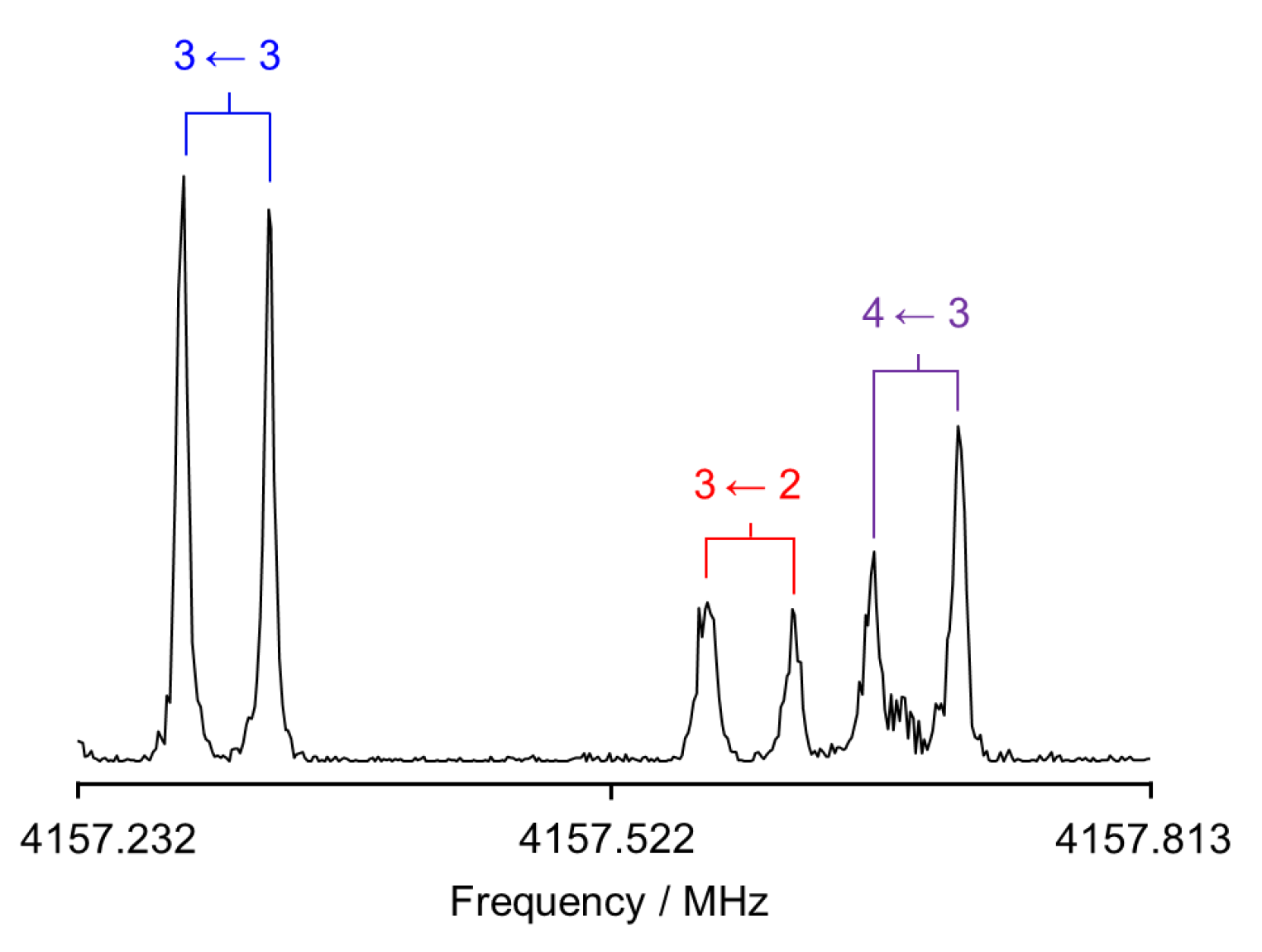
2.2. Rotational Spectrum
3. Discussion and Conclusions
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lammel, G.; Kitanovski, Z.; Kukučka, P.; Novák, J.; Arangio, A.M.; Codling, G.P.; Filippi, A.; Hovorka, J.; Kuta, J.; Leoni, C.; et al. Oxygenated and Nitrated Polycyclic Aromatic Hydrocarbons in Ambient Air—Levels, Phase Partitioning, Mass Size Distributions, and Inhalation Bioaccessibility. Environ. Sci. Technol. 2020, 54, 2615–2625. [Google Scholar] [CrossRef] [Green Version]
- Bandowe, B.A.M.; Meusel, H. Nitrated Polycyclic Aromatic Hydrocarbons (Nitro-PAHs) in the Environment—A Review. Sci. Total Environ. 2017, 581–582, 237–257. [Google Scholar] [CrossRef]
- Delgado-Saborit, J.M.; Alam, M.S.; Godri Pollitt, K.J.; Stark, C.; Harrison, R.M. Analysis of Atmospheric Concentrations of Quinones and Polycyclic Aromatic Hydrocarbons in Vapour and Particulate Phases. Atmos. Environ. 2013, 77, 974–982. [Google Scholar] [CrossRef]
- Mallah, M.A.; Changxing, L.; Mallah, M.A.; Noreen, S.; Liu, Y.; Saeed, M.; Xi, H.; Ahmed, B.; Feng, F.; Mirjat, A.A.; et al. Polycyclic Aromatic Hydrocarbon and Its Effects on Human Health: An Overview. Chemosphere 2022, 296, 133948. [Google Scholar] [CrossRef]
- Walgraeve, C.; Demeestere, K.; Dewulf, J.; Zimmermann, R.; Van Langenhove, H. Oxygenated Polycyclic Aromatic Hydrocarbons in Atmospheric Particulate Matter: Molecular Characterization and Occurrence. Atmos. Environ. 2010, 44, 1831–1846. [Google Scholar] [CrossRef]
- Minero, C.; Maurino, V.; Pelizzetti, E.; Vione, D. Assessing the Steady-State [•NO2] in Environmental Samples: Implication for Aromatic Photonitration Processes Induced by Nitrate and Nitrite. Environ. Sci. Pollut. Res. 2007, 14, 241–243. [Google Scholar] [CrossRef]
- Bejan, I.G.; Olariu, R.I.; Wiesen, P. Secondary Organic Aerosol Formation from Nitrophenols Photolysis under Atmospheric Conditions. Atmosphere 2020, 11, 1346. [Google Scholar] [CrossRef]
- Srivastava, D.; Vu, T.V.; Tong, S.; Shi, Z.; Harrison, R.M. Formation of Secondary Organic Aerosols from Anthropogenic Precursors in Laboratory Studies. NPJ Clim. Atmos. Sci. 2022, 5, 22. [Google Scholar] [CrossRef]
- Desyaterik, Y.; Sun, Y.; Shen, X.; Lee, T.; Wang, X.; Wang, T.; Collett, J.L. Speciation of “Brown” Carbon in Cloud Water Impacted by Agricultural Biomass Burning in Eastern China. J. Geophys. Res. Atmos. 2013, 118, 7389–7399. [Google Scholar] [CrossRef]
- Wang, H.; Gao, Y.; Wang, S.; Wu, X.; Liu, Y.; Li, X.; Huang, D.; Lou, S.; Wu, Z.; Guo, S.; et al. Atmospheric Processing of Nitrophenols and Nitrocresols From Biomass Burning Emissions. J. Geophys. Res. Atmos. 2020, 125, e2020JD033401. [Google Scholar] [CrossRef]
- Coeur-Tourneur, C.; Henry, F.; Janquin, M.A.; Brutier, L. Gas-Phase Reaction of Hydroxyl Radicals with m-, o- and p-Cresol. Int. J. Chem. Kinet. 2006, 38, 553–562. [Google Scholar] [CrossRef]
- Li, M.; Wang, X.; Lu, C.; Li, R.; Zhang, J.; Dong, S.; Yang, L.; Xue, L.; Chen, J.; Wang, W. Nitrated Phenols and the Phenolic Precursors in the Atmosphere in Urban Jinan, China. Sci. Total Environ. 2020, 714, 136760. [Google Scholar] [CrossRef] [PubMed]
- Kroll, J.H.; Seinfeld, J.H. Chemistry of Secondary Organic Aerosol: Formation and Evolution of Low-Volatility Organics in the Atmosphere. Atmos. Environ. 2008, 42, 3593–3624. [Google Scholar] [CrossRef]
- Hallquist, M.; Wenger, J.C.; Baltensperger, U.; Rudich, Y.; Simpson, D.; Claeys, M.; Dommen, J.; Donahue, N.M.; George, C.; Goldstein, A.H.; et al. The Formation, Properties and Impact of Secondary Organic Aerosol: Current and Emerging Issues. Atmos. Chem. Phys. 2009, 9, 5155–5236. [Google Scholar] [CrossRef] [Green Version]
- Park, G.B.; Field, R.W. Perspective: The First Ten Years of Broadband Chirped Pulse Fourier Transform Microwave Spectroscopy. J. Chem. Phys. 2016, 144, 200901. [Google Scholar] [CrossRef] [Green Version]
- Grabow, J.-U.; Caminati, W. Microwave Spectroscopy: Experimental Techniques. Front. Mol. Spectrosc. 2009, 383–454. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Caminati, W.; Grabow, J.U. The LAM of the Rings: Large Amplitude Motions in Aromatic Molecules Studied by Microwave Spectroscopy. Molecules 2022, 27, 3948. [Google Scholar] [CrossRef]
- Lin, C.C.; Swalen, J.D. Internal Rotation and Microwave Spectroscopy. Rev. Mod. Phys. 1959, 31, 841–891. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Kleiner, I. Understanding (Coupled) Large Amplitude Motions: The Interplay of Microwave Spectroscopy, Spectral Modeling, and Quantum Chemistry. In Theoretical and Computational Chemistry: Applications in Industry, Pharma, and Materials Science; De Gruyter: Berlin, Germany, 2021; pp. 41–92. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Mouhib, H.; Klahm, S.; Stahl, W.; Kleiner, I. A Touch of Lavender: Gas-Phase Structure and Dynamics of the Monoterpene Linalool Validated by Microwave Spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 10012–10018. [Google Scholar] [CrossRef]
- Uriarte, I.; Insausti, A.; Cocinero, E.J.; Jabri, A.; Kleiner, I.; Mouhib, H.; Alkorta, I. Competing Dispersive Interactions: From Small Energy Differences to Large Structural Effects in Methyl Jasmonate and Zingerone. J. Phys. Chem. Lett. 2018, 9, 5906–5914. [Google Scholar] [CrossRef]
- Murugachandran, S.I.; Tang, J.; Peña, I.; Loru, D.; Sanz, M.E. New Insights into Secondary Organic Aerosol Formation: Water Binding to Limonene. J. Phys. Chem. Lett. 2021, 12, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
- Baweja, S.; Panchagnula, S.; Sanz, M.E.; Evangelisti, L.; West, C.; Pate, B.H. Competition between In-Plane vs Above-Plane Configurations of Water with Aromatic Molecules: Non-Covalent Interactions in 1,4- Naphthoquinone-(H2O)1−3 Complexes. J. Phys. Chem. Lett. 2022, 13, 9510–9516. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.V.L.; Stahl, W. The Effects of Nitrogen Inversion Tunneling, Methyl Internal Rotation, and 14N Quadrupole Coupling Observed in the Rotational Spectrum of Diethyl Amine. J. Chem. Phys. 2011, 135, 024310. [Google Scholar] [CrossRef] [PubMed]
- Vigorito, A.; Calabrese, C.; Maris, A.; Loru, D.; Peña, I.; Sanz, M.E.; Melandri, S. The Shapes of Sulfonamides: A Rotational Spectroscopy Study. Molecules 2022, 27, 2820. [Google Scholar] [CrossRef] [PubMed]
- Burevschi, E.; Peña, I.; Sanz, M.E. Geminal Diol Formation from the Interaction of a Ketone with Water in the Gas Phase: Structure and Reactivity of Cyclooctanone-(H2O)1,2 Clusters. J. Phys. Chem. Lett. 2021, 12, 12419–12425. [Google Scholar] [CrossRef] [PubMed]
- Delhomme, O.; Morville, S.; Millet, M. Seasonal and Diurnal Variations of Atmospheric Concentrations of Phenols and Nitrophenols Measured in the Strasbourg Area, France. Atmos. Pollut. Res. 2010, 1, 16–22. [Google Scholar] [CrossRef] [Green Version]
- Lüttke, J.; Scheer, V.; Levsen, K.; Wünsch, G.; Cape, J.N.; Hargreaves, K.J.; Storeton-West, R.L.; Acker, K.; Wieprecht, W.; Jones, B. Occurrence and Formation of Nitrated Phenols in and out of Cloud. Atmos. Environ. 1997, 31, 2637–2648. [Google Scholar] [CrossRef]
- Belloli, R.; Barletta, B.; Bolzacchini, E.; Meinardi, S.; Orlandi, M.; Rindone, B. Determination of Toxic Nitrophenols in the Atmosphere by High-Performance Liquid Chromatography. J. Chromatogr. A 1999, 846, 277–281. [Google Scholar] [CrossRef]
- Cecinato, A.; Di Palo, V.; Pomata, D.; Tomasi Scianò, M.C.; Possanzini, M. Measurement of Phase-Distributed Nitrophenols in Rome Ambient Air. Chemosphere 2005, 59, 679–683. [Google Scholar] [CrossRef]
- Leuenberger, C.; Czuczwa, J.; Tremp, J.; Giger, W. Nitrated Phenols in Rain: Atmospheric Occurrence of Phytotoxic Pollutants. Chemosphere 1988, 17, 511–515. [Google Scholar] [CrossRef]
- Nishioka, M.G.; Lewtas, J. Quantification of Nitro- and Hydroxylated Nitro-Aromatic/Polycyclic Aromatic Hydrocarbons in Selected Ambient Air Daytime Winter Samples. Atmos. Environ. Part A Gen. Top. 1992, 26, 2077–2087. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09, Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 3785–3789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5656. [Google Scholar] [CrossRef] [Green Version]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Bailey, W.C. DFT and HF-DFT Calculations of 14N Quadrupole Coupling Constants in Molecules. Chem. Phys. 2000, 252, 57–66. [Google Scholar] [CrossRef]
- Roucou, A.; Kleiner, I.; Goubet, M.; Bteich, S.; Mouret, G.; Bocquet, R.; Hindle, F.; Meerts, W.L.; Cuisset, A. Towards the Detection of Explosive Taggants: Microwave and Millimetre-Wave Gas-Phase Spectroscopies of 3-Nitrotoluene. ChemPhysChem 2018, 19, 1056–1067. [Google Scholar] [CrossRef]
- Roucou, A.; Goubet, M.; Kleiner, I.; Bteich, S.; Cuisset, A. Large Amplitude Torsions in Nitrotoluene Isomers Studied by Rotational Spectroscopy and Quantum Chemistry Calculations. ChemPhysChem 2020, 21, 2523–2538. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.; Panchagnula, S.; Sanz, M.E.; Pérez, C.; Evangelisti, L.; Pate, B.H. Structural Changes Induced by Quinones: High Resolution Microwave Study of 1,4-Naphthoquinone. ChemPhysChem 2020, 21, 2579–2584. [Google Scholar] [CrossRef]
- Tsoi, V.W.Y.; Burevschi, E.; Saxena, S.; Sanz, M.E. Conformational Panorama of Cycloundecanone: A Rotational Spectroscopy Study. J. Phys. Chem. A 2022, 126, 6185–6193. [Google Scholar] [CrossRef] [PubMed]
- Burevschi, E.; Eugenia Sanz, M. Seven Conformations of the Macrocycle Cyclododecanone Unveiled by Microwave Spectroscopy. Molecules 2021, 26, 5162. [Google Scholar] [CrossRef] [PubMed]
- Graneek, J.B.; Bailey, W.C.; Schnell, M. Electron-Withdrawing Effects on the Molecular Structure of 2- and 3-Nitrobenzonitrile Revealed by Broadband Rotational Spectroscopy and Their Comparison with 4-Nitrobenzonitrile. Phys. Chem. Chem. Phys. 2018, 20, 22210–22217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Juanes, M.; Usabiaga, I.; León, I.; Evangelisti, L.; Fernández, J.A.; Lesarri, A. The Six Isomers of the Cyclohexanol Dimer: A Delicate Test for Dispersion Models. Angew. Chem.-Int. Ed. 2020, 59, 14081–14085. [Google Scholar] [CrossRef] [PubMed]
- Salvitti, G.; Blanco, S.; Lòpez, J.C.; Melandri, S.; Evangelisti, L.; Maris, A. Probing Intra- and Inter-Molecular Interactions through Rotational Spectroscopy: The Case of the Odorant 2′-Aminoacetophenone and Its 1:1 Water and Neon Complexes. J. Chem. Phys. 2022, 157, 144303. [Google Scholar] [CrossRef]
- Kannengießer, R.; Stahl, W.; Nguyen, H.V.L.; Bailey, W.C. 14N Quadrupole Coupling in the Microwave Spectra of N-Vinylformamide. J. Mol. Spectrosc. 2015, 317, 50–53. [Google Scholar] [CrossRef]
- Ferro-Costas, D.; Cordeiro, M.N.D.S.; Truhlar, D.G.; Fernández-Ramos, A. Q2DTor: A Program to Treat Torsional Anharmonicity through Coupled Pair Torsions in Flexible Molecules. Comput. Phys. Commun. 2018, 232, 190–205. [Google Scholar] [CrossRef]
- Fernández-Ramos, A. Accurate Treatment of Two-Dimensional Non-Separable Hindered Internal Rotors. J. Chem. Phys. 2013, 138, 134112. [Google Scholar] [CrossRef]
- Pickett, H.M. The Fitting and Prediction of Vibration-Rotation Spectra with Spin Interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
- Watson, J.K.G. Simplification of the Molecular Vibration-Rotation Hamiltonian. Mol. Phys. 1968, 15, 479–490. [Google Scholar] [CrossRef]
- Hartwig, H.; Dreizler, H. The Microwave Spectrum of Trans-2,3-Dimethyloxirane in Torsional Excited States. Zeitschrift fur Naturforsch.-Sect. A J. Phys. Sci. 1996, 51, 923–932. [Google Scholar] [CrossRef]
- Kannengießer, R.; Stahl, W.; Nguyen, H.V.L.; Kleiner, I. 14N Nuclear Quadrupole Coupling and Methyl Internal Rotation in N-Tert-Butylacetamide As Observed by Microwave Spectroscopy. J. Phys. Chem. A 2016, 120, 3992–3997. [Google Scholar] [CrossRef] [PubMed]
- Hougen, J.T.; Kleiner, I.; Godefroid, M. Selection Rules and Intensity Calculations for a Cs Asymmetric Top Molecule Containing a Methyl Group Internal Rotor. J. Mol. Spectrosc. 1994, 163, 559–586. [Google Scholar] [CrossRef]
- Kleiner, I. Asymmetric-Top Molecules Containing One Methyl-like Internal Rotor: Methods and Codes for Fitting and Predicting Spectra. J. Mol. Spectrosc. 2010, 260, 1–18. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Scheiner, A.C.; Lee, T.J.; Rice, J.E.; Schaefer, H.F. The Closed-Shell Coupled Cluster Single and Double Excitation (CCSD) Model for the Description of Electron Correlation. A Comparison with Configuration Interaction (CISD) Results. J. Chem. Phys. 1987, 86, 2881–2890. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Da Chai, J.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [Green Version]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Heineking, N.; Dreizler, H. Nitrogen Quadrupole Coupling Constants of Nitrobenzene and o-Nitrophenol. Ber. Bunsenges. Phys. Chem. 1993, 97, 663–665. [Google Scholar] [CrossRef]
- Gordy, W.; Cook, R.L. Microwave Molecular Spectra; John Wiley & Sons: Hoboken, NJ, USA, 1984; Chapter 14. [Google Scholar]
- Pinacho, P.; Obenchain, D.A.; Schnell, M. New Findings from Old Data: A Semi-Experimental Value for the eQq of the Nitrogen Atom. J. Chem. Phys. 2020, 153, 234307. [Google Scholar] [CrossRef] [PubMed]
- Bohn, R.K.; Montgomery, J.A.; Michels, H.H.; Fournier, J.A. Second Moments and Rotational Spectroscopy. J. Mol. Spectrosc. 2016, 325, 42–49. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C. On the Internal Rotations in p-resol in its Ground and First Electronically Excited States. J. Chem. Phys. 2007, 127, 024307. [Google Scholar] [CrossRef]
- Loru, D.; Bermúdez, M.A.; Sanz, M.E. Structure of Fenchone by Broadband Rotational Spectroscopy. J. Chem. Phys. 2016, 145, 074311. [Google Scholar] [CrossRef] [Green Version]
- Loru, D.; Peña, I.; Sanz, M.E. Ethanol Dimer: Observation of Three New Conformers by Broadband Rotational Spectroscopy. J. Mol. Spectrosc. 2017, 335, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Grabow, J.-U.; Stahl, W.; Dreizler, H. A Multioctave Coaxially Oriented Beam-Resonator Arrangement Fourier-Transform Microwave Spectrometer. Rev. Sci. Instrum. 1996, 67, 4072–4084. [Google Scholar] [CrossRef]
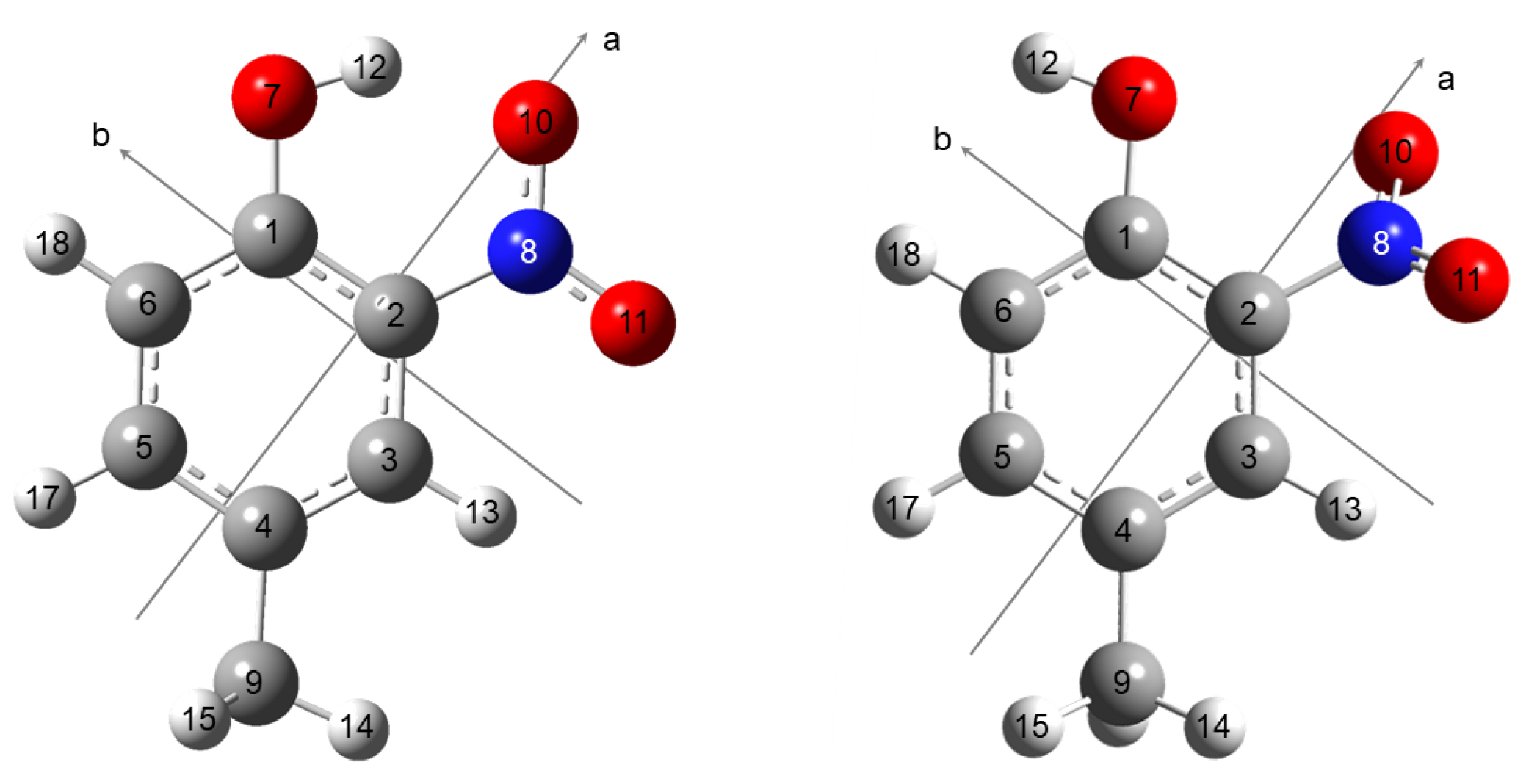
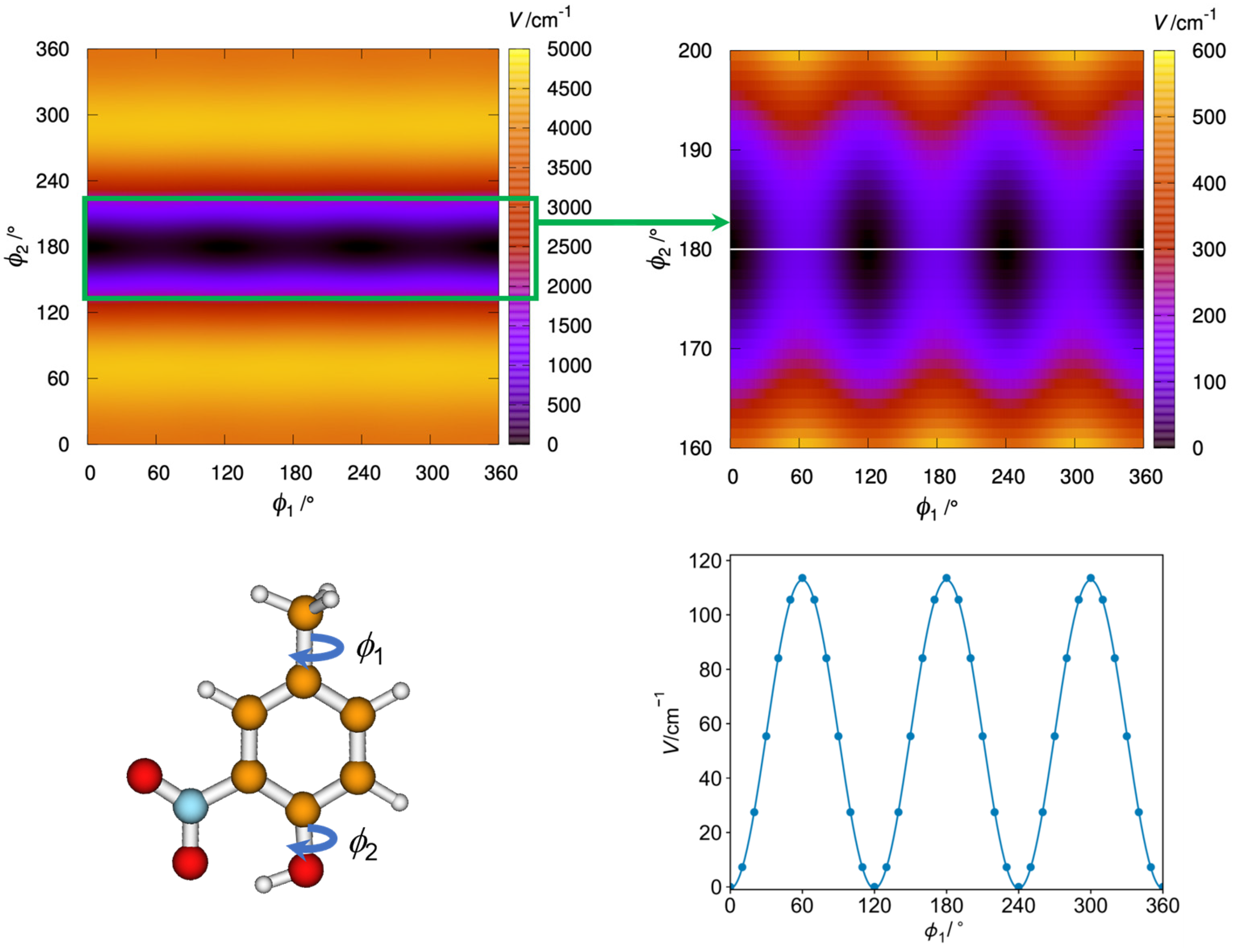
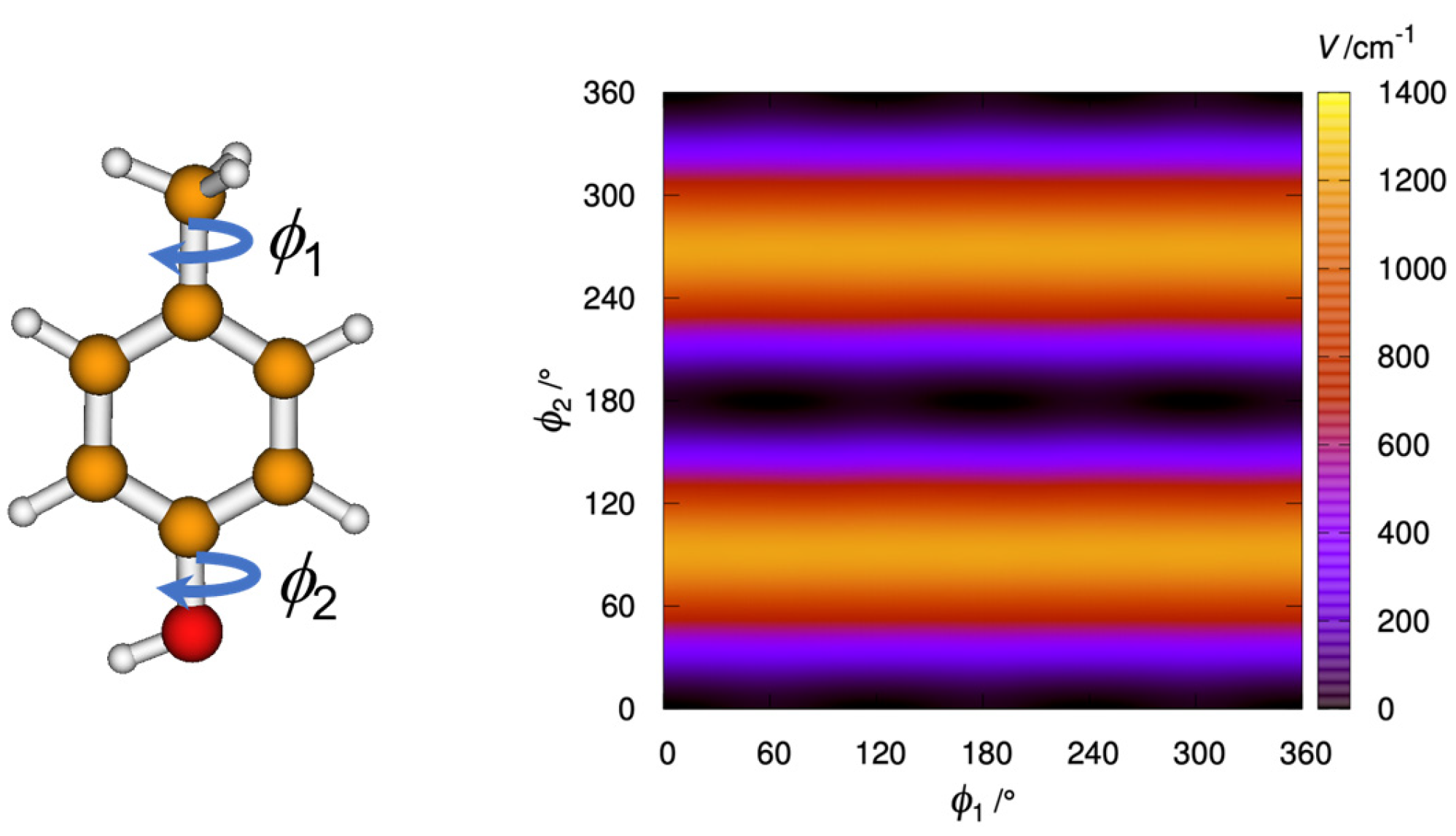
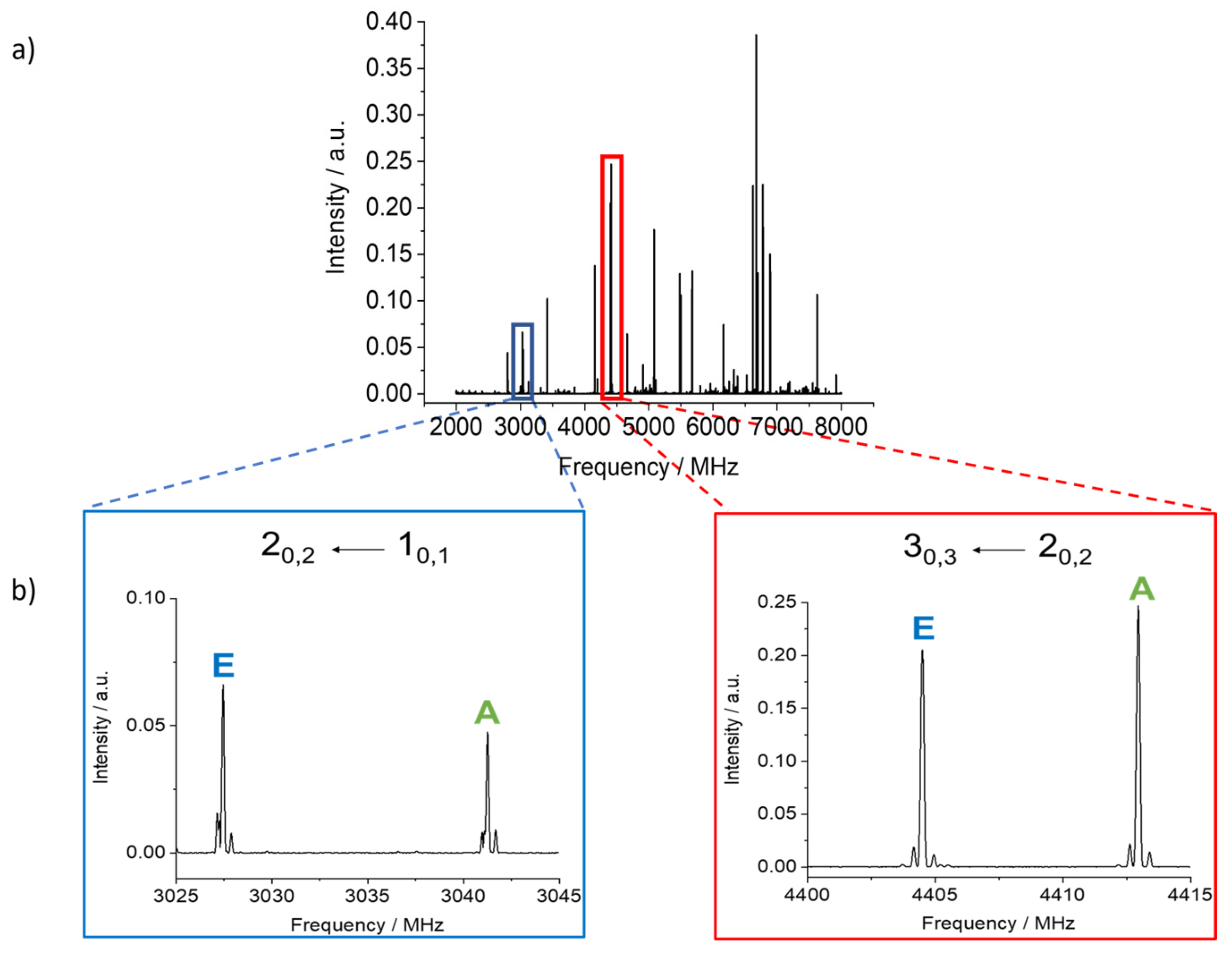
| Parameter | 4MNP-1 | 4MNP-2 | ||||
|---|---|---|---|---|---|---|
| B3LYP-D3BJ | B3PW91 | MP2 | B3LYP-D3BJ | B3PW91 | MP2 | |
| Aa (MHz) | 1840.5 | 1855.7 | 1820.1 | 1804.8 | 1808.7 | 1816.2 |
| B (MHz) | 933.8 | 935.6 | 930.5 | 925.0 | 929.1 | 902.3 |
| C (MHz) | 621.9 | 624.4 | 618.1 | 629.4 | 631.5 | 641.8 |
| Δb(uÅ2) | −3.16 | −3.12 | −3.16 | −23.42 | −23.08 | −51.03 |
| μa c (D) | 4.3 | 4.3 | 3.8 | 5.5 | 5.4 | 4.9 |
| μb (D) | −0.7 | −0.8 | −0.3 | −3.2 | −3.2 | −2.7 |
| μc (D) | 0.0 | 0.0 | 0.0 | −0.2 | −0.2 | −0.2 |
| χaa d (MHz) | −0.76 | −0.72 | −0.34 | −0.76 | −0.73 | −0.39 |
| χbb (MHz) | 0.02 | 0.01 | −0.16 | 0.12 | 0.10 | −0.01 |
| χcc (MHz) | 0.74 | 0.71 | 0.50 | 0.65 | 0.62 | 0.38 |
| V3e (cm−1) | 119.6 | 114.7 | 89.4 | 31.3 | 28.8 | 28.0 |
| ΔE f (kJ mol−1) | 0.0 | 0.0 | 0.0 | 44.0 | 45.5 | 27.1 |
| ΔE0 g (kJ mol−1) | 0.0 | 0.0 | 0.0 | 43.1 | 44.3 | 31.2 |
| Parameter | Unit | XIAM | BELGIa | Calc. |
|---|---|---|---|---|
| A | MHz | 1841.7616 (26) b | 1841.8415961 (43) | 1837.267 c |
| B | MHz | 932.06085 (19) | 932.3075 (47) | 925.714 c |
| C | MHz | 621.56246 (20) | 621.53031 (89) | 618.216 c |
| DJ | kHz | 0.0076 (11) | - | 0.05921 c |
| DJK | kHz | 0.0153 (58) | - | −0.06727 c |
| F0 | GHz | 160.336 d | 160.34966 (44) | 160.336 e |
| F | GHz | 161.9023 f | 161.9023 g | - |
| V3 | cm−1 | 106.4456 (8) | 105.995 (14) | 117.8 |
| unitless | 0.0100 f | 0.0099412 (28) | - | |
| kHz | −20.331 (88) | - | - | |
| MHz | 0.1158 (36) | - | - | |
| kHz | −17.9 (2) | - | - | |
| χaa | MHz | −0.8150 (43) | −0.811 (27) | −0.7053 h |
| χbb | MHz | −0.0702 (70) i | −0.075 (50) | 0.0379 h |
| χcc | MHz | 0.885 (17) i | 0.89 (12) | 0.6674 h |
| ∠(i,a) | ° | 34.4141 (12) | 34.37469 (49) | 34.40 |
| ∠(i,b) | ° | 55.5859 (12) | 55.62532 (49) | 55.61 |
| ∠(i,c) | ° | 90.0 j | 90.0 j | 89.00 |
| rmsk | kHz | 7.8 | 3.9 | - |
| NA/NE/Nhf l | 168/159/327 | 168/159/327 | - |
| Parameter | Unit | Value | Operator a |
|---|---|---|---|
| A | MHz | 1744.2236 (35) | |
| B | MHz | 1029.6800 (40) | |
| C | MHz | 621.53031 (89) | |
| Dab | MHz | 281.1730 (48) | } |
| ΔJ | kHz | 0.0 | |
| ΔK | kHz | −0.576 (33) | |
| ΔJK | kHz | 0.211 (11) | |
| δJ | kHz | 0.0 | |
| δK | kHz | 0.0 | |
| χaa | MHz | −0.630 (46) | - |
| χbb | MHz | −1.140 (46) | - |
| χab | MHz | −1.515 (57) | - |
| V3 | cm−1 | 105.995 (14) | (1/2)(1 − cos 3α) |
| ρ | unitless | 0.0099412 (28) | |
| F | GHz | 161.9023 b | |
| c2 | MHz | −0.0842 (25) | |
| Δab | MHz | 0.15048 (56) | |
| rmsc | kHz | 3.9 | - |
| NA/NE/Nhf d | 168/159/327 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baweja, S.; Antonelli, E.; Hussain, S.; Fernández-Ramos, A.; Kleiner, I.; Nguyen, H.V.L.; Sanz, M.E. Revealing Internal Rotation and 14N Nuclear Quadrupole Coupling in the Atmospheric Pollutant 4-Methyl-2-nitrophenol: Interplay of Microwave Spectroscopy and Quantum Chemical Calculations. Molecules 2023, 28, 2153. https://doi.org/10.3390/molecules28052153
Baweja S, Antonelli E, Hussain S, Fernández-Ramos A, Kleiner I, Nguyen HVL, Sanz ME. Revealing Internal Rotation and 14N Nuclear Quadrupole Coupling in the Atmospheric Pollutant 4-Methyl-2-nitrophenol: Interplay of Microwave Spectroscopy and Quantum Chemical Calculations. Molecules. 2023; 28(5):2153. https://doi.org/10.3390/molecules28052153
Chicago/Turabian StyleBaweja, Shefali, Eleonore Antonelli, Safia Hussain, Antonio Fernández-Ramos, Isabelle Kleiner, Ha Vinh Lam Nguyen, and M. Eugenia Sanz. 2023. "Revealing Internal Rotation and 14N Nuclear Quadrupole Coupling in the Atmospheric Pollutant 4-Methyl-2-nitrophenol: Interplay of Microwave Spectroscopy and Quantum Chemical Calculations" Molecules 28, no. 5: 2153. https://doi.org/10.3390/molecules28052153
APA StyleBaweja, S., Antonelli, E., Hussain, S., Fernández-Ramos, A., Kleiner, I., Nguyen, H. V. L., & Sanz, M. E. (2023). Revealing Internal Rotation and 14N Nuclear Quadrupole Coupling in the Atmospheric Pollutant 4-Methyl-2-nitrophenol: Interplay of Microwave Spectroscopy and Quantum Chemical Calculations. Molecules, 28(5), 2153. https://doi.org/10.3390/molecules28052153







