Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry
Abstract
:1. Introduction
2. Theory
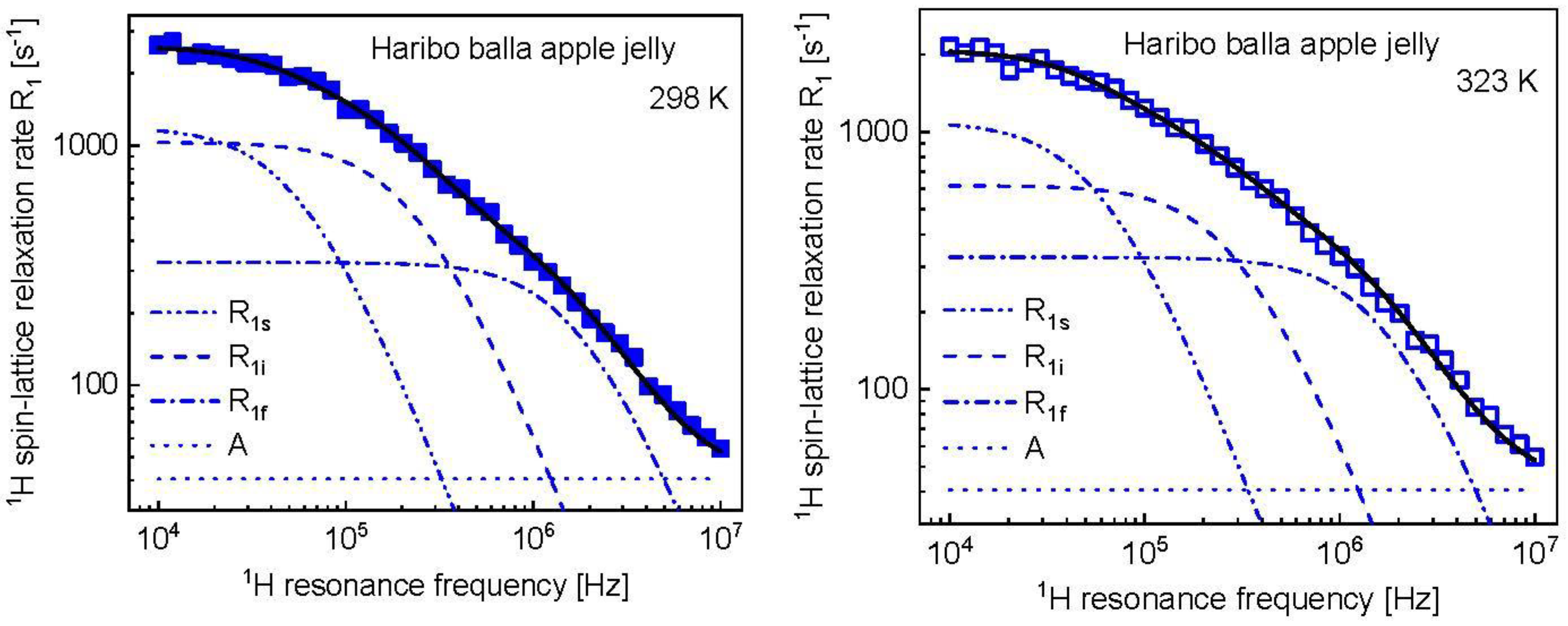
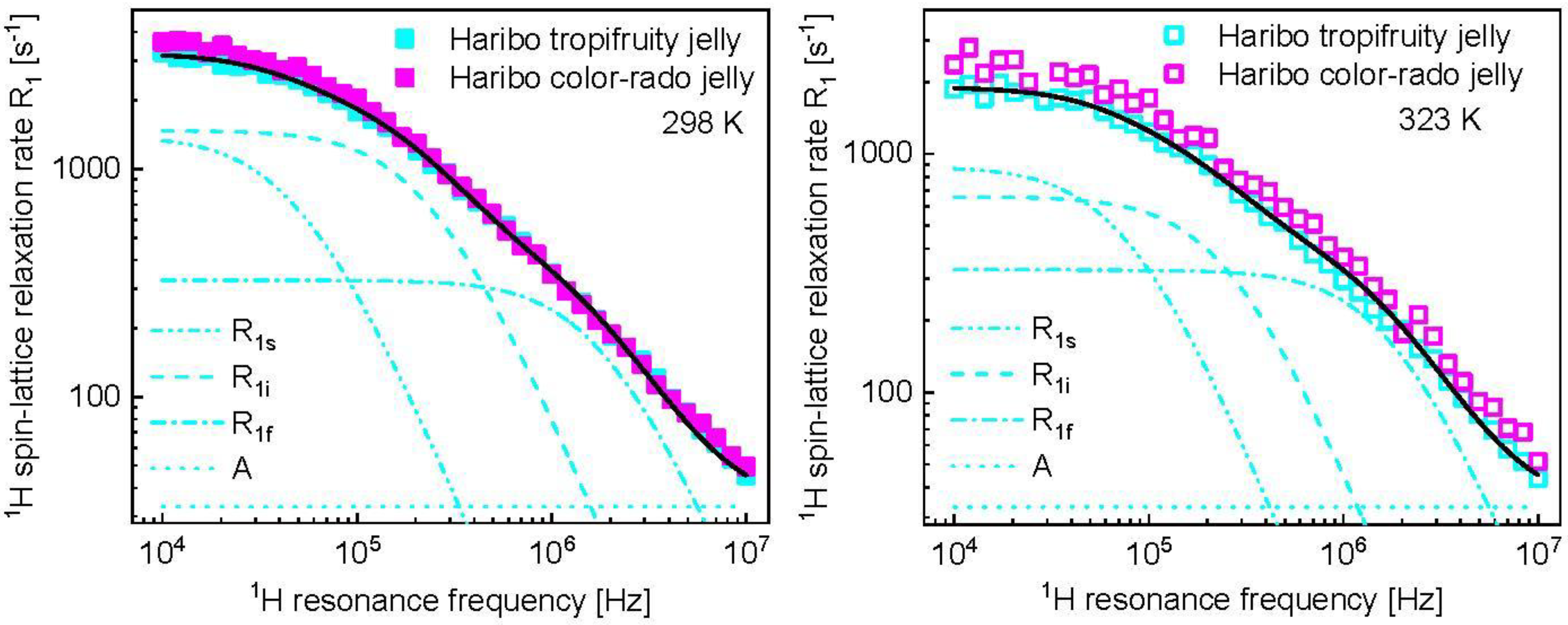
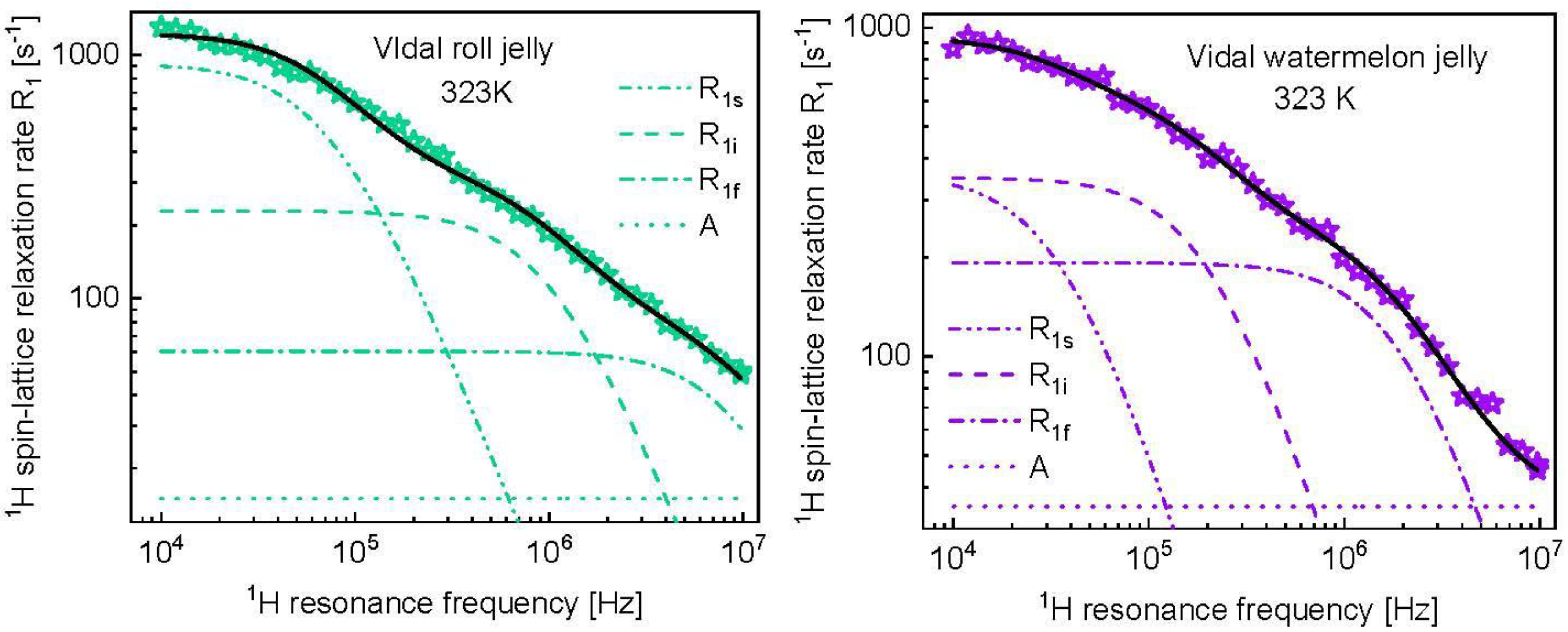
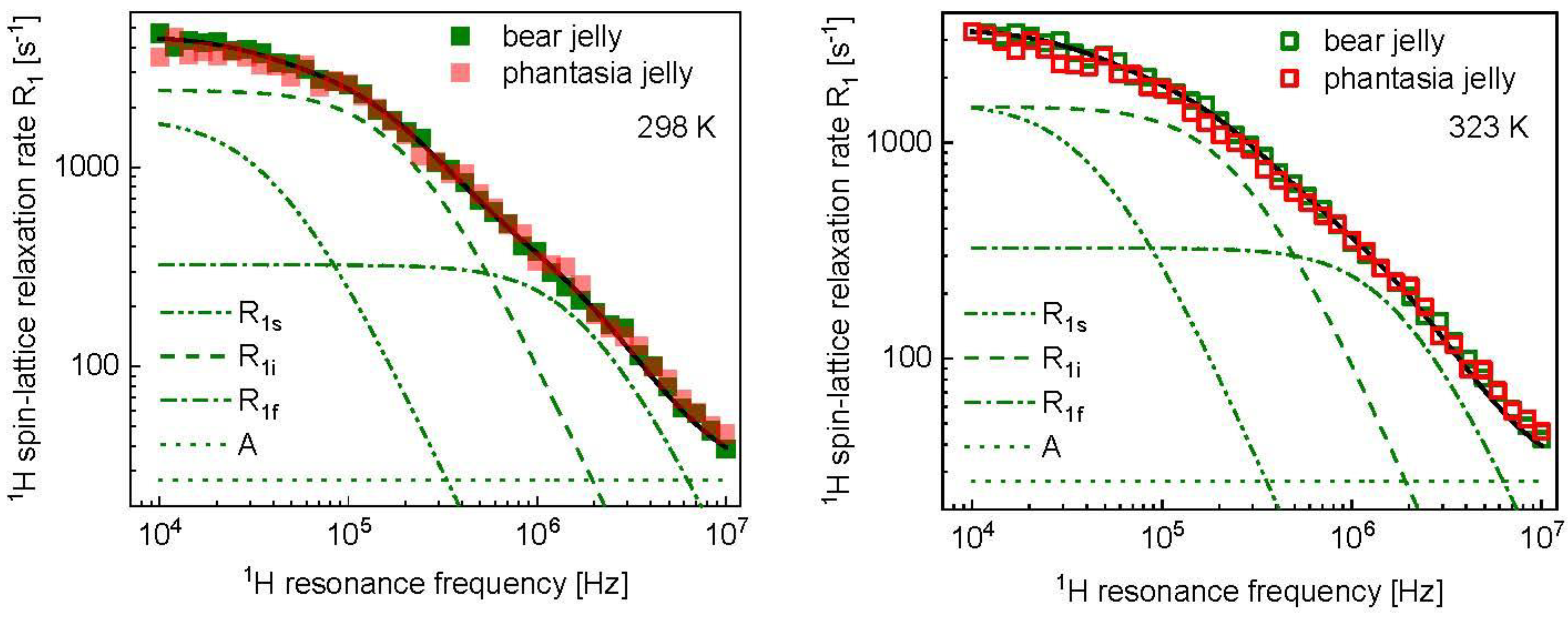
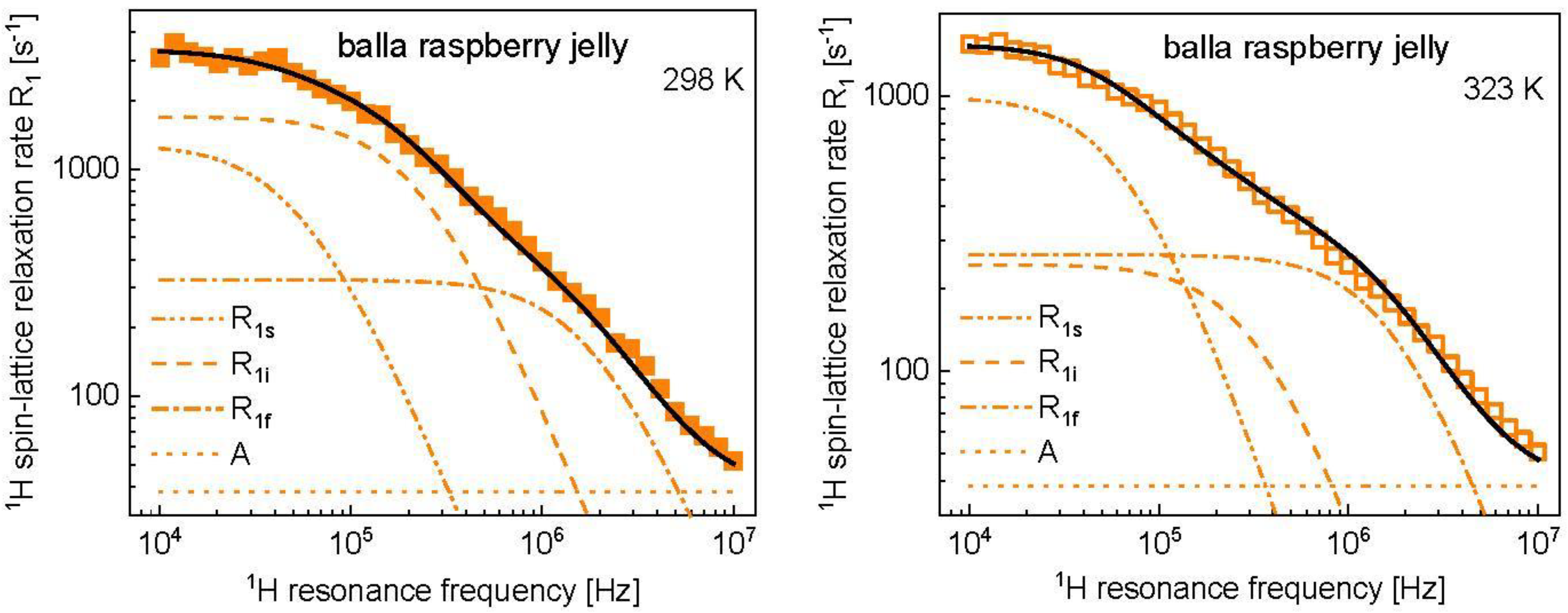
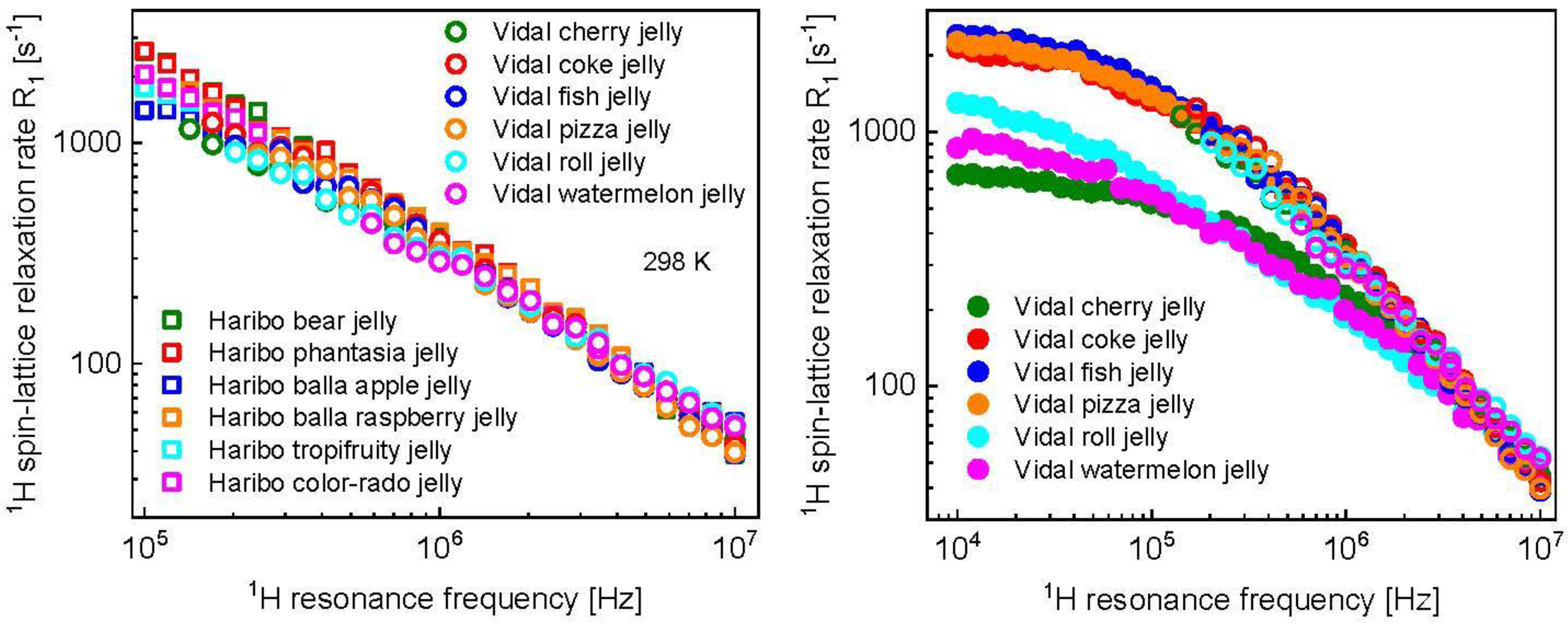
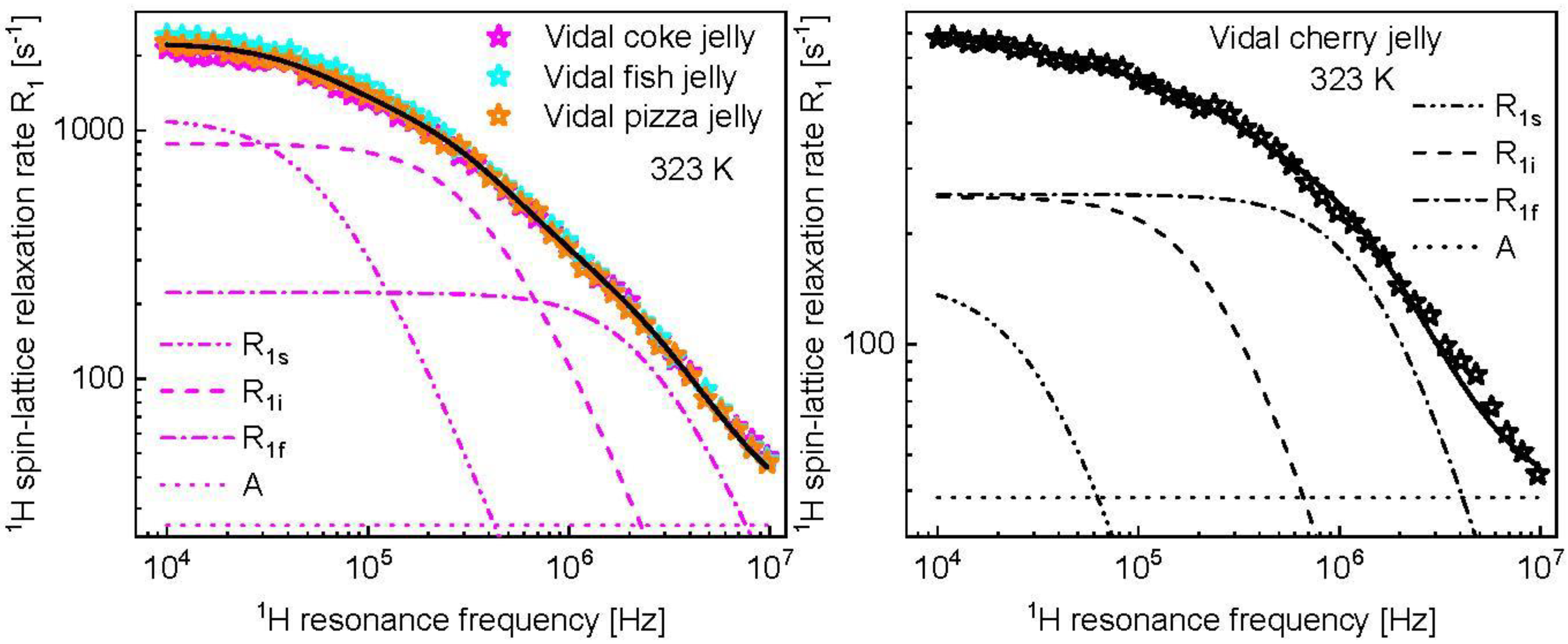
3. Results and Analysis
4. Discussion
5. Materials and Methods
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Korb, J.P. Multiscale Nuclear Magnetic Relaxation Dispersion of Complex Liquids in Bulk and Confinement. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 104, 12–55. [Google Scholar] [CrossRef]
- Kruk, D.; Meier, R.; Rachocki, A.; Korpała, A.; Singh, R.K.; Rössler, E.A. Determining Diffusion Coefficients of Ionic Liquids by Means of Field Cycling Nuclear Magnetic Resonance Relaxometry. J. Chem. Phys. 2014, 140, 244509. [Google Scholar] [CrossRef] [PubMed]
- Carignani, E.; Juszyńska-Gałązka, E.; Gałązka, M.; Forte, C.; Geppi, M.; Calucci, L. Translational and Rotational Diffusion of Three Glass Forming Alcohols by 1H Field Cycling NMR Relaxometry. J. Mol. Liq. 2021, 330, 115597. [Google Scholar] [CrossRef]
- Overbeck, V.; Golub, B.; Schröder, H.; Appelhagen, A.; Paschek, D.; Neymeyr, K.; Ludwig, R. Probing Relaxation Models by Means of Fast Field-Cycling Relaxometry, NMR Spectroscopy and Molecular Dynamics Simulations: Detailed Insight into the Translational and Rotational Dynamics of a Protic Ionic Liquid. J. Mol. Liq. 2020, 319, 114207. [Google Scholar] [CrossRef]
- Ordikhani Seyedlar, A.; Stapf, S.; Mattea, C. Nuclear Magnetic Relaxation and Diffusion Study of the Ionic Liquids 1-Ethyl- and 1-Butyl-3-Methylimidazolium Bis(Trifluoromethylsulfonyl)Imide Confined in Porous Glass. Magn. Reson. Chem. 2019, 57, 818–828. [Google Scholar] [CrossRef]
- Ordikhani Seyedlar, A.; Stapf, S.; Mattea, C. Dynamics of the Ionic Liquid 1-Butyl-3-Methylimidazolium Bis(Trifluoromethylsulphonyl)Imide Studied by Nuclear Magnetic Resonance Dispersion and Diffusion. Phys. Chem. Chem. Phys. 2015, 17, 1653–1659. [Google Scholar] [CrossRef]
- Jayakody, N.K.; Fraenza, C.C.; Greenbaum, S.G.; Ashby, D.; Dunn, B.S. NMR Relaxometry and Diffusometry Analysis of Dynamics in Ionic Liquids and Ionogels for Use in Lithium-Ion Batteries. J. Phys. Chem. B 2020, 124, 6843–6856. [Google Scholar] [CrossRef]
- Kimmich, R.; Fatkullin, N. Self-Diffusion Studies by Intra- and Inter-Molecular Spin-Lattice Relaxometry Using Field-Cycling: Liquids, Plastic Crystals, Porous Media, and Polymer Segments. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 101, 18–50. [Google Scholar] [CrossRef]
- Kimmich, R.; Fatkullin, N. Polymer Chain Dynamics and NMR. In NMR• 3D Analysis• Photopolymerization; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–113. [Google Scholar]
- Goddard, Y.; Korb, J.-P.; Bryant, R.G. The Magnetic Field and Temperature Dependences of Proton Spin-Lattice Relaxation in Proteins. J. Chem. Phys. 2007, 126, 175105. [Google Scholar] [CrossRef]
- Bertini, I.; Fragai, M.; Luchinat, C.; Parigi, G. H NMRD Profiles of Diamagnetic Proteins: A Model-Free Analysis. Magn. Reson. Chem. 2000, 38, 543–550. [Google Scholar] [CrossRef]
- Ravera, E.; Parigi, G.; Mainz, A.; Religa, T.L.; Reif, B.; Luchinat, C. Experimental Determination of Microsecond Reorientation Correlation Times in Protein Solutions. J. Phys. Chem. B 2013, 117, 3548–3553. [Google Scholar] [CrossRef]
- Kruk, D.; Masiewicz, E.; Borkowska, A.M.; Rochowski, P.; Fries, P.H.; Broche, L.M.; Lurie, D.J. Dynamics of Solid Proteins by Means of Nuclear Magnetic Resonance Relaxometry. Biomolecules 2019, 9, 625. [Google Scholar] [CrossRef] [Green Version]
- Kruk, D.; Fujara, F.; Gumann, P.; Medycki, W.; Privalov, A.F.; Tacke, C. Field Cycling Methods as a Tool for Dynamics Investigations in Solid State Systems: Recent Theoretical Progress. Solid State Nucl. Magn. Reson. 2009, 35, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Kruk, D.; Lips, O. Field-Dependent Nuclear Relaxation of Spins 1/2 Induced by Dipole-Dipole Couplings to Quadrupole Spins: LaF3 Crystals as an Example. J. Magn. Reson. 2006, 179, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Fujara, F.; Kruk, D.; Privalov, A.F. Solid State Field-Cycling NMR Relaxometry: Instrumental Improvements and New Applications. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 82, 39–69. [Google Scholar] [CrossRef] [PubMed]
- Kimmich, R.; Anoardo, E. Field-Cycling NMR Relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 2004, 44, 257–320. [Google Scholar] [CrossRef]
- Baroni, S.; Consonni, R.; Ferrante, G.; Aime, S. Relaxometric Studies for Food Characterization: The Case of Balsamic and Traditional Balsamic Vinegars. J. Agric. Food Chem. 2009, 57, 3028–3032. [Google Scholar] [CrossRef]
- Rachocki, A.; Tritt-Goc, J. Novel Application of NMR Relaxometry in Studies of Diffusion in Virgin Rape Oil. Food Chem. 2014, 152, 94–99. [Google Scholar] [CrossRef]
- Kruk, D.; Masiewicz, E.; Budny, J.; Stankiewicz, A.; Lotarska, S.; Oztop, M.; Wieczorek, Z. Diffusion in Oils versus Their Viscosity–Insight from Nuclear Magnetic Resonance Relaxometry. J. Food Eng. 2022, 317, 110848. [Google Scholar] [CrossRef]
- Conte, P.; Mineo, V.; Bubici, S.; De Pasquale, C.; Aboud, F.; MacCotta, A.; Planeta, D.; Alonzo, G. Dynamics of Pistachio Oils by Proton Nuclear Magnetic Resonance Relaxation Dispersion. Anal. Bioanal. Chem. 2011, 400, 1443–1450. [Google Scholar] [CrossRef]
- Kruk, D.; Masiewicz, E.; Budny, J.; Kolodziejski, K.; Zulewska, J.; Wieczorek, Z. Relationship between Macroscopic Properties of Honey and Molecular Dynamics–Temperature Effects. J. Food Eng. 2022, 314, 110782. [Google Scholar] [CrossRef]
- Kruk, D.; Florek-Wojciechowska, M.; Oztop, M.; Ilhan, E.; Wieczorek, Z. Water Dynamics in Eggs by Means of Nuclear Magnetic Resonance Relaxometry. J. Magn. Reson. 2021, 327, 106976. [Google Scholar] [CrossRef]
- Kruk, D.; Florek–Wojciechowska, M.; Masiewicz, E.; Oztop, M.; Ploch-Jankowska, A.; Duda, P.; Wilczynski, S. Water Mobility in Cheese by Means of Nuclear Magnetic Resonance Relaxometry. J. Food Eng. 2021, 298, 110483. [Google Scholar] [CrossRef]
- İlhan, E.; Poçan, P.; Kruk, D.; Wojciechowski, M.; Osuch, M.; Markiewicz, R.; Jurga, S.; Oztop, M.H. Water Dynamics in Starch Based Confectionery Products Including Different Types of Sugar. Molecules 2022, 27, 2216. [Google Scholar] [CrossRef]
- Ozel, B.; Kruk, D.; Wojciechowski, M.; Osuch, M.; Oztop, M.H. Water Dynamics in Whey-Protein-Based Composite Hydrogels by Means of Nmr Relaxometry. Int. J. Mol. Sci. 2021, 22, 9672. [Google Scholar] [CrossRef] [PubMed]
- Burey, P.; Bhandari, B.R.; Rutgers, R.P.G.; Halley, P.J.; Torley, P.J. Confectionery Gels: A Review on Formulation, Rheological and Structural Aspects. Int. J. Food Prop. 2009, 12, 176–210. [Google Scholar] [CrossRef] [Green Version]
- Delgado, P.; Bañón, S. Determining the Minimum Drying Time of Gummy Confections Based on Their Mechanical Properties. CYTA-J. Food 2015, 13, 329–335. [Google Scholar] [CrossRef]
- Kasapis, S.; Mitchell, J.; Abeysekera, R.; MacNaughtan, W. Rubber-to-Glass Transitions in High Sugar/Biopolymer Mixtures. Trends Food Sci. Technol. 2004, 15, 298–304. [Google Scholar] [CrossRef]
- Pocan, P.; Ilhan, E.; Oztop, M.H. Effect of D-Psicose Substitution on Gelatin Based Soft Candies: A TD-NMR Study. Magn. Reson. Chem. 2019, 57, 661–673. [Google Scholar] [CrossRef]
- Kastner, H.; Einhorn-Stoll, U.; Senge, B. Structure Formation in Sugar Containing Pectin Gels-Influence of Ca2+ on the Gelation of Low-Methoxylated Pectin at Acidic PH. Food Hydrocoll. 2012, 27, 42–49. [Google Scholar] [CrossRef] [Green Version]
- Ates, E.G.; Ozvural, E.B.; Oztop, M.H. Understanding the Role of D-Allulose and Soy Protein Addition in Pectin Gels. J. Appl. Polym. Sci. 2021, 138, 49885. [Google Scholar] [CrossRef]
- Ilhan, E.; Pocan, P.; Ogawa, M.; Oztop, M.H. Role of ‘D-Allulose’ in a Starch Based Composite Gel Matrix. Carbohydr. Polym. 2020, 228, 115373. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.; Ahn-Jarvis, J.H.; Vodovotz, Y. Development and Characterization of Different Black Raspberry Confection Matrices Designed for Delivery of Phytochemicals. J. Food Sci. 2015, 80, E610–E618. [Google Scholar] [CrossRef]
- Slichter, C.P. Principles of Magnetic Resonance; Springer Science & Business Media: Berlin, Germany, 2013; Volume 1. [Google Scholar]
- Kruk, D. Understanding Spin Dynamics; Pan Stanford: Boca Raton, FL, USA, 2015; ISBN 9814463507. [Google Scholar]
- Kowalewski, J.; Maler, L. Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, 2nd ed.; Taylor & Francis: New York, NY, USA, 2006; ISBN 9780750309646. [Google Scholar]
- Kowalewski, J.; Egorov, A.; Kruk, D.; Laaksonen, A.; Nikkhou Aski, S.; Parigi, G.; Westlund, P.-O. Extensive NMRD Studies of Ni(II) Salt Solutions in Water and Water–Glycerol Mixtures. J. Magn. Reson. 2008, 195, 103–111. [Google Scholar] [CrossRef] [PubMed]


| Temp. (K) | (s) | (Hz2) | (s) | (s−1) |
|---|---|---|---|---|
| Haribo bear jelly and Haribo phantasia jelly | ||||
| 298 | 2.43 × 10−6 (± 5.2 × 10−7) | 1.00 × 109 (± 1.2 × 107) | 4.83 × 10−7 (± 3.9 × 10−8) | 27.0 (±3.2) |
| 323 | 2.43 × 10−6 | 8.02 × 108 (± 4.3 × 107) | 3.49 × 10−7 (± 2.6 × 10−8) | 27.0 |
| Haribo balla apple jelly | ||||
| 298 | 1.64 × 10−6 (± 6.9 × 10−8) | 5.20 × 108 (± 3.3 × 107) | 3.97 × 10−7 (± 2.9 × 10−8) | 40.6 (±5.3) |
| 323 | 1.50 × 10−6 (± 5.7 × 10−8) | 4.12 × 108 (± 2.9 × 107) | 3.00 × 10−7 (± 2.8 × 10−8) | 40.6 |
| Haribo balla raspberry jelly | ||||
| 298 | 1.76 × 10−6 (± 1.3 × 10−7) | 7.86 × 108 (± 3.9 × 107) | 4.34 × 10−7 (± 3.0 × 10−8) | 37.8 (±3.3) |
| 323 | 1.37 × 10−6 (± 3.6 × 10−8) | 1.78 × 108 (± 2.1 × 107) | 2.74 × 10−7 (± 4.2 × 10−8) | 37.8 |
| Haribo tropifruity jelly and Haribo color-rado jelly | ||||
| 298 | 1.92 × 10−6 (± 5.0 × 10−8) | 7.08 × 108 (± 1.6 × 107) | 4.17 × 10−7 (± 1.3 × 10−8) | 33.1 (±3.7) |
| 323 | 1.20 × 10−6 (± 5.8 × 10−8) | 3.61 × 108 (± 2.2 × 107) | 3.66 × 10−7 (± 3.3 × 10−8) | 33.1 |
| (Hz2) | (s) | (Hz2) | (s) | (Hz2) | [s] | [s−1] |
|---|---|---|---|---|---|---|
| Vidal coke jelly, Vidal fish jelly and Vidal pizza jelly | ||||||
| 1.46 × 108 | 1.53 × 10−6 (± 2.8 × 10−8) | 6.98 × 108 (± 6.9 × 107) | 2.53 × 10−7 (± 1.6 × 10−8) | 1.25 × 109 | 3.55 × 10−8 (± 6.3 × 10−9) | 25.6 (±1.2) |
| Vidal cherry jelly | ||||||
| 1.16 × 107 (± 3.1 × 106) | 2.55 × 10−6 (± 5.3 × 10−7) | 1.38 × 108 (± 1.7 × 107) | 3.45 × 10−7 (± 2.4 × 10−8) | 9.11 × 108 (± 3.1 × 107) | 5.61 × 10−8 (± 2.4 × 10−9) | 38.4 (±2.2) |
| Vidal roll jelly | ||||||
| 1.46 × 108 | 1.26 × 10−6 (± 3.0 × 10−8) | 4.90 × 108 (± 2.0 × 108) | 9.32 × 10−8 (± 2.6 × 10−8) | 1.25 × 109 | 9.68 × 10−9 (± 6.1 × 10−9) | 15.1 (±0.8) |
| Vidal watermelon jelly | ||||||
| 2.94 × 107 (± 8.8 × 107) | 2.44 × 10−6 (± 4.7 × 10−7) | 1.64 × 108 (± 2.5 × 107) | 4.27 × 10−7 (± 8.8 × 10−8) | 8.79 × 108 (± 6.6 × 107) | 4.39 × 10−8 (± 6.7 × 10−9) | 35.0 (±3.3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruk, D.; Grunin, L.; Stankiewicz, A.; Kołodziejski, K.; Ilhan, E.; Oztop, M.H. Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry. Molecules 2023, 28, 2230. https://doi.org/10.3390/molecules28052230
Kruk D, Grunin L, Stankiewicz A, Kołodziejski K, Ilhan E, Oztop MH. Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry. Molecules. 2023; 28(5):2230. https://doi.org/10.3390/molecules28052230
Chicago/Turabian StyleKruk, Danuta, Leonid Grunin, Aleksandra Stankiewicz, Karol Kołodziejski, Esmanur Ilhan, and Mecit Halil Oztop. 2023. "Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry" Molecules 28, no. 5: 2230. https://doi.org/10.3390/molecules28052230
APA StyleKruk, D., Grunin, L., Stankiewicz, A., Kołodziejski, K., Ilhan, E., & Oztop, M. H. (2023). Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry. Molecules, 28(5), 2230. https://doi.org/10.3390/molecules28052230






