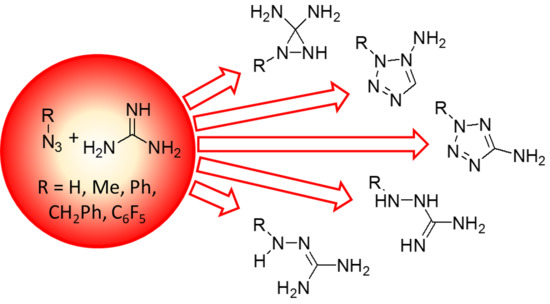
Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine
Abstract
:1. Introduction
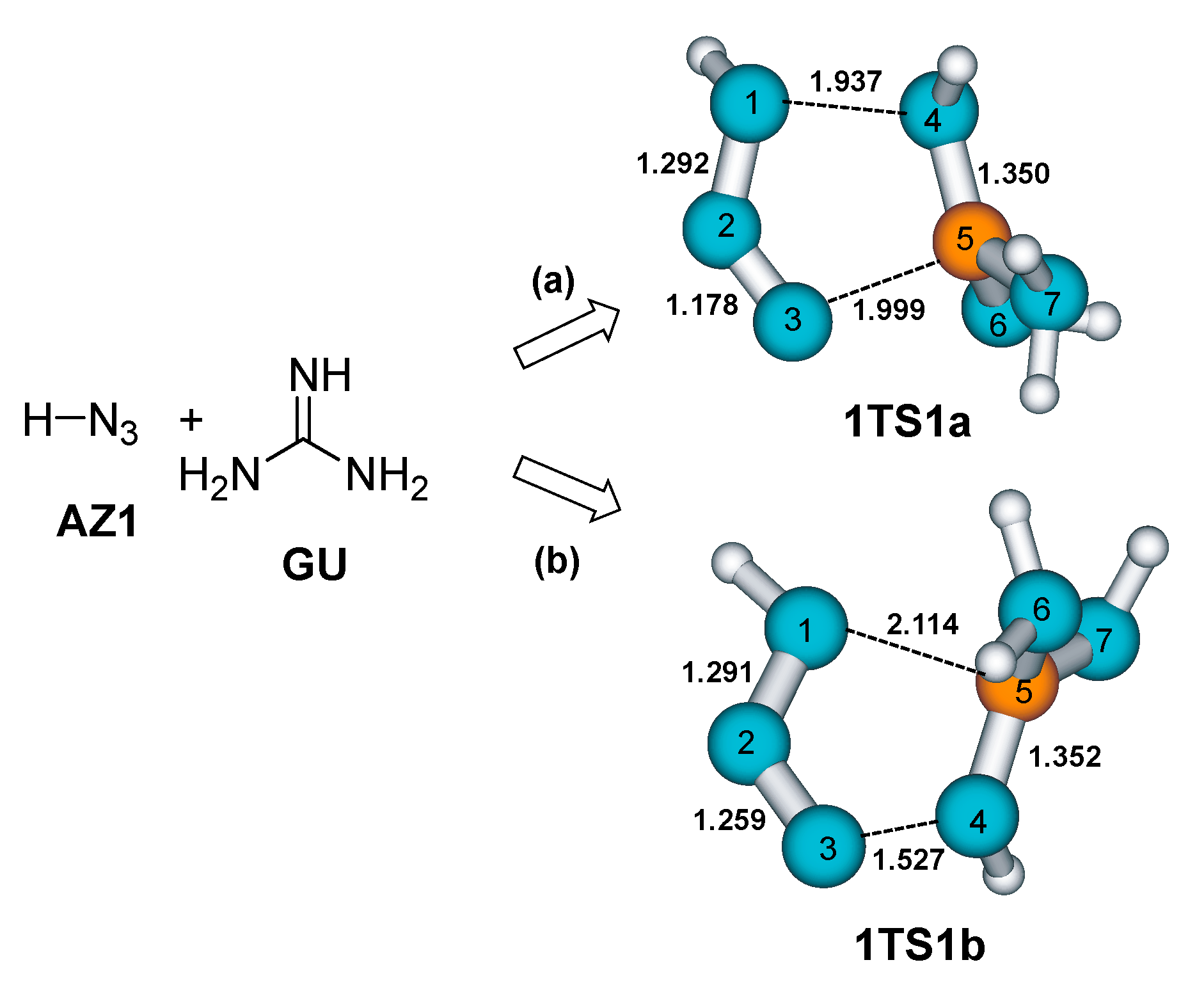
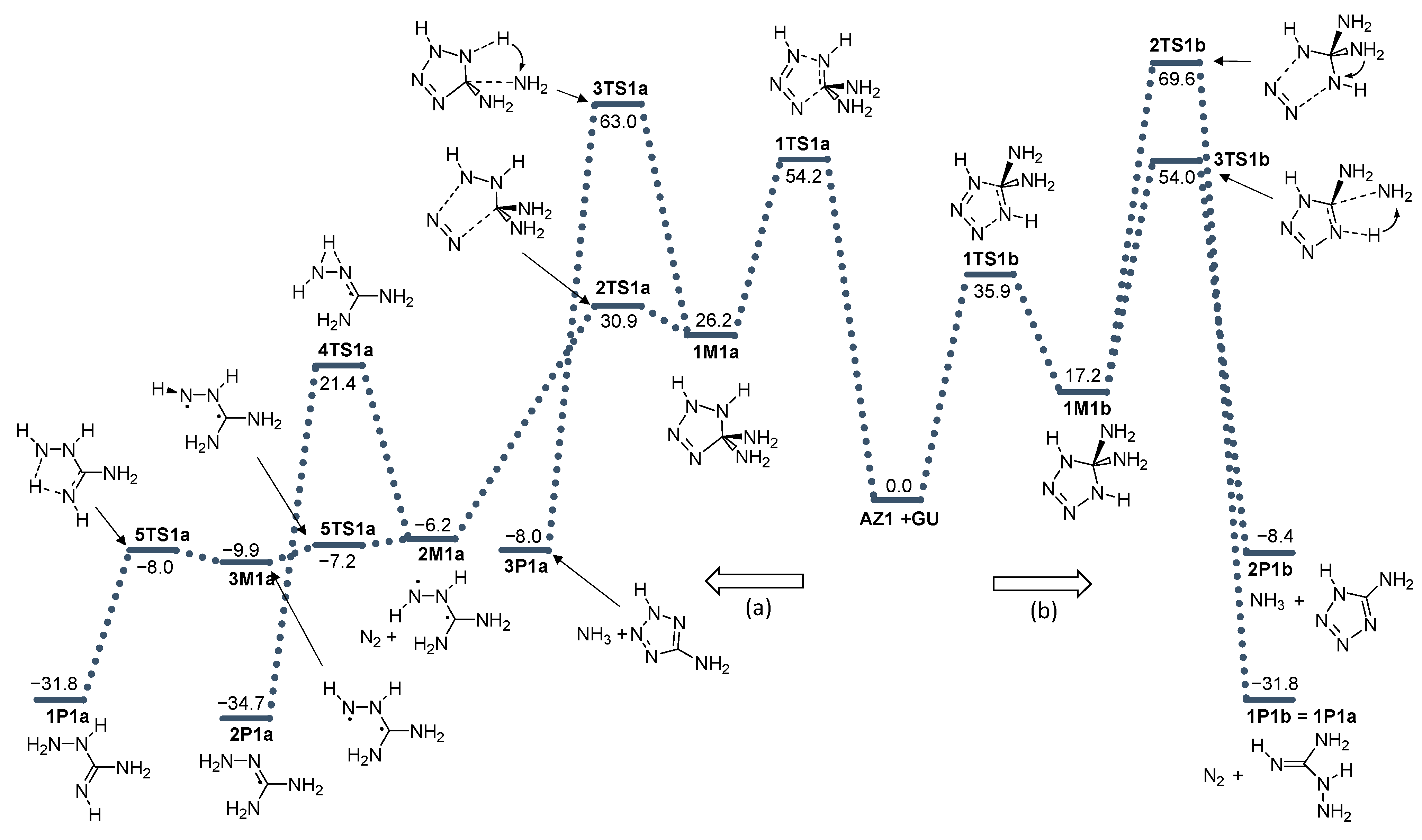
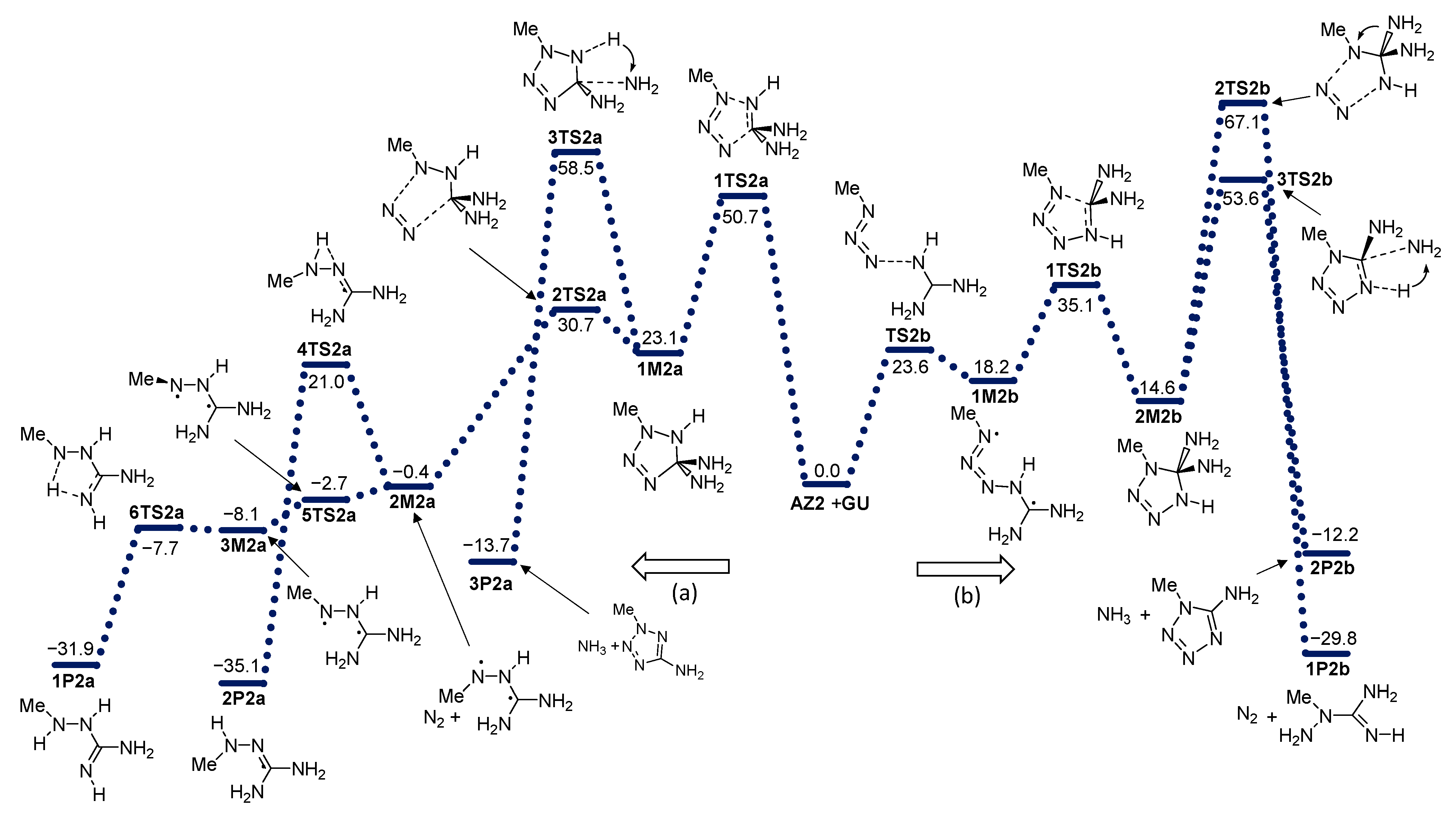
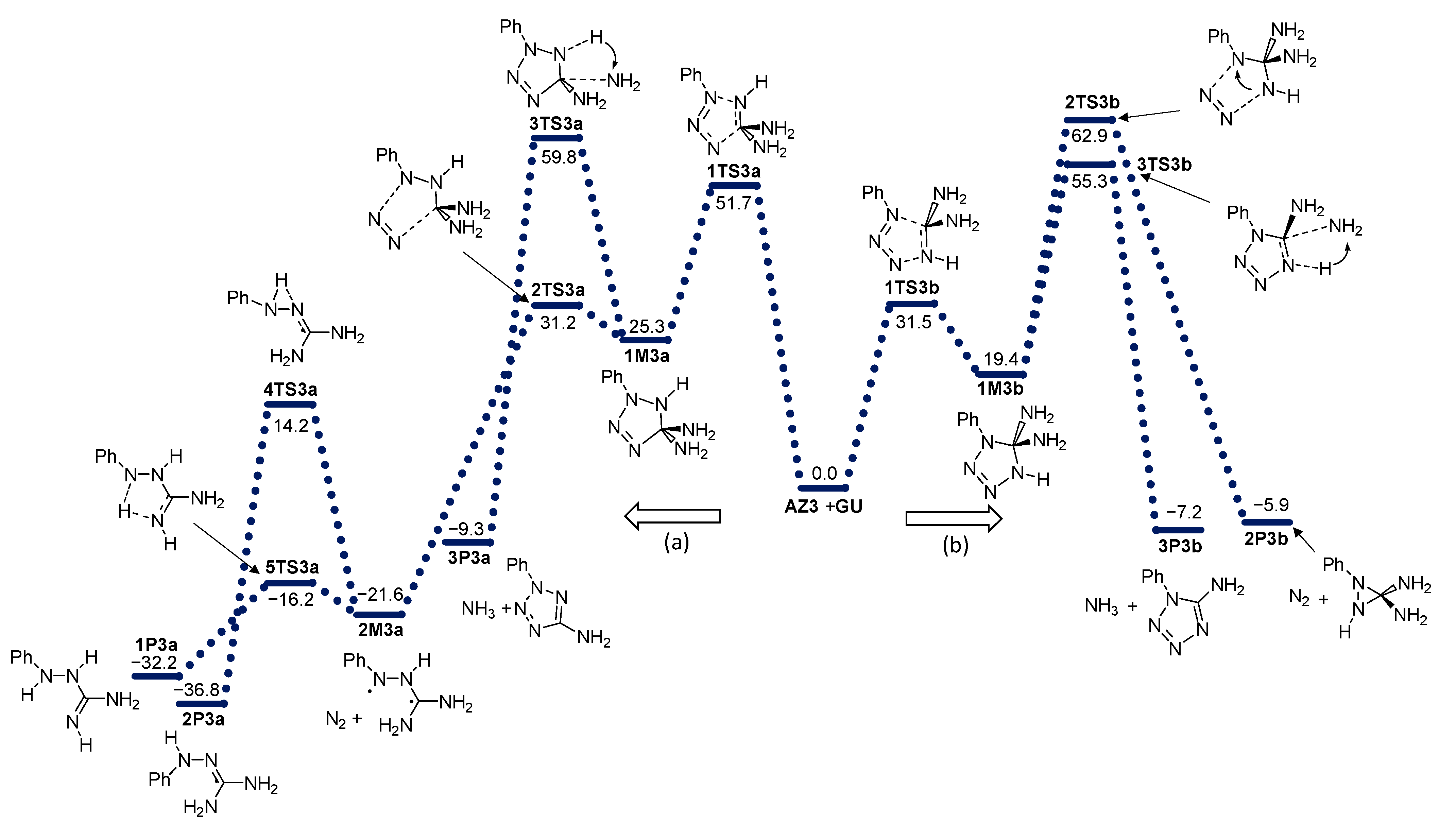
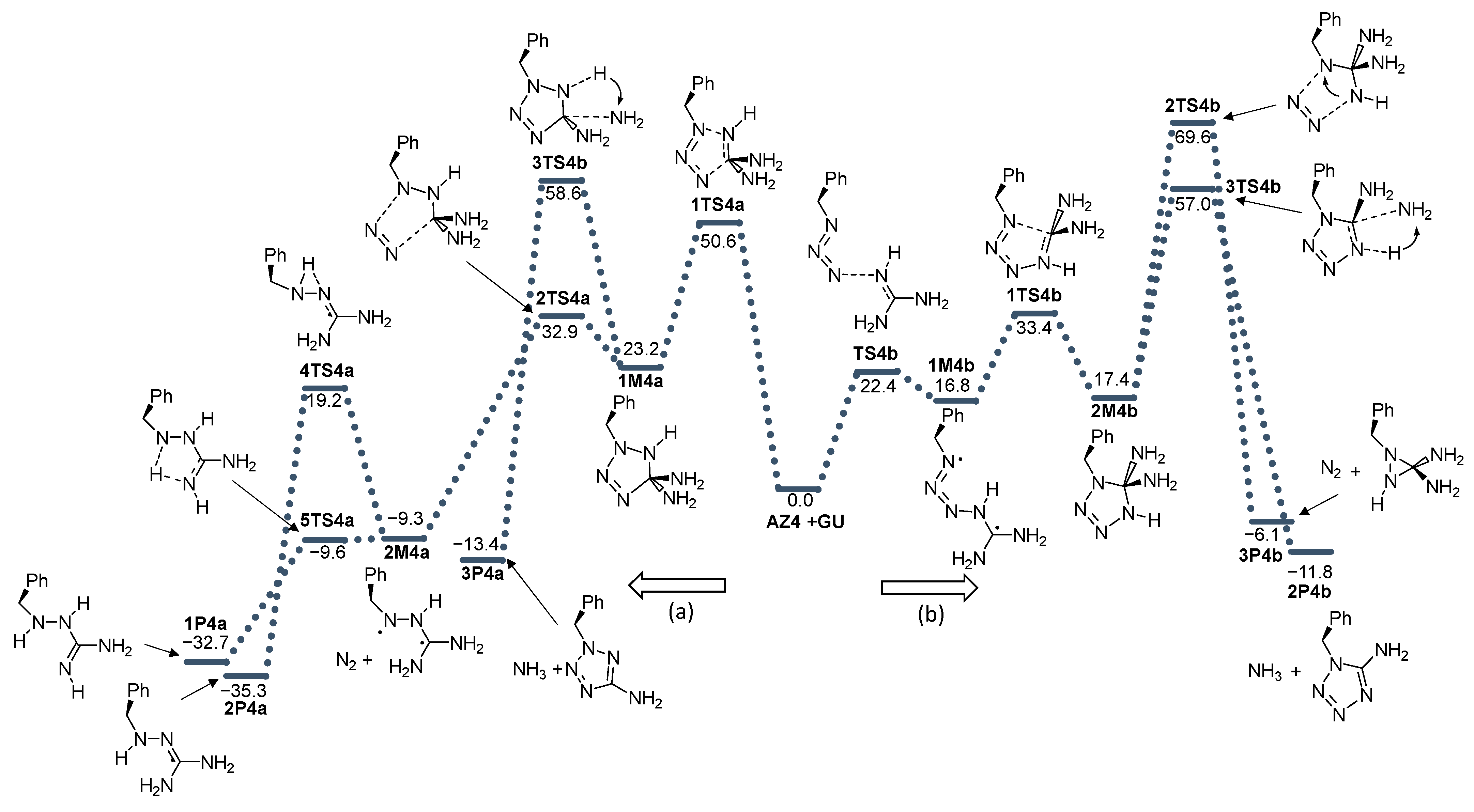
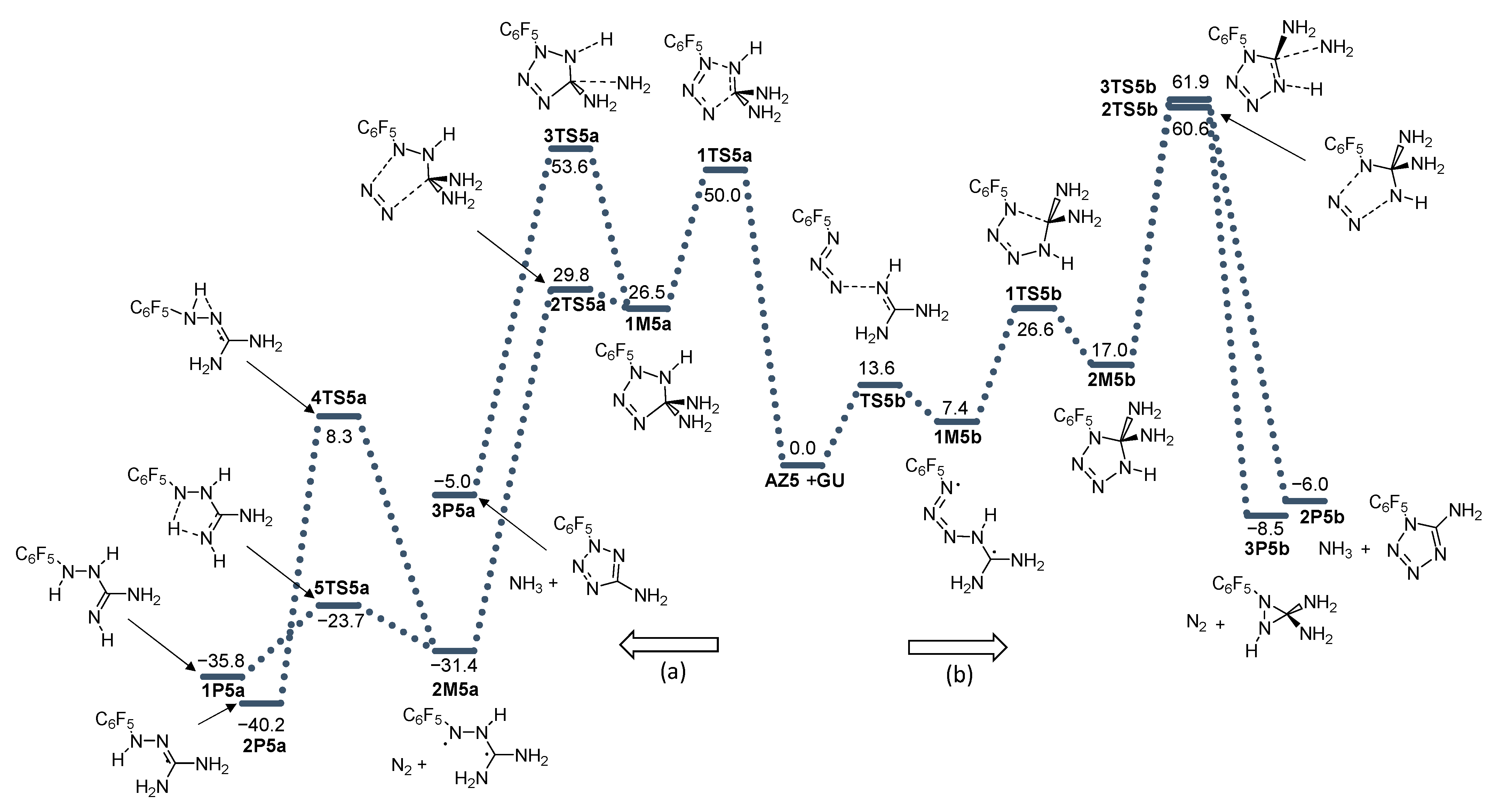
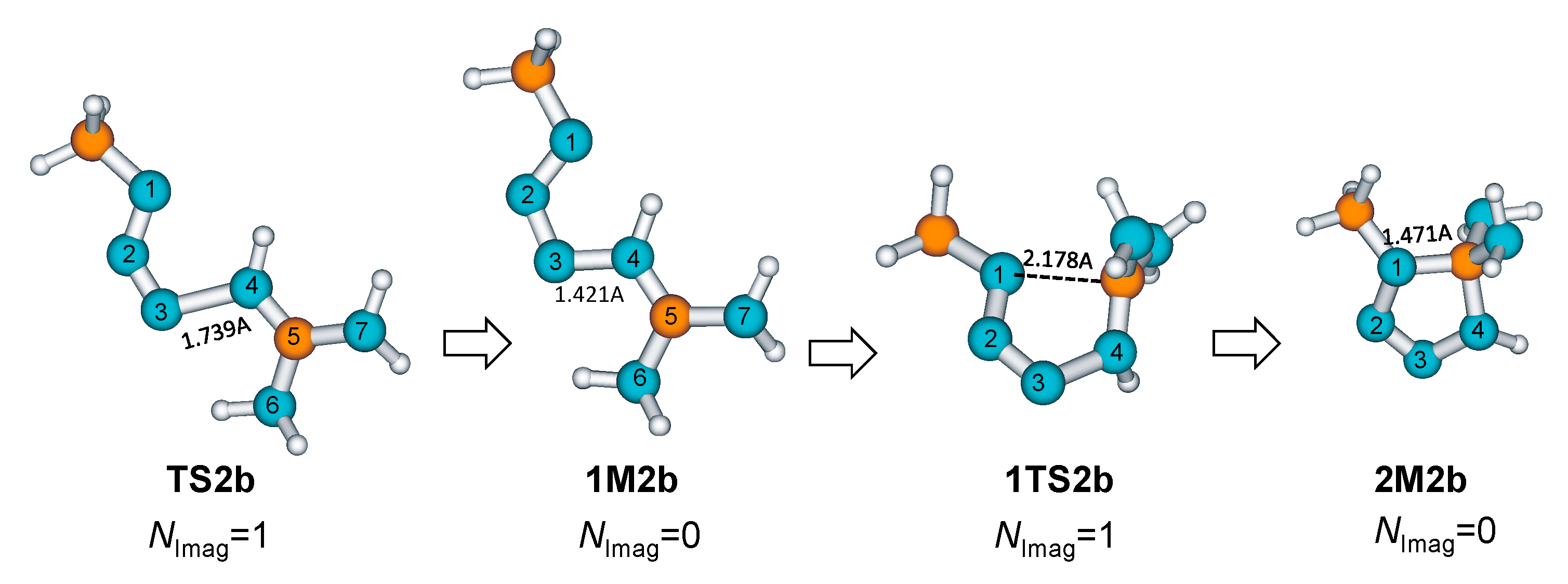
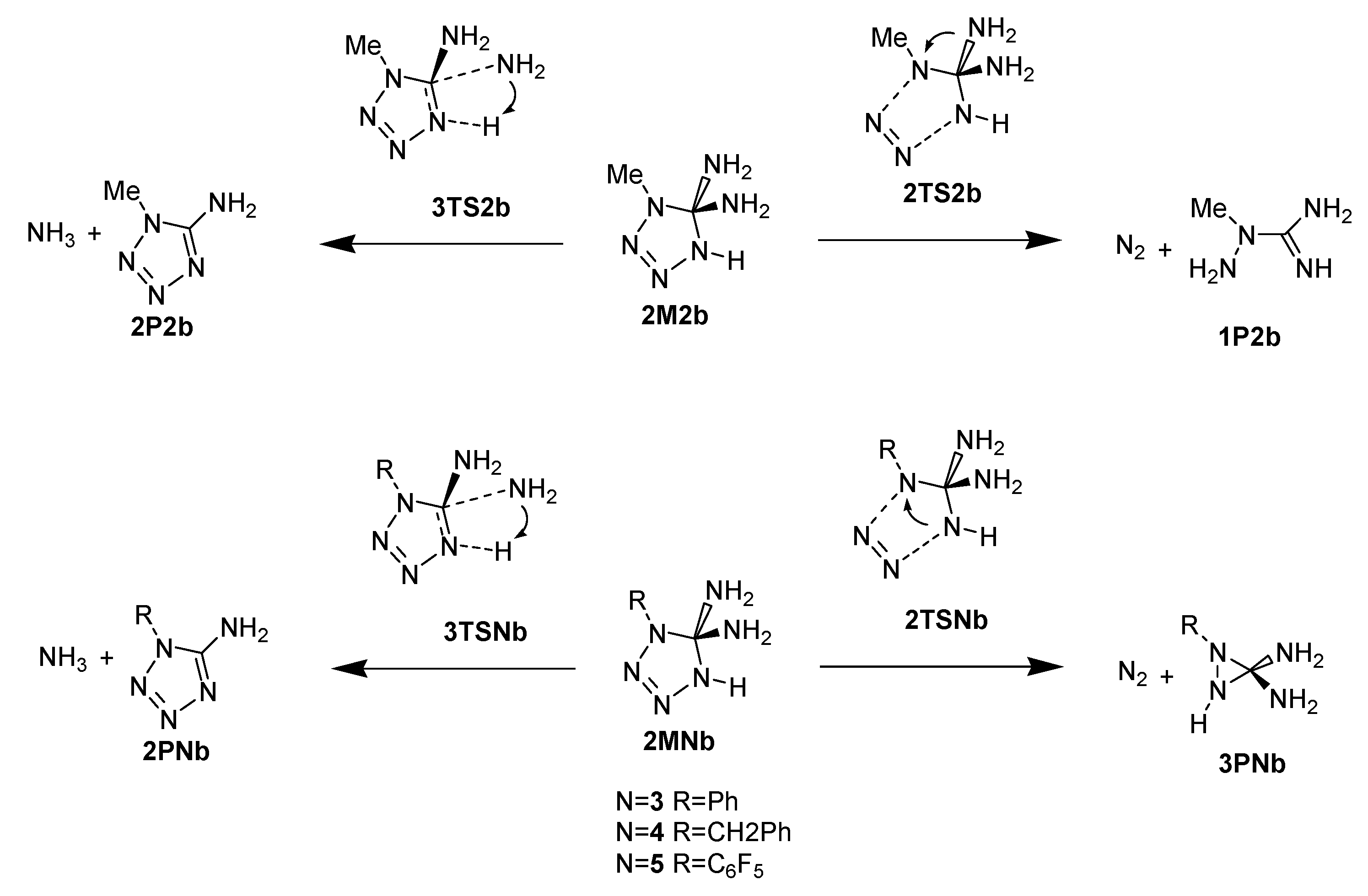
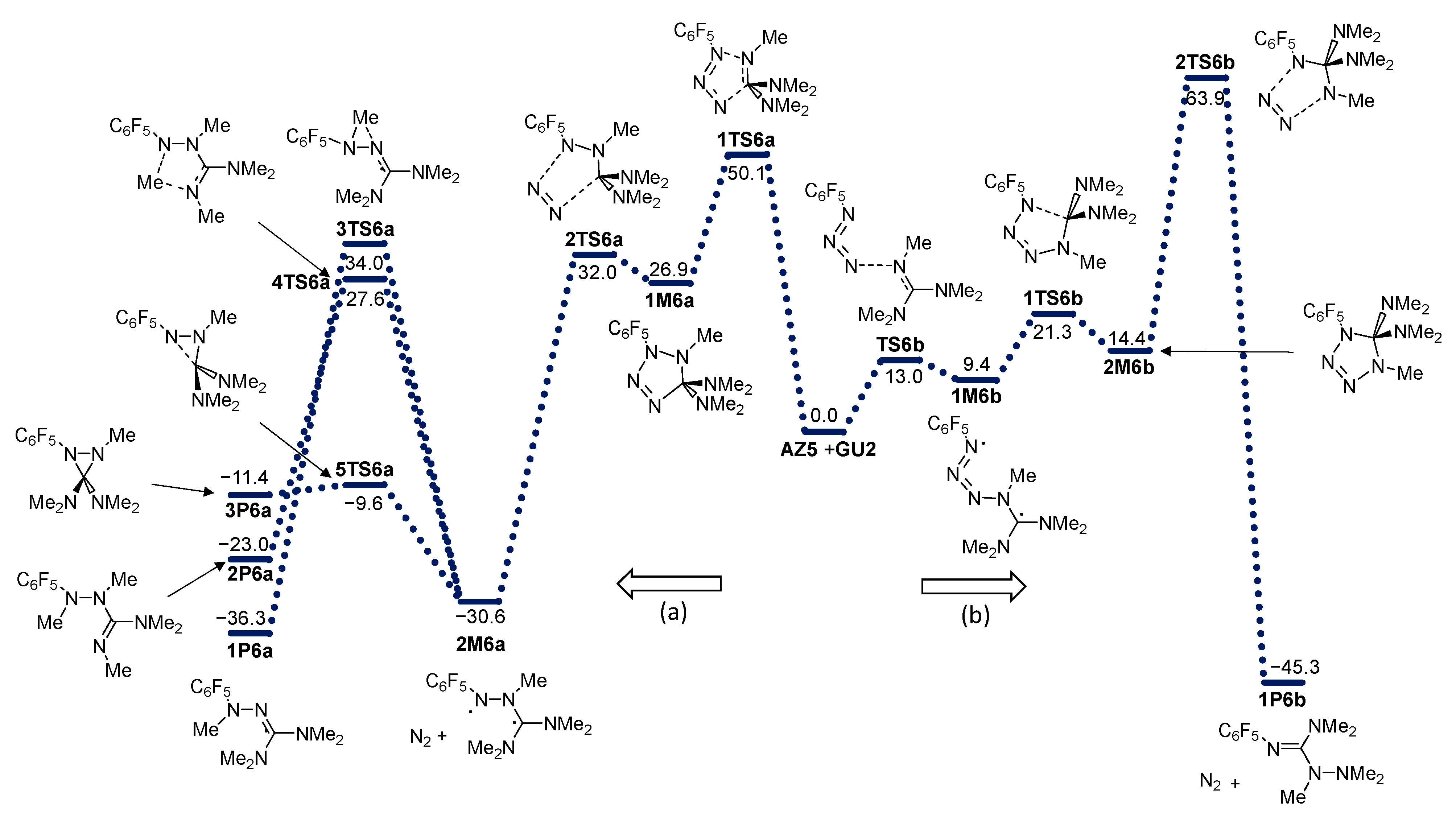
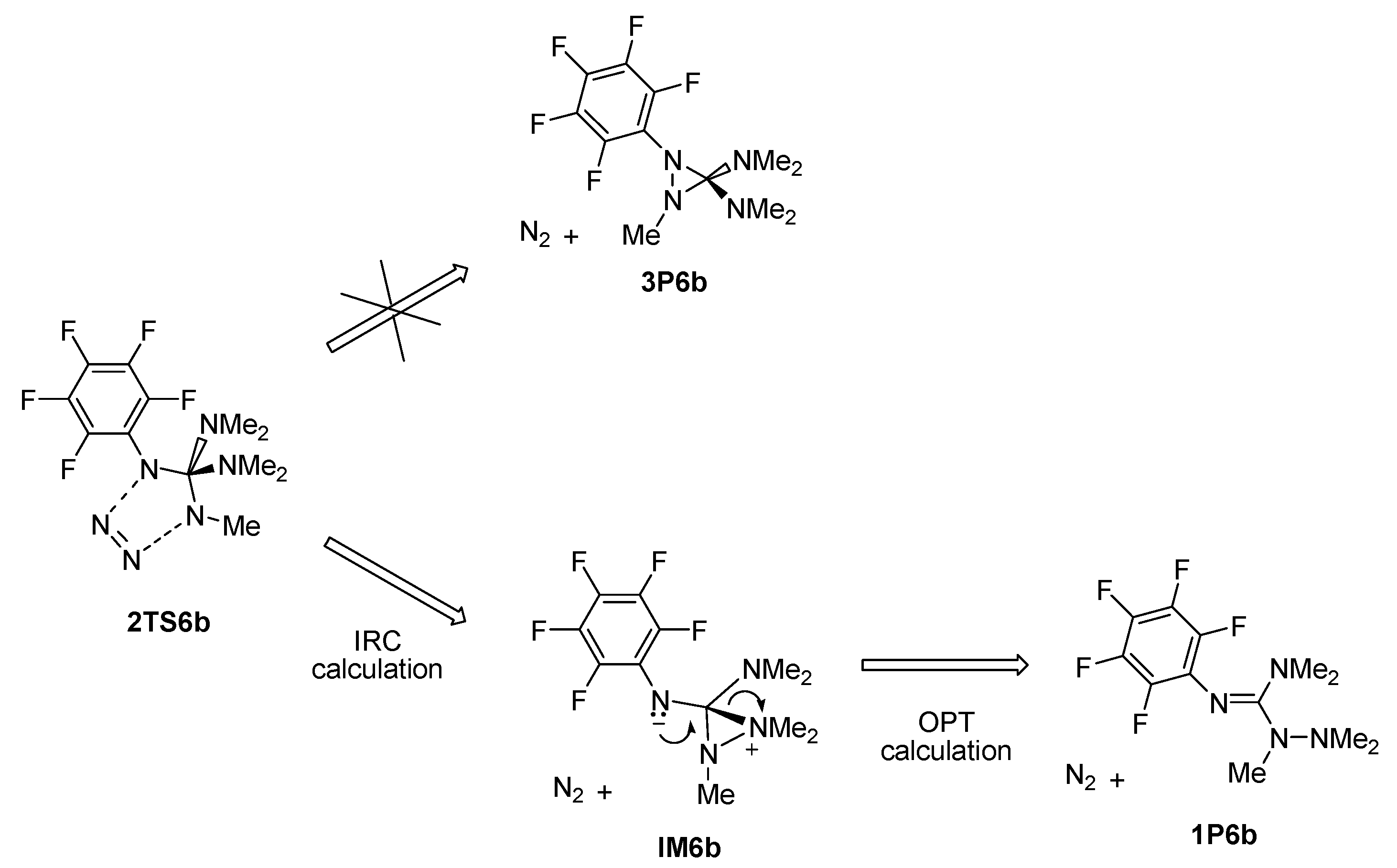
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Maksić, Z.B.; Kovačević, B.; Vianello, R. Advances in Determining the Absolute Proton Affinities of Neutral Organic Molecules in the Gas Phase and Their Interpretation: A Theoretical Account. Chem. Rev. 2012, 112, 5240–5270. [Google Scholar] [CrossRef]
- Vazdar, K.; Margetić, D.; Kovačević, B.; Sundermeyer, J.; Leito, I.; Jahn, U. Design of Novel Uncharged Organic Superbases: Merging Basicity and Functionality. Acc. Chem. Res. 2021, 54, 3108–3123. [Google Scholar] [CrossRef]
- Saczewski, F.; Balewski, Ł. Biological Activities of Guanidine Compounds. Expert Opin. Ther. Pat. 2009, 19, 1417–1448. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T. (Ed.) Superbases for Organic Synthesis: Guanidines, Amidines, Phosphazenes and Related Organocatalysts; Wiley: Chichester, UK, 2009. [Google Scholar]
- Bailey, P.J.; Pace, S. The Coordination Chemistry of Guanidines and Guanidinates. Coord. Chem. Rev. 2009, 214, 91–141. [Google Scholar] [CrossRef]
- Thiele, M.; Octa-Smolin, F.; Thölke, S.; Wölper, C.; Linders, J.; Mayer, C.; Haberhauer, G.; Niemeyer, J. A Supramolecular Double-helix Based on Complementary Phosphate–Guanidinium Pairing. Chem. Commun. 2021, 57, 9842–9845. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-H.; Semenya, D.; Castagnolo, D. Antimicrobial Drugs Bearing Guanidine Moieties: A Review. Eur. J. Med. Chem. 2021, 216, 113293. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.-H.; Lovreković, V.; Kussayeva, A.; Chen, D.-Y.; Margetić, D.; Chen, Z.-L. The Photodynamic Activities of Dimethyl 131-[2-(guanidinyl)ethylamino] Chlorin e6 Photosensitizers in A549 Tumor. Eur. J. Med. Chem. 2019, 177, 144–152. [Google Scholar] [CrossRef]
- Glasovac, Z.; Barešić, L.; Antol, I.; Margetić, D. Benzoylguanidines as Anion-Responsive Systems. ChemPlusChem 2018, 83, 845–854. [Google Scholar] [CrossRef]
- Pacheco-Liñán, P.J.; Alonso-Moreno, C.; Carrillo-Hermosilla, F.; Garzón-Ruiz, A.; Martín, C.; Sáez, C.; Albaladejo, J.; Bravo, I. Novel Fluorescence Guanidine Molecules for Selective Sulfate Anion Detection in Water Complex Samples over a Wide pH Range. ACS Sens. 2021, 6, 3224–3233. [Google Scholar] [CrossRef]
- Margetić, D. Cycloadditions of guanidines. In Cycloaddition Reactions: Advances in Research and Applications; Margetić, D., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2019; Chapter 7; pp. 243–280. [Google Scholar]
- Yang, Y.-L.; Li, S.; Zhang, F.-G.; Ma, J.-A. N-Iodosuccinimide-Promoted [3+2] Annulation Reaction of Aryldiazonium Salts with Guanidines To Construct Aminotetrazoles. Org. Lett. 2021, 23, 8894–8898. [Google Scholar] [CrossRef]
- Ramanathan, M.; Wang, Y.-H.; Liu, S.-T. One-Pot Reactions for Synthesis of 2,5-Substituted Tetrazoles from Aryldiazonium Salts and Amidines. Org. Lett. 2015, 17, 5886–5889. [Google Scholar] [CrossRef]
- Myznikov, L.V.; Hrabalek, A.; Koldobskii, G.I. Drugs in the tetrazole series. Chem. Heterocycl. Compd. 2007, 43, 1–9. [Google Scholar] [CrossRef]
- Leyva-Ramos, S.; Cardoso-Ortiz, J. Recent Developments in the Synthesis of Tetrazoles and their Pharmacological Relevance. Curr. Org. Chem. 2021, 25, 388–403. [Google Scholar] [CrossRef]
- Brigas, A.F. Product Class 30: Tetrazoles. In Science of Synthesis, 13: Category 2, Hetarenes and Related Ring Systems, Five-Membered Hetarenes with Three or More Heteroatoms; Storr, R.C., Gilchrist, T.L., Eds.; Thieme: Stuttgart, Germany, 2004; pp. 861–915. [Google Scholar] [CrossRef]
- Margetić, D.; Warrener, R.N.; Butler, D.N.; Jin, C.-M. A Cascade Thermal Isomerisation of Cyclobutane di-(carbomethoxy) Δ2-1,2,3-Triazolines with Intramolecular 1,3-Dipolar Cycloreversion as the Key Step. Tetrahedron 2012, 68, 3306–3318. [Google Scholar] [CrossRef]
- Briš, A.; Marinić, Ž.; Chen, Z.-L.; Margetić, D. Synthesis of Chlorins by Diels–Alder Cycloadditions of Pheophorbide a and Its Derivatives. Synlett 2015, 26, 991–994. [Google Scholar] [CrossRef]
- Antol, I.; Barešić, L.; Glasovac, Z.; Margetić, D. Computational Study of Electronic Influence of Guanidine Substitution on Diels-Alder Reactions of Heterocyclic Dienes. Croat. Chem. Acta 2019, 92, 279–286. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Esmaeeli, Z.; Khodabakhshi, M.R.; Mirjafary, Z.; Saeidian, H. A Robust Three-component Synthesis of Dispiroheterocycles Containing Aurone Scaffold via 1,3-Dipolar Cycloaddition Reaction of Azomethine Ylides: Regioselectivity and Mechanistic Overview Using DFT Calculations. Struct. Chem. 2022, 33, 147–157. [Google Scholar] [CrossRef]
- Molteni, G.; Ponti, A. Site- and Regioselectivity of Nitrile Oxide–allene Cycloadditions: DFT-Based Semiquantitative Predictions. J. Org. Chem. 2017, 82, 10710–10714. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Wang, B.; Wang, X.-R.; Zhang, J.-H.; Fang, D.-C. An Experimental and Theoretical Study on the Interaction of N-heterocyclic Carbene-derived 1,3-Dipoles with Methoxycarbonylallenes: Highly Regio- and Stereoselective [3+2]-Cycloadditions Controlled by the Structures of n-Heterocycles of 1,3-Dipoles. J. Org. Chem. 2009, 74, 2357–2367. [Google Scholar] [CrossRef] [PubMed]
- Yavari, I.; Ravaghi, P.; Safaei, M.; Kayanian, J. Regio- and Stereoselectivity in the 1,3-Dipolar Cycloaddition Reactions of Isoquinolinium Ylides with Cyclopenta[a]acenaphthylen-8-ones. Synlett 2020, 31, 1691–1695. [Google Scholar] [CrossRef]
- Chandra, A.K.; Uchimaru, T.; Nguyen, M.T. Regiochemistry of 1,3-dipolar cycloadditions between azides and substituted ethylenes: A theoretical study. J. Chem. Soc. Perkin Trans. 1999, 2, 2117–2121. [Google Scholar] [CrossRef]
- Himo, F.; Demko, Z.P.; Noodleman, L.; Sharpless, K.B. Mechanisms of Tetrazole Formation by Addition of Azide to Nitriles. J. Am. Chem. Soc. 2002, 124, 12210–12216. [Google Scholar] [CrossRef] [PubMed]
- Lopez, S.A.; Munk, M.E.; Houk, K.N. Mechanisms and Transition States of 1,3-Dipolar Cycloadditions of Phenyl Azide with Enamines: A Computational Analysis. J. Org. Chem. 2013, 78, 1576–1582. [Google Scholar] [CrossRef]
- Chen, P.-P.; Ma, P.; He, X.; Svatunek, D.; Liu, F.; Houk, K.N. Computational Exploration of Ambiphilic Reactivity of Azides and Sustmann’s Paradigmatic Parabola. J. Org. Chem. 2021, 86, 5792–5804. [Google Scholar] [CrossRef] [PubMed]
- Sebest, F.; Lachhani, K.; Pimpasri, C.; Casarrubios, L.; White, A.J.P.; Rzepa, H.S.; Díez-González, S. Cycloaddition Reactions of Azides and Electron-Deficient Alkenes in Deep Eutectic Solvents: Pyrazolines, Aziridines and Other Surprises. Adv. Synth. Catal. 2020, 362, 1877–1886. [Google Scholar] [CrossRef] [Green Version]
- Huisgen, R. 1,3-Dipolar Cycloadditions—Introduction, Survey, Mechanism. In 1,3-Dipolar Cycloaddition Chemistry; Padwa, A., Ed.; Wiley-Interscience: New York, NY, USA, 1984; Volume 1, pp. 1–176. [Google Scholar]
- Yoshida, S.; Goto, S.; Nishiyama, Y.; Hazama, Y.; Kondo, M.; Matsushita, T.; Hosoya, T. Effect of Resonance on the Clickability of Alkenyl Azides in the Strain-promoted Cycloaddition with Dibenzo-fused Cyclooctynes. Chem. Lett. 2019, 48, 1038–1041. [Google Scholar] [CrossRef] [Green Version]
- Hioe, J.; Šakić, D.; Vrček, V.; Zipse, H. The Stability of Nitrogen-centered Radicals. Org. Biomol. Chem. 2015, 13, 157–169. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Sundhoro, M.; Houk, K.N.; Yan, M. Electrophilic Azides for Materials Synthesis and Chemical Biology. Acc. Chem. Res. 2020, 53, 937–948. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chem. Acc. 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Ritchie, J.P.; Bachrach, S.M. Some methods and applications of electron density distribution analysis. J. Comp. Chem. 1987, 8, 499–509. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural-population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Computer Software Program (Gaussian 09, Revision D.01 and Gaussian 16, Revision C.01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre- and post-Processing Program for Molecular and Electronic Structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antol, I.; Glasovac, Z.; Margetić, D. Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine. Molecules 2023, 28, 2342. https://doi.org/10.3390/molecules28052342
Antol I, Glasovac Z, Margetić D. Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine. Molecules. 2023; 28(5):2342. https://doi.org/10.3390/molecules28052342
Chicago/Turabian StyleAntol, Ivana, Zoran Glasovac, and Davor Margetić. 2023. "Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine" Molecules 28, no. 5: 2342. https://doi.org/10.3390/molecules28052342
APA StyleAntol, I., Glasovac, Z., & Margetić, D. (2023). Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine. Molecules, 28(5), 2342. https://doi.org/10.3390/molecules28052342