Thermodynamic Parameters of Berberine with Kolliphor Mixtures Adsorption and Micellization
Abstract
:1. Introduction
2. Theory
3. Results and Discussion
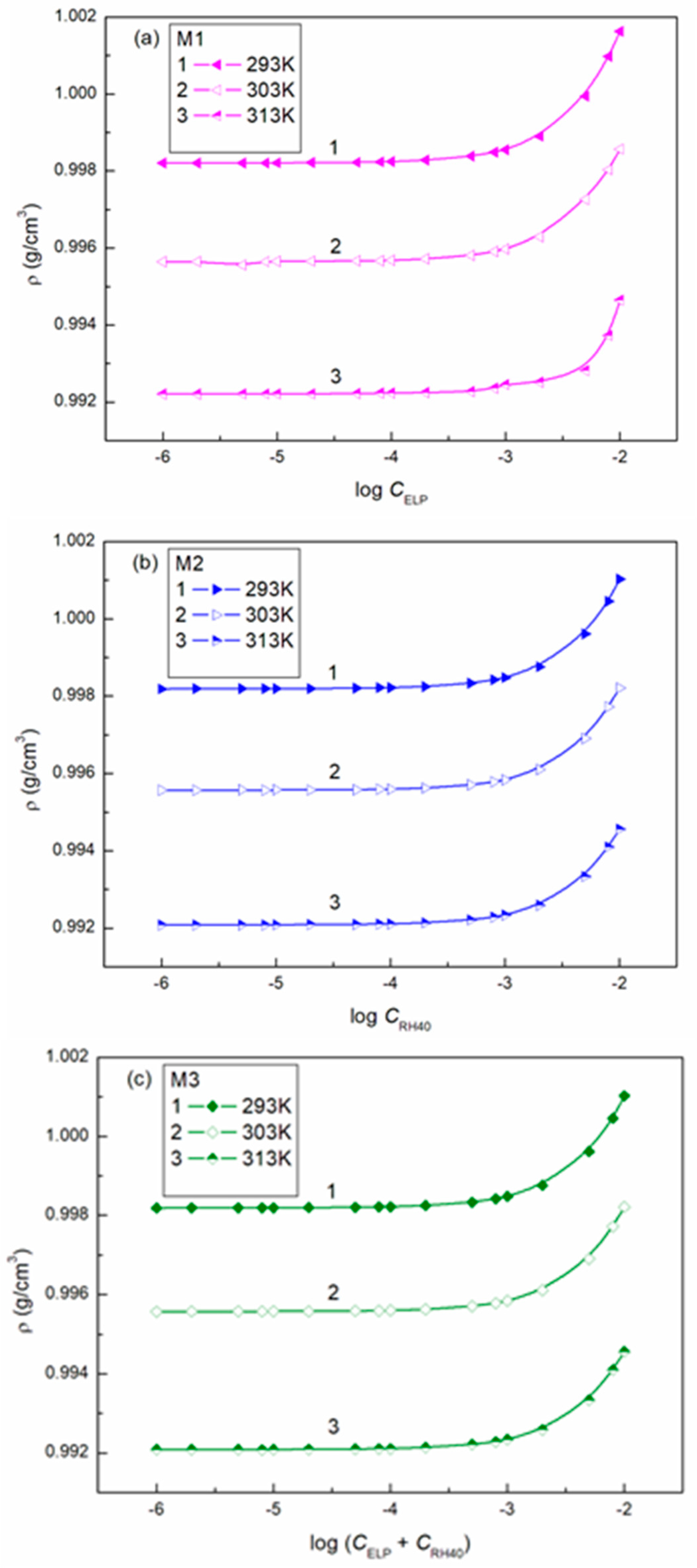
3.1. Some Physicochemical Properties of Ber, ELP and RH40
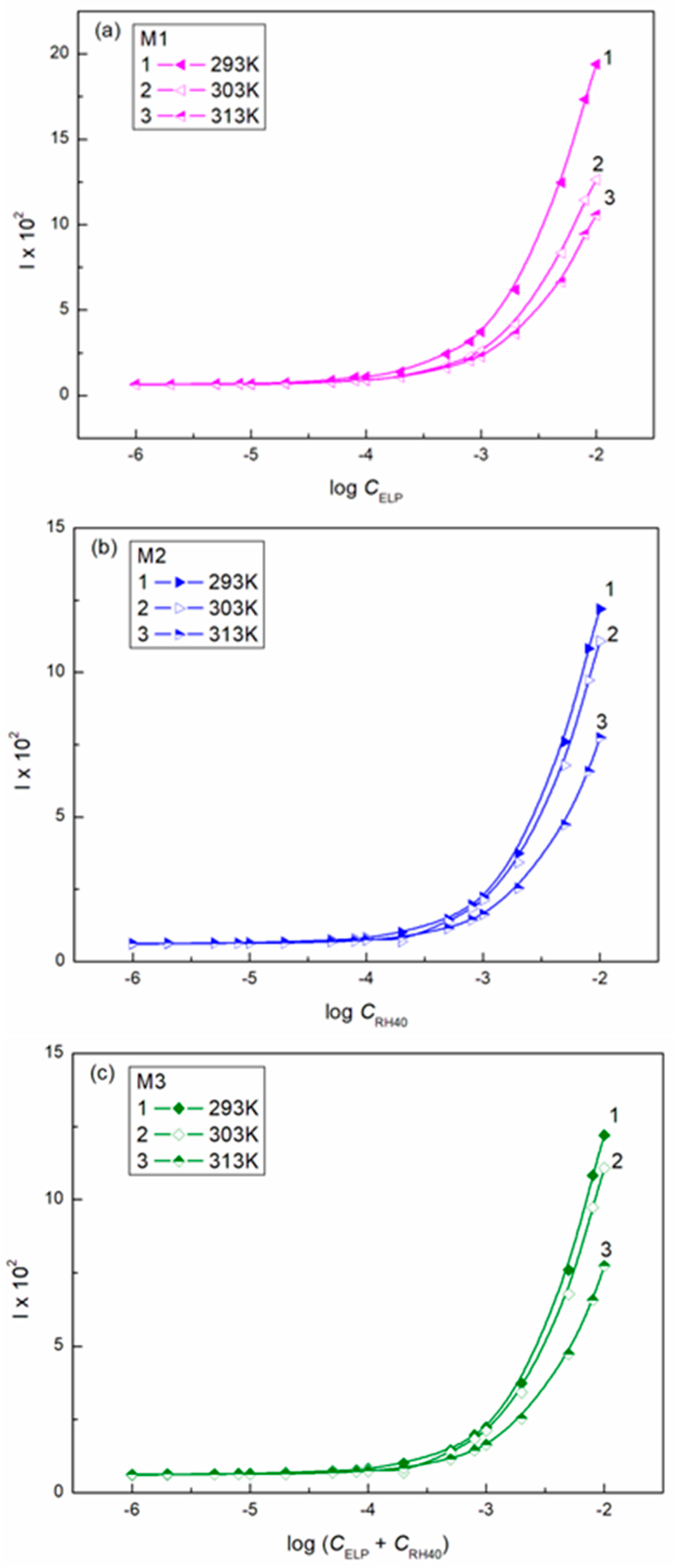
3.2. Surface Tension of the Aqueous Solution of ELP, RH40, and ELP + RH40 Mixtures with Ber; Concentration and Composition of Mixed Monolayers at the Water-Air Interface
3.3. CMC of ELP + Ber, RH40 + Ber and ELP + RH40 + Ber Mixtures
3.4. Thermodynamic Parameters of the Adsorption and Micellization
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Zhang, X.; Dai, K.; Liu, C.; Hu, H.; Luo, F.; Qi, Q.; Wang, L.; Ye, F.; Jin, J.; Tang, J.; et al. Berberine-coated biomimetic composite microspheres for simultaneously hemostatic and antibacterial performance. Polymers 2021, 13, 360. [Google Scholar]
- Patel, P. A bird’s eye view on a therapeutically ‘wonder molecule’: Berberine. Phytomed. Plus 2021, 1, 100070. [Google Scholar] [CrossRef]
- Pang, B.; Zhao, L.H.; Zhou, Q.; Zhao, T.Y.; Wang, H.; Gu, C.J.; Tong, X.-L. Application of berberine on treating type 2 diabetes mellitus. Int. J. Endocrinol. 2015, 2015, 905749. [Google Scholar] [CrossRef] [Green Version]
- Xue, M.; Yang, M.-X.; Zhang, W.; Li, X.-M.; Gao, D.-H.; Ou, Z.-M.; Li, Z.-P.; Liu, S.-H.; Li, X.-J.; Yang, S.-Y. Characterization, pharmacokinetics, and hypoglycemic effect of berberine loaded solid lipid nanoparticles. Int. J. Nanomed. 2013, 8, 4677–4687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Younis, F.A.; Saleh, S.R.; Abd El-Rahman, S.S.; Newairy, A.-S.A.; El-Demellawy, M.A.; Ghareeb, D.A. Preparation, physicochemical characterization, and bioactivity evaluation of berberine-entrapped albumin nanoparticles. Sci. Rep. 2022, 12, 17431. [Google Scholar] [CrossRef]
- Wang, L.; Ye, X.; Hua, Y.; Song, Y. Berberine alleviates adipose tissue fibrosis by inducing AMP-activated kinase signaling in high-fat diet-induced obese mice. Biomed. Pharmacother. 2018, 105, 121–129. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kim, W.S.; Kim, K.H.; Yoon, M.J.; Cho, H.J.; Shen, Y.; Ye, J.-M.; Lee, C.H.; Oh, W.K.; Kim, C.H.; et al. Berberine, a natural plant product, activates AMP-activated protein kinase with beneficial metabolic effects in diabetic and insulin resistant states. Diabetes 2006, 55, 2256–2264. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, X.; Zou, D.; Liu, W.; Yang, J.; Zhu, N.; Huo, L.; Wang, M.; Hong, J.; Wu, P.; et al. Treatment of type 2 diabetes and dyslipidemia with the natural plant alkaloid berberine. J. Clin. Endocrinol. Metab. 2008, 93, 2559–2565. [Google Scholar] [CrossRef] [Green Version]
- Pirillo, A.; Catapano, A.L. Berberine, a plant alkaloid with lipid- and glucoselowering properties: From in vitro evidence to clinical studies. Atherosclerosis 2015, 243, 449–461. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Lam, K.S.; Li, Y.; Wong, W.T.; Ye, H.; Lau, C.W.; Vanhoutte, P.M.; Xu, A. Berberine prevents hyperglycemia-induced endothelial injury and enhances vasodilatation via adenosine monophosphate-activated protein kinase and endothelial nitric oxide synthase. Cardiovasc. Res. 2009, 82, 484–492. [Google Scholar] [CrossRef] [Green Version]
- Sahibzada, M.U.K.; Sadiq, A.; Faidah, H.S.; Khurram, M.; Amin, M.U.; Haseeb, A.; Kakar, M. Berberine nanoparticles with enhanced in vitro bioavailability: Characterization and antimicrobial activity. Drug Des. Dev. Ther. 2018, 12, 303–312. [Google Scholar] [CrossRef] [Green Version]
- Behl, T.; Singh, S.; Sharma, N.; Zahoor, I.; Albarrati, A.; Albratty, M.; Meraya, A.M.; Najmi, A.; Bungau, S. Expatiating the pharmacological and nanotechnological aspects of the alkaloidal drugberberine: Current and future trends. Molecules 2022, 27, 3705. [Google Scholar] [CrossRef]
- Guo, J.; Xia, Y.; Liu, Y.; Liu, S.; Zhang, L.; Li, B. Microscopic adsorption behaviors of ionic surfactants on lignite surface and its effect on the wettability of lignite: A simulation and experimental study. J. Mol. Liq. 2022, 345, 117851. [Google Scholar] [CrossRef]
- Corona, R.R.B.; Sad, C.M.S.; da Silva, M.; Lopes, D.L.; Leite, J.S.D.; Viegas, G.M.D.F.; Gonçalves, G.R.; Filgueiras, P.R.; de Castro, E.V.R. Adsorption of anionic surfactant in graphite oxide: A study for treatment of laundry wastewater. J. Environ. Chem. Eng. 2021, 9, 106858. [Google Scholar] [CrossRef]
- Abu-Huwaij, R.; Al-Assaf, S.F.; Hamed, R. Recent exploration of nanoemulsions for drugs and cosmeceuticals delivery. J. Cosmet. Dermatol. 2022, 21, 3729–3740. [Google Scholar] [CrossRef]
- Yu, F.; Miao, Y.; Wang, M.; Liu, G.; Yuan, L.; Geng, R.; Qiu, Q.; Ni, C.; Kay, M. Predicting nanoemulsion formulation and studying the synergism mechanism between surfactant and cosurfactant: A combined computational and experimental approach. Int. J. Pharm. 2022, 615, 121473. [Google Scholar] [CrossRef]
- van Oss, C.J.; Constanzo, P.M. Adhesion of anionic surfactants to polymer surfaces and low-energy materials. J. Adhes. Sci. Technol. 1992, 4, 477–487. [Google Scholar] [CrossRef]
- van Oss, C.J. Interfacial Forces in Aqueous Media; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- van Oss, C.J.; Good, R.J. Surface tension and the solubility of polymers and biopolymers: The role of polar and apolar interfacial free energies. J. Macromol. Sci. Chem. 1989, 26, 1183–1203. [Google Scholar] [CrossRef]
- van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Monopolar surfaces. Adv. Coll. Interface Sci. 1987, 28, 35–64. [Google Scholar] [CrossRef]
- Szymczyk, K.; Lewandowski, A.; Zdziennicka, A.; Szaniawska, M.; Jańczuk, B. Behavior of Auramine O in the aqueous solution of two Kolliphors and their mixture. Molecules 2022, 27, 8493. [Google Scholar] [CrossRef] [PubMed]
- Szaniawska, M.; Szymczyk, K.; Zdziennicka, A.; Jańczuk, B. Adsorption properties and composition of binary Kolliphor mixtures at the water-air interface at different temperatures. Molecules 2022, 27, 877. [Google Scholar] [CrossRef]
- Markarian, S.A.; Sargsyan, H.R.; Grigoryan, G.S.; Ghazoyan, H.H.; Chaban, V.V. Dimethyl sulfoxide fosters larger micelles of docusate sodium in the mixed solutions with water. J. Mol. Liq. 2023, 369, 120960. [Google Scholar] [CrossRef]
- Lalthlengliani, J.; Gurung, J.; Pulikkal, A.K. Solubilization of aqueous-insoluble phenothiazine drug in TX-100 micellar solution and interactions of cationic/anionic surfactants with phenothiazine–TX-100 system. J. Mol. Liq. 2022, 354, 118823. [Google Scholar] [CrossRef]
- Adamson, W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; Wiley Interscience: New York, NY, USA, 1997. [Google Scholar]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry; Eighth Edition; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Rosen, J.M.; Hua, X.Y. Surface concentrations and molecular interactions in binary mixtures of surfactants. J. Colloid Interface Sci. 1982, 86, 164–172. [Google Scholar] [CrossRef]
- 28. Rubingh, D.N. Solution Chemistry of Surfactants; Mittal, K.L., Ed.; Plenum Press: New York, NY, USA, 1979; Volume 3, pp. 337–354. [Google Scholar]
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2004; pp. 34–178. [Google Scholar]
- Butler, J.A.V. The Thermodynamics of the Surfaces of the Solutions. Proc. Roy. Soc. Ser. A 1932, 138, 348–375. [Google Scholar]
- Jańczuk, B.; Méndez-Sierra, J.A.; González-Martin, M.L.; Bruque, J.M.; Wójcik, W. Properties of decylammonium chloride and cesium perfluorooctanoate at interfaces and standard free energy of their adsorption. J. Colloid Interface Sci. 1997, 192, 408–414. [Google Scholar] [CrossRef] [PubMed]
- Zdziennicka, A.; Krawczyk, J.; Szymczyk, K.; Jańczuk, B. Macroscopic and microscopic properties of some surfactants and biosurfactants. Int. J. Mol. Sci. 2018, 19, 1934. [Google Scholar] [CrossRef] [Green Version]
- Groszek, A.J. Selective adsorption at graphite/hydrocarbon interfaces. Proc. R. Soc. Lond. A Math. Phys. Sci. 1970, 314, 473–478. [Google Scholar]
- Beyer, K. Phase structures, water binding, and molecular dynamics in liquid crystalline and frozen states of the system Triton X-100-D2O: A deuteron and carbon NMR study. J. Colloid Interface Sci. 1982, 86, 73–89. [Google Scholar] [CrossRef]
- Desai, T.R.; Dixit, S.G. Interaction and viscous properties of aqueous solutions of mixed cationic and nonionic surfactants. J. Colloid Interface Sci. 1996, 177, 471–477. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Szymczyk, K.; Krawczyk, J.; Jańczuk, B. Some remarks on the solid surface tension determination from contact angle measurements. Appl. Surf. Sci. 2017, 405, 88–101. [Google Scholar] [CrossRef]
- Szymczyk, K.; Zdziennicka, A.; Jańczuk, B. Properties of some nonionic fluorocarbon surfactants and their mixtures with hydrocarbon ones. Adv. Colloid Interface Sci. 2021, 292, 102421. [Google Scholar] [CrossRef]
- Bhadra, P.; Siu, S.W.I. Effect of concentration, chain length, hydrophobicity, and an external electric field on the growth of mixed alkanethiol self-assembled monolayers: A Molecular dynamics study. Langmuir 2021, 37, 1913–1924. [Google Scholar] [CrossRef]
- Hubbe, M.A.; McLean, D.S.; Stack, K.R.; Lu, X.; Strand, A.; Sundberg, A. Self-assembly of alkyl chains of fatty acids in papermaking systems: A review of related pitch issues, hydrophobic sizing, and pH effects. BioResources 2020, 15, 4591–4635. [Google Scholar] [CrossRef]
- Kloubek, J. Orientation of aliphatic hydrocarbons at the liquid-air interface. Colloids Surfaces 1990, 48, 323–335. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Szymczyk, K.; Krawczyk, J.; Jańczuk, B. Critical micelle concentration of some surfactants and thermodynamic parameters of their micellization. Fluid Phase Equilibria 2012, 322–323, 126–134. [Google Scholar] [CrossRef]
- De Boer, J.H. The Dynamic Character of Adsorption; Oxford University: Oxford, UK, 1953. [Google Scholar]
- Rathod, K.; Ahmed, H.; Gomte, S.S.; Chougule, S.; Prabakaran, A.; Dethe, M.R.; Patel, R.J.; Bharadwaj, D.; Alexander, A. Exploring the potential of anti-inflammatory activity of berberine chloride-loaded mesoporous silica nanoparticles in carrageenan-induced rat paw edema model. J. Solid State Chem. 2023, 317, 123639. [Google Scholar] [CrossRef]
- Sailor, G.U.; Ramani, V.D.; Shah, N.; Parmar, G.R.; Gohil, D.; Balaram, R.; Seth, A. Design Of Experiment Approach Based Formulation Optimization Of Berberine Loaded Solid Lipid Nanoparticle For Antihyperlipidemic Activity. Indian J. Pharm. Sci. 2021, 83, 204–218. [Google Scholar] [CrossRef]
- Xiong, W.; Sang, W.; Linghu, K.G.; Cheang, W.S.; Li, J.; Hu, Y.J.; Yu, H.; Wang, Y.T. Dual-functional Brij-S20-modified nanocrystal formulation enhances the intestinal transport and oral bioavailability of berberine. Int. J. Nanomed. 2018, 13, 3781–3793. [Google Scholar] [CrossRef] [Green Version]
- Zdziennicka, A.; Szymczyk, K.; Jańczuk, B.; Longwic, R.; Sander, P. Adhesion of canola and diesel oils to some parts of diesel engine in the light of surface tension components and parameters of these substrates. Int. J. Adhes. Adhes. 2015, 60, 23–30. [Google Scholar] [CrossRef]
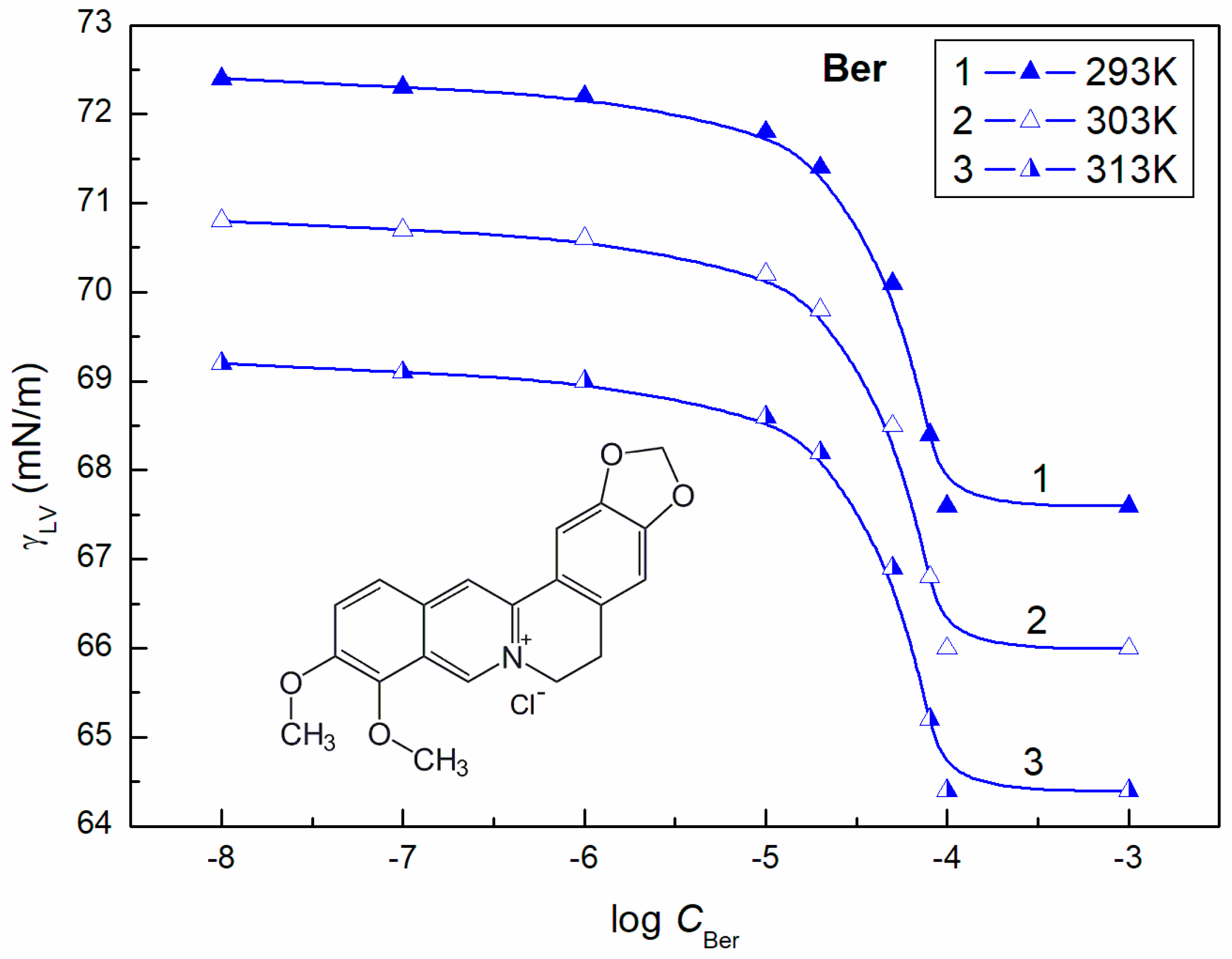
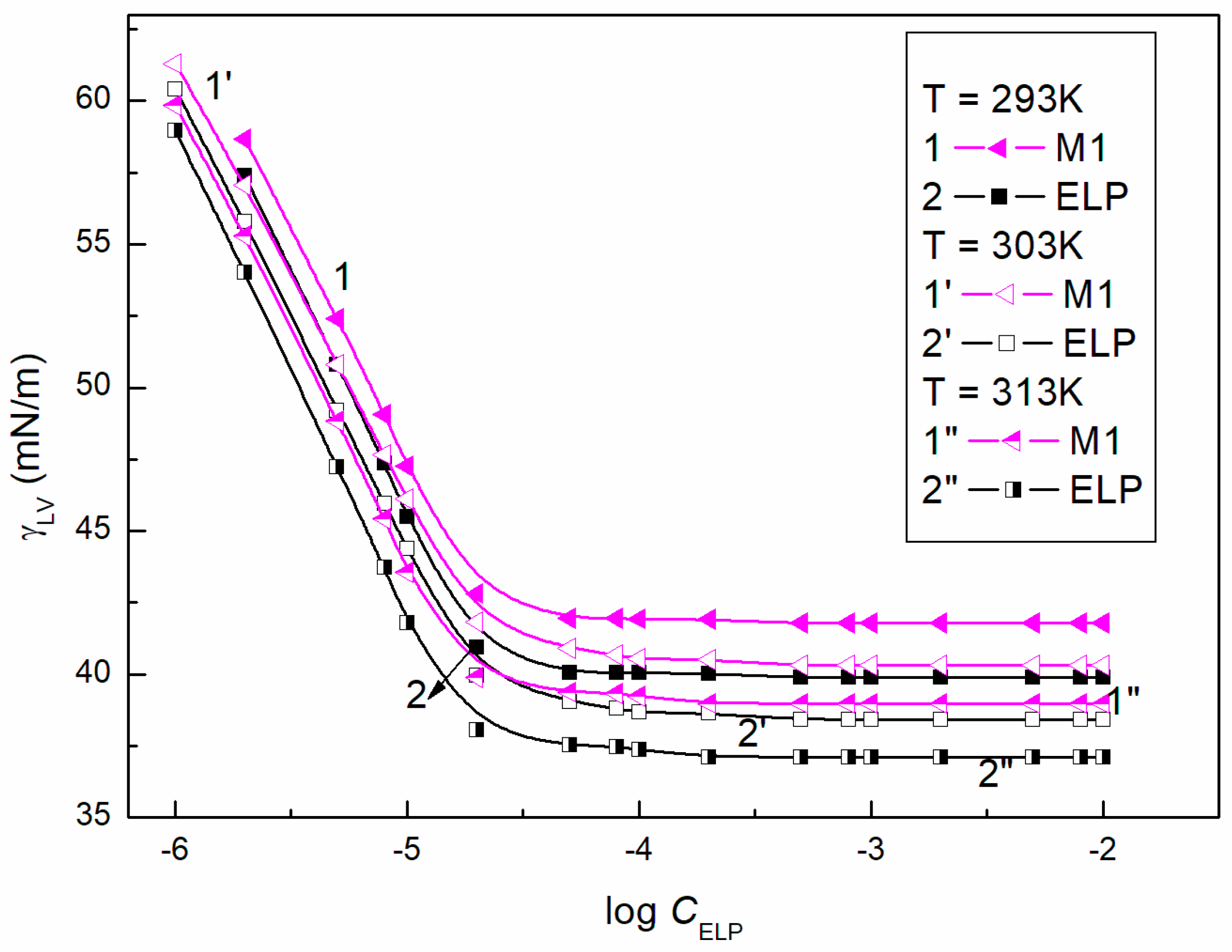

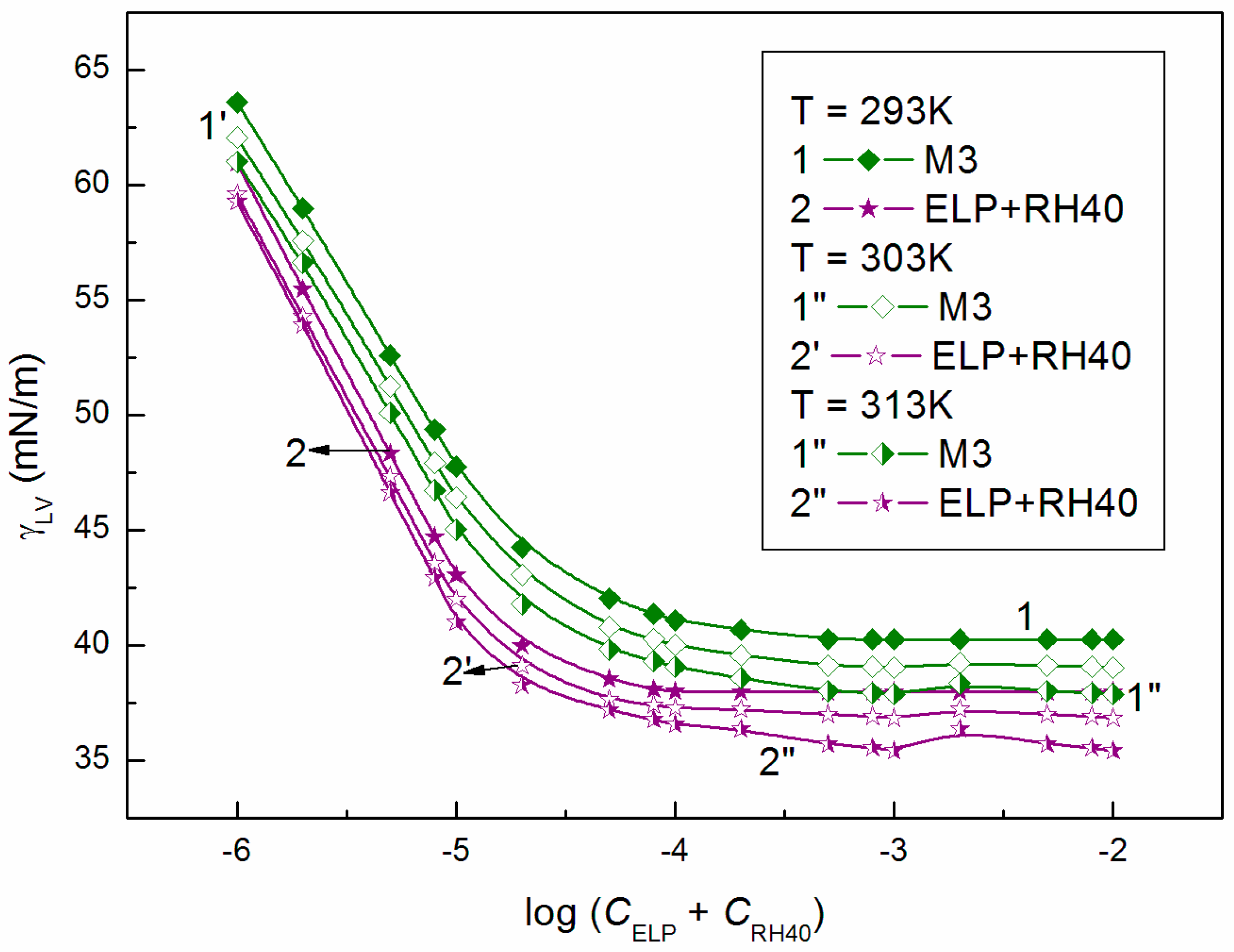
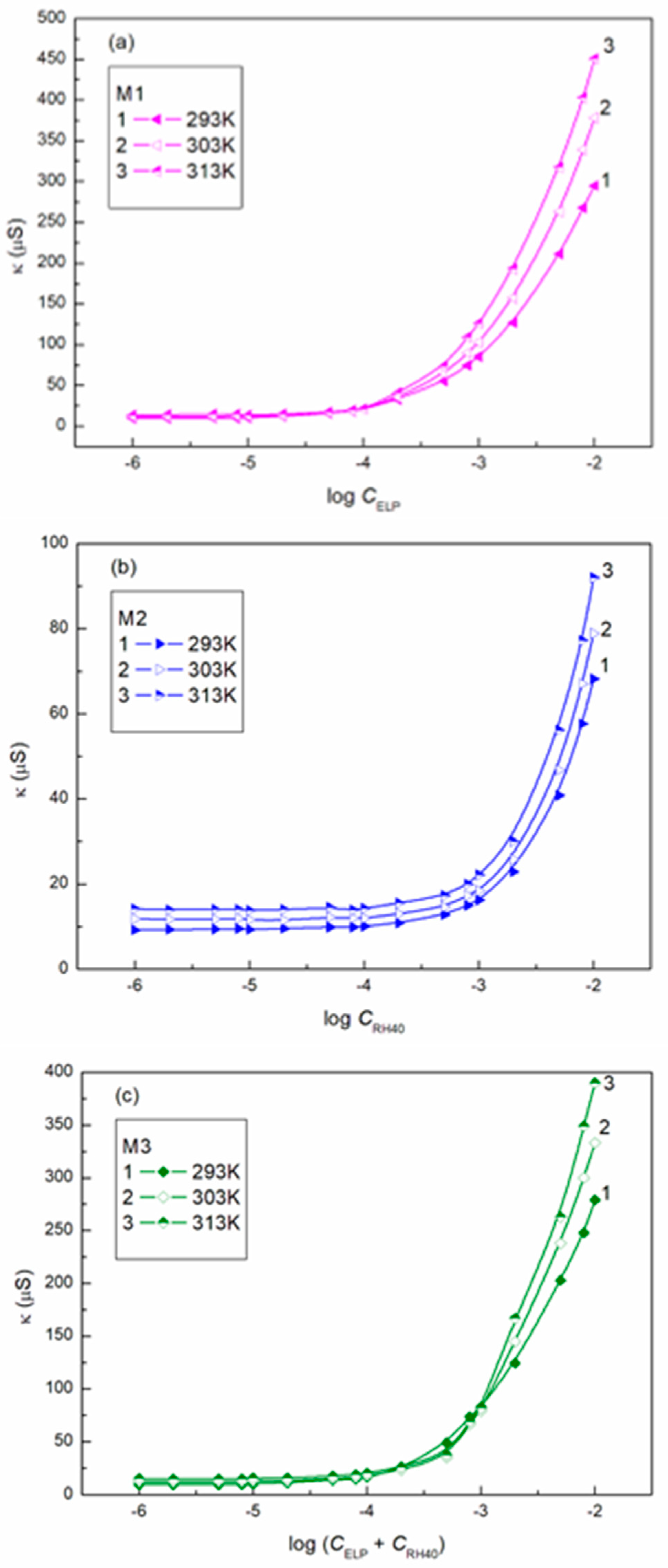

| Ber | 56.2 | 38.4 | 46.1 | |
| PTFE | PMMA | |||
| ELP | 74 | 23 | ||
| RH40 | 75 | 25 | ||
| Ber | 36.42 | 1.556 | 16.38 | 46.52 |
| ELP head | 27.51 | 0.460 | 48.95 | 37.00 |
| RH40 head | 27.38 | 0.565 | 44.42 | 37.40 |
| Water | 26.85 | 22.975 | 22.975 | 72.80 |
| TX165 head | 27.70 | 0.33 | 50.20 | 35.84 |
| PTFE | 20.24 | - | - | 20.24 |
| PMMA | 41.28 | - | 7.28 | 41.28 |
| T (K) | CMC from | CMC from | CMC from | CMC from I | |
|---|---|---|---|---|---|
| ELP + Ber (M1) | 293 | 2.11 × 10−5 | 3.87 × 10−4 | 5.92 × 10−4 | |
| 303 | 2.78 × 10−5 | 4.02 × 10−4 | 5.40 × 10−4 | ||
| 313 | 2.72 × 10−5 | 4.67 × 10−4 | 5.05 × 10−4 | ||
| ELP | 293 | 2.14 × 10−5 | 5.13 × 10−4 | 6.03 × 10−4 | |
| 303 | 2.03 × 10−5 | 7.78 × 10−4 | 4.16 × 10−4 | ||
| 313 | 1.91 × 10−5 | 5.32 × 10−4 | 3.71 × 10−4 | ||
| RH40 + Ber (M2) | 293 | 4.24 × 10−5 | 7.31 × 10−4 | 4.97 × 10−4 | |
| 303 | 5.62 × 10−5 | 7.70 × 10−4 | 4.67 × 10−4 | ||
| 313 | 5.05 × 10−5 | 4.46 × 10−4 | 4.16 × 10−4 | ||
| RH40 | 293 | 6.64 × 10−5 | 6.03 × 10−4 | 4.97 × 10−4 | |
| 303 | 2.50 × 10−5 | 5.77 × 10−4 | 4.67 × 10−4 | ||
| 313 | 2.12 × 10−5 | 5.22 × 10−4 | 4.42 × 10−4 | ||
| ELP + RH40 + Ber (M3) | 293 | 3.13 × 10−5 | 3.81 × 10−4 | 4.74 × 10−4 | |
| 303 | 2.81 × 10−5 | 4.23 × 10−4 | 4.33 × 10−4 | ||
| 313 | 2.80 × 10−5 | 4.74 × 10−4 | 4.16 × 10−4 | ||
| ELP + RH40 | 293 | 1.92 × 10−5 | 8.76 × 10−4 | 4.89 × 10−4 | |
| 303 | 1.84 × 10−5 | 7.21 × 10−4 | 4.40 × 10−4 | ||
| 313 | 1.70 × 10−5 | 7.03 × 10−4 | 3.90 × 10−4 |
| T = 293 K | T = 303 K | T = 313 K | |
|---|---|---|---|
| CMC | 3.13 × 10−5 | 2.81 × 10−5 | 2.80 × 10−5 |
| C1 | 2.50 × 10−5 | 2.25 × 10−5 | 2.24 × 10−5 |
| C2 | 6.26 × 10−6 | 5.63 × 10−6 | 5.60 × 10−6 |
| C3 | 1 × 10−4 | 1 × 10−4 | 1 × 10−4 |
| CMC | 40.27 | 39.17 | 37.92 |
| 0.3954 | 0.4568 | 0.4508 | |
| 0.2313 | 0.0418 | 0.0024 | |
| 0.3733 | 0.5014 | 0.5467 | |
| −5.0834 | 0.3762 | 1.0993 | |
| −0.4159 | −1.5256 | −1.1598 | |
| 0.7619 | 1.0007 | 1.0007 | |
| 0.0496 | 1.4125 | 2.8469 | |
| 0.9371 | 0.7273 | 0.7900 | |
| 0.8590 | 0.6376 | 0.7048 | |
| −2.2018 | 0.0380 | 0.0682 | |
| −0.2422 | −0.9536 | −0.7472 |
| T = 293 K | T = 303 K | T = 313 K | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ELP | −46.91 | −1.64 | 45.27 | −47.97 | −1.16 | 46.81 | −50.00 | −1.64 | 48.36 |
| ELP from M1 | −44.62 | −0.23 | 44.39 | −46.16 | −0.26 | 45.90 | −47.65 | −0.23 | 47.42 |
| ELP from M3 | −43.64 | 2.65 | 46.29 | −45.25 | 2.62 | 47.87 | −46.80 | 2.65 | 49.45 |
| RH40 | −48,12 | 4.62 | 52.74 | −50.11 | 4.43 | 54.54 | −51.72 | 4.62 | 56.34 |
| RH40 from M2 | −45.69 | 2.54 | 48.23 | −47.57 | 2.30 | 49.87 | −48.98 | 2.54 | 51.52 |
| RH40 from M3 | −44.45 | −8.85 | 35.6 | −45.72 | −8.91 | 36.81 | 46.88 | 84.91 | 38.03 |
| Ber | −32.00 | −1.97 | 30.03 | −33.10 | −2.04 | 31.06 | −34.05 | −1.97 | 32.08 |
| Ber from M1 | −31.63 | −1.89 | 29.74 | −32.62 | −1.87 | 30.75 | −43.66 | −11.89 | 31.77 |
| Ber from M2 | −31.42 | −3.15 | 28.27 | −32.32 | −3.08 | 29.24 | −33.45 | −3.25 | 30.20 |
| Ber from M3 | −31.02 | −1.28 | 29.74 | −32.02 | −1.27 | 30.75 | −32.95 | −1.18 | 31.77 |
| T = 293 K | T = 303 K | T = 313 K | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ELP | −35.97 | 4.17 | 40.14 | −37.33 | 4.18 | 41.51 | −38.71 | 4.17 | 42.88 |
| ELP from ELP + RH40 | −35.81 | 6.68 | 42.49 | −37.33 | 6.61 | 43.94 | −38.71 | 6.68 | 45.39 |
| ELP from M3 | −32.96 | 1.47 | 34.43 | −33.96 | 1.64 | 35.60 | −35.31 | 1.47 | 36.78 |
| RH40 | −33.21 | 8.98 | 42.19 | −36.80 | 6.83 | 43.63 | −38.44 | 6.63 | 45.07 |
| RH40 from RH40 + ELP | −36.19 | −3.23 | 32.96 | −36.80 | −2.71 | 34.09 | −38.44 | −3.23 | 35.21 |
| RH40 from M3 | −31.28 | 16.92 | 48.20 | 39.88 | 89.72 | 49.84 | −43.71 | 7.78 | 51.49 |
| Ber from M3 | −29.15 | 4.55 | 33.70 | −31.57 | 3.28 | 34.85 | −32.72 | 3.28 | 36.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szaniawska, M.; Szymczyk, K.; Zdziennicka, A.; Jańczuk, B. Thermodynamic Parameters of Berberine with Kolliphor Mixtures Adsorption and Micellization. Molecules 2023, 28, 3115. https://doi.org/10.3390/molecules28073115
Szaniawska M, Szymczyk K, Zdziennicka A, Jańczuk B. Thermodynamic Parameters of Berberine with Kolliphor Mixtures Adsorption and Micellization. Molecules. 2023; 28(7):3115. https://doi.org/10.3390/molecules28073115
Chicago/Turabian StyleSzaniawska, Magdalena, Katarzyna Szymczyk, Anna Zdziennicka, and Bronisław Jańczuk. 2023. "Thermodynamic Parameters of Berberine with Kolliphor Mixtures Adsorption and Micellization" Molecules 28, no. 7: 3115. https://doi.org/10.3390/molecules28073115
APA StyleSzaniawska, M., Szymczyk, K., Zdziennicka, A., & Jańczuk, B. (2023). Thermodynamic Parameters of Berberine with Kolliphor Mixtures Adsorption and Micellization. Molecules, 28(7), 3115. https://doi.org/10.3390/molecules28073115








