Modulating Optoelectronic and Elastic Properties of Anatase TiO2 for Photoelectrochemical Water Splitting
Abstract
:1. Introduction
Computational Methods and Details
2. Results and Discussion
2.1. Geometrical Analysis
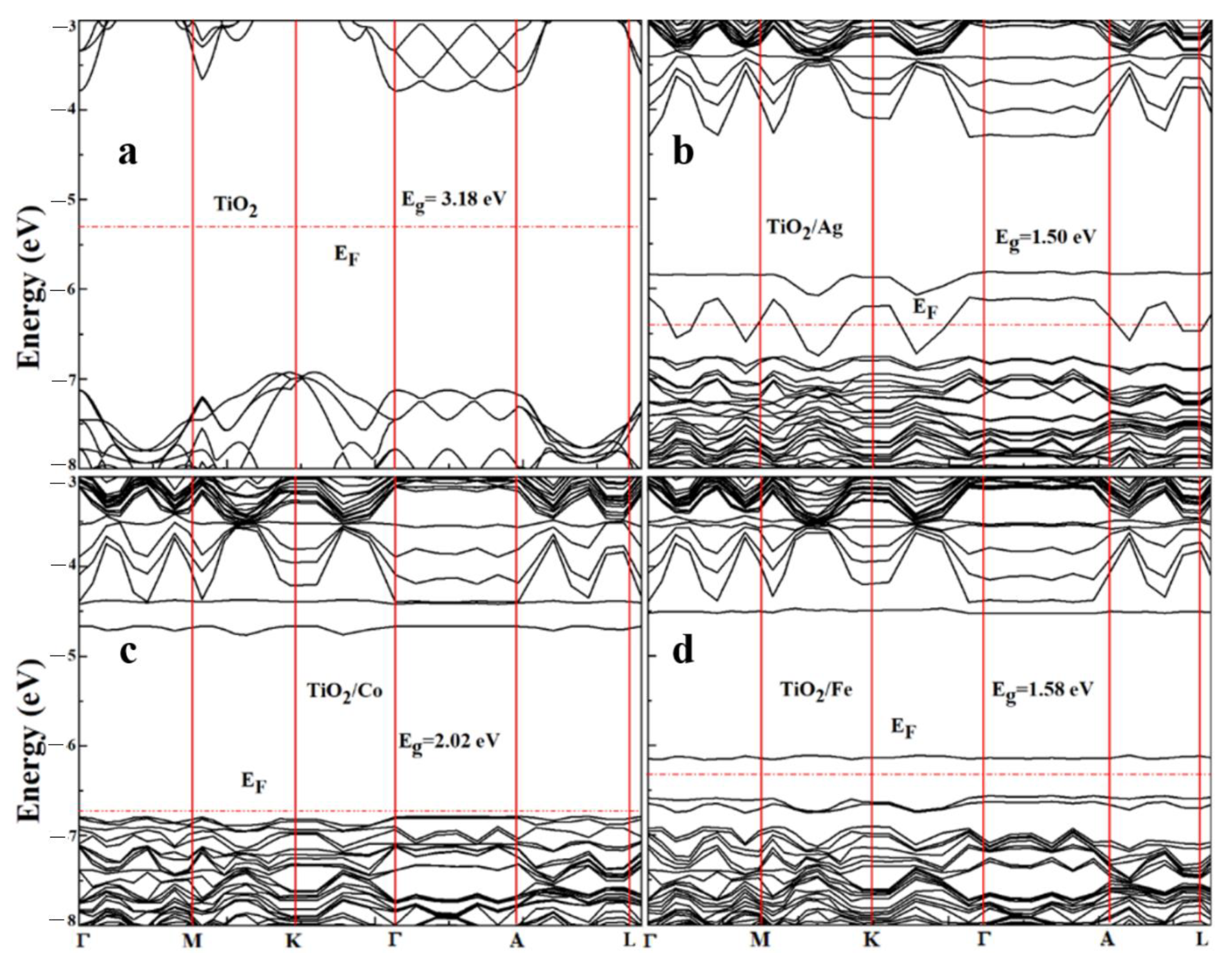
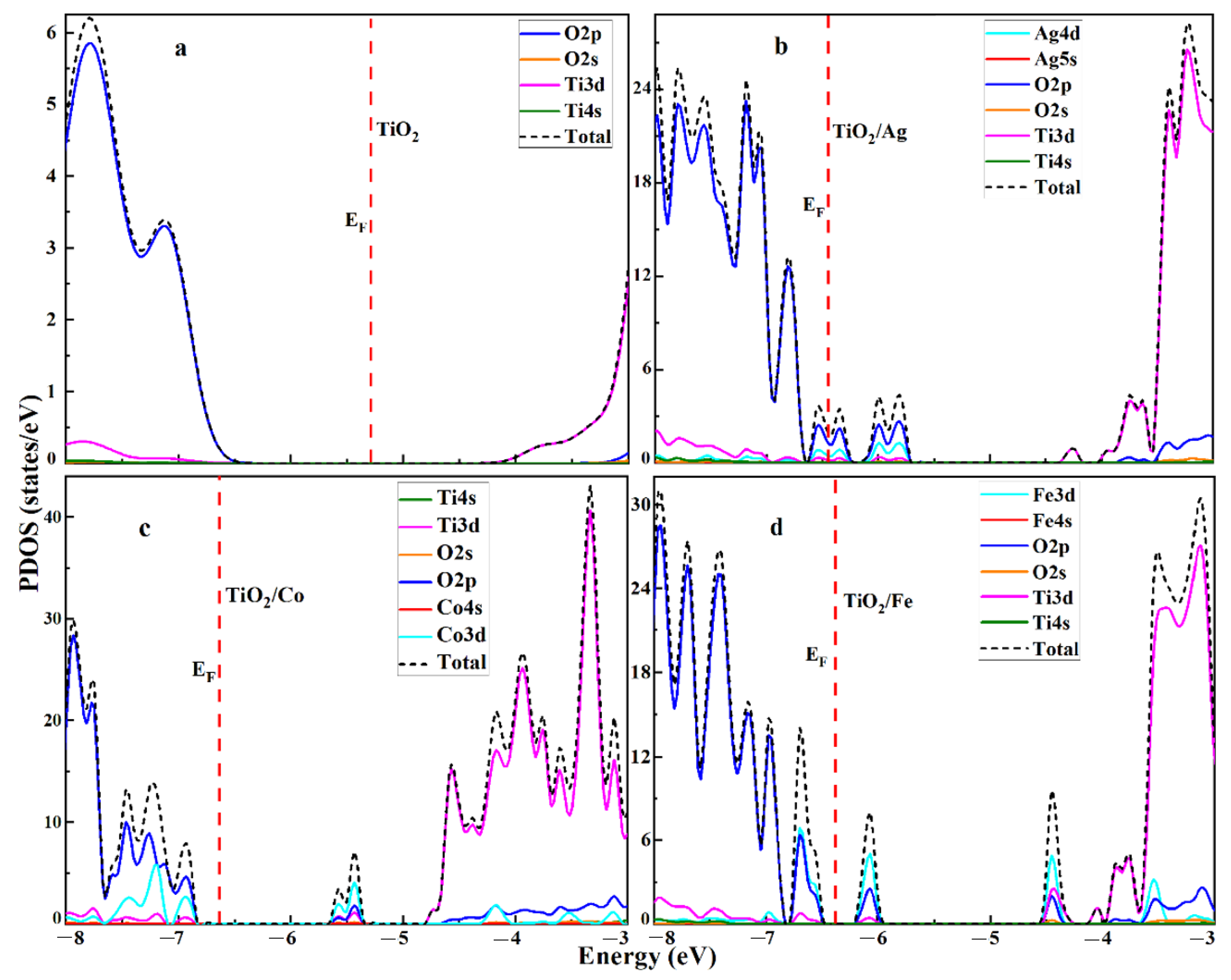
2.2. Electronic Properties
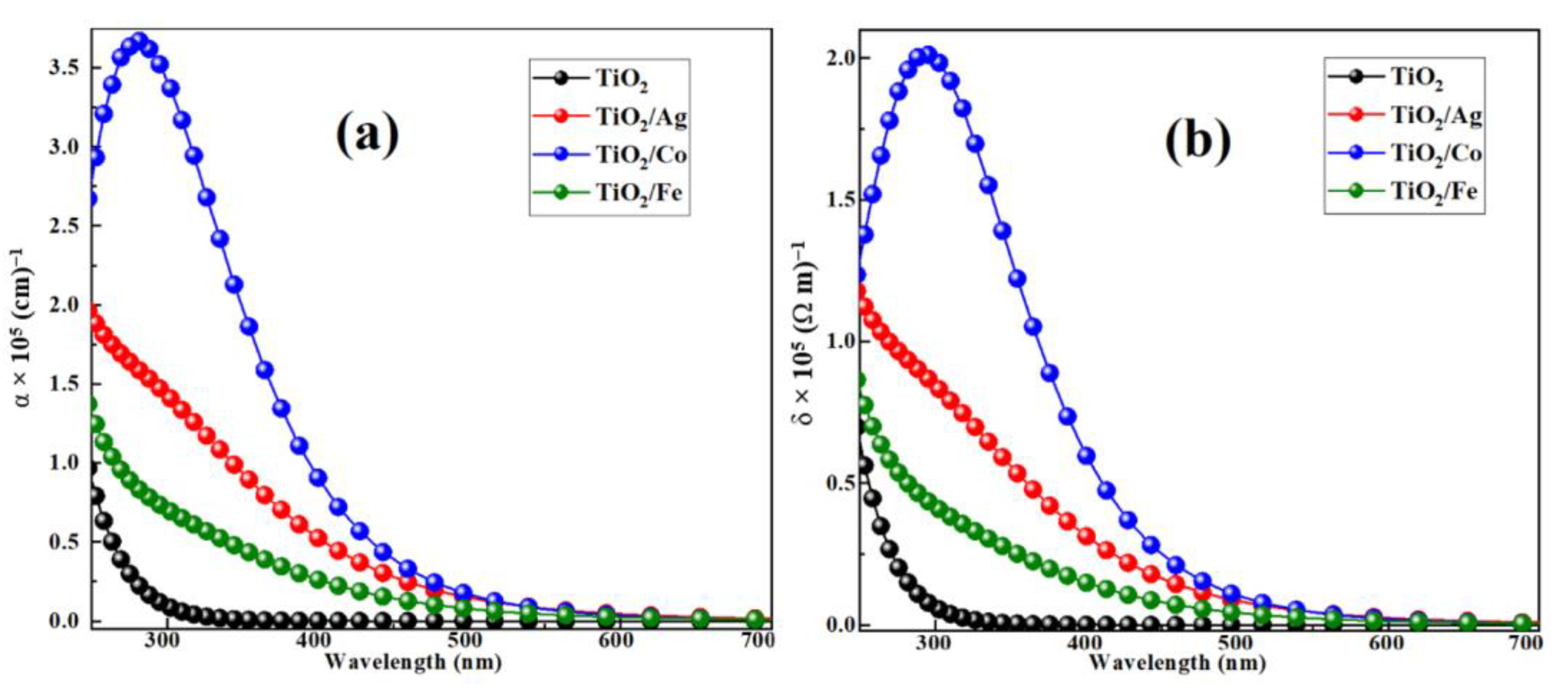
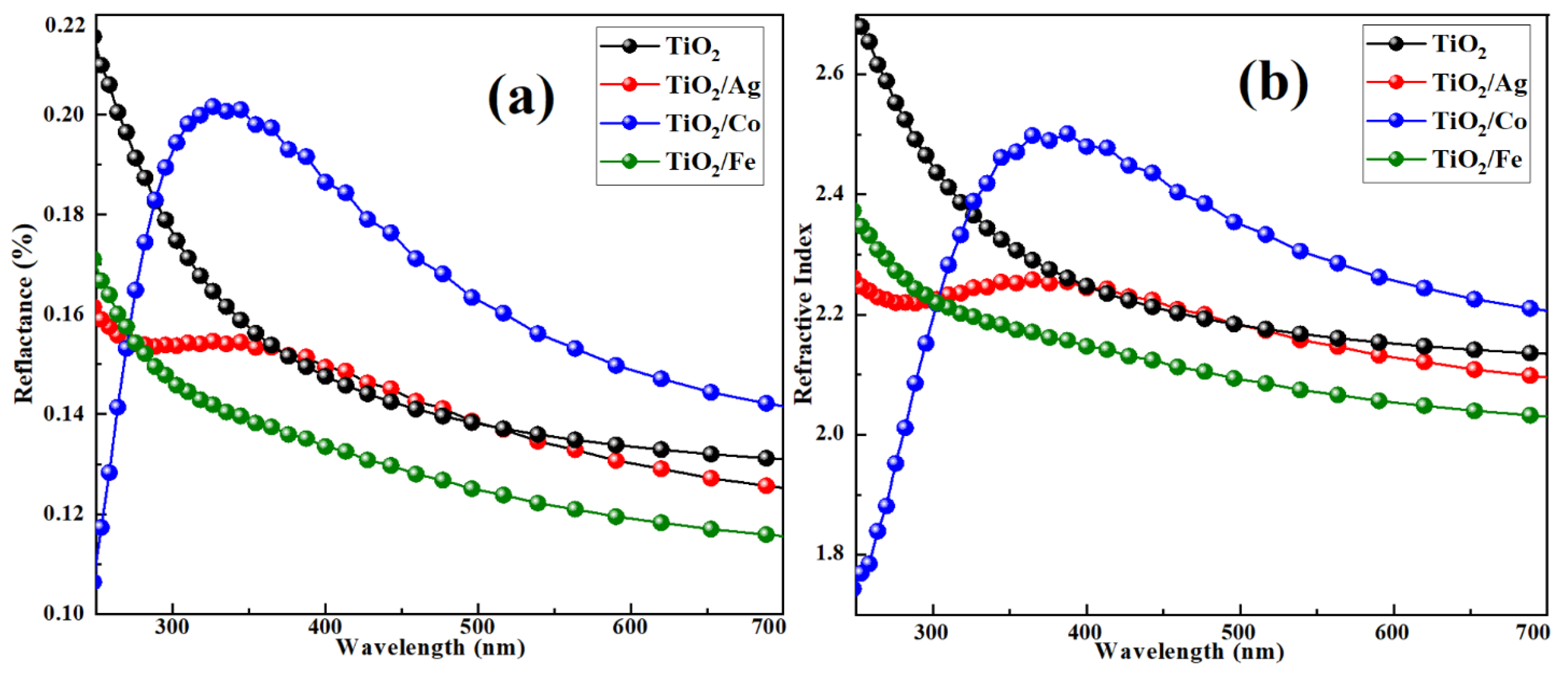
2.2.1. Real and Imaginary Parts of Dielectric Functions
2.2.2. Optical Absorption and Conductivity
2.3. Elastic Properties
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Vorontsov, A.V.; Valdés, H.; Smirniotis, P.G.; Paz, Y. Recent advancements in the understanding of the surface chemistry in TiO2 photocatalysis. Surfaces 2020, 3, 72–92. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, P.; Liu, J.; Yu, J. New understanding of the difference of photocatalytic activity among anatase, rutile and brookite TiO2. Phys. Chem. Chem. Phys. 2014, 16, 20382–20386. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Wei, Z.; Shi, L. A Fundamental DFT Study of Anatase (TiO2) Doped with 3d Transition Metals for High Photocatalytic Activities. J. Wuhan Univ. Technol. Sci. Ed. 2018, 33, 403–408. [Google Scholar] [CrossRef]
- Ilyas, M.; Hussain, A.; Rauf, A.; Rahman, I.U.; Naveed, A.; Basit, M.A.; Rabbani, F.; Khan, S.U.; Ahmed, E.; Hussain, M.; et al. Tailoring the antifouling agent titanium dioxide in the visible range of solar spectrum for photoelectrochemical activity with hybrid DFT & DFT+ U approach. Mater. Today Commun. 2021, 27, 102366. [Google Scholar]
- Dharmale, N.; Chaudhury, S.; Kar, J. Technology. Pressure-Induced Phase Transition Study on Brookite to Rutile TiO2 Transformation. ECS J. Solid State Sci. Technol. 2021, 10, 071021. [Google Scholar] [CrossRef]
- Chen, T.; Chen, W.-L.; Foley, B.J.; Lee, J.; Ruff, J.P.; Ko, J.P.; Brown, C.M.; Harriger, L.W.; Zhang, D.; Park, C.; et al. Origin of long lifetime of band-edge charge carriers in organic–inorganic lead iodide perovskites. Proc. Natl. Acad. Sci. USA 2017, 114, 7519–7524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huy, H.A.; Aradi, B.; Frauenheim, T.; Deák, P. Calculation of carrier-concentration-dependent effective mass in Nb-doped anatase crystals of TiO2. Phys. Rev. B 2011, 83, 155201. [Google Scholar] [CrossRef]
- Tamirat, A.G.; Rick, J.; Dubale, A.A.; Su, W.-N.; Hwang, B.-J. Using hematite for photoelectrochemical water splitting: A review of current progress and challenges. Nanoscale Horiz. 2016, 1, 243–267. [Google Scholar] [CrossRef]
- Du, C.; Yang, X.; Mayer, M.T.; Hoyt, H.; Xie, J.; McMahon, G.; Bischoping, G.; Wang, D. Hematite-based water splitting with low turn-on voltages. Angew. Chem. 2013, 125, 12924–12927. [Google Scholar] [CrossRef]
- Sivula, K.; Le Formal, F.; Grätzel, M. Solar water splitting: Progress using hematite (α-Fe2O3) photoelectrodes. Chemsuschem 2011, 4, 432–449. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, W.; Chen, C.; Xu, W.; Li, L. Tungsten trioxide nanostructures for photoelectrochemical water splitting: Material engineering and charge carrier dynamic manipulation. Adv. Funct. Mater. 2019, 29, 1809036. [Google Scholar] [CrossRef]
- Enesca, A.; Duta, A.; Schoonman, J. Study of photoactivity of tungsten trioxide (WO3) for water splitting. Thin Solid Films 2007, 515, 6371–6374. [Google Scholar] [CrossRef]
- Park, J.H.; Park, O.O.; Kim, S. Photoelectrochemical water splitting at titanium dioxide nanotubes coated with tungsten trioxide. Appl. Phys. Lett. 2006, 89, 163106. [Google Scholar] [CrossRef]
- Fujishima, A.; Zhang, X.; Tryk, D.A. TiO2 photocatalysis and related surface phenomena. Surf. Sci. Rep. 2008, 63, 515–582. [Google Scholar] [CrossRef]
- Hisatomi, T.; Kubota, J.; Domen, K. Recent advances in semiconductors for photocatalytic and photoelectrochemical water splitting. Chem. Soc. Rev. 2014, 43, 7520–7535. [Google Scholar] [CrossRef]
- Khan, S.U.; Al-Shahry, M.; Ingler, W.B., Jr. Efficient photochemical water splitting by a chemically modified n-TiO2. Science 2002, 297, 2243–2245. [Google Scholar] [CrossRef]
- Guerrero, A.; Bisquert, J. Perovskite semiconductors for photoelectrochemical water splitting applications. Curr. Opin. Electrochem. 2017, 2, 144–147. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, H.; Inoue, T.; Yao, Q. Band gap engineering of SrTiO3 for water splitting under visible light irradiation. Int. J. Hydrogen Energy 2014, 39, 12507–12514. [Google Scholar] [CrossRef]
- Yang, Y.; Niu, S.; Han, D.; Liu, T.; Wang, G.; Li, Y. Progress in developing metal oxide nanomaterials for photoelectrochemical water splitting. Adv. Energy Mater. 2017, 7, 1700555. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Yao, L.; Deng, L.; Bowen, C.; Zhang, Y.; Chen, S.; Lin, Z.; Peng, F.; Zhang, P. Recent advances in metal sulfides: From controlled fabrication to electrocatalytic, photocatalytic and photoelectrochemical water splitting and beyond. Chem. Soc. Rev. 2019, 48, 4178–4280. [Google Scholar] [CrossRef]
- Rueda, D.; Arias, V.; Zhang, Y.; Cabot, A.; Agudelo, A.C.; Cadavid, D. Monitoring; Management. Low-cost tangerine peel waste mediated production of titanium dioxide nanocrystals: Synthesis and characterization. Environ. Nanotechnol. Monit. Manag. 2020, 13, 100285. [Google Scholar]
- Kanakaraju, D.; Glass, B.D.; Oelgemöller, M. Titanium dioxide photocatalysis for pharmaceutical wastewater treatment. Environ. Chem. Lett. 2014, 12, 27–47. [Google Scholar] [CrossRef]
- Yang, X.; Cui, F.; Guo, X.; Li, D. Effects of nanosized titanium dioxide on the physicochemical stability of activated sludge flocs using the thermodynamic approach and Kelvin probe force microscopy. Water Res. 2013, 47, 3947–3958. [Google Scholar] [CrossRef]
- Pelaez, M.; Nolan, N.T.; Pillai, S.C.; Seery, M.K.; Falaras, P.; Kontos, A.G.; Dunlop, P.S.; Hamilton, J.W.; Byrne, J.A.; O’shea, K.; et al. A review on the visible light active titanium dioxide photocatalysts for environmental applications. Appl. Catal. B Environ. 2012, 125, 331–349. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Takata, T.; Domen, K. Particulate photocatalysts for overall water splitting. Nat. Rev. Mater. 2017, 2, 1–17. [Google Scholar] [CrossRef]
- Qian, R.; Zong, H.; Schneider, J.; Zhou, G.; Zhao, T.; Li, Y.; Yang, J.; Bahnemann, D.W.; Pan, J.H. Charge carrier trapping, recombination and transfer during TiO2 photocatalysis: An overview. Catal. Today 2019, 335, 78–90. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Yang, M.; Zhang, G.; Dionysiou, D.D. HNO3-involved one-step low temperature solvothermal synthesis of N-doped TiO2 nanocrystals for efficient photocatalytic reduction of Cr (VI) in water. Appl. Catal. B Environ. 2013, 142, 249–258. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Li, J.; Xu, H.Y. One-step in situ solvothermal synthesis of SnS2/TiO2 nanocomposites with high performance in visible light-driven photocatalytic reduction of aqueous Cr (VI). Appl. Catal. B Environ. 2012, 123, 18–26. [Google Scholar] [CrossRef]
- Basavarajappa, P.S.; Patil, S.B.; Ganganagappa, N.; Reddy, K.R.; Raghu, A.V.; Reddy, C.V. Recent progress in metal-doped TiO2, non-metal doped/codoped TiO2 and TiO2 nanostructured hybrids for enhanced photocatalysis. Int. J. Hydrogen Energy 2020, 45, 7764–7778. [Google Scholar] [CrossRef]
- Yalçın, Y.; Kılıç, M.; Çınar, Z. The role of non-metal doping in TiO2 photocatalysis. J. Adv. Oxid. Technol. 2010, 13, 281–296. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Li, J.; Li, L.; Lin, S. First-principles study on transition metal-doped anatase TiO2. Nanoscale Res. Lett. 2014, 9, 46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, G.; Zhu, L.; Liu, M.; Fang, Q.; Zhang, L. Optical and electrical properties of plasma-oxidation derived HfO2 gate dielectric films. Appl. Surf. Sci. 2007, 253, 3413–3418. [Google Scholar] [CrossRef]
- Pandey, S.C.; Xu, X.; Williamson, I.; Nelson, E.B.; Li, L. Electronic and vibrational properties of transition metal-oxides: Comparison of GGA, GGA+ U, and hybrid approaches. Chem. Phys. Lett. 2017, 669, 1–8. [Google Scholar] [CrossRef]
- Orhan, O.K.; O’Regan, D.D. TDDFT+ U: A critical assessment of the Hubbard U correction to exchange-correlation kernels and potentials. Phys. Rev. B 2019, 99, 165120. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G. Density functional theory of atoms and molecules. In Horizons of Quantum Chemistry; Springer: Dordrecht, The Netherlands, 1980; pp. 5–15. [Google Scholar]
- Arshad Javid, M.; Khan, Z.U.; Mehmood, Z.; Nabi, A.; Hussain, F.; Imran, M.; Nadeem, M.; Anjum, N. Structural, electronic and optical properties of LiNbO3 using GGA-PBE and TB-mBJ functionals: A DFT study. Int. J. Mod. Phys. B 2018, 32, 1850168. [Google Scholar] [CrossRef]
- Nisar, J.; Århammar, C.; Jämstorp, E.; Ahuja, R. Optical gap and native point defects in kaolinite studied by the GGA-PBE, HSE functional, and GW approaches. Phys. Rev. B 2011, 84, 075120. [Google Scholar] [CrossRef]
- Sharma, S.B. Optoelectronic and elastic response of fluorinated hexagonal boron nitride monolayer. ChemRxiv 2021. ahead of print. [Google Scholar]
- Mazumder, J.T.; Mayengbam, R.; Tripathy, S. Theoretical investigation on structural, electronic, optical and elastic properties of TiO2, SnO2, ZrO2 and HfO2 using SCAN meta-GGA functional: A DFT study. Mater. Chem. Phys. 2020, 254, 123474. [Google Scholar] [CrossRef]
- Uspenskii, Y.A.; Kulatov, E.; Halilov, S. Effect of anisotropy on magneto-optical properties of uniaxial crystals: Application to CrO2. Phys. Rev. B 1996, 54, 474. [Google Scholar] [CrossRef]
- Wanbayor, R.; Ruangpornvisuti, V. Adsorption of CO, H2, N2O, NH3 and CH4 on the anatase TiO2 (0 0 1) and (1 0 1) surfaces and their competitive adsorption predicted by periodic DFT calculations. Mater. Chem. Phys. 2010, 124, 720–725. [Google Scholar] [CrossRef]
- Howard, C.; Sabine, T.; Dickson, F. Structural and thermal parameters for rutile and anatase. Acta Crystallogr. Sect. B Struct. Sci. 1991, 47, 462–468. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Wen, M. Noble metals enhanced catalytic activity of anatase TiO2 for hydrogen evolution reaction. Int. J. Hydrogen Energy 2018, 43, 22055–22063. [Google Scholar] [CrossRef]
- Wu, H.-C.; Li, S.-H.; Lin, S.-W. Effect of Fe concentration on Fe-doped anatase TiO2 from GGA+ U calculations. Int. J. Photoenergy 2012, 2012, 823498. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Ai, M.; Huang, C.; Yin, L.; Liu, X.; Zhang, R.; Wang, S.; Jiang, Z.; Zhang, X.; Zou, J.-J.; et al. Manipulating spin polarization of titanium dioxide for efficient photocatalysis. Nat. Commun. 2020, 11, 418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cendula, P.; Tilley, S.D.; Gimenez, S.; Bisquert, J.; Schmid, M.; Grätzel, M.; Schumacher, J.O. Calculation of the energy band diagram of a photoelectrochemical water splitting cell. J. Phys. Chem. C 2014, 118, 29599–29607. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wang, L.-W. Thermodynamic oxidation and reduction potentials of photocatalytic semiconductors in aqueous solution. Chem. Mater. 2012, 24, 3659–3666. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Jiang, Z.; Zhu, C.; Hu, X.; Zhu, H.; Zhang, X.; Fan, J.; Lin, S.H. The optical absorption and hydrogen production by water splitting of (Si, Fe)-codoped anatase TiO2 photocatalyst. Int. J. Hydrog. Energy 2013, 38, 5209–5214. [Google Scholar] [CrossRef]
- Dash, L.; Vast, N.; Baranek, P.; Cheynet, M.-C.; Reining, L. Electronic structure and electron energy-loss spectroscopy of ZrO2 zirconia. Phys. Rev. B 2004, 70, 245116. [Google Scholar] [CrossRef]
- Sharma, P.; Katyal, S. Determination of optical parameters of a-(As2Se3)90Ge10 thin film. J. Phys. D Appl. Phys. 2007, 40, 2115. [Google Scholar] [CrossRef]
- Khoshman, J.M.; Kordesch, M.E. Optical properties of a-HfO2 thin films. Surf. Coat. Technol. 2006, 201, 3530–3535. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Ouyang, L.; Ching, W.Y. Ab initio calculation of elastic constants of ceramic crystals. J. Am. Ceram. Soc. 2007, 90, 3194–3204. [Google Scholar] [CrossRef]
- Mahmood, T.; Malik, H.; Batool, R.; Perveen, Z.; Saleemi, F.; Rasheed, H.; Saeed, M.; Cao, C.; Rizwan, M. Elastic, electronic and optical properties of anatase TiO2 under pressure: A DFT approach. Chin. J. Phys. 2017, 55, 1252–1263. [Google Scholar] [CrossRef]
- Liu, X.; Fu, J. Electronic and elastic properties of the tetragonal anatase TiO2 structure from first principle calculation. Optik 2020, 206, 164342. [Google Scholar] [CrossRef]
- Lü, X.; Yang, W.; Quan, Z.; Lin, T.; Bai, L.; Wang, L.; Huang, F.; Zhao, Y. Enhanced electron transport in Nb-doped TiO2 nanoparticles via pressure-induced phase transitions. J. Am. Chem. Soc. 2014, 136, 419–426. [Google Scholar] [CrossRef] [PubMed]




| Type | a (Å) | c(Å) | c/a | V (Å)3 |
|---|---|---|---|---|
| TiO2-Pure DFT [41] Experiment [42] | 3.791 3.737, 3.741 3.785 | 9.510 9.981, 9.964 9.514 | 2.51 2.57, 2.66 2.51 | 549.537 |
| TiO2/Ag DFT [43] | 3.821 3.905 | 9.588 9.825 | 2.51 2.52 | 559.621 |
| TiO2/Co | 3.802 | 9.447 | 2.48 | 545.971 |
| TiO2/Fe DFT [44] | 3.785 3.771 | 9.496 9.489 | 2.51 2.49 | 545.984 |
| Materials | This Work | Other DFT | Experimental |
|---|---|---|---|
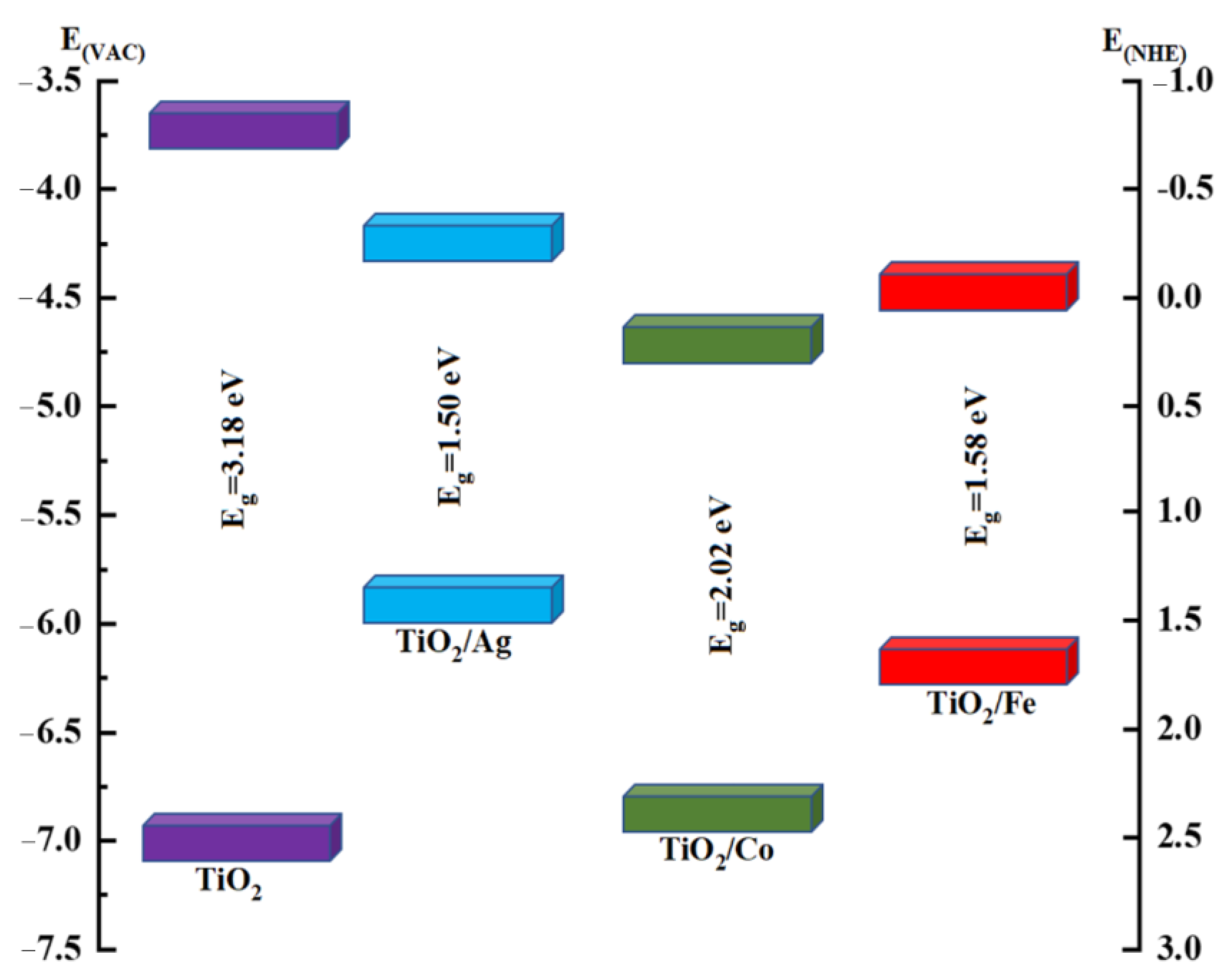
| TiO2 | 3.18 eV | 3.3 eV [45] | 3.2 eV [42] |
| TiO2/Ag | 1.50 eV | 0.9 eV [43] | --- |
| TiO2/Co | 2.02 eV | --- | --- |
| TiO2/Fe | 1.58 eV | 1.74 eV [44] | --- |
| Elastic Constants | This Work TiO2 | Other DFT [39]a [53]b | This Work TiO2/Co |
|---|---|---|---|
| C11 | 369.140 | a399.1, b336.5 | 340.595 |
| C12 | 153.918 | a167.6, b138.6 | 155.326 |
| C13 | 153.260 | a159.9, b136.0 | 138.609 |
| C33 | 215.389 | a250.8, b192.1 | 196.803 |
| C44 | 44.281 | a70.49, b49.4 | 60.523 |
| C66 | 58.665 | a61.28, b58.3 | 63.446 |
| Elastic Properties | Current Work TiO2 | Other Work TiO2 [55] | Current Work Co dope TiO2 |
|---|---|---|---|
| BV | 208.283 | 221.982 | 193.675 |
| BR | 192.736 | 204.210 | 176.590 |
| BH | 200.510 | 213.096 | 185.132 |
| Gv | 62.327 | 51.275 | 66.595 |
| GR | 55.230 | 32.085 | 63.099 |
| GH | 58.779 | 41.680 | 64.847 |
| EV | 170.023 | 142.829 | 179.241 |
| ER | 151.243 | 91.466 | 169.152 |
| EH | 160.640 | 117.388 | 174.203 |
| υV | 0.363 | 0.393 | 0.346 |
| υR | 0.369 | 0.425 | 0.340 |
| υH | 0.366 | 0.408 | 0.343 |
| BV/GV | 3.342 | 4.329 | 2.908 |
| BR/GR | 3.489 | 6.365 | 2.799 |
| BH/GH | 3.411 | 5.113 | 2.855 |
| AU | 0.423 | 0.368 | 0.374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Rauf, A.; Ahmed, E.; Khan, M.S.; Mian, S.A.; Jang, J. Modulating Optoelectronic and Elastic Properties of Anatase TiO2 for Photoelectrochemical Water Splitting. Molecules 2023, 28, 3252. https://doi.org/10.3390/molecules28073252
Hussain A, Rauf A, Ahmed E, Khan MS, Mian SA, Jang J. Modulating Optoelectronic and Elastic Properties of Anatase TiO2 for Photoelectrochemical Water Splitting. Molecules. 2023; 28(7):3252. https://doi.org/10.3390/molecules28073252
Chicago/Turabian StyleHussain, Akbar, Abdur Rauf, Ejaz Ahmed, Muhammad Saleem Khan, Shabeer Ahmad Mian, and Joonkyung Jang. 2023. "Modulating Optoelectronic and Elastic Properties of Anatase TiO2 for Photoelectrochemical Water Splitting" Molecules 28, no. 7: 3252. https://doi.org/10.3390/molecules28073252
APA StyleHussain, A., Rauf, A., Ahmed, E., Khan, M. S., Mian, S. A., & Jang, J. (2023). Modulating Optoelectronic and Elastic Properties of Anatase TiO2 for Photoelectrochemical Water Splitting. Molecules, 28(7), 3252. https://doi.org/10.3390/molecules28073252






