Molecular Dynamics Simulation of Helium Barrier Performance of Modified Polyamide 6 Lining of IV Hydrogen Storage Tank with Montmorillonite
Abstract
1. Introduction
2. Simulation
2.1. Modified Montmorillonite (OMMT)/Polyamide-6 (PA6) Model Construction
2.2. Simulation of the Calculation Process
3. Results and Discussion
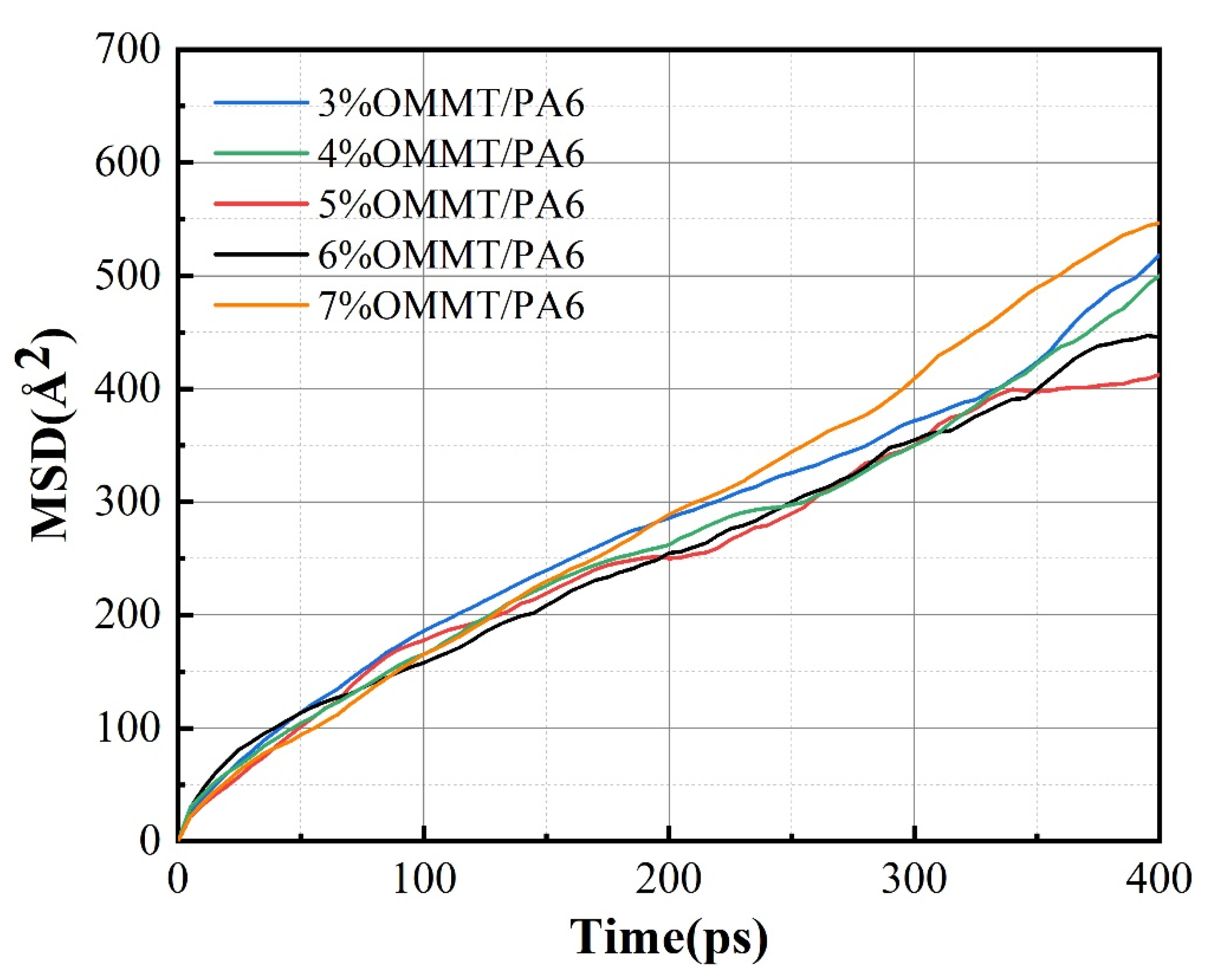
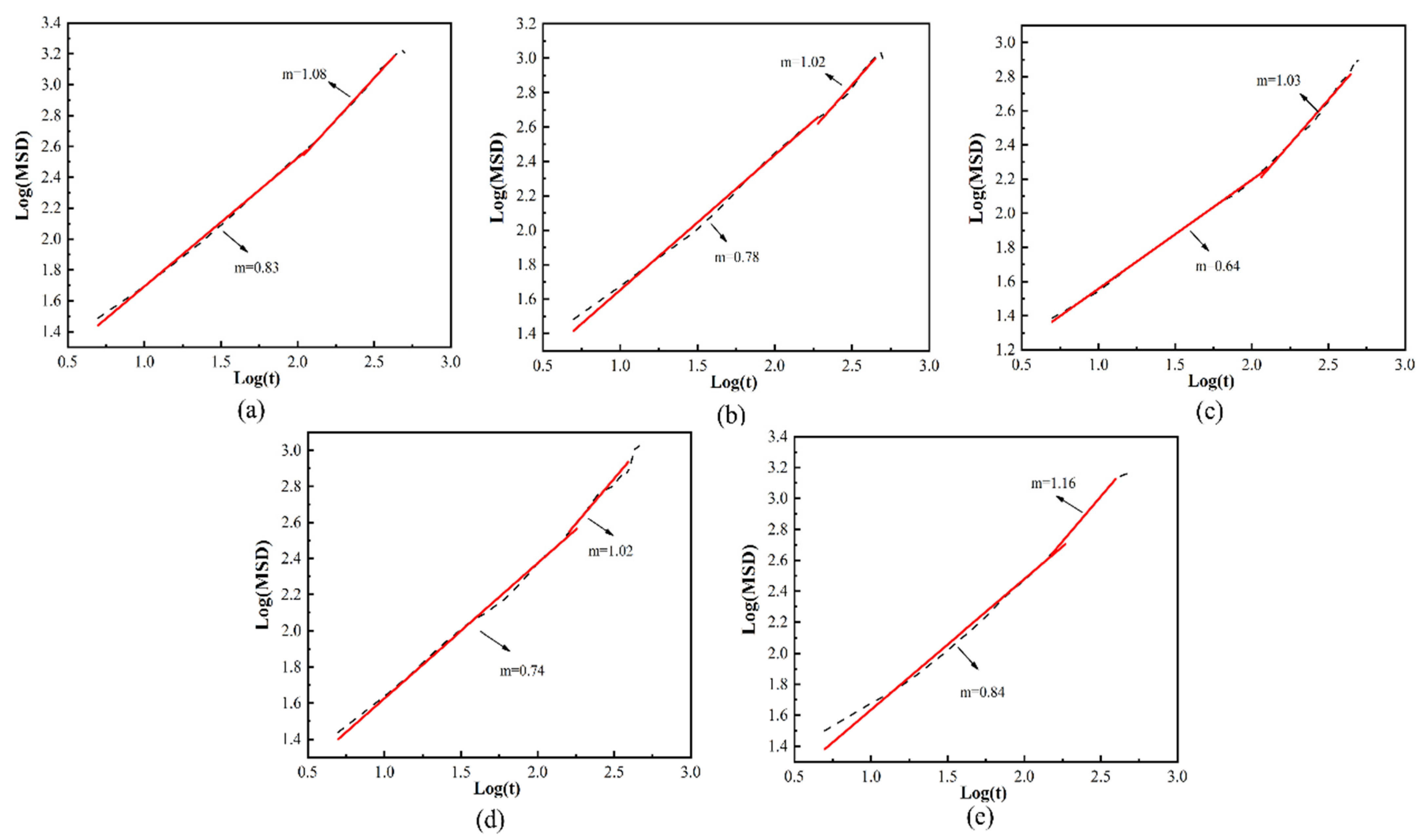
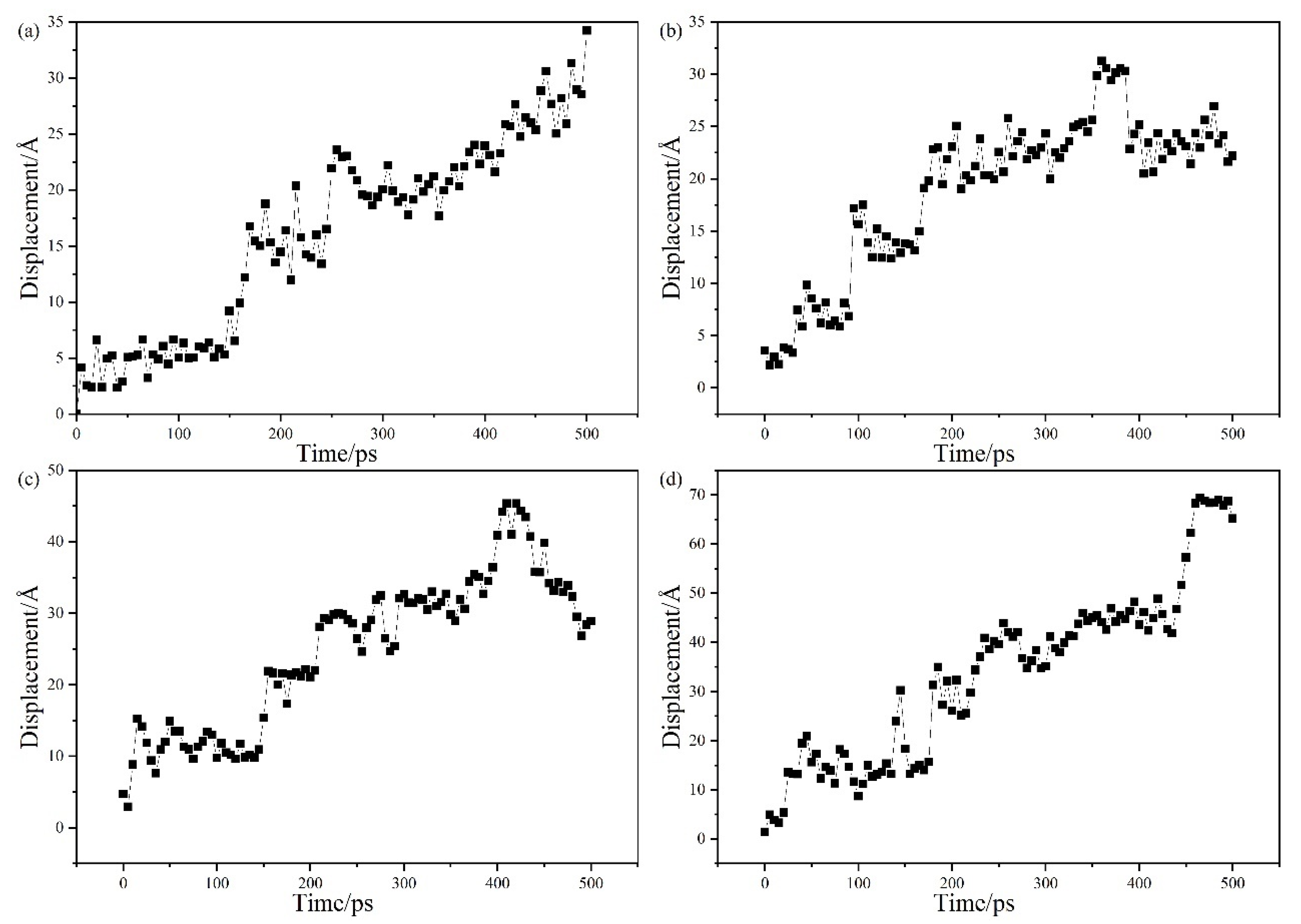
3.1. Influence of Filler Ratio on Permeability Coefficient
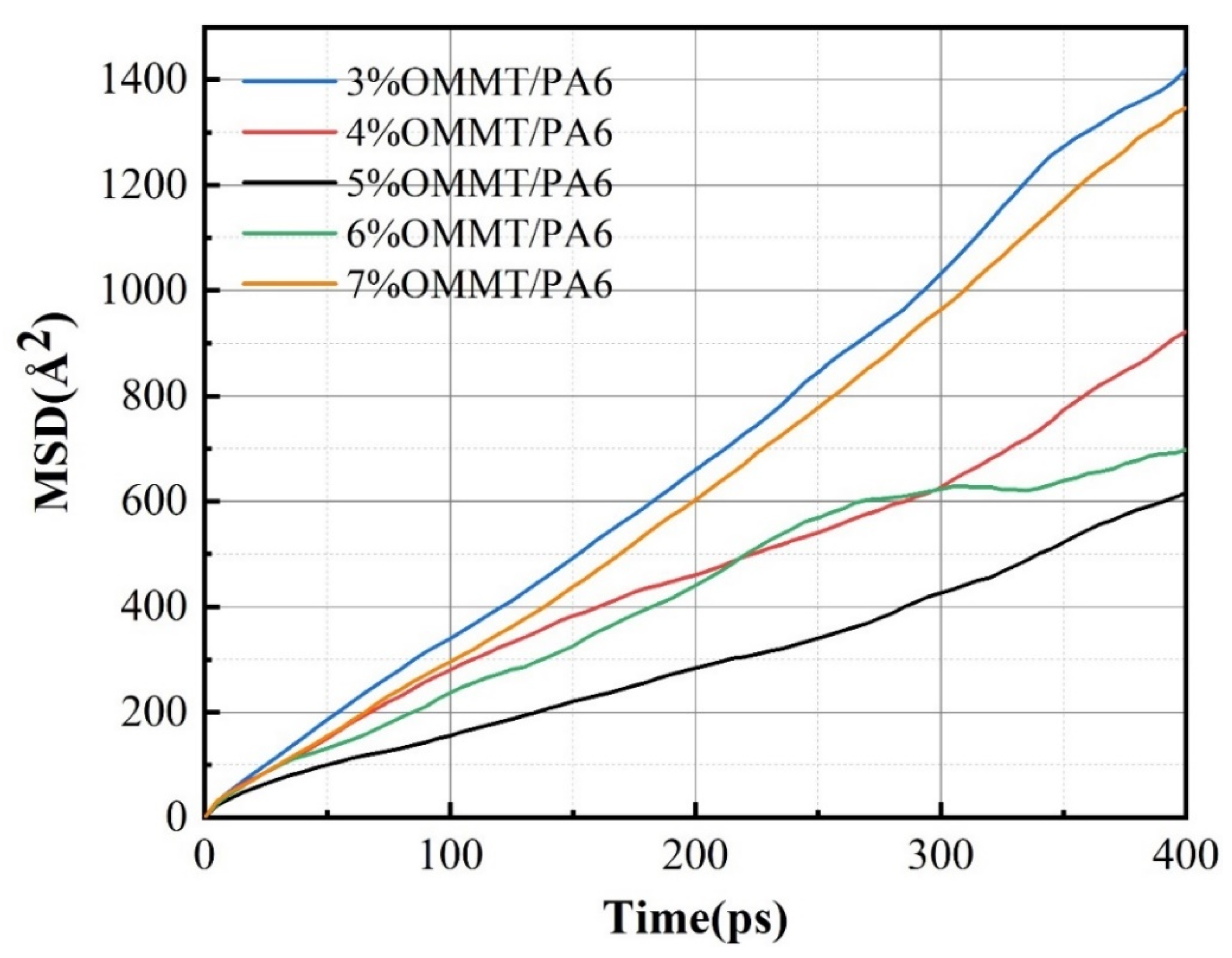
3.2. Effect of Temperature on Permeability Coefficient
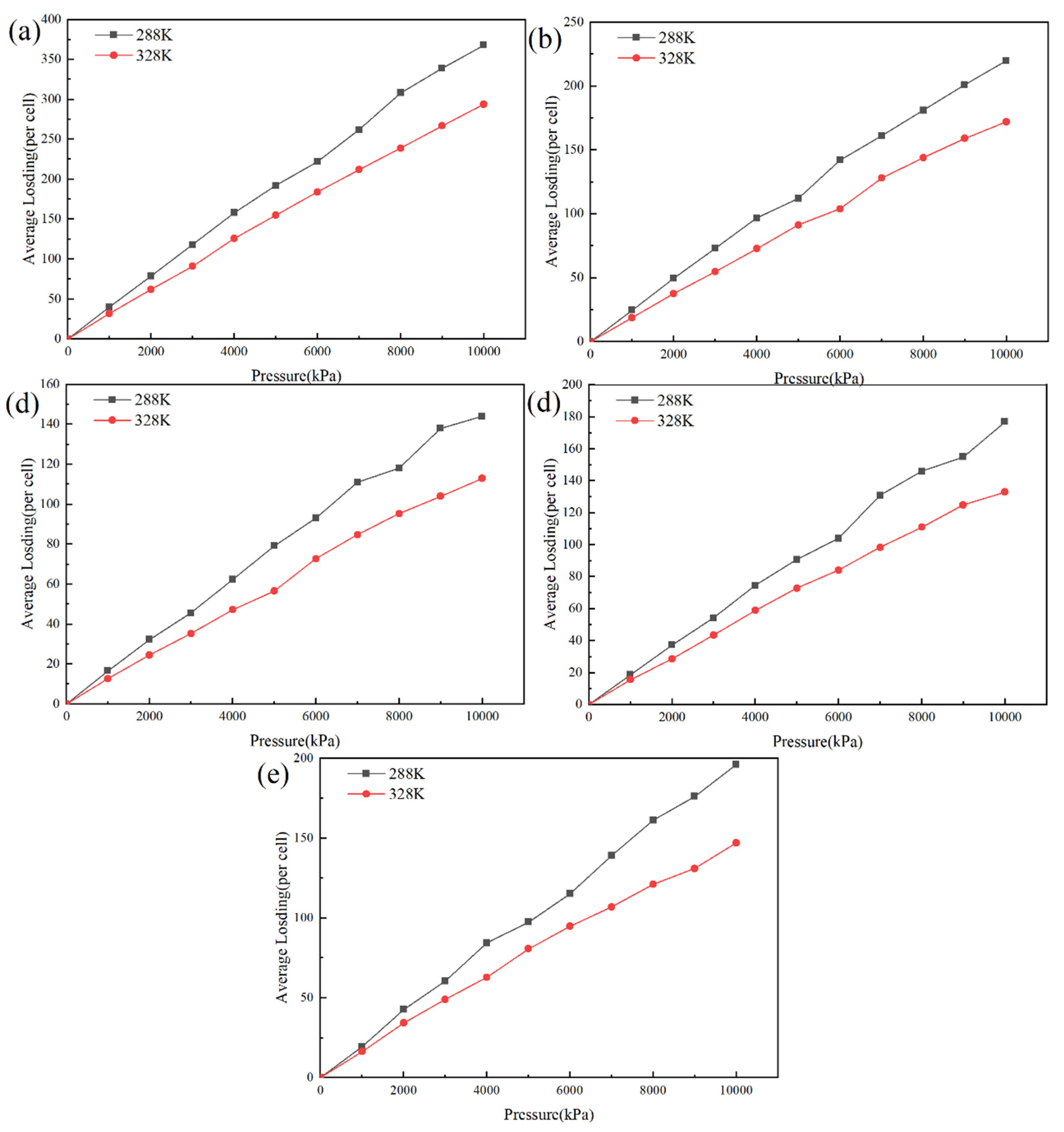
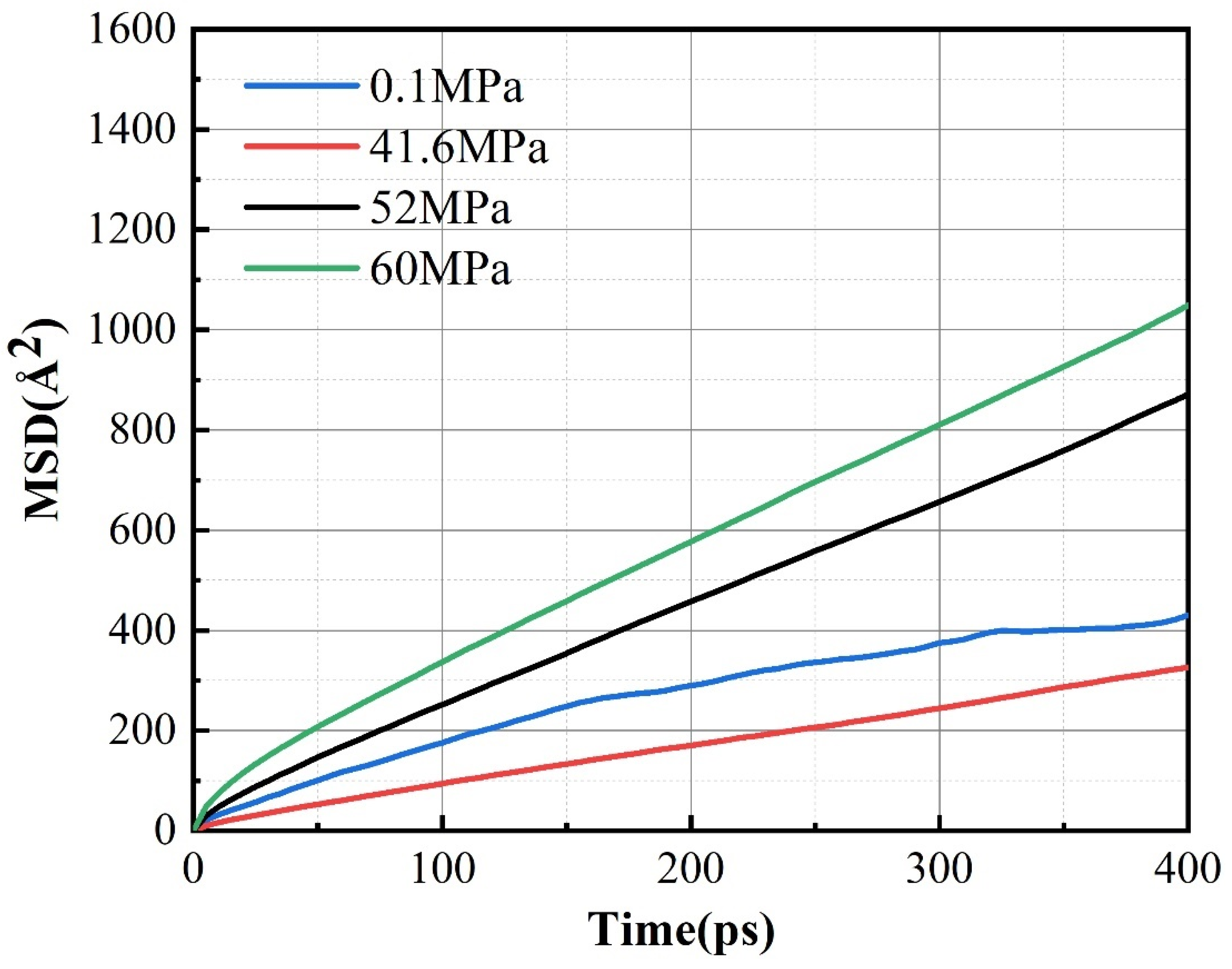
3.3. Effect of Pressure on Permeability Coefficient
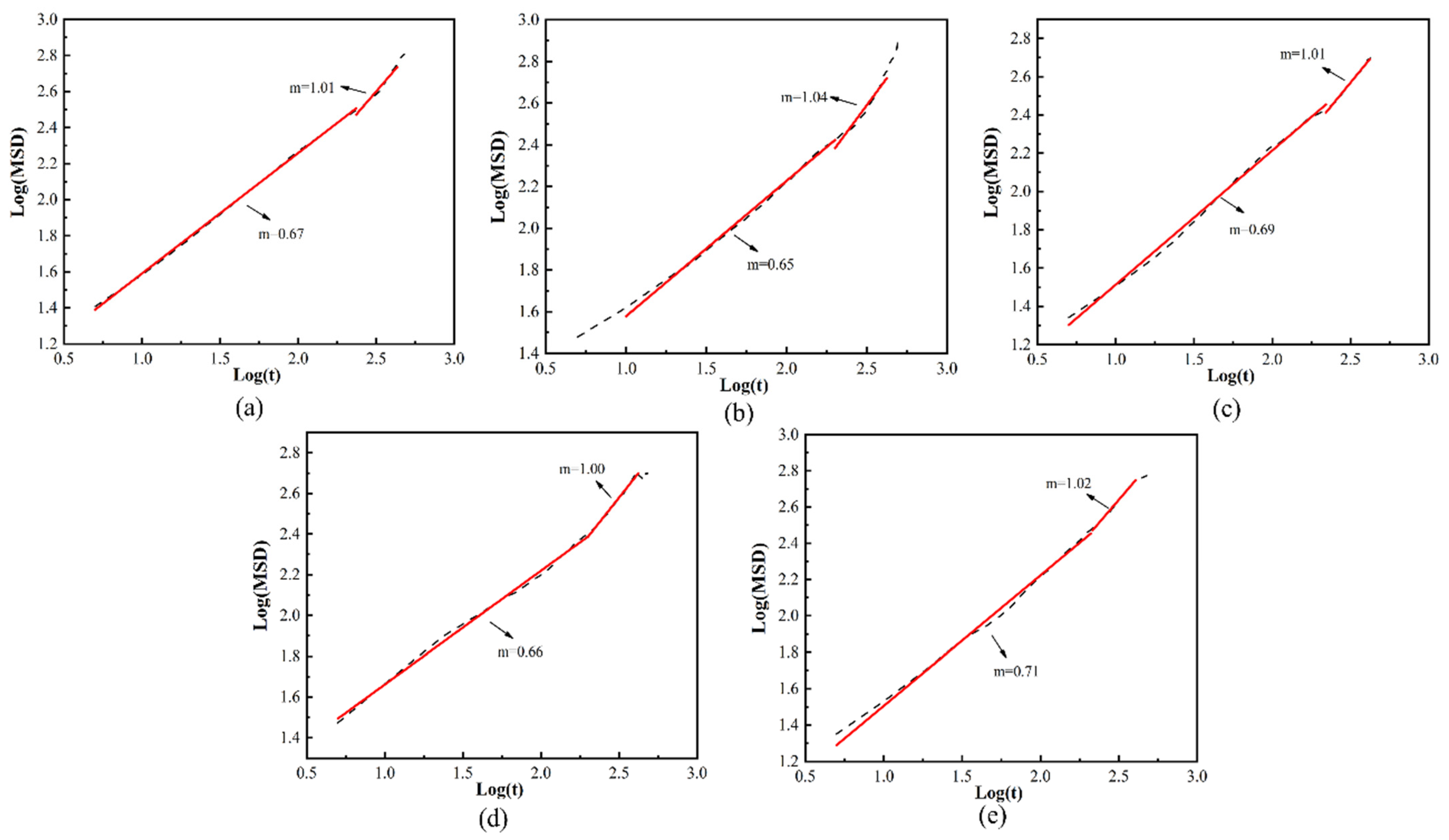
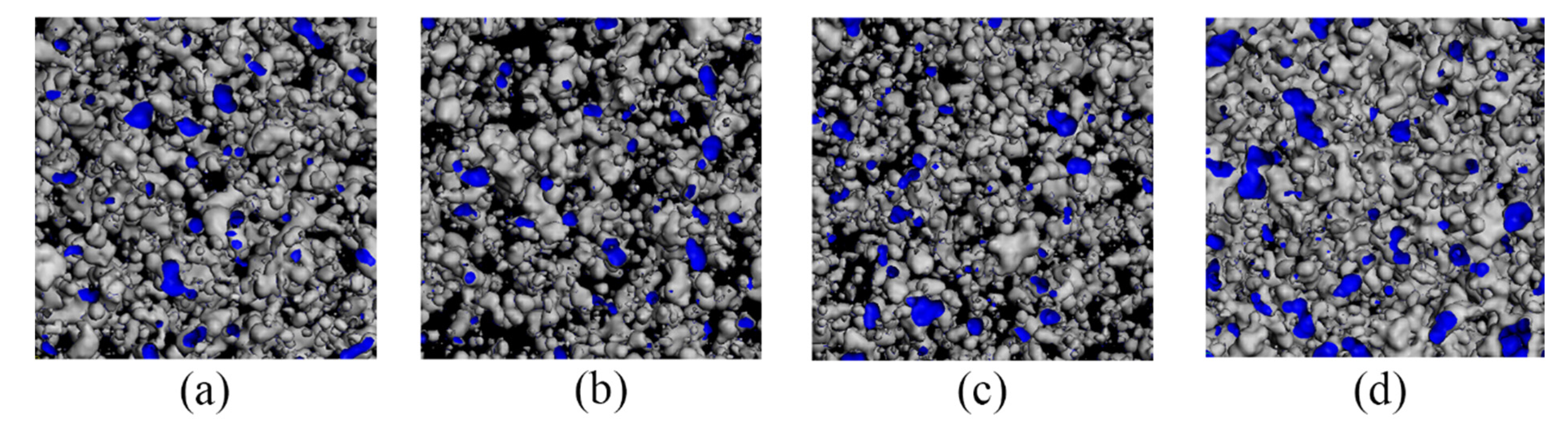
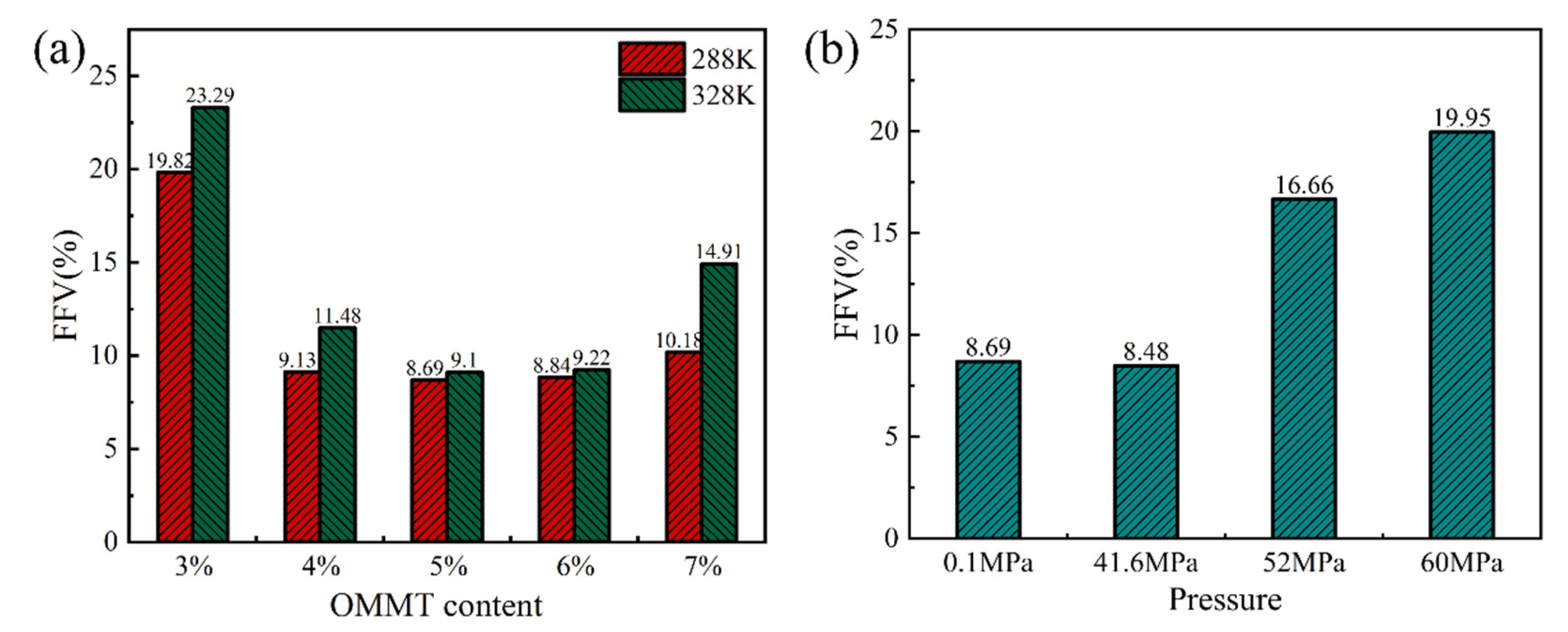
3.4. Analysis of the Effect of Free Volume
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Jiang, Z.; Pan, Q.; Xu, J.; Fang, T. Current situation and prospect of hydrogen storage technology with new organic liquid. Int. J. Hydrogen Energy 2014, 39, 17442–17451. [Google Scholar] [CrossRef]
- Müller, K.; Arlt, W. Status and Development in Hydrogen Transport and Storage for Energy Applications. Energy Technol. 2013, 1, 501–511. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Jia, Z.-C.; Yuan, Z.-M.; Yang, T.; Qi, Y.; Zhao, D.-L. Development and Application of Hydrogen Storage. J. Iron Steel Res. Int. 2015, 22, 757–770. [Google Scholar] [CrossRef]
- Li, M.; Bai, Y.; Zhang, C.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the research of hydrogen storage system fast refueling in fuel cell vehicle. Int. J. Hydrogen Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef]
- Johnson, T.; Bozinoski, R.; Ye, J.; Sartor, G.; Zheng, J.; Yang, J. Thermal model development and validation for rapid filling of high pressure hydrogen tanks. Int. J. Hydrogen Energy 2015, 40, 9803–9814. [Google Scholar] [CrossRef]
- Zheng, J.; Guo, J.; Yang, J.; Zhao, Y.; Zhao, L.; Pan, X.; Ma, J.; Zhang, L. Experimental and numerical study on temperature rise within a 70 MPa type III cylinder during fast refueling. Int. J. Hydrogen Energy 2013, 38, 10956–10962. [Google Scholar] [CrossRef]
- Cousins, K.; Zhang, R. Highly Porous Organic Polymers for Hydrogen Fuel Storage. Polymers 2019, 11, 690. [Google Scholar] [CrossRef]
- Kato, R.; Nishide, H. Polymers for carrying and storing hydrogen. Polym. J. 2018, 50, 77–82. [Google Scholar] [CrossRef]
- He, J.; Kokgil, E.; Wang, L.; Ng, H.D. Assessment of similarity relations using helium for prediction of hydrogen dispersion and safety in an enclosure. Int. J. Hydrogen Energy 2016, 41, 15388–15398. [Google Scholar] [CrossRef]
- Lee, I.D.; Smith, O.I.; Karagozian, A.R. Hydrogen and Helium Leak Rates from Micromachined Orifices. AIAA J. 2003, 41, 457–464. [Google Scholar] [CrossRef]
- Punetha, M.; Choudhary, A.; Khandekar, S. Stratification and mixing dynamics of helium in an air filled confined enclosure. Int. J. Hydrogen Energy 2018, 43, 19792–19809. [Google Scholar] [CrossRef]
- Kan, L.; Ouyang, X.; Gao, S.; Li, R.; Ma, N.; Han, S.-H.; Wei, H.; Liu, L.-H. High damping and mechanical properties of hydrogen-bonded polyethylene materials with variable contents of hydroxyls: Effect of hydrogen bonding density. Chin. J. Polym. Sci. 2017, 35, 649–658. [Google Scholar] [CrossRef]
- Backens, S.; Siering, J.; Schmidt, S.; Glück, N.; Flügge, W. Comparative study of thermoplastic liner materials with regard to mechanical and permeation barrier properties before and after cyclic thermal aging. Mater. Test. 2021, 63, 311–316. [Google Scholar] [CrossRef]
- Sun, Y.; Lv, H.; Zhou, W.; Zhang, C. Research on hydrogen permeability of polyamide 6 as the liner material for type IV hydrogen storage tank. Int. J. Hydrogen Energy 2020, 45, 24980–24990. [Google Scholar] [CrossRef]
- Humpenöder, J. Gas permeation of fibre reinforced plastics. Cryogenics 1998, 38, 143–147. [Google Scholar] [CrossRef]
- Pepin, J.; Lainé, E.; Grandidier, J.-C.; Castagnet, S.; Blanc-Vannet, P.; Papin, P.; Weber, M. Determination of key parameters responsible for polymeric liner collapse in hyperbaric type IV hydrogen storage vessels. Int. J. Hydrogen Energy 2018, 43, 16386–16399. [Google Scholar] [CrossRef]
- Lafitte, G.; Espuche, E.; Gérard, J.-F. Polyamide 11/poly(hydroxy amino ether) blends: Influence of the blend composition and morphology on the barrier and mechanical properties. Eur. Polym. J. 2011, 47, 1994–2002. [Google Scholar] [CrossRef]
- Jordan, J.; Jacob, K.I.; Tannenbaum, R.; Sharaf, M.A.; Jasiuk, I. Experimental trends in polymer nanocomposites—A review. Mater. Sci. Eng.-Struct. Mater. Prop. Microstruct. Process. 2005, 393, 1–11. [Google Scholar] [CrossRef]
- He, W.; Song, P.; Yu, B.; Fang, Z.; Wang, H. Flame retardant polymeric nanocomposites through the combination of nanomaterials and conventional flame retardants. Prog. Mater. Sci. 2020, 114, 100687. [Google Scholar] [CrossRef]
- Mousavi, S.R.; Estaji, S.; Kiaei, H.; Mansourian-Tabaei, M.; Nouranian, S.; Jafari, S.H.; Ruckdäschel, H.; Arjmand, M.; Khonakdar, H.A. A review of electrical and thermal conductivities of epoxy resin systems reinforced with carbon nanotubes and graphene-based nanoparticles. Polym. Test. 2022, 112, 107645. [Google Scholar] [CrossRef]
- Fasihi, M.; Abolghasemi, M.R. Oxygen barrier and mechanical properties of masterbatch-based PA6/nanoclay composite films. J. Appl. Polym. Sci. 2012, 125, E2–E8. [Google Scholar] [CrossRef]
- Bee, S.-L.; Abdullah, M.A.A.; Bee, S.-T.; Sin, L.T.; Rahmat, A.R. Polymer nanocomposites based on silylated-montmorillonite: A review. Prog. Polym. Sci. 2018, 85, 57–82. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Niu, Y.Q.; Liu, J.H.; Chen, X.X.; Li, C.S.; Gates, W.P.; Zhou, C.H. Functional Montmorillonite/Polymer Coatings. Clays Clay Miner. 2022, 70, 209–232. [Google Scholar] [CrossRef]
- Bhattacharya, M. Polymer Nanocomposites—A Comparison between Carbon Nanotubes, Graphene, and Clay as Nanofillers. Materials 2016, 9, 262. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.T.; Baird, D.G. Preparation of polymer–clay nanocomposites and their properties. Adv. Polym. Technol. 2006, 25, 270–285. [Google Scholar] [CrossRef]
- Shabanian, M.; Mirzakhanian, Z.; Basaki, N.; Khonakdar, H.A.; Faghihi, K.; Hoshyargar, F.; Wagenknecht, U. Flammability and thermal properties of novel semi aromatic polyamide/organoclay nanocomposite. Thermochim. Acta 2014, 585, 63–70. [Google Scholar] [CrossRef]
- Bilgiç, C.; Karakehya, N. Inverse gas chromatographic characterization of polystyrene and organo-montmorillonite/polystyrene nanocomposites. J. Adhes. Sci. Technol. 2016, 30, 1945–1956. [Google Scholar] [CrossRef]
- Liu, G.; Wu, S.; van de Ven, M.; Yu, J.; Molenaar, A. Influence of sodium and organo-montmorillonites on the properties of bitumen. Appl. Clay Sci. 2010, 49, 69–73. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Das, T.K.; Ganguly, S.; Nath, K.; Paul, S.; Ganguly, D.; Das, N.C. Silane functionalization of sodium montmorillonite and halloysite (HNT) nanoclays by ‘grafting to’ method to improve physico-mechanical and barrier properties of LLDPE/clay nanocomposites. Polym. Bull. 2022, 80, 4307–4335. [Google Scholar] [CrossRef]
- Gómez, M.; Palza, H.; Quijada, R. Influence of Organically-Modified Montmorillonite and Synthesized Layered Silica Nanoparticles on the Properties of Polypropylene and Polyamide-6 Nanocomposites. Polymers 2016, 8, 386. [Google Scholar] [CrossRef]
- Song, J.; Zhang, S.; Li, G.; Du, Q.; Yang, F. Preparation of montmorillonite modified biochar with various temperatures and their mechanism for Zn ion removal. J. Hazard. Mater. 2019, 391, 121692. [Google Scholar] [CrossRef] [PubMed]
- Marry, V.; Turq, P. Microscopic Simulations of Interlayer Structure and Dynamics in Bihydrated Heteroionic Montmorillonites. J. Phys. Chem. B 2003, 107, 1832–1839. [Google Scholar] [CrossRef]
- Na, P.; Zhang, F.; Li, Y. Molecular Dynamics Simulation of Na-montmorillonite and Na/Mg-montmorillonite Hydrates. Acta Physico-Chim. Sin. 2006, 22, 1137–1142. [Google Scholar] [CrossRef]
- Wu, L.; Liao, L.; Lv, G. Influence of interlayer cations on organic intercalation of montmorillonite. J. Colloid Interface Sci. 2015, 454, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.; Casewit, C.; Colwell, K.; Goddard, W.; Skiff, W. Uff, a Full Periodic-Table Force-Field for Molecular Mechanics and Molecular-Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Atomistic modeling of mechanical properties of polymeric glasses. Macromolecules 1986, 19, 139–154. [Google Scholar] [CrossRef]
- Charati, S.G.; Stern, S.A. Diffusion of Gases in Silicone Polymers: Molecular Dynamics Simulations. Macromolecules 1998, 31, 5529–5535. [Google Scholar] [CrossRef]
- Fried, J.; Sadat-Akhavi, M.; Mark, J. Molecular simulation of gas permeability: Poly(2,6-dimethyl-1,4-phenylene oxide). J. Membr. Sci. 1998, 149, 115–126. [Google Scholar] [CrossRef]
- Hu, H.; Li, X.; Fang, Z.; Wei, N.; Li, Q. Small-molecule gas sorption and diffusion in coal: Molecular simulation. Energy 2010, 35, 2939–2944. [Google Scholar] [CrossRef]
- Yu, S.; Fangkai, Q.; Junhong, Y. Diffusion of guest molecules in coal: Insights from simulation. Fuel 2022, 323, 124295. [Google Scholar] [CrossRef]
- Yang, Y.; Nair, A.K.N.; Sun, S. Adsorption and Diffusion of Methane and Carbon Dioxide in Amorphous Regions of Cross-Linked Polyethylene: A Molecular Simulation Study. Ind. Eng. Chem. Res. 2019, 58, 8426–8436. [Google Scholar] [CrossRef]
- Klopffer, M.H.; Flaconneche, B. Transport Properdines of Gases in Polymers: Bibliographic Review. Oil Gas Sci. Technol.–Rev. d’IFP Energies Nouv. 2001, 56, 223–244. [Google Scholar] [CrossRef]
- Naito, Y.; Kamiya, Y.; Terada, K.; Mizoguchi, K.; Wang, J. Pressure dependence of gas permeability in a rubbery polymer. J. Appl. Polym. Sci. 1996, 61, 945–950. [Google Scholar] [CrossRef]
- Kanesugi, H.; Ohyama, K.; Fujiwara, H.; Nishimura, S. High-pressure hydrogen permeability model for crystalline polymers. Int. J. Hydrogen Energy 2023, 48, 723–739. [Google Scholar] [CrossRef]
- Cui, L.; Yeh, J.-T.; Wang, K.; Tsai, F.-C.; Fu, Q. Relation of free volume and barrier properties in the miscible blends of poly(vinyl alcohol) and nylon 6-clay nanocomposites film. J. Membr. Sci. 2009, 327, 226–233. [Google Scholar] [CrossRef]
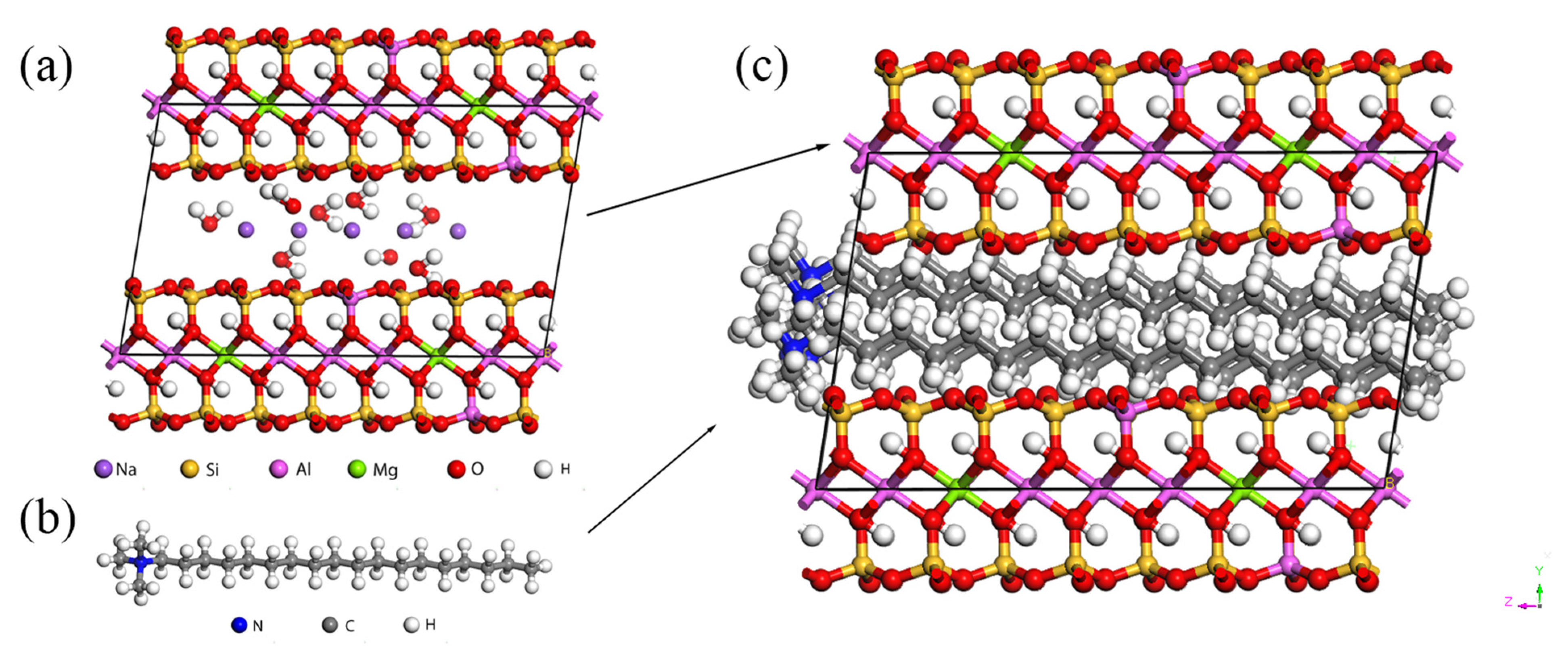

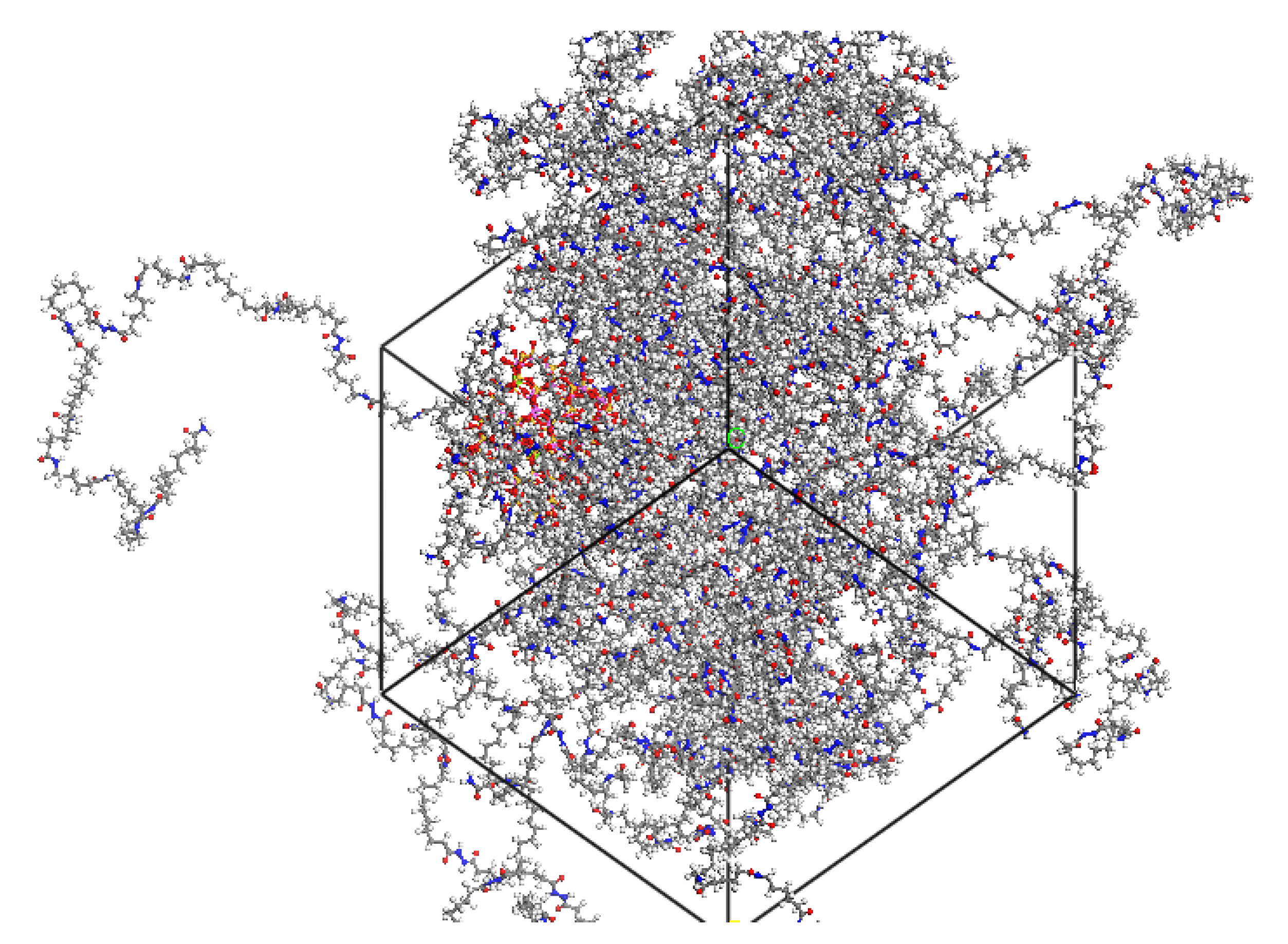
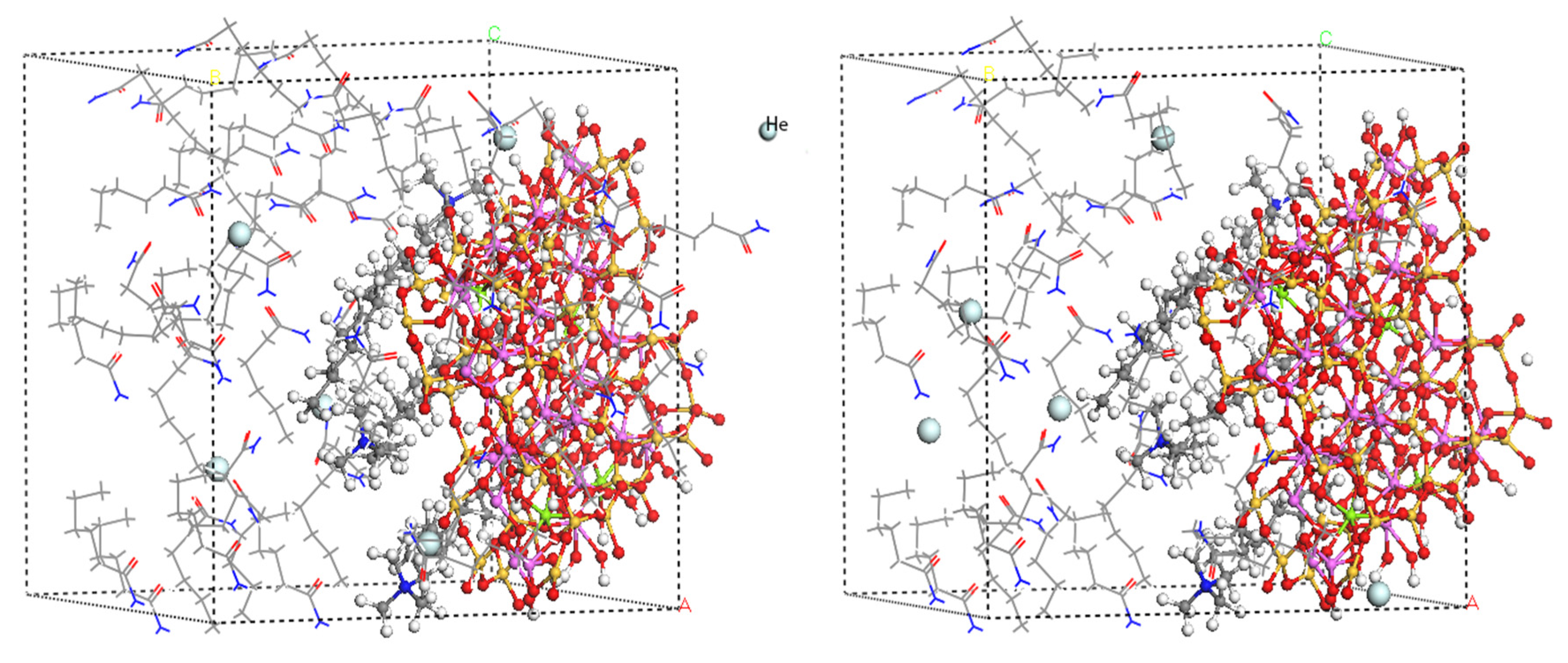
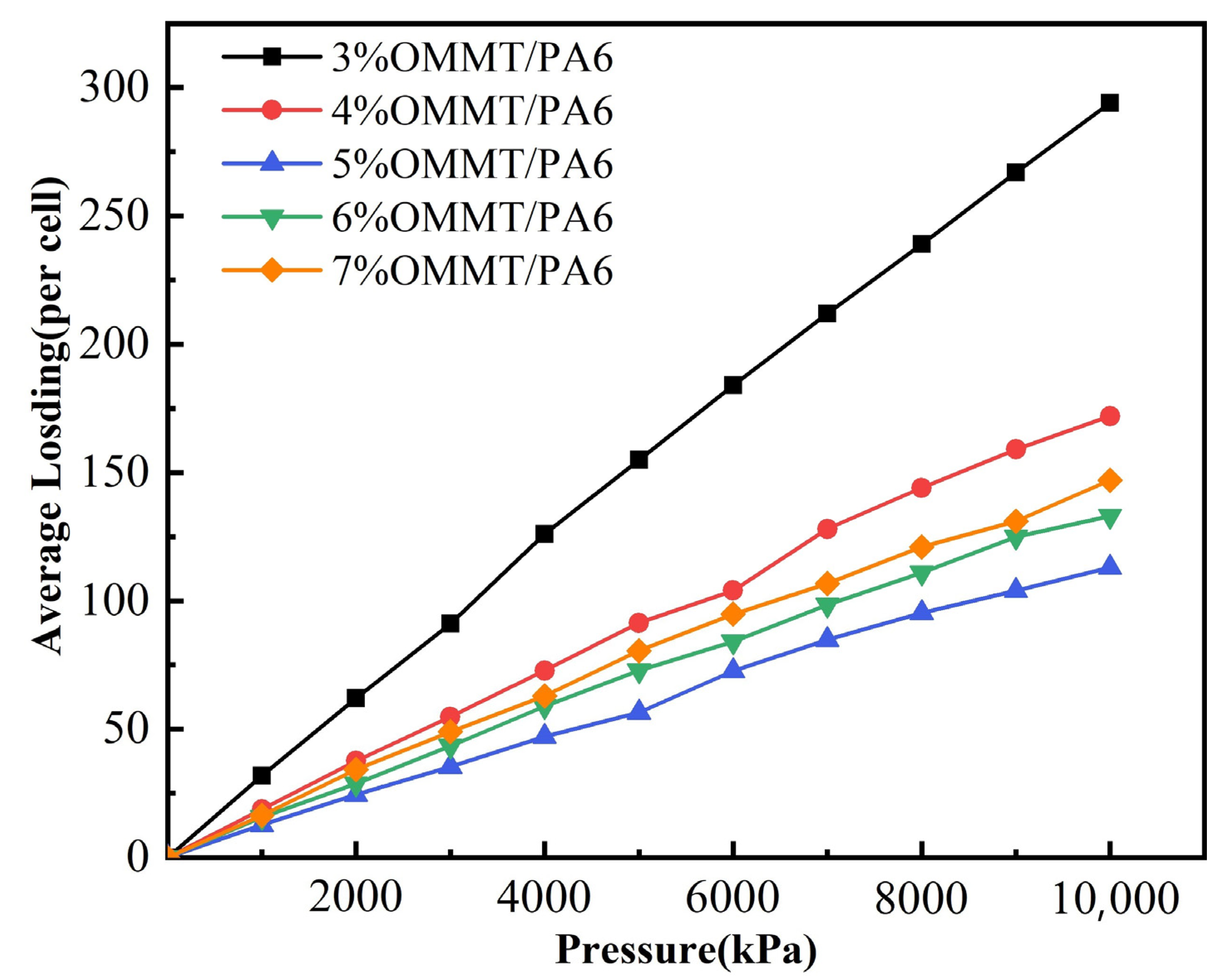

| Atom | X/Å | Y/Å | Z/Å | |||
|---|---|---|---|---|---|---|
| Al | 0.000 | 3.020 | 12.500 | 3.000 | 0.000 | 0.000/13.192 |
| Si | 0.472 | 1.510 | 9.580 | 1.200 | 1.840 | 13.192 |
| O(a) | 0.122 | 0.000 | 9.040 | −1.000 | 3.166 | 0.653 |
| O(o) | −0.686 | 2.615 | 9.240 | −1.424 | 3.166 | 0.653 |
| O(t) | 0.772 | 1.510 | 11.200 | −0.800 | 3.166 | 0.653 |
| O(OH) | 0.808 | 4.530 | 11.250 | −0.848 | 3.166 | 0.653 |
| H(OH) | −0.103 | 4.530 | 10.812 | 0.424 | 0.000 | 0.000 |
| Na+ | 0.000 | 4.530 | 6.250 | 1.000 | 2.586 | 0.418 |
| Material System | Solubility | Diffusion Coefficient | Permeation Coefficient |
|---|---|---|---|
| 3% OMMT/PA6 | |||
| 4% OMMT/PA6 | |||
| 5% OMMT/PA6 | |||
| 6% OMMT/PA6 | |||
| 7% OMMT/PA6 |
| Material System | Solubility | Diffusion Coefficient | Permeation Coefficient |
|---|---|---|---|
| 3% OMMT/PA6 | |||
| 4% OMMT/PA6 | |||
| 5% OMMT/PA6 | |||
| 6% OMMT/PA6 | |||
| 7% OMMT/PA6 |
| Material System | Solubility | Diffusion Coefficient | Permeation Coefficient |
|---|---|---|---|
| 0.1 MPa | |||
| 41.6 MPa | |||
| 52 MPa | |||
| 60 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Zhang, J.; Yang, Z.; Zhao, J. Molecular Dynamics Simulation of Helium Barrier Performance of Modified Polyamide 6 Lining of IV Hydrogen Storage Tank with Montmorillonite. Molecules 2023, 28, 3333. https://doi.org/10.3390/molecules28083333
Wu P, Zhang J, Yang Z, Zhao J. Molecular Dynamics Simulation of Helium Barrier Performance of Modified Polyamide 6 Lining of IV Hydrogen Storage Tank with Montmorillonite. Molecules. 2023; 28(8):3333. https://doi.org/10.3390/molecules28083333
Chicago/Turabian StyleWu, Ping, Jiaming Zhang, Zhenhan Yang, and Jianping Zhao. 2023. "Molecular Dynamics Simulation of Helium Barrier Performance of Modified Polyamide 6 Lining of IV Hydrogen Storage Tank with Montmorillonite" Molecules 28, no. 8: 3333. https://doi.org/10.3390/molecules28083333
APA StyleWu, P., Zhang, J., Yang, Z., & Zhao, J. (2023). Molecular Dynamics Simulation of Helium Barrier Performance of Modified Polyamide 6 Lining of IV Hydrogen Storage Tank with Montmorillonite. Molecules, 28(8), 3333. https://doi.org/10.3390/molecules28083333





