Benchmarking First-Principles Reaction Equilibrium Composition Prediction
Abstract
:1. Introduction
2. Results
2.1. Errors for Constant Equilibrium Compositions
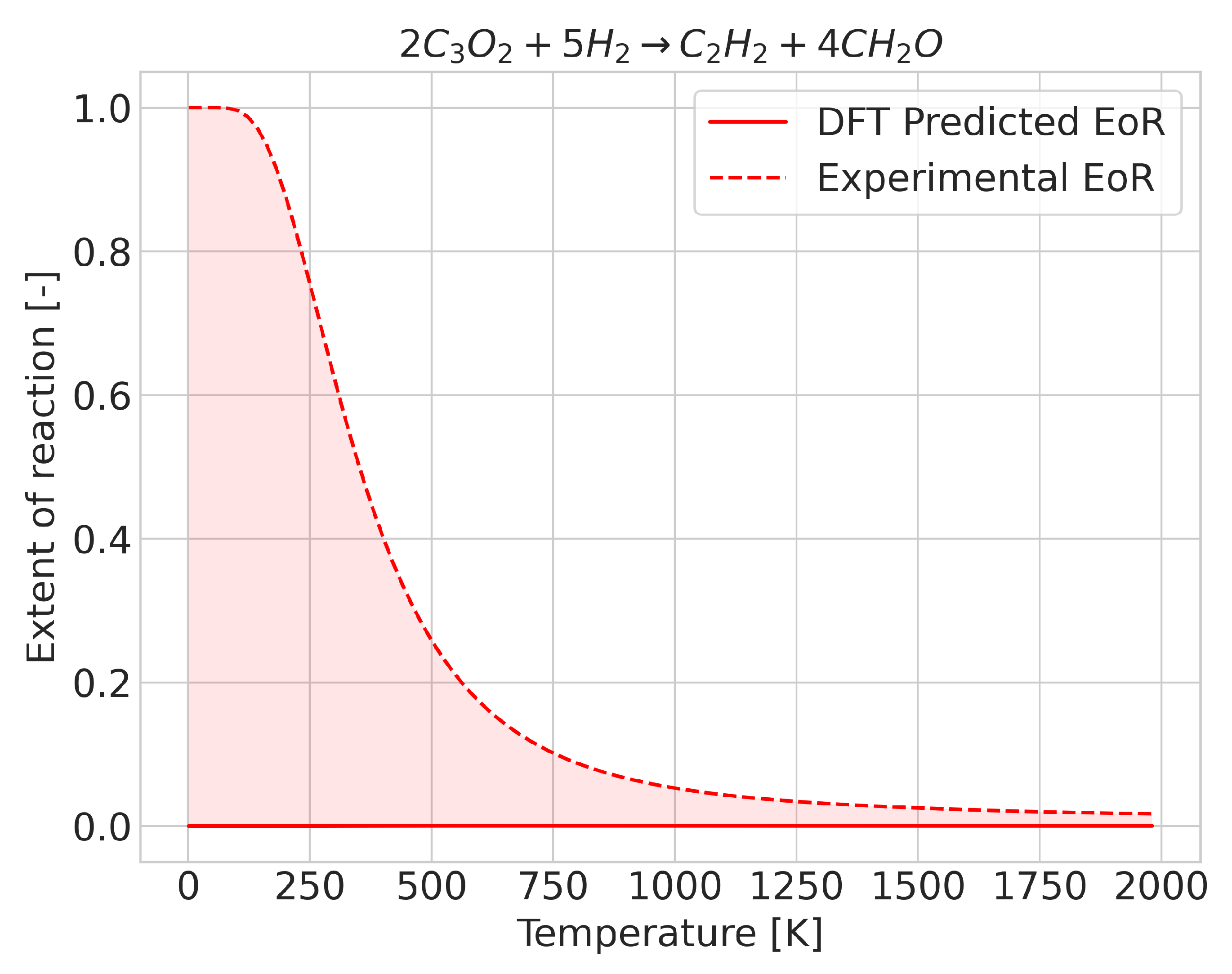
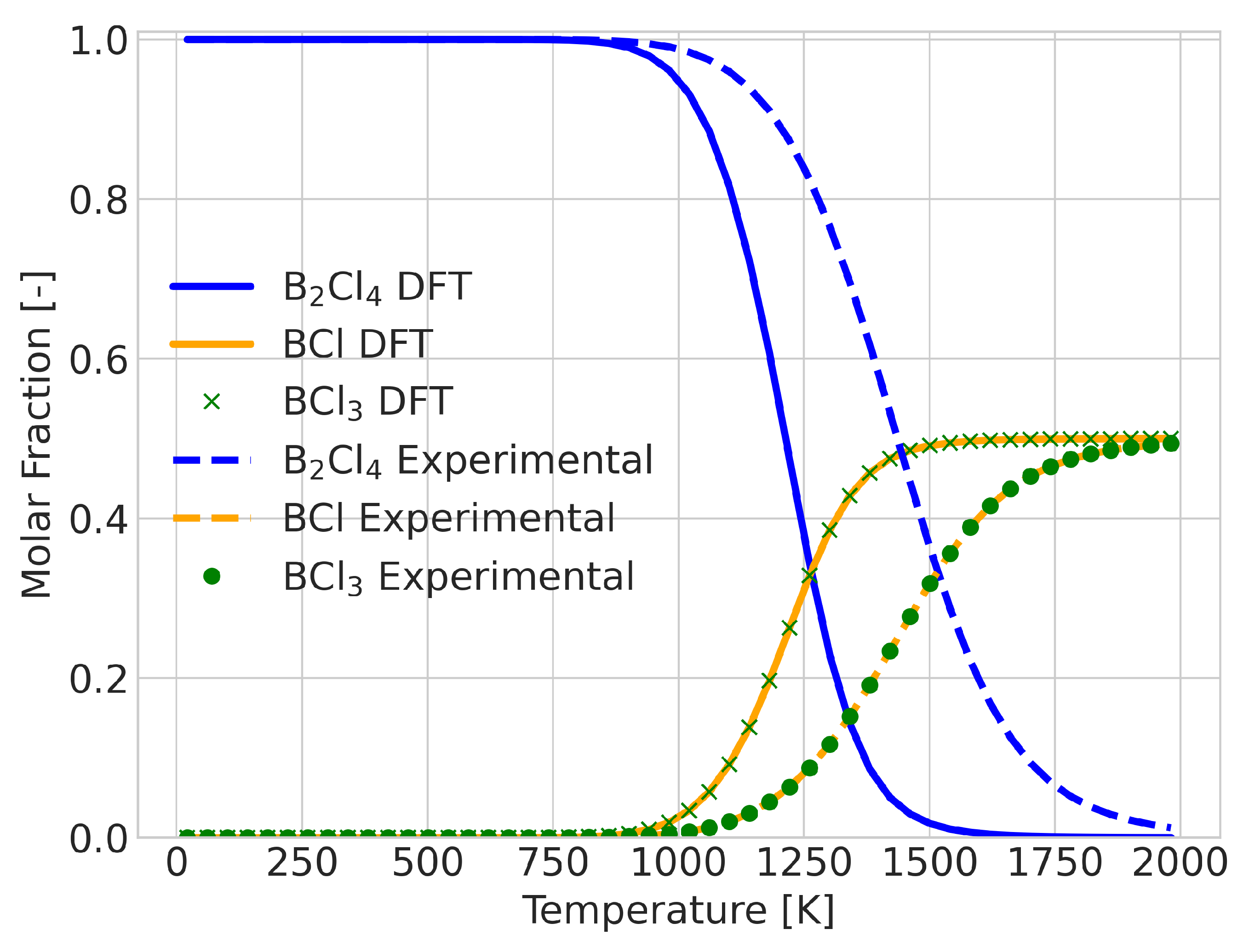
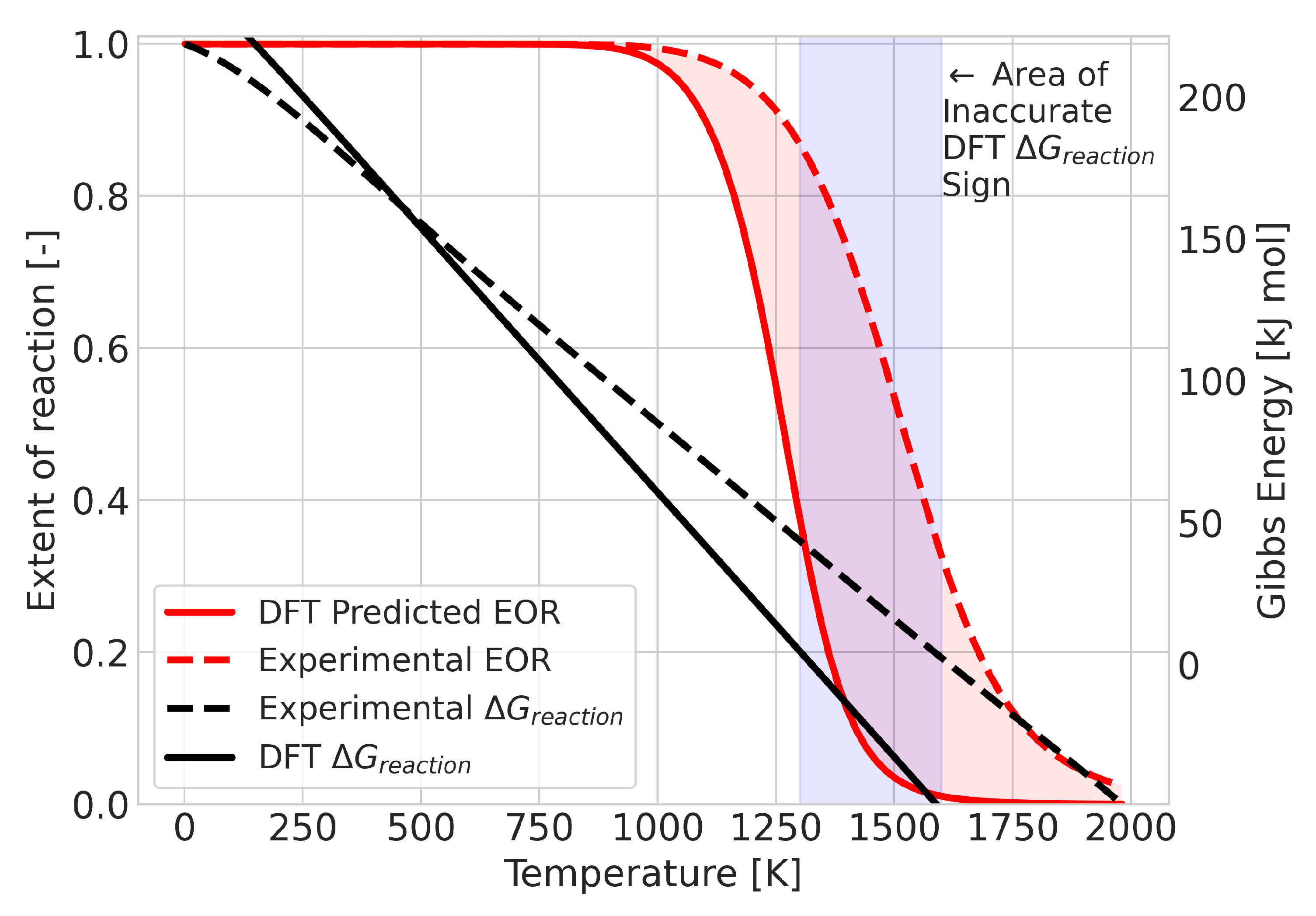
2.2. Errors for Temperature-Dependent Equilibrium Compositions
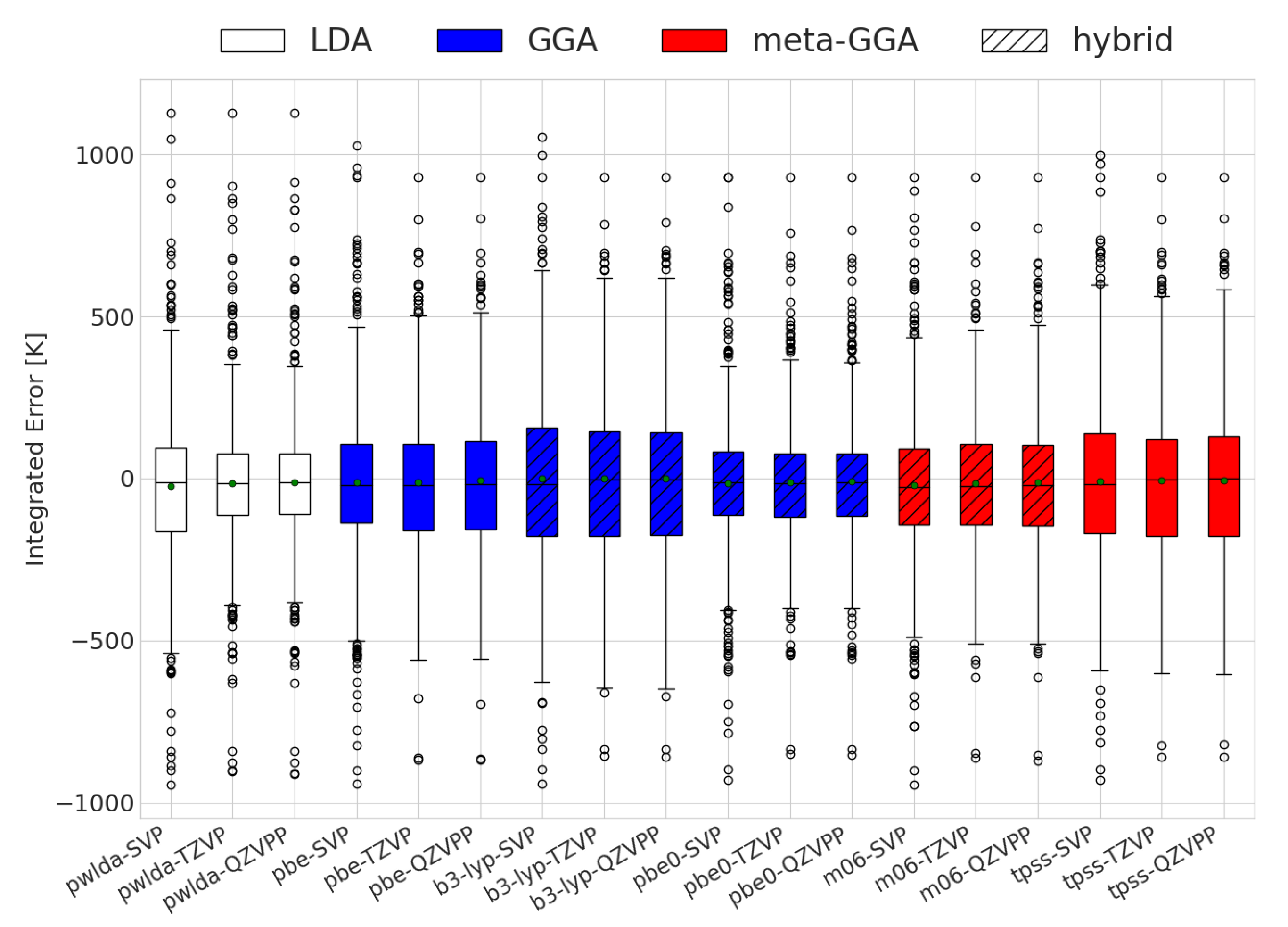
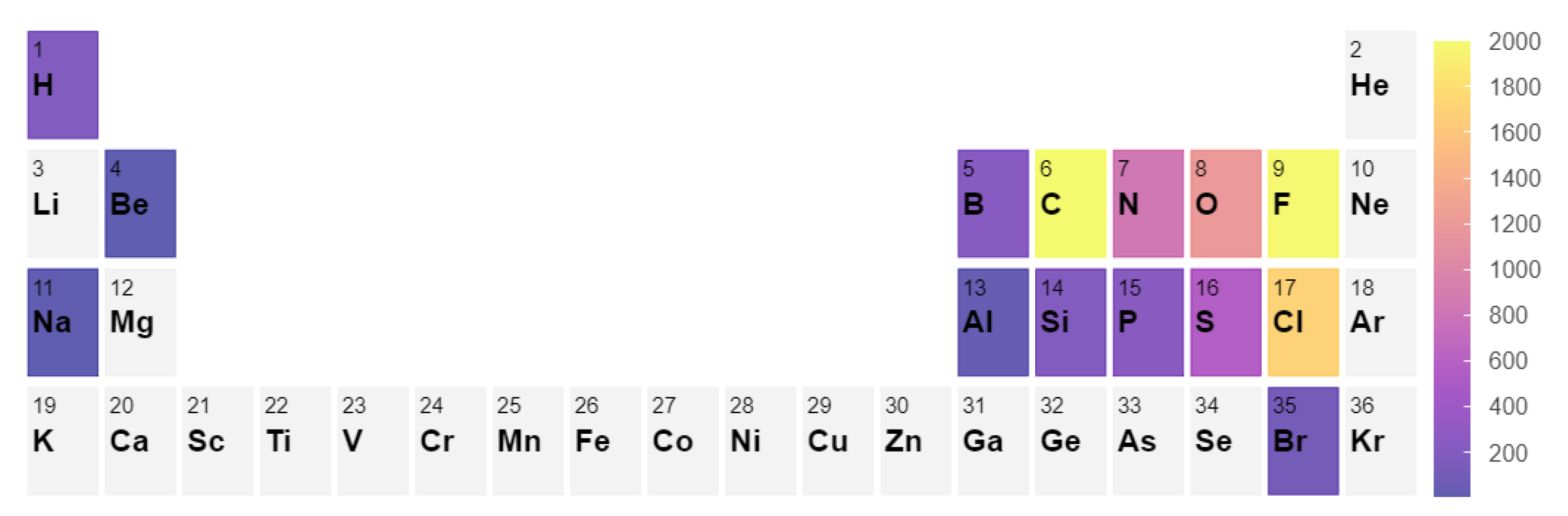
2.3. Error Analysis
- Errors made on , whose dominant contribution comes from the DFT ground state energy.
- Errors in the transition temperature for the Gibbs free energy, which mostly come from harmonic approximation inaccuracies.
3. Methods
3.1. Molecule Set Collection and Reaction Generation
3.2. Molecular Gibbs Free Energy Calculation
3.3. Calculation of the Equilibrium Composition
3.4. Error Calculation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| CVD | Chemical Vapor Deposition |
| DFT | Density Functional Theory |
| EoR | Extent of Reaction |
| ASALD | Area Selective Atomic Layer Deposition |
| ALD | Atomic Layer Deposition |
References
- Jocz, J.N.; Medford, A.J.; Sievers, C. Thermodynamic Limitations of the Catalyst Design Space for Methanol Production from Methane. ChemCatChem 2019, 11, 593–600. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, Y.; Ponge, D.; Zaefferer, S.; Jägle, E.A.; Gault, B.; Rollett, A.D.; Raabe, D. Thermodynamics-guided alloy and process design for additive manufacturing. Nat. Commun. 2022, 13, 4361. [Google Scholar] [CrossRef] [PubMed]
- Chase, M.W. NIST-JANAF Thermochemical Tables; American Institute of Physics: College Park, MD, USA, 1998. [Google Scholar]
- Mackus, A.J.; Merkx, M.J.; Kessels, W.M. From the Bottom-Up: Toward Area-Selective Atomic Layer Deposition with High Selectivity. Chem. Mater. 2019, 31, 2–12. [Google Scholar] [CrossRef]
- Grillo, F.; Soethoudt, J.; Marques, E.A.; de Martín, L.; van Dongen, K.; van Ommen, J.R.; Delabie, A. Area-selective deposition of ruthenium by area-dependent surface diffusion. Chem. Mater. 2020, 32, 9560–9572. [Google Scholar] [CrossRef]
- Shareef, I.A.; Rubloff, G.W.; Anderle, M.; Gill, W.N.; Cotte, J.; Kim, D.H. Subatmospheric chemical vapor deposition ozone/TEOS process for SiO2 trench filling. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 1995, 13, 1888–1892. [Google Scholar] [CrossRef]
- Mehta, A.N.; Zhang, H.; Dabral, A.; Richard, O.; Favia, P.; Bender, H.; Delabie, A.; Caymax, M.; Houssa, M.; Pourtois, G.; et al. Structural characterization of SnS crystals formed by chemical vapour deposition. J. Microsc. 2017, 268, 276–287. [Google Scholar] [CrossRef]
- Powell, C.F.; Oxley, J.H.; Blocher, J.M.; Klerer, J. Vapor Deposition. J. Electrochem. Soc. 1966, 113, 266C. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Fleszar, A.; Gonze, X. First-principles thermodynamical properties of semiconductors. Phys. Rev. Lett. 1990, 64, 2961. [Google Scholar] [CrossRef]
- Palafox, M.A. DFT computations on vibrational spectra: Scaling procedures to improve the wavenumbers. Phys. Sci. Rev. 2018, 3, 20170184. [Google Scholar] [CrossRef]
- Fromsejer, R.; Maribo-Mogensen, B.; Kontogeorgis, G.M.; Liang, X. Evaluating the harmonic approximation for the prediction of thermodynamic formation properties of solids. Comput. Mater. Sci. 2023, 223, 112152. [Google Scholar] [CrossRef]
- McQuarrie, D. Statistical Mechanics; University Science Books: Sausalito, CA, USA, 2000. [Google Scholar]
- Sandler, S. An Introduction to Applied Statistical Thermodynamics; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Becke, A.D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140, 18A301. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Corso, A.D.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, 1394. [Google Scholar] [CrossRef] [PubMed]
- Van Setten, M.J.; Caruso, F.; Sharifzadeh, S.; Ren, X.; Scheffler, M.; Liu, F.; Lischner, J.; Lin, L.; Deslippe, J.R.; Louie, S.G.; et al. GW100: Benchmarking G0W0 for Molecular Systems. J. Chem. Theory Comput. 2015, 11, 5665–5687. [Google Scholar] [CrossRef]
- Dilena, G.; Pistillo, S.; Bodo, E. About the Formation of NH2OH + from Gas Phase Reactions under Astrochemical Conditions. Molecules 2023, 28, 2932. [Google Scholar] [CrossRef] [PubMed]
- Antol, I.; Glasovac, Z.; Margetić, D. Mechanistic DFT Study of 1,3-Dipolar Cycloadditions of Azides with Guanidine. Molecules 2023, 28, 2342. [Google Scholar] [CrossRef]
- Al-Hazmy, S.M.; Zouaghi, M.O.; Amri, N.; Arfaoui, Y.; Alhagri, I.A.; Hamdi, N. DFT Study of Regio- and Stereoselective 13DC Reaction between Diazopropane and Substituted Chalcone Derivatives: Molecular Docking of Novel Pyrazole Derivatives as Anti-Alzheimer’s Agents. Molecules 2023, 28, 1899. [Google Scholar] [CrossRef]
- Laref, S.; Wang, B.; Gao, X.; Gojobori, T. Computational Studies of Auto-Active van der Waals Interaction Molecules on Ultra-Thin Black-Phosphorus Film. Molecules 2023, 28, 681. [Google Scholar] [CrossRef]
- Widjaja, H.; Miran, H.A.; Altarawneh, M.; Oluwoye, I.; Lim, H.N.; Huang, N.M.; Jiang, Z.T.; Dlugogorski, B.Z. DFT + U and ab initio atomistic thermodynamics approache for mixed transitional metallic oxides: A case study of CoCu2O3 surface terminations. Mater. Chem. Phys. 2017, 201, 241–250. [Google Scholar] [CrossRef]
- Herrera, M.; Serra, R.M.; D’Amico, I. DFT-inspired methods for quantum thermodynamics. Sci. Rep. 2017, 7, 4655. [Google Scholar] [CrossRef] [PubMed]
- Dianat, A.; Seriani, N.; Bobeth, M.; Pompe, W.; Ciacchi, L.C. DFT study of the thermodynamic stability of Pd-Pt bulk oxide phases. J. Phys. Chem. C 2008, 112, 13623–13628. [Google Scholar] [CrossRef]
- Cervantes, J.M.; Pilo, J.; Rosas-Huerta, J.L.; Antonio, J.E.; Muñoz, H.; Oviedo-Roa, R.; Carvajal, E. DFT Electronic Properties and Synthesis Thermodynamics of LixLa1-xTiO3 Electrolytes for Li-Ion Batteries. J. Electrochem. Soc. 2021, 168, 080516. [Google Scholar] [CrossRef]
- Wei, M.; Marrakchi, F.; Yuan, C.; Cheng, X.; Jiang, D.; Zafar, F.F.; Fu, Y.; Wang, S. Adsorption modeling, thermodynamics, and DFT simulation of tetracycline onto mesoporous and high-surface-area NaOH-activated macroalgae carbon. J. Hazard. Mater. 2022, 425, 127887. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, B.W.; Peng, G.; Mavrikakis, M. Density functional theory study of thermodynamic and kinetic isotope effects of H2/D2 dissociative adsorption on transition metals. Catal. Sci. Technol. 2018, 8, 3321–3335. [Google Scholar] [CrossRef]
- van Setten, M.J.; Lohstroh, W.; Fichtner, M. A new phase in the decomposition of Mg(BH4)2: First-principles simulated annealing. J. Mater. Chem. 2009, 19, 7081–7087. [Google Scholar] [CrossRef]
- van Setten, M.; Fichtner, M. On the enthalpy of formation of aluminum diboride, AlB2. J. Alloys Compd. 2009, 477, L11–L12. [Google Scholar] [CrossRef]
- Mole, S.J.; Zhou, X.; Liu, R. Density Functional Theory (DFT) Study of Enthalpy of Formation. 1. Consistency of DFT Energies and Atom Equivalents for Converting DFT Energies into Enthalpies of Formation. J. Phys. Chem. 1996, 100, 14665–14671. [Google Scholar] [CrossRef]
- Huenerbein, R.; Schirmer, B.; Moellmann, J.; Grimme, S. Effects of London dispersion on the isomerization reactions of large organic molecules: A density functional benchmark study. Phys. Chem. Chem. Phys. 2010, 12, 6940–6948. [Google Scholar] [CrossRef]
- Minenkov, Y.; Wang, H.; Wang, Z.; Sarathy, S.M.; Cavallo, L. Heats of Formation of Medium-Sized Organic Compounds from Contemporary Electronic Structure Methods. J. Chem. Theory Comput. 2017, 13, 3537–3560. [Google Scholar] [CrossRef]
- Korth, M.; Grimme, S. Mindless DFT benchmarking. J. Chem. Theory Comput. 2009, 5, 993–1003. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Tang, Z.X.; Zhang, X.Z.; Li, X.H. DFT Study of the C-Cl Bond Dissociation Enthalpies and Electronic Structure of Substituted Chlorobenzene Compounds. J. Struct. Chem. 2009, 50, 34–40. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Moran, A.; Pieniazek, S.N.; Houk, K.N. Accurate reaction enthalpies and sources of error in DFT Thermochemistry for aldol, mannich, and a-aminoxylation reactions. J. Phys. Chem. A 2009, 113, 10376–10384. [Google Scholar] [CrossRef]
- Ghahremanpour, M.M.; Van Maaren, P.J.; Ditz, J.C.; Lindh, R.; Van Der Spoel, D. Large-scale calculations of gas phase thermochemistry: Enthalpy of formation, standard entropy, and heat capacity. J. Chem. Phys. 2016, 145, 114305. [Google Scholar] [CrossRef]
- Sirirak, J.; Lawan, N.; der Kamp, M.W.V.; Harvey, J.N.; Mulholland, A.J. Benchmarking quantum mechanical methods for calculating reaction energies of reactions catalyzed by enzymes. PeerJ Phys. Chem. 2020, 2, e8. [Google Scholar] [CrossRef]
- Kumar, A.; Arantes, P.R.; Saha, A.; Palermo, G.; Wong, B.M. GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems. Molecules 2023, 28, 1277. [Google Scholar] [CrossRef] [PubMed]
- Letterman, R.G.; DeYonker, N.J.; Burkey, T.J.; Webster, C.E. Calibrating reaction enthalpies: Use of density functional theory and the correlation consistent composite approach in the design of photochromic materials. J. Phys. Chem. A 2016, 120, 9982–9997. [Google Scholar] [CrossRef] [PubMed]
- Ventura, O.N.; Kieninger, M.; Irving, K. Density Functional Theory: A Useful Tool for the Study of Free Radicals. Adv. Quantum Chem. 1997, 28, 293–309. [Google Scholar] [CrossRef]
- Reinhardt, A.; Cheng, B. Quantum-mechanical exploration of the phase diagram of water. Nat. Commun. 2021, 12, 588. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Hamel, S.; Bethkenhagen, M. Diamond formation from hydrocarbon mixtures in planets. Nat. Commun. 2022, 14, 1104. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.D., III. NIST Computational Chemistry Comparison and Benchmark Database. Available online: https://webbook.nist.gov/ (accessed on 1 July 2019).
- Sharma, D.; Kumar, J.; Vajpayee, A.; Kumar, R.; Ahluwalia, P.K.; Awana, V.P. Comparative experimental and density functional theory (DFT) study of the physical properties of MgB 2 and AlB 2. J. Supercond. Nov. Magn. 2011, 24, 1925–1931. [Google Scholar] [CrossRef]
- Rosen, A. Periodic Trend Plotter. 2018. Available online: https://github.com/arosen93/ptable_trends (accessed on 1 July 2019).
- Ahlrichs, R.; Bar, M.; Haser, M.; Horn, H.; Kolmel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Weigend, F.; Häser, M.; Patzelt, H.; Ahlrichs, R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143–152. [Google Scholar] [CrossRef]
- Boese, A.D.; Klopper, W.; Martin, J.M.L. Anharmonic force fields and thermodynamic functions using density functional theory. Mol. Phys. 2005, 103, 863–876. [Google Scholar] [CrossRef]
- Liton, M.A.K.; Nuruzzaman, M.; Helen, S. Calculation of Gas-Phase Gibb’s free Energy Changes of Some Small Molecules with Monte Carlo, DFT (MPW1PW91), Composite (CBS-QB3), Gaussian-n (G1, G2) and Gaussian Modified (G2MP2) Methods. Orient. J. Chem. 2019, 35, 947–957. [Google Scholar] [CrossRef]
- Treutler, O.; Ahlrichs, R. Efficient molecular numerical integration schemes. J. Chem. Phys. 1995, 102, 346–354. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://scipy.org/ (accessed on 1 July 2019).

| Percentage of Correctly Described Reactions (%) | ||||||
|---|---|---|---|---|---|---|
| Functional | ||||||
| Basis Set | PWLDA | PBE | B3-LYP | PBE0 | M06 | TPSS |
| SVP | 88.7 | 92.1 | 92.7 | 92.8 | 92.6 | 91.5 |
| TZVP | 90.5 | 94.2 | 94.7 | 94.8 | 94.4 | 95.1 |
| QZVPP | 90.7 | 94.6 | 94.8 | 95.2 | 94.5 | 94.9 |
| Temperature | Error at 1500 K [Kj mol] | Error at 400 K [Kj mol] | |||||
|---|---|---|---|---|---|---|---|
| Functional | Basis Set | Max | Min | Mean | Max | Min | Mean |
| b3-lyp | QZVPP | 296.21 | −309.67 | 60.94 | 60.19 | −45.08 | 11.07 |
| b3-lyp | SVP | 295.18 | −310.7 | 59.9 | 60.05 | −45.22 | 10.93 |
| b3-lyp | TZVP | 296.26 | −309.62 | 60.98 | 60.20 | −45.07 | 11.08 |
| m06 | QZVPP | 295.07 | −310.81 | 59.8 | 60.03 | −45.25 | 10.91 |
| m06 | SVP | 293.16 | −312.72 | 57.89 | 59.74 | −45.53 | 10.62 |
| m06 | TZVP | 294.96 | −310.91 | 59.69 | 60.01 | −45.27 | 10.89 |
| pbe0 | QZVPP | 295.65 | −310.23 | 60.38 | 60.12 | −45.15 | 11.00 |
| pbe0 | SVP | 294.96 | −310.92 | 59.69 | 60.05 | −45.23 | 10.93 |
| pbe0 | TZVP | 295.72 | −310.16 | 60.44 | 60.14 | −45.14 | 11.02 |
| pbe | QZVPP | 298.07 | −307.81 | 62.79 | 60.52 | −44.76 | 11.40 |
| pbe | SVP | 297.16 | −308.72 | 61.88 | 60.41 | −44.86 | 11.29 |
| pbe | TZVP | 298.2 | −307.68 | 62.92 | 60.54 | −44.73 | 11.42 |
| pwlda | QZVPP | 297.26 | −308.62 | 61.99 | 60.44 | −44.84 | 11.32 |
| pwlda | SVP | 296.12 | −309.76 | 60.84 | 60.28 | −44.99 | 11.16 |
| pwlda | TZVP | 297.43 | −308.45 | 62.15 | 60.47 | −44.80 | 11.35 |
| tpss | QZVPP | 297.7 | −308.18 | 62.42 | 60.46 | −44.81 | 11.34 |
| tpss | SVP | 296.79 | −309.09 | 61.52 | 60.35 | −44.92 | 11.23 |
| tpss | TZVP | 297.78 | −308.1 | 62.5 | 60.48 | −44.79 | 11.36 |
| Percentage of Correctly Described Reactions (%) | ||||||
|---|---|---|---|---|---|---|
| Functional | ||||||
| Basis Set | PWLDA | PBE | B3-LYP | PBE0 | M06 | TPSS |
| SVP | 89.1 | 93.1 | 93.5 | 94.5 | 93.6 | 93.5 |
| TZVP | 91.3 | 95.3 | 95.9 | 96.7 | 95.9 | 96.1 |
| QZVPP | 91.4 | 95.9 | 96.0 | 96.9 | 96.0 | 96.2 |
| Percentage of Correctly Described Reactions (%) | ||||||
|---|---|---|---|---|---|---|
| Functional | ||||||
| Basis Set | PWLDA | PBE | B3-LYP | PBE0 | M06 | TPSS |
| SVP | 65.9 | 71.3 | 72.9 | 71.5 | 71.3 | 74.0 |
| TZVP | 69.2 | 73.6 | 76.2 | 74.4 | 74.4 | 75.0 |
| QZVPP | 69.4 | 73.3 | 76.4 | 74.0 | 74.0 | 74.6 |
| Percentage of Correctly Described Reactions (%) | ||||||
|---|---|---|---|---|---|---|
| Functional | ||||||
| Basis Set | PWLDA | PBE | B3-LYP | PBE0 | M06 | TPSS |
| SVP | 85.5 | 83.5 | 87.0 | 82.4 | 83.7 | 85.7 |
| TZVP | 88.2 | 85.1 | 87.8 | 82.9 | 84.7 | 85.7 |
| QZVPP | 88.2 | 84.7 | 87.6 | 82.9 | 84.5 | 85.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marques, E.A.; De Gendt, S.; Pourtois, G.; van Setten, M.J. Benchmarking First-Principles Reaction Equilibrium Composition Prediction. Molecules 2023, 28, 3649. https://doi.org/10.3390/molecules28093649
Marques EA, De Gendt S, Pourtois G, van Setten MJ. Benchmarking First-Principles Reaction Equilibrium Composition Prediction. Molecules. 2023; 28(9):3649. https://doi.org/10.3390/molecules28093649
Chicago/Turabian StyleMarques, Esteban A., Stefan De Gendt, Geoffrey Pourtois, and Michiel J. van Setten. 2023. "Benchmarking First-Principles Reaction Equilibrium Composition Prediction" Molecules 28, no. 9: 3649. https://doi.org/10.3390/molecules28093649
APA StyleMarques, E. A., De Gendt, S., Pourtois, G., & van Setten, M. J. (2023). Benchmarking First-Principles Reaction Equilibrium Composition Prediction. Molecules, 28(9), 3649. https://doi.org/10.3390/molecules28093649







