First Principle Study on Structural, Electronic, Magnetic, and Optical Properties of Co-Doped Middle Size Silver Clusters
Abstract
:1. Introduction
2. Model and Computational Methods
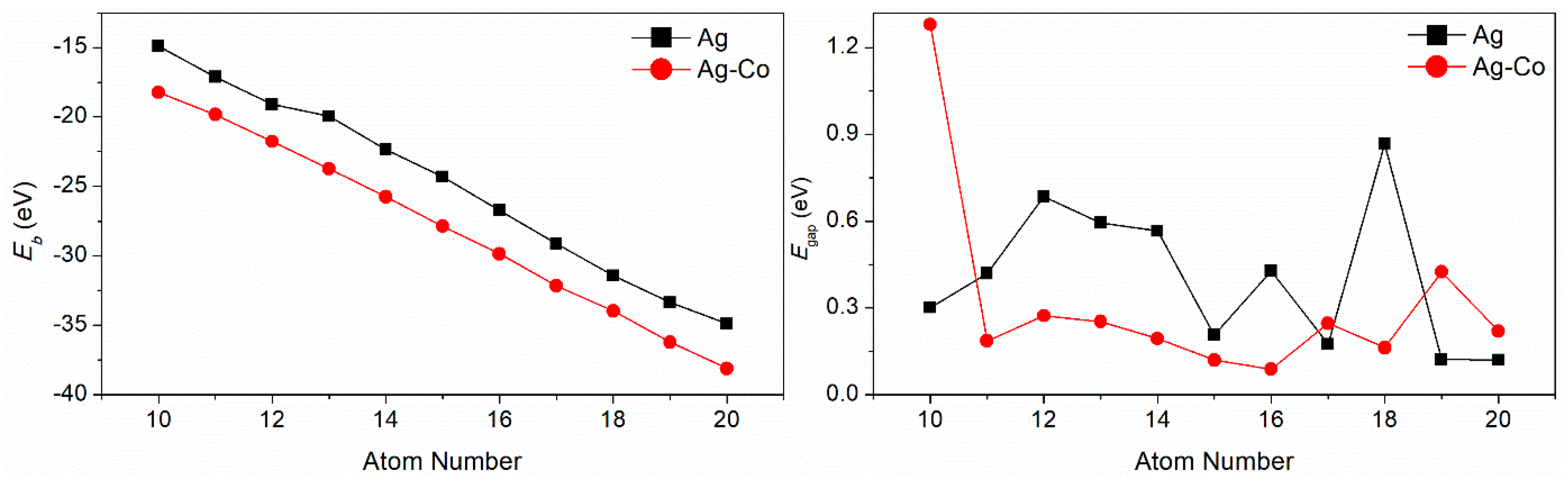
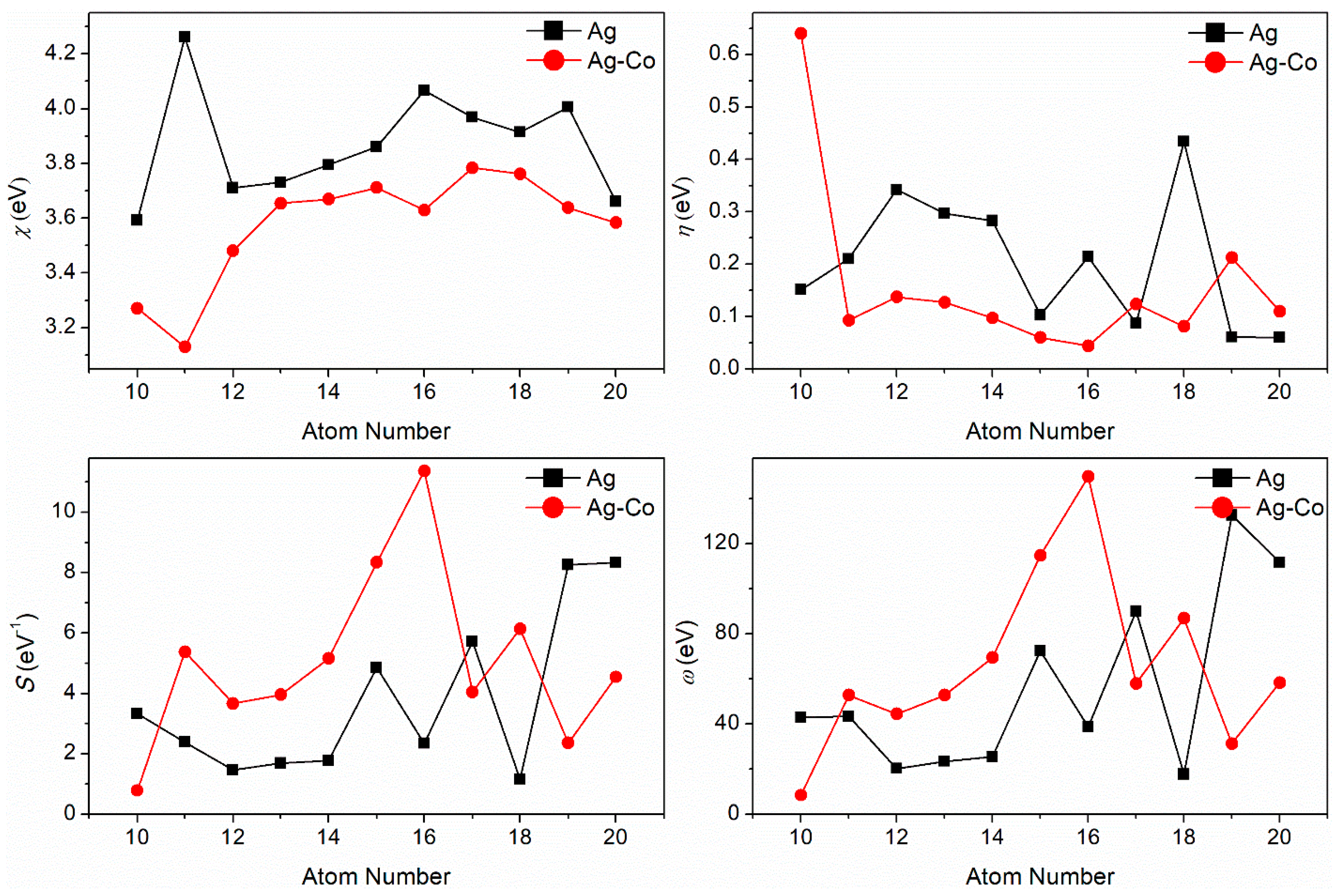
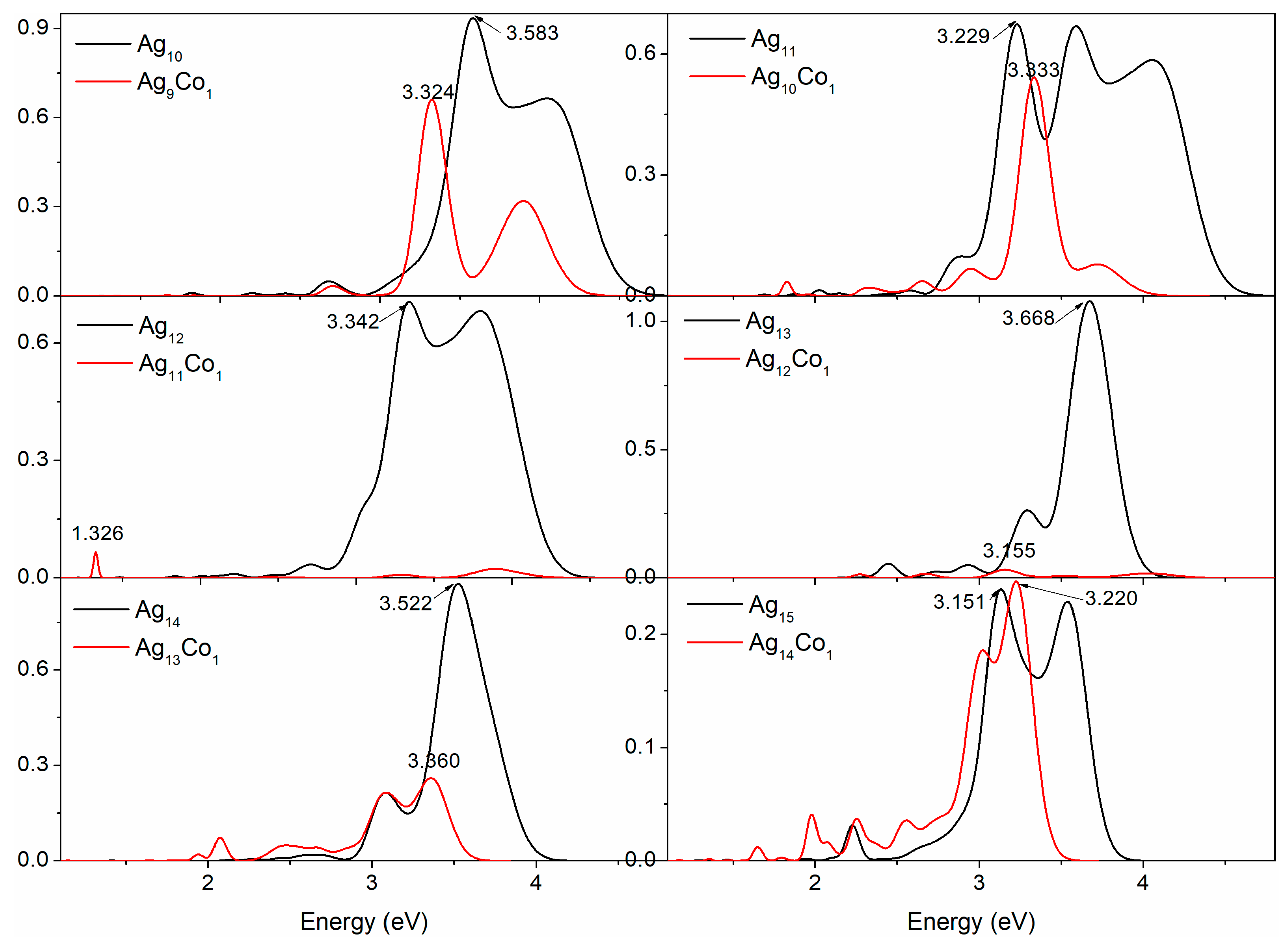
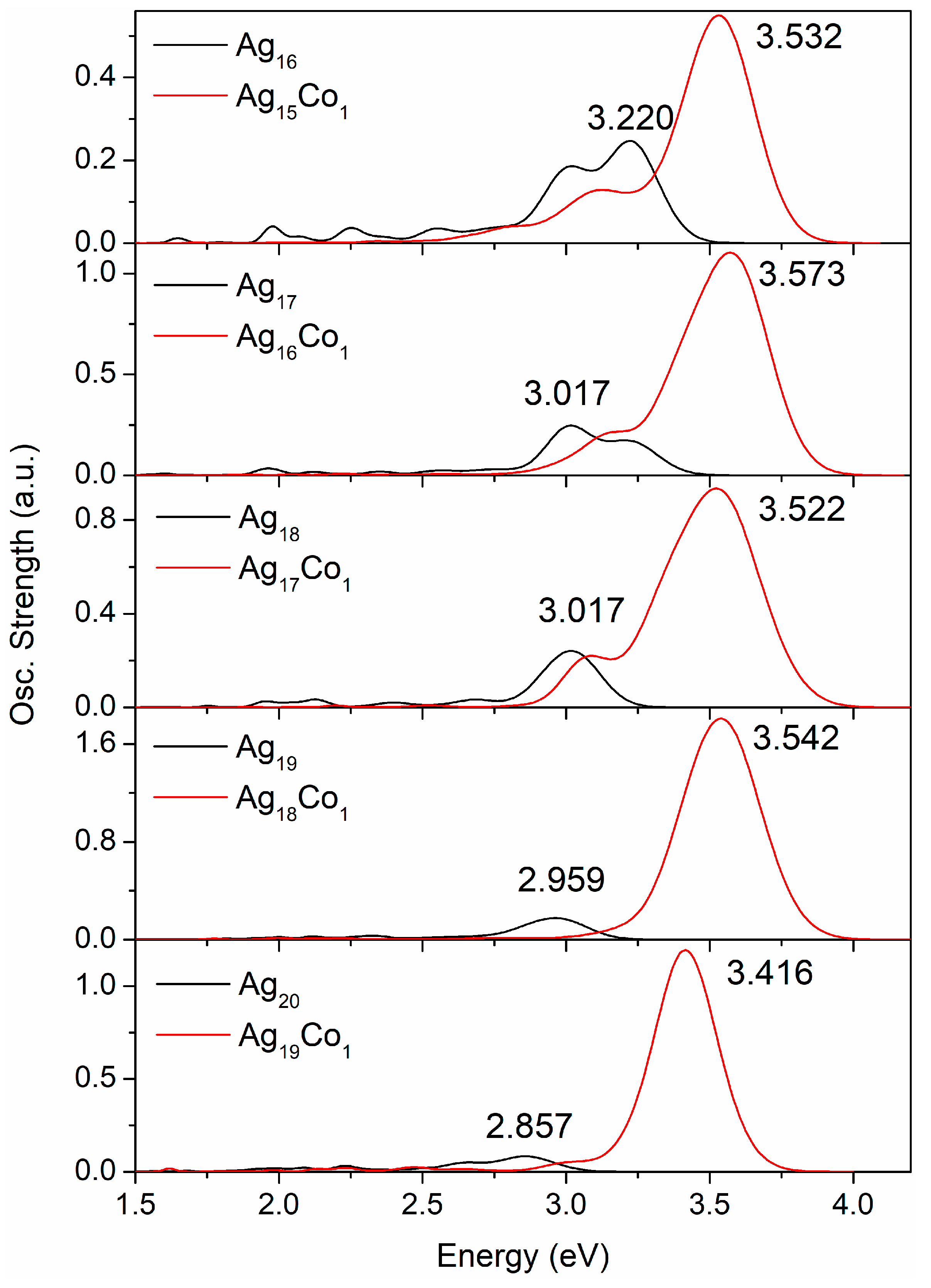
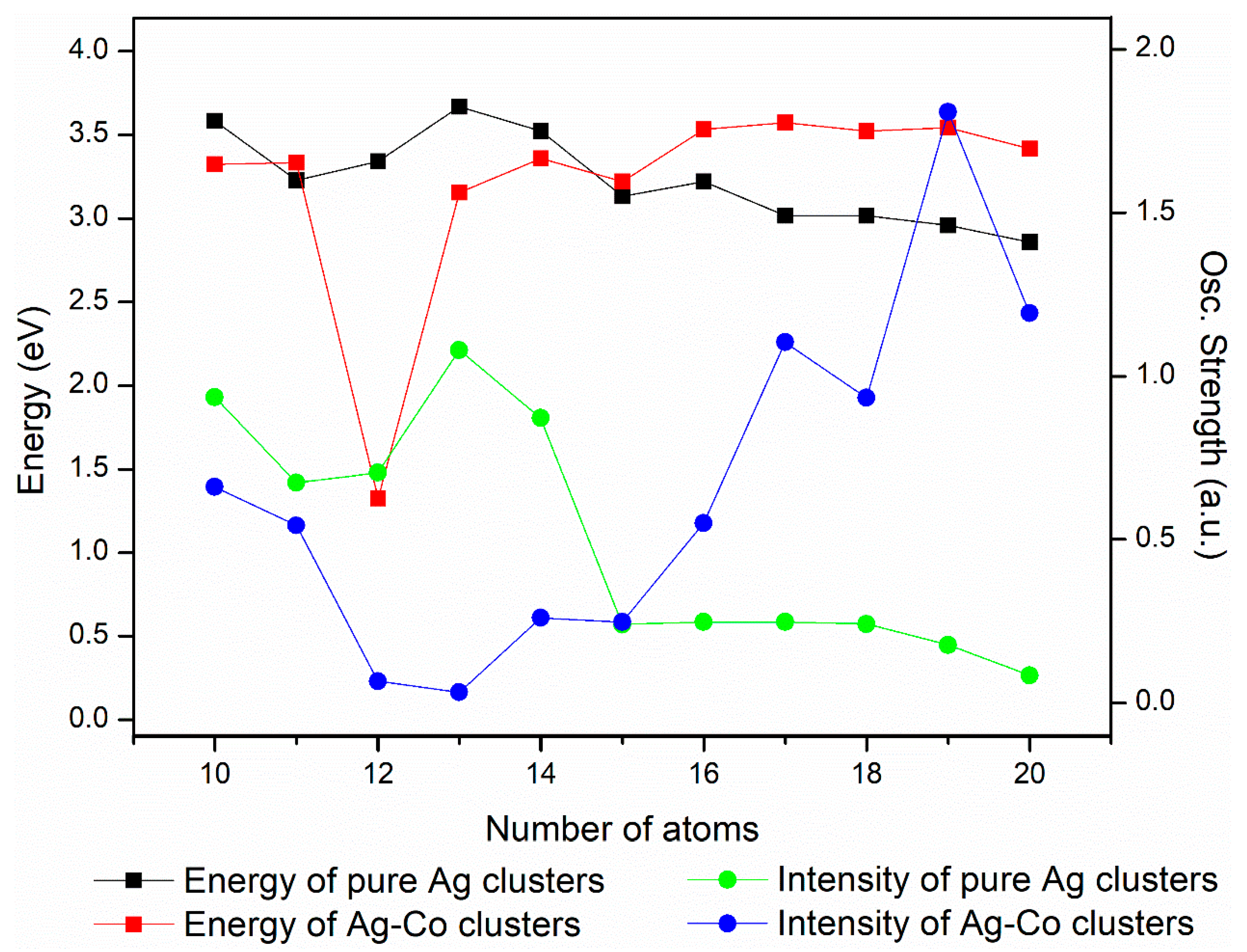
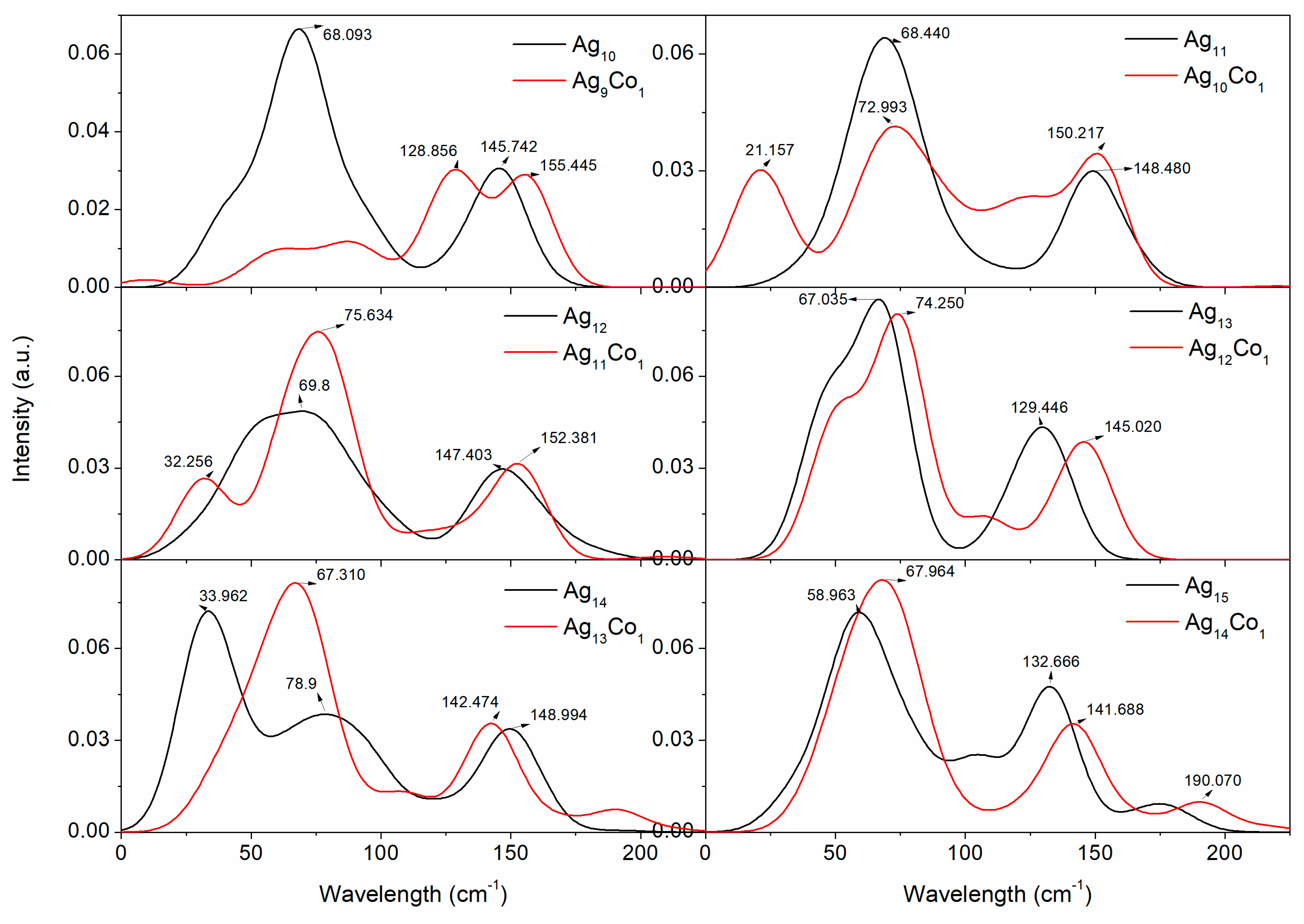
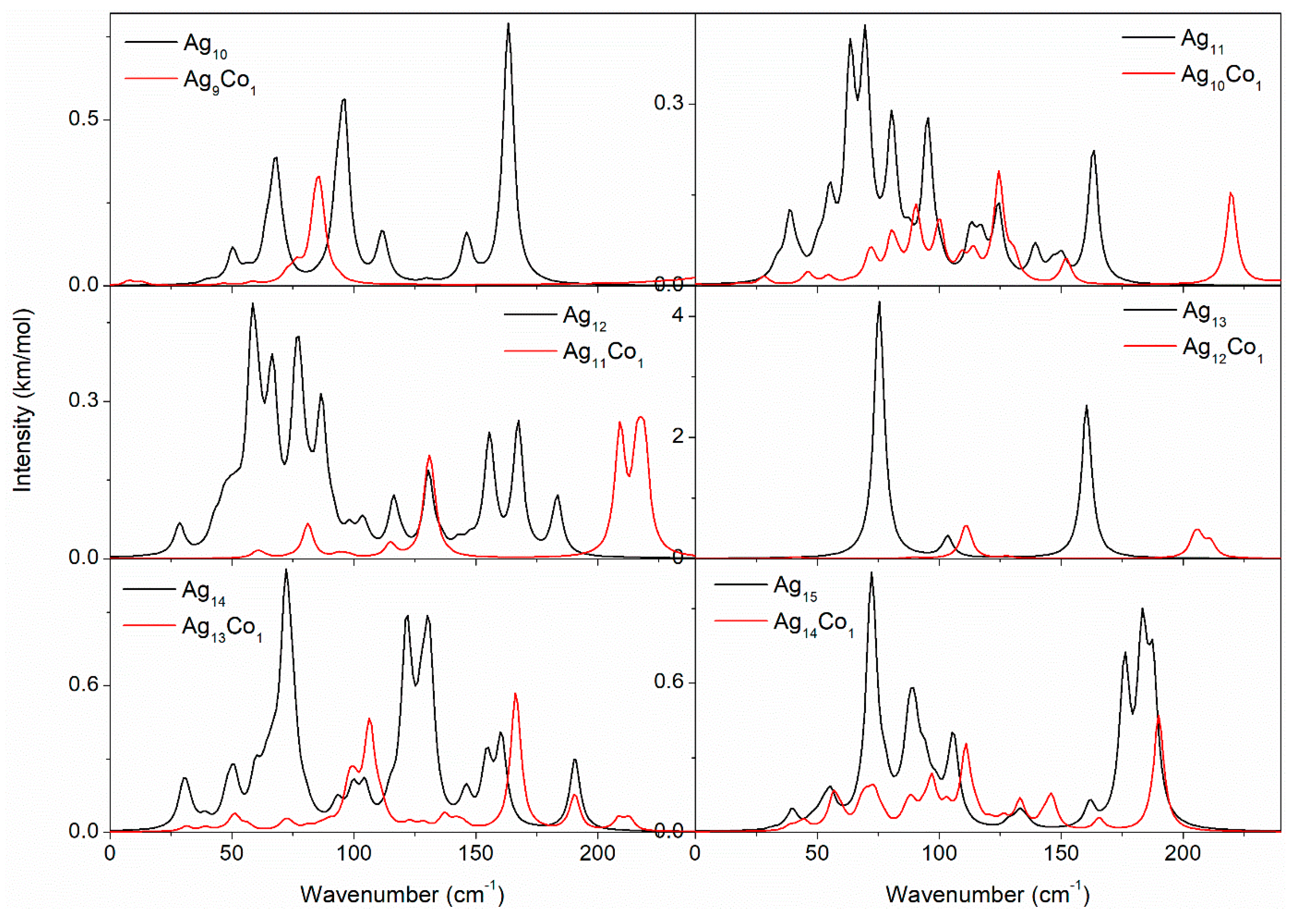
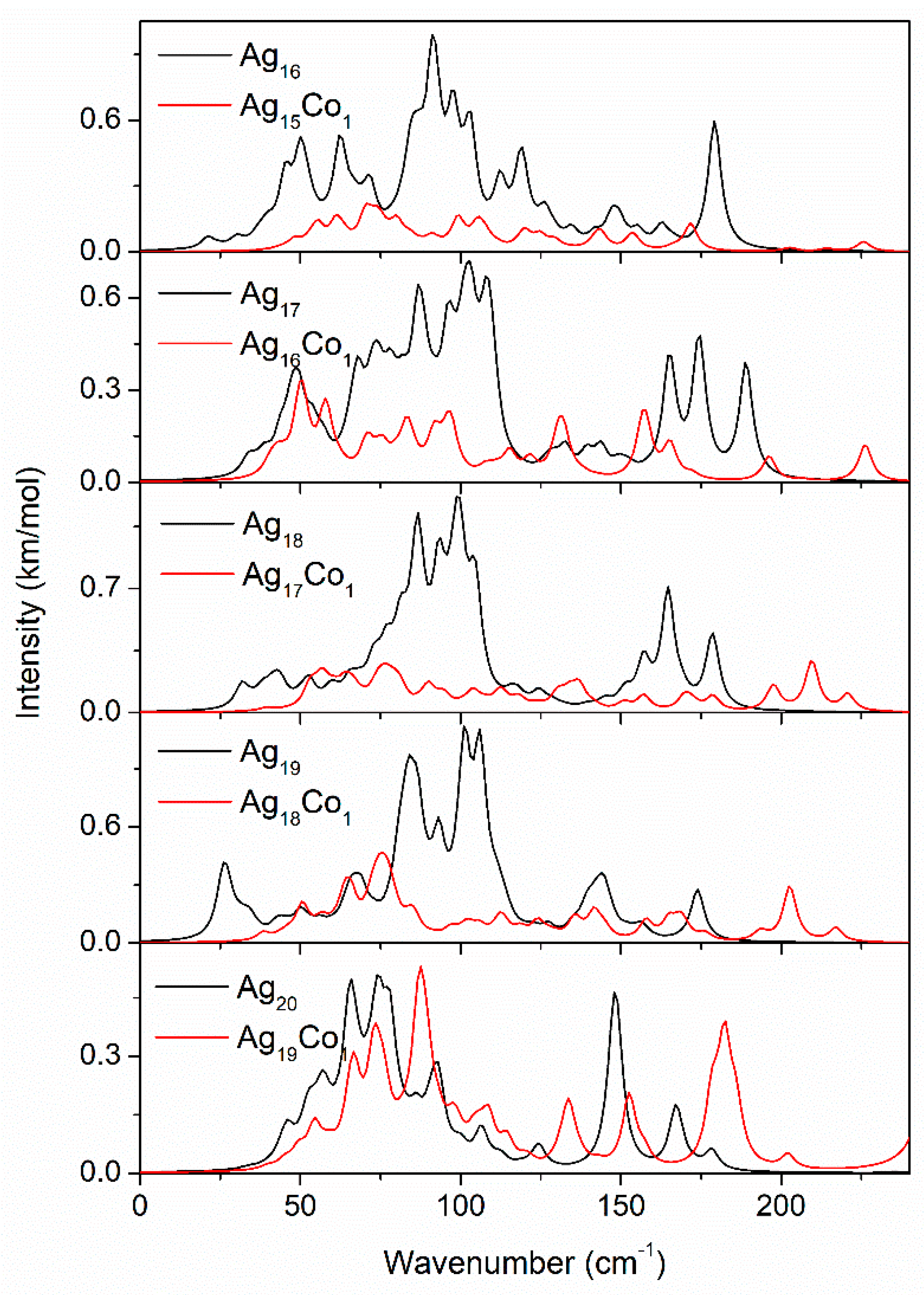
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ferrando, R.; Jellinek, J.; Johnston, R.L. Nanoalloys: From theory to applications of alloy clusters and nanoparticles. Chem. Rev. 2008, 108, 845–910. [Google Scholar] [CrossRef] [PubMed]
- Lewis, L.N. Chemical Catalysis by Colloids and Clusters. Chem. Rev. 1993, 93, 2693–2730. [Google Scholar] [CrossRef]
- Darbha, G.K.; Ray, A.; Ray, P.C. Gold nanoparticle-based miniaturized nanomaterial surface energy transfer probe for rapid and ultrasensitive detection of mercury in soil, water, and fish. ACS Nano 2007, 1, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Dreaden, E.C.; Mackey, M.A.; Huang, X.H.; Kang, B.; El-Sayed, M.A. Beating cancer in multiple ways using nanogold. Chem. Soc. Rev. 2011, 40, 3391–3404. [Google Scholar] [CrossRef] [PubMed]
- Mirkin, C.A.; Letsinger, R.L.; Mucic, R.C.; Storhoff, J.J. A DNA-based method for rationally assembling nanoparticles into macroscopic materials. Nature 1996, 382, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Nicewarner-Pena, S.R.; Freeman, R.G.; Reiss, B.D.; He, L.; Pena, D.J.; Walton, I.D.; Cromer, R.; Keating, C.D.; Natan, M.J. Submicrometer metallic barcodes. Science 2001, 294, 137–141. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Chen, F. Ultraviolet-visible absorption, Raman, vibration spectra of pure silver and Ag-Cu clusters: A density functional theory study. Phys. B 2014, 451, 96–105. [Google Scholar] [CrossRef]
- Li, W.; Ding, L.; Wang, K.; Wang, W.; Zhang, S. A density functional theory study of structural, electronic and optical properties of 9-atom silver-copper clusters. Mater. Today Commun. 2020, 25, 101248. [Google Scholar] [CrossRef]
- Li, W.; Ding, L.; Zhao, T.; Liu, Y. Structural, electronic, and optical properties of the Ag-Cu clusters with the equal number atoms. J. Nanoparticle Res. 2022, 24, 11. [Google Scholar] [CrossRef]
- Li, W.Y.; Zhang, S.; Hai, L. Structural, optical, electronic, and magnetic properties of Ag-Cu bimetallic clusters: A density functional theory study. J. Nanoparticle Res. 2018, 20, 188. [Google Scholar] [CrossRef]
- Gaudry, M.; Cottancin, E.; Pellarin, M.; Lermé, J.; Arnaud, L.; Huntzinger, J.R.; Vialle, J.L.; Broyer, M.; Rousset, J.L.; Treilleux, M.; et al. Size and composition dependence in the optical properties of mixed (transition metal/noble metal) embedded clusters. Phys. Rev. B 2003, 67, 5409. [Google Scholar] [CrossRef]
- Ma, W.Q.; Chen, F.Y. Optical and electronic properties of Cu doped Ag clusters. J. Alloys Compd. 2012, 541, 79–83. [Google Scholar] [CrossRef]
- Wang, L.; Die, D.; Wang, S.J.; Zhao, Z.Q. Geometrical, electronic, and magnetic properties of CunFe (n = 1–12) clusters: A density functional study. J. Phys. Chem. Solids 2015, 76, 10–16. [Google Scholar] [CrossRef]
- Bhatt, M.D.; Lee, G.; Lee, J.S.; Lee, J.Y. Electrocatalytic property of water oxidation reaction depends on charging state of intermediates on Ag-M (M = Fe, co, Ni, Cu) in alkaline media. Int. J. Hydrogen Energy 2019, 44, 5863–5871. [Google Scholar] [CrossRef]
- Andreazza, P.; Lemoine, A.; Coati, A.; Nelli, D.; Ferrando, R.; Garreau, Y.; Creuze, J.; Andreazza-Vignolle, C. From metastability to equilibrium during the sequential growth of Co-Ag supported clusters: A real-time investigation. Nanoscale 2021, 13, 6096–6104. [Google Scholar] [CrossRef] [PubMed]
- Zhevnenko, S.N.; Chernyshikhin, S.V. The effect of cobalt on surface energy of Ag(Co) alloys. Mater. Lett. 2020, 258, 126800. [Google Scholar] [CrossRef]
- Amaya-Roncancio, S.; Reinaudi, L.; Gimenez, M.C. Adsorption and dissociation of CO on metal clusters. Mater. Today Commun. 2020, 24, 101158. [Google Scholar] [CrossRef]
- Cesari, C.; Berti, B.; Calcagno, F.; Femoni, C.; Garavelli, M.; Iapalucci, M.C.; Rivalta, I.; Zacchini, S. Polymerization Isomerism in Co-M (M = Cu, Ag, Au) Carbonyl Clusters: Synthesis, Structures and Computational Investigation. Molecules 2021, 26, 1529. [Google Scholar] [CrossRef]
- Cesari, C.; Berti, B.; Calcagno, F.; Lucarelli, C.; Garavelli, M.; Mazzoni, R.; Rivalta, I.; Zacchini, S. Bimetallic Co–M (M = Cu, Ag, and Au) Carbonyl Complexes Supported by N-Heterocyclic Carbene Ligands: Synthesis, Structures, Computational Investigation, and Catalysis for Ammonia Borane Dehydrogenation. Organometallics 2021, 40, 2724–2735. [Google Scholar] [CrossRef]
- Jia, N.N.; Song, S.P.; Zhang, Y.Z.; Zhou, H.R.; Wang, J.Z. First-principles study on adsorption C2H4 on the surface of ConAgm clusters (n + m = 13). J. At. Mol. Phys. 2018, 35, 592. [Google Scholar] [CrossRef]
- Cheng, Z.F.; Fu, C.P.; Bai, J. First-principles study of the geometry and properties of ComAgn(m + n = 13) clusters. J. At. Mol. Phys. 2015, 32, 993. [Google Scholar]
- Dzhurakhalov, A.A.; Atanasov, I.; Hou, M. Calculation of binary and ternary metallic immiscible clusters with icosahedral structures. Phys. Rev. B 2008, 77, 115415. [Google Scholar] [CrossRef]
- Garcia-Torres, J.; Gomez, E.; Valles, E. Evolution of magnetic and structural properties from Ag nanolayers to several microns Co–Ag deposits prepared by electrodeposition. J. Electroanal. Chem. 2009, 635, 63. [Google Scholar] [CrossRef]
- Laasonen, K.; Panizon, E.; Bochicchio, D.; Ferrando, R. Competition between Icosahedral Motifs in AgCu, AgNi, and AgCo Nanoalloys: A Combined Atomistic–DFT Study. J. Phys. Chem. C 2013, 117, 26405–26413. [Google Scholar] [CrossRef]
- Ferrando, R.; Fortunelli, A.; Johnston, R.L. Searching for the optimum structures of alloy nanoclusters. Phys. Chem. Chem. Phys. 2008, 10, 640. [Google Scholar] [CrossRef] [PubMed]
- Bochicchio, D.; Ferrando, R. Size-dependent transition to high-symmetry chiral structures in AgCu, AgCo, AgNi, and AuNi nanoalloys. Nano Lett. 2010, 10, 4211–4216. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Zhang, R.; Li, Z.; Liu, B.X. Magnetic properties of Co and Co-Ag alloys in equilibrium/nonequilibrium structures studied by ab initio calculations. Phys. Rev. B 2003, 68, 134446. [Google Scholar] [CrossRef]
- Van Hoof, T.; Dzhurakhalov, A.; Hou, M. Interface formation by low energy deposition of core-shell Ag-Co nanoclusters on Ag(100). Eur. Phys. J. D 2007, 43, 159–163. [Google Scholar] [CrossRef]
- Van Hoof, T.; Hou, M. Structural and thermodynamic properties of Ag-Co nanoclusters. Phys. Rev. B 2005, 72, 115434. [Google Scholar] [CrossRef]
- Janssens, E.; Neukermans, S.; Nguyen, H.M.; Nguyen, M.T.; Lievens, P. Quenching of the magnetic moment of a transition metal dopant in silver clusters. Phys. Rev. Lett. 2005, 94, 113401. [Google Scholar] [CrossRef]
- Janssens, E.; Van Hoof, T.; Veldeman, N.; Neukermans, S.; Hou, M.; Lievens, P. Mass spectrometric and modeling investigations of bimetallic silver–cobalt clusters. Int. J. Mass Spectrom. 2006, 252, 38–46. [Google Scholar] [CrossRef]
- Li, W.; Shang, R.; Lei, Y.; Liu, Y.; Ma, C. Density Functional Theory Study on Structural, Electronic, Magnetic, and Optical Properties of Au, Cu, Cr, Mn, Co, Ni, and Fe Atoms Doped 13-Atom Silver Clusters. Nano 2023, 18, 2350077. [Google Scholar] [CrossRef]
- Li, W.; Shang, R.; Wang, C.; Zhang, Y. Study on the structural, electronic and optical properties of the Ag-Co clusters based on density functional theory. J. At. Mol. Phys. 2025, 42, 022001. [Google Scholar] [CrossRef]
- Zhang, J.; Dolg, M. ABCluster: The artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 2015, 17, 24173. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Dolg, M. Global optimization of clusters of rigid molecules using the artificial bee colony algorithm. Phys. Chem. Chem. Phys. 2016, 18, 3003. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.P. Lattice-Relaxation at a Metal-Surface. Phys Rev B 1981, 23, 6265–6270. [Google Scholar] [CrossRef]
- Cleri, F.; Rosato, V. Tight-Binding Potentials for Transition-Metals and Alloys. Phys. Rev. B 1993, 48, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Delley, B. Hardness conserving semilocal pseudopotentials. Phys. Rev. B 2002, 66, 155125. [Google Scholar] [CrossRef]
- Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Delley, B. An All-Electron Numerical-Method for Solving the Local Density Functional for Polyatomic-Molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Delley, B. Time dependent density functional theory with DMol3. J. Phys.-Condens. Mat. 2010, 22, 384208. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Dyer, J.E.; Li, K.; Dixon, D.A. Prediction of Structures and Atomization Energies of Small Silver Clusters, (Ag)n, n < 100. J. Phys. Chem. A 2013, 117, 8298–8313. [Google Scholar] [CrossRef] [PubMed]
- Harb, M.; Rabilloud, F.; Simon, D.; Rydlo, A.; Lecoultre, S.; Conus, F.; Rodrigues, V.; Felix, C. Optical absorption of small silver clusters: Agn, (n = 4–22). J. Chem. Phys. 2008, 129, 194108. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Zhang, H.; Zhao, J. Structure and structural evolution of Agn (n = 3–22) clusters using a genetic algorithm and density functional theory method. Solid State Commun. 2007, 144, 174–179. [Google Scholar] [CrossRef]
- Li, W.; Chen, F. Effects of shape and dopant on structural, optical absorption, Raman, and vibrational properties of silver and copper quantum clusters: A density functional theory. Chin. Phys. B 2014, 23, 117103. [Google Scholar] [CrossRef]
- Li, W.; Chen, F. A density functional theory study of structural, electronic, optical and magnetic properties of small Ag-Cu nanoalloys. J. Nanoparticle Res. 2013, 15, 1809. [Google Scholar] [CrossRef]
- Baishya, K.; Idrobo, J.C.; Ogut, S.; Yang, M.L.; Jackson, K.; Jellinek, J. Optical absorption spectra of intermediate-size silver clusters from first principles. Phys. Rev. B 2008, 78, 075439. [Google Scholar] [CrossRef]
- Conus, F.; Lau, J.T.; Rodrigues, V.; Félix, C. High sensitivity absorption measurement of small metal clusters embedded in an argon matrix. Rev. Sci. Instrum. 2006, 77, 113103. [Google Scholar] [CrossRef]
- Harbich, W.; Fedrigo, S.; Buttet, J. The Optical-Absorption Spectra of Small Silver Clusters (N = 5–11) Embedded in Argon Matrices. Chem. Phys. Lett. 1992, 195, 613–617. [Google Scholar] [CrossRef]
- Harbich, W.; Fedrigo, S.; Buttet, J. The Optical-Absorption Spectra of Small Silver Clusters (N = 8–39) Embedded in Rare-Gas Matrices. Z. Phys. D At. Mol. Clust. 1993, 26, 138. [Google Scholar] [CrossRef]




| A (eV) | (eV) | p | q | r0 (Å) | |
|---|---|---|---|---|---|
| Ag–Ag | 0.1043 | 1.1940 | 2.8900 | 10.7900 | 3.1900 |
| Ag–Co | 0.1444 | 1.4776 | 2.6950 | 10.0100 | 3.0850 |
| Co–Co | 0.1757 | 1.8430 | 2.5000 | 9.2100 | 2.7950 |
| Unpaired Electrons | Closed- or Open-Shell | Spin Multiplicity | |
|---|---|---|---|
| Ag10 | 2 | open-shell | 3 |
| Ag9Co1 | 0 | closed-shell | 1 |
| Ag11 | 1 | open-shell | 2 |
| Ag10Co1 | 1 | open-shell | 2 |
| Ag12 | 0 | closed-shell | 1 |
| Ag11Co1 | 2 | open-shell | 3 |
| Ag13 | 1 | open-shell | 2 |
| Ag12Co1 | 3 | open-shell | 4 |
| Ag14 | 0 | closed-shell | 1 |
| Ag13Co1 | 2 | open-shell | 3 |
| Ag15 | 3 | open-shell | 4 |
| Ag14Co1 | 3 | open-shell | 4 |
| Ag16 | 0 | closed-shell | 1 |
| Ag15Co1 | 0 | closed-shell | 1 |
| Ag17 | 1 | open-shell | 2 |
| Ag16Co1 | 1 | open-shell | 2 |
| Ag18 | 0 | closed-shell | 1 |
| Ag17Co1 | 0 | closed-shell | 1 |
| Ag19 | 1 | open-shell | 2 |
| Ag18Co1 | 1 | open-shell | 2 |
| Ag20 | 0 | closed-shell | 1 |
| Ag19Co1 | 2 | open-shell | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Feng, H.; Shang, R. First Principle Study on Structural, Electronic, Magnetic, and Optical Properties of Co-Doped Middle Size Silver Clusters. Molecules 2024, 29, 2670. https://doi.org/10.3390/molecules29112670
Li W, Feng H, Shang R. First Principle Study on Structural, Electronic, Magnetic, and Optical Properties of Co-Doped Middle Size Silver Clusters. Molecules. 2024; 29(11):2670. https://doi.org/10.3390/molecules29112670
Chicago/Turabian StyleLi, Weiyin, Hao Feng, and Ruiyong Shang. 2024. "First Principle Study on Structural, Electronic, Magnetic, and Optical Properties of Co-Doped Middle Size Silver Clusters" Molecules 29, no. 11: 2670. https://doi.org/10.3390/molecules29112670
APA StyleLi, W., Feng, H., & Shang, R. (2024). First Principle Study on Structural, Electronic, Magnetic, and Optical Properties of Co-Doped Middle Size Silver Clusters. Molecules, 29(11), 2670. https://doi.org/10.3390/molecules29112670





