Experimental and Modeling Analysis of Mechanical Response of Composite Electrodes in Lithium Batteries
Abstract
:1. Introduction
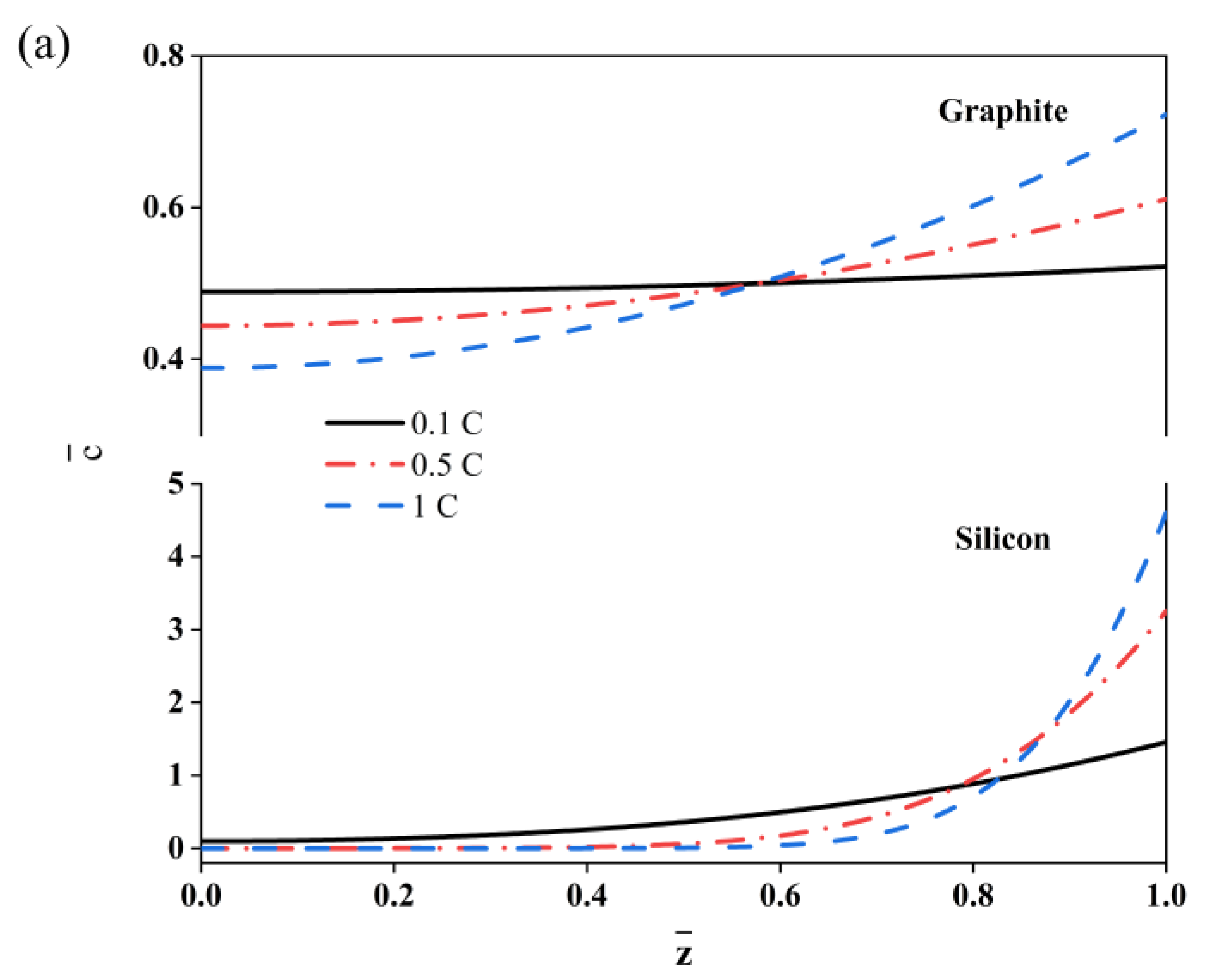
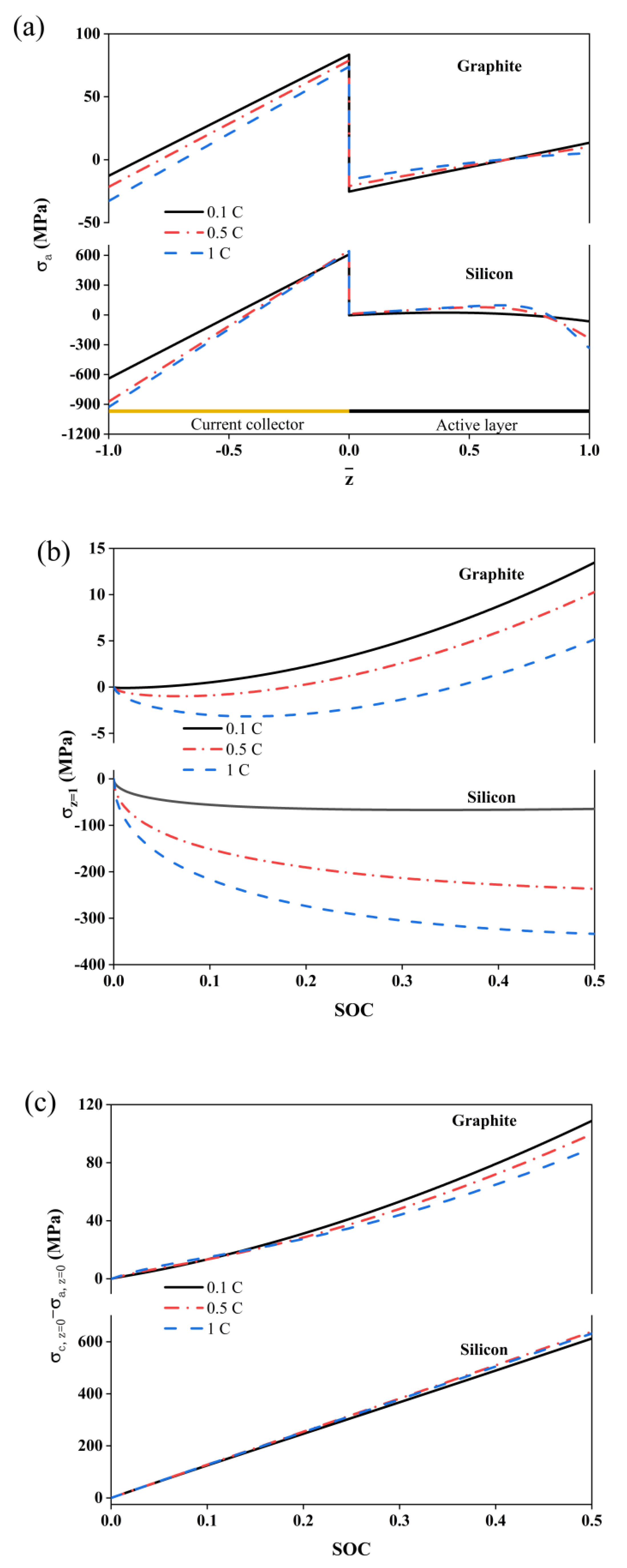
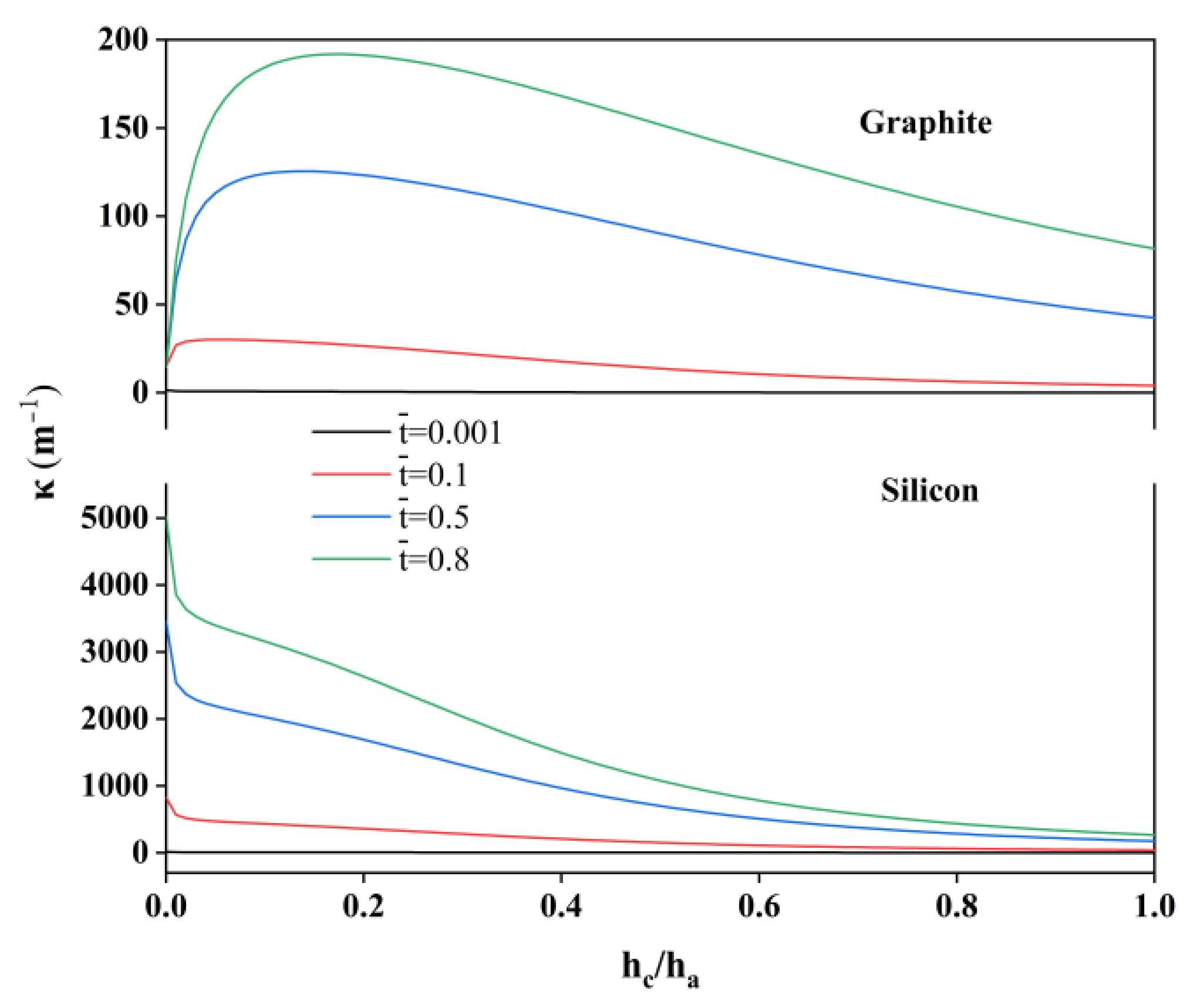
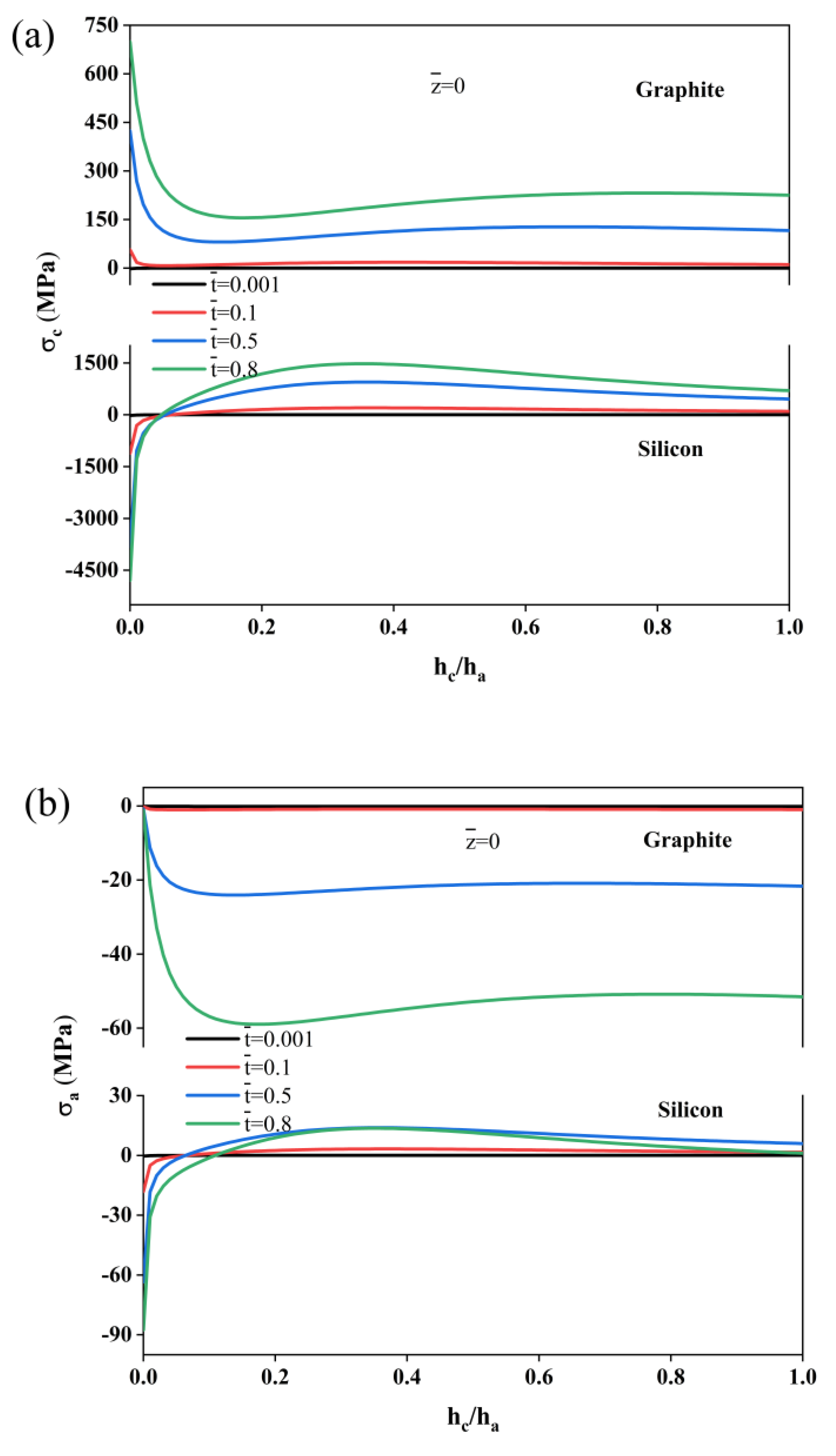
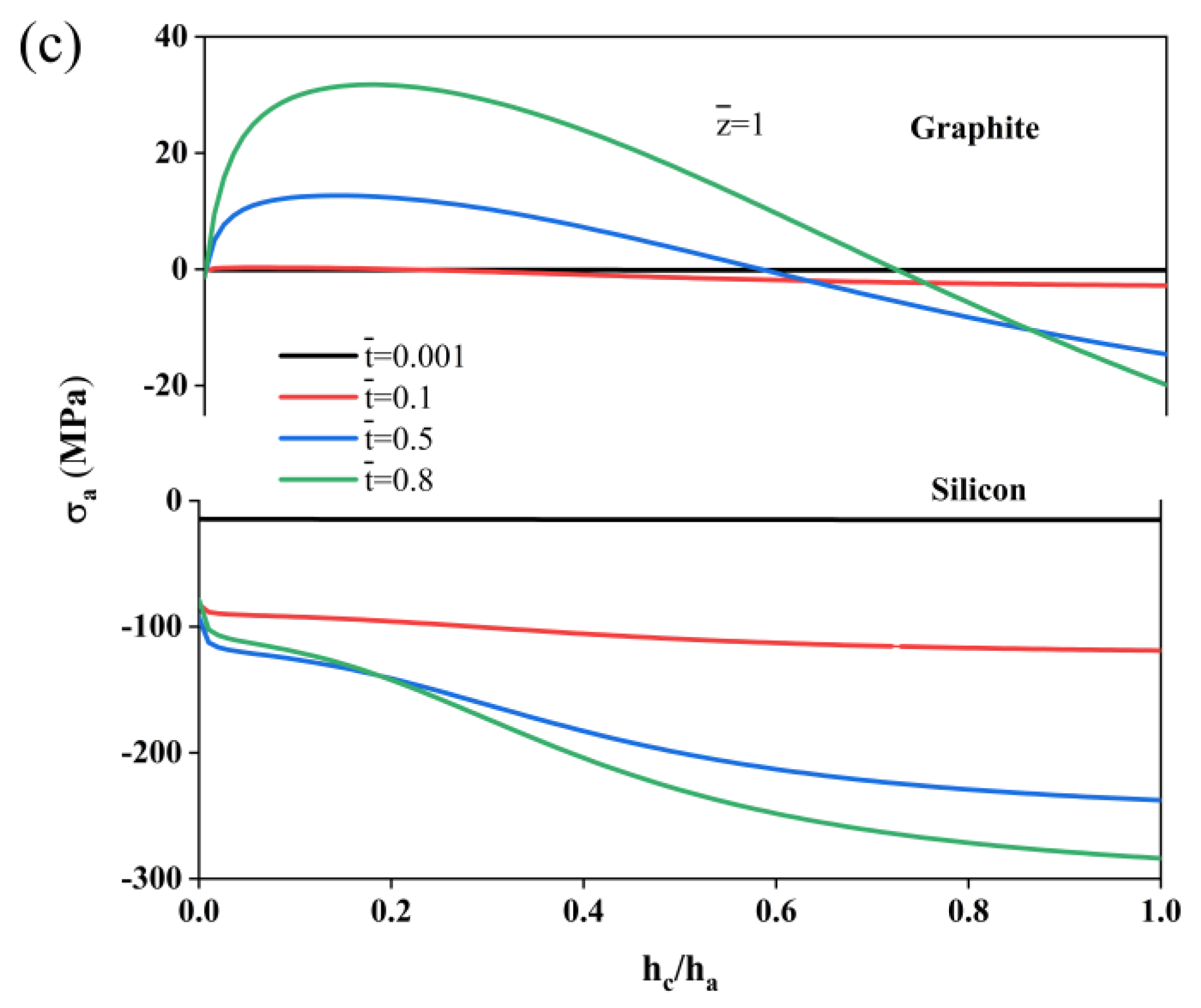
2. Results
3. Experimental Section
3.1. Electrode Preparation
3.2. Assembly of the Model Cell
3.3. Electrochemical Measurements
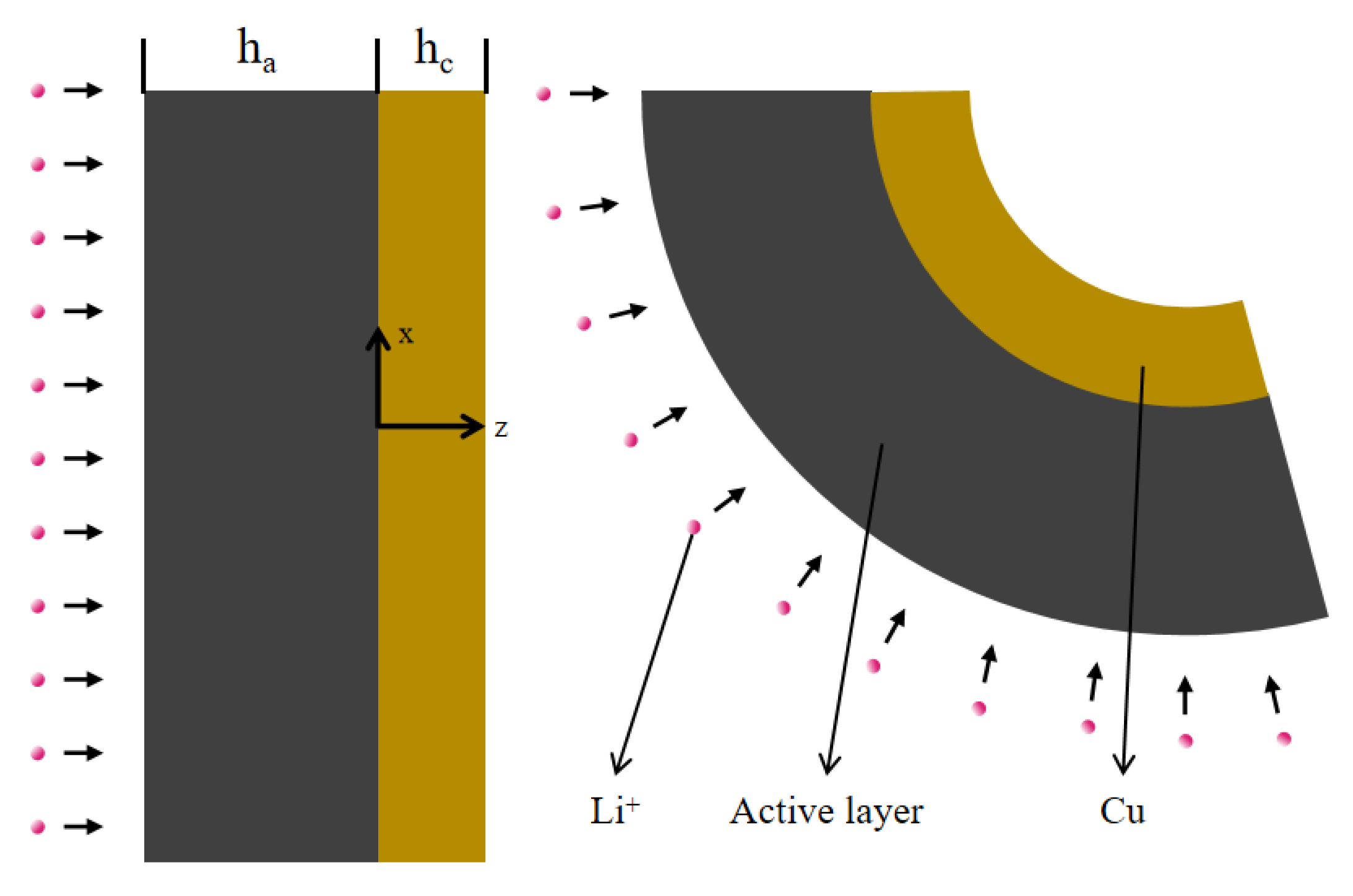
4. Modeling of the Bending Deformation of the Composite Electrodes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Jaguemont, J.; Goutam, S.; Gopalakrishnan, R.; Firouz, Y.; Kalogiannis, T.; Omar, N.; Van Mierlo, J. Concept of reliability and safety assessment of lithium-ion batteries in electric vehicles: Basics, progress, and challenges. Appl. Energy 2019, 251, 113343. [Google Scholar] [CrossRef]
- Eftekhari, A. Lithium Batteries for Electric Vehicles: From Economy to Research Strategy; ACS Publications: Washington, DC, USA, 2019. [Google Scholar]
- Li, Y.; Song, J.; Yang, J. A review on structure model and energy system design of lithium-ion battery in renewable energy vehicle. Renew. Sustain. Energy Rev. 2014, 37, 627–633. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-energy lithium-ion batteries: Recent progress and a promising future in applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Wu, F.; Maier, J.; Yu, Y. Guidelines and trends for next-generation rechargeable lithium and lithium-ion batteries. Chem. Soc. Rev. 2020, 49, 1569–1614. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Li, H.; Zhai, T. Reviving lithium-metal anodes for next-generation high-energy batteries. Adv. Mater. 2017, 29, 1700007. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; He, Y.; Li, X.; Jin, Z.; Yu, H.; Li, D. Effect of the charge rate on the mechanical response of composite graphite electrodes: In situ experiment and mathematical analysis. Phys. Chem. Chem. Phys. 2024, 26, 1245–1254. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; Jiang, H.; Li, W.; Li, G.; Li, D. Chemo-Mechanical Coupling Measurement of LiMn2O4 Composite Electrode during Electrochemical Cycling. Batteries 2023, 9, 209. [Google Scholar] [CrossRef]
- Ye, Z.; Li, Z.; Roberts, J.; Zhang, P.; Wang, J.; Zhao, G. Electromagnetic wave absorption properties of carbon nanotubes-epoxy composites at microwave frequencies. J. Appl. Phys. 2010, 108, 054315. [Google Scholar] [CrossRef]
- Jangid, M.K.; Mukhopadhyay, A. Real-time monitoring of stress development during electrochemical cycling of electrode materials for Li-ion batteries: Overview and perspectives. J. Mater. Chem. A 2019, 7, 23679–23726. [Google Scholar] [CrossRef]
- Gao, Y.; Zheng, F.; Wang, D.; Wang, B. Mechanoelectrochemical issues involved in current lithium-ion batteries. Nanoscale 2020, 12, 20100–20117. [Google Scholar] [CrossRef] [PubMed]
- Yim, T.; Choi, S.J.; Jo, Y.N.; Kim, T.-H.; Kim, K.J.; Jeong, G.; Kim, Y.-J. Effect of binder properties on electrochemical performance for silicon-graphite anode: Method and application of binder screening. Electrochim. Acta 2014, 136, 112–120. [Google Scholar] [CrossRef]
- Finegan, D.P.; Darcy, E.; Keyser, M.; Tjaden, B.; Heenan, T.M.; Jervis, R.; Bailey, J.J.; Malik, R.; Vo, N.T.; Magdysyuk, O.V. Characterising thermal runaway within lithium-ion cells by inducing and monitoring internal short circuits. Energy Environ. Sci. 2017, 10, 1377–1388. [Google Scholar] [CrossRef]
- Jaumann, T.; Balach, J.; Langklotz, U.; Sauchuk, V.; Fritsch, M.; Michaelis, A.; Teltevskij, V.; Mikhailova, D.; Oswald, S.; Klose, M. Lifetime vs. rate capability: Understanding the role of FEC and VC in high-energy Li-ion batteries with nano-silicon anodes. Energy Storage Mater. 2017, 6, 26–35. [Google Scholar] [CrossRef]
- Li, D.; Wan, H.; Liu, J.; Jiang, H.; Wang, Y.; Zhang, J.; Zheng, Y. Effects of calendering state on coupled electrochemical-mechanical performance of silicon based composite electrodes. Green Energy Intell. Transp. 2024, 100154. [Google Scholar] [CrossRef]
- Yu, H.; Liu, X.; Li, D. Experimental measurement of stress evolution in silicon carbide composite electrode during electrochemical cycling. Mater. Sci. Semicond. Process. 2022, 138, 106275. [Google Scholar] [CrossRef]
- Nation, L.; Li, J.; James, C.; Qi, Y.; Dudney, N.; Sheldon, B.W. In situ stress measurements during electrochemical cycling of lithium-rich cathodes. J. Power Sources 2017, 364, 383–391. [Google Scholar] [CrossRef]
- Jones, E.; Silberstein, M.; White, S.R.; Sottos, N.R. In situ measurements of strains in composite battery electrodes during electrochemical cycling. Exp. Mech. 2014, 54, 971–985. [Google Scholar] [CrossRef]
- Allen, J.M.; Weddle, P.J.; Verma, A.; Mallarapu, A.; Usseglio-Viretta, F.; Finegan, D.P.; Colclasure, A.M.; Mai, W.; Schmidt, V.; Furat, O. Quantifying the influence of charge rate and cathode-particle architectures on degradation of Li-ion cells through 3D continuum-level damage models. J. Power Sources 2021, 512, 230415. [Google Scholar] [CrossRef]
- Zhang, X.; Shyy, W.; Sastry, A.M. Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles. J. Electrochem. Soc. 2007, 154, A910. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Cai, S.; Vlassak, J.J.; Suo, Z. Large plastic deformation in high-capacity lithium-ion batteries caused by charge and discharge. J. Am. Ceram. Soc. 2011, 94, s226–s235. [Google Scholar] [CrossRef]
- Song, Y.; Soh, A.; Zhang, J. On stress-induced voltage hysteresis in lithium ion batteries: Impacts of material property, charge rate and particle size. J. Mater. Sci. 2016, 51, 9902–9911. [Google Scholar] [CrossRef]
- Cui, Z.; Gao, F.; Qu, J. A finite deformation stress-dependent chemical potential and its applications to lithium ion batteries. J. Mech. Phys. Solids 2012, 60, 1280–1295. [Google Scholar] [CrossRef]
- Liu, P.; Xu, R.; Liu, Y.; Lin, F.; Zhao, K. Computational modeling of heterogeneity of stress, charge, and cyclic damage in composite electrodes of Li-ion batteries. J. Electrochem. Soc. 2020, 167, 040527. [Google Scholar] [CrossRef]
- Landesfeind, J.; Eldiven, A.; Gasteiger, H.A. Influence of the binder on lithium ion battery electrode tortuosity and performance. J. Electrochem. Soc. 2018, 165, A1122–A1128. [Google Scholar] [CrossRef]
- Vu, A.; Qian, Y.; Stein, A. Porous electrode materials for lithium-ion batteries–how to prepare them and what makes them special. Adv. Energy Mater. 2012, 2, 1056–1085. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Zinn, A.-H.; Zampardi, G.; Borhani-Haghighi, S.; La Mantia, F.; Ludwig, A.; Schuhmann, W.; Ventosa, E. Wet nanoindentation of the solid electrolyte interphase on thin film Si electrodes. ACS Appl. Mater. Interfaces 2015, 7, 23554–23563. [Google Scholar] [CrossRef]
- Li, D.; Wan, H.; Liu, H.; Wang, Y.; Zhang, J. Experimental measurement of electro-chemo-mechanical properties of a composite silicon electrode in lithium ion batteries. Phys. Chem. Chem. Phys. 2022, 24, 25580–25587. [Google Scholar] [CrossRef]
- Xie, H.; Qiu, W.; Song, H.; Tian, J. In situ measurement of the deformation and elastic modulus evolution in Si composite electrodes during electrochemical lithiation and delithiation. J. Electrochem. Soc. 2016, 163, A2685. [Google Scholar] [CrossRef]




| Silicon | Graphite | |
|---|---|---|
| 0.5 (Gpa) | ||
| −0.17 | 15 | |
| 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Jin, Z.; He, Y.; Li, D. Experimental and Modeling Analysis of Mechanical Response of Composite Electrodes in Lithium Batteries. Molecules 2024, 29, 3316. https://doi.org/10.3390/molecules29143316
Shen Z, Jin Z, He Y, Li D. Experimental and Modeling Analysis of Mechanical Response of Composite Electrodes in Lithium Batteries. Molecules. 2024; 29(14):3316. https://doi.org/10.3390/molecules29143316
Chicago/Turabian StyleShen, Zheru, Zhiyao Jin, Yaolong He, and Dawei Li. 2024. "Experimental and Modeling Analysis of Mechanical Response of Composite Electrodes in Lithium Batteries" Molecules 29, no. 14: 3316. https://doi.org/10.3390/molecules29143316
APA StyleShen, Z., Jin, Z., He, Y., & Li, D. (2024). Experimental and Modeling Analysis of Mechanical Response of Composite Electrodes in Lithium Batteries. Molecules, 29(14), 3316. https://doi.org/10.3390/molecules29143316







