Experimental and Theoretical Study of the Reaction of F2 with Thiirane
Abstract
:1. Introduction
2. Results and Discussion
2.1. Products of Reaction (1)
2.1.1. Measurements of HF Yield
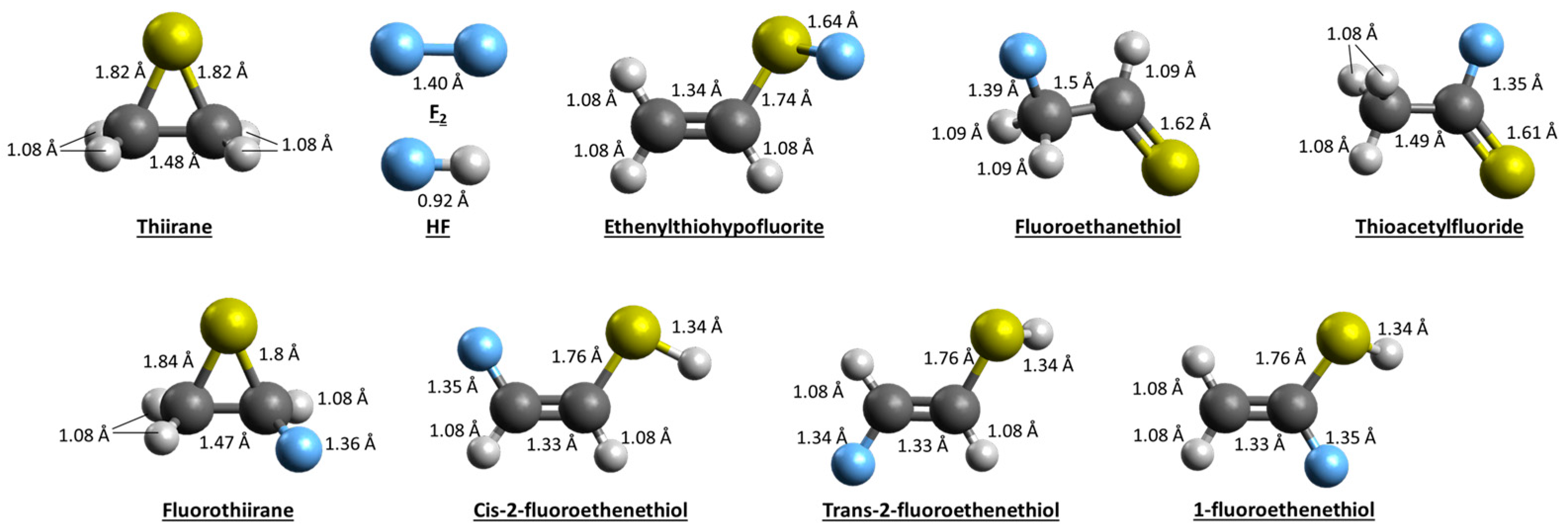
2.1.2. Theoretical Findings
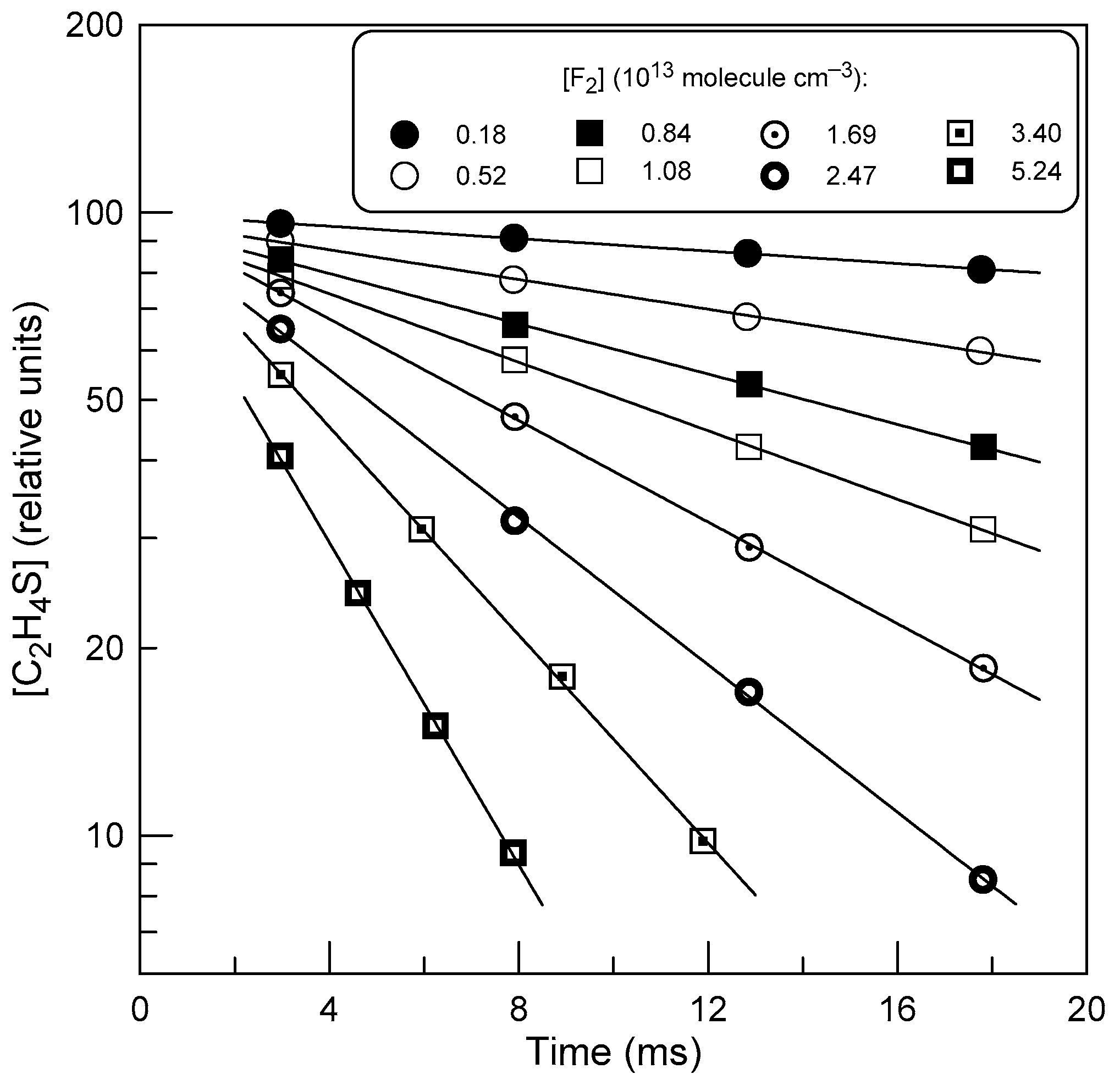
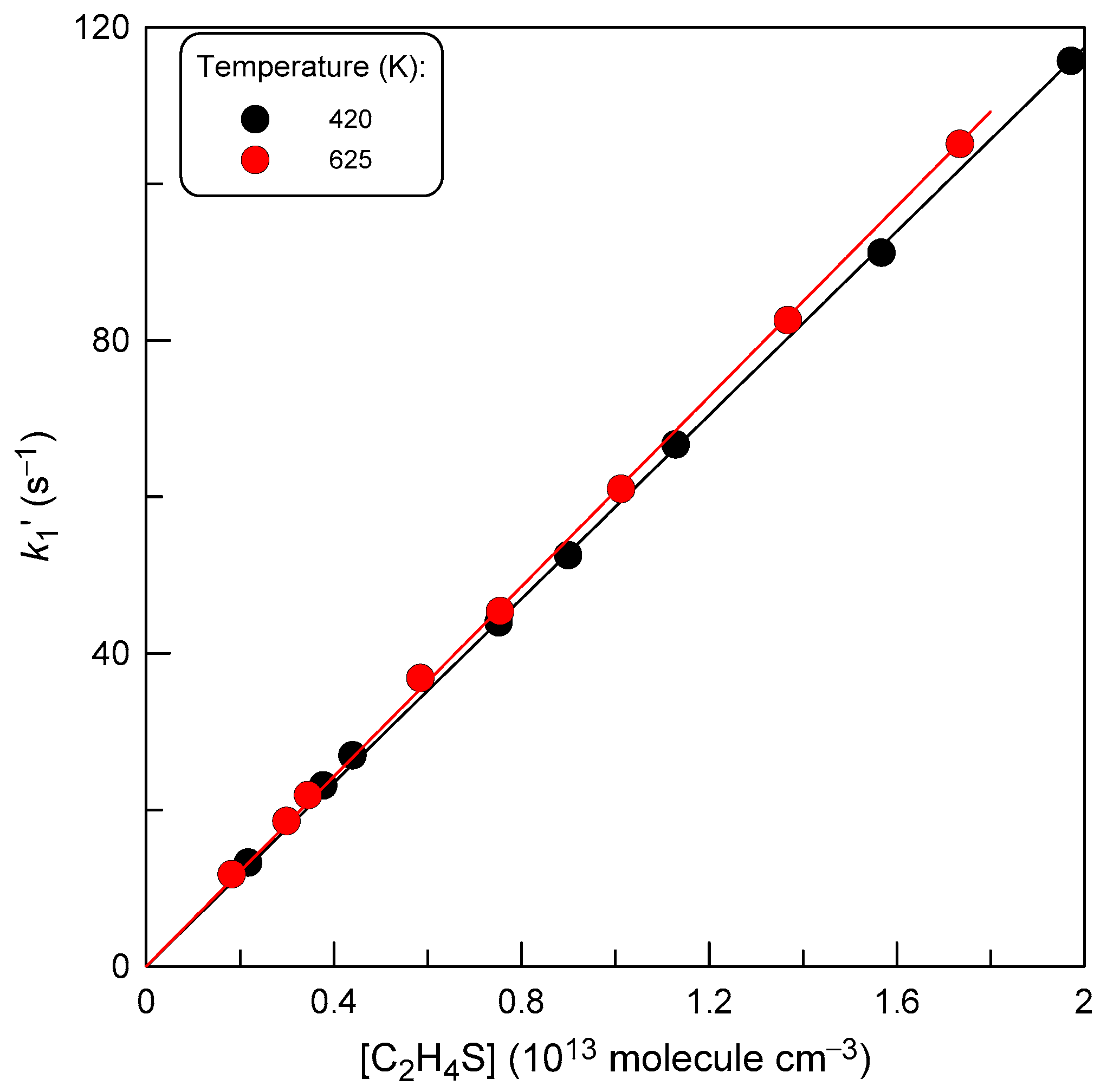
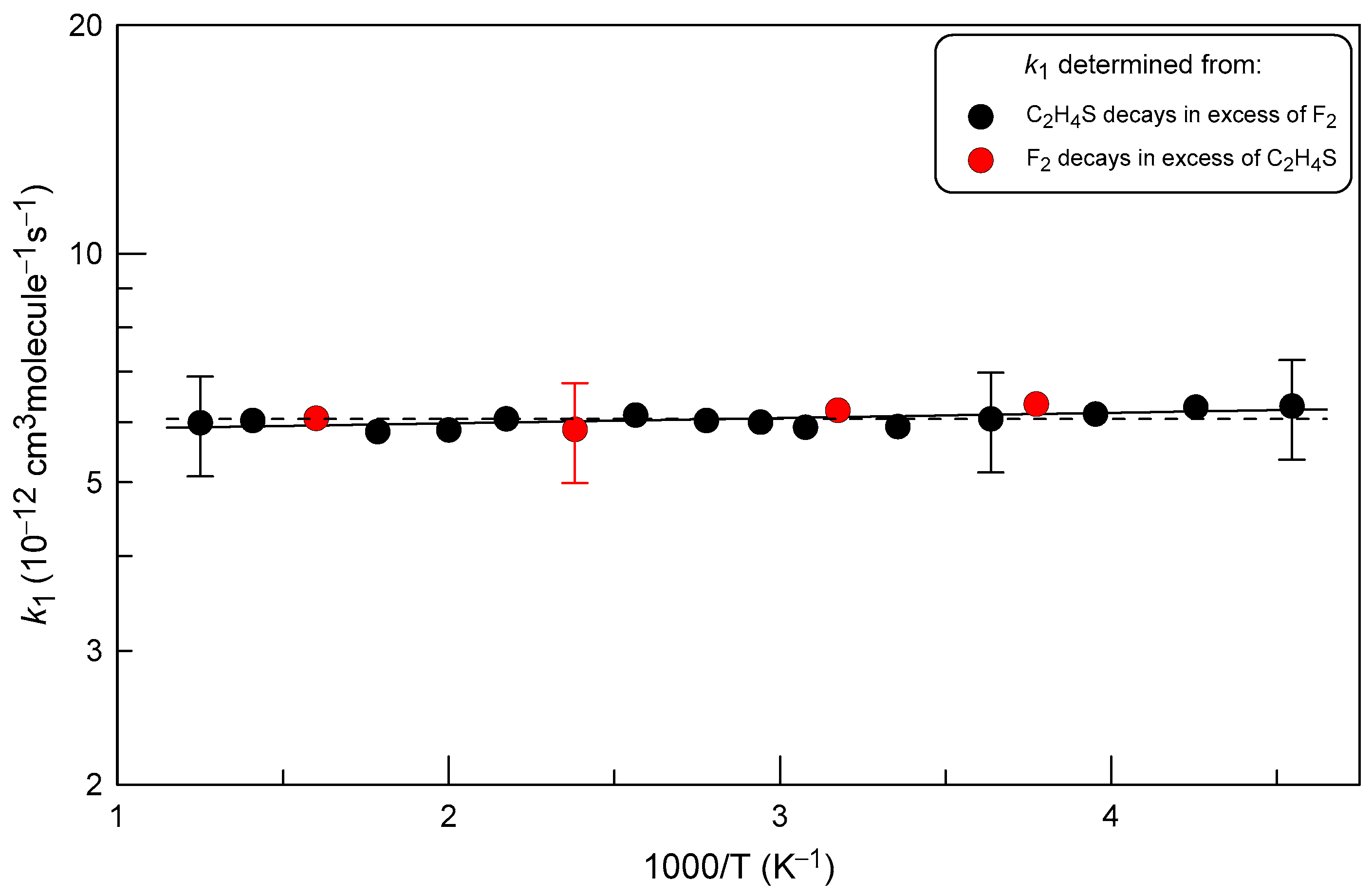
2.2. Measurements of the Rate Constant of Reaction (1)
3. Materials and Methods
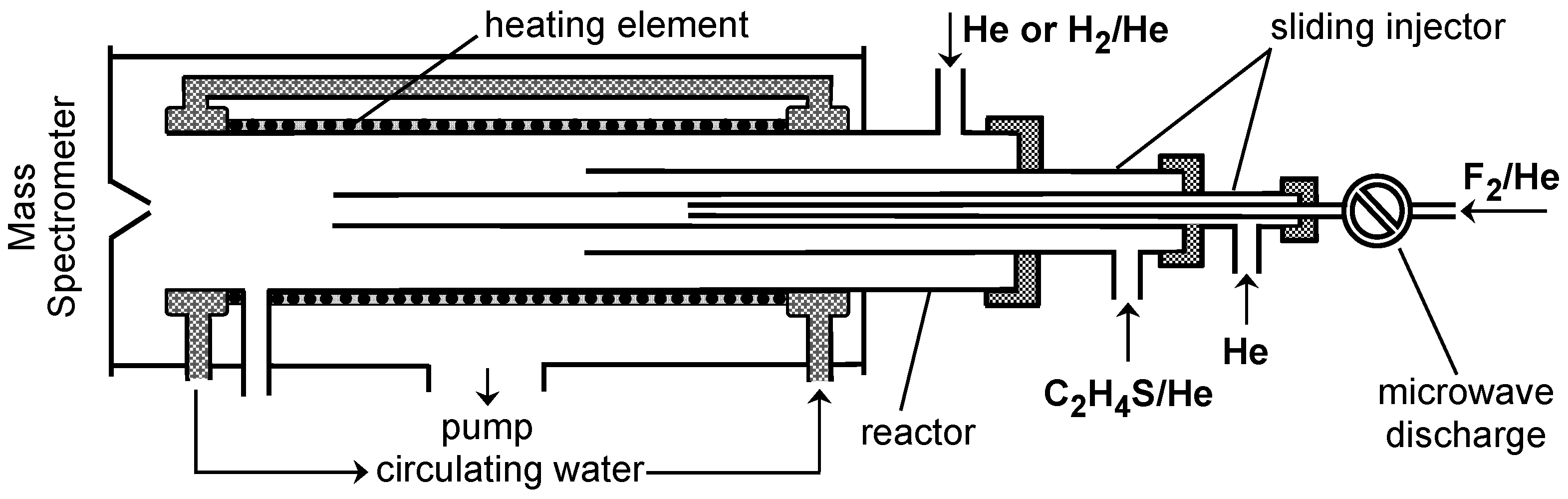
3.1. Experimental
3.2. Computational Methodology
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.-J.; Lee, L.; Pan, J.-W.; Xie, T.; Witek, H.A.; Lin, J.J. Barrierless reactions between two closed-shell molecules. I. Dynamics of F2+CH3SCH3 reaction. J. Chem. Phys. 2008, 128, 104317. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.-C.; Xie, T.; Lu, Y.-J.; Chang, C.-H.; Pan, J.-W.; Lin, J.J. Barrierless reactions between two closed-shell molecules. II. Dynamics of F2+CH3SSCH3 reaction. J. Chem. Phys. 2009, 130, 014301. [Google Scholar] [CrossRef] [PubMed]
- Bedjanian, Y.; Romanias, M.N.; Morin, J. Reaction of Limonene with F2: Rate Coefficient and Products. J. Phys. Chem. A 2014, 118, 10233–10239. [Google Scholar] [CrossRef] [PubMed]
- Turnipseed, A.A.; Birks, J.W. Kinetics of the reaction of molecular fluorine with dimethyl sulfide. J. Phys. Chem. 1991, 95, 6569–6574. [Google Scholar] [CrossRef]
- Manion, J.A.; Huie, R.E.; Levin, R.D.; Burgess, D.R.; Orkin, V.L.; Tsang, W.; McGivern, W.S.; Hudgens, J.W.; Knyazev, V.D.; Atkinson, D.B.; et al. NIST Chemical Kinetics Database, NIST Standard Reference Database 17, Version 7.0 (Web Version), Release 1.6.8, Data version 2015.12, National Institute of Standards and Technology, Gaithersburg, Maryland, 20899-8320. Available online: http://kinetics.nist.gov/ (accessed on 3 July 2024).
- Nelson, J.K.; Getty, R.H.; Birks, J.W. Fluorine induced chemiluminescence detector for reduced sulfur compounds. Anal. Chem. 1983, 55, 1767–1770. [Google Scholar] [CrossRef]
- Kaufman, F. Kinetics of elementary radical reactions in the gas phase. J. Phys. Chem. 1984, 88, 4909–4917. [Google Scholar] [CrossRef]
- Butler, J.J.; Baer, T. A photoionization study of organosulfur ring compounds—Thiirane, thietane and tetrahydrothiophene. Org. Mass Spectrom. 1983, 18, 248–253. [Google Scholar] [CrossRef]
- Bartmess, J.E.; McIver, R.T. Chapter 11—The gas-phase acidity scale. In Gas Phase Ion Chemistry; Bowers, M.T., Ed.; Academic Press: Cambridge, MA, USA, 1979; pp. 87–121. [Google Scholar]
- Bedjanian, Y. Rate Coefficients of the Reactions of Fluorine Atoms with H2S and SH over the Temperature Range 220–960 K. Molecules 2022, 27, 8365. [Google Scholar] [CrossRef] [PubMed]
- Bedjanian, Y. Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S. Molecules 2023, 28, 7883. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.; Romanias, M.N.; Bedjanian, Y. Experimental study of the reactions of OH radicals with propane, n-pentane, and n-heptane over a wide temperature range. Int. J. Chem. Kinet. 2015, 47, 629–637. [Google Scholar] [CrossRef]
- Bedjanian, Y. Rate constants for the reactions of F atoms with H2 and D2 over the temperature range 220–960 K. Int. J. Chem. Kinet. 2021, 53, 527–535. [Google Scholar] [CrossRef]
- Vila, A.; Puente, E.d.l.; Mosquera, R.A. QTAIM study of the electronic structure and strain energy of fluorine substituted oxiranes and thiiranes. Chem. Phys. Lett. 2005, 405, 440–447. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016.
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Celani, P.; Györffy, W.; Hesselmann, A.; Kats, D.; Knizia, G.; Köhn, A.; Korona, T.; Kreplin, D.; et al. MOLPRO, Version, a Package of ab Initio Programs. Available online: https://www.molpro.net (accessed on 3 July 2024).


| T (K) | [C2H4S]0 a | Δ[F2] b | Δ[HF]/Δ[C2H4S] c | Δ[HF]/Δ[F2] d |
|---|---|---|---|---|
| 220 | 3.5–3.8 | 0.18–1.80 | 1.04 ± 0.01 | 1.01±0.01 |
| 253 | 4.5–5.0 | 0.12–2.08 | 1.02 ± 0.01 | 1.01±0.01 |
| 298 | 3.2–5.0 | 0.19–2.07 | 1.01 ± 0.02 | 1.01±0.01 |
| 325 | 4.5–5.0 | 0.15–2.04 | 1.06 ± 0.01 | 1.05 ± 0.01 |
| 360 | 2.0–3.8 | 0.09–1.51 | 0.98 ± 0.01 | 0.95 ± 0.01 |
| 500 | 3.1–3.5 | 0.10–1.09 | 1.01 ± 0.01 | 1.00 ± 0.01 |
| 670 | 2.0–2.5 | 0.08–0.72 | 1.02 ± 0.01 | 1.00 ± 0.01 |
| 800 | 3.32–4.0 | 0.10–1.89 | 0.97 ± 0.01 | 0.96 ± 0.01 |
| Molecule | ∆G (kJ/mol) | ∆H (kJ/mol) | Boltzmann Population T = 298 K | Boltzmann Population T = 500 K | Boltzmann Population T = 1000 K |
|---|---|---|---|---|---|
| 1-fluoroethenethiol | −470.7 | −473.1 | 2.0 × 10−7 | 1.0 × 10−4 | 9.8 × 10−3 |
| Cis-2-fluoroethenethiol | −467.1 | −467.8 | 2.4 × 10−8 | 2.9 × 10−5 | 5.2 × 10−3 |
| Ethenylthyohypofluorite | −409.9 | −411.3 | 3.0 × 10−18 | 3.6 × 10−11 | 5.9 × 10−6 |
| Fluoroethanethiol | −456.3 | −456.6 | 2.6 × 10−10 | 1.9 × 10−6 | 1.4 × 10−3 |
| Fluorothiirane | −462.0 | −466.2 | 1.3 × 10−8 | 2.0 × 10−5 | 4.3 × 10−3 |
| Thioacetylfluoride | −509.1 | −511.3 | 1 | 1 | 9.8 × 10−1 |
| Trans-2-fluoroethenethiol | −463.4 | −465.5 | 9.3 × 10−9 | 1.6 × 10−5 | 4.0 × 10−3 |
| T (K) a | Excess Reactant | [Excess Reactant] b | k1(±2σ) c | Reactor Surface d |
|---|---|---|---|---|
| 220 | F2 | 0.52–5.35 | 6.30 ± 0.08 | HW |
| 235 | F2 | 0.39–4.70 | 6.28 ± 0.09 | HW |
| 253 | F2 | 0.39–5.53 | 6.15 ± 0.06 | HW |
| 265 | C2H4S | 0.24–4.82 | 6.34 ± 0.05 | HW |
| 275 | F2 | 0.30–4.60 | 6.06 ± 0.06 | HW |
| 298 | F2 | 0.36–5.45 | 5.92 ± 0.07 | HW |
| 315 | C2H4S | 0.23–2.31 | 6.22 ± 0.09 | Q |
| 325 | F2 | 0.18–5.24 | 5.91 ± 0.09 | HW |
| 340 | F2 | 0.20–4.00 | 6.00 ± 0.06 | Q |
| 360 | F2 | 0.36–4.02 | 6.03 ± 0.07 | Q |
| 390 | F2 | 0.35–4.68 | 6.13 ± 0.10 | Q |
| 420 | C2H4S | 0.22–1.94 | 5.87 ± 0.05 | Q |
| 460 | F2 | 0.36–3.69 | 6.06 ± 0.12 | Q |
| 500 | F2 | 0.29–3.19 | 5.86 ± 0.06 | Q |
| 560 | F2 | 0.22–3.30 | 5.83 ± 0.11 | Q |
| 625 | C2H4S | 0.18–1.73 | 6.07 ± 0.06 | Q |
| 710 | F2 | 0.21–2.88 | 6.03 ± 0.09 | Q |
| 800 | F2 | 0.27–2.51 | 5.99 ± 0.06 | Q |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedjanian, Y.; Roose, A.; Vallet, V.; Romanias, M.N. Experimental and Theoretical Study of the Reaction of F2 with Thiirane. Molecules 2024, 29, 3636. https://doi.org/10.3390/molecules29153636
Bedjanian Y, Roose A, Vallet V, Romanias MN. Experimental and Theoretical Study of the Reaction of F2 with Thiirane. Molecules. 2024; 29(15):3636. https://doi.org/10.3390/molecules29153636
Chicago/Turabian StyleBedjanian, Yuri, Antoine Roose, Valérie Vallet, and Manolis N. Romanias. 2024. "Experimental and Theoretical Study of the Reaction of F2 with Thiirane" Molecules 29, no. 15: 3636. https://doi.org/10.3390/molecules29153636
APA StyleBedjanian, Y., Roose, A., Vallet, V., & Romanias, M. N. (2024). Experimental and Theoretical Study of the Reaction of F2 with Thiirane. Molecules, 29(15), 3636. https://doi.org/10.3390/molecules29153636








